Abstract
There has been enormous recent interest in heterostructures of two-dimensional van der Waals materials. Integrating materials with different quantum ground states in vertical heterostructures is predicted to lead to novel electronic properties that are not found in the constituent layers. Here, we present direct synthesis of a superconductor-magnet hybrid heterostructure by combining superconducting niobium diselenide (NbSe2) with the monolayer vanadium diselenide (VSe2). Molecular-beam epitaxy growth in ultra-high vacuum yields clean and atomically sharp interfaces. Combining different characterization techniques and density-functional theory calculations, we investigate the electronic and magnetic properties of VSe2 on NbSe2. Low temperature scanning tunneling microscopy measurements show an absence of the typical charge density wave on VSe2 and demonstrate a reduction of the superconducting gap of NbSe2 on the VSe2 layer. This suggests magnetization of the VSe2 sheet, at least on the local scale. Our work demonstrates superconducting-magnetic hybrid materials with potential applications in future electronics devices.
Similar content being viewed by others
Introduction
There has been a surge of interest in designer materials that would realize electronic responses not found in naturally occurring materials. There are many routes toward this goal and they are all being explored vigorously, e.g., artificial atomic lattices1,2,3,4,5, atomically precise graphene nanoribbons6,7,8, and controlled heterostructures of two-dimensional (2D) materials9,10,11,12,13,14,15. The designer concept is well illustrated in systems combining magnetism with superconductivity to realize topological superconductivity16,17,18,19,20. Individual magnetic impurity atoms give rise to the so-called Yu–Shiba–Rusinov states21, which can be coupled in extended structures to give rise to bands (inside the superconducting gap). Eventually, the system can be driven into a topological phase in the presence of certain spin textures or spin–orbit coupling18,22,23,24,25,26. Topological superconductors are a distinct form of matter that is predicted to host boundary Majorana fermions. Experimental realization of Majorana fermions is exciting in its own right, but this is compounded by the proposal that systems with non-abelian statistics can serve as the basis for topological quantum computation27,28,29. Experimentally, these systems have been realized in one-dimensional chains of magnetic adatoms on the surface of s-wave superconductors18,23,30, and this has been extended to 2D systems by using magnetic metal islands31,32. However, these types of systems can be sensitive to disorder, and interface engineering through, e.g., the use of an atomically thin separation layer, might be required32.
Issues with interface inhomogeneities can potentially be avoided in van der Waals (vdW) heterostructures, where the different layers interact only through vdW forces9,10. Layered materials that remain magnetic down to the monolayer (ML) limit have been recently demonstrated11,12. While the first report relied on mechanical exfoliation for the sample preparation, related materials CrBr3 and Fe3GeTe2 have also been grown using molecular-beam epitaxy (MBE) in ultrahigh vacuum (UHV)33,34. This is essential for realizing clean edges and interfaces. Very recently, monolayer magnetism was suggested in the transition-metal dichalcogenide (TMD) vanadium diselenide (VSe2), which can be readily grown using MBE on various layered materials13. Later reports have questioned the existence of magnetism in VSe2 as no magnetic signal was detected in X-ray magnetic circular dichroism (XMCD) experiments35,36. Angle-resolved photoemission spectroscopy revealed an enhanced charge-density wave (CDW) transition at a higher temperature than in the bulk, and it was suggested that the presence of CDW driven by Fermi-surface nesting removes the usual mechanism for achieving a magnetic ground state35,37,38,39. It has also been suggested that spin frustration plays a role in VSe2 samples grown by MBE36. Support for this comes from recent experiments on chemically exfoliated VSe2 flakes that show ferromagnetic behavior with a Curie temperature of ca. 470 K and also nonzero XMCD signal40. While there still is no consensus on the nature of the possible magnetic ground state of VSe2, it is clear that there is a delicate balance between different competing interacting states and phases in monolayer transition-metal dichalcogenides, which may also depend on the nature of the substrate35,36,39,40,41,42,43.
Combining 2D magnetic and superconducting TMDs would create a promising material platform for investigating the coexistence of superconductivity, magnetism, and the resulting emergent quantum phases of matter. The inherent lack of surface-bonding sites due to the layered nature of these materials prevents chemical bonding between the layers and results in a better control of the interfaces. We report the growth of single-layer vanadium diselenide (VSe2) by molecular-beam epitaxy on superconducting niobium diselenide (NbSe2) substrate and study the magnetic and electrical properties of these heterostructures. MBE growth under UHV conditions facilitates the formation of clean edges and interfaces, and we characterize the electronic structure of the resulting hybrid materials down to the atomic scale using low-temperature scanning tunneling microscopy (STM) and spectroscopy (STS). Our results give further experimental information on the magnetic properties of VSe2 and demonstrate a clean and controllable platform for creating superconducting–magnetic hybrid TMD materials with great potential of integrating TMDs into future electronic devices.
Results
Growth and characterization of VSe2
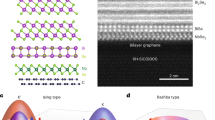
VSe2 was grown on NbSe2 by MBE, and the results are illustrated in Fig. 1 (see “Methods” for details). Briefly, vanadium was evaporated under excess flux of selenium onto a NbSe2 crystal cleaved in situ in UHV and held at T = 520–540 K during the growth. The samples were characterized in situ by STM and X-ray photoelectron spectroscopy (XPS). In addition, after capping the films with a thick Se layer, the samples were characterized ex situ by temperature-dependent magnetization measurements. Figure 1a shows STM characterization of submonolayer VSe2 films on NbSe2 substrate. VSe2 grows atomically smooth, large uniform ML islands. Higher coverages result in the formation of a second layer. The profile along the blue line in Fig. 1a shows that the apparent height of the VSe2 film is 6.5 Å (Fig. 1b) consistent with the unit-cell height44. Atomically resolved STM images of the VSe2 monolayer and NbSe2 crystal surface are shown in Fig. 1c, d, respectively. While NbSe2 shows the well-known 3 × 3 charge-density wave modulation in the atomic contrast, we do not detect a charge-density wave on VSe2 (even at temperature of T = 4.2 K). This is in contrast to reports on HOPG and bilayer graphene substrates13,35,37. The lattice constants can be measured from the atomically resolved images, as depicted in Fig. 1e. This yields values of 3.5 ± 0.1 Å and 3.4 ± 0.1 Å for VSe2 and NbSe2, respectively. These values match well with previous experimental results38,44,45. The lattice mismatch is roughly 3%; this together with the fact that we observe several different orientations of VSe2 w.r.t. the underlying NbSe2 suggests that there is no lattice match between VSe2 and NbSe2.
a Large-scale scanning tunneling microscopy (STM) image of submonolayer VSe2 on NbSe2. Scale bar: 25 nm. b Line profile along the blue line shown in panel a. c, d Atomically resolved images on VSe2 (c) and NbSe2 (d). Scale bars: 1 nm. e Line profiles along the lines in panels c and d (VSe2 (black), NbSe2 (red)) showing the atomic periodicities and the charge-density wave modulation on the NbSe2 substrate. f Computed structure of VSe2 on NbSe2.
XPS was used to study the chemical composition of the as-grown VSe2 films on NbSe2. Characteristic peaks of V, Se, and Nb are found in the XPS spectra (see Supplementary Note 1). The binding energies of the V 2p3/2 peak at 513.7 eV and the Se 3d5/2 peak at 53.4 eV are similar to those previously observed for VSe2 on HOPG13,45. The Nb 3d5/2 peak is found at 203.5 eV, which is typical for NbSe2. Both VSe2 and NbSe2 have similar selenium-binding energies and thus they cannot be resolved from the Se 3d spectrum46. The V:Se:Nb stoichiometry for a 0.6 ML VSe2 film was found to be roughly 1:5:2 (estimated from integrated peak areas, which were normalized to the elements’ atomic sensitivity factors). No other elements, such as possible magnetic impurities, were detected above the detection limit of ~1 atomic percent.
We have complemented the experiments by density-functional theory (DFT) calculations. According to previous DFT calculations, the lowest energy phase of VSe2 can be H or T phase, in the FM or AFM configuration, with or without CDW, depending on the choice of adopted functional, strain, and doping35,39,42,43,47,48. Despite the theoretical prediction of the existence of the 2H-VSe2, all of the recent experimental results using MBE report the formation of the 1T phase with no evidence of a successful growth of 2H phase. We also tested several different functionals, as shown in Supplementary Note 2, and have chosen vdw-DF functional revB86b with +U parameter of 2 eV, since it reproduces the larger lattice constant and the lowest energy phase being ferromagnetic 1T-VSe2. In contrast, LDA would lead to CDW phase and PBE to H phase, as in the previous reports35,39,42,43,47. Figure 1f shows the fully relaxed geometry of VSe2/NbSe2 heterostructure from the side and top views. The energetically most favorable stacking has the lower-layer Se atoms of VSe2 on top of the hollow site of the NbSe2 (2.94 Å from Se in NbSe2 to Se in VSe2) and V on top of Nb, with a distance of 6.16 Å from Nb to V.
Electronic properties of VSe2
We have probed the electronic structure of single-layer VSe2/NbSe2 heterostructure by both scanning tunneling spectroscopy (STS) and DFT. Figure 2a shows typical differential conductance (dI/dV) spectra taken on the ML VSe2 and on the bulk NbSe2 substrate over a large bias range. We will first focus on the NbSe2 response. At positive bias (empty states) region, the most pronounced features on bulk NbSe2 are the broad resonances at ~0.3 V and ~1.8 V, while at negative bias, the dI/dV signal is broad and rising. The measured dI/dV spectrum on NbSe2 is in agreement with earlier STS studies on bulk NbSe249. The features in our dI/dV spectroscopy also match the simulated local density-of-states (LDOS) spectra on a three-layer slab of NbSe2 (Fig. 2b), and can be compared with the bulk density of states (DOS) (Fig. 2c). The first resonance at positive bias arises from the Nb-derived band, while the broad feature at negative bias overlaps with mostly selenium-derived bands below EF. On VSe2, at positive bias, there are pronounced features close to the Fermi level and also at 0.9 V and 1.45 V. At negative bias, we observe a peak at –0.5 V, and a shallow feature at ~−1 V. These VSe2 features are discussed in more detail below.
a Typical long-range experimental dI/dV spectra on a monolayer (ML) VSe2 and on the NbSe2 substrate as a function of the sample bias. b Simulated scanning tunneling spectroscopy (STS) obtained by integrating the local density of states (LDOS) at a constant height on top of the NbSe2 surface. The solid and dashed lines show different values of the energy broadening. c Calculated density of states (DOS) of bulk NbSe2 as a function of energy. Density-of-states plots show both the total DOS and the DOS projected to the metal and Se atoms.
The electronic structure and the simulated and experimental STS are shown in Fig. 3a–f. First focusing on the experimental spectra for monolayer and bilayer VSe2 in Fig. 3d, we observe peaks close to the Fermi level at both positive and negative bias, and they are more pronounced for the bilayer compared with the monolayer. Their energy spacing (gap) is ~0.2 eV with an abrupt edge at positive energy (peak p1) and smoother edge at negative energy that develops into peaks labeled with n1/n2. At larger positive or negative bias, several peaks can be distinguished with the peak positions shifting between the mono- and bilayer spectra. The spectra are not noticeably position-dependent in the middle of the VSe2 islands.
a Calculated band structure of VSe2 (nonmagnetic state). The color of the symbols reflects the character of the states with blue corresponding to vanadium and orange to selenium. b, c Calculated projected density of states (PDOS) as a function of energy (b) and simulated dI/dV spectra (with two different broadenings, panel c) for the nonmagnetic and charge-density wave states. d Typical long-range experimental dI/dV spectra on 1 and 2 monolayer (ML) VSe2 on NbSe2 as a function of sample bias. e, f Simulated dI/dV spectra (with two different broadenings, panel e) and calculated PDOS (panel f) for the ferromagnetic ground state. All the calculations correspond to unstrained monolayer VSe2.
Starting from the nonmagnetic (NM) phase, the calculated band structure shows the partially filled d band (Fig. 3a). There is a flat region between Γ and K points, which also happens to coincide with the Fermi level. This leads to a strong peak at the Fermi level in the DOS and also in the simulated STS, which obviously contrasts the experimental spectra. NM phase is also unstable in calculations and may either develop CDW or ferromagnetism, depending on conditions (strain, doping, and defects) and on computational parameters (see Supplementary Note 2). In the CDW phase, DOS exhibits a clear pseudogap formation, although not at the Fermi level, but just above it. While the simulated STS would be relatively consistent with the experimental one, we do not detect CDW in the STM topography and also do not observe a hard gap at the Fermi level as reported by M. Bonilla et al.13.
In the ferromagnetic (FM) phase, the spin-up and -down band structures are only shifted in energy as in itinerant FM. The calculated magnetic moment depends moderately on strain and the computational parameters (e.g., the Hubbard U), see Supplementary Note 2 for details47. Consequently, also the DOS and simulated STS show splitting of the peaks w.r.t. NM phase. Due to the splitting of the DOS peak at Fermi level, the lower branch could explain the peaks n1/n2 with the higher branch falling slightly above Fermi level (feature p1 in the experimental spectra). The FM phase also seems to yield better agreement between the simulated and experimental STS for the peaks p2 and p3 in the monolayer sample. Note that while some experiments show nonuniform sampling of the states with different in-plane momenta50,51, the most prominent features on the VSe2 spectra close to the Fermi level are predicted to arise from the high density of states from bands close to the Γ point, and we do not observe strong variations in the dI/dV spectra depending on the microscopic tip apex. Even though the magnetic response of VSe2 is rather complex, taken together with the lack of CDW in the STM images, our STM and STS results are the most consistent with simulated response of the FM phase.
Magnetic properties of VSe2
After the electronic characterization of the samples, we will next focus on their magnetic properties. To explore the magnetic properties of ML VSe2 on NbSe2, we carried out magnetization measurements at various sample temperatures (see “Methods” for details). All the VSe2 samples measured showed an in-plane magnetic response similar to that shown in Fig. 4a, where the loops have a small coercivity and remanence, but show saturation ~200–300 mT38, apart from a linear background. As shown in Fig. 4b, the coercive field (Hc) is very small and the saturation magnetization (Ms) is practically independent of temperature in the range of T = 10–300 K. Supplementary Fig. 17 from Supplementary Note 3 shows a direct comparison between the substrate and VSe2 responses. We fit a Brillouin function to the T = 10 K data in Fig. 4a, similarly to previous literature52, which assumes the presence of a paramagnetic background signal. The goodness of fit suggests that such a background contributes significantly to the measured magnetisation. In the inset to Fig. 4b, the difference between the data and fit is plotted, which suggests that a small ferromagnetic signal is also present in the sample. However, due to the paramagnetic contribution, we cannot quantitatively assess the possible underlying ferromagnetic response with bulk magnetization measurements. Further discussion and details of the fitting are presented in Supplementary Note 4.
Experiments on chemically exfoliated VSe2 flakes exhibit a ferromagnetic response with a Curie temperature of ca. 470 K40. As there is no strict alignment between the substrate and the VSe2 layer, MBE growth results in a polycrystalline 2D layer, which also may be affected by substrate interactions. Furthermore, as indicated by the DFT calculations, the energy differences between the different ground states (CDW and magnetism) of the VSe2 monolayer are small. Minor perturbations due to the substrate, capping, sample quality, and adsorbates, could cause variations in the observed behavior. However, local measurements (such as STM) should still probe the ferromagnetic phase suggested in the data above that corresponds to the DFT calculations.
It has been argued that there is no conventional ferromagnetism in VSe2 on graphite and graphene substrates35,36,37,38,43,53. Here, one potentially important difference between our samples and those on graphite and graphene is the absence of a charge-density wave: we find no evidence of CDW in either the STM images or the dI/dV spectroscopy. Based on the recent experimental works54,55, the absence of the CDW in our system might also be related to the underlying NbSe2 substrate. Our DFT calculations also suggest that the stability of the CDW is sensitive to the strain, doping, and amount of the defects in the system as discussed extensively in Supplementary Information. Furthermore, in previous studies13, monolayer VSe2 sample exhibits a maximum in Ms and Hc in a range around T = 100 K and this nonmonotonic behavior is ascribed to the CDW transition. This is in contrast to our data on Ms and Hc as a function of temperature. The absence of CDW transition is also independently determined from the magnetization measurement under zero-field-cooled (ZFC) and field-cooled (FC) regimes, where we do not observe noticeable changes in the slope of the ZFC and FC curves due to the CDW (see Supplementary Note 5).
The magnetic response of the sample below the superconducting transition temperature (Tc = 7.2 K) is dominated by the superconducting NbSe2 substrate. Magnetization M(H) curves measured at 2 K for bulk NbSe2 and VSe2/NbSe2 (see also Supplementary Note 5) show superconducting diamagnetic behavior as reported previously56,57. Moreover, there is no obvious difference between these magnetization curves, which indicates that the signal is mostly dominated by the bulk NbSe2. This conclusion is further supported by the temperature-dependent magnetization curves for the zero-field cooling (ZFC) of a bulk NbSe2 and VSe2/NbSe2 heterostructure (see Supplementary Note 5). They show a rapid decrease at the onset of the diamagnetic signal below the critical temperature Tc for both samples and, again, there is no obvious change in Tc, which further indicates the dominance of the bulk signals. It is worth to mention that Tc is very sensitive to the magnetic doping, with studies suggesting that Tc drops rapidly upon metal atom doping58,59. This suggests that we do not lose any vanadium due to intercalation at the normal growth temperatures. Increasing the growth temperature to T > 300 °C results in intercalation of vanadium, which is clearly seen in atomically resolved images of the NbSe2 surface, and results in the loss of the long-range order of the NbSe2 CDW60 (see Supplementary Note 6 for details).
Proximity-induced superconductivity in monolayer VSe2
There is a particular interest in the interaction between the superconducting substrate and the magnetic layer, both in terms of the proximity effect induced in the single-layer VSe2 and conversely, the effect of the magnetic layer on the underlying superconductor. The superconducting proximity effect can be used to spontaneously drive a nonsuperconducting material (normal metal) into superconductivity; however, this picture is altered when the superconductor makes contact with a magnetic layer. In the case of a ferromagnet, the superconducting order parameter is expected to decay exponentially with a very short coherence length ζF (typically some nm) at the superconductor–ferromagnet (SF) interface. Moreover, the pairing potential Δp inside the ferromagnet shows a strong oscillatory and damped behavior due to the internal exchange field of the ferromagnet61,62. This type of phenomena could also occur in our hybrid VSe2/NbSe2 layers, and it will allow us to shed some light on the nature of the magnetism in VSe2 on the atomic scale.
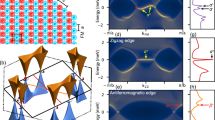
Figure 5a shows the dI/dV spectra measured on the NbSe2 substrate as well as VSe2 layers with different thicknesses. On NbSe2, we observe a typical superconducting gap: a pronounced dip in the DOS at the Fermi level and coherence peaks on both sides of the gap63,64. The spectra measured on the VSe2 films with thicknesses of 1 ML and 2 ML also show a superconducting gap, but the gap width is significantly reduced compared with the bare NbSe2 substrate. We do not observe oscillatory behavior of the pairing potential as bilayer VSe2 is not sufficiently thick for this. To further quantify the reduction of the SC gap width, we use a simple analytical relation between a superconducting gap Δ and decay length λ65,66,67: \(\Delta \approx {\Delta }_{{{\rm{NbSe}}}_{2}}{e}^{-d/\lambda }\), where the d is the VSe2 film thickness and \({\Delta }_{{{\rm{NbSe}}}_{2}}\) is the gap of bare NbSe2, respectively. We extract the apparent gap widths from the spectra shown in Fig. 5a by fitting them (see Supplementary Note 7 for details) and plot the results in Fig. 5b (error bars show the confidence interval of the fit). The decrease in the energy gap follows an exponential dependence with a decay length of λ = 1.3 ± 0.1 nm (1 ML thickness is roughly 0.65 nm). This is a measure of the quasi-particle coherence length associated with Andreev reflections. However, this decay length is much shorter than recent experimental results on Bi2Se3 on NbSe268: they observe a decay length of λ = 4.3 ± 0.3 nm, which is shown as a dashed blue line in Fig. 5b. In the case of Bi2Se3 on Nb, an even much higher value of λ = 8.4 nm was reported67. A possible explanation for the faster decay we observe in VSe2 would be given by magnetism of the VSe2 layer. In this case, one would expect a shorter coherence length ζF governed by the magnetization in the VSe2 layer and not by the diffusion (which is a case in Bi2Se3/NbSe2). The reduced gap is very uniform within the VSe2 islands and also between different islands. This shows that the observed response is not affected by the orientation of the VSe2 islands w.r.t. the underlying NbSe2, and that it is related to bulk properties of ML VSe2 and not simply an effect arising from impurities, vacancies, and structural imperfections (e.g., layer edges).
a Spectra measured on clean NbSe2 and on 1 and 2 monolayer (ML) of VSe2 (spectra offset vertically for clarity). b The measured energy gap as a function of the VSe2 thickness (the error bars shown in panel b are 0.02, 0.02, and 0.04 meV, respectively, and represent the confidence interval of the fit). c Spectra measured at different locations, including over the edge of a VSe2 island. d Topographic scanning tunneling microscopy (STM) image and a constant-height dI/dV map at zero bias over an edge of a VSe2 island. Scale bars: 6 nm.
Spectroscopy on the edges of the VSe2 islands
We have also probed the spatially dependent spectroscopic response over the edges of the VSe2 islands, and typical spectra are shown in Fig. 5c (more results in Supplementary Note 8). The spectra evolve from the typical gapped structure over the NbSe2 into a sharp peak at zero bias at the edge of the VSe2 island. This feature is very localized at the edge of the VSe2 layer. Furthermore, it is inhomogeneously distributed along the edges of VSe2 islands, and there are strong intensity variations as illustrated in Fig. 5d. In addition to the spatial distribution of the zero-bias peak, its width is also strongly position-dependent. We observe both zero-bias peaks that are confined within the superconducting gap (e.g., Fig. 5c), but on some other locations (see Supplementary Note 9), its width can be a couple of times larger than the superconducting gap width. Features inside the superconducting gap could arise from Yu–Shiba–Rusinov bands or topological edge modes, but the broader peaks suggest the presence of free unpaired spins giving rise to the Kondo effect21,69. In any case, the reason is likely related to the changes of the gap structure of the underlying superconductor due to local magnetic fields arising from the edges of the VSe2 layer.
Discussion
In conclusion, we have demonstrated high-quality epitaxial growth of VSe2–NbSe2 hybrid structures using MBE. We have observed significant and spatially uniform reduction of the superconducting gap of the NbSe2 substrate on the VSe2 islands with the reduction being thickness-dependent and stronger on bilayer VSe2. This would be most naturally explained to result from magnetization of the VSe2 layer. The other electronic and magnetic characterization results are also more consistent with magnetization than with charge-density waves. Finally, we observe strongly position-dependent, enhanced dI/dV intensity at the Fermi level around the edges of the VSe2 layer likely related to the changes of the gap structure of the underlying superconductor due to local magnetic fields arising from the edges of the VSe2 layer.
On a broad scale, our work contributes to the efforts in designer materials that would realize electronic responses not found in naturally occurring materials, but arising from engineered interactions between the different components. Van der Waals heterostructures are ideally suited for this purpose as the different layers interact only through vdW forces and hence retain their intrinsic properties. This results in very high-quality interfaces and allows for a rational design of the emergent properties of the heterostructure. Our work suggests that it will be possible to combine 2D TMDs with different quantum ground states to stimulate new work in the field of 2D-TMD hybrids.
Methods
Sample preparation
Monolayer VSe2 was grown on NbSe2 substrates by e-beam evaporation of V (99.8%, Goodfellow Cambridge Ltd.) and simultaneous deposition of atomic Se (99.99%, Sigma-Aldrich) from a Knudsen cell under ultra-high-vacuum conditions (UHV, base pressure ~10−10 mbar). The NbSe2 substrate (HQ Graphene) was cleaved in vacuum and subsequently annealed in ultrahigh vacuum at T = 600 K for 1 h before film growth, which did not adversely affect the substrate quality. VSe2 was grown at a substrate temperature of T = 520–540 K. During growth, the V flux (10 nA) is maintained at a beam-equivalent pressure (BEP) of ~10−10 mbar, whereas approximately an order of magnitude greater Se flux (under Se-rich conditions, pressure ~10−8 mbar) is used. Our growth rate of 1 ML per hour is dictated by the V flux due to the near-unity sticking coefficient of V at the growth temperature. The excess selenium desorbs from the substrate since the substrate temperature was higher than the evaporation temperature of selenium atoms (T = 393 K). The samples were either characterized in situ by XPS and STM or capped with Se by deposition of Se at room temperature before transferring them out of the UHV system.
Sample characterization
XPS measurements (Surface Science Instruments SSX-100 spectrometer) were performed using monochromated Al K-alpha radiation with X-ray power of 200 W, a pass energy of 100 eV, and a measurement spot size of 1 mm.
Magnetic characterization was carried out using a Quantum Design Dynacool PPMS operating as a vibrating sample magnetometer (VSM). For magnetization measurements, the sample is attached to a quartz rod. The magnetization measurements were done on the samples with mixed mono- and bilayer VSe2 coverage. In the experiments shown in Fig. 4, the coverage of VSe2 was 0.57 (consisting of 0.44 monolayer and 0.13 bilayer).
The STM experiments (Unisoku USM-1300) of the samples were performed at T = 4 K. STM images were taken in the constant current mode. dI/dV spectra were recorded by standard lock-in detection while sweeping the sample bias in an open-feedback loop configuration, with a peak-to-peak bias modulation of 5 mV (long-range spectra) or 0.1 mV (short-range spectra of the superconducting gap) at a frequency of 709 Hz.
DFT calculations
All density-functional theory calculations are carried out in the plane-wave basis in the projector-augmented wave framework as implemented in VASP70,71,72. In all calculations, we use 500 eV cut-off and k-point sampling corresponding to 24 × 24 mesh in the primitive cell. High k-point mesh is required to correctly describe, e.g., the CDW phases.
Vanadium tends to exhibit strong Coulomb correlations, which usually necessitate using hybrid functionals, LDA+U or DMFT. We benchmarked several exchange-correlations functionals, and the results are collected in the SI. For the results shown in the main paper, we have adopted to use revB86b vdw-DF functional73 augmented with +U correction of 2 eV (on Mn-d orbitals). Further computational details are given in Supplementary Information.
Data availability
The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.
References
Gomes, K. K., Mar, W., Ko, W., Guinea, F. & Manoharan, H. C. Designer Dirac fermions and topological phases in molecular graphene. Nature 483, 306–310 (2012).
Slot, M. R. et al. Experimental realization and characterization of an electronic Lieb lattice. Nat. Phys. 13, 672–676 (2017).
Drost, R., Ojanen, T., Harju, A. & Liljeroth, P. Topological states in engineered atomic lattices. Nat. Phys. 13, 668–671 (2017).
Khajetoorians, A. A., Wegner, D., Otte, A. F. & Swart, I. Creating designer quantum states of matter atom-by-atom. Nat. Rev. Phys. 1, 703–715 (2019).
Yan, L. & Liljeroth, P. Engineered electronic states in atomically precise artificial lattices and graphene nanoribbons. Adv. Phys. X 4, 1651672 (2019).
Talirz, L., Ruffieux, P. & Fasel, R. On-surface synthesis of atomically precise graphene nanoribbons. Adv. Mater. 28, 6222–6231 (2016).
Gröning, O. et al. Engineering of robust topological quantum phases in graphene nanoribbons. Nature 560, 209–213 (2018).
Rizzo, D. J. et al. Topological band engineering of graphene nanoribbons. Nature 560, 204–208 (2018).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & CastroNeto, A. H. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Bonilla, M. et al. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 13, 289–293 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Gibertini, M., Koperski, M., Morpurgo, A. F. & Novoselov, K. S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 14, 408–419 (2019).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602 (2014).
Sato, M. & Ando, Y. Topological superconductors: a review. Rep. Prog. Phys. 80, 076501 (2017).
Zhou, J. et al. Large tunneling magnetoresistance in VSe2/MoS2 magnetic tunnel junction. ACS Appl. Mater. Interfaces 11, 17647–17653 (2019).
Heinrich, B. W., Pascual, J. I. & Franke, K. J. Single magnetic adsorbates on s-wave superconductors. Prog. Surf. Sci. 93, 1–19 (2018).
Pöyhönen, K., Westström, A., Röntynen, J. & Ojanen, T. Majorana states in helical Shiba chains and ladders. Phys. Rev. B 89, 115109 (2014).
Kim, H. et al. Toward tailoring Majorana bound states in artificially constructed magnetic atom chains on elemental superconductors. Sci. Adv. 4, eaar5251 (2018).
Röntynen, J. & Ojanen, T. Topological superconductivity and high Chern numbers in 2D ferromagnetic Shiba lattices. Phys. Rev. Lett. 114, 236803 (2015).
Li, J. et al. Two-dimensional chiral topological superconductivity in Shiba lattices. Nat. Commun. 7, 12297 (2016).
Rachel, S., Mascot, E., Cocklin, S., Vojta, M. & Morr, D. K. Quantized charge transport in chiral Majorana edge modes. Phys. Rev. B 96, 205131 (2017).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Wilczek, F. Majorana returns. Nat. Phys. 5, 614 (2009).
Ruby, M. et al. End states and subgap structure in proximity-coupled chains of magnetic adatoms. Phys. Rev. Lett. 115, 197204 (2015).
Ménard, G. C. et al. Two-dimensional topological superconductivity in Pb/Co/Si(111). Nat. Commun. 8, 2040 (2017).
Palacio-Morales, A. et al. Atomic-scale interface engineering of Majorana edge modes in a 2D magnet-superconductor hybrid system. Sci. Adv. 5, eaav6600 (2019).
Liu, S. et al. Wafer-scale two-dimensional ferromagnetic Fe3GeTe2 thin films grown by molecular beam epitaxy. npj 2D Mater. Appl. 1, 30 (2017).
Chen, W. et al. Direct observation of van der Waals stacking-dependent interlayer magnetism. Science 366, 983–987 (2019).
Feng, J. et al. Electronic structure and enhanced charge-density wave order of monolayer VSe2. Nano Lett. 18, 4493–4499 (2018).
Wong, P. K. J. et al. Evidence of spin frustration in a vanadium diselenide monolayer magnet. Adv. Mater. 31, 1901185 (2019).
Chen, P. et al. Unique gap structure and symmetry of the charge density wave in single-layer VSe2. Phys. Rev. Lett. 121, 196402 (2018).
Duvjir, G. et al. Emergence of a metal-insulator transition and high-temperature charge-density waves in VSe2 at the monolayer limit. Nano Lett. 18, 5432–5438 (2018).
Coelho, P. M. et al. Charge density wave state suppresses ferromagnetic ordering in VSe2 monolayers. J. Phys. Chem. C. 123, 14089–14096 (2019).
Yu, W. et al. Chemically exfoliated VSe2 monolayers with room-temperature ferromagnetism. Adv. Mater. 31, 1903779 (2019).
Sugawara, K. et al. Monolayer VTe2: incommensurate Fermi surface nesting and suppression of charge density waves. Phys. Rev. B 99, 241404 (2019).
Kim, T. J., Ryee, S., Han, M. J. & Choi, S. Sub-room temperature ferromagnetism and its nature in VSe2 monolayer Preprint at http://arXiv.org/abs/1907.04790 (2019).
Fumega, A. O. et al. Absence of ferromagnetism in VSe2 caused by its charge density wave phase. J. Phys. Chem. C. 123, 27802–27810 (2019).
Bayard, M. & Sienko, M. J. Anomalous electrical and magnetic properties of vanadium diselenide. J. Solid State Chem. 19, 325–329 (1976).
Liu, Z.-L. et al. Epitaxially grown monolayer VSe2: an air-stable magnetic two-dimensional material with low work function at edges. Sci. Bull. 63, 419–425 (2018).
Wang, H. et al. High-quality monolayer superconductor NbSe2 grown by chemical vapour deposition. Nat. Commun. 8, 394 (2017).
Ma, Y. et al. Evidence of the existence of magnetism in pristine VX2 monolayers (X = S, Se) and their strain-induced tunable magnetic properties. ACS Nano 6, 1695–1701 (2012).
Popov, Z. I. et al. The electronic structure and spin states of 2D graphene/VX2 (X = S, Se) heterostructures. Phys. Chem. Chem. Phys. 18, 33047–33052 (2016).
Arguello, C. J. et al. Visualizing the charge density wave transition in 2H -NbSe2 in real space. Phys. Rev. B 89, 235115 (2014).
Zhang, Y. et al. Giant phonon-induced conductance in scanning tunnelling spectroscopy of gate-tunable graphene. Nat. Phys. 4, 627–630 (2008).
Leicht, P. et al. In situ fabrication of quasi-free-standing epitaxial graphene nanoflakes on gold. ACS Nano 8, 3735–3742 (2014).
O’Hara, D. J., Zhu, T. & Kawakami, R. Importance of paramagnetic background subtraction for determining the magnetic moment in epitaxially grown ultrathin van der Waals magnets. IEEE Magn. Lett. 9, 1405805 (2018).
Chen, G.et al. Correlating structural, electronic, and magnetic properties of epitaxial VSe2 thin films. Preprint at http://arXiv.org/abs/1912.12798 (2019).
Duvjir, G. et al. Novel polymorphic phase of two-dimensional VSe2: the 1T’ structure and its lattice dynamics. Nanoscale 11, 20096–20101 (2019).
Kolekar, S. et al. Controlling the charge density wave transition in monolayer TiSe2: substrate and doping effects. Adv. Quantum Technol. 1, 1800070 (2018).
delValle, J. et al. Force-free state in a superconducting single crystal and angle-dependent vortex helical instability. Phys. Rev. B 95, 224510 (2017).
Galvan, D. H. et al. Superconductivity of NbSe2 samples subjected to electron irradiation. Phys. C. 398, 147–151 (2003).
Naik, I., Tiwari, G. C., Yadav, C. S. & Rastogi, A. K. Effect of magnetic exchange interaction in resistivity on 2H-Nb1−xVxSe2. Indian J. Phys. 87, 1075–1078 (2013).
Pervin, R. et al. Enhancement of superconducting critical current density by Fe impurity substitution in NbSe2 single crystals and the vortex pinning mechanism. Phys. Chem. Chem. Phys. 19, 11230–11238 (2017).
Chatterjee, U. et al. Emergence of coherence in the charge-density wave state of 2H-NbSe2. Nat. Commun. 6, 6313 (2015).
Linder, J. & Robinson, J. W. A. Superconducting spintronics. Nat. Phys. 11, 307 (2015).
Buzdin, A. I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 77, 935–976 (2005).
Hudson, E. W. Investigating High-Tc Superconductivity on the Atomic Scale by Scanning Tunneling Microscopy. PhD Thesis, University of California (1999).
Noat, Y. et al. Quasiparticle spectra of 2H-NbSe2: two-band superconductivity and the role of tunneling selectivity. Phys. Rev. B 92, 134510 (2015).
Reeg, C. R. & Maslov, D. L. Hard gap in a normal layer coupled to a superconductor. Phys. Rev. B 94, 020501 (2016).
Belzig, W., Bruder, C. & Schön, G. Local density of states in a dirty normal metal connected to a superconductor. Phys. Rev. B 54, 9443–9448 (1996).
Flötotto, D. et al. Superconducting pairing of topological surface states in bismuth selenide films on niobium. Sci. Adv. 4, eaar7214 (2018).
Wang, M.-X. et al. The coexistence of superconductivity and topological order in the Bi2Se3 thin films. Science 336, 52 (2012).
Franke, K. J., Schulze, G. & Pascual, J. I. Competition of superconducting phenomena and Kondo screening at the nanoscale. Science 332, 940–944 (2011).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mat. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Hamada, I. Van der Waals density functional made accurate. Phys. Rev. B 89, 121103 (2014).
Acknowledgements
This research made use of the Aalto Nanomicroscopy Center (Aalto NMC) facilities and was supported by the European Research Council (ERC-2017-AdG no. 788185 “Artificial Designer Materials”) and Academy of Finland (Academy professor funding no. 318995 and 320555, Academy postdoctoral researcher no. 309975, and Academy research fellow no. 311058). Our DFT calculations were performed using computer resources within the Aalto University School of Science “Science-IT” project and the Finnish CSC-IT Center for Science. M.M.U. acknowledges support by the Spanish MINECO under grant no. MAT2017-82074-ERC and by the ERC Starting grant LINKSPM (Grant 758558).
Author information
Authors and Affiliations
Contributions
S.K., M.N.H., P.D., and I.M. carried out the sample growth under the supervision of P.L. and M.M.U. R.M. and Y.Z. performed the magnetic characterizations under supervision of S.v.D., and J.S. made the XPS measurements. H.P.K. carried out the DFT calculations. S.K., M.N.H., and P.D. carried out the low-temperature STM measurements. S.K. and P.L. wrote the paper with input from all coauthors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kezilebieke, S., Huda, M.N., Dreher, P. et al. Electronic and magnetic characterization of epitaxial VSe2 monolayers on superconducting NbSe2. Commun Phys 3, 116 (2020). https://doi.org/10.1038/s42005-020-0377-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0377-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.