Abstract
The discovery of unconventional superconductivity in hole doped NdNiO2, similar to CaCuO2, has received enormous attention. However, different from CaCuO2, RNiO2 (R = Nd, La) has itinerant electrons in the rare-earth spacer layer. Previous studies show that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and rare-earth-d orbitals is very weak and thus RNiO2 is still a promising analog of CaCuO2. Here, we perform first-principles calculations to show that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons in RNiO2 is substantially stronger than previously thought. The dominant hybridization comes from an interstitial-s orbital rather than rare-earth-d orbitals, due to a large inter-cell hopping. Because of the hybridization, Ni local moment is screened by itinerant electrons and the critical UNi for long-range magnetic ordering is increased. Our work shows that the electronic structure of RNiO2 is distinct from CaCuO2, implying that the observed superconductivity in infinite-layer nickelates does not emerge from a doped Mott insulator.
Similar content being viewed by others
Introduction
Since the discovery of high-temperature superconductivity in cuprates1, people have been attempting to search for superconductivity in other materials whose crystal and electronic structures are similar to those of cuprates2,3. One of the obvious candidates is La2NiO4 which is iso-structural to La2CuO4 and Ni is the nearest neighbor of Cu in the periodic table. However, superconductivity has not been observed in doped La2NiO44. This is in part due to the fact that in La2NiO4, two Ni-eg orbitals are active at the Fermi level, while in La2CuO4 only Cu-\({d}_{{x}^{2}-{y}^{2}}\) appears at the Fermi level. Based on this argument, a series of nickelates and nickelate heterostructures have been proposed with the aim of realizing a single orbital Fermi surface in nickelates. Those attempts started from infinite-layer nickelates2,5,6, to LaNiO3/LaAlO3 superlattices7,8,9,10, to tri-component nickelate heterostructures11,12 and to reduced Ruddlesden–Popper series13,14. Eventually, superconductivity with a transition temperature of about 15 K has recently been discovered in hole doped infinite-layer nickelate NdNiO215, injecting new vitality into the field of high-Tc superconductivity16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33.
However, there is an important difference between infinite-layer nickelate RNiO2 (R = Nd, La) and infinite-layer cuprate CaCuO2 in their electronic structures: in infinite-layer cuprates, only a single Cu-\({d}_{{x}^{2}-{y}^{2}}\) band crosses the Fermi level, while in infinite-layer nickelates, in addition to Ni-\({d}_{{x}^{2}-{y}^{2}}\) band, another conduction band also crosses the Fermi level6,21,22,23. First-principles calculations show that the other non-Ni conduction band originates from rare-earth spacer layers6,21,22,23. Hepting et al.20 propose that itinerant electrons on rare-earth-d orbitals may hybridize with Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital, rendering RNiO2 an “oxide-intermetallic” compound. But previous studies find that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and rare-earth-d orbitals is very weak21,22,23,29. Therefore other than the self-doping effect27, infinite-layer nickelates can still be considered as a promising analog of infinite-layer cuprates21,16.
In this work, we combine density functional theory (DFT)34,35 and dynamical mean-field theory (DMFT)36,37 to show that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons in rare-earth spacer layers is substantially stronger than previously thought. However, the largest source of hybridization comes from an interstitial-s orbital due to a large inter-cell hopping. The hybridization with rare-earth-d orbitals is weak, about one order of magnitude smaller. We also find that weak-to-moderate correlation effects on Ni lead to a charge transfer from Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital to hybridization states, which provides more itinerant electrons to couple to Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital. In the experimentally observed paramagnetic metallic state of RNiO2, we explicitly demonstrate that the coupling between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons screens the Ni local moment, as in Kondo systems38,39,40. Finally we find that the hybridization increases the critical UNi that is needed to induce long-range magnetic ordering.
Our work provides the microscopic origin of a substantial hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons in RNiO2, which leads to an electronic structure that is distinct from that of CaCuO2. As a consequence of the hybridization, spins on Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital are affected by itinerant electrons and the physical property of RNiO2 is changed. This implies that the observed superconductivity in infinite-layer nickelates does not emerge from a doped Mott insulator as in cuprates.
The computational details of our DFT and DMFT calculations can be found in the Method section. For clarity, we study NdNiO2 as a representative of infinite-layer nickelates. The results of LaNiO2 are very similar (see Supplementary Note 1 and Note 2 in the Supplementary Information).
Results
Electronic structure and interstitial-s orbital
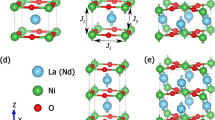
In Fig. 1a, b, we show the DFT-calculated band structure and Wannier function fitting of NdNiO2 and CaCuO2 in the non-spin-polarized state, respectively. We use altogether 17 Wannier projectors to fit the DFT band structure: 5 Ni/Cu-d orbitals, 5 Nd/Ca-d orbitals, 3 O-p orbitals (for each O atom), and an interstitial-s orbital. The interstitial-s orbital is located at the position of the missing apical oxygen. The importance of interstitial-s orbitals has been noticed in the study of electrides and infinite-layer nickelates22,41,42. Our Wannier fitting exactly reproduces not only the band structure of the entire transition-metal and oxygen pd manifold, but also the band structure of unoccupied states about 5 eV above the Fermi level. In particular, the Ni/Cu-\({d}_{{x}^{2}-{y}^{2}}\) Wannier projector is highlighted by red dots in Fig. 1a, b. The details of the Wannier fitting can be found in Supplementary Note 3 in the Supplementary Information. For both compounds, Ni/Cu-\({d}_{{x}^{2}-{y}^{2}}\) band crosses the Fermi level. However, as we mentioned in the Introduction, in addition to Ni-\({d}_{{x}^{2}-{y}^{2}}\) band, another conduction band also crosses the Fermi level in NdNiO2. Using Wannier analysis, we find that the non-Ni conduction electron band is mainly composed of three orbitals: Nd-\({d}_{3{z}^{2}-{r}^{2}}\), Nd-dxy, and interstitial-s orbitals. The corresponding Wannier projectors are highlighted by dots in the panels of Fig. 1c–e. An iso-value surface of the three Wannier functions (Nd-\({d}_{3{z}^{2}-{r}^{2}}\), Nd-dxy, and interstitial-s orbitals) is explicitly shown in Fig. 1f–h. We note that interstitial-s orbital is more delocalized than Nd-\({d}_{3{z}^{2}-{r}^{2}}\) and Nd-dxy orbitals. Because all these three orbitals are located in the Nd spacer layer between adjacent NiO2 planes, if these three orbitals can hybridize with Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital, then they will create a three-dimensional electronic structure, distinct from that of CaCuO220.
a, b DFT-calculated band structures and 17 Wannier functions fitting of NdNiO2 (a) and CaCuO2 (b). The thick blue lines are DFT-calculated bands and the red thin lines are bands reproduced by the Wannier functions. The red dots show the Wannier projection onto Ni-\({d}_{{x}^{2}-{y}^{2}}\) and Cu-\({d}_{{x}^{2}-{y}^{2}}\) orbitals, respectively. c–e Band structures reproduced by Wannier functions in an energy window close to the Fermi level. The dots show the weights of Wannier projections onto Nd-\({d}_{3{z}^{2}-{r}^{2}}\) orbital (c), Nd-dxy orbital (d), and interstitial-s orbital (e). The coordinates of the high-symmetry points on the k-path are Γ(0,0,0)-X(0.5,0,0)-M(0.5,0.5,0)-Γ(0,0,0)-Z(0,0,0.5)-R(0.5,0,0.5)-A(0.5,0.5,0.5)-Z(0,0,0.5). The Fermi level EF (black dashed line) is shifted to zero energy. f–h An iso-value surface of the Wannier functions of Nd-\({d}_{3{z}^{2}-{r}^{2}}\) orbital (f), Nd-dxy orbital (g), and interstitial-s orbital (h). The large orange atom is Nd, the gray atom is Ni, and the small red atom is O.
Analysis of hybridization
However, from symmetry consideration, within the same cell the hopping between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and any of those three orbitals (Nd-\({d}_{3{z}^{2}-{r}^{2}}\), Nd-dxy, and interstitial-s) is exactly equal to zero22, which leads to the conclusion that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and rare-earth-d orbitals is weak20,22,29. While this conclusion is correct by itself, the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and interstitial-s orbital has been omitted in previous studies20,21,22,23,27,29. We find that due to a large inter-cell hopping, Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital hybridizes with interstitial-s orbital much more substantially than with rare-earth-d orbitals by about one order of magnitude.
The direct inter-cell hopping between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and any of the three orbitals (Nd-\({d}_{3{z}^{2}-{r}^{2}}\), Nd-dxy and interstitial-s) is negligibly small. The effective hopping is via O-p orbitals. Figure 2 shows the inter-cell hopping between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and the other three orbitals via one O-p orbital. Among Nd-\({d}_{3{z}^{2}-{r}^{2}}\), Nd-dxy and interstitial-s orbitals, we find that the largest effective hopping (via one O-p orbital) is the one with interstitial-s orbital (see Table 1). The effective hopping between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and Nd-dxy/\({d}_{3{z}^{2}-{r}^{2}}\) orbitals is one order of magnitude smaller because Nd atom is located at the corner of the cell, which is further from the O atom than the interstitial site is. Furthermore, the energy difference between interstitial-s and O-p orbitals is about 1 eV smaller than that between Nd-dxy/\({d}_{3{z}^{2}-{r}^{2}}\) and O-p orbitals (see Table 1). These two factors combined lead to the fact that Ni-\({d}_{{x}^{2}-{y}^{2}}\) has a significant coupling with interstitial-s orbital, substantially stronger than that with Nd-d orbitals. This challenges the previous picture that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons in the Nd spacer layer is weak20,21,22,23,27,29.
To further confirm that the hybridization is substantial, we downfold the full band structure to a noninteracting model that is based on the above four orbitals (Ni-\({d}_{{x}^{2}-{y}^{2}}\), Nd-\({d}_{3{z}^{2}-{r}^{2}}\), Nd-dxy, and interstitial-s orbitals). Equation (1) shows the Wannier-based Hamiltonian 〈0∣H0∣a1〉 = H0(a1) in the matrix form (not the usual Hamiltonian 〈0∣H0∣0〉 = H0(0), H0(0) is shown in Supplementary Note 3 in the Supplementary Information). The important information is in the first row. The largest hopping is the one between neighboring Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbitals (this is due to the σ bond between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and O-px/py orbitals). However, the hopping between Ni-\({d}_{{x}^{2}-y2}\) and interstitial-s orbitals is even comparable to the largest hopping. By contrast, the hopping between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and Nd-dxy/\({d}_{3{z}^{2}-{r}^{2}}\) orbitals is about one order of magnitude smaller than the hopping between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and interstitial-s orbitals, which is consistent with the preceding analysis.
Charge transfer and screening of Ni local moment
Since infinite-layer nickelates are correlated materials, next we study correlation effects arising from Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital. We focus on whether the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons in the rare-earth spacer layer may affect the correlated properties of NdNiO2, such as magnetism.
We use the above four orbitals (see Eq. (1)) to build an interacting model:
where \(mm^{\prime}\) labels different orbitals, i labels Ni sites and σ labels spins. \({\hat{n}}_{i\sigma }\) is the occupancy operator of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital at site i with spin σ and the onsite Coulomb repulsion is only applied on the Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital. H0(k) is the Fourier transform of the Wannier-based Hamiltonian H0(R)9 and \({\hat{V}}_{{\mathrm{dc}}}\) is the double counting potential. That we do not explicitly include O-p states in the model is justified by noting that in NdNiO2 O-p states have much lower energy than Ni-d states, which is different from perovskite rare-earth nickelates and charge-transfer-type cuprates20,19. In the model Eq. (2), the Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is the correlated state while the other three orbitals (interstitial-s and Nd-\({d}_{3{z}^{2}-{r}^{2}}\)/dxy) are noninteracting, referred to as hybridization states.
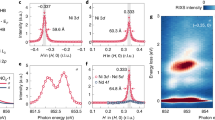
We perform dynamical mean-field theory calculations on Eq. (2). We first study paramagnetic state (paramagnetism is imposed in the calculations). Figure 3a–c shows the spectral function with an increasing UNi on Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital. At UNi = 0 eV, the system is metallic with all the four orbitals crossing the Fermi level (the main contribution comes from Ni-\({d}_{{x}^{2}-{y}^{2}}\)). As UNi increases to 3 eV, a quasi-particle peak is evident with the other three orbitals still crossing the Fermi level. We find a critical UNi of about 7 eV, where the quasi-particle peak becomes completely suppressed and a Mott gap emerges. As UNi further increases to 9 eV (not shown in Fig. 3), a clear Mott gap of about 1 eV is opened.
a–c Spectral function of the 4-orbital interacting model Eq. (2) calculated by density functional theory plus dynamical mean-field theory (DFT+DMFT) method in the paramagnetic state at T = 116 K with UNi = 0 eV (a), UNi = 3 eV (b), and UNi = 7 eV (c). UNi is the Hubbard U on each Ni atom. A(ω) is the frequency-dependent spectral function and ω represents the frequency. The Fermi level (black dashed line) is shifted to zero energy. The red, blue, magenta, yellow, and green curves are Ni-\({d}_{{x}^{2}-{y}^{2}}\) projected spectral function, Nd-\({d}_{3{z}^{2}-{r}^{2}}\) projected spectral function, Nd-dxy projected spectral function, interstitial-s projected spectral function, and total spectral function, respectively. The Ni-\({d}_{{x}^{2}-{y}^{2}}\) projected spectral function is highlighted by red shades. d Wannier function occupancy Nα as a function of UNi. Left axis is the occupancy of Nd-\({d}_{3{z}^{2}-{r}^{2}}\) (blue solid symbols), Nd-dxy (magenta solid symbols), interstitial-s (yellow solid symbols), and their sum (dark blue solid symbols). Right axis is the occupancy of Ni-\({d}_{{x}^{2}-{y}^{2}}\) (red open symbols). The light blue and light red shades show the range of UNi in which the total occupancy of hybridization states increases and decreases, respectively. e, f Local spin susceptibility \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital as a function of temperature T. e The blue symbols are calculated using UNi = 7 eV. The brown symbols are calculated using UNi = 2 eV. The black dashed line is a Curie–Weiss fitting. (f) The solid symbols are the same as in (e), in which the hybridization between itinerant electrons and Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is “turned on”. The open symbols are the local spin susceptibility \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) recalculated at UNi = 2 eV with the hybridization “turned off”. The black dashed line is a Curie–Weiss fitting.
The presence of hybridization states means that there could be charge transfer between correlated Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and interstitial-s/Nd-d orbitals. We calculate the occupancy of each Wannier function Nα and study correlation-driven charge transfer in NdNiO2. Figure 3d shows Nα of each hybridization state and Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital as well as the total occupancy of hybridization states as a function of UNi. We first note that at UNi = 0, the total occupancy of hybridization states is 0.14, which is significant. As UNi becomes larger, the total occupancy of hybridization states first increases and then decreases. This is because when UNi is small, the system is still metallic with all the hybridization states crossing the Fermi level, while the upper Hubbard band of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is just formed and pushed to higher energy. This leads to charge transfer from Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital to hybridization states, providing more itinerant electrons to couple to Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital. However, when UNi is large, hybridization states are also pushed above the Fermi level, which causes electron to transfer back to Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital (in the lower Hubbard band). In the strong UNi limit where the Mott gap opens, itinerant electrons in the Nd spacer layer disappear. Figure 3d also shows that for all UNi considered, the occupancy on interstitial-s orbital is always the largest among the three hybridization states, confirming the importance of the interstitial-s orbital in infinite-layer nickelates. We note that because we calculate the occupancy at finite temperatures, even when the gap is opened, the occupancy of hybridization states does not exactly become zero.
Because of the hybridization, we study possible screening of Ni local magnetic moment by itinerant electrons. We calculate local spin susceptibility of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital:
where Sz(τ) is the local spin operator for Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital, at the imaginary time τ. g denotes the electron spin gyromagnetic factor and β = 1/(kBT) is the inverse temperature. Figure 3e shows \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) for two representative values of UNi. The blue symbols are \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) for UNi = 7 eV when the system becomes insulating. The local spin susceptibility nicely fits to a Curie–Weiss behavior, as is shown by the black dashed line in Fig. 3e. \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) has a strong enhancement at low temperatures. However, for UNi = 2 eV when the system is metallic, we find a completely different \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\). The local spin susceptibility has very weak dependence on temperatures (see Fig. 3f for the zoomin). In particular, at low temperatures (T < 250 K), \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) reaches a plateau. We note that the weak temperature dependence of \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) is consistent with the experimental result of LaNiO2 paramagnetic susceptibility5, in particular our simple model calculations qualitatively reproduce the low-temperature plateau feature that is observed in experiment5.
To explicitly understand how the hybridization between itinerant electrons and Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital affects local spin susceptibility, we perform a thought-experiment: we manually “turn off” hybridization, i.e., for each R, we set \(\langle s| {H}_{0}({\bf{R}})| {d}_{{x}^{2}-{y}^{2}}\rangle =\langle {d}_{xy}| {H}_{0}({\bf{R}})| {d}_{{x}^{2}-{y}^{2}}\rangle =\langle {d}_{3{z}^{2}-{r}^{2}}| {H}_{0}({\bf{R}})| {d}_{{x}^{2}-{y}^{2}}\rangle =0\). Then we recalculate \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) using the modified Hamiltonian with UNi = 2 eV. The chemical potential is adjusted so that the total occupancy remains unchanged in the modified Hamiltonian. The two local spin susceptibilities are compared in Fig. 3f. With hybridization, \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) saturates at low temperatures, implying that μeff decreases or even vanishes with lowering temperatures. However, without hybridization, \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) shows an evident enhancement at low temperatures and a Curie–Weiss behavior is restored (black dashed line). This shows that in paramagnetic metallic NdNiO2, the hybridization between itinerant electrons and Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is substantial and as a consequence, it screens the Ni local magnetic moment, as in Kondo systems38,39,40. Such a screening mechanism may be used to explain the low-temperature upturn in the resistivity of NdNiO2 observed in experiment27,15. We note that while we only fix the total occupancy by adjusting the chemical potential, the occupancy of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital is almost the same in the original and modified models. In Fig. 3f, “with hybridization”, Ni-\({d}_{{x}^{2}-{y}^{2}}\) occupancy is 0.84 and “without hybridization”, Ni-\({d}_{{x}^{2}-{y}^{2}}\) occupancy is 0.83. This indicates that the screening of Ni moment is mainly due to the hybridization effects, while the change of Ni-\({d}_{{x}^{2}-{y}^{2}}\) occupancy (0.01e per Ni) plays a secondary role.
Correlation strength and phase diagram
We estimate the correlation strength for NdNiO2 by calculating its phase diagram. We allow spin polarization in the DMFT calculations and study both ferromagnetic and checkerboard antiferromagnetic states. We find that ferromagnetic ordering cannot be stabilized up to UNi = 9 eV. Checkerboard antiferromagnetic state can emerge when UNi exceeds 2.5 eV. The phase diagram is shown in Fig. 4a in which Md is the local magnetic moment on each Ni atom. Md is zero until UNi ≃ 2.5 eV and then increases with UNi and finally saturates to 1 μB/Ni which corresponds to a \(S=\frac{1}{2}\) state. We note that the critical value of UNi is model-dependent. If we include O-p states and semi-core states, the critical value of UNi will be substantially larger43. The robust result here is that with UNi increasing, antiferromagnetic ordering occurs before the metal-insulator transition. In the antiferromagnetic state, the critical UNi for the metal-insulator transition is about 6 eV, slightly smaller than that in the paramagnetic phase. The spectral function of antiferromagnetic metallic and insulating states is shown in Fig. 4b and c, respectively. Experimentally long-range magnetic orderings are not observed in NdNiO244. The calculated phase diagram means that NdNiO2 can only be in a paramagnetic metallic state (instead of a paramagnetic insulating state), in which the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and itinerant electrons screens the Ni local magnetic moment. We note that using our model Eq. (2), the calculated phase boundary indicates that Ni correlation strength is moderate in NdNiO2 with UNi/tdd < 7 (tdd is the effective hopping between the nearest-neighbor Ni-\({d}_{{x}^{2}-{y}^{2}}\) due to the σpd bond). This contrasts with the parent compounds of superconducting cuprates which are antiferromagnetic insulators and are described by an effective single-orbital Hubbard model with a larger correlation strength (UNi/tdd = 8–20)45,46,47,48. Finally, we perform a self-consistent check on the hybridization. When the system is metallic, the hybridization between itinerant electrons and Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital screens the spin on Ni site and reduces the local spin susceptibility \({\chi }_{{\rm{loc}}}^{\omega = 0}(T)\) in the paramagnetic phase. This implies that once we allow antiferromagnetic ordering, a smaller critical UNi may be needed to induce magnetism. To test that, we recalculate the phase diagram using the modified Hamiltonian with the hybridization manually “turned off”. The chemical potential is adjusted in the modified model so that the total occupancy remains unchanged. Figure 4d shows that without the hybridization, the Ni magnetic moment increases and the antiferromagnetic phase is expanded with the critical UNi reduced to 1.8 eV (UNi/tdd ≃ 5). This shows that the coupling to the conducting electrons affects Ni spins and changes the magnetic property of NdNiO240.
a Phase diagram of NdNiO2, calculated by using density functional theory plus dynamical mean-field theory (DFT+DMFT) method based on the 4-orbital interacting model Eq. (2). Md is the local moment on each Ni atom and UNi is the Hubbard U on each Ni atom. PM, paramagnetic state; AFM, checkerboard antiferromagnetic state; M, metallic; I, insulating. b Spectral function of the 4-orbital interacting model Eq. (2) in the antiferromagnetic state with UNi = 3 eV. A(ω) is the frequency-dependent spectral function and ω represents the frequency. The states above (below) zero correspond to spin up (down). The Fermi level (vertical dashed line) is set at zero energy. The red, blue, magenta, yellow, and green curves represent Ni-\({d}_{{x}^{2}-{y}^{2}}\) projected spectral function, Nd-\({d}_{3{z}^{2}-{r}^{2}}\) projected spectral function, Nd-dxy projected spectral function, interstitial-s projected spectral function, and total spectral function, respectively. The inset shows the spectral function of a single Ni atom projected onto its \({d}_{{x}^{2}-{y}^{2}}\) orbital. c Same as (b) with UNi = 9 eV. d The solid symbols are the same as in (a). The open symbols are local moment on each Ni atom recalculated with the hybridization “turned off”.
Discussion
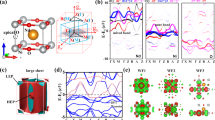
Our minimal model Eq. (2) is different from the standard Hubbard model (single-orbital, two-dimensional square lattice, and half filling) due to the presence of hybridization. It is also different from a standard periodic Anderson model in that (1) the correlated orbital is a 3d-orbital with a strong dispersion instead of a 4f or 5f orbital whose dispersion is usually neglected20,49,50; (2) the hybridization of Ni-\({d}_{{x}^{2}-{y}^{2}}\) with the three noninteracting orbitals is all inter-cell rather than onsite and anisotropic with different types of symmetries, which may influence the symmetry of the superconducting order parameter in the ground state51. Figure 5 explicitly shows the symmetry of hybridization. The dominant hybridization of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital, the one with interstitial-s orbital, has \({d}_{{x}^{2}-{y}^{2}}\) symmetry. Second, the hybridization of Ni-\({d}_{{x}^{2}-{y}^{2}}\) with Nd-dxy and Nd-\({d}_{3{z}^{2}-{r}^{2}}\) orbitals has \({g}_{xy({x}^{2}-{y}^{2})}\) and \({d}_{{x}^{2}-{y}^{2}}\) symmetries, respectively52.
Inter-cell hopping from Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital to interstitial-s orbital (a), to Nd-dxy orbital (b), and to Nd-\({d}_{3{z}^{2}-{r}^{2}}\) orbital (c). All the hoppings here are between second nearest neighbors. Brown and green arrows represent positive and negative hoppings, respectively. Note this is a top view. Nd spacer layer and NiO2 layer are not in the same plane.
d-wave superconducting states can be stabilized in the doped single-orbital Hubbard model from sophisticated many-body calculations53,54,55,56. However, the hybridization between correlated Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons fundamentally changes the electronic structure of a single-orbital Hubbard model, in particular when the system is metallic. This probably creates a condition unfavorable for superconductivity51, implying that new mechanisms such as interface charge transfer, strain engineering, etc. are needed to fully explain the phenomena observed in infinite-layer nickelates15.
Before we conclude, we briefly discuss other models for RNiO2 (R = La, Nd). In literature, some models focus on low-energy physics and include only states that are close to the Fermi level; others include more states which reproduce the electronic band structure within a large energy window around the Fermi level. Kitatani et al.57 propose that RNiO2 can be described by the one-band Hubbard model (Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital) with an additional electron reservoir, which is used to directly estimate the superconducting transition temperature. Hepting et al.20 construct a two-orbital model using Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and a R-\({d}_{3{z}^{2}-{r}^{2}}\)-like orbital. Such a model is used to study hybridization effects between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and rare-earth R-d orbitals. Zhang et al.28, Werner et al.32, and Hu et al.33 study a different type of two-orbital models which consist of two Ni-d orbitals. Hu et al.33 include Ni-\({d}_{{x}^{2}-{y}^{2}}\) and Ni-dxy orbitals, while Zhang et al. and Werner et al.32,28 include Ni-\({d}_{{x}^{2}-{y}^{2}}\) and Ni-\({d}_{3{z}^{2}-{r}^{2}}\) orbitals. This type of two-orbital model aims to study the possibility of high-spin S = 1 doublon when the system is hole doped. Wu et al.21 and Nomura et al.22 study three-orbital models. Wu et al.21 include Ni-dxy, R-dxy, and R-\({d}_{3{z}^{2}-{r}^{2}}\) orbitals. This model is further used to calculate the spin susceptibility and to estimate the superconducting transition temperature. Nomura et al.22 compare two choices of orbitals: one is Ni-dxy orbital, R-\({d}_{3{z}^{2}-{r}^{2}}\) orbital, and interstitial-s; and the other is Ni-dxy-orbital, R-\({d}_{3{z}^{2}-{r}^{2}}\) orbital, and R-dxy. The model is used to study the screening effects on the Hubbard U of Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital. Gao et al.23 construct a general four-orbital model B1g@1a⨁A1g@1b which consists of two Ni-d orbitals and two R-d orbitals. The model is used to study the topological property of the Fermi surface. Jiang et al.29 use a tight-binding model that consists of five Ni-d orbitals and five R-d orbitals to comprehensively study the hybridization effects between Ni-d and R-d orbitals; Jiang et al. also highlight the importance of Nd-f orbitals in the electronic structure of NdNiO2. Botana et al.16, Lechermann26, and Karp et al.58 consider more orbitals (including Nd-d, Ni-d, and O-p states) in the modeling of NdNiO2 with the interaction applied to Ni-d orbitals and make a comparison to infinite-layer cuprates. Botana et al.16 extract longer-range hopping parameters and the eg energy splitting. Lechermann26 studies hybridization and doping effects. Karp et al.58 calculate the phase diagram and estimates the magnetic transition temperature.
Conclusion
In summary, we use first-principles calculations to study the electronic structure of the parent superconducting material RNiO2 (R = Nd, La). We find that the hybridization between Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and itinerant electrons is substantially stronger than previously thought. The dominant hybridization comes from an interstitial-s orbital due to a large inter-cell hopping, while the hybridization with rare-earth-d orbitals is one order of magnitude weaker. Weak-to-moderate correlation effects on Ni cause electrons to transfer from Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital to the hybridization states, which provides more itinerant electrons in the rare-earth spacer layer to couple to correlated Ni-d orbital. Further increasing correlation strength leads to a reverse charge transfer, antiferromagnetism on Ni sites, and eventually a metal-insulator transition. In the experimentally observed paramagnetic metallic state of RNiO2, we find that the strong coupling between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and itinerant electrons screens the Ni local moment, as in Kondo systems. We also find that the hybridization increases the critical UNi that is needed to induce long-range magnetic ordering. Our work shows that the electronic structure of RNiO2 is fundamentally different from that of CaCuO2, which implies that the observed superconductivity in infinite-layer nickelates does not emerge from a doped Mott insulator as in cuprates.
Methods
We perform first-principles calculations using density functional theory (DFT)34,35, maximally localized Wannier functions (MLWF) to construct the noninteracting tight-binding models59, and dynamical mean field theory (DMFT)36,37 to solve the interacting models.
DFT calculations
The DFT method is implemented in the Vienna ab initio simulation package (VASP) code60 with the projector augmented wave (PAW) method61. The Perdew–Burke–Ernzerhof (PBE)62 functional is used as the exchange-correlation functional in DFT calculations. The Nd-4f orbitals are treated as core states in the pseudopotential. We use an energy cutoff of 600 eV and sample the Brillouin zone by using Γ-centered k-mesh of 16 × 16 × 16. The crystal structure is fully relaxed with an energy convergence criterion of 10−6 eV, force convergence criterion of 0.01 eV/Å, and strain convergence of 0.1 kBar. The DFT-optimized crystal structures are in excellent agreement with the experimental structures, as shown in our Supplementary Note 1. To describe the checkerboard antiferromagnetic ordering, we expand the cell to a \(\sqrt{2}\times \sqrt{2}\times 1\) supercell. The corresponding Brillouin zone is sampled by using a Γ-centered k-mesh of 12 × 12 × 16.
MLWF calculations
We use maximally localized Wannier functions59, as implemented in Wannier90 code63 to fit the DFT-calculated band structure and build an ab initio tight-binding model which includes onsite energies and hopping parameters for each Wannier function. We use two sets of Wannier functions to do the fitting. One set uses 17 Wannier functions to exactly reproduce the band structure of entire transition-metal and oxygen pd manifold as well as the unoccupied states that are a few eV above the Fermi level. The other set uses 4 Wannier functions to reproduce the band structure close to the Fermi level. The second tight-binding Hamiltonian is used to study correlation effects when onsite interactions are included on Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital.
DMFT calculations
We use DMFT method to calculate the 4-orbital interacting model, which includes a correlated Ni-\({d}_{{x}^{2}-{y}^{2}}\) orbital and three noninteracting orbitals (interstitial-s, Nd-dxy, and Nd-\({d}_{3{z}^{2}-{r}^{2}}\)). We also cross-check the results using a 17-orbital interacting model which includes five Ni-d, five Nd-d, six O-p, and one interstitial-s orbital (the results of the 17-orbital model are shown in Supplementary Note 4 of the Supplementary Information). DMFT maps the interacting lattice Hamiltonian onto an auxiliary impurity problem which is solved using the continuous-time quantum Monte Carlo algorithm based on hybridization expansion64,65. The impurity solver is developed by K. Haule66. For each DMFT iteration, a total of 1 billion Monte Carlo samples are collected to converge the impurity Green function and self-energy. We set the temperature to be 116 K. We check all the key results at a lower temperature of 58 K and no significant difference is found. The interaction strength UNi is treated as a parameter. We calculate both paramagnetic and magnetically ordered states. For magnetically ordered states, we consider ferromagnetic ordering and checkerboard antiferromagnetic ordering. For checkerboard antiferromagnetic ordering calculation, we double the cell, and the noninteracting Hamiltonian is 8 × 8. We introduce formally two effective impurity models and use the symmetry that electrons at one impurity site are equivalent to the electrons on the other with opposite spins. The DMFT self-consistent condition involves the self-energies of both spins.
To obtain the spectral functions, the imaginary axis self-energy is continued to the real axis using the maximum entropy method67. Then the real axis local Green function is calculated using the Dyson equation, and the spectral function is obtained in the following equation:
where m is the label of a Wannier function. 1 is an identity matrix, H0(k) is the Fourier transform of the Wannier-based Hamiltonian H0(R). Σ(ω) is the self-energy, understood as a diagonal matrix only with nonzero entries on the correlated orbitals. μ is the chemical potential. Vdc is the fully localized limit (FLL) double counting potential, which is defined as68:
where Nd is the d occupancy of a correlated site. Here the Hund’s J term vanishes because we have a single correlated orbital Ni-\({d}_{{x}^{2}-{y}^{2}}\) in the model. A 40 × 40 × 40 k-point mesh is used to converge the spectral function. We note that double counting correction affects the energy separation between Ni-\({d}_{{x}^{2}-{y}^{2}}\) and Nd-d/interstitial-s orbitals. However, because the charge transfer is small (around 0.1e per Ni), the effects from the double counting correction are weak in the 4-orbital model, compared with those in the p–d model in which double counting correction becomes much more important69. That is because O-p states are included in the p–d model. The double counting correction affects the p–d energy separation and thus the charge transfer between metal-d and oxygen-p orbitals, which can be as large as 1e per metal atom for late transition-metal oxides such as rare-earth nickelates69.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The electronic structure calculations were performed using the proprietary code VASP60, the open-source code Wannier9063, and the open-source impurity solver implemented by Kristjan Haule at Rutgers University (http://hauleweb.rutgers.edu/tutorials/). Both Wannier90 and Haule’s impurity solver are freely distributed on academic use under the Massachusetts Institute of Technology (MIT) License.
References
Bednorz, J. G. & Müller, K. A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. f.ür. Phys. B 64, 189–193 (1986).
Anisimov, V. I., Bukhvalov, D. & Rice, T. M. Electronic structure of possible nickelate analogs to the cuprates. Phys. Rev. B 59, 7901–7906 (1999).
Hu, J. Identifying the genes of unconventional high temperature superconductors. Sci. Bull. 61, 561–569 (2016).
Rao, C. N. R., Ganguli, A. K. & Nagarajan, R. Superconductivity in layered nickel oxides. Pramana 32, L177–L179 (1989).
Hayward, M., Green, M., Rosseinsky, M. & Sloan, J. Sodium hydride as a powerful reducing agent for topotactic oxide deintercalation: Synthesis and characterization of the nickel (I) oxide LaNiO2. J. Am. Chem. Soc. 121, 8843–8854 (1999).
Lee, K.-W. & Pickett, W. Infinite-layer LaNiO2: Ni1+ is not Cu2+. Phys. Rev. B 70, 165109 (2004).
Freeland, J. et al. Orbital control in strained ultra-thin LaNiO3/LaAlO3 superlattices. Europhys. Lett. 96, 57004 (2011).
Chaloupka, J. & Khaliullin, G. Orbital order and possible superconductivity in LaNiO3/LaMO3 superlattices. Phys. Rev. Lett. 100, 016404 (2008).
Hansmann, P. et al. Turning a nickelate fermi surface into a cupratelike one through heterostructuring. Phys. Rev. Lett. 103, 016401 (2009).
Han, M. J., Wang, X., Marianetti, C. A. & Millis, A. J. Dynamical mean-field theory of nickelate superlattices. Phys. Rev. Lett. 107, 206804 (2011).
Chen, H. et al. Modifying the electronic orbitals of nickelate heterostructures via structural distortions. Phys. Rev. Lett. 110, 186402 (2013).
Disa, A. S. et al. Orbital engineering in symmetry-breaking polar heterostructures. Phys. Rev. Lett. 114, 026801 (2015).
Botana, A. S., Pardo, V. & Norman, M. R. Electron doped layered nickelates: Spanning the phase diagram of the cuprates. Phys. Rev. Mater. 1, 021801 (2017).
Zhang, J. et al. Large orbital polarization in a metallic square-planar nickelate. Nat. Phys. 13, 864–869 (2017).
Li, D. et al. Superconductivity in an infinite-layer nickelate. Nature 572, 624–627 (2019).
Botana, A. & Norman, M. Similarities and differences between LaNiO2 and CaCuO2 and implications for superconductivity. Phys. Rev. X 10, 011024 (2020).
Sakakibara, H. et al. Model construction and a possibility of cuprate-like pairing in a new d9 nickelate superconductor (Nd,Sr)NiO2. Preprint at https://arxiv.org/abs/1909.00060 (2019).
Hirsch, J. & Marsiglio, F. Hole superconductivity in infinite-layer nickelates. Physica C 566, 1353534 (2019).
Jiang, M., Berciu, M. & Sawatzky, G. A. Doped holes in NdNiO2 and high-Tc cuprates show little similarity. Preprint at https://arxiv.org/abs/1909.02557 (2019).
Hepting, M. et al. Electronic structure of the parent compound of superconducting infinite-layer nickelates. Nat. Mater. 19, 381–385 (2020).
Wu, X. et al. Robust \({d}_{x}^{2}-{y}^{2}\)-wave superconductivity of infinite-layer nickelates. Phys. Rev. B 101, 60504 (2020).
Nomura, Y. et al. Formation of a two-dimensional single-component correlated electron system and band engineering in the nickelate superconductor NdNiO2. Phys. Rev. B 100, 205138 (2019).
Gao, J., Wang, Z., Fang, C. & Weng, H. Electronic structures and topological properties in nickelates Lnn+1NinO2n+2. In press, SCIENCE CHINA Physics, Mechanics & Astronomy (2019).
Ryee, S., Yoon, H., Kim, T. J., Jeong, M. Y. & Han, M. J. Induced magnetic two-dimensionality by hole doping in the superconducting infinite-layer nickelate Nd1−xSrxNiO2. Phys. Rev. B 101, 064513 (2020).
Zhang, H. et al. Effective hamiltonian for nickelate oxides Nd1−xSrxNiO2. Phys. Rev. Res. 2, 13214 (2020).
Lechermann, F. Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates. Phys. Rev. B 101, 81110 (2020).
Zhang, G.-M., Yang, Y.-f. & Zhang, F.-C. Self-doped mott insulator for parent compounds of nickelate superconductors. Phys. Rev. B 101, 20501 (2020).
Zhang, Y.-H. & Vishwanath, A. Type II t-J model in superconducting nickelate Nd_{1-x}Sr_{x}NiO_2. Physical Review Research, in press (2019).
Jiang, P., Si, L., Liao, Z. & Zhong, Z. Electronic structure of rare-earth infinite-layer RNiO2(R = La, Nd). Phys. Rev. B 100, 201106 (2019).
Hirayama, M., Tadano, T., Nomura, Y. & Arita, R. Materials design of dynamically stable d9 layered nickelates. Phys. Rev. B 101, 75107 (2020).
Zhou, T., Gao, Y. & Wang, Z. D. Spin excitations in nickelate superconductors. Preprint at https://arxiv.org/abs/1910.05757 (2019).
Werner, P. & Hoshino, S. Nickelate superconductors: multiorbital nature and spin freezing. Phys. Rev. B 101, 41104 (2020).
Hu, L.-H. & Wu, C. Two-band model for magnetism and superconductivity in nickelates. Phys. Rev. Res. 1, 032046 (2019).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13–125 (1996).
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865–951 (2006).
Kondo, J. Resistance minimum in dilute magnetic alloys. Prog. Theor. Phys. 32, 37–49 (1964).
Wilson, K. G. The renormalization group and critical phenomena. Rev. Mod. Phys. 55, 583–600 (1983).
Sawatzky, G. A. Superconductivity seen in a non-magnetic nickel oxide. Nature 572, 592–593 (2019).
Hirayama, M., Matsuishi, S., Hosono, H. & Murakami, S. Electrides as a new platform of topological materials. Phys. Rev. X 8, 031067 (2018).
Matsuishi, S. et al. High-density electron anions in a nanoporous single crystal: [Ca24Al28O64]4+4e−). Science 301, 626–629 (2003).
Sakuma, R. & Aryasetiawan, F. First-principles calculations of dynamical screened interactions for the transition metal oxides M O (M = Mn, Fe, Co, Ni). Phys. Rev. B 87, 165118 (2013).
Hayward, M. & Rosseinsky, M. Synthesis of the infinite layer Ni (I) phase NdNiO2+x by low temperature reduction of NdNiO3 with sodium hydride. Solid State Sci. 5, 839–850 (2003).
Tokura, Y. et al. Cu-o network dependence of optical charge-transfer gaps and spin-pair excitations in single-CuO2-layer compounds. Phys. Rev. B 41, 11657–11660 (1990).
Comanac, A., De’Medici, L., Capone, M. & Millis, A. Optical conductivity and the correlation strength of high-temperature copper-oxide superconductors. Nat. Phys. 4, 287–290 (2008).
de’ Medici, L., Wang, X., Capone, M. & Millis, A. J. Correlation strength, gaps, and particle-hole asymmetry in high-Tc cuprates: a dynamical mean field study of the three-band copper-oxide model. Phys. Rev. B 80, 054501 (2009).
W., C., Haule, K. & Kotliar, G. Strength of correlations in electron- and hole-doped cuprates. Nat. Phys. 6, 574–578 (2010).
Bulla, R., Costi, T. A. & Pruschke, T. Numerical renormalization group method for quantum impurity systems. Rev. Mod. Phys. 80, 395–450 (2008).
Held, K., Huscroft, C., Scalettar, R. T. & McMahan, A. K. Similarities between the Hubbard and periodic anderson models at finite temperatures. Phys. Rev. Lett. 85, 373–376 (2000).
Sarasua, L. & Continentino, M. A. Superconductivity in the periodic Anderson model with anisotropic hybridization. Phys. C. 384, 41–46 (2003).
Dresselhauss, M., Dresselhauss, G. & Jorio, A. Group Theory: Application to the Physics of Condensed Matter (Springer-Verlag Berlin Heidelberg, 2007).
Zheng, B.-X. et al. Stripe order in the underdoped region of the two-dimensional Hubbard model. Science 358, 1155–1160 (2017).
Gull, E., Parcollet, O. & Millis, A. J. Superconductivity and the pseudogap in the two-dimensional Hubbard model. Phys. Rev. Lett. 110, 216405 (2013).
Maier, T. A., Jarrell, M., Schulthess, T. C., Kent, P. R. C. & White, J. B. Systematic study of d-wave superconductivity in the 2d repulsive Hubbard model. Phys. Rev. Lett. 95, 237001 (2005).
Halboth, C. J. & Metzner, W. d-wave superconductivity and pomeranchuk instability in the two-dimensional Hubbard model. Phys. Rev. Lett. 85, 5162–5165 (2000).
Kitatani, M. et al. Nickelate superconductors—a renaissance of the one-band Hubbard model. Preprint at https://arxiv.org/abs/2002.12230 (2020).
Karp, J. et al. Many-body electronic structure of NdNiO2 and CaCuO2. In press, Physical Review X (2020).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 84, 1419–1475 (2012).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Werner, P., Comanac, A., De’Medici, L., Troyer, M. & Millis, A. J. Continuous-time solver for quantum impurity models. Phys. Rev. Lett. 97, 076405 (2006).
Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349–404 (2011).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Silver, R. N., Sivia, D. S. & Gubernatis, J. E. Maximum-entropy method for analytic continuation of quantum Monte Carlo data. Phys. Rev. B 41, 2380–2389 (1990).
Czyżyk, M. T. & Sawatzky, G. A. Local-density functional and on-site correlations: the electronic structure of La2CuO4 and LaCuO3. Phys. Rev. B 49, 14211–14228 (1994).
Park, H., Millis, A. J. & Marianetti, C. A. Computing total energies in complex materials using charge self-consistent DFT + DMFT. Phys. Rev. B 90, 235103 (2014).
Acknowledgements
We thank Danfeng Li, Jean-Marc Triscone, Andrew Millis, Dong Luan and Qiang Zhang for useful discussions. H.C. is supported by the National Natural Science Foundation of China under project number 11774236 and NYU University Research Challenge Fund. Y.G. and J.H. are supported by the Ministry of Science and Technology of China 973 program (Grant No. 2015CB921300, No. 2017YFA0303100, and No. 2017YFA0302900), National Science Foundation of China (Grant No. NSFC-11334012), the Strategic Priority Research Program of CAS (Grant No. XDB07000000), and High-performance Computing Platform of Peking University. Computational resources are provided by High-performance Computing Platform of Peking University, NYU High-performance computing at New York, Abu Dhabi, and Shanghai campuses.
Author information
Authors and Affiliations
Contributions
H.C. conceived the project. Y.G. and H.C. performed the calculations. S.Z. and X.W. analyzed data. J.H. participated in the discussion. H.C. and Y.G. wrote the manuscript. All the authors commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gu, Y., Zhu, S., Wang, X. et al. A substantial hybridization between correlated Ni-d orbital and itinerant electrons in infinite-layer nickelates. Commun Phys 3, 84 (2020). https://doi.org/10.1038/s42005-020-0347-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0347-x
This article is cited by
-
Structural phase transition, s±-wave pairing, and magnetic stripe order in bilayered superconductor La3Ni2O7 under pressure
Nature Communications (2024)
-
Charge density wave ordering in NdNiO2: effects of multiorbital nonlocal correlations
npj Computational Materials (2024)
-
Emergence of antiferromagnetic correlations and Kondolike features in a model for infinite layer nickelates
npj Quantum Materials (2024)
-
Optimization for epitaxial fabrication of infinite-layer nickelate superconductors
Frontiers of Physics (2024)
-
Orbital-overlap-driven hybridization in 3d-transition metal perovskite oxides LaMO3 (M = Ti-Ni) and La2CuO4
Communications Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.