Abstract
Electrostatic superlattices have been known to significantly modify the electronic structure of low-dimensional materials. Studies of graphene superlattices were triggered by the discovery of moiré patterns in van der Waals stacks of graphene and hexagonal boron nitride (hBN) layers a few years ago. Very recently, gate-controllable superlattices using spatially modulated gate oxides have been achieved, allowing for Dirac band structure engineering of graphene. Despite these rapid experimental progresses, technical advances in quantum transport simulations for large-scale graphene superlattices have been relatively limited. Here, we show that transport experiments for both graphene/hBN moiré superlattices and gate-controllable superlattices can be well reproduced by transport simulations based on a scalable tight-binding model. Our finding paves the way to tuning-parameter-free quantum transport simulations for graphene superlattices, providing reliable guides for understanding and predicting novel electric properties of complex graphene superlattice devices.
Similar content being viewed by others
Introduction
Hexagonal boron nitride (hBN), one of the most popular dielectric materials due to its atomic flatness1, has been playing a crucial role in studying two-dimensional materials using so-called van der Waals heterostructures2. The graphene/hBN moiré pattern3 arising from the large-scale lattice interference led to the discovery of graphene superlattices. First experiments revealing new transport phenomena, such as the emergence of the Hofstadter butterfly, were reported in 20134,5,6. In the following years, other exciting transport experiments have been reported7,8,9,10,11,12,13, as well as a dynamic band structure tuning14,15. More recently, another approach for inducing a superlattice potential in graphene has been demonstrated by using patterned dielectrics16, allowing for mini-band structure engineering. On the theory side, most works related to graphene superlattices focus either on calculations for the superlattice-induced mini-band structures17,18,19,20,21,22,23, or on predicting transport properties by solving the Dirac equation with simplified superlattice model potential24,25. Quantum transport simulations considering realistic experimental conditions have been relatively rare in the literature26,27, not to mention a theory work combining transport simulations and mini-band structure calculations, together with transport experiments.
This article aims at providing a straightforward method to perform reliable quantum transport simulations for graphene superlattices. As shown in the following, our transport simulations based on the real-space Green’s function method for two-terminal structures with the superlattice potential arising either from the graphene/hBN moiré pattern or from periodically modulated gating are consistent with transport experiments as well as mini-band structures based on the continuum model. Our method is applicable equally well to multi-terminal structures for simulating, for example, four-probe measurements using the Landauer–Büttiker approach28.
Results
Superlattice on a scaled graphene lattice
To perform quantum transport simulations for graphene working in real-space, the scalable tight-binding model29 has been proved to be a very convenient numerical tool30,31,32,33,34: the physics of a real graphene system can be captured by a graphene lattice scaled by a factor of s such that the lattice spacing and nearest-neighbor hopping parameter are given by a = sa0 and t = t0/s, respectively, where a0 ≈ 0.142 nm and t0 ≈ 3 eV are the tight-binding parameters for a genuine graphene lattice. The scaling is justified as long as a remains much shorter than all important physical length scales in the considered graphene system.
In dealing with graphene superlattices (such as the one sketched in Fig. 1a), the newly introduced physical length scale not previously considered29 is the periodicity λ of the superlattice. The advantage of the scaling can be easily appreciated by comparing Fig. 1b, c: The former considers a genuine graphene lattice involving lots of carbon atoms, while the latter depicts a scaled graphene lattice (here s = 2 for illustrative purposes) involving a strongly reduced number of lattice sites that down-scales with s2. As long as a ≪ λ is satisfied, a reasonably large area covering enough superlattice periods can be implemented in real-space quantum transport simulations (see Methods) to reveal transport properties arising from the superlattice effects.
a Schematic of a two-terminal graphene device of length L and width W in the presence of a superlattice potential of periodicity λ within the scattering region only, but not in the attached two leads. The red box is magnified in the surface plot shown at the right to indicate the smoothing of the superlattice potential. The white box is magnified in (b) for a genuine graphene lattice of site spacing a0 equal to the carbon–carbon bond length and (c) for a scaled graphene lattice of site spacing a given by a0 up-scaled by a factor s.
In the following, we demonstrate the reliability of transport simulations for graphene superlattices based on scaled graphene lattices, considering both graphene/hBN moiré superlattice and gate-controlled superlattice.
Graphene/hBN moiré superlattice model potential
Formation of the moiré pattern due to the stacking of hBN and graphene lattices has been understood in one of the earliest experiments3. Following their model, the moiré pattern results in a triangular periodic scalar potential described by
where V = 0.06 eV is the amplitude of the model potential and \({\mathbf{G}}_1(\tilde \lambda ,\tilde \theta )\) is the reciprocal primitive vector of the moiré pattern corresponding to the primitive vector L1(λ, θ) = λ(cos θ, sin θ) in real space. The orientation angle \(\tilde \theta\) and wavelength \(\tilde \lambda\) are related to those in real-space through \(\tilde \theta = \theta + \pi {\mathrm{/}}2\) and \(\tilde \lambda = 4\pi {\mathrm{/}}\sqrt 3 \lambda\). The other two reciprocal vectors are given by \({\mathbf{G}}_2(\tilde \lambda ,\tilde \theta ) = {\mathbf{G}}_1(\tilde \lambda ,\tilde \theta + \pi {\mathrm{/}}3)\) and \({\mathbf{G}}_3(\tilde \lambda ,\tilde \theta ) = {\mathbf{G}}_1(\tilde \lambda ,\tilde \theta + 2\pi {\mathrm{/}}3)\). Following Moon and Koshino23 with the zigzag lattice direction arranged along the x axis, the moiré wavelength λ and the orientation angle θ of the pattern are given by
and
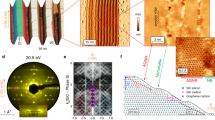
respectively, where \(a_{\mathrm{g}} = \sqrt 3 a_0 \approx 0.246\) nm is the graphene lattice constant, ϵ = (ahBN − ag)/ag ≈ 1.81% is the lattice constant mismatch with ahBN ≈ 0.2504 nm the hBN lattice constant, and ϕ is the twist angle of the hBN lattice relative to the graphene lattice. An illustrative example with ϕ = 5° is sketched in Fig. 2a, where an overlay of Us(x, y) given by Eq. (1) is shown to match perfectly the lattice structure of the resulting graphene/hBN moiré pattern. For self-containment, λ and θ as functions of the twist angle ϕ are plotted in Fig. 2b, c, respectively, where the hollow squares mark the ϕ = 5° example of Fig. 2a and the hollow circles mark the ϕ = 0.9° case corresponding to our transport experiments and simulations to be elaborated below.
a An example of stacked graphene and hBN lattices with twist angle ϕ = 5° showing the resulting moiré pattern with wavelength λ and the orientation angle θ. The overlay of the color map is given by the moiré model potential (1) with yellow (bright) and blue (dark) representing the maximum 3V and minimum −3V/2, respectively. The ϕ dependence of λ and θ are shown in (b, c), respectively, based on Eqs. (2a) and (2b). d Experimentally measured two-terminal conductance G as a function of back gate voltage Vbg at low temperature. Inset: the atomic force microscopy (AFM) image of a typical junction similar to the measured device. e Simulated conductance as a function of Vbg at zero temperature with Fermi energy in the leads fixed (black dashed) and floating (red). Scale bar: 5 nm on (a) and 1 μm on the inset of (d). Calculated f conductance, g density of states, and h mini-band structures as functions of energy E, all based on the same moiré superlattice potential (1) with ϕ = 0.9°. Side plot of (h): three-dimensional mini-band structure showing only the lowest two conduction and two valence bands.
Transport experiment
To confirm the validity of our simulation scheme illustrated above, the most convincing way is to fabricate a real device, perform a transport measurement, and finally simulate the experiment. Our single-gated two-terminal device was fabricated with a graphene/hBN stack (see the inset of Fig. 2d and Methods) and measured at low temperature (≈4.1 K), using standard low-frequency (≈13 Hz) lock-in technique. Figure 2d shows the two-terminal differential conductance of our sample as a function of the back gate voltage Vbg. Conductance dips at around −60 and +58 V are basic characteristics of the moiré superlattice potential4,5,6, showing that our graphene and hBN lattices are nearly aligned. By analyzing from the Brown–Zak oscillation12,13, the moiré wavelength λ ≈ 10.9 nm of our graphene/hBN sample was deduced. Note that although our graphene sample was encapsulated by two hBN layers, the single dip structure (in each of the electron and hole branches) of our conductance measurement (Fig. 2d) suggests that only one hBN layer exhibits a measurable moiré superlattice effect arising from a small twist angle, contrary to a recent report on doubly aligned hBN/graphene/hBN heterostructures35. In the following simulations, therefore, we model our experiment with graphene/hBN, instead of hBN/graphene/hBN.
Transport simulation
To simulate such a conductance measurement, we have calculated the transmission T(E) as a function of Fermi energy E at zero temperature, and hence the conductance G(E) = (2e2/h)T(E), based on an s = 4 tight-binding model Hamiltonian, for a two-terminal device similar to Fig. 1a with L = W = 500 nm (see Supplementary Fig. 1 and Supplementary Note 1 for sample size dependence), implementing the moiré model potential (1) with a twist angle ϕ. To compare with the experiment on the same voltage axis, we adopt the parallel-plate capacitor formula to convert from the Fermi energy to the gate voltages; see Supplementary Note 2 for the conversion. With the chosen ϕ = 0.9° for the moiré model potential Eq. (1) corresponding to λ ≈ 10.4 nm consistent with the experimentally deduced value, the simulated conductance G(Vbg) transformed from G(E) and reported in Fig. 2e is found to show excellent agreement with the experiment, Fig. 2d, in the positions of the conductance dips. Note that the red curve reported in Fig. 2e considers leads with on-site and Fermi energies identical to those at the lattice sites attached to the leads; see Fig. 1a. In this way, the Fermi energy in the leads “floats” with that in the scattering region such that the interface between the lead and the scattering region is as transparent as possible. Compared to Fig. 2d, the electron–hole asymmetry is less pronounced due to the simple model of Eq. (1) from Yankowitz et al.3. Although accounting for an electron doping from the metal contacts simply by fixing the Fermi energy in the leads with a positive value can make the conductance curve (black dashed curve in Fig. 2e with Fermi energy 0.32 eV in the leads) even more similar to the experiment, the nature of the electron–hole asymmetry observed in Fig. 2d comes from more subtle interactions between graphene and hBN lattices which require more advanced model Hamiltonians21,22,23 beyond the simple model of Eq. (1). We will not further address the electron–hole asymmetry but continue our discussions with calculations based on leads with “floating” Fermi energies.
Density of states and mini-band structures
Without transforming to the gate voltage axis, the original conductance data of Fig. 2e as a function of energy is reported in Fig. 2f with a wider energy range up to ±0.4 eV. Compared to the density of states (Fig. 2g) and the band structure (Fig. 2h) which are calculated based on the same moiré superlattice model potential but within the continuum model (see Methods), consistent features in the energy spectrum can be seen. In view of Fig. 2d–h, our calculations significantly capture basic properties of the graphene/hBN moiré superlattice, at least at zero magnetic field.
Dependence on moiré orientation angle
In all the transport simulations for the moiré superlattice shown in the main text of this article, we have considered realistic moiré orientation angle θ prescribed by Eq. (2b), relative to the zigzag direction. We have further tested that the simulation results are insensitive to θ. See Supplementary Fig. 2 and Supplementary Note 3.
Magnetotransport experiment and simulation
We continue our comparison of the experimentally measured and theoretically calculated conductance G(Vbg) with finite magnetic field B perpendicular to the graphene plane, which can be modeled by associating the Peierls phase28,36 to the hopping t → teiΦ in Eq. (3), where \({\mathrm{\Phi }} = (e{\mathrm{/}}\hbar ){\int}_{{\mathbf{r}}_j}^{{\mathbf{r}}_i} {{\mathbf{A}} \cdot d{\mathbf{r}}}\), choosing the Landau gauge A = (−yB, 0, 0) for the vector potential A; see the axes shown in Fig. 1. Conductance maps of G(Vbg, B) are reported in Fig. 3a (b) from the experiment (theory) showing magnetic field up to 5 T and the same gate voltage range as Fig. 2d (e), which corresponds exactly to the horizontal line cuts at B = 0 in Fig. 3a (b). The original data of the calculated conductance as a function of Fermi energy and magnetic field, G(E, B), is shown in Supplementary Fig. 3 with the full range. Within the gate voltage range of about −45 V ≲ Vbg ≲ +45 V, typical relativistic Landau fans can be seen in both experiment and theory. To compare further, we magnify the regions marked by the black dashed box in Fig. 3a (b) in Fig. 3c (d) painted by a different color code to highlight the quantized conductance plateaus. Numbers −6, −10, ⋯, −38 on Fig. 3d label the filling factor ν on the corresponding plateau with the expected conductance |ν|e2/h. Good agreement between experiment (Fig. 3a, c) and theory (Fig. 3b, d) within the main Dirac cone can be seen.
Conductance G as a function of back gate voltage Vbg and magnetic field B from a experiment and b theory, with regions marked by the black dashed boxes magnified and recolored in (c, d), respectively. The color bar in (c) is shared with (d), calibrating the conductance in units of e2/h. Numbers on (d) are filling factors on the corresponding plateaus. e The simulated conductance map with high gate voltages surrounding the electron-branch secondary Dirac point. The red line corresponds to the horizontal line cut shown in (f), where the Vbg range marked by yellow corresponds to the energy window marked by yellow in Fig. 2h.
Unobserved 12-fold quantum Hall plateaus
At gate voltages |Vbg| ≳ 45 V, transport properties are dominated by the extra Dirac cones arising from the modulating moiré superlattice. Discrepancies between the experiment and theory are evident. This suggests that the neglected higher-order terms of a more complete model Hamiltonian21,22,23 become important when the magnetic field is strong. Interestingly, we note that in the theory map of Fig. 3b, some unusual plateaus in the energy range around the electron-branch secondary Dirac point can be observed. We magnify this region in Fig. 3e with a horizontal line cut shown in Fig. 3f, where the gate voltage range showing quantized conductance plateaus is highlighted by a yellow background.
This Vbg range, transformed back to the energy through Eq. (S1) of Supplementary Note 2, corresponds to an energy window where part of the electron branch of the secondary Dirac cones at M points of the superlattice mini-Brillouin zone are completely isolated. The respective energy window is highlighted also by yellow in Fig. 2h. Since there are effectively three such Dirac cones (six cones on six M points within each mini-Brillouin zone but each cone shared by two neighboring mini-Brillouin zones), the degeneracy factor is expected to be 3 × 2 × 2 = 12 with ×2 accounting for spin and another ×2 for valley. Indeed, in the quantum Hall regime, the calculated conductance is quantized to 6, 18, 30, 42 e2/h as shown in Fig. 3f. Outside this energy (and hence back gate voltage) range, the higher-order Dirac cones are always mixed with background bands, so that no quantized conductance is observed. However, such a special energy window leading to the 12-fold-degeneracy of the Landau levels at the secondary DP is never observed in transport experiments with graphene/hBN moiré superlattices4,5,10,11,12, including ours shown in Fig. 3a, indicating once again that the simplified model3 of Eq. (1) containing only the electrostatic scalar potential term is not sufficient to capture transport properties of graphene/hBN moiré superlattices at higher magnetic fields.
At this stage, we comment that the periodic scalar potential enters the tight-binding model Hamiltonian through the on-site energy term (see Methods), so that it is readily compatible with the scaling method29. Including higher-order terms21,22,23 of the graphene/hBN moiré superlattice should be possible but is beyond the scope of the present study. As we will see below, when the graphene superlattice potential arises solely from the electrostatic gating, our method becomes even more precise because in such systems the scalar potential is the only term comprising the superlattice.
Gate-controllable superlattices
To observe any superlattice effects in graphene, the mean free path must exceed enough periods of the superlattice potential. This means that either the sample quality must be extraordinary, or the superlattice periodicity must be short enough. When the periodicity is too short, however, the resulting extra Dirac cones appear at too high energy, exceeding the experimentally reachable range. This is why the discovery of the graphene/hBN moiré pattern3 led to studies on the graphene superlattice of its first kind—the periodicity corresponding to small twist angles turns out to be naturally in a suitable range for experiments; see Fig. 2b. A more flexible approach to design artificial graphene superlattice structures for band structure engineering was pursued with the realization of electrostatic gating schemes16. To create an externally controllable periodic potential, the most intuitive way is to pattern an array of periodic fine metal gates on top of the graphene sample37,38. However, due to technical difficulties such as instabilities of nanometer-scale local gates, the low adhesion between metal gates and the inert hBN, etc., such superlattice graphene devices often suffer the problem of very low sample yield39. The basic idea of the new technical breakthrough is to keep the hBN/graphene/hBN sandwich intact, while periodically modulating the gate capacitance. This can be achieved either by using few-layer graphene as a local gate which is subsequently etched with a periodic pattern39,40, or by etching the dielectric layer with a periodic pattern using a standard uniform back gate underneath the modulated substrate16. In the following, we revisit the experiment of the latter by Forsythe et al.16 and reproduce the observed transport features by our transport simulations.
Electrostatic simulation
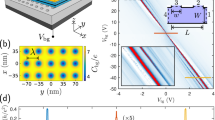
Following the geometry of the device subject to a square superlattice potential with periodicity λ = 35 nm presented in the work by Forsythe et al.16, we have performed our own electrostatic simulation to obtain the back gate capacitance showing periodic spatial modulation. We consider an hBN/graphene/hBN sandwich (showing no measurable moiré superlattice effects) gated by a global top gate contributing a uniform carrier density ntg, and a bottom gate at voltage Vbg with a pre-patterned SiO2 substrate in between. See Figure 1 of Forsythe et al.16. The bottom gate capacitance therefore shows a spatial modulation with a square lattice symmetry, as shown in the lower left inset of Fig. 4a.
a Inverse transmission 1/T as a function of top-gate-contributed carrier density ntg and back gate voltage Vbg for the simulated virtual device similar to one of those reported by Forsythe et al.16. Upper inset: Device geometry with the modulated back gate capacitance profile Cbg showing a spatial modulation of periodicity λ = 35 nm. The boxed region is magnified in the lower inset with the color bar calibrating the value of Cbg in units of 1010 cm−2 V−1. The three horizontal color lines marked on the main panel of (a) correspond to the line cuts shown in (b–d). e–g Mini-band structures based on the continuum model, showing six bands closest to the main Dirac point, labeled from high to low energy by C3 (yellow), C2 (blue), C1 (red), V1 (green), V2 (orange), and V3 (purple), implementing Us(x, y) displayed over a range of 2λ × 2λ above each main panel. Panels (e–g) correspond to (ntg, Vbg) configurations labeled by the left, middle, and right black arrows marked in (b), respectively. The black dashed boxes mark the E = 0 Fermi level hosting low-bias transport, where the intersected sub-band Fermi contours are shown below the corresponding mini-band structure: V1 (green) and V2 (orange) in (e), C1 (red) in (f), and C1 (red) and C2 (blue) in (g). Symmetry points on the square mini-Brillouin zone (Γ for the central point, M for the corner points, and X for the midpoints on the edges) are labeled in a way that avoids disturbing the Fermi contours shown.
With the electrostatically simulated position-dependent back gate capacitance per unit area Cbg(x, y), contributing carrier density nbg(x, y) = [Cbg(x, y)/e]Vbg, together with the uniform ntg, the resulting superlattice potential is given by \(U_{\mathrm{s}}(x,y) = - {\mathrm{sgn}}[n(x,y)]\hbar v_{\mathrm{F}}\sqrt {\pi \left| {n(x,y)} \right|}\) with n = nbg + ntg, in order to set the global transport Fermi level at zero41. Slightly different from the case of the graphene/hBN moiré superlattice where the model potential Us(x, y) given by Eq. (1) is independent of the gating, we consider U(x, y) = Us(x, y) for the on-site energy term (4), and implement it in the tight-binding Hamiltonian (3) with s = 6 (such that a = sa0 ≈ 0.85 nm ≪ λ = 35 nm) to perform quantum transport simulations over a two-terminal structure with L = 420 nm and W = 385 nm; see the upper right inset of Fig. 4a.
Transport simulation
To compare with the resistance measurements reported by Forsythe et al.16, we plot the inverse transmission 1/T as a function of ntg and Vbg in the main panel of Fig. 4a, where most areas show high transmission (white regions correspond to low 1/T). Along the diagonal dark thick line showing high 1/T values due to the main Dirac point, multiple satellite peaks can be seen when increasing |Vbg| and hence the magnitude of the square superlattice potential, signifying the emerging multiple extra Dirac points due to the gate-controlled square superlattice potential. Exemplary line cuts are plotted in Fig. 4b–d to show clearly the single- and multiple-peak structures, in excellent agreement with the experiment (see Figure 2b of Forsythe et al.16). Note that the peak positions of the secondary Dirac points at the electron and hole side seen in Fig. 4b, d are not symmetric due to the asymmetric superlattice potential shape obtained from the electrostatic simulation. When implementing a model periodic function symmetric in its potential profile, the density spacing from the main Dirac point to the secondary Dirac points at electron and hole sides becomes identical (not shown).
Gate-dependent mini-band structures
We have also checked the consistency between the calculated mini-band structures and the simulated inverse transmission. Overall, we obtain band structures similar to those reported in the work by Forsythe et al.16, but since each (ntg, Vbg) point corresponds to a different Us(x, y) profile and hence a different mini-band structure, an overview consistency-check like in Fig. 2f–h is technically not possible. Instead, the consistency can be checked by comparing the 1/T peaks and their corresponding mini-band structure around E = 0. We have chosen three particular (ntg, Vbg) configurations corresponding to the three black arrows in Fig. 4b marking three of the 1/T peaks, at which the E = 0 Fermi level is expected to hit either the main or the extra Dirac points.
These mini-band structures, along with the actual Us(x, y) profiles implemented individually in the continuum model (see Methods) are shown in Fig. 4e–g. Going from low to high ntg (left, middle, and right black arrow in Fig. 4b), the highest filled energy rises relative to the main Dirac point, corresponding to the sinking of the whole band structure due to our choice of fixing the Fermi level at E = 0 (Fig. 4e–g). As expected, the highest peak in Fig. 4b marked by the middle black arrow corresponds to Fig. 4f, where the main Dirac point is nearly hit; see the lower sub-panel therein and the relevant caption. From the E = 0 Fermi contours of Fig. 4e, g, the two satellite 1/T peaks seen in Fig. 4b are mainly contributed by the secondary Dirac points at X, labeling the midpoints on the edges of the square mini-Brillouin zone. Note that the mini-band structures shown in Fig. 4e–g, though corresponding to an increasing uniform ntg, do not exhibit simply an energy shift without changing the band shape. Compare, for example, the shapes of the lowest shown sub-bands (purple).
Discussion
We have shown that quantum transport simulations based on the scalable tight-binding model29 correctly capture transport properties of electrostatic graphene superlattices. In the case of graphene/hBN moiré superlattice, the consistency of our simulation and experiment at zero and low magnetic field is rather satisfactory but breaks down at too strong magnetic field due to the adopted simple moiré model potential3 that neglects higher order terms. In the other case of gated superlattices, without such higher order terms the simulations are expected to be precise for all magnetic field range. Compared to the recent transport experiment on a gate-controlled square superlattice device reported by Forsythe et al.16, our simulations show an excellent agreement in revealing the emergence of multiple extra Dirac cones at zero magnetic field. Transport simulations at finite magnetic field for the gated superlattices are expected to reveal also consistent behaviors compared to the experiment, but are left as future work.
Our finding significantly lowers the computation burdens and hence paves the way to tuning-parameter-free quantum transport simulations for graphene superlattices, providing reliable guides for understanding and predicting novel electric properties of complex graphene superlattice devices. We note some recent studies working on developing numerical techniques that allow large-scale efficient transport simulations42,43,44, but properly scaling the graphene lattice seems to be of least technical complexity and is readily applicable to anyone who is familiar with quantum transport using, for example, real-space Green’s function methods28 or the open-source python package KWANT45.
Methods
Real-space Green’s function method
The model Hamiltonian including the superlattice potential Us(x, y) using the scaled graphene lattice can be written as
where the operator cj (\(c_j^\dagger\)) annihilates (creates) an electron at site rj = (xj, yj). The first term in Eq. (3) represents the clean part of the Hamiltonian which contains nearest neighbor hoppings summing over site indices i and j with 〈i, j〉 standing for |ri − rj| = a, and the second term is the on-site energy
containing the superlattice potential Us(x, y) smoothed by a model function Fs(x, y) = fs(x, −L/2 + d)fs(−x, L/2 − d)fs(y, −W/2 + d)fs(−y, W/2 − d) with \(f_{\mathrm{s}}(z,z_0) = \{ 1 + {\mathrm{tanh}}[(z - z_0){\mathrm{/}}\ell _{\mathrm{s}}]\} {\mathrm{/}}2\), where \(\ell _{\mathrm{s}}\) is a smoothing parameter typically taken as \(\ell _{\mathrm{s}} = \lambda {\mathrm{/}}4\). The purpose of smearing off the superlattice potential function Us to zero at a distance d (typically taken as λ) away from the edges and the leads (see Fig. 1a and its inset) is to avoid any spurious effects due to the combination of the superlattice potential and the physical edges of the graphene lattice, as well as to avoid oversized unit cells for the lead self-energies. Any contributions to the on-site energy term other than the superlattice potential are collected in the U0 term in Eq. (4).
With the model Hamiltonian Eq. (3) constructed, together with self-energies Σ1 and Σ2 describing the attached two leads (following, for example, Wimmer46), the retarded Green’s function at energy E is given by
leading to the transmission function
where \({\mathrm{\Gamma }}_j = i({\mathrm{\Sigma }}_j - {\mathrm{\Sigma }}_j^\dagger )\) with j = 1, 2 is the broadening function. In the low-temperature low-bias limit, the conductance across the modeled scattering region is given by the Landauer formula G = (2e2/h)T, where the factor of 2 accounts for the spin degeneracy. For a pedagogical introduction to the above outlined real-space Green’s function, see, for example, Datta28. Note that in most simulations, the full matrix of Eq. (5) is not needed, suggesting that a partial inversion should be implemented in the numerics to avoid wasting computer memories and CPU time. On the other hand, the matrix version of the Fisher–Lee relation (6) can be implemented as the way it reads.
Device fabrication
Our two-terminal device contains a hBN/graphene/hBN stack on a Si/SiO2 substrate, where the crystallographic axis of the graphene flake is aligned with respect to one of the hBN flakes. Electric contact to the graphene is made from the edge of the mesa47 with self-aligned Ti/Al electrodes. We use the Si wafer as an overall back gate with a two-layer dielectric consisting of SiO2 with thickness \(d_{{\mathrm{SiO}}_{\mathrm{2}}}\) = 300 nm and the bottom hBN flake with thickness dhBN = 20 nm. A typical exemplary junction similar to the measured device is shown by the atomic-force microscope (AFM) image in the inset of Fig. 2d and marked by the white dashed box.
Continuum model for mini-bands and density of states
To calculate the mini-band structure of graphene in the presence of a superlattice potential Us(r), we consider an infinitely large two-dimensional pristine graphene described by \({\cal{H}}_0\) in k-space. Following Park et al.17, we start with the continuum model Hamiltonian near the K valley:
where the first term is \({\cal{H}}_0\) and superlattice potential in the second term is treated as a perturbation. In Eq. (7), the product of the reduced Planck constant ħ and Fermi velocity vF is related to the tight-binding parameters through ħvF = (3/2)ta, and the two-dimensional wave vector (kx, ky) = k is small relative to the K point. Using the eigenstates of \({\cal{H}}_0({\mathbf{k}})\) as a new basis, we solve the eigenvalue problem of Eq. (7) to obtain a set of linear equations:
where E is the energy eigenvalue of the graphene superlattice, εs(k) = sħvFk is the eigenenergy of \({\cal{H}}_0({\mathbf{k}})\) associated with the s branch (s = 1 for electron above the Dirac point and s = −1 for hole below the Dirac point), \({\cal{U}}({\mathbf{G}})\) is the Fourier component of Us(r) with the reciprocal lattice vector G = m1G1 + m2G2 of the superlattice potential, θk,k−G is the angle from k − G to k, and cs(k) are the expansion coefficients of the pristine graphene eigenstates.
The infinite-dimensional matrix spanned by the states with wave vectors \(\mathop {\sum}\nolimits_{m_1,m_2} {\mathbf{k}} + m_1{\mathbf{G}}_1 + m_2{\mathbf{G}}_2\) in Eq. (8) allows for solving for E and hence calculating the band structure. Since we focus on the low-energy region, a matrix involving states with |m1| ≤ 3 and |m2| ≤ 3 is found to be sufficient to attain the convergence of the band structure. With the eigenenergies obtained, the density of states D as a function of energy can be calculated by
where the integration is taken over the first Brillouin zone.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nano 5, 722–726 (2010).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Yankowitz, M. et al. Emergence of superlattice Dirac points in graphene on hexagonal boron nitride. Nat. Phys. 8, 382–386 (2012).
Ponomarenko, L. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Dean, C. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moire superlattices. Nature 497, 598–602 (2013).
Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).
Gorbachev, R. V. et al. Detecting topological currents in graphene superlattices. Science 346, 448–451 (2014).
Wang, L. et al. Evidence for a fractional fractal quantum Hall effect in graphene superlattices. Science 350, 1231–1234 (2015).
Wang, P. et al. Topological winding number change and broken inversion symmetry in a Hofstadter’s butterfly. Nano Lett. 15, 6395–6399 (2015).
Lee, M. et al. Ballistic miniband conduction in a graphene superlattice. Science 353, 1526–1529 (2016).
Handschin, C. et al. Fabry–Pérot resonances in a graphene/hBN moiré superlattice. Nano Lett. 17, 328–333 (2017).
Krishna Kumar, R. et al. High-temperature quantum oscillations caused by recurring Bloch states in graphene superlattices. Science 357, 181–184 (2017).
Chen, G. et al. Emergence of tertiary Dirac points in graphene moiré superlattices. Nano Lett. 17, 3576–3581 (2017).
Yankowitz, M. et al. Dynamic band-structure tuning of graphene moiré superlattices with pressure. Nature 557, 404–408 (2018).
Ribeiro-Palau, R. et al. Twistable electronics with dynamically rotatable heterostructures. Science 361, 690–693 (2018).
Forsythe, C. et al. Band structure engineering of 2d materials using patterned dielectric superlattices. Nat. Nanotechnol. 13, 566 (2018).
Park, C.-H., Yang, L., Son, Y.-W., Cohen, M. L. & Louie, S. G. New generation of massless Dirac fermions in graphene under external periodic potentials. Phys. Rev. Lett. 101, 126804 (2008).
Brey, L. & Fertig, H. A. Emerging zero modes for graphene in a periodic potential. Phys. Rev. Lett. 103, 046809 (2009).
Wu, S., Killi, M. & Paramekanti, A. Graphene under spatially varying external potentials: Landau levels, magnetotransport, and topological modes. Phys. Rev. B 85, 195404 (2012).
Ortix, C., Yang, L. & van den Brink, J. Graphene on incommensurate substrates: trigonal warping and emerging dirac cone replicas with halved group velocity. Phys. Rev. B 86, 081405 (2012).
Kindermann, M., Uchoa, B. & Miller, D. L. Zero-energy modes and gate-tunable gap in graphene on hexagonal boron nitride. Phys. Rev. B 86, 115415 (2012).
Wallbank, J. R., Patel, A. A., Mucha-Kruczyński, M., Geim, A. K. & Fal’ko, V. I. Generic miniband structure of graphene on a hexagonal substrate. Phys. Rev. B 87, 245408 (2013).
Moon, P. & Koshino, M. Electronic properties of graphene/hexagonal-boron-nitride moiré superlattice. Phys. Rev. B 90, 155406 (2014).
Barbier, M., Vasilopoulos, P. & Peeters, F. M. Extra Dirac points in the energy spectrum for superlattices on single-layer graphene. Phys. Rev. B 81, 075438 (2010).
Burset, P., Yeyati, A. L., Brey, L. & Fertig, H. A. Transport in superlattices on single-layer graphene. Phys. Rev. B 83, 195434 (2011).
Diez, M., Dahlhaus, J. P., Wimmer, M. & Beenakker, C. W. J. Emergence of massless Dirac fermions in graphene’s Hofstadter butterfly at switches of the quantum hall phase connectivity. Phys. Rev. Lett. 112, 196602 (2014).
Hu, J. et al. Quantum transport in graphene p-n junctions with moiré superlattice modulation. Phys. Rev. B 98, 045412 (2018).
Datta, S. Electronic Transport in Mesoscopic Systems. (Cambridge University Press, Cambridge, 1995).
Liu, M.-H. et al. Scalable tight-binding model for graphene. Phys. Rev. Lett. 114, 036601 (2015).
Rickhaus, P. et al. Snake trajectories in ultraclean graphene p-n junctions. Nat. Commun. 6, 6470 (2015).
Mreńca-Kolasińska, A. & Szafran, B. Lorentz force effects for graphene Aharonov–Bohm interferometers. Phys. Rev. B 94, 195315 (2016).
Kolasiński, K., Mreńca-Kolasińska, A. & Szafran, B. Imaging snake orbits at graphene n-p junctions. Phys. Rev. B 95, 045304 (2017).
Petrović, M. D., Milovanović, S. P. & Peeters, F. M. Scanning gate microscopy of magnetic focusing in graphene devices: quantum versus classical simulation. Nanotechnology 28, 185202 (2017).
Ma, Q., Parmentier, F. D., Roulleau, P. & Fleury, G. Graphene n-p junctions in the quantum hall regime: numerical study of incoherent scattering effects. Phys. Rev. B 97, 205445 (2018).
Wang, L. et al. New generation of moiré superlattices in doubly aligned hBN/graphene/hBN heterostructures. Nano Lett. 19, 2371–2376 (2019).
Peierls, R. Zur Theorie des Diamagnetismus von Leitungselektronen. Z. Phys. A Hadrons Nucl. 80, 763–791 (1933).
Dubey, S. et al. Tunable superlattice in graphene to control the number of Dirac points. Nano Lett. 13, 3990–3995 (2013).
Drienovsky, M. et al. Towards superlattices: lateral bipolar multibarriers in graphene. Phys. Rev. B 89, 115421 (2014).
Drienovsky, M. et al. Few-layer graphene patterned bottom gates for van der Waals heterostructures. Preprint at: arXiv:1703.05631 (2017).
Drienovsky, M. et al. Commensurability oscillations in one-dimensional graphene superlattices. Phys. Rev. Lett. 121, 026806 (2018).
Liu, M.-H. & Richter, K. Efficient quantum transport simulation for bulk graphene heterojunctions. Phys. Rev. B 86, 115455 (2012).
Beconcini, M. et al. Scaling approach to tight-binding transport in realistic graphene devices: the case of transverse magnetic focusing. Phys. Rev. B 94, 115441 (2016).
Calogero, G., Papior, N. R., Bøggild, P. & Brandbyge, M. Large-scale tight-binding simulations of quantum transport in ballistic graphene. J. Phys.: Condens. Matter 30, 364001 (2018).
Papior, N., Calogero, G., Leitherer, S. & Brandbyge, M. Removing all periodic boundary conditions: efficient non-equilibrium Green function calculations. Phys. Rev. B 100, 195417 (2019).
Groth, C. W., Wimmer, M., Akhmerov, A. R. & Waintal, X. Kwant: a software package for quantum transport. N. J. Phys. 16, 063065 (2014).
Wimmer, M. Quantum Transport in Nanostructures: From Computational Concepts to Spintronics in Graphene and Magnetic Tunnel Junctions. PhD thesis, Universität Regensburg (2008).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Acknowledgements
The authors thank R. Huber and J. Eroms for valuable and stimulating discussions, R. Rückner for technical support on using the Athene Cluster of Rechenzentrum of Universität Regensburg, where most of the computations were performed, and J. Bundesmann for building and maintaining the Mordor Cluster of NCKU Physics, where part of the transport simulations were performed. Financial supports from Taiwan Ministry of Science and Technology (107-2112-M-006-004-MY3 and 107-2627-E-006-001) and Ministry of Education (Higher Education Sprout Project), Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 10314695032—CRC 1277 (Subproject A07) and Project No. Ri681/13-1, and Helmholtz Society (Program STN) are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
S.-C.C. calculated the mini-band structures and density of states within the continuum model. R.K. performed experiment with the support of R.D. on the graphene/hBN moiré device. M.-H.L. performed transport and electrostatic simulations, and wrote the draft of the manuscript. R.D., K.R., and M.-H.L. guided the project. All authors contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, SC., Kraft, R., Danneau, R. et al. Electrostatic superlattices on scaled graphene lattices. Commun Phys 3, 71 (2020). https://doi.org/10.1038/s42005-020-0335-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0335-1
This article is cited by
-
Probing miniband structure and Hofstadter butterfly in gated graphene superlattices via magnetotransport
npj 2D Materials and Applications (2023)
-
Biperiodic superlattices and transparent states in graphene
Scientific Reports (2022)
-
Long-range ballistic transport of Brown-Zak fermions in graphene superlattices
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.