Abstract
Bacterial swarming is a rapid mass-migration, in which thousands of cells spread collectively to colonize surfaces. Physically, swarming is a natural example for active particles that use energy to generate motion. Accordingly, understanding the constraints physics imposes on these dynamics is essential for understanding the mechanisms underlying swarming. We present new experiments of swarming Bacillus subtilis mutants with different aspect ratios and at different densities; two physical quantities known to be associated with collective behavior. Analyzing the dynamics reveals a rich phase diagram of qualitatively distinct swarming regimes, describing how cell shape and population density govern the dynamical characteristics of the swarm. In particular, we show that under standard conditions, bacteria inhabit a region of phase space that is associated with rapid mixing and robust dynamics, with homogeneous density and no preferred direction of motion. The results suggest that bacteria have adapted their physical properties to optimize the principle functions assumed for swarming.
Similar content being viewed by others
Introduction
Microorganisms such as bacteria, sperm, epithelial, and cancer cells, as well as immune T cells and even inanimate active particles, generate collective flows and demonstrate a wealth of newly discovered emergent dynamical patterns1,2,3,4,5,6,7,8. This report addresses the dynamics of swarming bacteria—a biological state to which some bacterial species transition, in which rod-shaped cells, powered by flagellar rotation, migrate rapidly on surfaces en masse9,10,11,12. Swarming allows efficient expansion and colonization of new territories, even under harsh and adverse conditions such as starvation or antibiotic stress13,14. Revealing the biological and physical mechanisms underlying bacterial swarming is therefore a key to our understanding of how bacteria spread and invade new niches.
The transition to swarming involves several critical intracellular processes such as an increase in flagellar number and changes in cell aspect ratio, suggesting that these changes promote favorable swarming conditions8,9,11,12,15. Quantifying the “quality” of swarming can be done using the tools of statistical physics by analyzing the dynamical properties of large, out-of-equilibrium, self-propelled collectives3,16,17. Accordingly, one of the primary goals of such quantification is to obtain a phase diagram that would describe the possible dynamical states of swarms as a function of independent parameters such as density and cell aspect ratio; density because individual sparsely distributed cells do not swarm, and aspect ratio because this often changes in the cell prior to swarming. Thus a phase diagram provides a map that explains how the microscopic mechanical properties of cells, which are regulated by complex bio-chemical cellular processes, may govern the global dynamical characteristics of the entire swarm.
The surface density, ρ (the fraction of surface covered by bacteria), within bacterial cultures in general, and in the swarm in particular, is typically extremely high (up to 0.8), resulting in a combination of short-range steric repulsion and long-range hydrodynamic interactions. Both forces strongly depend on cell aspect ratio and particle density, see e.g., refs. 2,8,10,18,19,20,21,22,23,24. Recently, Jeckel et al.24 studied expanding colonies of swarming Bacillus subtilis and discovered regions in the colony corresponding to single cells, rafts, biofilm, and mixed states. Despite the recent progress in understanding the physics of active matter in general and swarming bacteria in particular, the different pieces does not yet fit together into a comprehensive picture. In particular, it is not clear how the properties of cells determine the dynamical state of a swarm.
In this paper, monolayer swarms of four strains of B. subtilis with different aspect ratios—ranging from 5.5 to 19, were analyzed as a function of surface density. A custom algorithm enabled tracking of individual cell trajectories, which in turn allowed a comprehensive analysis of both the individual and collective dynamics of bacteria in a swarm. The main results are then expressed in a phase diagram of bacterial swarming. The novel two-dimensional set-up of a thin, single layer of cells, brings out a complex experimentally based phase diagram with various features that could not be obtained with earlier multilayer studies19,20,22,25 or naturally expanding colonies24. Our analysis identified five dynamical states for bacterial swarms. Each state showed distinct dynamical features, as detailed below, which are expressed both at the individual and collective levels.
Results
Experimental set-up
Small drops of overnight bacterial cultures were inoculated at the center of agar plates; each colony grew from a single strain, with no mixing between strains (see “Methods” for details). Within a few hours, cells collectively migrated outwards of the initial inoculum, forming a swarm, with a boundary that expanded toward the plate perimeter. When the colonies reached a diameter of 5 cm (approximately 4 h after inoculation), a wide (>2 cm in thickness) and highly active ring-shaped band was formed. High-resolution microscopy was used to observe the dynamics within a smaller ring, approximately 300 μm in width, close to the colony’s edge; see Fig. 1a and Supplementary Fig. 1. Different regions of this this band showed a range of cell densities. Note that this is different from Jeckel et al.24, who were interested in scanning and characterizing different regions and time periods within the expanding colony. Here we concentrate on the most active part of the swarm for different strains that differ in their aspect ratios. In particular, we study “unnaturally” short and long cells, with aspect ratios that are not manifested in freely growing colonies. This point of view, which is complementary to ref. 24, allows us to probe the swarming regimes as a function of the two independent parameters.
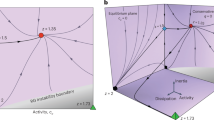
a Snapshots of monolayer bacterial swarms with different aspect ratios and densities, representative of the motile phases. Colors represent moving clusters (gray or non-labeled cells are not moving). The scale bar corresponds to 50 μm. For short cells (S phase), almost all cells are moving coherently. For long cells, spatial ordering into local (SC) or global (LC) clusters is apparent. b The inferred phase diagram as a function of aspect ratio (α) and surface density (ρ), showing five distinct phases: immotile (IM), swarming (S), small clusters (SCs), large clusters (LCs), and jammed (J).
Deriving a phase diagram requires measuring a large number of collective and individual dynamical statistics for swarms with particular parameter values. As described above, we concentrate on cell aspect ratio (α) and surface density (ρ) as the fundamental mechanical parameters (Fig. 1b). Since the typical expansion rate of the colony is about 10 times slower than the typical microscopic swarming speed, different regions of the actively migrating colony can be considered to be in a quasi-steady state. Therefore, the effect of density can be evaluated by sampling regions that occupy a different number of bacteria per unit area, e.g., refs. 20,24. Cell shape was manipulated genetically by mutating a few of the robust mechanisms that maintain aspect ratio during growth. Artificially long cells were generated using cells mutated for either MinD or MinJ that control proper medial division in B. subtilis. Artificially short cells were generated by overexpression of SwrA, the master activator of flagellar biosynthesis15,26. Overall, four different strains of the same species with various average aspect ratios of 5.5, 7 (the wild type (WT)), 13, and 19 (Supplementary Table 1) were compared. Changes in aspect ratio of a specific strain stemming from different regions in a colony are negligible. A wide range of benchmark tests verified that all other motility and expansion-related parameters were the same (including swimming speeds and doubling times in broth, colony expansion rates, and surfactant production). See “Methods,” Supplementary Note 1, and Supplementary Figs. 2 and 3.
Quantifying swarming regimes
Figure 2a depicts the mean cell speed, which is monotonically increasing with density for each aspect ratio, a hallmark of collective motion—showing that many cells cooperate to produce faster motion, e.g., refs. 2,27,28. The mean speed is not monotonic in the aspect ratio where WT cells seem to be optimal in this regard (see also ref. 22). However, speeds depend smoothly on cell density, showing no sharp transitions. In addition, Fig. 2a identifies lower and upper density thresholds, beyond which swarming cannot occur. At very low densities, cells are practically immotile (IM), suggesting a minimal surface or number density below which cells cannot move29. The minimal speed at which swarming was observed marks the edge of the IM phase depicted in Fig. 1b. At very high densities, cells cannot move efficiently due to confinement21,30, suggesting an additional jammed phase J. This phase is not observed in our experiments, as we concentrate on the active regions.
a The denser the cells, the faster they move. The average speed increases with density but is non-monotonic in aspect ratio. Wild-type cells are the fastest. Surface density ρ corresponds to the fraction of the viewing area that is covered by cells. Error bars are the standard deviation and are of the same size as the markers. b The mean squared displacement exponent shows that cell trajectories are super-diffusive. However, the exponent of long cells (small cluster (SC) and large cluster (LC) phases) decreases rapidly with density, showing that their super-diffusive property degrades at high densities. Inset shows the log–log plot of the mean square displacement (MSD) versus time interval from which we have fitted each exponent value. This specific MSD corresponds to the hollow red square. Full lines are the best linear fit, providing the slope value reported in the legend. c–f The distribution of densities among a 10 × 10 partition of the viewing area (15 × 15 μm bins) for different (average) surface densities. c, d At small aspect ratios (S phase), the swarm is characterized by a unimodal spatial distribution, with the mode increasing with mean surface density. e, f At large aspect ratios (SC and LC phases), the swarm is segregated into two populations. The proportion of each population changes with the mean surface density.
At intermediate surface densities, our analysis below revealed three phases of motile bacteria with distinct dynamical characteristics: (i) A swarm phase S at small aspect ratios, in which cells move and flow efficiently, (ii) a low-density phase of long cells, which consists of small moving clusters (SCs), and (iii) a high-density phase of long cells, in which large moving clusters (LCs) of the size of viewing area cause large (but finite) fluctuations in time. While we find trajectories are always super-diffusive (Fig. 2b), we first focus on the differences between short and long cells. Note that, given our relatively small number of possible aspect ratios, we cannot establish a sharp phase transition or its properties (first or second, critical exponents, etc.). Nonetheless, several qualitative differences between short and long cells are apparent: at small aspect ratios (S phase), the swarm is characterized by a unimodal spatial distribution of surface densities (Fig. 2c, d, Supplementary Fig. 4) and the velocities exhibit a Gaussian distribution (kurtosis close to 3, Supplementary Fig. 5). In contrast, at large aspect ratios (SC and LC phases), the swarm is segregated into two populations, corresponding to low- and high-density regions (Fig. 2e, f). The proportion of each population changes with the mean surface density. The distribution of velocities exhibits very large kurtosis (indicating a heavy-tailed distribution) at the large aspect ratios (Supplementary Fig. 5). Another key statistic, which has been theoretically shown to describe different regimes of collective dynamics, is the distribution of cluster sizes (DCS)18: In the S phase (Fig. 3a, b), the DCS is close to a power law with an exponential cut-off. In contrast, in the SC/LC phases, the DCS at low densities (a power law with a cut-off) is different than at higher ones, where LCs emerge whose sizes are comparable with the observed system size (Fig. 3c, d). Lastly, it has been shown that WT swarming bacteria are super-diffusive, with trajectories that are consistent with Lévy walks31,32. Figure 2b shows that trajectories are super-diffusive at all aspect ratios and surface densities. However, the associated characteristic exponent is varying. While the exponent in the S phase is approximately constant (1.6–1.7), it is clearly decreasing in the SC/LC phases. Therefore, the super-diffusive property of long cells degrades at high surface densities, indicating slower mixing and spreading.
a, b For short cells (S phase), the distribution of cluster sizes is approximately a power law with an exponential cutoff. c, d For long cells (small cluster (SC) and large cluster (LC) phases), the distribution is more complex: at low densities, it is a power law. However, at higher densities, e.g., ρ = 0.6, large clusters emerge whose sizes are comparable with the system size. Error bars are the standard deviation and are of the same size as the markers.
At large aspect ratios, the phase diagram is divided into two distinct regions (Fig. 1b). The transition (as a function of density) is pronounced in the spatial correlation functions (Fig. 4a–d), both in cell directional alignment λ|| and in the velocity (direction of motion) λν. At low surface densities, the correlation lengths grow sharply with density, exhibiting small fluctuations (<5%). However, at densities >0.3, the correlation lengths are practically constant, with large fluctuations between samples (up to 55%). The transition region is narrow, suggesting a critical phenomenon. Further examination reveals that the jump in the standard deviation of measurements is mostly due to density fluctuations in time (Fig. 4e). A time series analysis reveals a sharp increase in the Hurst exponent, which quantifies the roughness of temporal fluctuations, indicating that the density varies sharply in time (Fig. 4f, Supplementary Fig. 6). For small aspect ratios, the Hurst exponent is around 0.5 at all densities, as expected for finitely correlated series. See Supplementary Note 2 and Supplementary Fig. 6 for details of the effect of the field of view size.
a Average correlation length of cells′ directions and b cells′ velocities. Standard deviations of the correlation length for c directions and d velocities show a sharp increase within a narrow region of surface densities corresponding with the SC/LC transition. e The standard deviation of temporal fluctuations in surface density suggests large number of fluctuations in time. f The Hurst exponent, which indicates the roughness of a time series, shows a sharp jump in the SC/LC transition region. The gray rectangle represents the transition region. Error bars are the standard deviation and are of the same size as the markers.
Interpretation as a self-propelled particle system
From an active matter perspective, our results reveal some successful theoretical predictions upon comparison to earlier work on simulations17,18,21,23,24,33,34 and experiments with artificial inanimate systems35,36. However, the swarming phase diagram also has several unique characteristics that are not observed in other active systems. For example, several phases that have been observed in simulations, such as the bio-nematic and laning phases21,34, were not realized. Other predictions, such as the emergence of bimodal cluster-size distributions (Fig. 3)18, motility-induced spatial segregation into low- and high-density regions37, large number fluctuations (Supplementary Fig. 7)3, long-tailed auto-correlations functions (Supplementary Figs. 8 and 9)3, and meso-scale turbulence21, have been inferred from agent-based and continuous models and are found, to some extent, in the present experiments. See Supplementary Note 3 for further discussions.
Collective motion of bacteria changes, quite dramatically, if the aspect ratio is increased above a threshold value (around 10 for B. subtilis in our study here). Strikingly, above densities of around 0.25, cells transition into another phase and form LCs that can become of the order of the observation window employed here (see Supplementary Fig. 6c for a variety of window sizes). This transition is reminiscent of behavior of self-propelled rods with short-range alignment interactions (typically due to volume exclusion) in simulations and experiments; see ref. 17 and references therein. The observed cluster-size distributions are in line with a kinetic theory describing occurrence of LCs as a specific type of microphase separation characteristic for rod-shaped moving particles like bacteria18,38. DCS is also related to the increase in temporal fluctuations. We hypothesize that large temporal fluctuations correlate with the occurrence of giant number fluctuations, which indicate the occurrence of LCs, similar to previous findings in bacterial systems19,20 and in contrast to experimental reports and theoretical predictions, e.g., for active nematic phases that are assumed to be homogeneous on the large scale3,35.
We conclude that, in the SC and LC phases, collective behavior is dominated by short-range alignment or excluded volume interactions. This is in line with findings for filamentous, very large aspect ratio mutants of Escherichia coli that display behavior dominated by short-range alignment interaction39. At small aspect ratios, the collective behavior deviates from the self-propelled rod paradigm. We rationalize that this is due to long-range hydrodynamic interactions, which suppress the clustering and density inhomogeneities. This is in accordance with recent simulation findings, e.g., with circular microswimmers40 showing that hydrodynamic interactions indicate a complex dependency of clustering behavior on the shape and the swimming mechanism of the microswimmers41. Thus our observation should stimulate more detailed model studies.
Independently of the aspect ratio, at low cell densities (<0.1) cells do not move at all—hence we have an IM phase. At high densities (>0.7) a jamming phase (J) is observed, where cells stop moving, possibly due to lack of space. While jamming of high-density active systems has been predicted theoretically21,30,34, the IM phase does not occur in typical active matter systems. This includes swimming (not swarming) bacteria in bulk or thin films2,42, in driven inanimate particles35,36, or most models of self-propelled particles, either discrete or continuous, e.g., refs. 21,30,34, in which isolated particles typically move. During swarming, on the other hand, the reason for the absence of motion of isolated individuals (or cells at very low densities) is unclear. It has been suggested that the cells are trapped in areas that are temporarily too dry8. In such regions, the surface may exert a large drag force that the thrust of the flagella cannot overcome.
Another possibility is that quorum sensing (or some sort of quorum signaling) may play a role in the onset of swarming. Indeed, it is known that the quorum sensing in B. subtilis controls surfactin production, which is required for swarming (quorum sensing controls many other things including genetic competence but these do not appear to be essential for swarming)43,44,45. Therefore, introducing quorum signaling to current bacterial swarming models may be crucial for successfully modeling the transition between the IM and the motile phases. However, in the swarming regimes that are considered in this work, corresponding to extremely high bacterial densities in the interior of the colony, surfactin at the colony edge is abundant46, and we do not expect that quorum sensing plays a major role in the dynamics of the cells in the outer band. In particular, the absence of motion of sparsely distributed cells does not seem to be the result of quorum signaling effects, which does not fluctuate on the micrometer scale; individual cells that are placed on the agar with the system already above the threshold for surfactant secretion are still immobile. Indeed, the increase in the average speed as a function of cell density can be explained in terms of collective-motion models that do not take quorum sensing into account30,47.
Overall, many of the prominent features of the swarm dynamics, including the non-trivial Hurst exponent (marking the SC–LC transition) and the lack of phase changes at small aspect ratios cannot be explained by current theories. Therefore, the phase diagram, Fig. 1b, and the subsequent detailed statistical analysis of key dynamic quantities provide a rich data set against which future models for swarming and swimming bacteria with competing alignment and hydrodynamic interactions can be calibrated or tested.
Discussion
From a biological perspective, the physical properties described above may alter, constrain, or even control cells’ ability to move collectively in an efficient manner, mix within the colony, and spread. As a result, it has direct biological consequences in terms of the ability of bacteria to swarm efficiently. With a typical aspect ratio of 7 and a wide range of densities (0.2–0.7), WT bacteria show rapid movement and highly efficient spreading. Within the S region, the swarming statistics were not sensitive to the density as well as to small changes in the aspect ratio, suggesting that the collective behavior of WT swarming cells is particularly robust to fluctuations in density and cell shape. Thus the physical robustness of the swarming phase (S) may be advantageous for maintaining efficient swarming, particularly under stress.
B. subtilis is a representative of a group of bacteria called “temperate swarmers” such as Serratia marcescens, Pseudomonas, Salmonella, and E. coli that swarm at similar conditions48. Thus we expect their phase diagram to be qualitatively similar. Other bacteria, termed “robust swarmers,” such as Proteus mirabilis and Vibrio parahaemolyticus, are capable of migrating atop harder surfaces12. These cells are typically longer (~20 µm) and may show a truncated diagram eliminating the S phase49. In addition, such cells have a “life cycle” of repeated elongation, migration, division, and sessility, which implies different biological functions. Moreover, the difference between phase states may be a critical determinant that differentiates temperate from robust swarmers and thus the kinds of surface hardness a bacterium can traverse.
Bacterial swarming is a natural state, i.e., cells appear to enter a swarming state when introduced to a surface. This suggests that the changes in cells prior to the onset of swarming may be advantageous to the colony’s survival. The phase diagram discussed above describes the range of possible dynamical regimes for the swarm, highlighting the subtle interplay between the physical and biological characteristics of the swarm. We find that under standard conditions bacteria inhabit a region of phase space in which the swarm dynamics is highly robust and insensitive to fluctuations. In this regime, bacteria do not cluster and do not form an orientational order that would bias the bacterial flow toward a particular direction. Global alignment would reduce the assumed biological function for swarming, which is rapid isotropic expansion (given no external directional cues). In addition, the super-diffusive property of trajectories does not deteriorate at high surface densities. These conditions are pivotal for rapid spreading and mixing of bacteria within the swarm, which may be crucial for efficient growth and colony expansion.
Methods
Growth protocol and observation
B. subtilis is a Gram-positive, rod-shaped, flagellated bacterial species used as a model system in many quantitative swarming experiments29. Four different variants of B. subtilis 3610 were tested, all with the same width (~0.8 µm) but varying lengths. The cells were grown on agar plates; monolayer swarming colonies were obtained by growing the colonies on 25 g/l Luria Bertani (LB) and 0.5% agar (Difco). Plates were filled with 20 ml of molten agar and aged for 24 h in the laboratory (20 °C and 45% relative humidity) prior to inoculation. The cells were incubated at 30 °C and 95% relative humidity for about 5 h. B. subtilis is normally kept at −80 °C in 50% glycerol stocks and grown overnight in LB broth at 30 °C and shaking (200 RPM) prior to plate inoculation (5 µl at the center of each plate; OD650 = 1, corresponding to approximately 107 cells/ml).
All mutants were obtained from the same laboratory (Daniel B. Kearns, Indiana)22. Supplementary Table 1 lists the strain name and the mean aspect ratio with the standard deviation (the table includes strain DS860 too, with which we performed few control tests only). The mean was obtained from 500 randomly chosen cells in the active part of swarm, close to its edge. In most cases, the large variety of cell lengths in a specific sample is due to proliferation and cell division, thus the mean cell length does not have a Gaussian distribution (the size is bounded in the range 1–2 times the length of a single cell).
An optical microscope (Zeiss Axio Imager Z2; ×5, ×10, ×20, ×40, and ×63 LD-Phase contrast lenses) equipped with a camera (GX 1050, Allied Vision Technologies) was used to capture the microscopic motion at 100 frames/s and 1024 × 1024 pixels. For each aspect ratio, at least 30 independent plates were created.
Data analysis
In each experimental plate, individual cells were identified using a custom tracking software implemented in Matlab. The number density at each frame was estimated by counting the number of cells. Surface density was estimated by measuring the area of a threshold filter applied to either the pixel intensity or the local entropy of the image.
Snapshots were binned according to densities with a width of 0.02 surface density. In some of the figures, results with very sparse or very dense bins (e.g., 0.10 or 0.80) are not shown due to insufficient data.
The tracking algorithm receives as input a video of bacteria given as a sequence of frame images. It outputs the trajectories of all cells in the video. The algorithm is separated into two conceptual parts: image analysis and motion reconstruction. In the image analysis step, following standard filtering and sharpening preprocessing, the location and orientation of every bacterium in each frame is obtained by thresholding an intensity histogram and segmenting cells compared to the background. Cells that overlap or are too close to be distinguished are separated using two custom algorithms. The first estimates the orientation of a bacteria using axis matching. The second applies a skeleton cutting algorithm as suggested in ref. 50. Finally, the motion reconstruction algorithm matches cells in consecutive frames using a nearest-neighbor greedy algorithm to approximate continuous trajectories.
Measured statistics
The dynamical properties of single cells and the swarm were quantified using several measurements and observables, which were calculated from the binned trajectory data.
Speed: Following standard smoothing using Matlab’s malowess command, speed was obtained by calculating the displacement between adjacent frames.
Mean squared displacement (MSD) exponent of trajectories. Denoting the trajectory of cell i by \({\mathbf{r}}_i(t) \in {\Bbb R}^2\), the MSD is defined as
where \(\left\| \cdot \right\|\) is the Euclidean norm and \(\left\langle \cdot \right\rangle _{s,i}\) denotes averaging over all times S and particles i. Assuming that for sufficiently large t, \({\mathrm{MSD}}(t)\sim At^\gamma\), the exponent γ is obtained using linear regression on a log–log scale.
The spatial distribution of densities at a given average density ρ was computed as follows. We collect all frames with a given aspect ratio and with overall density in the range \([\rho - 0.01,\rho + 0.01]\). Each frame is divided into 10 × 10 subsections. We compute the standard deviation, the kurtosis (centered, scaled fourth moment), and the histogram of densities within all subsections.
Clustering: Two bacteria appearing in the same frame are considered neighbors if their distance between their centers is less than the mean bacterium length (which depends on the aspect ratio) and their relative speed is <20% the average speed in the corresponding density. Clusters are defined as connected components of the graph obtained using the above definition.
Spatial correlation functions: For a given distance r, define the set Af (r) as the pairs of all cells in a frame f whose centers are separated by a distance (r − ε, r + ε), Af (r) = {(i, j)| ║ri − rj║ ∈ (r − ε, r + ε)} for some 0 < ε ≪ r. The spatial velocity correlation is then given by
where \({\mathbf{v}}_{i}^{\;f}\) is the velocity of the ith cell in frame f, \(|A_f(r)|\) is the number of elements in \(A_f(r)\), \(\left\langle \cdot \right\rangle _f\) denotes averaging over all frames f frames with a given aspect ratio and with overall density in the range \([\rho - 0.01,\rho + 0.01]\), and Z is a normalization constant such that Cv(0) = 1. Similarly, the angle correlation (cell orientation) is given by
where \(\theta_{i}^{\;f}\) is the orientation of the ith cell in frame f. Figure 4 shows both the correlation lengths obtained by averaging over all experiments in the density range (Fig. 4a, b) or the standard deviation, normalized by the average (Fig. 4c, d).
Temporal auto-correlation functions: Auto-correlation functions are defined as \(C(t) = Z^{ - 1}\left\langle {{\mathbf{r}}(s + t) \cdot {\mathbf{r}}(s)} \right\rangle _{s,f}\), where Z is a normalization constant such that C(0) = 1 and \(\left\langle \cdot \right\rangle _{s,f}\) denotes averaging with respect to all trajectories in frames at a given density range and times s along a trajectory. We study three auto-correlation functions in different vector fields r(t): the instantaneous velocity, normalized instantaneous velocity (direction of movement), and cell orientation.
Hurst exponent H: Given a time series, the Hurst exponent quantifies the roughness of fluctuations in the series. For a time series \(X_1,\,X_2, \ldots\), we define \(h(n) = E\left[ {R(n)/S(n)} \right]\), where \(R(n) = \max \left\{ {Z_1, \ldots ,Z_n} \right\} - \min \left\{ {Z_1, \ldots ,Z_n} \right\}\) is the range of the cumulative (centered) first n observations, \(Z(n) = \mathop {\sum}\nolimits_{i = 1}^n {(X_i - E[X_i])}\), and S(n) is the standard deviation obtained in the first n observations. Assuming that asymptotically, for large n, \(h(n)\sim Bn^H\) defines the Hurst exponent H. When data are sparse, the Hurst exponent can be approximated using the following method, which was used here: Let \(w(n) = \left\langle {{\mathrm{std}}\left\{ {X_k, \ldots ,X_{k + n - 1}} \right\}} \right\rangle _k\), i.e., the average standard deviation of n sequential observations. Then, for large n, \(w(n)\sim Bn^H\). Figure 4f was generated using the density obtained in ×40 magnification; see additional magnifications for this data in Supplementary Fig. 6c.
Large number fluctuations: Cells with particular aspect ratio and density were partitioned into 1–30 bins in each dimension. The variance among all bins was calculated.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
All relevant data are available from the authors.
Code availability
All relevant codes are available from the authors.
References
Szabó, B. et al. Phase transition in the collective migration of tissue cells: Experiment and model. Phys. Rev. E 74, 061908 (2006).
Sokolov, A., Aranson, I. S., Kessler, J. O. & Goldstein, R. E. Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 98, 158102 (2007).
Ramaswamy, S. The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1, 323 (2010).
Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143 (2013).
Zhou, S., Sokolov, A., Lavrentovich, O. D. & Aranson, I. S. Living liquid crystals. Proc. Natl Acad. Sci. USA 111, 1265 (2014).
Elgeti, J., Winkler, R. G. & Gompper, G. Physics of microswimmers - single particle motion and collective behavior: a review. Rep. Prog. Phys. 78, 056601 (2015).
Blanch-Mercader, C. et al. Turbulent dynamics of epithelial cell cultures. Phys. Rev. Lett. 120, 208101 (2018).
Be’er, A. & Ariel, G. A statistical physics view of swarming bacteria. Mov. Ecol. 7, 9 (2019).
Harshey, R. M. Bacterial motility on a surface: many ways to a common goal. Annu. Rev. Microbiol. 57, 249 (2003).
Darnton, N. C., Turner, L., Rojevsky, S. & Berg, H. C. Dynamics of bacterial swarming. Biophys. J. 98, 2082 (2010).
Kearns, D. B. A field guide to bacterial swarming motility. Nat. Rev. Microbiol. 8, 634 (2010).
Tuson, H. H., Copeland, M. F., Carey, S., Sacotte, R. & Weibel, D. B. Flagellum density regulates proteus mirabilis swarmer cell motility in viscous environments. J. Bacteriol. 195, 368 (2013).
Lai, S., Tremblay, J. & Deziel, E. Swarming motility: a multicellular behaviour conferring antimicrobial resistance. Environ. Microbiol 11, 126 (2009).
Benisty, S., Ben-Jacb, E., Ariel, G. & Be’er, A. Antibiotic-induced anomalous statistics of collective bacterial swarming. Phys. Rev. Lett. 114, 018105 (2015).
Mukherjee, S. et al. Adaptor-mediated Lon proteolysis restricts Bacillus subtilis hyperflagellation. Proc. Natl Acad. Sci. USA 112, 250 (2015).
Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71 (2012).
Bär, M., Großmann, R., Heidenreich, S. & Peruani, F. Self-propelled rods: insights and perspectives for active matter. Annu. Rev. Condens. Matter Phys. 11, 441–466 (2020).
Peruani, F., Deutsch, A. & Bär, M. Nonequilibrium clustering of self-propelled rods. Phys. Rev. E 74, 030904 (2006).
Zhang, H. P., Be’er, A., Florin, E.-L. & Swinney, H. L. Collective motion and density fluctuations in bacterial colonies. Proc. Natl Acad. Sci. USA 107, 13626 (2010).
Peruani, F. et al. Collective motion and nonequilibrium cluster formation in colonies of gliding bacteria. Phys. Rev. Lett. 108, 098102 (2012).
Wensink, H. H. et al. Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. USA 109, 14308 (2012).
Ilkanaiv, B., Kearns, D. B., Ariel, G. & Be’er, A. Effect of cell aspect ratio on swarming bacteria. Phys. Rev. Lett. 118, 158002 (2017).
Shi, X.-q. & Chaté, H. Self-propelled rods: linking alignment-dominated and repulsion-dominated active matter. Preprint at https://arxiv.org/abs/1807.00294 (2018).
Jeckel, H. et al. Learning the space-time phase diagram of bacterial swarm expansion. Proc. Natl Acad. Sci. USA 116, 1489 (2019).
Li, H. et al. Data-driven quantitative modeling of bacterial active nematics. Proc. Natl Acad. Sci. USA 116, 777 (2019).
Guttenplan, S. B., Shaw, S. & Kearns, D. B. The cell biology of peritrichous flagella in Bacillus subtilis. Mol. Microbiol. 87, 211 (2013).
Aranson, I. S., Sokolov, A., Kessler, J. O. & Goldstein, R. E. Model for dynamical coherence in thin films of self-propelled microorganisms. Phys. Rev. E 75, 040901R (2007).
Rabani, A., Ariel, G. & Be’er, A. Collective motion of spherical bacteria. PLoS ONE 8, e83760 (2013).
Kearns, D. B. & Losick, R. Swarming motility in undomesticated Bacillus subtilis. Mol. Microbiol. 49, 581 (2003).
Ariel, G. et al. Collective dynamics of two-dimensional swimming bacteria: experiments and models. Phys. Rev. E 98, 032415 (2018).
Ariel, G. et al. Swarming bacteria migrate by Lévy walk. Nat. Commun. 6, 8396 (2015).
Ariel, G., Be’er, A. & Reynolds, A. A chaotic model for Lévy walks in swarming bacteria. Phys. Rev. Lett. 118, 228102 (2017).
Ginelli, F., Peruani, F., Bär, M. & Chaté, H. Large-scale collective properties of self-propelled rods. Phys. Rev. Lett. 104, 184502 (2010).
Abkenar, M., Marx, K., Auth, T. & Gompper, G. Collective behavior of penetrable self-propelled rods in two dimensions. Phys. Rev. E. 88, 062314 (2013).
Narayan, V., Ramaswamy, S. & Menon, N. Long-lived giant number fluctuations in a swarming granular nematic. Science 317, 105 (2007).
Bricard, A., Caussin, J. B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95 (2013).
Mishra, S. & Ramaswamy, S. Active nematics are intrinsically phase separated. Phys. Rev. Lett. 97, 090602 (2006).
Peruani, F. & Bär, M. A kinetic model and scaling properties of non-equilibrium clustering of self-propelled particles. N. J. Phys. 15, 065009 (2013).
Nishiguchi, D., Nagai, K. H., Chaté, H. & Sano, M. Long-range nematic order and anomalous fluctuations in suspensions of swimming filamentous bacteria. Phys. Rev. E 95, 020601(R) (2017).
Zöttl, A. & Stark, H. Hydrodynamics determines collective motion and phase behavior of active colloids in quasi-two-dimensional confinement. Phys. Rev. Lett. 112, 118101 (2014).
Theers, M., Westphal, E., Qi, K., Winkler, R. G. & Gompper, G. Clustering of microswimmers: interplay of shape and hydrodynamics. Soft Matter 14, 8590 (2018).
Sokolov, A. & Aranson, I. S. Physical properties of collective motion in suspensions of bacteria. Phys. Rev. Lett. 109, 248109 (2012).
Turgay, K., Hahn, J., Burghoorn, J. & Dubnau, D. Competence in Bacillus subtilis is controlled by regulated proteolysis of a transcription factor. EMBO J. 17, 6730 (1998).
Nakano, M. M. & Zuber, P. The primary role of comA in establishment of the competent state in Bacillus subtilis is to activate expression of srfA. J. Bacteriol. 173, 7269 (1991).
D’Souza, C., Nakano, M. M. & Zuber, P. Identification of comS, a gene of the srfA operon that regulates the establishment of genetic competence in Bacillus subtilis. Proc. Natl Acad. Sci. USA 91, 9397 (1994). erratum Proc. Natl Acad. Sci. USA 17, 646 (1995).
Be’er, A. & Harshey, R. M. Collective motion of surfactant-producing bacteria imparts superdiffusivity to their upper surface. Biophys. J. 101, 1017 (2011).
Ryan, S. D., Sokolov, A., Berlyand, L. & Aranson, I. S. Correlation properties of collective motion in bacterial suspensions. N. J. Phys. 15, 105021 (2013).
Partridge, J. & Harshey, R. M. Swarming: flexible roaming plans. J. Bacteriol. 195, 909 (2013).
Little, K., Austerman, J., Zheng, J. & Gibbs, K. A. Cell shape and population migration are distinct steps of Proteus mirabilis swarming that are decoupled on high-percentage agar. J. Bacteriol. 201, e00726-18 (2019).
Liu, X., Harvey, C. W., Wang, H., Alber, M. S. & Chen, D. Z. Detecting and tracking motion of myxococcus xanthus bacteria in swarms. In International Conference on Medical Image Computing and Computer-Assisted Intervention (eds Ayache, N., Delingette, H., Golland, P. & Mori, K.) 373–380 (Springer, Berlin, Heidelberg, 2012).
Acknowledgements
Partial support from The Israel Science Foundation’s Grant 373/16 and the Deutsche Forschungsgemeinschaft (The German Research Foundation DFG) Grant No. HE5995/3–1 and Grant No. BA1222/7–1 are thankfully acknowledged.
Author information
Authors and Affiliations
Contributions
A.B. and G.A. designed the experiments; A.B. and B.I. performed the experiments; D.B.K. produced the bacterial strains; R.G. wrote the code; A.B., D.B.K., G.A., M.B., S.H., and R.G. analyzed the data; A.B., D.B.K., G.A., M.B., and S.H. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Be’er, A., Ilkanaiv, B., Gross, R. et al. A phase diagram for bacterial swarming. Commun Phys 3, 66 (2020). https://doi.org/10.1038/s42005-020-0327-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0327-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.