Abstract
Metal-halide semiconductor perovskites have received great attention for the development of stable and efficient light emitting diodes and lasers, since they combine high charge carrier mobility and light emission spectral-purity with low-cost fabrication methods. Nevertheless, the role of excitons, free carries and trap states in perovskite light emission properties is still unclear due to their interdependence. In this paper we selectively manage trapping and light emission mechanisms by a reversible laser-assisted trap-passivation process performed on a CH3NH3PbBr3 perovskite layer, coupled to the inner modes of a high-quality micro-cavity, which only affects the radiative recombination. We show that photoluminescence is dominated by exciton radiative decay process and that trap states passivation increases the exciton gemination rate by reducing coulombic scattering of free electrons due to the ionized impurities. This picture provides a more general description than the model based on trap states-free Saha thermodynamic equilibrium between photo-generated species.
Similar content being viewed by others
Introduction
The understanding and the control of the light spontaneous emission process in semiconductors are essential for the realization of efficient optoelectronic devices, such as light-emitting diodes (LEDs), solid state lasers (SSLs) or semiconductor solar cells (SSCs). Indeed, for these class of devices, the spontaneous emission process represents, respectively, the device-output (LEDs), the trigger for the stimulated emission process (SSLs), and the intrinsic detrimental channel for the photogenerated carriers loss (SSCs).
Recently, metal-halide semiconductor perovskites have received great attention in the aforesaid fields1,2,3,4,5,6,7,8,9,10,11,12,13,14, since they combine the main characteristics of inorganic semiconductors, namely high charge carrier mobility and light emission spectral-purity, with those of conjugated organic semiconductors, such as easy fabrication processes15,16,17 and wide tuning of the energy gap (Eg) in the visible and NIR spectral range.
Despite outstanding power conversion/external-quantum efficiencies as high as 25 and 20%, recently reached in SSCs and LEDs, respectively5,11, the interdependence of excitons (EX), free carriers (FC), and trap states (TS) in the spontaneous emission process of metal-halide perovskites is still an open issue18,19,20,21. This is especially true for those perovskites with energy gap in the visible spectral range, which are more interesting for light-emitting applications (LEDs, SSLs)20. In this respect, the main issue in the radiative recombination mechanisms understanding relies in the missing of an unambiguous identification of the emitting species (FC vs EX).
In the literature, studies based on both continuous-wave and transient photoluminescencet experiments (hereafter CWPL and TRPL, respectively) typically identify three kinds of dominant processes: (i) a monomolecular non-radiative carrier trapping mechanism assisted by thermally activated ionized impurities; (ii) the bimolecular FC radiative recombination process and (iii) the trimolecular non-radiative Auger process. FC usually results the dominant radiative species, EX having a negligible role in the light emission process22,23,24. These statements are supported by Saha equation, which describes, at the thermal equilibrium, the ratio between photo-excited species densities (EX vs FC) as a function of EX binding energy Eb, temperature T and photogenerated-carrier density n025,26. This equation forecasts, at room temperature (RT) and in 3D-perovskite materials with Eb < 100 meV, a relative EX concentration of the order of few percentage units, at the photogenerated population density typical of perovskite LED and SSC24,27. Therefore, the possibility to realize exciton-based optoelectronic devices seems greatly limited by the characteristic low EX binding energy of metal-halide perovskites. However, this standard picture is not conclusive. In fact, a significant presence of TS may affect the FC-EX equilibrium and in turn the validity of Saha equation application to these systems. Additionally, even though EX represent the minority radiative species, their radiative rate coefficient can result higher than the FC bimolecular one (at excitation densities typically reported in the literature, lower than 1017 cm−3)24. Anyway, the monomolecular radiative EX recombination process is hardly distinguishable from monomolecular non-radiative one (TS related) by means of conventional analysis, without a suitable experiment conceived in order to discriminate and/or to control TS. Moreover, a method that distinctively separates the radiative from non-radiative contribution to the spontaneous emission has not been developed to date, thus making the analysis of EX, FC, and TS not clear.
In this work, we present a study on the competition/interaction between FC, EX, and TS in the emission processes of CH3NH3PbBr3 thin films28,29, showing that PL is dominated by the EX monomolecular radiative recombination rather than the FC bimolecular one. Radiative and non-radiative processes are distinguished by a reversible TS laser-assisted passivation performed on the material coupled with a high-quality resonant microcavity30,31,32,33, unveiling that the reduction of FC-Coulomb scattering due to ionic Pb2+ and Br− vacancies enhances electron–hole pairing exciton formation. Our experimental results highlight that the two radiative species (FC and EX) do not form an isolated system at thermodynamic equilibrium, as assumed by Saha equation model, since their kinetics are affected by charge carrier mobility which is limited by ionized impurities, well described by the Conwell–Weisskopf semiconductor theory. It is worth to underline that the tool herein proposed can be spread to the study of all perovskite materials so far developed, allowing for the unambiguous understanding of spontaneous emission process and opening the possibility to realize optoelectronic perovskite devices based on EX emitting species.
Results
Morphological characterization
We have grown thin films of CH3NH3PbBr3 by dual source thermal vapor deposition of the precursors at 10−7 mbar (see Methods section for further details) with an equimolar concentration of CH3NH3Br (methylammonium bromide, hereinafter referred as MABr) and PbBr2. We underline that thermal deposition guarantees a fine control on the relative precursors concentration28,29, and it is compatible with a possible industrial implementation in optoelectronic devices production.
The sample surface has been studied by means of atomic force microscope (AFM) revealing that it consists of randomly distributed large grains with size of the order of 1 μm, as shown in Supplementary Fig. 1a of Supplementary Note 1. This is useful to rule out the possible inter-grains diffusion that can influence the recombination process of FC and EX. Since the perovskite coverage of the substrate is 20 ± 5%, the average thickness of the layer, considering perovskite grains and voids, is around 50 nm (see Supplementary Note 1). The X-ray diffraction (XRD) spectrum of the MAPbBr3 film is reported in Supplementary Fig. 1b of Supplementary Note 1, showing peaks corresponding to the cubic phase of MAPbBr328,34.
Trap passivation role on the optical properties
In order to tune the TS density, we exploited a physical passivation procedure, that has been recently explored30,31,32. It consists in irradiating the sample with UV (405 nm) laser under air exposure. This procedure ensured effective physisorption-based passivation and, most of all, allowed to control TS density due to the reversibility of its effects.
In Fig. 1a the absorbance of the as-deposited sample is reported. A strong EX peak, emerging from the continuum, is well evident at E = 2.35 eV (528 nm). The fitting procedure by means of the Elliott model35 (red-line through the experimental data) returns an EX binding energy of about (53.0 ± 0.2) meV, in agreement with the values reported in literature20 (details are reported in Supplementary Note 2).
a Absorption spectrum with Elliott theory fitting. b Photoluminescence (PL) spectrum with line-shape analysis. The red lines through the experimental data (blue symbols, indicating the obtained continuous-wave PL, named PL-CW in the legend) represent the best fit curves as returned by the model reported in Supplementary Note 2. The single PL components are also highlighted for free/localized excitons (EX/EXLOC in the legend, indicated by the light-orange-shadowed areas) and for free carriers (FC in the legend, indicated by the dark-orange-shadowed area). The contribution of the single components to the total PL area results to be 66% (25%) for free (localized) excitons, and less than 9% for free carriers.
The CWPL experiments have been performed on the sample after passivation, under 405 nm CW laser fluence of 30 mW mm−2, corresponding to a photogenerated carrier density of 1017 cm−3. The representative CWPL spectrum is reported in Fig. 1b. The emission peak is located at about 2.31 eV (537 nm), showing a Stokes shift of about 40 meV and a FWHM of 82 meV (about 20 nm). In order to identify the emitting species (EX and/or FC) in the spontaneous emission, we performed a line-shape analysis of the CWPL spectrum. In this analysis we take advantage of the different excitons (PLX) and free carriers (PLFC) emission features, originating from their different density of states (DOS), Gaussian-like and 3D Elliott continuum, respectively (details are reported of Supplementary Note 2). As reported in Fig. 1b, two DOS components for EX (orange-shadowed areas) and one for FC (dark-orange-shadowed area)22,36,37,38,39 have been used to fit the spectrum. We remark that, for the continuum 3D-Elliott DOS, we fixed the same parameters used for the absorption analysis by Elliott model (Fig. 1a), while at least two Gaussian distributions have been required to fit the exciton resonances, attributed to free and localized excitons40,41. A localization energy of about 15 meV emerges from the comparison of localized (EXLOC) and free (EX) exciton. The main result arising from the analysis, as reported in Fig. 1b, consists in the evidence of the dominance of EX contributions (Free-EX and Localised-EX) in PL spectrum, leading to a total PLX component that is about 36 times larger than the PLFC one (at 535 nm).
The passivation effects on the emission properties have been investigated in detail, comparing PL emission at RT in vacuum and in wet-air environmental conditions. In particular, we have evaluated the change induced in the PL intensity by the laser-assisted air exposure as a function of the exposure time, in the range of few tens of minutes, until PL intensity saturation value has been reached. The pressure has been varied from 10−3 mbar (vacuum) to the atmospheric value (wet air) and vice versa, over repeated cycles. Figure 2a shows the variation of the integrated PL signal in the spectral region around the PLmax. The signal increases exponentially when wet-air (50% of humidity) fills the chamber, increasing by more than two orders of magnitude in 900 s, at the moment the highest switch-on/off ratio never reported, at the best of our knowledge, then reaching a saturation value. The signal rapidly decreases when the chamber is evacuated, reducing by 98% in the first 10 s. As reported in Fig. 2a, the increases and decreases of integrated PL in presence/absence of wet-air atmosphere result reversible over repeated cycles of experiments, indicating that air molecules are just physically adsorbed without forming strong chemical bonds with the material. The reversibility of this process allowed us to monitor over time the trapping mechanism, thus making easier the understanding of the role of EX, FC, and TS in the radiative emission process. It deserves to be stressed that in our experiments the density of active traps (NT) is not constant over time. In fact, we have modulated NT value by means of the CW laser-assisted wet-air adsorption procedure, as above reported. As a consequence, the intensity of the excitation laser has been kept fixed in the experiments.
In Fig. 2b, the normalized TRPL traces recorded on the sample at different laser-assisted wet-air exposure times, are shown. We point out that TRPL experiments have been performed by exciting the sample with a pulsed laser delivering 63 mW at 402 nm, corresponding to a photogenerated carrier density of 6 × 1015 cm−3. It is worth to note that the integrated PL spectrum under pulsed excitation regime (dotted line in Fig. 1b) presents the same line shape of the CWPL.
Optical cavity and Purcell factor
In order to discriminate the non-radiative trapping mechanisms from the radiative processes, we carried out TRPL experiments by coupling the perovskite material with the inner modes of a high-quality optical microcavity33. This has been realized by mechanically approaching two distributed Bragg reflectors (DBR), consisting of 7.5 alternate pairs of quarter-wavelength TiO2 and SiO2 thin layers33,42 (fabrication details are reported in Methods). In fact, by mechanically removing/tuning the top DBR we modified the coupling of the material with the photonic modes, thus changing the Purcell factor and allowing us to identify the radiative components among all the relaxation and/or recombination mechanisms occurring after the carriers photo-generation, being only the radiative recombination processes affected by the Purcell effect. We underline that top DBR is never stacked on the bottom DBR/perovskite layer.
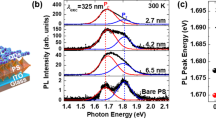
Figure 3 shows the PL spectrum of the perovskite sample, coupled to the optical cavity modes. Five narrow modes are visible in the stop-band of the DBR, one of them being nearly resonant to the out-cavity PL peak at 2.32 eV (535 nm). A Purcell factor P = 6 ± 1 has been experimentally and theoretically estimated at resonance (see Supplementary Note 3 and 4).
Photoluminescence (PL) spectra of CH3NH3PbBr3 perovskite out of the cavity (grey) and inside the cavity (green). Inset: Distributed Bragg Reflector (DBR)-based microcavity. The ultraviolet laser-assisted air passivation process is simplified by representing water molecules that passivate the trap centers in perovskite grains (orange/green cubes for bare/passivated CH3NH3PbBr3 grains).
The thin crawlspace of about 8 microns between the two mirrors (see Supplementary Note 4) allowed us to control the TS density by reversible laser-assisted physical adsorption of air molecules also when radiative processes are modified by the perovskite-cavity coupling30,31,32. A scheme of the microcavity is also reported in the inset of Fig. 3. Evidences that passivation effects occur in the case of in-cavity sample are reported in Supplementary Note 5.
Light-emitting species identification in optical cavity
In Fig. 4a, b we reported the normalized TRPL traces recorded in four different experimental conditions: (i) after wet-air passivation out of the cavity (P = 1, blue full circles in Fig. 4a); (ii) after wet-air passivation coupled with the cavity (P = 6, green open circles in Fig. 4a); (iii) under vacuum out of the cavity (P = 1, blue full circles in Fig. 4b) and (iv) under vacuum coupled with the cavity (P = 6, green open circles in Fig. 4b). The laser instrumental response in the first 10 ns is also reported in the figure (red-dotted lines in the grey area).
a Time-resolved photoluminescence traces of the perovskite film recorded after wet-air passivation in (open green circles) and out (full blue circles) of the cavity. Laser response in the first 10ns (red-dotted lines) and simulation curves (red continuous lines) are also reported. b Time-resolved photoluminescence traces of the perovskite film recorded in vacuum in (open green circles) and out (full blue circles) the cavity. NT and n0 stand for trap density and photogenerated carrier density (6 × 1015 cm−3), respectively. P is the Purcell factor. c Scheme of the processes involved in the spontaneous emission according to the rate equation system (see Supplementary Note 9). ET is the trap energy; kT (kDT) is the trapping (detrapping) coefficient usually related to electrons traps; Br is the bimolecular radiative band-to-band free carriers recombination coefficient; kT (kDT) is the exciton gemination (dissociation) rate; Ar is the excitons monomolecular radiative recombination rate; hν is the energy of emitted photons.
Few general considerations deserve to be pointed out. First of all in both out-cavity and in-cavity conditions, the passivated sample shows a TRPL time evolution slower than the not-passivated one, in agreement with the trap-passivation effect30,31; moreover, the Purcell effect due to the coupling of sample to the microcavity is clearly evidenced by the shortening of PL lifetime; lastly in all cases the time evolution of the TRPL signal is clearly not monomolecular (mono-exponential).
In literature the perovskite PL dynamics is typically described by the so-called ABC rate equation model, namely \(\frac{{{\rm{d}}n}}{{{\rm{d}}t}} = - An - Bn^2 - Cn^3\), where n is the volume density of the photogenerated carriers27,43, and A, B, C coefficients are related to monomolecular carrier trapping, FC bimolecular radiative recombination and Auger process43, respectively, the last one being usually neglected at the exploited excitation regimes. Nevertheless, by using this model to our case, the assumption that FC are the dominant emitting photogenerated species leads to contradictory results, as reported in Supplementary Note 6, supporting that, as suggested by CWPL line-shape analysis, also the TRPL signal is strongly affected by EX species contribution.
For the sake of completeness, we have performed the previous experiments also on a spin-coated MAPbBr3 sample, whose morphology and optical analysis were reported in Supplementary Note 7. Also in this case, the sample showed the presence of EX species at RT and the ABC model failed as well, due to the strong contribution to PL from EX states.
To study in depth the relaxation mechanisms involved in the light emission processes we assumed that the recombination dynamic after photo-generation of FC is governed by the following mechanisms: (i) EX gemination/dissociation; (ii) carriers Trapping/Detrapping; (iii) FC and EX radiative recombination. We highlight that in this model the trapping process is only associated with the FC. Details concerning this point are reported in Supplementary Note 8.
Therefore, in this frame, we analyzed the PL decay signals by using the outputs of the coupled rate equations accounting for electrons, holes, EX and filled TS densities (ne, nh, nX and nT respectively), which have been derived by the aforementioned processes, sketched in Fig. 4c (see Supplementary Note 9 for further details). In the rate equations system, kT (kDT) is the trapping (detrapping) coefficient usually related to electrons traps22 (NT being the full trap density); Br is the bimolecular radiative band-to-band FC recombination coefficient; kX (kDX) is the exciton gemination (dissociation) rate; Ar is the EX monomolecular radiative recombination rate. To reproduce the temporal evolution of the emission signal, we simulate the TRPL traces by taking into account the electron/hole/exciton densities and the radiative recombination rates/coefficients (Ar and Br) as returned by the calculation procedure. The photo-doping effect22 has been taken into account in the simulation, as described in Supplementary Note 9.
We performed the trace analysis on the TRPL data recorded at different experimental conditions, namely passivated/not-passivated and in-cavity/out-cavity sample. The simulated PL decays are shown in Fig. 4a, b by red continuous lines through the experimental data, and the corresponding values of the parameters used in the calculation are reported in Table 1. The simulated curves well reproduce the TRPL traces, after the laser response range.
We point out that an analysis performed by using the same model on high-quality perovskite crystal or nanostructure have been reported in the literature with similar qualitative fitting to the experimental curves17,44. Furthermore, contrarily to what obtained in the ABC model application, all the parameter values used in the simulations (reported in Table 1) are in agreement with those typically reported in the literature27,43. The set of parameters related to the four different experimental conditions evidences some important results which deserve to be stressed. Firstly, the set of parameters corresponding to the passivated and not-passivated experimental conditions in the out-cavity case (first and second columns of Table 1), differs from the one describing the corresponding in-cavity case (third and fourth columns of Table 1) only in Ar and Br values, which result 6 times increased by the Purcell factor (P = 6). This result shows that not only the bimolecular decay process but also the monomolecular one is related to radiative recombination, confirming the relevant role of EX in the spontaneous emission processes (monomolecular behavior) occurring in these materials, as suggested by CWPL line-shape analysis. Secondly, the values of parameters corresponding to the not-passivated and passivated experimental conditions (in both in-cavity/out-cavity cases) are the same with the only exception of NT and kX, suggesting an unexpected dependence of the EX gemination coefficient by the passivation conditions. We attribute the reduction of trap density to the intercalation, by the perovskite grains, of the O2 and H2O air molecules that induce ion passivation, thus affecting the EX gemination rate.
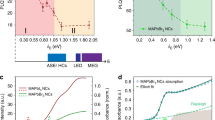
For a better understanding and to clarify the relationship between kX and NT, we have also analyzed the TRPL traces carried out in the case of out-cavity sample, by exploiting the rate equation model to all the TRPL data reported in Fig. 2b. The values of kX and NT, as a function of laser-assisted wet-air exposure time, are reported in Fig. 5a. As we can see, in the investigated time range, NT decreases by a factor 4 while kX increases by a factor 2, thus resulting in a first evidence of clear dependence of the EX geminate rate on trap density, in perovskite systems. We stress that in the TRPL traces simulations, recorded in all the different experimental conditions (eight traces), five parameters have been fixed, namely kT, kDT, kDX, Ar, Br, and only two acted as free, that is NT and kX, as reported in details in Supplementary Note 9.
a Trap states density (red) and excitons gemination rate (blue) versus exposure time. Vertical bars are related to the values range of KX and NT parameters for which the simulation curves well describe time-resolved photoluminescence (TRPL) traces for each exposure time while the error bars of exposure time are within the markers size. b Excitons gemination rate versus trap states density. Continuous line represents the theoretical excitons gemination rate as calculated by Langevin and scattering limited mobility models for a net charge value of Z = 1 (red line) and Z = 2 (purple line); grey line represents the best fitting-curve of the experimental data, resulting in an average value of Z = 1.6, indicating a larger dominion of Z = 2 ionic traps than Z = 1 ones. The bars are related to the values range of KX and NT parameters for which the simulation curves well describe time-resolved photoluminescence (TRPL) traces for each exposure time. c Excitons, electrons and holes density fractions versus passivation time after 20 ns from laser pulse. The grey line, labeled as Saha equilibrium, indicates the exciton density as extracted by Saha equation for a photogenerated carrier density value of n0 = 6 × 1015 cm−3. nk reported in the y axis stay for electrons ne, holes nh and excitons nX populations. The error bars are within the markers size. d Equilibrium population versus trap states density as extracted by the electrons ne, holes nh and excitons nX populations taken from time-resolved photoluminescence fits at different times after laser pulse (from 20 to 50 ns). Red and purple lines represent the theoretical equilibrium density calculated by the ratio kDX/kX (where kX and kDX are the excitons gemination/dissociation rate, respectively) as extracted by the time-resolved photoluminescence fit against the trap density by using modified Langevin model. The grey line, labeled as Saha equilibrium, indicates the equilibrium population as extracted by Saha equation for n0 = 6 × 1015 cm−3. The black line represents the photogenerated carrier density. Horizontal bars are related to the values range of NT parameter for which the simulation curves well describe time-resolved photoluminescence (TRPL) traces for each exposure time while the vertical error bars are within the markers size.
Finally, we observe that, concerning the radiative recombination, in the case of out-cavity sample, the model returns a value of 20 ns for exciton lifetime (1/Ar) and 1 µs for free-carrier initial-time constant (1/Brn0), respectively. All these results suggest that, at least at the beginning of the relaxation, FC and EX can be treated as a trap-dependent system in quasi-equilibrium.
Discussion
In order to describe the EX gemination rate dependence on trap states density we have developed a theoretical framework based on the Langevin model. This model was so far used to qualitatively describe the FC bimolecular recombination process in metal-halide perovskites, but it failed from a quantitative point of view, returning a value of the bimolecular recombination coefficient, six order of magnitude larger than the one experimentally observed20. Nevertheless, this model can be used, as we will demonstrate here, to explain the kX behavior in our sample, namely its relationship with the trapping states. In the frame of the Langevin model, in fact, the EX gemination rate can be expressed as kX = eμ/ε, where ε is the dielectric function of the perovskite material and μ the free-charge mobility, that is influenced by the trapping mechanisms. Concerning the mobility, in fact, we assume that it depends both on lattice and on ionized species presence (scattering limited mobility—SLM). In more details, we consider in our sample a total mobility value derived by the Matthiessen’s rule μ−1 = μL−1 + μI−1, where μL is the mobility due to the carriers interaction with lattice and μI is the ionized impurity SLM45, accounting for Coulomb potential generated by unsaturated ion vacancies, able to modify the electron scattering cross section. As resulting from the well-known scattering theory, we consider for μI the following expression:
where \({\it{\epsilon }}_{\mathrm{r}}\), kB, m, Z are, respectively, the relative dielectric constant, the Boltzmann constant, the electron mass and the net charge in the vacancy. F value is a function of trap states density and temperature, and it is dependent on the collision integral value describing the scattering process. We calculate F by means of the Conwell–Weisskopf model46. F parameter has been truncated because of the divergence due to long range Coulomb potential. Since the trap density is in the order of 1016 cm−3 (roughly 1 trap in a cube of 108 unit cells) we used the Conwell–Weisskopf truncation46 of the collision integral at a value of the impact parameter corresponding to half the distance between two impurities \(\left( {b_{{\mathrm{max}}} = 1/2\root {3} \of {{N_{\mathrm{T}}}}} \right)\).
The mobility related to the lattice interaction μL has been derived by means of the following considerations: as already reported, since in all the samples conditions the trapping process results to be slower than EX formation rate coefficient (Table 1) we expect that the FC-EX equilibrium can be reached just after the laser pulse. In these conditions the FC-EX kinetics equilibrium leads to an equilibrium population density of \(n_{{\mathrm{eq}}} = \frac{{n_{\mathrm{e}}n_{\mathrm{h}}}}{{n_{\mathrm{X}}}} = \frac{{k_{{\mathrm{DX}}}}}{{k_{\mathrm{X}}}}\). Under CW conditions we expect that, in the passivated sample, TS play a minor role in the emission process. Since the ratio between PL emitted by EX and FC (resulting to be 36 at the emission peak; Fig. 1b), is simply given by \(\frac{{PL_{{\mathrm{EX}}}}}{{PL_{{\mathrm{FC}}}}} = \frac{{A_{\mathrm{r}}k_{\mathrm{X}}}}{{B_{\mathrm{r}}k_{{\mathrm{DX}}}}}\), a value of 1.2 × 10−4 cm3s−1 is achieved for the passivated gemination rate kX, corresponding to an equilibrium density neq of 8 × 1015 cm−3. This leads to a mobility dominated by the lattice resulting, from Langevin model, in \(\mu \cong \mu _L = \varepsilon k_{\mathrm{X}}/e = 350\,{\mathrm{cm}}^2\,{\mathrm{V}}^{ - 1}\,{\mathrm{s}}^{ - 1}\), a value in the range reported in the literature for crystals47. We remark that, since our value is extracted by optical analysis, it is expected to be larger than that extracted by electrical transport measurements for polycrystalline films, which are affected also by inter-grain surface boundary scattering of electrical charges.47 Assuming the same concentration of electrons and holes (ne ≈ nh), we can solve the second order equation \(\frac{{x^2}}{{1 - x}} = \frac{{n_{{\mathrm{eq}}}}}{{n_0}}\), x being the FC fraction, for \(n_0({\mathrm{CWPL}}) \cong 10^{17}\,{\mathrm{cm}}^{ - 3}\), resulting in a maximum exciton fraction 1−x of about 75%. Saha equation (see Supplementary Note 10) foresees, at RT, an equilibrium population density of about 8 × 1016 cm−3, thus underestimating the EX fraction to the value of 42% (see Supplementary Fig. 13 in Supplementary Note 10).
To check the validity of our model that assumes ionized impurity SLM, we compare in Fig. 5b the EX gemination coefficient kX values as a function of trap density NT, as derived from TRPL traces simulation model, with the theoretical curves calculated by means of Eq. (1) at Z = 1 and Z = 2 (corresponding to the charge of Br- and Pb2+ ionic vacancies). As we can see, the kX values, extracted from the experimental data, match very well the theoretical curves, clearly showing that SLM model accurately describes the kX behavior in our sample. The correlation between data and theoretical model in the case of Z = 1 and Z = 2 suggests that vacancies can be concurrently attributed to doubly-charged species as well as singly-charged species. In particular, since the data are better described by Z = 2, we can assume a larger contribution by doubly-charged vacancies (i.e. Pb2+ ions) in the determination of the scattering mobility.
TS saturation combines two atmosphere-dependent passivation channels occurring via: (i) adsorption of molecules onto promptly-accessible and widely-extended surfaces and grain boundary interfaces, and (ii) bulk inclusion, namely intercalation of molecules in the material lattice framework.
As well documented in the literature, cubic MAPbBr3 results stable in the ambient conditions31 and, more specifically, is prone to exhibit MABr-terminated (001) surfaces that are energetically more favorable than PbBr2-terminated (001) as confirmed by calculations48 and experiments49. Therefore, such surface states specifically contribute to electronic properties and provide a n-type character to that region, because of an excess of Pb. Indeed, a surface stoichiometry close to MAPb1.27Br3 reveals a bromine deficient area (or lead rich) and points out the straightforward tendency to oxidation49,50. Calculations have shown that the dominant defects in MAPbBr3, namely Pb and Br vacancies, create shallow energy levels51 in the vicinity of valence band maximum, with a significant contribution of lead52, which will affect charge carrier dynamics. In this view, Wei H. et al. unequivocally showed the deactivation of surface trap states via oxygen-assisted passivation with the subsequent photoluminescence enhancement of organolead tribromide perovskites (see Fig. 2a) and the formation of chemical bonds with lead50,53. Apart from O2 and H2O neutral molecules, also hydroxide- and superoxide-based ligands can have a more straightforward role in the perovskite surface passivation53. At the same extent, grain boundaries TS passivation occur because of oxygen segregation into such states54.
The adsorption of H2O-deriving species onto the perovskite film actively depends also on the orientation of MA+ of surface terminated facets. In the event of MABr-exposing surfaces, whether NH3+ points outward, precise hydrogen bonds can be formed between water molecules and MA+ molecules. By contrast, in the less-favored case that the exposed surface shows a PbBr2 composition, water will preferably interact with lead ions, with NH3+ pointing inward and forming hydrogen bonds with the inorganic framework55,56.
The inclusion of gaseous molecules from ambient into the perovskite lattice cannot be ruled out as well; the cases of MAPbI3 for which H2O molecules can promote the chemical complexation with the formation of mono- and di-hydrate forms, due to their ability to penetrate into the lattice framework57,58 or oxygen can diffuse into the lattice, via interaction with interstitial iodine59, are significant. Oxygen and water infiltration of organolead tribromide perovskites can occur, when exposed to ambient condition, via intrinsic defects present in polycrystalline materials. Also, a contribution to the intercalation of molecules is made by the light irradiation at energies larger than the band gap, a phenomenon that causes a structural lattice expansion, even persisting for some dozens of minutes after lighting off. The event occurs due to the photogenerated charge carriers that populate the relative states of the conduction and valence bands, inducing a distortion (or elongation) of specific perovskite chemical bonds60. The intercalation of O2 and H2O molecules in the bulk structure of the MAPbBr3 can results in an annihilation of Frenkel pairs, namely bromine-related vacancies and interstitial defects, thus effecting the TS associated with them and the bulk charge carrier dynamics in accordance with our experimental data61.
From the analysis of TRPL data by means of the rate equations model, we have also calculated the electrons, holes and excitons densities at different laser-assisted wet-air exposure time. In Fig. 5c the values of \(n_i/\mathop {\sum}\nolimits_i {n_i} \left( {i = e,h,X} \right)\) at 20 ns after the laser pulse are reported. Contrarily to what stated by Saha equation, which does not consider the influence of traps states, the relative populations result to be dependent on trap density NT. In particular exciton density increases from 7 to 15% of the total population after passivation and it consists in 50% of the electron density, thus overcoming the limits of Saha prediction of 6.6% at \(n_0({\mathrm{TRPL}}) \cong 6 \times 10^{15}\,{\mathrm{cm}}^{ - 3}\) (see Supplementary Fig. 13 in Supplementary Note 10). Therefore, the FC-EX equilibrium is limited by kinetics rather than thermodynamics also in TRPL conditions. This is better shown in Fig. 5d, where we reported the trap dependence of the equilibrium population density \(n_{{\mathrm{eq}}} = \frac{{n_{\mathrm{e}}n_{\mathrm{h}}}}{{n_{\mathrm{X}}}}\), as extracted by the electrons, holes and excitons population densities, for different times after the pulse (from 20 to 50 ns). It appears that Saha equation greatly over-estimates the equilibrium density value by one order of magnitude. In Fig. 5d we have also reported neq determined by the kinetic equilibrium condition \(n_{{\mathrm{eq}}} = \frac{{k_{{\mathrm{DX}}}}}{{k_{\mathrm{X}}}}\), where kX dependence on NT has been calculated by SLM model. As we see, the data match nearly the two curves corresponding to Z = 1 and Z = 2. Moreover, the SLM model well describes also the trend of neq as a function of TS density, thus promoting it as an efficient framework able to explain the relationship between EX and FC density in presence of trap states.
In conclusion, we report on a thermally deposited 3D MAPbBr3 thin film whose PL spontaneous emission is dominated by the radiative exciton recombination. We demonstrate that the monomolecular decay process cannot be solely attributed to non-radiative trapping process, as usually reported for low exciton-binding energy perovskites, but also to efficient radiative exciton recombination. In order to discriminate the contribution of excitons, free carriers and trap states and their role in the radiative emission process, we conceived an appropriate experimental method, that can be extended to other perovskite films: we control the trap states density by means of reversible laser-assisted exposure to air molecules, and we simultaneously discriminate radiative from non-radiative processes by coupling the sample to the inner modes of a high-quality microcavity, being only the radiative recombination affected by the Purcell effect. Additionally, we developed a theoretical framework which well describes the exciton formation by means of the Langevin model adapted to the Conwell-Weisskopf theory of semiconductor mobility, based on the Coulomb scattering of free-electron by ionized impurities. In particular, we have shown that the trap states passivation reduces the mobility scattering cross-section, thus improving the exciton gemination rate in our systems. These results clearly highlight that the two radiative species (free carriers and excitons) cannot be treated as an isolated system at thermodynamic equilibrium, as assumed by Saha equation model, but rather as an open system whose kinetics are affected by the trap-states density. It is worth to underline that the tool herein proposed is independent of the perovskite compound and deposition technique selected.
Methods
Perovskite deposition
We deposited MAPbBr3 films on glass substrates as well as on dielectric cavity mirrors (DBR). The perovskite film was fabricated by co-depositing in a vacuum chamber the precursors methylammonium bromide and lead (II) bromide from two independent sources. The stoichiometry of the two perovskite precursors was MABr:PbBr2 = 1:1, co-evaporated at a rate of 0.3Å s−1 (reached at about 150 °C) and 0.25 Å s−1 (reached at about 300 °C), respectively. Perovskite film was not annealed after the deposition.
Cavity fabrication
The open microcavity was made by two DBR made by sputtering, on a glass substrate, 7.5 pairs of TiO2/SiO2 alternating quarter-wavelength layers. Both SiO2 and TiO2 layers were deposited at 250W, heating the substrates at 250 °C. Moreover, in order to maintain a balanced stoichiometry, SiO2 was grown adding reactive oxygen at 10% of the nitrogen flow. The optical constants and thickness of the employed materials were measured using a J.A. Wollam M-2000XI ellipsometer, while the theoretical modelling of DBRs’ optical behavior and cavity were carried out by using the Transfer Matrix Method (TMM)42, taking into account the experimental thickness and the optical constants of the employed materials.
To shed light on the behavior of the enquired cavity mode in presence of perovskite grains, electromagnetic simulations have been carried out using a software based on Finite Element code (COMSOL Multiphysics).
The microcavity was simply realized by approaching the top mirror onto the bottom one by micrometric mechanical setup, obtaining the optical system reported in Fig. 3. The cavity mode resonances were tuned in situ by finely controlling the mirrors separation distance, until one of the few optical modes appearing in the cavity transmission spectrum was in resonance with the emission peak of perovskite film (λ = 535 nm).
AFM and XRD measurements
AFM image was recorded by a Park XE-100 model in non-contact mode.
XRD patterns were recorded from 10° to 60° 2θ with a step size of 0.02° and an acquisition time of 25 s per degree, using a Panalytical X’PERT Pro X-ray diffractometer.
Optical constants of perovskite layer
Real and imaginary parts of refractive index (n, k) of perovskite layers were carried out by ellipsometric measurements performed by means of a J. A. Wollam M-2000XI ellipsometer. The shift angles psi and delta have been fitted by using general oscillators (genosc function).
PL experiments
CWPL experiments were performed by exiting the sample by a solid state CW laser delivering 100 mW at 405 nm with a spot \(D \cong 2\,{\mathrm{mm}}\). The emission signal was collected in backscattering configuration by an optical fiber (diameter 1 mm) and dispersed by a Triax320 (focal length of 0.32 m) Horiba monochromator, coupled to a Peltier cooled CCD in kinetic acquisition mode. CWPL measurements for sample in microcavity were also recorded by using an iHR320 (focal length of 0.32 m) Horiba monochromator equipped with a Peltier cooled Hamamatsu photomultiplier (Head-on mod R943-02), operating in single photon counting mode.
TRPL measurements were performed exciting the samples by a solid state pulsed laser (mod. PLP10-040, Hamamatsu), which provided pulses at a wavelength of 402 nm of about 58 ps, at repetition rate of 1MHz. The photogenerated carrier density at time zero from the pulse was estimated following the equation \(n_0 = \frac{{\alpha \bar P}}{{\left( {RR} \right)h\nu S}}\), where α is the absorption coefficient (6.6 × 104 cm−1); P̄ is the average power of pulsed laser under a full period (3.8 µW), hν is the laser energy (3.08 eV; 402 nm), S is the laser spot area on the sample (about 0.1 mm2), and RR is the repetition rate (1 MHz). With all these input data, we estimate for n0 a value of 6 × 1015 cm−3. In the TRPL experiment, the PL was dispersed by an iHR320 (focal length of 0.32 m) Horiba monochromator equipped with a Peltier cooled Hamamatsu photomultiplier (Head-on mod R943-02), operating in single photon counting mode. The instrumental laser response (about 10 ns) was also recorded and reported in Fig. 4a, b (red-dotted line in the gray area).
Data availability
All relevant data are available from the authors.
References
Green, M. A. & Ho-Baillie, A. Perovskite solar cells: the birth of a new era in photovoltaics. ACS Energy Lett. 2, 822–830 (2017).
Yang, W. S. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 356, 1376–1379 (2017).
Tan, H. et al. Efficient and stable solution-processed planar perovskite solar cells via contact passivation. Science 355, 722–726 (2017).
Luo, D. et al. Enhanced photovoltage for inverted planar heterojunction perovskite solar cells. Science 360, 1442–1446 (2018).
Sahli, F. et al. Fully textured monolithic perovskite/silicon tandem solar cells with 25.2% power conversion efficiency. Nat. Mater. 17, 820–826 (2018).
Tan, Z.-H. et al. Bright light-emitting diodes based on organometal halide perovskite. Nat. Nanotech. 9, 687–692 (2014).
Kim, Y.-H. et al. Multicolored Organic/Inorganic Hybrid Perovskite Light‐Emitting Diodes. Adv. Mater. 27, 1248–1254 (2015).
Cho, S. et al. Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes. Science 350, 1222–1225 (2015).
Yang, X. et al. Efficient green light-emitting diodes based on quasi-two-dimensional composition and phase engineered perovskite with surface passivation. Nat. Commun. 9, 570 (2018).
Tian, Y. et al. Highly efficient spectrally stable red perovskites light-emitting diodes. Adv. Mater. 30, 1707093 (2018).
Lin, K. et al. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent. Nature 562, 245–248 (2018).
Zhang, Q. et al. Advances in small perovskite-based lasers. Small Methods 1, 1700163 (2017).
Harwell, J. R., Whitworth, G. L., Turnbull, G. A. & Samuel, I. D. W. Green perovskite distributed feedback lasers. Sci. Rep. 7, 11727 (2017).
Ha, S.-T., Shen, C., Zhang, J. & Xiong, Q. Laser cooling of organic-inorganic lead halide perovskites. Nat. Photon. 10, 115–121 (2016).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013).
Stranks, S. D. & Snaith, H. J. Metal-halide perovskites for photovoltaic and light-emitting devices. Nat. Nanotechnol. 10, 391–402 (2015).
Shi, D. et al. Low trap-state density and long carrier diffusion in organo lead-trihalide perovskite single crystals. Science 347, 519–522 (2015).
Saba, M. et al. Correlated electron–hole plasma in organometal perovskites. Nat. Commun. 5, 5049 (2014).
Saba, M., Quochi, F., Mura, A. & Bongiovanni, G. Excited state properties of hybrid perovskites. Acc. Chem. Res. 49, 166–173 (2016).
Sarritzu, V. et al. Perovskite excitonics: primary exciton creation and crossover from free carriers to a secondary exciton phase. Adv. Opt. Mater. 6, 1700839 (2017).
Srimath Kandada, A. R. et al. Nonlinear carrier interactions in lead halide perovskites and the role of defects. J. Am. Chem. Soc. 138, 13604–13611 (2016).
Stranks, S. D. et al. Recombination kinetics in organic-inorganic perovskites. excitons, free charge, and subgap states. Phys. Rev. Appl. 2, 034007 (2014).
D’Innocenzo, V. et al. Excitons versus free charges in organo-lead tri-halide perovskites. Nat. Commun. 5, 3586 (2014).
Droseros, N. et al. Origin of the enhanced photoluminescence quantum yield in MAPbBr3 Perovskite with reduced crystal size. ACS Energy Lett. 3, 1458–1466 (2018).
Saha, M. N. On a physical theory of stellar spectra. Proc. R. Soc. Lond. A 99, 135–153 (1921).
Cingolani, R. et al. Radiative recombination processes in wide-band-gap II–VI quantum wells: the interplay between excitons and free carriers. J. Opt. Soc. Am. B 13, 1268–1277 (1996).
Johnston, M. B. & Herz, L. M. Hybrid perovskites for photovoltaics: charge-carrier recombination, diffusion, and radiative efficiencies. Acc. Chem. Res. 49, 146–154 (2016).
Mariano, F. et al. Thermally evaporated hybrid perovskite for hetero-structured green light-emitting diodes. Appl. Phys. Lett. 111, 163301 (2017).
Genco, A. et al. Fully vapor-deposited heterostructured light-emitting diode based on organo-metal halide perovskite. Adv. Electron. Mater. 2, 1500325 (2016).
Fang, H. H., Wang, F., Adjokatse, S., Zhao, N. & Loi, M. A. Photoluminescence enhancement in formamidinium lead iodide thin films. Adv. Funct. Mater. 26, 4653–4659 (2016).
Fang, H. H. et al. Ultrahigh sensitivity of methylammonium lead tribromide perovskite single crystals to environmental gases. Sci. Adv. 2, e1600534 (2016).
Brenes, R. et al. Metal halide perovskite polycrystalline films exhibiting properties of single. Cryst. Joule 1, 155–167 (2017).
Genco, A. et al. High quality factor microcavity OLED employing metal-free electrically active Bragg mirrors. Org. Electron. 62, 174–180 (2018).
Noh, J. H., Im, S. H., Heo, J. H., Mandal, T. N. & Seok, S. I. Chemical management for colorful, efficient, and stable inorganic-organic hybrid nanostructured solar cells. Nano Lett. 13, 1764–1769 (2013).
Elliot, R. Intensity of optical absorption by excitons. Phys. Rev. 108, 1384–1389 (1957).
Bebbs, H. B., Williams, E. W. Photoluminescence I: Theory. Semiconductors and Semimetals Vol. 8, Transport and Optical Phenomena (Academic Press, New York, 1972).
Bastard, G. Wave Mechanics Applied to Semiconductor Heterostructures. (Les Editions de Physique, Les Ulis Cedex, Halsted Press, New York, 1988).
Cingolani, R. & Ploog, K. Frequency and density dependent radiative recombination processes in III-V semiconductors quantum wells and superlattices. Adv. Phys. 40, 535–623 (1991).
Mitin, V. V., Kochelap, V. & Stroscio, M. A. Quantum Heterostructures: Microelectronics and Optoelectronics. (Cambridge University Press, Cambridge, 1999).
He, H. et al. Exciton localization in solution-processed organolead trihalide perovskites. Nat. Commun. 7, 10896 (2016).
Shi, J. et al. Identification of high-temperature exciton states and their phase-dependent trapping behaviour in lead halide perovskites. Energy Environ. Sci. 11, 1460–1469 (2018).
Yeh, P. Optical Waves in Layered Media. (Wiley-Interscience, John Wiley and Sons, New York, 2005).
Milot, R. L., Eperon, G. E., Snaith, H. J., Johnston, M. B. & Hertz, L. M. Temperature-dependent charge-carrier dynamics in CH3NH3PbI3 perovskite thin films. Adv. Funct. Mater. 25, 6218–6227 (2015).
Stranks, S. D. Nonradiative losses in metal halide perovskites. ACS Energy Lett. 2, 1515–1525 (2017).
Sze, S. M. Physics of Semiconductor Devices 2nd edn (John Wiley and Sons, New York, 1981).
Conwell, E. & Weisskopf, V. F. Theory of impurity scattering in semiconductors. Phys. Rev. 77, 388–390 (1950).
Herz, L. M. Charge-carrier mobilities in metal halide perovskites: fundamental mechanisms and limits. ACS Energy Lett. 2, 1539–1548 (2017).
Huang, X., Paudel, T. R., Dowben, P. A., Dong, S. & Tsymbal, E. Y. Electronic structure and stability of the CH3NH3PbBr3 (001) surface. Phys. Rev. B 94, 195309 (2016).
Komesu, T. et al. Surface electronic structure of hybrid organo lead bromide perovskite single crystals. J. Phys. Chem. C. 120, 21710–21715 (2016).
Wei, H. et al. Sensitive X-ray detectors made of methylammonium lead tribromide perovskite single crystals. Nat. Photonics 10, 333–339 (2016).
Shi, T., Yin, W.-J., Hong, F., Zhu, K. & Yan, Y. Unipolar self-doping behavior in perovskite CH3NH3PbBr3. Appl. Phys. Lett. 106, 103902 (2015).
Kirmani, A. R. et al. Contributions of the lead-bromine weighted bands to the occupied density of states of the hybrid tri-bromide perovskites. Appl. Phys. Lett. 113, 022101 (2018).
Che, X. et al. Charge trap formation and passivation in methylammonium lead tribromide. J. Phys. Chem. C. 123, 13812–13817 (2019).
Yin, W. ‐J., Chen, H., Shi, T., Wei, S. ‐H. & Yan, Y. Origin of high electronic quality in structurally disordered CH3NH3PbI3 and the passivation effect of Cl and O at grain boundaries. Adv. Electron. Mater. 1, 1500044 (2015).
Koocher, N. Z., Saldana-Greco, D., Wang, F., Liu, S. & Rappe, A. M. Polarization dependence of water adsorption to CH3NH3PbI3 (001) surfaces. J. Phys. Chem. Lett. 6, 4371–4378 (2015).
Mosconi, E., Azpiroz, J. M. & De Angelis, F. Ab initio molecular dynamics simulations of methylammonium lead iodide perovskite degradation by water. Chem. Mater. 27, 4885–4892 (2015).
Leguy, A. M. A. et al. Reversible hydration of CH3NH3PbI3 in films, single crystals, and solar cells. Chem. Mater. 27, 3397–3407 (2015).
Müller, C. et al. Water infiltration in methylammonium lead iodide perovskite: fast and inconspicuous. Chem. Mater. 27, 7835–7841 (2015).
Meggiolaro, D., Mosconi, E. & De Angelis, F. Mechanism of reversible trap passivation by molecular oxygen in lead-halide perovskites. ACS Energy Lett. 2, 2794–2798 (2017).
Tsai, H. et al. Light-induced lattice expansion leads to high-efficiency perovskite solar cells. Science 360, 67–70 (2018).
Mosconi, E., Meggiolaro, D., Snaith, H. J., Stranks, S. D. & De Angelis, F. Light-induced annihilation of Frenkel defects in organo-lead halide perovskites. Energy Environ. Sci. 9, 3180–3187 (2016).
Staub, F., Rau, U. & Kirchartz, T. Statistics of the Auger recombination of electrons and holes via defect levels in the band gap application to lead-halide perovskites. ACS Omega 3, 8009–8016 (2018).
Acknowledgements
The authors thank Mr. Diego Mangiullo (CNR Nanotec), Dr. Marco Bianco, Dr. Stefania Milanese, Dr. Domenico Licchelli (University of Salento) for expert technical support, Dr. Vittorianna Tasco (CNR Nanotec), for useful discussions and scientific support. The work was supported by the Italian project PON SE4I—Smart Energy Efficiency & Environment for Industry (Cod. ARS01_01137).
Author information
Authors and Affiliations
Contributions
F.M. contributed in the preparation and characterization of perovskite layers, in the setting up the perovskite trap states passivation process and analysis of data. A.C. performed CWPL/TRPL experiments and analysis; A.G. fabricated DBR mirrors and performed optical simulations of the cavity. L.C. contributed in writing the manuscript and analysis of the data. S.D’A. performed COMSOL Multiphysics simulations of the perovskite-cavity by using finite element code. S.C. performed AFM images. G.M. implemented the Cash-Karp method (differential equations solver) in a user-friendly interface developed in LabView environment. M.L. and M.M. conceived the idea and the experiments, performed the analysis and developed the theoretical model. F.M. and A.C. equally contributed in writing the manuscript. All authors assisted in the manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mariano, F., Cretì, A., Carbone, L. et al. The enhancement of excitonic emission crossing Saha equilibrium in trap passivated CH3NH3PbBr3 perovskite. Commun Phys 3, 41 (2020). https://doi.org/10.1038/s42005-020-0309-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0309-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.