Abstract
Besides the mechanism responsible for high critical temperature superconductivity, the grand unresolved issue of the cuprates is the occurrence of a strange metallic state above the so-called pseudogap temperature T*. Even though such state has been successfully described within a phenomenological scheme, the so-called Marginal Fermi-Liquid theory, a microscopic explanation is still missing. However, recent resonant X-ray scattering experiments identified a new class of charge density fluctuations characterized by low characteristic energies and short correlation lengths, which are related to the well-known charge density waves. These fluctuations are present over a wide region of the temperature-vs-doping phase diagram and extend well above T*. Here we investigate the consequences of charge density fluctuations on the electron and transport properties and find that they can explain the strange metal phenomenology. Therefore, charge density fluctuations are likely the long-sought microscopic mechanism underlying the peculiarities of the metallic state of cuprates.
Similar content being viewed by others
Introduction
Among the different phases and orders populating the phase diagram of superconducting cuprates, the region where the strange metal occurs has a preeminent role for this class of compounds over a rather wide doping range pivoting around optimal doping (see Fig. 1). Experimentally, the most evident benchmark of this region is represented by the linear behaviour of the electrical resistivity ρ(T) as a function of the temperature T, from above a doping-dependent pseudogap crossover temperature T* up to the highest attained temperatures. Such occurrence is less evident in the underdoped regime, where T* is almost as high as room temperature (e.g. at doping p ≈ 0.11, see Fig. 1), while it dominates the transport properties of the metallic state in its entirety above optimal doping (p ≈ 0.17–0.20, see Fig. 1), where T* decreases and eventually merges with the superconducting critical temperature Tc. Beyond such occurrence, the main deviations from the paradigmatic behaviour dictated by the Landau Fermi-liquid theory of standard metals are the optical conductivity, following a non-Drude-like frequency dependence σ(ω) ~ 1/ω, and the Raman scattering intensity, starting linearly in frequency and then saturating into a flat electron continuum, as expressed by the dependence of the susceptibility of the scattering mediator, \({\rm{Im}}\ P(\omega ) \sim \omega /\max \ (T,| \omega | )\). It was shown long ago1 that the phenomenological assumption of this form for \({\rm{Im}}\ P(\omega )\) accounts for the above anomalous properties. In particular, the related low-energy excitations, mediating a momentum-independent electron–electron effective interaction, give rise to a linear dependence of the imaginary part of the electron self-energy both in frequency and temperature
Although there are theories that do not rely on a specific mediator2, a huge effort has been devoted along the years to identify the excitations mediating this scattering, mostly based on the idea of proximity to some form of order: circulating currents3, spin4,5, charge order6,7,8,9,10 or the phenomenological coupling to incoherent fermions11.
In the red region encompassed between the pseudogap temperature T* and the upturn temperature Tup of the resistance, above the superconducting critical temperature Tc, in particular close to the optimally doped regime (e.g. at hole doping p ≈ 0.17), these compounds display a strange-metal behaviour. This is revealed in the experimental resistance R data by the presence of a linear temperature dependence, displayed as a red thick solid line in the R(T) curves above the phase diagram. In the underdoped regime (e.g. at p ≈ 0.11), below T* (blue region) a downturn from the linear-in-T resistance is observed, since additional mechanisms lead to deviations from the strange-metal regime. In the overdoped regime (e.g. at p ≈ 0.21), below Tup (yellow region) the upturn from the linear-in-T resistance is due to the setting in of the Fermi-liquid regime. Recent Resonant X-Ray Scattering experiments12 showed that also the charge order phenomenon is widespread in the phase diagram. In particular, short-ranged dynamical charge density fluctuations (sketched by red waves highlighted in the red circle, and observed in the striped area) populate the strange-metal region, while in the underdoped region, below the onset temperature TCDW, they coexist with the usual longer-ranged charge density waves (sketched by blue waves in the blue circle, and observed in the wavy area). TN is the Néel temperature. The data of the R(T) curves are taken from Refs. 12,40.
A step forward in the identification of low energy excitations that might be responsible for the strange-metal behaviour was recently taken by means of resonant X-ray scattering (RXS), performed on Nd1+xBa2−xCu3O7−δ (NBCO) and YBa2Cu3O7−δ (YBCO) thin films12. After the first experimental evidence, these excitations have been demonstrated to be a common feature of different families of cuprates, namely HgBa2CuO4+δ13, La2−xSrxCuO414,15,16, La2−xBaxCuO417,18, and La1.675Eu0.2Sr0.125CuO419, thereby indicating that these excitations may well provide a generic scattering mechanism in all cuprates.
In the following we will focus on NBCO or YBCO investigated in the precursor experiment. These experiments not only confirmed the occurrence of incommensurate charge density waves (CDWs), correlated over several lattice spacings, in the underdoped region and below T*20,21,22,23,24,25,26,27,28, but, quite remarkably, also identified a much larger amount of very short-ranged (≈3 lattice spacings) dynamical charge density fluctuations (CDFs, see Fig. 1), with a characteristic energy scale ω0 ≈ 10–15 meV. These CDFs are peaked at a wave vector, along the (1,0) and (0,1) directions, which is very close to that of the intermediate-range CDWs12, arising below a given temperature TCDW(p) for each measured doping p. We also notice that, when the temperature is raised towards TCDW(p), the CDWs correlation length decreases down to values close to those of the CDFs. These facts suggest that the two charge fluctuations have a common origin. One possibility is that they develop differently in different regions, with CDFs remaining noncritical, whereas CDWs evolve towards order. This is also supported by the possibility that the narrow peak (NP) of the RXS response function, customarily associated to the CDWs, arises at the expense of the broad peak (BP) due to CDFs. However, differently from CDWs, CDFs are quite robust both in temperature (they survive essentially unaltered up to the highest explored temperatures, T ≈ 270 K) and doping. These excitations are at low energy (≈15 meV in an optimally doped sample with Tc = 90 K) and so short ranged that in reciprocal space they produce the BP observed in the RXS scans. CDFs not only provide a strong scattering channel for the electrons, but also overcome the difficulty of the CDWs, which, being so peaked, give rise to anisotropic scattering dominated by the hot spots on the Fermi surface. CDFs, instead, being so broad, affect all states on the Fermi surface nearly equally, resulting in an essentially isotropic scattering rate. This isotropy is a distinguished feature of the strange-metal state and we show below that it can account for the peculiar behaviour of the electronic spectra and for the linear-in-T resistivity.
Results
Strange-metal behaviour of the electron self-energy
Figure 2a shows a qualitative explanation of the inherent isotropy of the scattering by CDFs. RXS experiments directly access the frequency and momentum-dependent charge susceptibility (see Methods) and find the above mentioned BP at a well-defined incommensurate wave vector Qc, but the large width of this peak means that a wealth of low-energy CDFs are present over a broad range of momenta. Therefore, an electron quasiparticle on a branch of the Fermi surface can always find a CDF that scatters it onto another region of the Fermi surface [see Fig. 2a)]. Thus the whole Fermi surface is hot in the sense that no regions exist over the Fermi surface that can avoid this scattering. This is visualized in Fig. 2a, where the overlap of the Fermi surface with its translated and broadened replicas (due to the scattered quasiparticles) is almost uniform, and no particular nesting condition is needed. Quite remarkably, the CDF-mediated scattering stays isotropic even in an energy window of ≈20 meV around the Fermi surface (see Supplementary note 1 and Supplementary Fig. 2).
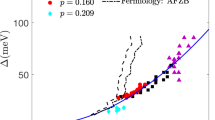
a Sketch of the charge density fluctuation (CDF) and charge density wave (CDW) mediated quasiparticle scattering on the Fermi surfaces. Points on the Fermi surface are identified by the angle ϕ. Owing to the broadness of CDFs in momentum space, all the states along the Fermi surface (thick black line) can be scattered by low-energy CDFs over other portions of the Fermi surface, and no particular nesting condition is needed. The involvement of only one branch of the Fermi surface in the Brillouin zone is displayed for clarity: The scattered portions of the Fermi surface (broad reddish areas) essentially cover the whole branch. Therefore the whole Fermi surface is affected in a nearly isotropic way. On the contrary, the CDWs are peaked in momentum space and scatter the Fermi surface states in rather restricted regions of other Fermi surface branches (hot spots). These occur where the bluish lines cross the thick black line. b Scattering rate [i.e. the imaginary part of the self-energy at zero frequency \({{\Gamma }}(\phi )=-{\rm{Im}}\ {{\Sigma }}(\phi ,T,\omega =0)\)] at a given temperature T = 80 K, as a function of the position on the Fermi surface, as identified by the angle ϕ defined in panel a. The nearly isotropic red line corresponds to the case when all the scattering would be due to CDFs, while the blue dashed line represents the scattering due to CDWs only. c Imaginary part of the electron self-energy as a function of the (negative) electron binding energy, at different temperatures above TCDW, below which the CDWs emerge to produce the narrow peak in resonant X-ray scattering. The coupling between fermion quasiparticles and CDFs is g = 0.166 eV. d Same as c, but with both frequency and self-energy axes rescaled by the temperature (kB is the Boltzmann constant), to highlight the approximate scaling behaviour at low frequency.
On the contrary, since CDWs are quite peaked, only a few of them around Qc are available to scatter quasiparticles at low energy: Only quasiparticles at the hot spot are then significantly scattered by CDWs [see Fig. 2a]. In a quantitative way, this is shown in Fig. 2b, where the actual scattering rate along the Fermi surface has been separately computed for CDFs (solid red line) and CDWs (dashed blue line) with parameters suitable to describe a slightly underdoped NBCO sample (p ≈ 0.15), where CDF and CDW coexist (see Supplementary note 2 and Supplementary Fig. 5). This feature makes these CDFs an appealing candidate to mediate the isotropic scattering required by the original marginal Fermi-liquid theory. We therefore test this expectation by explicitly calculating how the CDFs dress the electron quasiparticles modifying their spectrum. In many-body theory, this effect is customarily described by the electron self-energy. In particular, the imaginary part of the electron self-energy, \({\rm{Im}}\ {{\Sigma }}\), provides the broadening of the electron dispersion as measured, e.g. in angle-resolved photoemission experiments. We adopt the following strategy: (a) we extract from the experimental inelastic RXS spectra the information on the dynamics of the CDFs (see supplementary note 2) evaluated within the linear response theory; (b) we borrow from photoemission experiments the electron dispersion in the form of a tight-binding band structure29; (c) we calculate the electron self-energy resulting from the coupling between CDFs and the electron quasiparticles, as discussed in Supplementary note 1 and represented as a diagram in Supplementary Fig. 1.
With the extracted parameters, using the coupling between quasiparticles and CDFs obtained from the resistivity fit (see below) and taking the frequency derivative of the real part of the self-energy, we also calculated the dimensionless coupling λ at T ≈ T* finding λ ≈ 0.35–0.5 (see Supplementary note 1).
Of course, this perturbative approach, although supported by the low-moderate value of λ, is based on the Fermi-liquid as a starting point in the overdoped region. Its applicability can be safely extended to lower doping at high temperatures, in the metallic state and above T*, where the phenomenology is only marginally different from that of a Fermi-Liquid.
The result of our calculation for an optimally doped NBCO sample with Tc = 90 K is reported in Fig. 2c, d. After an initial quadratic behaviour, the scale of which is set by the energy scale ω0 of the CDFs30 (see Supplementary note 1), \({\rm{Im}}\ {{\Sigma }}\) displays an extended linear frequency dependence up to 0.10–0.15 eV (comparable to the one reported in the photoemission experiments of refs. 31,32). The overall value of this self-energy is comparable to, but it always stays smaller than, the Fermi energy scale of order 0.3–0.4 eV. This is an intrinsic manifestation of a strange-metal state, where the width of the quasiparticle peak must be of the same order of its typical energy. At low frequencies \({\rm{Im}}\ {{\Sigma }}\) saturates at a constant value that increases linearly with increasing T. This is precisely the behaviour expected from the strange-metal expression of Eq. (1). This self-energy is reported along a specific (1,1) direction, but it is crucial to recognize that it is also highly isotropic in momentum space. Figure 2b indeed reports the scattering rate (i.e. the imaginary part of the self-energy at zero frequency) Γ(ϕ) ≡ Γ0 + ΓΣ(ϕ). An isotropic scattering rate Γ0 representing the effect of quenched impurities has also been included. Our results in Fig. 2c, not only share with the data of ref. 31 a similar form, but also display a scaling behaviour, as reported in Fig. 2d. As mentioned in ref. 1, the isotropic linear-in-frequency self-energy behaviour, stemming from CDFs, is sufficient to produce a strange-metal behaviour in physical quantities like optical conductivity and Raman scattering.
Below TCDW = 150 K, an additional scattering due to the CDWs is present. This additional scattering has a significant anisotropic component, which is confined in a small region of momentum space, as shown by the dashed blue curve of Fig. 2b. This anisotropic character eventually leads to the departure from the strange-metal behaviour33 below temperatures comparable with T*.
CDFs produce linear resistivity
Once the dynamics of the CDFs is identified by exploiting RXS experiments, one can investigate their effects on transport properties. The calculation of the electron resistivity is carried out within a standard Boltzmann-equation approach along the lines of ref. 34 (see Supplementary note 3). An analogous calculation within the Kubo formalism gives very similar results (see Supplementary note 4 and Supplementary Fig. 7). From the electron self-energy we obtain the zero frequency quasiparticle scattering rate along the Fermi surface Γ(ϕ) defined above, and we use Γ0 as a fitting parameter, obtaining values (≈20-60 meV) that are reasonable for impurity scattering. We also use the anisotropic Fermi wave vector along the Fermi surface, as obtained from the same band structure in tight-binding approximation29 used for the self-energy calculation. Figure 3a displays the comparison between the ρ(T) curve of the optimally doped NBCO film (Tc = 90 K), studied in ref. 12 (yellow line) and the theoretical results (black line). At high temperatures, the famous linear-in-T behaviour of the resistivity is found and the data are quantitatively matched. This behaviour stems from the very isotropic scattering rate produced by the CDFs [red solid line in Fig. 2b], which, for this sample and in this temperature range, are the only observed charge excitations. At lower temperatures, below T*, a discrepancy emerges between the theoretical expectation and the experimental evidence, since the expected saturation, due to the onset of a Fermi-liquid regime and to (isotropic) impurity scattering Γ0, is experimentally replaced by a downturn of the resistivity. Such discrepancy occurs gradually in T when, entering the pseudogap state, the pseudogap itself and other intertwined incipient orders (CDWs, Cooper pairing,...) play their role. These effects, which are outside our present scope, obviously lead to deviations from our theory, which only considers the effect of CDFs. On the other hand, in the overdoped YBCO sample (Tc = 83 K), the pseudogap and the intertwined orders are absent, while the CDFs are the only surviving charge excitations, even down to Tc12. Here, our theoretical resistivity, related to the scattering rate produced by CDFs, matches very well the experimental data, in the whole range from room temperature almost down to Tc [see Fig. 3b]. In particular, the agreement is rather good even at the lowest temperatures above Tc. The data display an upward saturation due to the onset of a Fermi-liquid regime that is well described by our calculation: At temperatures lower than the characteristic energy of CDFs their scattering effect is suppressed and the strange-metal behaviour ceases. We find remarkable that our theory not only describes the linear-in-T regime, but also captures the temperature scale of upward deviation from it, without additional adjustments.
a Experimental resistivity for an optimally doped (Tc = 90 K) Nd1+xBa2−xCu3O7−δ sample (yellow thick curve) compared to the theoretical result as obtained from the charge density fluctuations (CDFs) only (black solid line). The dashed part demonstrates the continuation of linear-in-T behaviour up to temperatures > 500 K. The scattering rate includes an elastic scattering Γ0 due to quenched impurities, \({{\Gamma }}(\phi )={{{\Gamma }}}_{0}+{\rm{Im}}\ {{\Sigma }}(\phi ,T,\omega =0)\). Here, Γ0 = 52 meV, and the coupling g = 0.166 eV between quasiparticles and CDFs is the same as for the self-energy of Fig. 2. b Same as a for an overdoped YBa2Cu3O7−δ sample (Tc = 83 K). Here, Γ0 = 25.5 meV, g = 0.179 eV.
Discussion and conclusions
The above results clearly show that the main features for the CDFs to account for the strange-metal behaviour are a) a short coherence length of 1–2 wavelengths to scatter the low-energy electrons in a nearly isotropic way and b) a rather low energy (ω0 ≈ 10–15 meV) to produce a linear scattering rate down to 100–120 K. We emphasize here that ω0 is only a characteristic minimal scale of CDFs, but these are broad overdamped excitations from ω = 0 (due to damping) up to about 0.1 eV, because they have a dispersion \(\sim \overline{\nu }{({\bf{q}}-{{\bf{Q}}}_{c})}^{2}\) with a stiffness energy scale \(\overline{\nu }\approx 1.0-1.5\) eV(r.l.u.)−2 [see Eq. (3), the discussion in supplementary note 2, and Supplementary Figs. 5 and 6]. Moreover, our approach (extract information about CDFs from RXS experiments, and determine their effect on electron spectra and transport), not only captures the high-temperature linear behaviour of resistivity, but also the deviation from it in the overdoped case, where no other perturbing mechanisms, like CDWs, pairing, spin fluctuations, pseudogap, are present.
The question may also arises whether CDFs can also account for the so-called Planckian behaviour35: at some specific doping, when a strong magnetic field (several tens of Teslas) destroys superconductivity, the linear-in-T resistivity extends down to low temperatures of a few K. In order for our theory to account also for this behaviour, we should find CDFs with a lower characteristic energy of order 0.5–1.0 meV, while maintaining the correlation length short, to keep the scattering isotropic. Unfortunately at the moment no RXS experiments in the presence of such large magnetic fields are viable and we therefore cannot test these expectations. Nevertheless, we feel that it is not accidental that our theory accounts so well of the experiments done so far in the absence of magnetic field which show linearity up to very high temperature, well above T*, so far from the quantum region. No wonder if by lowering the temperature at special values of doping, other effects may come in to modify our parameters values.
One interesting question is why CDFs, even in the absence of the specific Planckian conditions have rather low characteristic energies ≈10–15 meV. In this regard, we notice that CDFs and CDWs have nearly the same characteristic wave vectors, indicating a close relationship. Since CDWs have a nearly critical character (that was theoretically predicted long ago6,36), it is likely that CDFs are aborted CDWs, that for several possible reasons (competition with superconductivity, low dimensionality, disorder, charge density inhomogeneity, ...) do not succeed in establishing longer-range correlations. Still, this tight affinity with CDWs, which are nearly critical and therefore at very low energy, implies that CDFs also may have a broad dynamical range extending down to a rather low-energy scale ω0. In this scenario, where CDWs and CDFs coexist in the system, one and the same theoretical scheme accounts for both excitations.
In conclusion, although some issues are still open, like the effects of magnetic field on CDFs to possibly account for Planckian transport, or the origin of the pseudogap features in transport, we were able to show that CDFs account for the anomalous metallic state of cuprates above T*. Indeed, once the dynamics of the CDFs is extracted from RXS experiments, we can well explain, with the same parameter set, both the strange-metal behaviour of the electron self-energy (therefore all the related anomalous spectral properties observed, e.g. in optical conductivity and Raman spectroscopy, are also explained) and the famous linear-in-T resistivity in the metallic state of high-temperature superconducting cuprates. We thus believe that our results provide a very sound step forward in the long-sought explanation of the violation of the normal Fermi-liquid behaviour in cuprates.
Methods
Fitting procedure to extract the CDW and CDF dynamics
The CDW and CDF contributions to the RXS spectra are captured by a density response-function diagram as reported in Supplementary Fig. 1. In this framework, we carry out a twofold task: on the one hand, we show that dynamical CDFs and nearly critical CDWs account both for the RXS high-resolution, frequency-dependent, spectra, and for the quasi-elastic momentum-dependent spectra. On the other hand, from the fitting of these experimental quantities, we extract the dynamical structure of these excitations needed to calculate the physical quantities discussed above.
According to this scheme, the CDW or CDF contribution to the low-energy RXS spectra is
where \(b(\omega )\equiv {[{{\rm{e}}}^{\omega /{k}_{B}T}-1]}^{-1}\) is the Bose distribution ruling the thermal excitation of CDFs and CDWs, and A is a constant effectively representing the intricate photon-conduction electron scattering processes27,37. In Eq. (2), \({\rm{Im}}\ D({\bf{q}},\omega )\) is the imaginary (i.e. absorptive) part of the (retarded) dynamical density fluctuation propagator, which can describe either CDWs or CDFs. For both we adopt the standard Ginzburg–Landau form of the dynamical density fluctuation propagator, typical of overdamped quantum critical Gaussian fluctuations6,7,36,
where \({\omega }_{0}=\bar{\nu }\ {\xi }^{-2}\) is the characteristic energy of the fluctuations, \(\nu ({\bf{q}})\approx \bar{\nu }\ | {\bf{q}}-{{\bf{Q}}}_{{\rm{c}}}{| }^{2}\), \(\bar{\nu }\) determines the dispersion of the density fluctuations, Qc ≈ (0.3, 0), (0, 0.3) is the characteristic critical wave vector (we work with dimensionless wave vectors, measured in reciprocal lattice units, r.l.u.) and \(\overline{{{\Omega }}}\) is a frequency cut-off. This form of the charge collective mode propagator is typical of metallic systems where the collective modes have a marked overdamped character at low energy, where they can decay into particle-hole pairs (Landau damping). At larger energies, above \(\overline{{{\Omega }}}\), they acquire a more propagating character. In both regimes, however, the maximum of their spectral weight is dispersive with a definite relation between ω and momentum, as it should be for well-defined collective modes. This is valid for both CDFs and CDWs, although the coherence length of the formers is weakly varying in doping and temperature and is generically very short (of the order of the wavelength itself). The sharper CDWs have a nearly critical character, with a marked temperature dependence of the square correlation length, \({\xi }_{{\rm{NP}}}^{2}(T)\). In particular, if these fluctuations had a standard quantum critical character around optimal doping6,7,36,38, one would expect \({\xi }_{{\rm{NP}}}^{2}(T) \sim 1/T\). The CDFs have a similar Qc, the main difference being in the behaviour of the correlation length, that, according to RXS experiments, increases significantly with decreasing the temperature and reaches up to 8–10 lattice spacings for the nearly critical CDWs, while the CDFs have correlation length in the range 2–3 lattice spacings, independently of the temperature.
Although high-resolution spectra provide a wealth of information, they are experimentally very demanding, so that RXS data are more often available in the form of quasi-elastic spectra corresponding to the frequency integration of the inelastic spectra, Eq. (2),
Our first goal is to extract from the experiments all the parameters entering the CDW and CDF correlators, \({\omega }_{0},\bar{\nu },{{\bf{Q}}}_{{\rm{c}}}\) and \(\overline{{{\Omega }}}\).
Since high-resolution and quasi-elastic spectra provide different complementary information, we adopted a bootstrap strategy in which we first estimated the dynamical scale ω0 from high resolution at the largest temperatures, where the NP due to CDWs is absent and all collective charge excitations are CDFs. Then, we used this information to fit the quasi-elastic peaks to extract the relative weight (intensity) of the narrow and broad contributions. Once this information is obtained, we go back to high-resolution spectra, since we now know the relative weight of the CDFs and CDWs contribution at all temperatures.
More specifically, the quasi-elastic peak has a composite character and, once the (essentially linear) background measured along the (1, 1) direction is subtracted (see, e.g. Fig. 2 A–D in ref. 12), the peak may be decomposed into two approximately Lorentzian curves, corresponding to a narrow, strongly temperature dependent, peak due to the standard nearly critical CDWs arising below T ≈ 200 K and to a BP due to the CDFs. This is the main outcome of the RXS experiments reported in ref. 12. We thus fitted each of the two peaks with Eq. (4). From the fits, one can extract the overall intensity parameter A and the ratio \({\omega }_{0}/\bar{\nu }={\xi }^{-2}\). Since only this ratio determines the width of the quasi-elastic spectra, we need a separate measure to disentangle ω0 and \(\bar{\nu }\), so we used the high-resolution information on ω0 for the BP at T = 150 K and T = 250 K to extract \({\bar{\nu }}_{{\rm{BP}}}\approx 1400\) meV(r.l.u.)−2 at these temperatures. The same procedure cannot be adopted for the narrow CDWs peaks, which always appear on top of (and are hardly unambiguously separated from) the broad CDFs contribution. Nevertheless, to obtain a rough estimate, we investigated the high-resolution spectra at low temperature (see Supplementary note 2), where the maximum intensity should mostly involve the NP to extract the characteristic energy of the quasi-critical CDWs obtaining, as expected, much lower values \({\omega }_{0}^{{\rm{NP}}}\approx 1-3\) meV (although these low values are less reliable, due to the relatively low resolution of the frequency-dependent spectra). These estimates allow to extract values of \({\bar{\nu }}_{{\rm{NP}}}\approx 800\) meV(r.l.u.)−2 for the CDWs, comparable with those of the CDFs, suggesting a common electronic origin of the two types of charge fluctuations. To reduce the fitting parameters to a minimum, although subleading temperature dependencies of the high-energy parameters \(\bar{\nu }\) and \(\overline{{{\Omega }}}\) over a broad temperature range can be expected, we kept those parameters constant. We also assumed a constant ω0 for the CDFs, to highlight the noncritical nature of these fluctuations.
Data availability
The experimental resistivity and RXS data (see Fig. 3 of the main text and supplementary figures 4–7) have already been published in ref. 12 and are therefore available in the related data repository39. They are also available from one of the corresponding authors [M.G.] on reasonable request. The datasets (resistivity curves, fitted RXS spectra and electron self-energy) generated during the current study are available from one of the corresponding authors [M.G.] on reasonable request.
Code availability
The theoretical analysis was carried out with FORTRAN codes to implement various required numerical integrations [Eq. (4) in Methods to fit the RXS data, supplementary Eq. (1) for the self-energy, in the supplementary note 1, and supplementary Eq. (6) for the resistivity, in supplementary note 3]. Although the same task could easily by performed with Mathematica or other standard softwares, the FORTRAN codes we used are available from one of the corresponding authors [M.G.] on reasonable request.
References
Varma, C. M., Littlewood, P. B., Schmitt-Rink, S., Abrahams, E. & Ruckenstein, A. E. Phenomenology of the normal state of Cu-O high-temperature superconductors. Phys. Rev. Lett. 63, 1996 (1989).
Kastrinakis, G. A Fermi liquid model for the overdoped and optimally doped cuprate superconductors: scattering rate, susceptibility, spin resonance peak and superconducting transition. Physica C 340, 119 (2000).
Aji, V. & Varma, C. M. Theory of the quantum critical fluctuations in cuprate superconductors. Phys. Rev. Lett. 99, 067003 (2007).
Abanov, A., Chubukov, A. & Schmalian, J. Quantum-critical theory of the spin-fermion model and its application to cuprates: normal state analysis. Adv. Phys. 52, 119 (2003).
Norman, M. R. & Chubukov, A. V. High-frequency behavior of the infrared conductivity of cuprates. Phys. Rev. B 73, 140501R (2006).
Castellani, C., DiCastro, C. & Grilli, M. Singular quasiparticle scattering in the proximity of charge instabilities. Phys. Rev. Lett. 75, 4650 (1995).
Castellani, C., DiCastro, C. & Grilli, M. Non-Fermi-liquid behavior and d-wave superconductivity near the charge-density-wave quantum critical point. Z. Phys. B 103, 137 (1996).
Kivelson, S. A. et al. How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201 (2003).
Caprara, S., Grilli, M., Di Castro, C. & Seibold, G. Pseudogap and (An)isotropic scattering in the fluctuating charge-density wave phase of cuprates. J. Supercond. Nov. Magn. 30, 25–30 (2017).
Caprara, S., Di Castro, C., Fratini, S. & Grilli, M. Anomalous optical absorption in the normal state of overdoped cuprates near the charge-ordering instability. Phys. Rev. Lett. 88, 147001 (2002).
Patel, A. A., McGreevy, J., Arovas, D. P. & Sachdev, S. Magnetotransport in a model of a disordered strange metal. Phys. Rev. X 8, 021049 (2018).
Arpaia, R. et al. Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor. Science 365, 906 (2019).
Yu, B. et al. Unusual dynamic charge-density-wave correlations in HgBa2 CuO4+δ. Phys. Rev. X 10, 021059 (2020).
Miao, H. et al. Discovery of charge density waves in cuprate superconductors up to the critical doping and beyond. arxiv:2001.10294; https://arxiv.org/abs/2001.10294.
Lin, J. Q. et al. Nature of the charge-density wave excitations in cuprates. arxiv:2001.10312; https://arxiv.org/abs/2001.10312.
Wen, J.-J. et al. Observation of two types of charge-density-wave orders in superconducting La2−x Srx CuO4. Nat. Commun. 10, 3269 (2019).
Miao, H. et al. High-temperature charge density wave correlations in La1.875 Ba0.125 CuO4 without spin-charge locking. PNAS 114, 12430 (2017).
Miao, H. et al. Formation of incommensurate charge density waves in cuprates. Phys. Rev. X 9, 031042 (2019).
Chang, J. et al. High-temperature charge-stripe correlations in La1.675 Eu0.2 Sr0.125 CuO4. Phys. Rev. Lett. 124, 187002 (2020).
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2 Cu3 O6+x. Science 337, 821–825 (2012).
Achkar, A. J. et al. Distinct charge orders in the planes and chains of ortho-III-ordered YBa2 Cu3 O6+δ superconductors identified by resonant elastic x-ray scattering. Phys. Rev. Lett. 109, 167001 (2012).
Tabis, W. et al. Charge order and its connection with Fermi-liquid charge transport in a pristine high-Tc cuprate. Nat. Commun. 5, 5875 (2014).
Comin, R. et al. Charge order driven by Fermi-arc instability in Bi2 Sr2−x Lax CuO6+δ. Science 343, 390–392 (2014).
Blanco-Canosa, S. et al. Resonant X-ray scattering study of charge-density wave correlations in YBa2 Cu3 O6+δ. Phys. Rev. B 90, 054513 (2014).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179 (2015).
Gerber, S. et al. Three-dimensional charge density wave order in YBa2 Cu3 O6.67 at high magnetic fields. Science 350, 949–952 (2015).
Comin, R. & Damascelli, A. Resonant X-ray scattering studies of charge order in cuprates. Annu. Rev. Condens. Matter Phys. 7, 369–405 (2016).
Peng, Y. Y. et al. Re-entrant charge order in overdoped (Bi, Pb)2.12 Sr1.88 CuO6+δ outside the pseudogap regime. Nat. Mater. 17, 697 (2018).
Meevasana, W. et al. Hierarchy of multiple many-body interaction scales in high-temperature superconductors. Phys. Rev. B 75, 174506 (2007).
Caprara, S., Sulpizi, M., Bianconi, A., Di Castro, C. & Grilli, M. Single-particle properties of a model for coexisting charge and spin quasicritical fluctuations coupled to electrons. Phys. Rev. B 59, 14980 (1999).
Valla, T. et al. Evidence for quantum critical behavior in the optimally doped cuprate Bi2 Sr2 CaCu2 O8+δ. Science 285, 2110 (1999).
Bok, J. M. et al. Momentum dependence of the single-particle self-energy and fluctuation spectrum of slightly underdoped Bi2 Sr2 CaCu2 O8+δ from high-resolution laser angle-resolved photoemission. Phys. Rev. B 81, 174516 (2010).
Hlubina, R. & Rice, T. M. Resistivity as a function of temperature for models with hot spots on the Fermi surface. Phys. Rev. B 51, 9253 (1995).
Hussey, N. E. The normal state scattering rate in high-Tc cuprates. Eur. Phys. J. B 31, 495 (2003).
Legros, A. et al. Universal T -linear resistivity and Planckian dissipation in overdoped cuprates. Nat. Phys. 15, 142 (2019).
Andergassen, S. et al. Anomalous isotopic effect near the charge-ordering quantum criticality. Phys. Rev. Lett. 87, 056401 (2001).
Ament, L. J. P. et al. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705 (2011).
Caprara, S., Di Castro, C., Seibold, G. & Grilli, M. Dynamical charge density waves rule the phase diagram of cuprates. Phys. Rev. B 95, 224511 (2017).
Arpaia, R. et al. Raw data for ‘Dynamical charge density fluctuations pervading the phase diagram of a Cu-based high-Tc superconductor’; https://doi.org/10.5281/zenodo.2641214 (2019).
Arpaia, R., Andersson, E., Trabaldo, E., Bauch, T. & Lombardi, F. Probing the phase diagram of cuprates with YBa2 Cu3 O7−δ thin films and nanowires. Phys. Rev. Mater. 2, 024804 (2018).
Acknowledgements
We thank C. Castellani, S. Kivelson, M. Le Tacon, M. Moretti Sala and T. P. Devereaux for stimulating discussions. We acknowledge financial support from the University of Rome Sapienza, through the projects Ateneo 2017 (Grant No. RM11715C642E8370), Ateneo 2018 (Grant No. RM11816431DBA5AF), Ateneo 2019 (Grant No. RM11916B56802AFE), from the Italian Ministero dell’Università e della Ricerca, through the Project No. PRIN 2017Z8TS5B, and from the Fondazione CARIPLO and Regione Lombardia, through the ERC-P-ReXS project (2016-0790). R.A. is supported by the Swedish Research Council (VR) under the project "Evolution of nanoscale charge order in superconducting YBCO nanostructures”. G.S. acknowledges support from the Deutsche Forschungsgemeinschaft.
Author information
Authors and Affiliations
Contributions
S.C., C.D.C. and M.G. conceived the project. G.S. performed the theoretical calculations of the self-energy and resistivity, with contributions from S.C., C.D.C. and M.G. R.A., R.F., Y.Y.P., L.B., M.G. and G.G. provided the RXS experimental data. M.G., S.C., R.A., L.B. and G.G. performed the fitting of the RXS data. The manuscript was written by S.C., C.D.C., M.G., G.S., R.A. and G.G., with contributions and suggestions from all coauthors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seibold, G., Arpaia, R., Peng, Y.Y. et al. Strange metal behaviour from charge density fluctuations in cuprates. Commun Phys 4, 7 (2021). https://doi.org/10.1038/s42005-020-00505-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00505-z
This article is cited by
-
Tuning the ground state of cuprate superconducting thin films by nanofaceted substrates
Communications Materials (2024)
-
Signature of quantum criticality in cuprates by charge density fluctuations
Nature Communications (2023)
-
Dissipation-driven strange metal behavior
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.