Abstract
Semiconductor quantum dots are excellent candidates for ultrafast coherent manipulation of qubits by laser pulses on picosecond timescales or even faster. In inhomogeneous ensembles a macroscopic optical polarization decays rapidly due to dephasing, which, however, is reversible in photon echoes carrying complete information about the coherent ensemble dynamics. Control of the echo emission time is mandatory for applications. Here, we propose a concept to reach this goal. In a two-pulse photon echo sequence, we apply an additional resonant control pulse with multiple of 2π area. Depending on its arrival time, the control slows down dephasing or rephasing of the exciton ensemble during its action. We demonstrate for self-assembled (In,Ga)As quantum dots that the photon echo emission time can be retarded or advanced by up to 5 ps relative to its nominal appearance time without control. This versatile protocol may be used to obtain significantly longer temporal shifts for suitably tailored control pulses.
Similar content being viewed by others
Introduction
Coherent nonlinear optics involving quantum emitters is an excellent playground for investigating advanced quantum mechanical phenomena1. Ensembles of quantum emitters in solids typically possess significant inhomogeneous broadening of the optical transition frequency. This might be considered as a drawback, as it leads to rapid dephasing of a macroscopic polarization in the medium. However, the ensemble may also be used to establish a unique collective phenomena in the coherent evolution of the system such as superradiance or entanglement2,3. Moreover, ultrafast optical control of quantum emitters in solid-state systems is possible on picosecond timescales, which is attractive for applications in quantum technologies4, where the use of an ensemble is advantageous for establishing efficient coupling with light5,6.
Semiconductor quantum dots (QDs) are outstanding quantum emitters7,8, showing a discrete energy level spectrum due to the three-dimensional carrier confinement. The transition to the elementary optical excitation of an exciton (electron-hole pair) can often be well approximated by a two-level system (TLS), for which the strong Coulomb attraction in QDs leads to a high spectral selectivity for resonant excitation. QD excitons possess a large oscillator strength, well defined optical selection rules, and long coherence times, which are limited by the radiative decay time of about 1 ns at low temperatures9. This allows one to perform their ultrafast initialization and coherent control with ps- or even sub-ps-optical pulses10,11. Rabi oscillations12,13,14,15,16 and adiabatic rapid passage17,18 were successfully demonstrated on QD excitons. Ramsey fringes and their control by time-dependent electric fields were implemented on single QD level, demonstrating the possibility of optical phase manipulation19,20. In contrast, phase control in an ensemble of emitters has remained difficult because of inhomogeneous broadening of the optical transitions due to fluctuations of QD size, composition, etc. In particular, it was shown that rapid dephasing has significant impact even during excitation with ps-pulses, leading to a complex temporal evolution of the coherent optical response21,22.
The inhomogeneous broadening of optical transitions in a TLS ensemble leads to decay of the macroscopic polarization. However, often the optical coherence on the microscopic level is preserved and the dephasing is reversible. Deterministic delayed emission of light by the QD ensemble can be achieved by the implementation of photon echo (PE) protocols9,21. In the simplest case of a primary two-pulse PE, the second excitation pulse is used to invert the phase distribution of the TLS ensemble, which leads to a subsequent rephasing: the appearance of macroscopic polarization and the emission of the PE. Therefore, modification of the TLS phase evolution during dephasing or rephasing must influence the temporal PE profile23. In nuclear magnetic resonance or electron spin resonance, a large variety of protocols involving complex pulse sequences has been established to shape the dephasing and observe multiple spin echoes on a long timescale24. The most prominent examples are dynamic decoupling (Carr–Purcell and Carr–Purcell–Meiboom–Gill sequences)25,26 and spin locking27. The latter requires elaborate control of the phase in the pulse sequence, which is hard to achieve for optical pulses. Nevertheless, inhibition of dephasing has been also demonstrated for atoms through locking of the macroscopic polarization and the PE shape28,29,30. Deterministic control of PE timing has been recently demonstrated in a rare-earth nanophotonic crystal using symmetrically detuned ac Stark pulses, which result in compression of the atomic frequency comb and subsequent delay of the emitted PE pulse31. However, optical control of the PE timing using resonant optical fields has not been considered yet. Moreover, the short duration of the PE pulses in semiconductor QDs enables us to extend the timing control into the picosecond range which is significantly faster as compared to previous studies.
In this work, we propose a simple approach to this problem and perform a proof of principle demonstration of resonant optical control of the PE timing in self-assembled semiconductor QDs, leveraging concepts of multi-wave mixing in TLS32. First, we show that exciton dephasing and rephasing in a QD ensemble can be efficiently slowed down by resonant excitation with a 2π optical control pulse on picosecond timescales. Moreover, we show that the freezing takes place even when the ensemble has lost its macroscopic polarization at the time of control pulse action. Second, we demonstrate that the application of the control pulse can be used to significantly alter the time of PE emission. Interestingly, this procedure is very robust as there is no need to adjust precisely the optical phase and exact timing of the control pulse. Therefore, our results pave the way to a versatile PE control in ensembles of TLS.
Results
PE timing via dephasing freezing
Here we describe the main principles underlying the control of PE emission time. Let us consider a TLS ensemble with optically allowed transition between the ground state \({\left|1\right\rangle }_{i}\) with energy E1,i and the excited state \({\left|2\right\rangle }_{i}\) with energy E2,i. In a semiconductor QD, these states correspond to the crystal ground state and the lowest energy exciton. The energy of this transition is ℏωi = E2,i − E1,i for the i-th QD, which varies due to QD fluctuations. For simplicity, we assume a Gaussian distribution with central frequency ω0 and inhomogeneous broadening Δ0. We note that in spite of the strong inhomogeneous broadening of the ensemble, i.e., Δ0 ≫ 1/T2, where T2 is the exciton coherence time in a single QD, the resonance frequency ω0 is well defined, because Δ0 ≪ ω0.
In the following, we concentrate on the primary two-pulse PE, resulting from resonant excitation of the ensemble with a sequence of two short optical pulses with areas π/2 and π, respectively. The pulse area is defined as
where \({\Omega }_{{\rm{R}}}(t)={d}_{12}{\mathcal{E}}(t)/\hslash\) is the Rabi frequency with \({\mathcal{E}}(t)\) being the time-dependent electric field amplitude of an optical pulse and d12 is the dipole matrix element of the optical transition. In addition, a control pulse with area 2πn (n is an integer) is applied, to freeze the dephasing. The central photon energy ℏω is the same for all pulses and corresponds to resonant excitation, i.e., ω = ω0. First, let us consider a simplified picture, where the excitation pulses are very short (δ-pulses), whereas the control pulse has a rectangular shape with duration tC. In this case, the ensemble dephasing during excitation by the first and second pulses can be neglected, simplifying the descriptive analysis. In addition, we neglect primarily any decoherence during PE formation and use the Bloch sphere presentation to describe the coherent dynamics of the TLS ensemble in the rotating frame.
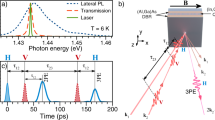
The quantum mechanical state of each QD is given by the coherent superposition of \({\left|1\right\rangle }_{i}\) and \({\left|2\right\rangle }_{i}\), and described by the Bloch vector \({\bf{U}}=(u,v,w)=(\sin \theta \sin \phi ,\sin \theta \cos \phi ,-\cos \theta )\) as shown in Fig. 1a–c. The colatitude θ gives the population difference between the excited and ground state, and the longitude ϕ determines the phase of the quantum state (see Fig. 1a). Initially, all QDs are in the ground state (θ = 0). At time t = 0, the π/2-pulse excitation leads to rotation of the Bloch vectors around the u-axis to the equator (θ = π/2). Then dephasing of the TLS kicks in. Excitons with frequency ω0 remain at the same point of the Bloch sphere (ϕ = 0), whereas for other excitons with detuning Δ = ωi − ω0, the phase evolves linearly with time ϕ = tΔ as shown in Fig. 1d. The Bloch vectors of the excited QDs get evenly distributed along the equator (see Fig. 1a). The second π-pulse, exciting the ensemble at t = τ12, inverts the phase distribution and leads subsequently to refocusing of the TLS at t = 2τ1223,33, when all QD Bloch vectors coincide. This is manifested in the recovery of the macroscopic polarization that was induced by the first pulse, and the emission of a PE pulse with duration of about \({\Delta }_{0}^{-1}\). In this evolution, two prominent time intervals between excitation and PE emission exist: time range 1, 0 < t < τ12 for dephasing; time range 2, τ12 < t < 2τ12 for rephasing.
Schematic illustration of coherent evolution of an exciton ensemble on the Bloch sphere. a Partial dephasing of excitons with different detunings at time t0 after excitation with a π/2-pulse. b Nutation of excitons by the action of control pulse with a pulse area of 2π (solid gray lines) and weak deviations from pure 2π rotations due to detunings at time t0 + tC with tC ≈ Δ−1, where Δ corresponds to maximum detuning of the inhomogeneous ensemble (red lines). For detuned excitons, the rotation occurs with the generalized Rabi frequency which is larger and consequently leads to a deviation from 2π rotation. c Distribution of Bloch vectors at the same time as in b; however, without impact of the control pulse. d Phase evolution of excitons in a two-pulse PE sequence from the excitation pulse at t = 0 to the photon echo at t = 2τ12. Positive (Δ > 0) and negative (Δ < 0) detunings of the exciton resonances are shown by red and blue lines, respectively. First and second excitation pulses are shown in red and magenta peak corresponds to the primary two-pulse PE. e, f Two-pulse PE in presence of the additional 2π pre-pulse (blue) or post-pulse (green) leading to an advanced and retarded PE peak. The evolution of optical phase in presence of the control pulse is shown by solid lines, whereas dashed lines indicate the evolution without the control pulse.
Now we apply the control pulse to the dephased system, i.e., when the macroscopic polarization has decayed and all Bloch vectors are evenly distributed along the equator of the sphere. The area of the control pulse is ΩRtC = 2πn. In the resonant case (Δ = 0), the Bloch vector directed along the v-axis is rotated around the u-axis, transfering the excitons to the same point on the Bloch sphere after time tC. For detuned excitons, the rotation occurs with the generalized Rabi frequency \(\tilde{\Omega }=\sqrt{{\Omega }_{{\rm{R}}}^{2}+{\Delta }^{2}}\) around the vector Ω = (ΩR, 0, Δ), which can be visualized using the equation of motion of the Bloch vector
The analysis shows that there are deviations between the final and starting points of the rotation, as represented by the short red lines in Fig. 1b. For ΩR ≫ Δ, we obtain \(\tilde{\Omega }\approx {\Omega }_{{\rm{R}}}[1+{(\Delta /{\Omega }_{{\rm{R}}})}^{2}/2]\) (further details are provided in the Supplementary Note 1). Moreover, as Ω deviates only slightly from the u-axis, the increment mostly contributes to θ rather than to ϕ. The deviation of the phase after several Rabi rotations from the initial point is significantly smaller compared to free evolution of the system without control pulse after the same time tC (see Fig. 1b, c for comparison). Thus, the control pulse leads to an inhibition of dephasing after its action. It is noteworthy that there are no strict requirements regarding the duration tC of the control pulse, the freezing will take place also for tCΔ > 1. Here we assumed only that ΩR ≫ Δ and (Δ/ΩR)tCΔ ≪ 1 (see Supplementary Note 1).
The impact of the control pulse on the PE formation is manifested in a temporal shift of the PE peak. If the control pulse is applied in time range 1 (control pre-pulse) or 2 (control post-pulse), it effectively slows down the dephasing or rephasing process, respectively. The phase evolutions for these two scenarios are shown in Fig. 1e, f. A consequence of the partially suppressed dephasing in time range 1 is a shorter rephasing period after the arrival of the second pulse. As a result the PE is advanced by tC (blue peak in Fig. 1e). Vice versa, if the rephasing was frozen for the time tC, it will delay the PE appearance after the second pulse by this time (see Fig. 1f).
Interestingly, the effect is independent of the exact timing of the control pulse within the two time ranges and the optical phase of the control with respect to the first and second pulse is also not important. Thus, this method can be used as convenient and efficient tool to control the timing of two- or even multiple-pulse PEs. In addition, the area of the control pulse can be used to modulate the amplitude of PE. In the following sections, we present experimental data demonstrating that the concept can be easily implemented with self-assembled (In,Ga)As QDs. The measurements are analyzed using the optical Bloch equations (OBEs) from which good agreement between the experiment is obtained.
Coherent optical response in QDs
The experiments were performed on a single layer of (In,Ga)As QDs placed at the electric field antinode of a planar λ-microcavity formed by distributed Bragg reflectors as shown in Fig. 2a (for details see “Methods” and ref. 34). The quality factor of the microcavity is about 200, as evaluated from the photoluminescence spectrum in the inset of Fig. 2b. The photon energy of the optical pulses was tuned into resonance with the photonic mode. The use of the microcavity has several advantages16,21: first, it allows us to achieve Rabi rotations using moderate excitation intensities. Second, it enhances the intensity of the emitted PEs. Simultaneously, the spectral width of the cavity mode (ℏΔB ≈ 7.4 meV) is significantly larger than the spectral width of the laser pulses (ℏδω ~ 0.6 meV) and therefore does not influence the coherent dynamics of the optically addressed QD ensemble. On the other hand, we have to consider the QD ensemble as strongly inhomogeneous, as the total spectral width of the ensemble Δ0 is even larger than ΔB.
a Scheme of photon echo experiment, red arrows indicate the first and second pulses, and magenta arrow indicates direction of the PE emission. b PE decays with increasing delay time τ12 between pulses first and second for excitation with different first pulse areas Θ1. Blue, green, and dark red dots correspond to Θ1 ≈ π/2, 3π/2, and 5π/2, respectively. The second pulse area is Θ2 ≈ π. The inset shows photoluminescence spectrum for non-resonant cw excitation with photon energy ℏωexc = 2.33 eV. c–f Temporal profiles of two-pulse PE without control pulse (c), in presence of pre- (d) and post-control pulse (e, f). First and second pulses are schematically depicted in red, pre- and post-control pulses in blue and green. The pulse parameters are Θ1 ≈ π/2, Θ2 ≈ π, τ12 = 80 ps and the control pulse area is ΘC ≈ 2π.
The coherent optical response after the two excitation pulse sequence was measured using transient four-wave mixing (FWM) in reflection geometry at the temperature of 2 K (see Fig. 2a and “Methods”). All pulses are emitted from the same mode-locked laser source and have a duration of about 2.5 ps. Heterodyne detection allows us to measure the temporal profile of the electric field amplitude of the FWM signal from the PE21. A typical signal is shown in Fig. 2c for a delay time between the first and second pulses of τ12 = 80 ps. As expected, the PE peak occurs at the time t = 2τ12. The measured signal is well described by a Gaussian with full-width at half-maximum (FWHM) of about 6.5 ps, which corresponds to a PE duration of 4 ps FWHM (see details in Supplementary Note 2 for the evaluation of the PE pulse duration). The latter is determined by the spectral width of optically addressed excitons which is proportional to the spectral width of the laser. The PE duration can be even shorter if fs pulses are used for excitation9. The PE peak dependence on τ12 is shown in Fig. 2b. The PE amplitude decreases with increasing delay time between the first and second pulse, and is well described by \({P}_{{\rm{PE}}}\propto \exp (-2{\tau }_{12}/{T}_{2})\). Interestingly, an increase of the first pulse’s area Θ1 from π/2 to 5π/2 leaves T2 unchanged at ≈0.7 ns, which is approximately twice as long as the exciton lifetime T1 = 360 ps. Thus, we conclude that excitation-induced dephasing and further many-body interactions are weak in our system, which is essential for robust Rabi oscillations22.
The ensemble comprises neutral and charged QDs, which are occupied with resident electrons. To address only one type of TLS and avoid additional inhomogeneities of the Rabi frequency due to potential differences in the dipole matrix elements for trions (electron-hole pair excitation in a negatively charged QD) and excitons, we used a polarization configuration that results in a PE signal from charged QDs only35. This is ensured for a horizontally H-polarized first pulse and a V-vertically polarized second pulse with the resulting PE signal being H-polarized.
Impact of control pulse on PE timing
First, we demonstrate PE timing by a control pulse when the primary echo has maximum amplitude, which is achieved for the first and second pulse areas of Θ1 ≲ π/2 and Θ2 ≈ π. As will be shown below, the corresponding pulse energy densities are I1 = 4 nJ cm−2 and I2 = 23 nJ cm−2. In this case the PE peak appears at t = 2τ12 (see Fig. 2c). The application of a 2π control pulse has strong impact on the PE peak timing. According to our expectations, we observe an advancement or retardation of the PE by ~5 ps for application of a control pre- or post-pulse, respectively. It is noteworthy that the temporal shift is about two times larger than the duration of the control pulse. This is not surprising because we use a non-rectangular Gaussian pulse and proper calculations of the coherent optical response are required here. We emphasize that the temporal shift is independent of the exact moment of control pulse application within the time range 1 (pre-pulse in Fig. 2d) or 2 (post-pulse in Fig. 2e, f). In addition, we note that the duration of the detected PE signal remains constant with a FWHM of about 6.5 ps. Its amplitude is reduced by about 50%, which is attributed mainly to the damping of Rabi oscillations as will be discussed at the end of this section.
Due to the strong inhomogeneous broadening of the optical transitions, the PE temporal profile depends sensitively on the intensity of the first excitation pulse. In particular, previous studies on (In,Ga)As QDs demonstrated that the PE signal acquires a non-Gaussian shape and experiences a significant advancement for pulse areas larger than π due to inhomogeneity-induced dephasing of the excitons during the optical excitation21. Therefore, the area of the first pulse should be adjusted accurately to not too high values.
Figure 3 shows two-dimensional plots of the PE transients (horizontal axis) vs. pulse area \({\Theta }_{1}\propto \sqrt{{I}_{1}}\) (vertical axis). The top (Fig. 3a–c) and bottom (Fig. 3d–f) rows show experimental data and numerical simulations, respectively. The simulations show ∣PSignal∣, obtained from numerical solution of the extended OBEs22,23. These equations take into account the inhomogeneous broadening and the finite spot size of the laser pulses (for details, see “Methods”) and allow us to reproduce the measured coherent transients well. The results are presented for τ12 = 80 ps and Θ2 ≈ π in the presence of a pre-pulse (Fig. 3a) or a post-pulse (Fig. 3c) with area ΘC ≈ 2π and delays relative to the first and second pulse of 33 and 27 ps, respectively. The reference data without control pulse is shown in Fig. 3b. Clearly, oscillations of the PE amplitude are observed with increasing Θ1 that have to be attributed to Rabi oscillations33.
Two-dimensional plots showing dependence of PE temporal profiles on the amplitude of the first pulse \(\sqrt{{I}_{1}}\) (a, d) in presence of the control pre-pulse, (b, e) without control pulse, and (c, f) in the presence of the control post-pulse. Top row (a–c) and bottom row (d–f) show experiments and simulations, respectively. Data are shown for τ12 = 80 ps delay, Θ2 ≈ π pulse area of second pulse, and control pulse delays of 33 ps relative to the first pulse in a, d and of 27 ps relative to the second pulse in c, f.
In the simplest case of a TLS ensemble excited by a sequence of δ-pulses, the PE peak is centered at t = 2τ12 and its amplitude scales like \({P}_{{\rm{PE}}}\propto \sin ({\Theta }_{1})\). In our experimental setting, the FWM signal at t = 2τ12 is proportional to ∣PPE∣. It follows from Fig. 3b that we observe up to two full Rabi flops (2π rotations). In our measurement, each maximum as function of Θ1 is attributed to Θ1 = mπ/2, where m is an odd integer. In addition to the oscillatory behavior, we observe significant changes in the timing of the PE when Θ1 is varied. This is well reproduced by our numerical simulation (see Fig. 3e) and indicates that dephasing of the ensemble during excitation with the first and second pulses should be taken into account21.
The main result of Fig. 3 becomes obvious when comparing the plots with and without control pulse. Control pulse application shifts the PE signals along the time axis. Even though the PE transient profile may have a complex temporal shape, the impact of pre- or post-pulse with area 2π advances or retards the intensity-dependent transient, without strong changes in its shape. Thus, PE timing by the control pulse is demonstrated as confirmed for arbitrary intensities of the first pulse. Moreover, in our experiment where excitation and control pulses have the same duration the inhibition of dephasing for high intensity pulses may add up. For example, it follows from Fig. 3a that for Θ1 ≈ 3π/2 and ΘC ≈ 2π, the PE appears 8 ps earlier compared to the PE observed for Θ1 ≈ π/2 and in the absence of this control pulse. This advancement noticeably exceeds the PE pulse duration of 4 ps.
Finally, we discuss the influence of the area of the control pulse ΘC. Figure 4 shows the dependence of the PE temporal profile on the control pulse amplitude \(\sqrt{{I}_{{\rm{C}}}}\) for control pre-pulse (a) and post-pulse (b) application, whereas (c) and (d) show the corresponding simulations, where ∣PSignal∣ was calculated (see “Methods” for details). The time delays for pre- or post-pulses correspond to 33 and 27 ps relative to the first or second pulse, respectively. Here we also observe oscillatory behavior due to Rabi flopping. PE timing shifts occur in both cases but the induced delays are opposite for pre- or post-pulse, so that the contour plots are mirrored with respect to t = 2τ12. We concentrate on the PE timing in case of a pre-pulse. For weak pulse energies \(\sqrt{{I}_{{\rm{C}}}}<1.5\times 1{0}^{-4}{{\rm{J}}}^{1/2}{{\rm{cm}}}^{-1}\) (ΘC < π), we observe quenching of the PE amplitude, while its maximum slightly shifts towards longer times. For a pre-pulse amplitude of \(\sqrt{{I}_{{\rm{C}}}}\approx 1.5\times 1{0}^{-4}{{\rm{J}}}^{1/2}\,{{\rm{cm}}}^{-1}\) (ΘC ≈ π), the PE almost disappears. Further increase of IC leads to the appearance of a strong PE signal with its maximum at \(\sqrt{{I}_{{\rm{C}}}}\approx 3\times 1{0}^{-4}\,{{\rm{J}}}^{1/2}\,{{\rm{cm}}}^{-1}\) (ΘC ≈ 2π), which is temporally advanced by 5 ps. The next maximum around \(\sqrt{{I}_{{\rm{C}}}}=6\times 1{0}^{-4}\,{{\rm{J}}}^{1/2}\,{{\rm{cm}}}^{-1}\) (ΘC ≈ 4π) is sufficiently weaker compared to the first one and is only slightly further advanced. Thus, we conclude that the application of a control pre-pulse shows two different regimes depending on its pulse/intensity area. For ΘC < π, the maxima shift slightly to longer times, whereas the application of a more intense control pulse ΘC > π leads to an advanced PE and, in fact, a much larger temporal displacement (see Fig. 4e).
Temporal PE profile as function of the control pulse area \(\propto \sqrt{{I}_{{\rm{C}}}}\): a, b experimental data for contol pre- and post-pulses; c, d corresponding simulations. The delay times for the pre- or post-pulses correspond to 33 and 27 ps, respectively, τ12 = 80 ps, Θ1 ≈ π/2, and Θ2 ≈ π. e Temporal PE profiles for three different pre-pulse intensities IC corresponding to ΘC = π/3 (blue), 3π/4 (red), and 2π (green). Symbols and lines correspond to experiment and modeling, respectively. The associated intensities are labeled with arrows in a.
Discussion
The results of the simulations are in excellent agreement with the experimental data in Figs. 3 and 4, considering the temporal shifts of the PE, as well as their magnitude for pulse areas Θ1 and ΘC up to 2π. The model accounts for the spatially inhomogeneous distribution of the laser intensity on the sample which leads to a spread of Rabi frequencies within the laser spot, which consequently leads to a decay of the Rabi oscillations22. For pulse areas larger than 2π, the damping of the Rabi oscillations is not reproduced quantitatively by our simulations, predominantly due to the simplified description of the laser intensity distributions. It is established that an intensity-dependent damping of the Rabi oscillations can also arise from the coupling to acoustic phonons as demonstrated for spatially homogeneous systems36,37. However, in our case, the spatial inhomogeneity is likely the dominant damping process. A more detailed discussion of intensity-dependent damping is provided in the Supplementary Note 3.
Figure 4 shows that substantial PE shifts in time occur for control pulse areas up to ΘC = 2π. For larger areas, the PE shifts saturate, in agreement with our simulations, which confirm that there exists a maximum possible PE shift for a given pulse duration tC. Nevertheless, it is possible to vary the temporal shift of the PE by setting the proper tC. The exact dependence of the PEs on intensity and duration of the control pulse is determined by the shape of its envelope. For Gaussian pulses, the magnitude of retardation or advancement is linearly proportional to tC if the driving optical field is strong enough. However, if we increase tC while keeping the pulse area constant, the optical field amplitude \({{\mathcal{E}}}_{{\rm{C}}}\) becomes weaker and at some point the PE intensity decreases, whereas the PE pulse broadens and its shape is deformed, indicating that the freezing mechanism is not effective any more for the entire ensemble (for details see also Supplementary Note 4).
Apart from increasing the pulse area or the pulse duration of the control pulse, it is also possible to control the temporal shift by means of multiple pulses. Such an approach can be even more convenient from the application point of view. Our model predicts that the respective time shifts sum up, which is consistent with the interpretation of successive freezing events. Figure 5 shows the temporal profiles of the PE for different double pulse sequences with amplitudes \({{\mathcal{E}}}_{{\rm{C,1}}}\) and \({{\mathcal{E}}}_{{\rm{C,2}}}\), simulated with the OBEs. Two pre-pulses lead to a temporal advancement of the PE, twice as large as compared to one pre-pulse (see Fig. 5a) and two post-pulses to the retardation twice as large as compared to one post-pulse (see Fig. 5b). The resulting temporal shift is independent on the exact time of excitation with the control pulses. However, action of pre- and post-pulses induces opposite temporal shifts. Therefore, as shown in Fig. 5c, cooperative action of such pulses leads to cancellation of the PE shift.
Numerical simulation of PEs calculated using the optical Bloch equations. The first and second pulses are depicted by the electric field amplitudes \({{\mathcal{E}}}_{1}\) and \({{\mathcal{E}}}_{2}\), and excite the quantum dots at t = 0 and 80 ps, respectively. The three PEs in all panels result from a different control pulse sequences: (i) no control pulse, (ii) the single control pulse with amplitude \({{\mathcal{E}}}_{{\rm{C,1}}}\), and (iii) two control pulses with amplitudes \({{\mathcal{E}}}_{{\rm{C,1}}}\) and \({{\mathcal{E}}}_{{\rm{C,2}}}\) are considered. The control pulses \({{\mathcal{E}}}_{{\rm{C,1}}}\) and \({{\mathcal{E}}}_{{\rm{C,2}}}\) are positioned at (a) t = 33 and 45 ps (two pre-pulses), (b) t = 103 and 115 ps (two post-pulses), and (c) t = 50 and 140 ps (one pre-pulse and one post-pulse), respectively. For all simulations, Θ1 = π/2, Θ2 = π, and ΘC,1 = ΘC,2 = 2π.
It should be noted that also intense off-resonant control pulses can be used to influence the dephasing of excitons in QD ensembles. In this case, the ac Stark effect may lead to modulations of the PE amplitude as recently demonstrated in rare-earth solids38,39,40. This behavior has also been confirmed within our model where we find that the temporal shift of the PE decreases in the presence of a detuning, for which also the PE amplitude rapidly reduces with increasing intensity of the control pulse.
Thus, we conclude that the timing of PEs by optical freezing of exciton dephasing and rephasing in QDs is robust with respect to the exact time of arrival of the control pulse. The PE shifts for a large variety of excitation conditions, e.g., it occurs for arbitrary intensities of the first and the second pulses, and it is also independent of the optical phase of the control pulse. Our study shows that the temporal shift can be controlled (i) bidirectionally in a deterministic way (pre- or post-control pulse); (ii) the magnitude of the advancement or retardation is determined by the duration of the intensive control pulse; and (iii) the echo does not experience strong variations of its temporal shape under appropriate conditions, which correspond to a strong driving optical field. The accuracy of timing for the temporal shift is determined by the precision of control pulse parameters (pulse duration, temporal shape, and intensity). The latter can be adjusted to obtain shifts with an accuracy well below the duration of the echo pulse. Therefore, optical freezing can be applied for optical control of PE timing on ultrafast timescales, e.g., for timing corrections in memory protocols5,6,31. Furthermore, addressing the spin degrees of freedom in systems with more than two energy levels (V- and Λ-type arrangements) can be used to split the temporal profile of PEs in two counter-polarized pulses, making it possible to perform wave-function interferometry of electronic excitations in solid-state systems. This opens a vast novel possibilities for investigations of collective phenomena in exciton ensembles.
Methods
Experiment
The experiment was performed on a single layer of (In,Ga)As QDs, surrounded by an AlGaAs λ-microcavity grown by molecular-beam epitaxy. The growth procedure is decribed in ref. 34. The QD density is 1.8 × 109 cm−2. There is a Si δ-layer with donor density 8 × 109 cm−2 located in the barrier 10 nm below the QD layer. The Bragg mirrors consist of alternating GaAs and AlAs layers with thicknesses of 68 and 82 nm, respectively. The top and bottom mirror contain 5 and 18 of such pairs. The same sample was previously studied in ref. 21. The sample has a gradient axis along which the thickness of the cavity and of the layers in the Bragg structure slightly change. Thereby, the energy of the photonic resonator mode varies in the spectral range of 1.343–1.362 eV (910–923 nm) with a gradient of about 3.5 nm/mm. This spectral range corresponds approximately to the energy range of the photoluminescence from the QD ensemble. Therefore, the investigated structure shows strong photoluminescence with the maximum centered at the photon energy of the photonic mode and a FWHM of 7.4 meV, resulting in the quality factor of about 200 (see Fig. 2b).
The sample was kept in a bath cryostat and cooled down to 2 K. As source of the excitation and control pulses, we use a single mode-locked Ti : sapphire laser, which generates pulses with tunable central wavelength at a repetition rate of 75.75 MHz and duration of 2.5 ps, estimated from autocorrelation measurements (see Supplementary Note 2). The spectral width of the laser pulses (FWHM = 0.6 meV) is below the spectral width of the cavity mode and therefore the resonator impact can be considered mostly as enhancement of the electric field amplitude16,21. Degenerate transient FWM was measured in reflection geometry (see Fig. 2a). The first and second pulses hit the sample with wave vectors k1 and k2 at incidence angles of 3∘ and 4∘, respectively, and with the delay time τ12 between them. In addition, we applied a control pulse, which hits the sample with the wave vector k2, delayed relative to the first or second pulse. The delay times between the pulses are controlled by mechanical translation stages and their polarizations are set by Glan prisms combined with half-wave plates.
The laser beams are focused at the sample into spots with diameters of about 400 μm for the first pulse and about 250 μm for the second and control pulses. To record PEs from the charged QDs only, the first pulse had a horizontal (H) polarization, whereas the second and control pulses were vertically (V) polarized. The H-component of the signal was detected along the 2k2–k1 direction. The FWM signal was overlapped with the reference pulse and the resulting interference signal was heterodyne detected at the balanced photoreceiver41. The delay line of the reference pulse tref was scanned relative to the first pulse to obtain the temporal profile of the electric field amplitude of the FWM signal. As result, the modulus of the cross correlation of the electrical field amplitude was detected (see Eq. (9) in the next section). The area of the second pulse was fixed at π, whereas the areas of the exciting and control pulses were varied.
Theoretical modeling
The photoexcited TLS are theoretically described by the OBEs23,42 Their solution provides the dynamics of the microscopic polarization \(p=\left\langle 2\right|\hat{\rho }\left|1\right\rangle\) and the occupation of the upper energy level \(n=\left\langle 2\right|\hat{\rho }\left|2\right\rangle\) where \(\hat{\rho }\) is the density matrix of the system42. Taking into account the inhomogeneous broadening of the TLS ensemble and the finite spot size of the laser pulses leads to a set of extended OBEs22
where T2 and T1 are the coherence time and lifetime of the exciton, respectively. The index i describes the inhomogeneous broadening of the resonance as a superposition of many TLS with different transition frequencies ωi = (E2,i − E1,i)/ℏ. The fraction of TLS with transition frequency ωi is described by the weight function G(ωi), which is taken to be a Gaussian with FWHM ℏΔ0 = 7.5 meV. \({\mathcal{E}}({\bf{r}},t)={{\mathcal{E}}}_{1}({\bf{r}},t)+{{\mathcal{E}}}_{2}({\bf{r}},t)+{{\mathcal{E}}}_{{\rm{C}}}({\bf{r}},t)\) is the total electric field amplitude including the first, second, and control pulses. The temporal dependences of the pulse amplitudes are modeled as Gaussians with FWHM of the intensity profile τd = 2.5 ps, whereas their magnitudes are determined by the pulse areas (Eq. (1)). The finite spot size of the laser pulses is included by considering their spatial profiles as function of r = (x, y). These profiles are taken as
where \(r=\sqrt{{x}^{2}+{y}^{2}}\) is the distance from the laser spot center at (0, 0) and σR is the spot width. For simplicity, we assume that all spots have the same center and the same diameter. To obtain the macroscopic polarization P(r, t) that is created in the sample, the sum of all microscopic polarizations pi(r, t), weighted with G(ωi) and multiplied with d12 has to be calculated according to
The macroscopic polarization P(r, t) is the source of the electric field that is emitted from the spot at position r. The calculations can be performed with P(r, t), as its absolute value is proportional to the absolute value of the emitted electric field. The detector does not resolve each coordinate separately, but rather the spatial integral of all signals is measured, which requires spatial averaging. However, before the electric field that is induced by the macroscopic polarization P(r, t) is detected, it interferes with the reference pulse \({{\mathcal{E}}}_{{\rm{Ref}}}({\bf{r}},t)\); this interference is described by a temporal convolution of the macroscopic polarization and the electric field of the reference pulse that needs to be performed for each coordinate separately. The reference pulse is assumed to have the same spatial profile as \({\mathcal{E}}({\bf{r}},t)\), which results in a factor of \(\exp (-{r}^{2}/{\sigma }_{{\rm{R}}}^{2})\) for each P(r, t). We note that the convolution of two functions is a linear operation, which means that we can perform the spatial averaging first and calculate the temporal convolution in the end. The total signal that results from the spatial averaging then reads
Due to the rotational symmetry of all spatial profiles, it is advantageous to use a polar coordinate system. With this, the extended OBEs only need to be solved for all distances r instead of all coordinates. Discretizing the distance r with the index s, and therefore changing the integration to a summation, leads to the following expression
where Δr is the stepwidth for the discretization of r.
The final signal PSignal(t) is taken by calculating the temporal convolution of Paverage(t) and the temporal dependence of the reference pulse \({{\mathcal{E}}}_{{\rm{Ref}}}(t)\)
where \({{\mathcal{E}}}_{{\rm{Ref}}}(t)={{\mathcal{E}}}_{1}(t)/\max \{{{\mathcal{E}}}_{1}(t)\}\) is given by the normalized first pulse and the convolution of two functions f and g is defined as
For the implementation of the inhomogeneous ensemble, 1500 TLS are considered with frequencies from −15 meV to 15 meV and a resolution of 0.02 meV. For the spatial profile of the laser pulses, the value of σR is not needed in the calculation. Rather, the radii can be written in units of σR. Radii from r = 0.05σR to r = 3.5σR are considered with a stepwidth of Δr = 0.05σR. The coherence time and lifetime of the exciton are chosen according to the experimental values of T2 = 710 ps and T1 = 360 ps. The extended OBEs are integrated as function of time with the fourth-order Runge–Kutta method, using a temporal stepwidth of 0.01 ps. For scanning the pulse area, a stepwidth of ΔΘ = 0.05 was used.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code used for simulations in this study is available from the corresponding author upon reasonable request.
References
Scully, M. O. & Zubairy, M. S. Quantum Optics (Cambridge Univ. Press, 1997).
Rainò, G. et al. Superfluorescence from lead halide perovskite quantum dot superlattices. Nature 563, 671 (2018).
Zarkeshian, P. et al. Entanglement between more than two hundred macroscopic atomic ensembles in a solid. Nat. Commun. 8, 906 (2017).
Fox, M. Quantum Optics: An Introduction (Oxford Univ. Press, New York, 2006).
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nat. Photonics 3, 706 (2009).
Tittel, W. et al. Photon echo quantum memory in solid state systems. Laser Photonic Rev. 4, 244 (2010).
Lodahl, P., Mahmoodian, S. & Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 87, 347 (2015).
Bayer, M. Bridging two worlds: colloidal versus epitaxial quantum dots. Ann. Phys. 531, 1900039 (2019).
Borri, P., Langbein, W., Schneider, S. & Woggon, U. Ultralong dephasing time in InGaAs quantum dots. Phys. Rev. Lett. 87, 157401 (2001).
Bonadeo, N. H. et al. Coherent optical control of the quantum state of a single quantum dot. Science 282, 1473 (1998).
Flissikowski, T., Betke, A., Akimov, I. A. & Henneberger, F. Two-photon coherent control of a single quantum dot. Phys. Rev. Lett. 92, 227401 (2004).
Stievater, T. H. et al. Rabi oscillations of excitons in single quantum dots. Phys. Rev. Lett. 87, 133603 (2001).
Zrenner, A. et al. Coherent properties of a two-level system based on a quantum-dot photodiode. Nature 418, 612–614 (2002).
Ramsay, A. J. et al. Phonon-induced Rabi-frequency renormalization of optically driven single InGaAs/GaAs quantum dots. Phys. Rev. Lett. 105, 177402 (2010).
Suzuki, T. et al. Coherent control of the exciton-biexciton system in an InAs self-assembled quantum dot ensemble. Phys. Rev. Lett. 117, 157402 (2016).
Wigger, D. et al. Rabi oscillations of a quantum dot exciton coupled to acoustic phonons: coherence and population readout. Optica 5, 1442 (2018).
Wu, Y. et al. Population inversion in a single InGaAs quantum dot using the method of adiabatic rapid passage. Phys. Rev. Lett. 106, 067401 (2011).
Simon, C.-M. et al. Robust quantum dot exciton generation via adiabatic passage with frequency-swept optical pulses. Phys. Rev. Lett. 106, 166801 (2011).
Stufler, S., Ester, P., Zrenner, A. & Bichler, M. Ramsey fringes in an electric-field-tunable quantum dot system. Phys. Rev. Lett. 96, 037402 (2006).
Michaelis De Vasconcellos, S., Gordon, S., Bichler, M., Meier, T. & Zrenner, A. Coherent control of a single exciton qubit by optoelectronic manipulation. Nat. Photonics 4, 545 (2010).
Poltavtsev, S. V. et al. Photon echo transients from an inhomogeneous ensemble of semiconductor quantum dots. Phys. Rev. B 93, 121304 (2016).
Poltavtsev, S. V. et al. Damping of Rabi oscillations in intensity-dependent photon echoes from exciton complexes in a CdTe/(Cd,Mg)Te single quantum well. Phys. Rev. B 96, 075306 (2017).
Allen, L. & Eberly, J. H. Optical Resonance and Two-Level Atoms (Wiley, New York, 1975).
Slichter, C. P. Principles of Magnetic Resonance Ch. 8 (Springer, Berlin, 1990).
Carr, H. Y. & Purcell, E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 94, 630 (1954).
Meiboom, S. & Gill, D. Modified spin echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 29, 688 (1958).
Hartmann, S. R. & Hahn, E. L. Nuclear double resonance in the rotating frame. Phys. Rev. 128, 2042 (1962).
Sleva, E. T., Xavier, I. M. & Zewail, A. H. Photon locking. J. Opt. Soc. Am. B 3, 483 (1986).
Yodh, A. G., Golub, J., Carlson, N. W. & Mossberg, T. W. Optically inhibited collisional dephasing. Phys. Rev. Lett. 53, 659 (1984).
Carlson, N. W., Babbitt, W. R., Bai, Y. S. & Mossberg, T. W. Field-inhibited optical dephasing and shape locking of photon echoes. Optics Lett. 9, 232 (1983).
Zhong, T. et al. Nanophotonic rare-earth quantum memory with optically controlled retrieval. Science 357, 1392–1395 (2017).
Rose, H. Numerische Simulationen zum Multi-Wellen-Mischen an Ensemblen von Zwei-Niveau-Systemen, Bachelor Thesis (Universität Paderborn, 2018).
Berman, P. R. & Malinovsky, V. S. in Principles of Laser Spectroscopy and Quantum Optics Ch. 9 (Princeton Univ. Press, 2011).
Maier, S. et al. Bright single photon source based on self-aligned quantum dot-cavity systems. Opt. Express 22, 8136–8142 (2014).
Poltavtsev, S. V. et al. Polarimetry of photon echo on charged and neutral excitons in semiconductor quantum wells. Sci. Rep. 9, 5666 (2019).
Krügel, A., Axt, V. M., Kuhn, T., Machnikowski, P. & Vagov, A. The role of acoustic phonons for Rabi oscillations in semiconductor quantum dots. Appl. Phys. B 81, 897 (2005).
Monniello, L. et al. Excitation-induced dephasing in a resonantly driven InAs/GaAs quantum dot. Phys. Rev. Lett. 111, 026403 (2013).
Chaneliére, T. & Hetet, G. Light-shift-modulated photon-echo. Opt. Lett. 40, 1294–1297 (2015).
Ham, B. S. A controlled ac Stark echo for quantum memories. Sci. Rep. 7, 7655 (2017).
Bartholomew, J. G. et al. Controlling rare-earth ions in a nanophotonic resonator using the ac Stark shift. Phys. Rev. A 97, 063854 (2018).
Poltavtsev, S. V., Yugova, I. A., Akimov, I. A., Yakovlev, D. R. & Bayer, M. Photon echo from localized excitons in semiconductor nanostructures. Phys. Solid State 60, 1635 (2018).
Meier, T., Thomas, P. & Koch, S. W. Coherent Semiconductor Optics: From Basic Concepts to Nanostructure Applications (Springer, New York, 2007).
Acknowledgements
Support by Dr. S. Maier in the epitaxial growth of the sample is gratefully acknowledged. We are grateful to D. Suter and C. Schmidt for useful discussions. We acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) through the Collaborative Research Centre TRR 142 (project number 231447078, project A02). S.V.P. thanks the Russian Foundation for Basic Research (Project number 19-52-12046) and the Saint Petersburg State University (Grant number 51125686). The Würzburg group acknowledges financial support by the state of Bavaria.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
A.N.K., S.V.P., and I.A.A. performed the experiments and analyzed the data. H.R., M.R., and T.M. developed the theoretical model and performed the simulations. C.S., M.K., and S.H. fabricated the samples. A.N.K., H.R., S.V.P., M.R., M.B., T.M., and I.A.A. conceived the idea for the experiment and co-wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kosarev, A.N., Rose, H., Poltavtsev, S.V. et al. Accurate photon echo timing by optical freezing of exciton dephasing and rephasing in quantum dots. Commun Phys 3, 228 (2020). https://doi.org/10.1038/s42005-020-00491-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00491-2
This article is cited by
-
Extending the time of coherent optical response in ensemble of singly-charged InGaAs quantum dots
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.