Abstract
Magnons, as the most elementary excitations of magnetic materials, have recently emerged as a prominent tool in electrical and thermal manipulation and transport of spin, and magnonics as a field is considered as one of the pillars of modern spintronics. On the other hand, orbitronics, which exploits the orbital degree of freedom of electrons rather than their spin, emerges as a powerful platform in efficient design of currents and redistribution of angular momentum in structurally complex materials. Here, we uncover a way to bridge the worlds of magnonics and electronic orbital magnetism, which originates in the fundamental coupling of scalar spin chirality, inherent to magnons, to the orbital degree of freedom in solids. We show that this can result in efficient generation and transport of electronic orbital angular momentum by magnons, thus opening the road to combining the functionalities of magnonics and orbitronics to their mutual benefit in the realm of spintronics applications.
Similar content being viewed by others
Introduction
Spin-heat conversion is a guiding motive in spincaloritronics, which sets out to explore physical phenomena beyond the limits of conventional electronics for energy-efficient information processing1,2,3,4. In this light, spin-wave excitations, known as magnons, offer bright prospects as they mediate thermal spin transport via analogs of Seebeck5,6,7 and Nernst effects in magnetic and nonmagnetic materials8,9,10,11. It has been suggested that the complex spin arrangement exhibited by antiferromagnets and noncollinear magnets provides an alternative route for triggering spin-heat conversion through magnons12, which relies on a vector chirality Si × Sj among spin moments Si and Sj. However, while converting temperature gradients into transverse spin currents as a consequence of the Dzyaloshinskii−Moriya interaction10,13,14,15,16, the spin Nernst effect of magnons is rather inefficient in light materials as it is proportional to the strength of relativistic spin−orbit interaction10,16.
The situation here is quite similar to the one we are facing in the realm of the spin Hall effect17, where strong spin−orbit interaction is prerogative for generation of sizeable spin currents which can be in turn used to e.g. switch the magnetization via the effect of spin−orbit torque18,19,20. Recently, a new paradigm has emerged that relies on the generation of the currents of orbital angular momentum rather than spin, and which carries many advantages over conventional protocols in spinorbitronics21,22,23,24. The corresponding palette of effects evolving around orbitronics is largely grounded in the fundamental fact that the electric-field-driven currents of orbital angular momentum of electrons as a rule overshadow the accompanying currents of spin by far, while remaining large even in the lightest materials21,23. Although nothing is known about interaction of magnonic excitations with electronic orbital magnetism, it appears to be extremely beneficial to marry the promising ideas of orbitronics with the magnon-based philosophy which has been very successful in the domain of spin transport and spincaloritronics so far.
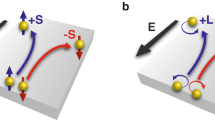
Nowadays, various magnetic phenomena in chiral spin systems are often interpreted based on a second flavor of chirality—the scalar spin chirality (SSC) \({\chi }_{ijk}={\hat{{\bf{S}}}}_{i}\cdot ({\hat{{\bf{S}}}}_{j}\times {\hat{{\bf{S}}}}_{k})\) between triplets of spins, where \({\hat{{\bf{S}}}}_{\alpha }\) is the unit vector along Sα. This type of chirality, which is inherent to skyrmions25,26,27,28,29 and frustrated magnets30,31,32, has been crucial for understanding of e.g. topological Hall effect33,34. In the context of skyrmions the SSC is known as the emergent magnetic field that impacts the dynamics of electrons in a way similar to usual but spin-dependent magnetic field25. In particular, it has been recently realized that the presence of SSC in frustrated magnets and skyrmions reflects in a nonvanishing contribution to the orbital moment of electrons hopping among triplets of non-coplanar spins—just as applying usual magnetic field would give rise to orbital magnetization; see Fig. 1a 28,35,36. The emergence of such chirality-driven orbital magnetization in various systems has been shown in recent years27,28,35,36,37,38,39.
a An electron hopping among noncollinear triplets of spins gives rise to so-called topological orbital moment (TOM), LTOM, which points out of the plane of the spins. The electronic TOM is effectively induced by the scalar spin chirality realized for example on a kagome spin lattice, which is shown in an oblique view. The unit cell is outlined with the dotted line. b Sketch of the orbital Nernst effect of magnons for a ferromagnet on an example kagome lattice. While the generation of a magnon (orange arrows) imprints an average scalar spin chirality into the system and leads to the generation of electronic TOM (red arrow), the generation of a magnon flow in a temperature gradient ∇T results in a transverse deflection of magnons and corresponding TOM-mediated drag of the orbital angular momentum, denoted by \(\left\langle {L}^{{\rm{TOM}}}\right\rangle_T\)—which we refer to as the orbital Nernst effect.
Here, we explore the idea that the coupling between chirality and electronic orbital magnetism presents a unique way to harvest orbital angular momentum by generating magnons. We ask the question whether magnonic excitations themselves can give rise to net SSC, even if it is absent in the ground state. If yes, then generating SSC by magnons would provide a unique mechanism for imprinting electronic orbital angular momentum into the system. Further, since an applied temperature gradient can drive magnon scattering, it is reasonable to ask whether this can result in a magnon “drag” of orbital angular momentum. If present, such an effect (Fig. 1b) would give an ability of driving orbital currents by magnons in addition to currents of spin. We provide confirmative answers to both questions, and discuss possible implications of our findings for spintronics applications.
Results
In order to demonstrate the emergence of magnon-mediated orbital magnetization and generation of the current of electronic orbital angular momentum, we refer to microscopic tight-binding and effective spin model of a ferromagnet on a kagome lattice. Conceptually, we separately consider the properties of the electronic bath that exhibits topological orbital magnetism, and the properties of the reservoir of magnons, while coupling both parts of the system by effective topological orbital electron−magnon interaction. First, we present the results that concern the generation of electronic orbital magnetism by the mechanism of SSC.
Electronic topological orbital magnetism
We model the electronic part of our system by making use of the tight-binding model of a magnet on a two-dimensional (in the xy-plane) kagome lattice (Fig. 1a), whose details are explained in “Methods”. The electronic Hamiltonian is set by considering hoppings among the atoms and an exchange splitting at each atomic site, in a way similar to that of refs. 40,41. To uncover the SSC-mediated mechanism of orbital moment generation, the spin−orbit interaction is explicitly not taken into account. We start with the ferromagnetic state with the spins pointing out of the plane (see the corresponding band structure in Fig. 2a) and then rotate all spins into the plane by an angle θ away from the z-axis, while keeping the azimuthal angles of the three spins at 0°, 120° and 240° (keeping z-axis as the threefold rotational symmetry axis). We find that the effect of such non-coplanarity on the band structure is most prominent in the vicinity of band degeneracies (Fig. 2a).
a The electronic band structure based on the tight-binding model of a kagome ferromagnet. The orange lines represent the bands of the ferromagnetic structure and the blue dotted lines mark the bands of the state canted by a polar angle of θ = 10°. b The total toplogical orbital moment (TOM) as a function of the canting angle for the electron density of ρ = 1.0 e(cell)−1. The red symbols mark the calculated values according to Eq. (2), while the black line is a fit according to Eq. (1). The inset displays the value of the topological orbital susceptibility κTO around the ferromagnetic state as a function of Fermi energy of the tight-binding model. c Topological phase diagram of the magnonic bands of a kagome ferromagnet as a function of the second nearest-neighbor Heisenberg coupling J2 and Dzyaloshinskii−Moriya interaction (DMI) (in units of the nearest-neighbor Heisenberg coupling J1), as well as external magnetic field B (in Tesla). Colors highlight different phases that are characterized by sets (C1,C2,C3) of Chern numbers. The unstable ferromagnetic phase is shown in red.
As has been realized in the past years, the nonvanishing SSC in canted spin systems gives rise to a special type of electronic orbital moment—the topological orbital moment (TOM). While being in its essence a Berry phase effect, microscopically, such TOM arises in response to breaking of symmetry by non-coplanarity, which allows for formation of nonlocal persistent orbital currents of electrons without any need for spin−orbit interaction28,38,42,43,44. The emergence of topological orbital magnetization in various systems, including celebrated MnGe and Mn3Ge compounds, has been shown in recent years from effective models, tight-binding and first-principles calculations27,28,35,36,37,38,39. The Zeeman interaction of TOM with an external magnetic field is known as the ring exchange, which contributes to the spin Hamiltonian of chiral spin systems45,46,47. By its nature, the TOM can be phenomenologically expressed in terms of the SSC as28,37,38:
where 〈ijk〉 indicates that spins i, j, and k are nearest neighbors forming a triangle (Fig. 1a), and a unit vector \({\hat{{\bf{e}}}}^{ijk}\) is normal to the triangle plane. The constant κTO is known as the topological orbital susceptibility28,38 and it characterizes the strength of the orbital response of electrons to the SSC. It has been shown that for materials with relatively small spin−orbit strength, the influence of the spin−orbit interaction on TOM is minor37,38. This is in contrast to collinear magnets, where the orbital magnetism appears solely as a result of spin−orbit interaction in the system. Here, we do not consider the so-called chiral, proportional to the vector spin chirality, contribution to the orbital magnetism in the system, as it is expected to arise in the regime of large spin−orbit interaction, not considered in this work28.
For our electronic system we numerically access the response of electronic orbital magnetization to canting by referring to the rigorous expression:
where \({\mathcal{H}}({\bf{k}})\) is an effective single-particle tight-binding electronic Hamiltonian of our system canted by an angle θ, unk is a periodic part of Bloch state with band index n and crystal momentum k, its corresponding energy eigenvalue is \({{\mathcal{E}}}_{n{\bf{k}}}\), and the summation goes over all occupied states below the Fermi energy \({{\mathcal{E}}}_{{\rm{F}}}\). We analyze the behavior of LTOM as a function of angle θ, and compare it to that expected from Eq. (1), finding that, overall, the explicitly calculated orbital response of the system to canting fits the TOM-picture very well; see for example the case with band filling of one electron per unit cell in Fig. 2b. In accord to this picture, the orbital moment vanishes for the coplanar and collinear cases, and the largest value of TOM is reached for the state with largest SSC. This type of behavior, when κTO with a good degree of accuracy can be assumed to be independent of θ in the whole range of possible canting, persists over large regions of energies. The deviations from it occur in the vicinity of band crossings where the response of the band structure to canting is very large, and where the orbital response is expected to be pronounced28.
Regardless, in our work, we focus on the interplay of orbital magnetism and magnons that cause small deviations of the magnetization from the ferromagnetic state; thus the value of the topological orbital susceptibility in the vicinity of θ = 0° is of primary interest. Our calculations, shown in the inset of Fig. 2b for the entire range of energies of the model, reveal that the magnitude of κTO in the limit of small canting exceeds the value of 1 μB over large regions of energy, and sensitively depends on the electronic structure.
Overall, our calculations demonstrate that even within the simplest electronic structure considered here, it is possible to generate sizable electronic orbital magnetization by the mechanism of SSC, the properties of which can be tuned by electronic structure design. We show below how to exploit the SSC generation by magnons in order to imprint electronic orbital magnetism into the system.
Modeling magnonic excitations
We consider the effect of magnons on electronic orbital magnetism by referring to an effective Hamiltonian of spin waves of a ferromagnet on a two-dimensional kagome lattice, which is given by
where Jij mediates the Heisenberg exchange between spins Si and Sj on sites i and j, the second term is the antisymmetric Dzyaloshinskii−Moriya interaction (DMI) quantified by vectors Dij, and the fourth term couples the spins to an external magnetic field B. In addition, we extend the Hamiltonian by the ring-exchange term in Eq. (3) to include explicitly the interaction between the magnetic field and the TOM45,47,48. This term is given by the product of the SSC and the topological orbital susceptibility κTO 28,38. Owing to the symmetry of the planar kagome lattice, the TOM and the DMI vectors are perpendicular to the film plane (along the z-axis), along which we also apply the external magnetic field of magnitude B.
We consider in our analysis only nearest-neighbor interactions except for the Heisenberg term, where we include next-nearest neighbors as well. We set the nearest-neighbor Heisenberg coupling to J1 = 1 meV, the next-nearest neighbor strength amounts to J2 = 0.1J1 unless stated otherwise, and the spin-moment length S is fixed to 1. For the magnitude of topological orbital susceptibility κTO we choose a representative value of −0.5 μB—a value not only motivated by recent material studies36,38,39, but also corresponding to the lower bound of κTO-range found above for small deviations from the ferromagnetic state. As follows from model considerations, the range of values for κTO exhibited by the electrons living on a kagome lattice is very large, and one should keep in mind that the effects discussed below can be further enhanced by engineering the electronic structure and the values of κTO. This route of material design is distinctly different from that associated with the design of the spin−orbit strength, taken routinely in conventional spinorbitronics.
We first analyze the magnonic bands and their topology in Figs. 2c and 3a−c. The dispersion of the three spin-wave branches in the presence of an external magnetic field of 10 T is presented in Fig. 3a. In the absence of DMI, the different magnon bands exhibit Chern numbers 1, 0, and −1 solely due to the coupling of the magnetic field to the SSC manifesting in a non-zero TOM carried by the magnons, as we show below. By including the effect of DMI, Fig. 3b, we find that the coupling to the vector spin chirality modifies the dispersion without changing the topology of the bands for this choice of parameters. While the microscopic origin of interactions with vector and scalar spin chiralities which enter Eq. (3) is fundamentally different, their roles for the resulting magnon dispersion are rather similar at the level of linear spin-wave theory. Based on the obtained spin-wave spectra and Berry curvature calculations, we present in Fig. 2c the complete topological phase diagram as a function of the model parameters entering the Hamiltonian. Sampling the nearest-neighbor coupling J2, the DMI strength, and the magnitude of the B-field, we identify eight nontrivial phases in addition to an unstable ferromagnetic state. These phases come in pairs with an opposite overall sign in the set of Chern numbers.
a−c Fat band analysis for the magnonic bands of the model for the values of the Dzyaloshinskii−Moriya interaction (DMI) (in units of the nearest-neighbor Heisenberg coupling J1), and magnetic field B specified at the bottom. Red and blue colors represent positive and negative sign of the local topological orbital moment (TOM) \({L}_{n{\bf{k}}}^{{\rm{TOM}}}\), respectively, and the line thickness denotes the corresponding magnitude. Bold integers indicate the Chern numbers of the spin-wave bands. d−g Distribution of the local TOM in the Brillouin zone for different temperatures, after summing over all magnon branches weighted by the Bose distribution. The color map is in units of μB, and the model parameters of panel (a) are used. h−k Overall TOM of the spin-wave system as a function of magnetic field and temperature. The panels (h−j) present phase diagrams for the DMI strengths of 0, 0.2J1, and −0.2J1, respectively, with the color map indicating the net TOM in units of μB per unit cell. In (k), solid and dotted lines correspond to DMI strengths of 0 and 0.2J1, respectively, and the magnetic field is given in Tesla.
Imprinting orbital magnetism by magnons
To uncover the role of magnons in giving rise to orbital magnetism of the electrons through SSC, we evaluate the average value of the SSC that a given magnon carries, and translate it into the topological orbital moment of the magnon via the SSC-mediated orbital electron−magnon coupling. We refer to this quantity as the local TOM of the nth magnon branch and access it according to \({L}_{n{\bf{k}}}^{{\rm{TOM}}}={\kappa }^{{\rm{TO}}}\left\langle {\Psi }_{n{\bf{k}}}| \chi ({\bf{k}})| {\Psi }_{n{\bf{k}}}\right\rangle\). Figure 3a−c illustrates the value of the local TOM of the magnon branches as represented by the line thickness. While either finite DMI or B-field are necessary to activate the local TOM, the Γ point typically hosts the minima and maxima of \({L}_{n{\bf{k}}}^{{\rm{TOM}}}\) in our model. Specifically, the local TOM of the lowest spin-wave branch reaches its global minimum at Γ whereas the higher magnon bands carry the maximal values as they correspond to precessional modes with an innately larger SSC. Clearly, the complex interplay between DMI and the orbital Zeeman coupling modifies not only the magnon topology but imprints also on the local TOM. In particular, the ordering of the states with positive and negative sign of \({L}_{n{\bf{k}}}^{{\rm{TOM}}}\) is inverted during the topological phase transition, which directly links the nature of electronic orbital magnetism with nontrivial topology of magnonic bands.
Since the local orbital moment carried by magnons depends strongly on the band and position in the Brillouin zone, the effect of finite temperature that results in the excitation of magnons with finite energy can give rise to a net magnon-mediated electronic orbital magnetization. To show this, we introduce a finite temperature T in our spin system, and calculate the orbital response of the electronic bath. In Fig. 3d−g we analyze the sum of the local TOM weighted by the occupation number of each spin-wave branch at a given temperature, i.e., \(\ell ({\bf{k}})={\sum }_{n}{L}_{n{\bf{k}}}^{{\rm{TOM}}}{n}_{{\rm{B}}}({\epsilon }_{n{\bf{k}}})\). Here, the magnons follow the Bose distribution function \({n}_{{\rm{B}}}(\epsilon )={[\exp (\beta \epsilon )-1]}^{-1}\) with β = 1/kBT. Depending on T, the number of excited magnons is different in each branch, which leads to a nontrivial distribution of ℓ(k) in momentum space, as shown in Fig. 3d−g for the model with finite B-field but zero DMI. At low T, Fig. 3d, only the Γ-point magnons from the first branch can be excited, leading only to small local contributions around the BZ center. As the temperature is increased, all spin-wave states from the first branch are excited such that ℓ(k) peaks in the M point with moderate magnitude as shown in Fig. 3e. If additionally magnons from the higher branches contribute at elevated temperatures, the maximum of ℓ(k) occurs at the Γ point, where the local TOM of the corresponding magnon states is the largest.
The overall TOM of the spin-wave system at given T can be then obtained as:
where \({\left\langle {L}^{{\rm{TOM}}}\right\rangle }_{T}\) is the total TOM carried by thermally activated magnons per unit cell (see Supplementary Note 1). Figure 3h−j illustrates the B, T-dependence of the overall TOM for various DMI coupling strengths. On the one hand, as more magnons become available to carry the TOM, higher temperatures enhance the magnitude of \({\left\langle {L}^{{\rm{TOM}}}\right\rangle }_{T}\) in the spin-wave system. On the other hand, the roles of orbital Zeeman coupling and DMI are intertwined in generating TOM. For example, while TOM locally vanishes at zero DMI and B-field, a DMI with positive coupling strength generally counteracts the effect of the magnetic field on TOM if κTO is negative. For nontrivial choices of these parameters, however, Fig. 3k illustrates that at low T the total TOM increases linearly, and, depending on the value of κTO, it can be sizeable.
The total topological orbital moment emerges as a quantity which can be readily measured experimentally by referring to techniques which are sensitive to orbital magnetization in solids23,24,49,50. The sizeable magnitude of the effect that we predict not only lends itself to an unambiguous observation, but can also influence significantly the temperature dependence of the overall magnetization in a sample, providing thus an additional “anomalous” orbital channel to the conventional mechanism of magnetization variation mediated by thermally excited magnons2,3,4. Given the much stronger sensitivity of topological orbital magnetism to electronic structure changes, as compared to the spin, we suggest that the magnon-driven orbital magnetism can serve as a unique tool in tracking the electronic structure dynamics in various types of setups. As we also observe that the sign of \({\left\langle {L}^{{\rm{TOM}}}\right\rangle }_{T}\) correlates with the ordering of the topological spin-wave bands and their respective Chern numbers, we suggest to exploit the total topological orbital moment as an indicator of topological dynamics of magnons.
Driving orbital currents by magnons
Answering the first question posed in the introduction, our analysis demonstrates that a finite TOM, stemming from orbital electronic currents, can be triggered by thermally activated magnons.
This observation suggests that TOM is intimately linked to thermal spin transport which is mediated by the coupling of the SSC to the bath of electrons in the system. As a consequence, the well-known magnon Nernst effect acquires a novel and fundamentally distinct contribution that we coin the orbital Nernst effect of magnons, which is illustrated in Fig. 1a. The phenomenon of orbital Nernst effect relates spatial temperature gradients to the emergence of topological orbital currents via \({j}_{x}^{{\rm{TOM}}}={\kappa }_{{\rm{ONE}}}^{xy}{(\nabla T)}_{y}\), where \({\kappa }_{{\rm{ONE}}}^{xy}\) stands for the topological orbital Nernst conductivity, which within the semiclassical theory reads
where \({c}_{1}(\tau )=\mathop{\int}\nolimits_{0}^{\tau }\mathrm{ln}\,[(1+t)/t]{\mathrm{d}}t=(1+\tau )\mathrm{ln}\,(1+\tau )-\tau \mathrm{ln}\,\tau\). In essence, the latter relation quantifies the fundamental mechanism behind a magnon—which develops a transverse velocity proportional to the Berry curvature in an applied temperature gradient—“dragging” with it the electronic orbital angular momentum which is generated by non-zero SSC inherent to the magnon. In contrast to the usual spin Nernst effect of magnons10,16,51, the conductivity in Eq. (5) characterizing the orbital Nernst effect depends explicitly on the local TOM of the magnon branches (see Supplementary Note 1).
Answering the second fundamental question posed in the introduction, below we reveal the existence of this effect by explicit calculation. In Fig. 4 we summarize the nontrivial dependence of the orbital Nernst effect on T and on the model parameters, as well as its correlation with the topology of the magnon bands. Although the orbital Nernst effect has a distinct microscopic origin in the orbital electron−magnon coupling, our prediction is that the corresponding conductivity can reach the order of π−1kB. If we assume a distance of 5 Å between two kagome layers, an orbital Nernst conductivity of (2π)−1kB is equivalent to the value 4.394 × 10−15 Jm−1 K−1, or 66,786 ℏe−1 μA cm−1 K−1, which is comparable to the values known for the spin Nernst effect of magnons or spin Nernst effect of electrons10,16,52,53,54,55. We emphasize that the magnitude of the effect can be further enhanced by proper electronic structure engineering of the topological orbital susceptibility, which in its nature does not rely on the presence of spin−orbit interaction in the system. This underlines the strong potential of the orbital Nernst effect for the realm of spincaloritronics and marks this effect as an entry point for ideas evolving around magnon-mediated orbitronics.
a Phase diagram of the orbital Nernst effect. Dependence of the orbital Nernst conductivity \({\kappa }_{{\rm{ONE}}}^{xy}\) on magnetic field B and second nearest-neighbor Heisenberg coupling J2 (in units of the nearest-neighbor Heisenberg coupling J1) at T = 200 K and zero Dzyaloshinskii−Moriya interaction (DMI). Solid black lines are the boundaries between different topological phases characterized by the Chern numbers of the three magnon branches. b \({\kappa }_{{\rm{ONE}}}^{xy}\) as a function of B and temperature T for the model with DMI strength of 0.2J1. c, d Comparison of the \({\kappa }_{{\rm{ONE}}}^{xy}\) (solid lines) and magnon Nernst conductivity \({\kappa }_{{\rm{N}}}^{xy}\) (dashed lines). c \({\kappa }_{{\rm{ONE}}}^{xy}\) and \({\kappa }_{{\rm{N}}}^{xy}\) as a function of B for the model at 200 K with DMI strength of 0 (red) and 0.2J1 (blue). The different topological phases are distinguished with a thin vertical line. d \({\kappa }_{{\rm{ONE}}}^{xy}\) and \({\kappa }_{{\rm{N}}}^{xy}\) as a function of T for different strengths of the DMI and B.
Our analysis, which is supported by our calculation (see Fig. 4 and Supplementary Note 1), reveals that both DMI and the coupling of external magnetic field to the SSC can generate a finite orbital Nernst conductivity. Comparing the two panels in more detail, we note that the sign of \({\kappa }_{{\rm{ONE}}}^{xy}\) is the same in topological phases for which the sets of Chern numbers differ by a global sign. This invariance stems from the product of the two microscopic quantities in Eq. (5), each of which changes its individual sign as the Chern numbers are reversed. Still, as exemplified in Fig. 4a−c, the orbital Nernst effect is characteristic to the nontrivial magnon topology of distinct phases. Close to topological phase transitions, the orbital Nernst effect changes abruptly and thus behaves rather differently compared to thermal Hall and magnon Nernst effects (see Fig. 4c and Supplementary Fig. 11). As a consequence, the conductivity \({\kappa }_{{\rm{ONE}}}^{xy}\) can in principle reach very large values near the phase boundary. Since the orbital Nernst effect is absent without the B-field and DMI (see Supplementary Fig. 9a), the peak structure in Fig. 4b, c for a magnetic field of about 7 T can be understood as a result of the competition between the effects of orbital Zeeman coupling and DMI, which results in a strongly suppressed orbital Nernst effect. On the other hand, Fig. 4d and Supplementary Fig. 9b reveal the qualitative difference in the temperature dependence of the orbital Nernst effect and conventional Nernst effect. The peculiar behavior of the orbital Nernst effect in response to an external magnetic field can be used to disentangle it from the magnon Nernst effect experimentally. Overall, the orbital Nernst effect presents a unique playground for generating orbital currents in magnonic systems, and we outline the prospects of this effect below.
Discussion
While in our work we consider ferromagnets on a kagome lattice, among material representatives of which one can name for example Cu(1-3,bdc)56 or Nd3Sb3Mg2O1457, the conclusions drawn from our analysis go well beyond this particular class of materials, and include for instance collinear or noncollinear states on a hexagonal, pyrochlore, B20 and Mn3Ge quasi-kagome type of lattice36,38,58,59,60, as well as their thin films. While in the latter classes the magnon drag of orbital momentum is nonvanishing, a precursor of prominent magnon-driven orbital phenomena is a large topological orbital susceptibility κTO in a given material of the order of that exhibited, e.g., by MnGe38, Mn/Cu(111)36, or Mn3Ge39. The latter quantity can be estimated from microscopic calculations, as well as from experiment, as to first approximation κTO is given by the orbital susceptibility of the system28.
To show this explicitly, we extract the rough magnitude of κTO from existing calculations and specifically consider the case of Mn3Ge39, exhibiting an almost coplanar noncollinear arrangement of spins. By using the exchange parameters used to fit the experimental magnonic spectra, and taking into account a small canting of spins in Mn3Ge in an external magnetic field (see Supplementary Note 2 and Supplementary Figs. 12−17 for a detailed discussion), in Fig. 5 we provide the orbital analysis of the bands, and the estimates for the magnon, \({\kappa }_{{\rm{N}}}^{xy}\), and orbital, \({\kappa }_{{\rm{ONE}}}^{xy}\), Nernst conductivities in this material as a function of temperature. Our calculations show that in Mn3Ge the magnitude of magnonic and orbital contributions to the transverse thermal currents is comparable and sizeable. As both contributions are opposite in sign, this potentially gives rise to a nontrivial dependence of the overall current of angular momentum on temperature, which can be accessed experimentally. This signifies the potential relevance of discussed here orbital effects for wide classes of diverse magnetic materials.
a Fat band analysis for the magnonic bands of Mn3Ge with the canting angle η = 1°. Red and blue colors represent positive and negative sign of the local topological orbital moment (TOM) \({L}_{n{\bf{k}}}^{{\rm{TOM}}}\), respectively, and the line thickness denotes the corresponding magnitude. b Comparison between the magnon Nernst conductivity (dotted line) and orbital Nernst conductivity (solid line) as the function of temperature for Mn3Ge. Different color represents two different canting angles η = 0.4° (red color) and η = 1° (black color). The unit of Nernst conductivity in (b) is 103ℏe−1μA (cm)−1 K−1. The schematic sketch of the magnetic structure of Mn3Ge is shown in the inset.
The uncovered mechanism of magnon-driven chirality accumulation has far-reaching consequences for the transport properties of systems which exhibit such chirality. For example, it will result in the generation of topological Hall or topological spin Hall effect of the underlying electronic bath61,62,63, which will contribute to the temperature dependence of the anomalous Hall conductivity even in nominally collinear magnets64. On the other hand, magnon-driven orbital magnetism brings the orbital angular momentum variable into the game of magnon-based spincaloritronics, which is conventionally associated with generation and transport of spin. Unleashing the orbital channel for the magnon-mediated effects poses a key question of the role of orbital magnetism for the temperature-dependent magnetization dynamics; however, it also opens a number of exciting possibilities for direct applications. For example, in analogy to the spin−orbit torques18,20, we envisage that the flow of orbital angular momentum generated by magnons can be used to generate sizeable orbital accumulation and orbital torques on adjacent magnets, which can go either via the mechanism of direct injection of the orbital current into the ferromagnet, or might involve an intermediate conversion of the orbital current into the spin current with the magnitude of the converted spin current larger by far than that driven by the local spin Hall effect23,24,50.
Given the sensitivity of the orbital effects to the topology of magnonic bands and generally magnonic properties, we suggest that accessing the magnon-mediated dynamics of orbital properties can serve as a unique tool of tracking the topological dynamics of magnons. Moreover, our findings also point at an exciting possibility of exploiting properly engineered orbital injection for excitation of specific magnonic modes via the inverse orbital Nernst effect. As in topologically complex materials the electronic topology is directly related to the orbital properties65, this link can be used for realizing hybrid nontrivial electron−magnon topologies. Overall, here, the uncovered orbital electron−magnon coupling bares various prospects for integration of spinorbitronics schemes into magnonic setups and vice versa, which shall be explored in the future.
Methods
Calculation of electronic TOM
For the calculation of the electronic structure and resulting TOM, we employ a tight-binding model on a two-dimensional kagome lattice. The Hamiltonian consists of hoppings and local exchange interactions,
where i and j are site indices, 〈 ⋯ 〉 and 〈〈 ⋯ 〉〉 indicate first and second nearest-neighbor pairs, respectively, and \({\hat{{\bf{m}}}}_{i}\) is the direction of the local magnetic moment at site i. The first and second nearest hopping amplitudes are chosen as t1 = 1.0 eV and t2 = 0.15 eV, respectively, and strength of the exchange interaction is set to J = 1.7 eV. For three basis atoms in the unit cell, namely A, B, and C, the directions of the local magnetic moments are parameterized by \({\hat{{\bf{m}}}}_{i}=(\sin \theta \cos {\phi }_{i},\sin \theta \sin {\phi }_{i},\cos \theta )\). The azimuthal angles ϕi are assumed to be chirally ordered, i.e., ϕi = ϕ0 for i ∈ A, ϕi = ϕ0 + 2π/3 for i ∈ B, and ϕi = ϕ0 + 4π/3 for i ∈ C. For the fitting of the TOM in Fig. 2b, we assume
To extract κTO near θ = 0 (inset of Fig. 2b), we use
where the second derivative is evaluated by a finite difference method.
Linear spin-wave theory
Linear spin-wave theory55,66 is used to obtain the eigenvalues and eigenvectors of the above Hamiltonian, which we reformulate first in terms of bosonic ladder operators ai and \({a}_{i}^{\dagger }\) via the Holstein−Primakoff transformation67. In the resulting spin-wave Hamiltonian, we keep only terms that are quadratic in the ladder operators. This approximation has been used before to treat the effect of chirality47. Within linear theory, the SSC χijk, coupling directly to the magnetic field in Eq. (3), can be expressed as47:
To map from real to momentum space, we perform a Fourier transform of the bosonic ladder operators, which leads to the Hamiltonian matrix H(k) at the spin-wave vector k = (kx, ky), which is diagonalized to obtain the eigenvectors and the energy spectrum of the spin waves. We address the topological character of the magnonic bands by computing the Chern number Cn, given by \({C}_{n}=\frac{1}{2\pi }\int {\Omega }_{n{\bf{k}}}^{xy}\ {\mathrm{d}}{\bf{k}}\), where the integral is performed over the Brillouin zone (BZ), and \({\Omega }_{n{\bf{k}}}^{xy}\) represents the magnon Berry curvature of the nth spin-wave branch:
where \(\left|{\Psi }_{n{\bf{k}}}\right\rangle\) is an eigenstate of the spin-wave Hamiltonian with the energy ϵnk (see Supplementary Methods).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code of this work is available from the corresponding author on request.
References
Žutić, I., Fabian, J. & Sarma, S. D. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323 (2004).
Bauer, G. E., Saitoh, E. & Van Wees, B. J. Spin caloritronics. Nat. Mater. 11, 391–399 (2012).
Boona, S. R., Myers, R. C. & Heremans, J. P. Spin caloritronics. Energy Environ. Sci. 7, 885 (2014).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Geballe, T. H. & Hull, G. W. Seebeck effect in silicon. Phys. Rev. 98, 940 (1955).
Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).
Xiao, J. et al. Theory of magnon-driven spin Seebeck effect. Phys. Rev. B 81, 214418 (2010).
Kikkawa, T. et al. Longitudinal spin Seebeck effect free from the proximity Nernst effect. Phys. Rev. Lett. 110, 067207 (2013).
Miyasato, T. et al. Crossover behavior of the anomalous Hall effect and anomalous Nernst effect in itinerant ferromagnets. Phys. Rev. Lett. 99, 086602 (2007).
Kovalev, A. A. & Zyuzin, V. Spin torque and Nernst effects in Dzyaloshinskii-Moriya ferromagnets. Phys. Rev. B 93, 161106(R) (2016).
Meyer, S. et al. Observation of the spin Nernst effect. Nat. Mater. 16, 977–981 (2017).
Menzel, M. et al. Information transfer by vector spin chirality in finite magnetic chains. Phys. Rev. Lett. 108, 197204 (2012).
Sergienko, I. A. & Dagotto, E. Role of the Dzyaloshinskii−Moriya interaction in multiferroic perovskites. Phys. Rev. B 73, 094434 (2006).
Heide, M., Bihlmayer, G. & Blügel, S. Dzyaloshinskii−Moriya interaction accounting for the orientation of magnetic domains in ultrathin films: Fe/W(110). Phys. Rev. B 78, 140403(R) (2008).
Zhang, L., Ren, J., Wang, J.-S. & Li, B. Topological magnon insulator in insulating ferromagnet. Phys. Rev. B 87, 144101 (2013).
Cheng, R., Okamoto, S. & Xiao, D. Spin Nernst effect of magnons in collinear antiferromagnets. Phys. Rev. Lett. 117, 217202 (2016).
Hirsch, J. E. Spin Hall effect. Phys. Rev. Lett. 83, 1834 (1999).
Miron, I. M. et al. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 9, 230–234 (2010).
Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Garello, K. et al. Symmetry and magnitude of spin-orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–593 (2013).
Kontani, H., Tanaka, T., Hirashima, D. S., Yamada, K. & Inoue, J. Giant orbital Hall effect in transition metals: origin of large spin and anomalous Hall effects. Phys. Rev. Lett. 102, 016601 (2009).
Tanaka, T. et al. Intrinsic spin Hall effect and orbital Hall effect in 4 d and 5d transition metals. Phys. Rev. B 77, 165117 (2008).
Go, D., Jo, D., Kim, C. & Lee, H.-W. Intrinsic spin and orbital Hall effects from orbital texture. Phys. Rev. Lett. 121, 086602 (2018).
Go, D. & Lee, H.-W. Orbital torque: torque generation by orbital current injection. Phys. Rev. Res. 2, 013177 (2020).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Seki, S., Yu, X. X., Ishiwata, S. & Tohura, Y. Observation of skyrmions in a multiferroic material. Science 336, 198–201 (2012).
dos Santos Dias, M., Bouaziz, J., Bouhassoune, M., Blügel, S. & Lounis, S. Chirality-driven orbital magnetic moments as a new probe for topological magnetic structures. Nat. Commun. 7, 13613 (2016).
Lux, F. R., Freimuth, F., Blügel, S. & Mokrousov, Y. Engineering chiral and topological orbital magnetism of domain walls and skyrmions. Commun. Phys. 1, 60 (2018).
Redies, M. et al. Distinct magnetotransport and orbital fingerprints of chiral bobbers. Phys. Rev. B 99, 140407(R) (2019).
Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N. & Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 291, 2573–2576 (2001).
Fujimoto, S. Hall effect of spin waves in frustrated magnets. Phys. Rev. Lett. 103, 047203 (2009).
Diep, H. T. Frustrated Spin Systems (World Scientific, 2005).
Neubauer, A. Topological Hall effect in the A phase of MnSi. Phys. Rev. Lett. 102, 186602 (2009).
Kanazawa, N. et al. Large topological Hall effect in a short-period helimagnet MnGe. Phys. Rev. Lett. 106, 156603 (2011).
Hoffmann, M. et al. Topological orbital magnetization and emergent Hall effect of an atomic-scale spin lattice at a surface. Phys. Rev. B 92, 020401(R) (2015).
Hanke, J.-P. et al. Role of Berry phase theory for describing orbital magnetism: from magnetic heterostructures to topological orbital ferromagnets. Phys. Rev. B 94, 121114(R) (2016).
Hanke, J.-P., Freimuth, F., Blügel, S. & Mokrousov, Y. Prototypical topological orbital ferromagnet γ -FeMn. Sci. Rep. 7, 41078 (2017).
Grytsiuk, S. et al. Topological−chiral magnetic interactions driven by emergent orbital magnetism. Nat. Commun. 11, 511 (2020).
Wimmer, S., Mankovsky, S. & Ebert, H. Chirality-induced linear response properties in non-coplanar Mn3 Ge. Preprint at https://arxiv.org/abs/1912.05211 (2019).
Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
Zhang, Y., Železný, J., Sun, Y., van den Brink, J. & Yan, B. Spin Hall effect emerging from a noncollinear magnetic lattice without spin-orbit coupling. N. J. Phys. 20, 073028 (2018).
Shindou, R. & Nagaosa, N. Orbital ferromagnetism and anomalous Hall effect in antiferromagnets on the distorted fcc lattice. Phys. Rev. Lett. 87, 116801 (2001).
Tatara, G. & Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 71, 2613 (2002).
Bulaevskii, L. N., Batista, C. D., Mostovoy, M. V. & Khomskii, D. I. Electronic orbital currents and polarization in Mott insulators. Phys. Rev. B 78, 024402 (2008).
Sen, D. & Chitra, R. Large-U limit of a Hubbard model in a magnetic field: chiral spin interactions and paramagnetism. Phys. Rev. B 51, 1922 (1995).
Gritsev, V., Normand, B. & Baeriswyl, D. Phase diagram of the Heisenberg spin ladder with ring exchange. Phys. Rev. B 69, 094431 (2004).
Katsura, H., Nagaosa, N. & Lee, P. A. Theory of the thermal Hall effect in quantum magnets. Phys. Rev. Lett. 104, 066403 (2010).
Motrunich, O. I. Orbital magnetic field effects in spin liquid with spinon Fermi sea: possible application to κ -(ET)2 Cu2 (CN)3. Phys. Rev. B 73, 155115 (2006).
Li, S.-Y., Ren, Y.-N., Liu, J., Dai, X. & He, L. Experimental evidence for orbital magnetic moments generated by moiré-scale current loops in twisted bilayer graphene. Phys. Rev. B 102, 121406(R) (2020).
Ding, S. et al. Harnessing orbital-to-spin conversion of interfacial orbital currents for efficient spin-orbit torques. Phys. Rev. Lett. 125, 177201 (2020).
Matsumoto, R. & Murakami, S. Theoretical prediction of a rotating magnon wave packet in ferromagnets. Phys. Rev. Lett. 106, 197202 (2011).
Mook, A., Henk, J. & Mertig, I. Thermal Hall effect in noncollinear coplanar insulating antiferromagnets. Phys. Rev. B 99, 014427 (2019).
Géranton, G., Freimuth, F., Blügel, S. & Mokrousov, Y. Spin-orbit torques in L10 -FePt/Pt thin films driven by electrical and thermal currents. Phys. Rev. B 91, 014417 (2015).
Long, N. H., Mavropoulos, P., Zimmermann, B., Blügel, S. & Mokrousov, Y. Giant spin Nernst effect induced by resonant scattering at surfaces of metallic films. Phys. Rev. B 93, 180406(R) (2016).
Mook, A., Henk, J. & Mertig, I. Magnon Hall effect and topology in kagome lattices: a theoretical investigation. Phys. Rev. B 89, 13409 (2014).
Chisnell, R. et al. Topological magnon bands in a Kagome lattice ferromagnet. Phys. Rev. Lett. 115, 147201 (2015).
Scheie, A. et al. Effective spin- \(\frac{1}{2}\) scalar chiral order on kagome lattices in Nd3 Sb3 Mg2 O14. Phys. Rev. B 93, 180407(R) (2016).
Chen, L. et al. Topological spin excitations in honeycomb ferromagnet CrI3. Phys. Rev. X 8, 041028 (2018).
Hirschberger, M., Krizan, J. W., Cava, R. J. & Ong, N. P. Large thermal Hall conductivity of neutral spin excitations in a frustrated quantum magnet. Science 348, 106–109 (2015).
Nayak, A. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3 Ge. Sci. Adv. 2, e1501870 (2016).
Bruno, P., Dugaev, V. K. & Taillefumier, M. Topological Hall effect and Berry phase in magnetic nanostructures. Phys. Rev. Lett. 93, 096806 (2004).
Buhl, P. M., Freimuth, F., Blügel, S. & Mokrousov, Y. Topological spin Hall effect in antiferromagnetic skyrmions. Phys. Status Solidi RRL 11, 1700007 (2017).
Franz, C. et al. Real-space and reciprocal-space Berry phases in the Hall effect of Mn1−x Fex Si. Phys. Rev. Lett. 112, 186601 (2014).
Ishizuka, H. & Nagaosa, N. Spin chirality induced skew scattering and anomalous Hall effect in chiral magnets. Sci. Adv. 4, eaap9962 (2018).
Niu, C. Mixed topological semimetals driven by orbital complexity in two-dimensional ferromagnets. Nat. Commun. 10, 3179 (2019).
Toth, S. & Lake, B. Linear spin wave theory for single-Q incommensurate magnetic structures. J. Phys. Condens. Matter 27, 166002 (2015).
Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098 (1940).
Acknowledgements
We acknowledge fruitful discussions with Marjana Ležaić and Olena Gomonay. L.-C.Z. acknowledges support from China Scholarship Council (CSC) (No. [2016]3100). This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—TRR 173—268565370 (project A11), TRR 288—422213477 (project B06), and SPP 2137 “Skyrmionics” (project MO 1731/7-1). We gratefully acknowledge financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant No. 856538, project “3D MAGiC”). We also gratefully acknowledge the Jülich Supercomputing Centre and RWTH Aachen University for providing computational resources under project jiff40.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
F.R.L. and Y.M. conceived the concept. F.R.L., D.G. and Y.M. designed the research. L.-C.Z. performed the magnonic part of the calculations and analysis, D.G. performed the calculations of the electronic properties. L.-C.Z., J.-P.H., D.G. and Y.M. wrote the manuscript. J.-P.H., S.G., P.M.B. and S.B. discussed the results and contributed to revising the manuscript with the rest of the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Lc., Go, D., Hanke, JP. et al. Imprinting and driving electronic orbital magnetism using magnons. Commun Phys 3, 227 (2020). https://doi.org/10.1038/s42005-020-00490-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00490-3
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.