Abstract
The convoluted nonlinear behaviors of heavily multimode photonic structures have been recently the focus of considerable attention. The sheer complexity associated with such multimode systems, allows them to display a host of phenomena that are otherwise impossible in few-mode settings. At the same time, however, it introduces a set of fundamental challenges in terms of comprehending and harnessing their response. Here, we develop an optical thermodynamic approach capable of describing the thermalization dynamics in large scale nonlinear photonic tight-binding networks. For this specific system, an optical Sackur-Tetrode equation is obtained that explicitly provides the optical temperature and chemical potential of the photon gas. Processes like isentropic expansion/compression, Joule expansion, as well as aspects associated with beam cleaning/cooling and thermal conduction effects in such chain networks are discussed. Our results can be used to describe in an effortless manner the exceedingly complex dynamics of highly multimoded nonlinear bosonic systems.
Similar content being viewed by others
Introduction
In recent years, there has been considerable interest in understanding the rich and complex dynamics of large-scale nonlinear multimoded optical systems1,2,3,4,5. To a great extent, what has fueled this effort is the ever-increasing quest for high information capacity photonic networks6,7,8,9,10 and high-power optical sources11. Similarly, the nonlinear physics of high-quality factor multimode microresonators has been intensively investigated in a number of areas, like comb-generation and optomechanics12,13,14,15,16. Yet, what kept us from fully expanding these classical settings, is the sheer complexity behind the nonlinear interactions taking place in such vastly many-moded environments. To appreciate this difficulty, consider for example a multimode optical fiber supporting thousands of modes. In this case, to correctly account for all the nonlinear processes unfolding in this structure, one has to first estimate at least a trillion or so four-wave mixing coefficients, before even attempting to numerically solve the evolution problem—a formidable task which is by itself computationally intensive. Clearly, to overcome these hurdles, a statistical approach has to be deployed that can effectively deal with many-body configurations. In essence, this calls for the development of a theoretical framework, akin to that of statistical mechanics, that has so far allowed us to understand the macroscopic properties of matter, in spite of the fact that on most occasions one has to deal with a great multitude of atoms or molecules—most often exceeding Avogadro’s number17.
Quite recently, an optical thermodynamic theory was put forward, that can self-consistently describe by means of statistical mechanics the utterly complex processes of energy exchange in nonlinear multimode systems at thermal equilibrium18. In accord with the axioms of thermodynamics19, the entropy of these systems was appropriately defined in terms of other extensive variables and a global equation of state was derived18,20. Moreover, the laws governing isentropic processes were obtained and the prospect for Carnot cycles was suggested. Similar results were derived from the perspective of the grand canonical ensemble along with the expected statistical fluctuations in these systems21,22.
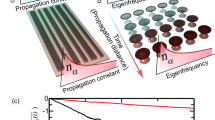
Here, by means of an optical Sackur–Tetrode equation, we investigate the entropic response of large-scale weakly nonlinear photonic chain networks. These classical networks may for example involve a large number of evanescently coupled waveguide lattices23 that exchange power in both crystalline (Fig. 1a) and other more complex arrangements (Fig. 1b), or could be comprised of arrays of optical resonators (CROWs)24 that allow for energy transfer in time—used as building blocks as shown in Fig. 1c. While in this work, we will be primarily dealing with coupled waveguide topologies in order to exemplify these notions, a similar discussion holds for heavily multimode chain cavity configurations and other bosonic systems25,26. In this case, the underlying Sackur–Tetrode equation can be expressed as a function of the electrodynamic momentum flow U, the number of available modes M, and the input optical power \({{{\mathcal{P}}}}\). This analytical formalism developed here is in turn used to study and predict several distinct phenomena that could be of practical importance. These include, for example, the prospect for beam cooling (leading to an improvement in beam quality) as well as Joule expansion and aspects associated with the photo-capacity and thermal conductivity of such chain networks. As opposed to previous works that were foundational in nature18,20, the results reported here (applicable to large-scale nonlinear tight-binding lattices) establish a tangible theoretical model through which many of these abstract ideas can be conceptually grasped and further developed.
Results and discussion
Optical Sackur–Tetrode equation
We begin our discussion by considering a lossless and leak-free, nonlinear array network of M single-mode elements that are coupled via nearest-neighbor interactions. In this nonlinear optical chain, the equation of motion is given by \(ida_m/d\xi + \kappa a_{m - 1} + \kappa a_{m + 1} + \left| {a_m} \right|^2a_m = 0\), where am represents the local mode amplitude at site m and κ stands for the coupling coefficient between two successive elements. These evolution equations can be obtained from the classical Hamiltonian \(\left\langle {H_{{{\mathrm{T}}}}} \right\rangle = \mathop {\sum}\nolimits_m {\kappa \left( {a_{m - 1}a_m^ \ast + a_{m + 1}a_m^ \ast } \right) + \left( {1/2} \right)\mathop {\sum}\nolimits_m {\left| {a_m} \right|^4.} }\) The linear eigenvalues εj corresponding to the optical supermodes |ϕj〉 of the arrangement shown in Fig. 1a are given by \(\varepsilon _j = 2\kappa {{{\mathrm{cos}}}}\left[ {\pi {\it{j}}/\left( {{\it{M}} + 1} \right)} \right]\) (refs. 23,24). In general, the evolution of this weakly nonlinear system can be described in terms of its supermodes, i.e., \({|\psi } \rangle =\mathop{\sum}\limits_{j = 1}^M {c_j( \xi )| {\phi _j} \rangle }\) where the square of the moduli (|cj|2) of the complex coefficients cj denotes modal occupancies. In this case, the norm in this conservative system \({{{\mathcal{P}}}} = \mathop{\sum}\limits_{j = 1}^M | {c_{j}} |^2\) is preserved, thus implying power/photon conservation in these coupled waveguide/cavity arrangements. In addition, in the weakly nonlinear regime, the expectation value of the total Hamiltonian 〈HT〉 = 〈HL〉 + 〈HNL〉 is dominated by its linear component 〈HL〉 and as a result the internal energy \(U = - \left\langle {\psi \left| {H_{{{\mathrm{L}}}}} \right|\psi } \right\rangle = - \mathop{\sum}\limits_{j = 1}^M {\varepsilon _j| {c_j} |^2}\) remains invariant during evolution, thus establishing the second conservation law associated with this class of structures. In fact, in multimode waveguide settings, the conserved internal energy U so happens to be the longitudinal electrodynamic momentum flow in these systems27. In this respect, the two normalized constants of the motion \({{{\mathcal{P}}}}\) and U are uniquely determined by the initial excitation amplitudes cj0, since \({{{\mathcal{P}}}} = \mathop{\sum}\limits_{j = 1}^M | {c_{j0}} |^2\) and \(U = - \mathop{\sum}\limits_{j = 1}^M \varepsilon _j| {c_{j0}} |^2\). At this point, it is important to stress that the sole role of the weak nonlinearity involved (χ(2), χ(3), etc.) is to chaotically reshuffle the optical power among modes through multi-wave mixing processes28—thus causing the complex amplitudes cj to vary randomly during propagation. In other words, the lack of M conserved quantities or integrability, allows this nonlinear array system to ergodically explore in a fair manner, all its accessible microstates (in its phase space) that lie on the constant energy (U) and power (\({{{\mathcal{P}}}}\)) manifolds. It is this ergodicity that provides the foundation for establishing an entropic thermodynamic theory for the aforementioned multimode chain networks. Moreover, in heavily multimode arrangements, the thermodynamically extensive variables \((U,M,{{{\mathcal{P}}}})\) are related to each other through the optical temperature T (henceforth called temperature) and chemical potential μ associated with the system. This relation is given through a global equation of state, given by \(U - \mu {{{\mathcal{P}}}} = MT\) that explicitly involves the total number of modes M (ref. 18). Here, the optical temperature is associated with the optical field itself and has nothing to do with the actual temperature of the environment the system is embedded in. In general, any system is expected to reach thermal equilibrium by maximizing its entropy. In this case, the thermalized average power levels conveyed by each mode are found to obey a Rayleigh–Jeans distribution29,30,31,32, i.e., \(| {c_j} |^2 = - T/(\varepsilon _j + \mu )\).
Based on the above premises, one can show that the relative entropy associated with a photonic monoatomic chain network (Fig. 1) is given by the following equation (see Supplementary Note 1 for the derivation), i.e.,
Equation (1) is analogous to the entropic Sackur–Tetrode equation—developed more than a century ago (based on an appropriate quantization of the phase space) in order to correctly account for the properties of monoatomic gases17,33. It was first derived in ref. 34 in order to account for the small fluctuation entropy of the defocusing nonlinear Schrödinger equation. Like its counterpart in statistical mechanics, the optical entropy of these nonlinear monoatomic chains is extensive with respect to the three other extensive variables \(\left( {U,M,{{{\mathcal{P}}}}} \right)\). In other words, if we let \(\left( {U,M,{{{\mathcal{P}}}}} \right) \to \left( {\lambda U,\lambda M,\lambda {{{\mathcal{P}}}}} \right)\), then from Eq. (1), one directly obtains S → λS. We note that this extensivity in entropy is crucial in developing a self-consistent thermodynamic formulation—free of Gibbs paradoxes. On the other hand, the optical entropy given above is by nature different from that of an ideal monoatomic gas in standard thermodynamics. This is apparent, since the prefactor in Eq. (1) is now given by the number of modes M (optical volume) as opposed to the optical power \({{{\mathcal{P}}}}\) which here plays the role of N—the number of gas particles. Figure 2a depicts the entropy of a chain system as a function of \(\left( {U,{{{\mathcal{P}}}}} \right)\) as obtained from Eq. (1), when M = 100. The three pertinent equations of state can in turn be derived from (1) by employing the fundamental equation of thermodynamics (see Supplementary Note 2 for the derivation), i.e.,
a Relative entropy S as a function of the internal energy U and input power \({{{\mathcal{P}}}}\). b Entropy cross-sections as a function of energy U for the power levels indicated in (a) with the same colored curves. The inset in (b) depicts the modal occupancies corresponding to different temperatures. While for positive temperatures the lowest group of modes is occupied, the converse is true for negative temperatures. When T→±∞, equipartition of power takes place among modes. c Energy–temperature diagrams pertaining to this family of lattices corresponding to the same power levels in (a) and (b), shown as colored curves. The gray shaded areas indicate physically inaccessible regions. In all cases, the number of modes was taken to be M = 100.
Equations (2–4), relate the three intensive thermodynamic variables \(\left( {T,\mu ,\hat p} \right)\) to their respective conjugate quantities \(\left( {U,{{{\mathcal{P}}}},M} \right)\). As in statistical mechanics, in this nonlinear multimoded setting, the temperature \(T = \left( {U^2 - 4\kappa ^2{{{\mathcal{P}}}}^2} \right)/(2MU)\) represents a thermodynamic force responsible for energy transfer ΔU from a hot to a colder subsystem whereas the chemical potential μ dictates the power exchange \({{\Delta }}{{{\mathcal{P}}}}\)—all aiming to maximize the entropy in accord with the second law of thermodynamics. Finally, \(\hat p\) represents the relative optical pressure in this configuration. From Eq. (2), one can readily deduce that as the system attains its lowest possible internal energy \(U_{{{{\mathrm{min}}}}} \to - 2\kappa {{{\mathcal{P}}}}\) (as imposed by the band structure of the monoatomic lattice), its temperature tends to zero (T → 0+) and as a result the photon gas becomes a condensate that exclusively occupies the ground state of the lattice. Conversely, when the internal energy is maximized \(U_{{{{\mathrm{max}}}}} \to 2\kappa {{{\mathcal{P}}}}\), the opposite is true (i.e., T → 0−), and hence the highest order mode is now solely occupied (anti-condensate)35. The first equation of state (Eq. (2)) directly indicates that the temperature of these lattices is positive for \(- 2\kappa {{{\mathcal{P}}}} \, < \, U \, < \, 0\) whereas is negative if the internal energy lies in the domain \(0 \, < \, U \, < \, 2\kappa {{{\mathcal{P}}}}\). On the other hand, when \(U \to 0^ \mp\), the temperature tends to T → ±∞ (as schematically shown in the inset of Fig. 2b), and as a result, equipartition of power takes place among modes, i.e., \(| {c_j} |^2 = - T/\mu = {{{\mathcal{P}}}}/M\). In general, negative temperatures correspond to bodies hotter than hot17—a relation that regulates the direction of the energy flow ΔU. While for positive temperatures the lower group of modes is mostly occupied (since \(| {c_j} |^2 = - T/(\varepsilon _j + \mu )\)), the opposite is true for negative temperatures where the higher-order modes are populated (Fig. 2b). We note that, the set of the three equations in (2–4) is complete, and is formally equivalent to the global equation of state (\(U - \mu {{{\mathcal{P}}}} = MT\)) as well as to the corresponding Euler equation (\(S = \left( {U - \mu {{{\mathcal{P}}}} + \hat pM} \right)/T\))—a relation that again reaffirms the extensivity of the entropy itself (see Supplementary Note 2). Meanwhile, Fig. 2c depicts energy–temperature curves (U – T) at various power levels, that as we will see dictate the photo-capacity of these photonic chain networks.
Thermodynamic processes
The above results can be used to predict the outcome of more complex processes like, for example, that associated with Joule expansion of the photon gas in such nonlinear heavily multimoded environments. This prospect is shown schematically in Fig. 3, where as an example, χ(3) nonlinear array supporting M modes suddenly expands to four times its size (M → 4M), while all the lattice parameters are kept the same. In this microcanonical scenario, both the internal energy U and power \({{{\mathcal{P}}}}\) remain constant during this abrupt transition. From Eqs. (2–3), one can quickly deduce that after Joule expansion, the temperature is reduced to one-fourth of its original value (T → T/4), while the chemical potential μ is entirely unaffected. This photonic response is in stark contrast to the Joule expansion behavior expected from ideal monoatomic gases where the temperature is constant whereas the chemical potential substantially changes. On the other hand, even in this case, the absolute entropy of the system always increases in response to this irreversible expansion (for details see Supplementary Note 3). In a similar vein, isentropic processes (S = const) can also be examined. These effects can be readily produced if, for example, a Kerr nonlinear multimode array adiabatically expands/contracts (in which case the mode occupancies |cj|2 are unaltered) while the individual single-mode elements remain the same (only the coupling coefficient κ adiabatically changes). Since M and \({{{\mathcal{P}}}}\) are invariant, an isentropic transition can only occur provided that U/κ = const (see Supplementary Note 4 for the derivation). This last relation can be justified given that \(U = -\mathop{\sum}\limits_{j = 1}^M \varepsilon _j| {c_j} |^2\) and εj ∝ κ. From the first two equations of state (Eqs. (2–3)), one can quickly conclude that U/T = const and μ/T = const. These latter isentropic relations, applicable for the photon gas in multimode chain networks, are to some extent reminiscent of their counterparts in the theory of monatomic gases, i.e., pV5/3 = const and TV2/3 = const (ref. 17). Nevertheless, there is a fundamental difference between these two physical settings, in the sense that in the former case there is a physical change in the lattice structure (and hence in the width of the density of states) while in the latter the gaseous substance stays the same.
Light conveying power \({{{\mathcal{P}}}}\) is allowed to suddenly expand in a larger chain network having four times as many waveguide elements (M→4M). In this case, if the temperature of the photon gas before this transition is T, after this abrupt and thermodynamically irreversible expansion, the system reaches equilibrium at T/4—a direct consequence of the way Joule expansion manifests itself in these heavily multimoded nonlinear optical environments.
Beam self-cleaning and cooling
The analytical formalism (Eqs. (2–4)) developed here, can now be utilized to predict the response of such nonlinear chain systems in settings of practical interest like those allowing for beam self-cleaning36,37,38,39 and cooling. Figure 4a schematically shows such a nonlinear multicore optical arrangement involving M = 30 sites. In this configuration, the power \(({{{\mathcal{P}}}} = 2)\) is injected in the \({\hat{{{\boldsymbol{y}}}}}\) polarization and is uniformly distributed (with random phases) between the supermodes having eigenvalues εj in the range of −0.5κ ≤ εj ≤ 1.2κ, in which case U = −0.77, as shown in Fig. 4b. For these initial conditions, Eqs. (2–4) predict the following equilibrium parameters T = 0.33, μ = −5.38. While at the input (z = 0) the intensity distribution displays considerable disorder (Fig. 4c), this speckle pattern disappears (Fig. 4d) after the system attains thermal equilibrium at the output (z = L). What facilitates this beam self-cleaning effect has to do with the fact that during thermalization, the power is reshuffled in such a way so as to favor the lower order modes (for T > 0) in the Rayleigh–Jeans distribution (Fig. 4b)—a process that removes the initial speckle in the beam. Yet, while the output beam at (z = L) seems to improve in the near-field, its multimode far-field is still highly divergent and thus is of poor quality as shown in Fig. 4e. Interestingly, the thermodynamic formulation developed here suggests that this situation can be greatly improved if in this same array structure, a cooler beam is launched—having a perpendicular polarization \({\hat{{{\boldsymbol{x}}}}}\) (Fig. 4f). In this latter arrangement, each waveguide site is assumed to be substantially birefringent, thus prohibiting any power exchange between the two beams. Instead, the two wavefronts only interact through cross-phase modulation24. In the example provided in Fig. 4f, the internal energy and power corresponding to each polarization is \(U_x = - 3.95,{{{\mathcal{P}}}}_{\it{x}} = 2,U_y = - 0.77,{{{\mathcal{P}}}}_{\it{y}} = 2\). Based on these initial conditions, Eq. (2) indicates that on its own, each polarization would have settled to an equilibrium temperature of Tx = 1.7 × 10−3, Ty = 0.33. On the other hand, once interacting together in a canonical-like arrangement, the two beams reach the same temperature T = 0.075 which can be exactly predicted following the procedure in Supplementary Note 5. In other words, the \({\hat{{{\boldsymbol{y}}}}}\) polarized beam can be considerably cooled after exchanging energy ΔU with its \({\hat{{{\boldsymbol{x}}}}}\) polarized counterpart. This in turn leads to a ~3-fold improvement in the far-field of the original beam (Fig. 4g).
a Propagation of a \({\hat{{{\boldsymbol{y}}}}}\) polarized optical beam in a nonlinear chain of waveguides involving 30 elements. The projected far-field after the beam exits the system at z = L is also shown. b Thermalization dynamics of the modal occupancies as a function of distance when \({{{\mathcal{P}}}} = 2\) and the modes are uniformly excited in the range of −0.5κ ≤ εj ≤ 1.2κ. At the output, the system settles into a Rayleigh–Jeans distribution with a temperature of T = 0.33. c The intensity distribution after ensemble average corresponding to the input used in (b) displays a strong speckle. d The beam self-cleans after thermalization takes place. e Far-field pattern associated with the thermalized \({\hat{{{\boldsymbol{y}}}}}\) polarized output field for the same conditions used in (b). f Cooling the \({\hat{{{\boldsymbol{y}}}}}\) polarized wavefront using cross-phase modulation with an \({\hat{{{\boldsymbol{x}}}}}\) polarized beam of equal power. g After cooling, the far-field of the \({\hat{{{\boldsymbol{y}}}}}\) polarized wave experiences considerable improvement. This cooling interaction can be analytically predicted from Eqs. (2–4).
Heat capacity and thermal conductivity of nonlinear chain networks
The formalism developed here, allows one to define a photo-capacity CM = ∂U/∂T associated with such nonlinear multimode photonic systems—a property that is in every respect analogous to that of the heat capacity pertaining to various phases of matter. Like its counterpart (heat capacity), this quantity critically depends on the density of states and hence it is characteristic of the multimode optical system itself. In this respect, it is formally possible to assign a CM capacity to any possible many-mode arrangement, irrespective of whether it is discrete or continuous. For the chain networks considered here, the photo-capacity can be explicitly obtained from Eq. (2) and it is given by \(C_M = M - \left| T \right|M^2\left( {T^2M^2 + 4\kappa ^2{{{\mathcal{P}}}}^2} \right)^{ - 1/2}\). Figure 5a shows the CM function (blue curve) for such a chain configuration, involving M = 200 sites while conveying a power of \({{{\mathcal{P}}}} = 20\). In this case, the photo-capacity function is an even function of temperature—as one should expect from the symmetry in the density of states. The photo-capacity curves corresponding to two different types of Lieb lattices are also displayed, as an example, in Fig. 5a for the same parameters (M = 200, \({{{\mathcal{P}}}} = 20\)). Note that the CM(T) function for the Lieb-2 lattice with cross-couplings is in this case highly asymmetric—a feature attributed to the band structure of this specific system.
a Photo-capacity curves corresponding to a standard chain network (blue curve), a Lieb lattice (Lieb-1) with only nearest-neighbor interactions (green) and a Lieb array (Lieb-2) with cross-couplings (red), when \({{{\mathcal{P}}}} = 20\) and M = 200. Note the asymmetry in the photo-capacity curve of the Lieb-2 system. b Energy transfer ΔU between a square L1 and a graphene L2 lattice when initially kept at different temperatures (T1 = 0.3, T2 = 0.1). This energy transfer takes place through a bridge chain composed of birefringent elements under non-equilibrium conditions. As required by the second law of thermodynamics, ΔU always flows from a hot to a cold subsystem. In this case, the temperature in the linking chain drops linearly, in accord with Fick’s law. c The internal energy transfer ceases when thermal equilibrium is reached in which case both subsystems attain the same temperature and the total entropy ST is maximized. In all cases, the nonlinearity was assumed to be of the Kerr type. The three surfaces shown at different planes are meant to illustrate the temperature difference between the two subsystems, where z represents the propagation distance along these arrays. Light is injected in the waveguides at z = 0.
We next explore the possibility for energy ΔU transport phenomena occurring when a hot and a cold optical nonlinear multimode system are linked together under non-equilibrium conditions. To some extent, these processes have much in common with heat conduction problems in solids. Figure 5b shows such an arrangement where a square multicore photonic lattice L1 with M1 = 900 sites is connected to a graphene-like system L2 (M2 = 896) via a chain bridge L3 involving M3 = 140 evanescently coupled waveguides. The bridge L3 is appropriately designed using birefringent elements so as to allow for energy exchange ΔU between the two lattices L1 and L2 while prohibiting any power transfer \({{\Delta }}{{{\mathcal{P}}}}\). System L1 together with the link array L3 are initially brought to thermal equilibrium where both share a temperature of T1 = 0.3 when conveying a total power of \({{{\mathcal{P}}}}_{1 + 3} = 65\) at a total internal energy U1+3 = −60. Similarly, lattice L2 (before is connected to the bridge) is kept at T2 = 0.1 when \({{{\mathcal{P}}}}_2 = 40\) and U2 = −46. Once L2 is put in contact with the L3 bridge, a non-equilibrium thermodynamical process ensues during which the entropy of the combined system starts to increase as expected from the second law of thermodynamics (Fig. 5c). During this non-equilibrium stage, internal energy ΔU starts to flow through the bridge from hot to cold (L1 → L2). In this case, the local temperature along this bridge (obtained after projecting on the local eigenfunctions) is found to linearly decrease from T1 to T2 in full accord to Fick’s law of heat diffusion40, J = −k∇T. This in turn allows one to express this energy transfer through an effective photo-conduction coefficient K as ΔU/Δz = −K(T1 − T2). From our simulations, we estimate that here the photo-conduction coefficient of the L3 chain is K ≈ 3.2 × 10−5.
Conclusion
By harnessing concepts from statistical mechanics, we have developed an optical thermodynamic theory that explicitly provides the Sackur–Tetrode entropy associated with large nonlinear photonic chain networks. Based on these premises, the temperature and chemical potential of such systems can be obtained in closed form as a function of the initial excitation conditions. The formalism developed here is general and can be readily deployed to describe a number of thermodynamic processes, like isentropic expansion/compression, Joule expansion, as well as aspects pertaining to beam self-cleaning and cooling in such chain networks. Of interest would be to explore similar possibilities in quasi-conversive systems under non-equilibrium conditions. Our results not only provide a platform to understand and predict in a systematic way the utterly complex dynamics of heavily multimoded nonlinear optical systems that are nowadays of importance in areas ranging from high-power photonic settings to cold atom condensates and optomechanics. In addition, they could be of practical importance in designing high-brightness multimode optical sources.
Methods
Simulations
Throughout this study, simulations were conducted by numerically solving the discrete nonlinear Schrödinger equations, using 4th order Runge–Kutta methods. Ensemble averages were obtained by performing a number of simulations with the same initial modal amplitudes but different random relative phases. The modal occupancies |cj|2 obtained were then averaged over several ensembles. More information concerning these results can be found in the Supplementary Methods.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code that support the findings of this study are available from the corresponding author upon reasonable request.
Change history
04 October 2023
A Correction to this paper has been published: https://doi.org/10.1038/s42005-023-01400-z
References
Renninger, W. H. & Wise, F. W. Optical solitons in graded-index multimode fibres. Nat. Commun. 4, 1719 (2013).
Wright, L. G., Christodoulides, D. N. & Wise, F. W. Controllable spatiotemporal nonlinear effects in multimode fibres. Nat. Photonics 9, 306–310 (2015).
Petersen, C. R. et al. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 8, 830–834 (2014).
Poletti, F. & Horak, P. Description of ultrashort pulse propagation in multimode optical fibers. J. Opt. Soc. Am. B 25, 1645–1654 (2008).
Longhi, S. Modulational instability and space time dynamics in nonlinear parabolic-index optical fibers. Opt. Lett. 28, 2363–2365 (2003).
Richardson, D., Fini, J. & Nelson, L. Space-division multiplexing in optical fibres. Nat. Photonics 7, 354–362 (2013).
Li, G., Bai, N., Zhao, N. & Xia, C. Space-division multiplexing: the next frontier in optical communication. Adv. Opt. Photon. 6, 413–487 (2014).
Ryf, R. et al. Mode-division multiplexing over 96 km of few-mode fiber using coherent 6 × 6 MIMO processing. J. Lightwave Technol. 30, 521–531 (2012).
Fan, S. & Kahn, J. M. Principal modes in multimode waveguides. Opt. Lett. 30, 135–137 (2005).
Ambichl, P. et al. Super- and anti-principal-modes in multimode waveguides. Phys. Rev. X 7, 041053 (2017).
Wright, L. G., Christodoulides, D. N. & Wise, F. W. Spatiotemporal mode-locking in multimode fiber lasers. Science 358, 94–97 (2017).
Del’Haye, P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214 (2007).
Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics. Nat. Photonics 7, 597 (2013).
Ferrera, M. et al. Low power four wave mixing in an integrated, micro-ring resonator with Q = 1.2 million. Opt. Express 17, 14098–14103 (2009).
Okawachi, Y. et al. Octave-spanning frequency comb generation in a silicon nitride chip. Opt. Lett. 36, 3398–3400 (2011).
Kippenberg, T. J. & Vahala, K. J. Cavity optomechanics: back-action at the mesoscale. Science 321, 1172–1176 (2008).
Pathria, R. K. & Beale, P. D. Statistical Mechanics. 3rd edn (Elsevier Science, 2011).
Wu, F. O., Hassan, A. U. & Christodoulides, D. N. Thermodynamic theory of highly multimoded nonlinear optical systems. Nat. Photonics 13, 776–782 (2019).
Callen, H. B. Thermodynamics and an Introduction to Thermostatistics. 2nd edn (Wiley, 1985).
Parto, M., Wu, F. O., Jung, P. S., Makris, K. & Christodoulides, D. N. Thermodynamic conditions governing the optical temperature and chemical potential in nonlinear highly multimoded photonic systems. Opt. Lett. 44, 3936–3939 (2019).
Makris, K. G., Wu, F. O., Jung, P. S. & Christodoulides, D. N. Statistical mechanics of weakly nonlinear optical multimode gases. Opt. Lett. 45, 1651–1654 (2020).
Ramos, A., Fernández-Alcázar, L., Kottos, T. & Shapiro, B. Optical Phase Transitions in Photonic Networks: a Spin-System Formulation. Physical Review X, 10 (2020).
Christodoulides, D. N., Lederer, F. & Silberberg, Y. Discretizing light behaviour in linear and nonlinear waveguide lattices. Nature 424, 817–823 (2003).
Yariv, A., Xu, Y., Lee, R. K. & Scherer, A. Coupled-resonator optical waveguide: a proposal and analysis. Opt. Lett. 24, 711–713 (1999).
Kottos, T. & Shapiro, B. Thermalization of strongly disordered nonlinear chains. Physical Review E, 83, 062103 (2011).
Davis, M. J., Morgan, S. A. & Burnett, K. Simulations of Bose fields at finite temperature. Phys. Rev. Lett. 87, 160402 (2001).
Haus, H. A. & Kogelnik, H. Electromagnetic momentum and momentum flow in dielectric waveguides. J. Opt. Soc. Am. 66, 320–327 (1976).
Boyd, R. W. Nonlinear Optics. 3rd edn (Academic Press, 2008).
Picozzi, A. et al. Optical wave turbulence: towards a unified nonequilibrium thermodynamic formulation of statistical nonlinear optics. Phys. Rep. 542, 1–132 (2014).
Dyachenko, S., Newell, A. C., Pushkarev, A. & Zakharov, V. E. Optical turbulence: weak turbulence, condensates and collapsing filaments in the nonlinear Schrödinger equation. Phys. D: Nonlinear Phenom. 57, 96–160 (1992).
Picozzi, A. Towards a nonequilibrium thermodynamic description of incoherent nonlinear optics. Opt. Express 15, 9063–9083 (2007).
Onorato, M., Vozella, L., Proment, D. & Lvov, Y. V. Route to thermalization in the α-Fermi–Pasta–Ulam system. Proc. Natl Acad. Sci. USA 112, 4208–4213 (2015).
Tetrode, H. V. Die chemische Konstante der Gase und das elementare Wirkungsquantum. Ann. der Phys. 343, 434–442 (1912).
Rumpf, B. Simple statistical explanation for the localization of energy in nonlinear lattices with two conserved quantities. Phys. Rev. E 69, 016618, https://doi.org/10.1103/PhysRevE.69.016618.
Braun, S. et al. Negative absolute temperature for motional degrees of freedom. Science 339, 52–55 (2013).
Krupa, K. et al. Spatial beam self-cleaning in multimode fibres. Nat. Photonics 11, 237–241 (2017).
Lopez-Galmiche, G. et al. Visible supercontinuum generation in a graded index multimode fiber pumped at 1064 nm. Opt. Lett. 41, 2553–2556 (2016).
Liu, Z., Wright, L. G., Christodoulides, D. N. & Wise, F. W. Kerr self-cleaning of femtosecond-pulsed beams in graded-index multimode fiber. Opt. Lett. 41, 3675–3678 (2016).
Fusaro, A., Garnier, J., Krupa, K., Millot, G. & Picozzi, A. Dramatic acceleration of wave condensation mediated by disorder in multimode fibers. Phys. Rev. Lett. 122, 123902 (2019).
Ashcroft, N. W. & Mermin, N. D. Solid State Physics. 1st edn (Cengage Learning, 1976).
Acknowledgements
This work was supported by the Office of Naval Research (ONR) through the grants (N00014-18-1-2347), and MURI (N00014-20-1-2789), the National Science Foundation (NSF) (EECS-1711230, CBET 1805200, ECCS 2000538, ECCS 2011171), the Army Research Office (ARO) (W911NF-17-1-0481), the Air Force Office of Scientific Research (AFOSR) (FA9550-14-1-0037, FA9550-20-1-0322), the US–Israel Binational Science Foundation (BSF; 2016381) and the Qatar National Research Fund (QNRF) (NPRP9-020-1-006). This work was partially supported by an MPS Simons collaboration (Simons grant 733682). P.S.J. thanks the Polish Ministry of Science and Higher Education for Mobility Plus scholarship (1654/MOB/V/2017/0).
Author information
Authors and Affiliations
Contributions
D.N.C. and M.K. conceived the idea. F.O.W. developed the theory. F.O.W., P.S.J., and M.P. conducted the simulations and data analysis. All the authors contributed to the writing of the original draft, review, and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wu, F.O., Jung, P.S., Parto, M. et al. Entropic thermodynamics of nonlinear photonic chain networks. Commun Phys 3, 216 (2020). https://doi.org/10.1038/s42005-020-00484-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00484-1
This article is cited by
-
Universality of light thermalization in multimoded nonlinear optical systems
Nature Communications (2023)
-
Physics of highly multimode nonlinear optical systems
Nature Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.