Abstract
Periodically forced, oscillatory fluid flows have been the focus of intense research for decades due to their richness as a nonlinear dynamical system and their relevance to applications in transportation, aeronautics, and energy conversion. Here we derive a mechanistic model of the dynamics of forced turbulent oscillator flows by leveraging a comprehensive experimental study of the turbulent wake behind a D-shaped body under periodic forcing. We confirm the role of resonant triadic interactions in the forced flow by studying the dominant components in the power spectra across multiple excitation frequencies and amplitudes. We then develop an extended Stuart-Landau model that captures the system dynamics and synchronization regions. Further, it is possible to identify the model coefficients from sparse measurement data.
Similar content being viewed by others
Introduction
Fluid flows that display unsteadiness characterized by a well-defined frequency and that are insensitive to low-level external noise are known as oscillator flows1,2. These flows have been the focus of research efforts for over 75 years3,4, in part because of their rich physics, and also because of their relevance to numerous applications where aerodynamic forces and mixing play a significant role, such as transportation, aeronautics, and energy conversion5.
Models that capture the evolution of dominant fluid coherent structures are of the utmost importance for prediction, control, and understanding of the underlying physical processes that drive these flows6. The wake past a bluff body is one example of an oscillator flow, where self-sustained periodic vortex shedding arises after an increase in the Reynolds number renders the flow incapable of maintaining a steady state. This scenario unfolds when a supercritical Hopf bifurcation takes place, where disturbances associated with a spatial structure, known as the global mode of the flow, become linearly unstable, leading to exponential growth of the mode amplitude A, followed by nonlinear saturation onto a stable limit cycle7,8. The Stuart−Landau model3,4
has been widely used to explain this nonlinear oscillator behavior of the wake past bluff bodies7,8,9,10,11,12. Sipp and Lebedev7 formally derived this model from the Navier−Stokes equations by means of a rigorous asymptotic expansion close to the Hopf bifurcation.
When periodically forced with certain frequencies, the wake past a bluff body has been observed to adjust its natural vortex shedding rate to some rational multiple of the forcing frequency, as first reported by Provansal et al.13 for the cylinder flow. This is synchronization—the spontaneous emergence of rhythmic oscillatory dynamics—an inherently nonlinear phenomenon that is abundant in natural and engineering systems such as chemical reactions, electric circuits, structural vibrations, cardiac cells, spiking neurons, and the locomotion of animals and robots14,15,16,17,18,19,20. More specifically, synchronization of an oscillating system to an external periodic forcing is usually referred to as phase or frequency entrainment18,20,21,22,23. In the context of fluid dynamics, the recent work of Taira and Nakao24 was the first to study the synchronization properties of the cylinder flow using phase-reduction analysis, a technique commonly used for biological and chemical systems25. Periodic forcing continues to present an appealing flow control strategy for a wide range of applications, as it has been shown to effectively reduce bluff body drag26, increase lift of airfoils27, and enhance mixing in heat exchangers28. Understanding synchronization in the context of unsteady aerodynamics is key to leverage periodic flow control and explain the mechanisms that lead to the performance improvements observed in these success stories.
Recent experimental work by Barros et al.29 and Rigas et al.30 reported synchronization in the harmonically forced turbulent wake past an Ahmed body and an axisymmetric blunt body, respectively. Both studies linked the spatial symmetry properties of the forcing mode to the type of response observed. They found the presence of a 1:2 subharmonic resonance for symmetric disturbances, where the vortex shedding frequency synchronizes to half of the forcing frequency. This lock-on phenomenon was attributed to resonant wave-triads, where the spatial structure of the interacting forcing and response modes are constrained by the triadic consistency condition31,32,33. This hypothesis suggests that studying the synchronization properties of forced flows past bluff bodies is a promising way to learn about the dominant nonlinear mode interactions present in the wake.
In previous work, the response of oscillator flows to periodic disturbances has been modeled using the Stuart−Landau equation with the addition of a forcing term13,30,34,35,36. In the work of Sipp35, this model was derived analytically by extending the weakly nonlinear analysis of laminar globally unstable flows to include the effects of external forcing. Rigas et al.30 used an eddy viscosity closure and the phase-averaged Navier−Stokes equations to extend the analysis to the turbulent regime. They validated the resulting model in the proximity of a subharmonic resonance by comparing against experiments of the turbulent wake past an axisymmetric body. Hence, weakly nonlinear analysis30,35 provides a theoretically based structure for a model of the form
where g(A, F) captures the excitation induced by the coupling between the global mode, with amplitude A, and the periodic forcing mode, with amplitude F. However, in practice, the computation of g(A, F) requires high-fidelity numerical simulations. Alternatively, recent data-driven techniques are enabling the identification of models directly from data37,38,39,40,41,42,43,44,45,46.
Our goal in this work is to derive a mechanistic model of the dynamics of forced turbulent oscillator flows by leveraging a more comprehensive experimental dataset than has been previously reported. As an example of this class of systems, we study the turbulent wake behind a D-shaped bluff body with a rectangular base, subject to spanwise-constant and time-periodic Coanda blowing, using wind tunnel experimental data, as shown in Fig. 1. Our experimental dataset characterizes the wake response to periodic forcing for a wide range of excitation parameters. We highlight the role of resonant triadic interactions by studying the finely resolved variations of the power spectral density (PSD) of the global mode response with the excitation frequency. Subsequently, we develop an extended Stuart−Landau model for the evolution of the forced global mode using a physically motivated ansatz for the coupling between forcing and response. Further analysis on the model shows that its structure describes the presence of multiple synchronization regions and offers analytic expressions for their boundaries, which depend on a priori unknown coefficients. Finally, after identifying these coefficients from experimental data, quantitative agreement is obtained between the low-order model and the resonances and frequency lock-on regions observed for the forced turbulent wake.
a Experimental setup to study the response of the global vortex shedding mode in the wake of a D-shaped bluff body with a rectangular base, subject to spanwise-constant and time-periodic Coanda blowing at Reynolds number Re = 5.62 × 104 based on the free-stream velocity U∞ and body height H. Time-resolved pressure measurements are obtained from five sensors located along the mid-span of the rear face of the body. Signals are weighted by ±1 and averaged to get the antisymmetric pressure average x(t) that characterizes the global mode amplitude response. b Normalized power spectral density (PSD) of x(t) in the unforced case, showing the natural frequency ω0, and periodically forced at a frequency ωf = 2ω0. The axis Ω denotes the frequency content of the response. c Panels show the PSD of the time-series of x(t) as a function of excitation frequencies ωf, for two types of actuation, symmetric and antisymmetric, and three forcing amplitudes ε.
Results and discussion
Power spectrum response
The dynamics of turbulent bluff body wakes exhibit self-sustained oscillations. The dominant coherent structure characterizing the oscillatory motion is known as the global vortex shedding mode6. Our experimental setup and our procedure for data post-processing used to investigate the response of the forced turbulent wake past a D-shaped body are detailed in the “Methods” section at the end of the paper. We use the antisymmetric average of pressure sensors located along the mid-span of the rear face of the body x(t) to capture the amplitude of the global vortex shedding mode, as shown in Fig. 1a. For the unforced flow, x(t) has a PSD with one distinct peak located at the fundamental shedding frequency ω0, corresponding to a Strouhal number based on the free-stream velocity and body height of St = ω0H/2πU∞ = 0.23, as shown in Fig. 1b. However, when the flow is periodically forced, the peak of the PSD of x(t) may change its magnitude and shift away from the natural frequency.
Like the peak of the PSD, the mean frequency ω and mean amplitude r of the global mode response, computed from x(t), provide information about resonances and lock-on regions that has already been discussed in previous studies29,30. A deeper insight into the underlying nonlinear interactions is obtained by examining all components of the PSD at different forcing frequencies. The power spectra obtained for each excitation frequency are stacked as columns to form a matrix that is plotted as a heat map, shown in Fig. 1c. The large number of test cases yields a fine resolution of the effect of ωf on the PSD of the global vortex shedding mode, resulting in a highly interpretable visualization that we refer to as the power spectrum response.
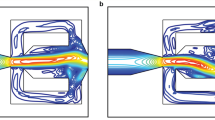
An enlarged version of the power spectrum response for the case of symmetric forcing is shown in Fig. 2a. Identification of the frequency components of the response that are dominant across all frequencies of the forcing, distinguishable as sharp straight lines on Fig. 2a, provides insight into the nature of the interactions between forcing and response modes. The highest energy component coincides with the measured mean vortex shedding rate, Ω = ω, shown by the white line overlay on the first panel of Fig. 2b. On the second panel of Fig. 2b, the green overlay corresponds to the linear function Ω = ωf, highlighting the component expected due to the footprint of the forcing frequency in the spectrum of the response. On the third panel of Fig. 2b, the yellow and blue overlays are obtained by adding and subtracting ωf from the measured mean shedding rate ω. Agreement of these overlays with the dominant components in the power spectrum response confirms that triadic interactions are readily seen in this visualization as side-bands to the forcing frequency component, i.e., Ω = ωf ± ω. All other relevant components for this case are explained as higher harmonics of the forcing and the triadic interactions with these higher harmonics. Figure 2c shows the results obtained by numerical integration of a hierarchy of low-order models, which we develop in the next section.
a Experimental response of the global vortex shedding mode amplitude characterized via its power spectral density (PSD) as function of the excitation frequency ωf normalized by the natural frequency ω0. The axis Ω denotes the frequency content of the response. b Interpretation of the dominant frequency components of the response across all frequencies of the forcing. Colored overlays highlight the response frequency components at the measured mean vortex shedding rate (white), the forcing frequency and its harmonics mωf, for integer m, (green), and those obtained by adding and subtracting the previous overlays as functions of the forcing frequency (yellow and blue). c The power spectrum response computed from simulations of a hierarchy of modified Stuart−Landau models, where A is the global mode amplitude, t is dimensionless time, σ and l are the Stuart−Landau coefficients, ε is the forcing amplitude, and \({\hat{F}}_{nm}\) are complex constants that model the interactions between the forcing and the wake. White measurement noise is added to all models.
For antisymmetric forcing, the power spectrum response is quite different, as shown in Fig. 3a. In this case, the dominant frequency components in the power spectrum response correspond to the vortex shedding rate Ω = ω and to harmonics of the forcing Ω = mωf, with m being an integer, as shown in Fig. 3b. The absence of components mωf ± ω induced by nonlinear interactions is expected because the forcing mode and the pair of conjugate response modes have spatial symmetries that are incompatible with the triadic consistency condition, i.e. their wavenumbers do not sum to zero. The other present frequency components correspond to interactions between the forcing and higher harmonics of the response, which are orders of magnitude weaker in power and do not play a significant role in the wake dynamics.
a Experimental response of the global vortex shedding mode amplitude characterized via its power spectral density (PSD) as function of the excitation frequency ωf normalized by the natural frequency ω0. The axis Ω denotes the frequency content of the response. b Interpretation of the dominant frequency components of the response across all frequencies of the forcing. Colored overlays highlight the response frequency components at the measured mean vortex shedding rate (white), and the forcing frequency and its harmonics mωf, for integer m (green). c The power spectrum response computed from simulations of a hierarchy of modified Stuart−Landau models, where A is the global mode amplitude, t is dimensionless time, σ and l are the Stuart−Landau coefficients, ε is the forcing amplitude, and \({\hat{F}}_{nm}\) are complex constants that model the interactions between the forcing and the wake. White measurement noise is added to all models.
Modified Stuart−Landau model
We derive a model for the evolution of the amplitude of the global vortex shedding mode in the turbulent wake behind a bluff body. We begin with the forced Stuart−Landau model in Eq. (2) obtained from weakly nonlinear theory7. Our goal is to obtain an interpretable model for the excitation function g(A, F) that explains the interactions with the periodic forcing F(t) = F(t + 2π/ωf). We posit a simple structure for g and proceed by systematically increasing its complexity until the resulting power spectrum response exhibits the same features observed in Fig. 2b. For easier comparison we evaluate each model in this hierarchy at the same actuation frequencies as our experimental data using the same number of sample records with the same length and sampling rate. Measurement noise is added to the numerical solutions before computing the power spectrum response to represent background turbulence27. Zero-mean white Gaussian noise is used with a standard deviation proportional to the corresponding response amplitude for each ωf. This enables unbiased comparison between the model response and experimental data, as in Fig. 2c and Fig. 2a, respectively.
We first show the power spectrum response in the absence of forcing (g = 0). As expected, the spectral power is localized at the natural shedding frequency, as shown in the first panel of Fig. 2c. Next, we consider the case of harmonic forcing at the known actuation frequency, \(F=\varepsilon \hat{F}{e}^{{\rm{i}}{\omega }_{f}t}\), where ε is the forcing amplitude and \(\hat{F}\) is a constant that depends on the spatial structure being excited in the flow. This harmonic forcing acts linearly on the dynamics, i.e. g = F, as shown in the second panel in Fig. 2c. As a third model in this hierarchy, we add terms involving quadratic interactions of the forcing mode with the global mode and with its complex conjugate, g = AF0 + F1 + A*F2, as shown in the third panel in Fig. 2c, where we allow for the possibility that different flow structures \({\hat{F}}_{j}\) are excited by each term. This ansatz is physically motivated, since quadratic interactions are the fundamental mechanism for energy transfer in fluid flows. Finally, we allow for nonharmonic external forcing, which can be expanded as a Fourier series
where \({\hat{F}}_{im}\) depends on the spatial structure being excited in the flow by the mth harmonic of the forcing. The generalization of the ansatz to include nonharmonic periodic forcing enables the model to express the response to inputs from actuators that are not capable of producing monochromatic signals, such as the valve actuators used in this work. The resulting model for the forced complex amplitude of the global mode is a modified Stuart−Landau equation:
The Stuart−Landau coefficients σ and l are identified from experimental data using a constrained least squares regression, as detailed in the “Methods” section. The coefficients \({\hat{F}}_{0m},\,{\hat{F}}_{1m}\) and \({\hat{F}}_{2m}\), for integer m, parametrize the direct and parametric excitation terms induced by the periodic forcing. These differ depending on the forcing configuration, symmetric or antisymmetric, and are also identified from data via the model-based analysis presented in the “Methods” section. The model power spectral response remarkably resembles the results obtained from the turbulent flow experiments, as shown in the last panel in Fig. 2c. When carrying out the analogous procedure for antisymmetric forcing, we find that the same model generalizes to both forcing modes. Nevertheless, in the latter case the terms \({\hat{F}}_{0m}\) and \({\hat{F}}_{2m}\) are negligible due to the absence of triadic interactions, as shown in Fig. 3c.
We use the method of averaging47 for further model-based analysis, as detailed in the methods section at the end of the paper. We find that, when under nearly resonant forcing, our extended Stuart−Landau model simplifies to the model of Rigas et al.30, generalized to nonharmonic excitation. In addition, our model also explains the response observed away from resonances in our extensive experimental dataset. Moreover, we obtain expressions bounding the regions where frequency locked solutions may exist, as follows
where \({\omega }_{0}^{\prime}={\omega }_{0}-\varepsilon {\hat{F}}_{00}{l}_{{\mathrm{i}}}/{l}_{{\mathrm{r}}}\), and the subscripts r and i denote the real and imaginary parts of the complex constants. The inequality in Eq. (5) delimits the n:1 synchronization region for n integer, and Eq. (6) delimits the n:2 synchronization region for n odd. Here, the notation n:m refers to a synchronization regime where n cycles of the oscillator take place every m cycles of the forcing. From Eqs. (5) and (6), the maximum allowable frequency offsets to stay inside the respective synchronization regions are given by
where \({\omega }_{{\mathrm{f}}}^{* }\) is the forcing frequency at the corresponding synchronization boundary. These expressions directly relate \({\hat{F}}_{1n}\) and \({\hat{F}}_{2n}\) with the width of the respective frequency lock-on regions, and therefore they can be exploited to identify these coefficients, as shown in Fig. 4 and detailed in the “Methods” section.
The plot reports the experimental long-term response to periodic forcing of the global vortex shedding mode frequency ω and oscillation amplitude r as a function of the excitation frequency ωf. Away from resonances, the response has amplitude \({r}_{0}^{\prime}\) and frequency \({\omega }_{0}^{\prime}\) which are different than those observed in the natural dynamics. The nth subharmonic and harmonic resonances, for integer n, are observed when \({\omega }_{{\mathrm{f}}}\approx 2{\omega }_{0}^{\prime}/n\) and \({\omega }_{{\mathrm{f}}}\approx {\omega }_{0}^{\prime}/n\), and the associated lock-on regions have frequency half-spans denoted by Δ2n and Δ1n, respectively. The model describes the evolution of the complex global mode amplitude A as a function of time t, and is parametrized by the coefficients σ and l that characterize the unforced dynamics, and by \({\hat{F}}_{0m}\), \({\hat{F}}_{1m}\), and \({\hat{F}}_{2m}\) that characterize the effect of the mth harmonic of the forcing mode with amplitude ε. The classical Stuart−Landau coefficients, σ and l, are identified via a regression onto data of the unforced dynamics. Colored markers highlight the training data used to identify the forcing coefficients. In particular, \({\hat{F}}_{00}\) acts as a correction to σ and is obtained from the nonresonant response shown by the yellow markers, whereas \({\hat{F}}_{0m}\) for m ≠ 0 play no role on the long-term response. The coefficient \({\hat{F}}_{2m}\) for m = n allows the model to capture the nth subharmonic resonance, and is identified using the width of the corresponding lock-on region calculated using the data points shown by the blue markers. Analogously, \({\hat{F}}_{1m}\) for m = n is obtained from the nth harmonic lock-on delimited by the green markers. Gray markers show the testing data reserved for comparison.
Modeling synchronization
In this section we present a comparison between simulations from our proposed model and experimental data, and discuss the synchronization properties of the forced turbulent wake past a D-shaped body. The unknown coefficients of our modified Stuart−Landau model are identified from experimental data. Only the data delimiting the synchronization regions and characterizing the nonresonant response was used to fit the model, as highlighted by the colored markers in Fig. 4. The rest of the data, shown by the gray markers in Fig. 4, were used for comparison. The details of the procedure as well as the identified coefficients are presented in the “Methods” section. Using the model, we compute the long-term amplitude and frequency response of the global vortex shedding mode under periodic forcing as a function of the excitation frequency. A comparison against experimental data for symmetric and antisymmetric forcing at three excitation amplitudes is shown in Fig. 5a−d. The modified Stuart−Landau model captures the experimental behavior very well, displaying multiple resonances and frequency lock-on regions. Moreover, the same model structure allows for the description of the long-term response with various forcing amplitudes and different forcing configuration, which translates into different dominating resonances, harmonic or subharmonic. It should be noted that the model is highly constrained by the data; therefore, special care is needed when tuning its coefficients to avoid overfitting.
a Mean amplitude of the global vortex shedding mode response to symmetric periodic forcing as function of the excitation frequency ωf for three forcing amplitudes ε. b The same as (a), but for antisymmetric forcing. c Mean frequency of the global vortex shedding mode response to symmetric periodic forcing as function of the excitation frequency ωf for three forcing amplitudes ε. Markers denote experimental results and solid lines correspond to the proposed model. d The same as (c), but for antisymmetric forcing. In panels (a−d), every other marker has been omitted for presentation purposes. e The Arnold tongues, i.e., regions in ωf−ε space where the wake response synchronizes to a rational multiple of the excitation frequency, for symmetric forcing. The blue markers show the experimentally observed boundaries of frequency locked regions, i.e., where \(| \omega -\frac{n}{2}{\omega }_{{\mathrm{f}}}| <\delta\) for n integer and δ a small threshold. Shaded regions correspond to the synchronization criteria according to Eqs. (5) and (6). f The same as (e), but for antisymmetric forcing.
In accordance with the work of Barros et al.29, when the forcing is symmetric, the largest amplification of the response occurs when the system is excited near twice the fundamental frequency ωf/ω0 ≈ 2, as shown in Fig. 5a. As pointed out by Rigas et al.30, this subharmonic resonance arises due to triadic interactions between the global mode, its complex conjugate, and the forcing mode. This can only occur when the spatial characteristics of these modes satisfy the triadic consistency conditions, meaning that, if expressed using a traveling wave ansatz, their wavenumbers and frequencies must add up to zero31,32. This requirement is clearly not satisfied for the case of antisymmetric forcing, where the largest amplification of the response occurs at the harmonic resonance ωf/ω0 ≈ 1, as shown in Fig. 5b.
We now investigate which combinations of the actuation frequency and amplitude cause the turbulent wake to synchronize with the external excitation. These regions in ωf–ε space are known as Arnold tongues16. From experimental data, the mean frequency of the response ω is used to find the excitation frequencies that delimit the n:1 harmonic and n:2 subharmonic lock-on regions. These are marked with blue crosses in Fig. 5e, f for both symmetric and antisymmetric forcing, respectively. The model-based Arnold tongues that are shaded in Fig. 5e, f correspond to the regions bounded by Eqs. (5) and (6). As the figure shows, our modified Stuart−Landau model captures the observed tongues and the position of the transition boundaries for the range of excitation amplitudes studied. In this particular example, significant drag reduction is observed outside the Arnold tongues, which highlights the relevance of modeling synchronization as a key enabler of effective periodic flow control.
Conclusions
In this work, we have leveraged a uniquely comprehensive experimental dataset of a periodically forced turbulent wake to develop a modified Stuart−Landau model for the response of the global vortex shedding mode. The breadth and quality of our dataset reveals previously unobserved resonances and frequency lock-on regions. Moreover, it enables the construction of heat maps showing the PSD of the wake response as a function of the excitation frequency. This novel visualization exposes triadic interactions as dominant frequency components, providing confirmation of their previously conjectured role in the forced wake response29,30.
We develop a mechanistic model for the evolution of the forced global mode that generalizes previous models to nonharmonic excitation and extends their applicability to a broader range of parameters. Although not derived from first principles, our model is shown to include the necessary nonlinear interactions to describe the response to forcing of a high-dimensional and turbulent oscillator flow with a single ordinary differential equation. After identifying the unknown model parameters using a small subset of experimental data, we find agreement between the model and the complete set of experiments, building a foundation for future investigations into effective periodic flow control. Low-order models that capture synchronization mechanisms are essential for the design of feedback controllers to manipulate periodic coherent structures that govern lift, drag and mixing in oscillator flows. Our approach to capture the synchronization properties of the system in an extensive parameter space using only a few measurements is promising, and its generalization to a large class of forced oscillator flows will be further studied in future work.
Methods
Experimental setup
A major contribution of this work is the exhaustive experimental investigation of the turbulent wake response to periodic blowing for a broad range of excitation frequencies, excitation amplitudes, and forcing configurations. The experiments are conducted in the “Leiser Niedriggeschwindigkeitswindkanal Braunschweig” (LNB) wind tunnel at the institute of fluid mechanics of the Technische Universität Braunschweig.
The experimental model is a D-shaped bluff body with a blunt trailing edge; it has a height of 53.4 mm, a length of 190.6 mm, and a width of 390 mm. The model is horizontally mounted in the wind tunnel and held by one steel tube on each side. The model nearly spans the entire width of the test section. Zigzag tape is applied to the upper and lower side at about 9% body length to trip the boundary layer and to prevent the formation of a laminar separation bubble. A sketch of the model is presented in Fig. 1a. The model is equipped with two Coanda actuators at the trailing corners, each fed by four plenum chambers. The Coanda surfaces have a 9.4 mm radius, which was determined by numerical optimization48. The jet slit height is set to 0.2 mm. The uniformity of each jet is verified with a fish mouth probe to be within 10% of the mean exit pressure.
Unsteady actuation is enabled through eight Festo MHJ9-QS4-MF monostable 2/2-way valves with an operating pressure range of 0.5−6 bar. The valves can be operated at maximum frequency of 1 kHz. Time-resolved pressure signals are acquired by five Honeywell SLP pressure sensors distributed along the mid-span of the rear face of the model. The sensors have a measurement range of ±1000 Pa differential pressure, a repeatability of 0.5% of the full scale, and a response time of 100 μs. Plenum pressure is monitored by two Kulite pressure sensors with a range of ±3.5 × 104 Pa differential pressure and an accuracy of ±0.1% of the full scale. All differential pressures are measured relative to the static pressure in the free stream. The instantaneous jet velocity is estimated from the pressure measurements in the plenum chambers.
Data post-processing
We study the long-term response of the global vortex shedding mode to periodic forcing for a broad range of parameters, including the forcing configuration, and the excitation amplitude and frequency. Two forcing configurations are considered: in-phase blowing through the top and bottom slits, leading to the excitation of a spatially symmetric flow structure, and 180° out-of-phase blowing, exciting a spatially antisymmetric structure. The effect of forcing amplitude is investigated for three blowing intensities quantified nondimensionally by the momentum coefficient as
where Ujet is the root mean square value of the jet velocity calculated from the plenum pressure measurements, h = 0.2 mm is the slot height, H = 53.4 mm is the body height, and the factor 2 accounts for the number of actuators. We define the excitation amplitude ε as the average of cμ over all excitation frequencies at a given tank pressure.
For each forcing configuration and amplitude, the base pressure is recorded for 8 s at a sampling rate of 5 kHz for blowing frequencies between 1 and 210 Hz with 1 Hz intervals. For all cases, the conditions are maintained for 5 s to ensure steady-state behavior before the measurements are taken. The complete dataset is conformed by a total of 1260 time-series of x(t), each consisting of 40,000 samples. The PSD of each time-series is computed using Welch’s method49, splitting the time-series into ten segments with 50% overlap and tapered by a Hanning window. In addition, the x(t) time-series are used to characterize the mean frequency and amplitude of the wake response. Each x(t) is low-pass filtered using a fifth-order Butterworth filter with a cutoff frequency of 1.3ω0. Its Hilbert transform xH(t) is then computed to build an analytic signal for the complex global mode amplitude A(t) = (x + ixH)(t), which is a common practice when studying oscillatory dynamics from data20. Once we have the complex time-series A(t), we compute its mean amplitude r, and its mean frequency ω from the mean of the time derivative of its instantaneous phase.
Model-based analysis
The dynamical system given by Eq. (4) is amenable to classical analysis of nonlinear oscillators. When there is no actuation, the solution to Eq. (4) for A = reiθ exhibits an unstable fixed point at r = 0 and a stable limit cycle of radius \({r}_{0}=\sqrt{{\sigma }_{{\mathrm{r}}}/{l}_{{\mathrm{r}}}}\) with frequency \({\omega }_{0}={\sigma }_{{\mathrm{i}}}-{l}_{{\mathrm{i}}}{r}_{0}^{2}\); the subscripts “r” and “i” denote the real and imaginary parts of the complex constants. In the presence of periodic excitation, we are interested in finding frequency locked solutions, where the phase of the complex amplitude rotates with a mean angular frequency \(\langle \dot{\theta }\rangle =\omega\), which is a rational multiple of the forcing frequency ωf. For this purpose, we introduce the change of variables \(A=r{e}^{{\rm{i}}\theta }=r{e}^{{\rm{i}}(\phi +\omega t)}=\tilde{A}{e}^{{\rm{i}}\omega t}\), where \(\tilde{A}=r{e}^{{\rm{i}}\phi }\) has a slowly varying amplitude r and phase ϕ. Substituting into Eq. (4) and rearranging yields
which describes the evolution of the slow complex amplitude \(\tilde{A}\). Up to this point, no approximations have been made. We have managed to turn the search for frequency locked solutions of A into the search for fixed points of \(\tilde{A}\). Nevertheless, Eq. (10) is nonautonomous, meaning that the dynamics depend explicitly on t. By applying the method of averaging47, also known as the Krylov−Bogoliubov method, we can further simplify this equation to an autonomous dynamical system. In practice, this is achieved by integrating over one period of the complex amplitude T = 2π/ω and neglecting the changes of the slow variables over that time horizon. The terms on the right-hand side of Eq. (10) that are kept after the averaging procedure are those that cancel out the fast oscillations ~ eiωt on the left. Therefore, the resulting expression for the slow dynamics depends on the actuation frequency. The three possible cases are analyzed below: nonresonant forcing, harmonic resonance nωf ≈ ω, and subharmonic resonance nωf ≈ 2ω, for integer n.
Away from any resonance of the system, nωf ≠ ω and nωf ≠ 2ω, the slow dynamics are governed by the balance between the left-hand side of Eq. (10) and the zeroth harmonic of F0, as follows
Notice that \({\hat{F}}_{00}\) changes the eigenvalue of the linear dynamics of the global mode at the origin to \(\sigma ^{\prime} =\sigma +\varepsilon {\hat{F}}_{00}\). As a consequence, the radius and frequency of the stable limit cycle are modified according to
The values identified for \({\hat{F}}_{00}\) in the cases of symmetric and antisymmetric forcing of the turbulent D-shaped bluff body wake are shown in Table 1.
In the proximity of an order n harmonic resonance, i.e., nωf = ω, the slow dynamics are governed by the balance between the left-hand side of Eq. (10) and the terms on the right-hand side that include \({\hat{F}}_{00}\), \({\hat{F}}_{1n}\), and \({\hat{F}}_{2m}\), where m = 2n. Furthermore, if the linear interaction of the global mode with the nth harmonic of the forcing dominates over the nonlinear interaction with its 2nth harmonic, then \({\hat{F}}_{1n}\gg {\hat{F}}_{2m}{\tilde{A}}^{* }\), resulting in
where \(\sigma ^{\prime}\) includes the contribution of the interaction with F0. Recasting the system in polar form we obtain
This system of equations has no explicit time dependence; hence, we can search for fixed points by setting \(\frac{{\rm{d}}r}{{\rm{d}}t}=\frac{{\rm{d}}\phi }{{\rm{d}}t}=0\), which represent frequency locked solutions of the form \(A=r{e}^{{\rm{i}}n{\omega }_{{\mathrm{f}}}t}\). Furthermore, equating the \(\left({r}^{2}-{r}_{0}^{^{\prime} 2}\right)\) terms and rearranging yields
Thus, a frequency locked solution exists only if the frequency detuning is in the range
where r0 approximates r evaluated at the synchronization boundary. Therefore, Eq. (16) represents the bounds for the n:1 synchronization region. Let \({\omega }_{{\mathrm{f}}}^{* }\) be the forcing frequency at the boundary of this region, then the maximum frequency detuning allowed to maintain the corresponding harmonic lock-on is given by
This expression is particularly useful since it directly relates \({\hat{F}}_{1n}\) with the width of the respective frequency lock-on region, and therefore it can be used to identify this family of coefficients, as shown in Fig. 4 and detailed in the following section.
We now investigate the cases where a subharmonic resonance of the type nωf = 2ω takes place, excluding even values of n as those were accounted for in the previous scenario. In the proximity of a subharmonic resonance, the slow dynamics are governed by the balance between the left-hand side of Eq. (10) and the terms on the right-hand side that include \({\hat{F}}_{00}\), and \({\hat{F}}_{2n}\), as follows
where \(\sigma ^{\prime}\) includes the contribution of the interaction with F0. Recasting Eq. (18) in polar form, we obtain
As in the previous case, these equations have no explicit time dependence; hence, we search for fixed points by setting \(\frac{{\rm{d}}r}{{\rm{d}}t}=\frac{{\rm{d}}\phi }{{\rm{d}}t}=0\), which represent frequency locked solutions that are now of the form \(A=r{e}^{{\rm{i}}n{\omega }_{{\mathrm{f}}}/2t}\). Again, equating the \(\left({r}^{2}-{r}_{0}^{^{\prime} 2}\right)\) terms and rearranging yields
for which a solution exists only for the range of the frequency detuning given by
This inequality determines the bounds for the n:2 synchronization region. Let \({\omega }_{{\mathrm{f}}}^{* }\) be the forcing frequency at the boundary of this region, then the maximum frequency detuning allowed to maintain the corresponding subharmonic lock-on is given by
This expression directly relates \({\hat{F}}_{2n}\) with the width of the respective frequency lock-on region, and therefore it can be exploited to identify this family of coefficients, as shown in Fig. 4 and detailed in the following section.
Identifying the model coefficients
In the absence of forcing, the proposed model, shown again in Fig. 4, reduces to the classic Stuart−Landau equation that is parametrized by the complex coefficients σ and l. Therefore, these unknown parameters can be identified using measurements of transients of the system when the forcing is not active. To characterize the unforced dynamics, we drive the system away from its long-term behavior using steady blowing and using resonant periodic forcing. Starting from each of these conditions, the forcing is turned off and we record the evolution of the global mode. These transients are low-pass filtered using a fifth-order Butterworth filter with a cutoff frequency of 1.3ω0 and then phase-averaged over an ensemble of 59 realizations. Figure 6a, b shows the evolution of the antisymmetric pressure average starting from larger and smaller amplitude oscillations, respectively. In both cases it takes on the order of ten shedding cycles for the wake to relax onto the limit cycle describing its long-term behavior.
The variable x(t) is our characterization of the global mode amplitude via the antisymmetric average of the transverse pressure distribution on the base of the body, t is dimensionless time, and T0 and r0 denote the fundamental period and amplitude of the unforced wake mode, respectively. a Evolution starting from the subharmonic resonant response to symmetric periodic forcing. b Evolution starting from the long-term response to steady blowing. Gray curves show the superposition of all experimental realizations, orange curves show their phase-average, and the dashed blue curves correspond to the identified model.
Based on the data for the unforced transients, we identify σ and l through a constrained least squares regression. The phase-averaged and filtered time-series x(t) and its Hilbert transform xH(t) are used to build an analytic signal for the complex global mode amplitude A(t) = (x + ixH)(t). Once we have the instantaneous complex amplitude, we can compute its instantaneous amplitude r(t) and phase θ(t), as well as the respective time derivatives using second-order central finite differences. In addition to the transients, we measure the mean amplitude and frequency, r0ω0, from the magnitude and position of the peak of the PSD of the long-term unforced time-series. In accordance with the Stuart−Landau equation, we know that these measurements must satisfy the solutions for the radius \({r}_{0}=\sqrt{{\sigma }_{{\mathrm{r}}}/{l}_{{\mathrm{r}}}}\) and frequency \({\omega }_{0}={\sigma }_{{\mathrm{i}}}-{l}_{{\mathrm{i}}}{r}_{0}^{2}\) of the stable limit cycle, where the subscripts “r“ and “i” denote the real and imaginary parts of the complex constants. Therefore, the regression problem is formulated by recasting the Stuart−Landau equation in polar form and deriving linear equality constraints from the known limit cycle solution, as follows
Here, the vector b and the matrix Θ are constructed by vertically stacking the time-series data for \(r,\dot{r},\) and \(\dot{\theta }\) and using null vectors of the same length. The matrix C and the vector d are also computed from experimental data, since we have measured r0 and ω0. Therefore, the coefficients ξ can be identified from
which is a convex optimization problem that can be solved using readily available software; we use CVXPY developed by Diamond and Boyd50. The identified model is simulated and compared against the experimental data in Fig. 6. The identified values for σ and l are shown in Table 1.
After identifying σ and l from the unforced dynamics, we can solve for \({\hat{F}}_{00}\) from Eq. (12) using measurements of the long-term unforced response, r0 and ω0, along with measurements of the modified response away from resonances, \({r}_{0}^{\prime}\) and \({\omega }_{0}^{\prime}\), as shown in Fig. 4. Furthermore, Eq. (17) is used to identify the coefficients \({\hat{F}}_{1n}\) from data. This is achieved using experimental measurements of the mean global mode frequency ω, and finding the values of \({\omega }_{{\mathrm{f}}}^{* }\) that delimit the corresponding n:1 frequency lock-on regions, i.e., where ∣ω − nωf∣ < δ is satisfied, with δ being a small threshold. Subsequently, we subtract the upper and lower bounds to compute the width of the frequency lock-on regions which is equal to twice the maximum frequency detuning Δ1n. Finally, as shown in Fig. 4, this measurement is used to solve for \({\hat{F}}_{1n}\), allowing the computation of one of these model parameters for every harmonic resonance observed. In the present experiment we observe three harmonic resonances for both symmetric and antisymmetric forcing. In a similar manner, the coefficients \({\hat{F}}_{2n}\) are identified using Eq. (21) and measurements of the width of the subharmonic frequency lock-on regions. This procedure allows the computation of one of these model parameters for every subharmonic resonance observed. For the present flow, we observe four subharmonic resonances for symmetric forcing, and one for antisymmetric. The identified coefficients are shown in Table 1.
As detailed in the previous section, the coefficients \({\hat{F}}_{2n}\) for even values of n are neglected because every subharmonic resonance caused by \({\hat{F}}_{2m}\), where m = 2n, overlaps with a harmonic resonance caused by \({\hat{F}}_{1n}\). The presence of non-zero (\({\hat{F}}_{2n}\)) \({\hat{F}}_{1n}\) coefficients for (anti-)symmetric forcing, is explained because the symmetry characteristics of the actuation are not perfect, as expected for any real setup. For the antisymmetric case, a small component of symmetric forcing is manifested as a narrow subharmonic resonance. For the symmetric case, multiple harmonic resonances of considerable size are observed, which we attribute to the direct excitation mechanism being more effective than the parametric one.
Data availability
The experimental dataset that supports the findings of this study is available from the corresponding author upon request.
Code availability
The custom-made Python codes that support the findings of this study are available from the corresponding author upon request.
References
Huerre, P. & Monkewitz, P. A. Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537 (1990).
Chomaz, J.-M. Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392 (2005).
Landau, L. D. On the problem of turbulence. C. R. Acad. Sci. URSS 44, 311–314 (1944).
Stuart, J. T. On the non-linear mechanics of wave disturbances in stable and unstable parallel flows Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9, 353–370 (1960).
Brunton, S. L. & Noack, B. R. Closed-loop turbulence control: progress and challenges. Appl. Mech. Rev. 67, 050801 (2015).
Holmes, P., Lumley, J. L., Berkooz, G. & Rowley, C. W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry (Cambridge University Press, Cambridge, 2012).
Sipp, D. & Lebedev, A. Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358 (2007).
Bagheri, S. Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596 (2013).
Mathis, C., Provansal, M. & Boyer, L. The Benard-Von Karman instability: an experimental study near the threshold. J. Phys. Lett. 45, 483–491 (1984).
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363 (2003).
Thompson, M. C. & Le Gal, P. The Stuart−Landau model applied to wake transition revisited. Eur. J. Mech. B/Fluids 23, 219–228 (2004).
Gallaire, F. et al. Pushing amplitude equations far from threshold: application to the supercritical Hopf bifurcation in the cylinder wake. Fluid Dyn. Res. 48, 061401 (2016).
Provansal, M., Mathis, C. & Boyer, L. Benard-von Karman instability: transient and forced regimes. J. Fluid Mech. 182, 1–22 (1987).
Winfree, A. T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16, 15–42 (1967).
Guckenheimer, J. Isochrons and phaseless sets. J. Math. Biol. 1, 259–273 (1975).
Arnold, V. I. Mathematical Methods of Classical Mechanics (Springer, 1997).
Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence (Springer, Berlin/Heidelberg, 1984).
Ermentrout, B. & Terman, D. Foundations of Mathematical Neuroscience (Springer, New York, 2008).
Strogatz, S. H. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Phys. D Nonlinear Phenom. 143, 1–20 (2000).
Pikovsky, A., Rosenblum, M. & Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge University Press, 2001).
Zlotnik, A., Chen, Y., Kiss, I. Z., Tanaka, H. A. & Li, J. S. Optimal waveform for fast entrainment of weakly forced nonlinear oscillators. Phys. Rev. Lett. 111, 024102 (2013).
Wilson, D., Holt, A. B., Netoff, T. I. & Moehlis, J. Optimal entrainment of heterogeneous noisy neurons. Front. Neurosci. 9, 192 (2015).
Diekman, C. O. & Bose, A. Entrainment maps: a new tool for understanding properties of circadian oscillator models. J. Biol. Rhythms 31, 598–616 (2016).
Taira, K. & Nakao, H. Phase-response analysis of synchronization for periodic flows. J. Fluid Mech. 846, R2 (2018).
Nakao, H. Phase reduction approach to synchronisation of nonlinear oscillators. Contemp. Phys. 57, 188–214 (2016).
Pastoor, M., Henning, L., Noack, B. R., King, R. & Tadmor, G. Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 608, 161–196 (2008).
Semaan, R. et al. Reduced-order modelling of the flow around a high-lift configuration with unsteady Coanda blowing. J. Fluid Mech. 800, 72–110 (2016).
Herrmann-Priesnitz, B., Calderón-Muñoz, W. R., Diaz, G. & Soto, R. Heat transfer enhancement strategies in a swirl flow minichannel heat sink based on hydrodynamic receptivity. Int. J. Heat Mass Transf. 127, 245–256 (2018).
Barros, D., Borée, J., Noack, B. R. & Spohn, A. Resonances in the forced turbulent wake past a 3D blunt body. Phys. Fluids 28, 065104 (2016).
Rigas, G., Morgans, A. S. & Morrison, J. F. Weakly nonlinear modelling of a forced turbulent axisymmetric wake. J. Fluid Mech. 814, 570–591 (2017).
Craik, A. D. D. Non-linear resonant instability in boundary layers. J. Fluid Mech. 50, 393–413 (1971).
Craik, A. D. D. Wave Interactions and Fluid Flows (Cambridge University Press, 1986).
Duvvuri, S. & McKeon, B. J. Triadic scale interactions in a turbulent boundary layer. J. Fluid Mech. 767, R4 (2015).
Le Gal, P., Nadim, A. & Thompson, M. Hysteresis in the forced Stuart−Landau equation: application to vortex shedding from an oscillating cylinder. J. Fluids Struct. 15, 445–457 (2001).
Sipp, D. Open-loop control of cavity oscillations with harmonic forcings. J. Fluid Mech. 708, 439–468 (2012).
Boury, S. et al. Forced wakes far from threshold: Stuart−Landau equation applied to experimental data. Phys. Rev. Fluids 3, 91901 (2018).
Schmid, P. J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28 (2010).
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127 (2009).
Mezić, I. Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378 (2013).
Kutz, J. N., Brunton, S. L., Brunton, B. W. & Proctor, J. L. Dynamic Mode Decomposition (Society for Industrial and Applied Mathematics, 2016).
Brunton, S. L., Proctor, J. L. & Kutz, J. N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113, 3932–3937 (2016).
Rudy, S. H., Brunton, S. L., Proctor, J. L. & Kutz, J. N. Data-driven discovery of partial differential equations. Sci. Adv. 3, e1602614 (2017).
Loiseau, J. C. & Brunton, S. L. Constrained sparse Galerkin regression. J. Fluid Mech. 838, 42–67 (2018).
Towne, A., Schmidt, O. T. & Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867 (2018).
Taira, K. et al. Modal analysis of fluid flows: applications and outlook. AIAA J. 1–36 (2019).
Brunton, S. L., Noack, B. R. & Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 52, 477–508 (2020).
Guckenheimer, J. & Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Applied Mathematical Sciences (Springer, New York, 2002).
Semaan, R. Shape optimization of active and passivedrag-reducing devices on a D-shaped blu body. In New Results Numer. Exp. Fluid Mech. XI, vol. 136, 327−336 (Springer, 2018).
Welch, P. D. The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73 (1967).
Diamond, S. & Boyd, S. CVXPY: a python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17, 1–5 (2016).
Acknowledgements
This work has been supported by the PRIME program of the German Academic Exchange Service (DAAD) with funds from the German Federal Ministry of Education and Research (BMBF) and by the Deutsche Forschungsgemeinschaft (DFG) project number SE 2504/3-1. S.L.B. acknowledges funding support from the Air Force Office of Scientific Research (AFOSR FA9550-18-1-0200) and the Army Research Office (ARO W911NF-19-1-0045).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
B.H., R.S. and S.L.B designed research; P.O. conducted experiments; B.H. performed research; B.H., P.O., R.S., and S.L.B. analyzed data; and B.H. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Herrmann, B., Oswald, P., Semaan, R. et al. Modeling synchronization in forced turbulent oscillator flows. Commun Phys 3, 195 (2020). https://doi.org/10.1038/s42005-020-00466-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00466-3
This article is cited by
-
Macroscopic waves, biological clocks and morphogenesis driven by light in a giant unicellular green alga
Nature Communications (2023)
-
Controlling fluidic oscillator flow dynamics by elastic structure vibration
Scientific Reports (2023)
-
The transformative potential of machine learning for experiments in fluid mechanics
Nature Reviews Physics (2023)
-
Aerodynamic optimization of a generic light truck under unsteady conditions using gradient-enriched machine learning control
Experiments in Fluids (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.