Abstract
Microscopy seeks to simultaneously maximize optical resolution, contrast, speed, volume size, and probe tolerability, which is possible by combining different complementary imaging techniques with their specific strengths. Here, we show how to combine three physical concepts to increase resolution and contrast in light-sheet microscopy by making the effective light-sheet thinner through phase shaping, fluorophores-switching, and dynamic blocking of fluorescence. This shape-switch-block principle is realized by illumination with two holographically shaped, sectioned Bessel beams. Second, by switching off fluorophores in the proximity of the excitation center using continuous-wave stimulated emission depletion (STED). And third, by blocking fluorescence outside the switching region by confocal line detection. Thereby, we reduce the light-sheet thickness by 35%, achieving an isotropic resolution with beads in a 300 × 70 × 50 µm³ volume. Without STED, we obtain 0.37 µm resolution in cell clusters at improved sectioning and penetration depth. The shape-switch-block concept promises high potential, also for other microscopy techniques.
Similar content being viewed by others
Introduction
Modern (super-resolution) microscopy techniques often use a combination of different lasers and phase shaping elements to clearly separate adjacent points in the image. While this combination is established in point-scanning approaches, it has hardly been applied to line-scanning approaches, such as light-sheet microscopy (LSM). LSM has enabled efficient imaging in 3D, with a variety of different illumination beams1,2,3, which are typically generated by holograms and which are scanned laterally (and axially4) within the focal plane of a camera. In combination with structured illumination, LSM has achieved resolutions even beyond the diffraction limit for weakly scattering samples5. It is widely accepted that LSM provides a valuable compromise between imaging speed of typically large objects, image resolution, and contrast while causing low levels of phototoxicity6, but further improvements in 3D image quality are necessary, to reveal even smaller structural cellular details and processes.
Particularly advantageous for LSM is fluorescence excitation with Bessel beams. In comparison to the popular Gaussian beams, Bessel beams provide an increased depth of field7 at the same focusing angle and penetrate deeper in scattering media2. For the same depth of field as a Gaussian beam, they feature a significantly lower diameter of the central beam lobe8. The concentric ring system of the Bessel beams, however, illuminates the object not only in the focal plane, but also in regions outside the focal plane, thereby reducing the contrast. Several approaches that aim to minimize the fluorescence excited by the ring system were demonstrated. These include multiple photon excitation9,10,11, line-confocal detection12,13,14, sectioned Bessel beams15, and for weak scattering samples, arranging Bessel beams to grids by incoherent9 or coherent superposition to a lattice16,17.
One recent approach to eliminate the unwanted fluorescence excited by the Bessel beam’s ring system is to use stimulated emission depletion (STED). The generation of so-called light needles formed by the undepleted fluorescence in the central lobe has been studied theoretically in idealized homogeneous media18, and in more realistic media containing scatterers19. The robustness in overlap and depletion efficiency of two Bessel beams for excitation and STED could be measured recently in scattering media20. However, attempts with conventional cylinder-lens generated light-sheets remain difficult21, since enormous STED powers are needed to realize an efficient depletion process. Utilizing the significantly slower process of reversible saturable optical fluorescence transitions (RESOLFT), the width of the remaining fluorescence layer, however, could be reduced in an—albeit limited—observation volume, thus increasing the spatial resolution in light-sheet microscopy22.
In this paper, we extend the principle of line-STED20 and apply it to a pair of non-rotationally symmetric Bessel beams23, so-called sectioned Bessel beams, which we use both for fluorescence excitation and depletion. Sectioned Bessel beams are supposed to have improved imaging properties since the overlap with the detection point spread function (PSF) is minimized outside the point focus15,16. Using an available continuous wave (CW) depletion laser, we maximize the STED illumination and fluorescence depletion efficiency by achieving a beam overlap only around the Bessel beam’s central lobe, while the fluorescence photons emitted from the outer region of the sectioned Bessel beam, are blocked by confocal slit-scanning. This way the established concepts of point-wise confocal and STED scanning are not only combined with a line-scanning mode, but they operate hand-in-hand by effectively reducing the width of the scanning beam in complementarity regions and thereby the width of light-sheet in detection direction.
Results
Basic principle and setup
All experimental results in this work were generated by measurements conducted on a modified version of a setup built in our laboratory and described in more detail in the ref. 20. A detailed set-up sketch is provided in Supplementary Fig. 1. The setup is based on two CW lasers: a 25 mW excitation laser (Cobolt Calypso 04–01 491 nm) and a 2 W STED laser (MPB Communications, VFL-P-2000-560). Both laser beams are expanded and coaligned by means of a beam splitter so that the beams propagate parallel in a distance of 6.5 mm to each other.
Each beam illuminates one half of the spatial light modulator (SLM) (Hamamatsu X10468-04), which generates the holograms for fluorescence excitation and STED, \(\phi _{{\mathrm{EX}}}(x,y)\) and \(\phi _{{\mathrm{ST}}}(x,y)\), on its right and left half, respectively, as sketched in Fig. 1 and Supplementary Fig. 2. The phase shaped beams show intensity profiles \(I_{{\mathrm{EX}}}(x,y)\) and \(I_{{\mathrm{ST}}}(x,y)\) of sectioned Bessel beams (SBB), which are characterized by dark cones in the vertical y-direction, indicated by yellow and blue dashed lines. Because of a π-phase step in the hologram \(\phi _{{\mathrm{ST}}}(x,y)\) for the STED beam, the corresponding intensity \(I_{{\mathrm{ST}}}(x,y)\) reveals a horizontal dark line. The width of this zero intensity area and the total intensity of the SBB define the thickness of the light-sheet. The beams are then combined and superimposed by beam splitters resulting in a common beam propagation axes. Lenses L1, L2 generate and project the angular spectrum of the beams onto a single-axis scan mirror (G8320KM44B, Cambridge Technology, not shown), which is imaged by an auxiliary 4f-system (not shown) into the back focal plane (BFP) of the water immersion illumination objective lens (IO, Nikon 40XW NAill = 0.8). The superimposed beams for excitation and depletion form a fluorescent line with single beam cross-section \(F_{{\mathrm{SB}}}(x - x_{\mathrm{s}},y)\), or after lateral scanning, the effective light-sheet in the sample chamber, resulting in a thin fluorescence slice \({\int} {F_{{\mathrm{SB}}}(x,y){\mathrm{d}}x}\) (see green particles in Fig. 1). The process of fluorescence excitation, spontaneous emission and depletion with intensity-dependent transition rates kEX, kFL, kST is sketched in the inset box. The fluorescence light (indicated in green) is collected by the water immersion detection objective lens (DO, Nikon 40XW) with a detection numerical aperture (NA) of NAdet = 0.8 and imaged via a tube lens onto a camera (Hamamatsu ORCA-Flash4.0 V2). In order to suppress fluorescence from the ring system and reject multiple scattered fluorescence photons, all images are recorded in rolling shutter mode, i.e., with a synchronized, sweeping confocal slit aperture. The coherent light from both SBBs propagates through the sample and is collected by a third objective lens (L3, Nikon 40XW) with NAsca = 0.8 (sca = scattering). The angular spectra \(\tilde I_{{\mathrm{EX}}}(k_{\mathrm{x}},k_{\mathrm{y}})\) and \(\tilde I_{{\mathrm{ST}}}(k_{\mathrm{x}},k_{\mathrm{y}})\) of both beams are recorded by a second camera (PhotonFocus DS1-D1024-80-CL-10). The imaging of the transmitted light facilitates the alignment and superposition of the beams and reveals the different diameters of the spectra, the sectioning angles (indicated by the yellow and blue dashed lines) as well as the horizontal zero intensity of the STED beam. In addition, the transmitted light permits to analyze the scattering behavior of different parts of the sample and for different illumination beam parameters.
a A single spatial light modulator (SLM) generates two phase holograms \(\phi _{{\mathrm{EX}}}(x,y)\) and \(\phi _{{\mathrm{ST}}}(x,y)\) resulting in two sectioned Bessel beams (SBB) for fluorescence excitation (blue frame) and depletion (yellow frame) with intensities \(I_{{\mathrm{EX}}}(x,y)\) and \(I_{{\mathrm{ST}}}(x,y)\). The SBBs are characterized by two angular sections 2(π−β) of zero intensity indicated by the yellow and blue cones (dashed lines). After beam combining, both SBBs are focused through lenses, a scan mirror (not shown) and an illumination objective (IO) into the sample. The STED beam has a line of zero intensity in the center of the light-sheet (xz-plane). Fluorescence excitation and depletion lead to the effective fluorescence intensity profile \(F(x - x_{\mathrm{s}},y)\) at an exemplary beam position xs, which is scanned in x-direction during image acquisition. Fluorescence excited in the SBB ring system is blocked by confocal slit sweeping parallel to the illumination beams. The angular spectra \(\tilde I(k_{\mathrm{x}},k_{\mathrm{y}})\) of both laser beams are recorded and analyzed in the back focal plane (BFP) of lens L3. b Shape-switch-block: the light-sheet width is reduced in several steps: i) Line scans normal to the light-sheet reveal fewer side lobes for sectioned Bessel beam SBB (blue). ii) A STED SBB (yellow) with zero intensity depletes the fluorescence close to the main lobe (yellow shading), iii) the confocal slit blocks fluorescence from the first side lobes (red shading).
The maximum beam scanning speed and the imaging speed is 50 Hz. The rolling shutter of the Hamamatsu sCMOS camera enables the confocal slit to move parallel to the illumination beam (a typical slit-width is 650 nm corresponding to four pixels). The galvometric mirror and camera triggers are synchronized using data acquisition cards and our custom microscope operating system MicPy. However, the imaging speed is usually limited by the fluorescent sample, not by the hardware. With our nonoptimal CW-STED laser, image acquisition takes 1–2 s per frame. Without the STED process, one frame takes 50–100 ms depending on the sample and the number of required image stacks.
Line-STED with sectioned Bessel beams (SBB)
SBB as introduced in detail earlier15 do not show rotational symmetry but have a bowtie-like profile characterized by a sectioning angle \(\beta\,<\,\pi\) as shown in Fig. 1. The bowtie-light transmission function for a SBB can be described by the sum of two rect-functions, i.e., \(T_\beta (\varphi )\,=\,{\mathrm{rect}}( {{\textstyle{\varphi \over \beta }}} ) + {\mathrm{rect}}( {{\textstyle{{\varphi\,+\,\pi } \over \beta }}})\), with azimuthal angle φ = 0…2π, and generates an electric field \(E_{\mathrm{q}}(x,y,z_{{\mathrm{SLM}}})\,\approx\,E_0 \cdot T_\beta (\varphi )\cdot \exp ( { - i\phi _{\mathrm{q}}(x,y)} )\) at the SLM.
The slope of the conical phase profile \(\phi ( {r = \sqrt {x^2 + y^2} } ) \,=\,r \cdot (\alpha \cdot k_0{\mathrm{NA}})\) is defined by the focusing angle NA = n·sinθ, the vacuum wave number \(k_0 = 2\pi /\lambda _0\) and the dimensionless parameter α ≥ 1. For both the excitation and depletion beam, the phase profile generated at the SLM (see plane [P1] at zSLM = –4f − zR in Fig. 1 and Supplementary Fig. 2) can be written as
Here zR is the depth of field and f the focal length of lens L1/2. The parameter q defines an additional π-phase step along y and is described by the Heaviside step function \({\Theta}(y)\). For the excitation beam we set \(\alpha = 1,\;\;q = 0\) (no phase step), for the depletion beam with zero intensity at y = 0 we need \(\alpha\,> \,1,\;\;q = 1\). The π-phase step is equivalent to an amplitude switch, i.e., \(\exp \left( { - i\pi {\Theta}(y)} \right) = 1 - 2 \cdot {\Theta}(y)\), such that the field right behind the SLM is
The field behind the SLM propagates over the distance zR (typically > 1 cm) to the plane [P2] according to \(E_{\mathrm{q}}(x,y,z = - 4f) ={\mathop{\rm{FT}}\nolimits} ^{ - 1}[ {{\mathop{\rm{FT}}\nolimits} [ {E_{\mathrm{q}}(x,y,z_{{\mathrm{SLM}}})} ] \cdot \exp ( { - iz_{\mathrm{R}}\sqrt {n^2k_0^2 - k_{\mathrm{x}}^2 - k_{\mathrm{y}}^2} } )} ]\), where FT stands for a lateral Fourier transform in xy. At the back focal plane [P3], the ring-like angular field spectrum \(\tilde E_{\mathrm{q}}(k_{\mathrm{x}},k_{\mathrm{y}},z = - 2f)\,=\,\tilde E_{\mathrm{q}}(k_{\mathrm{x}},k_{\mathrm{y}},z = + 2f)\) of the SBBs can be described at best by a multiplication of the conventional Bessel beam’s ring spectrum with a vertical rect-function15, which limits the extent of the sectioning angle β through Δk(β) = 2αk0NA·sin(β/2) (plane [P5] in Fig. 1). The upper and the lower parts of the angular spectrum are still phase-shifted by \(\exp \left( { - i\pi {\Theta}(y)} \right)\) in plane [P3] such that
The power spectra \(\tilde I_{\mathrm{q}}(k_{\mathrm{x}},k_{\mathrm{y}})\,=\,| {\tilde E_{\mathrm{q}}(k_{\mathrm{x}},k_{\mathrm{y}},z = 2f)} |^2\) without scattering object are imaged by a camera in a 4f-distance, as shown by the two sectioned, annular spectra in plane [P5] in Fig. 1: \(\tilde I_{{\mathrm{EX}}}(k_{\mathrm{x}},k_{\mathrm{y}}) + \tilde I_{{\mathrm{ST}}}(k_{\mathrm{x}},k_{\mathrm{y}})= \tilde I_{{\mathrm{q}} = 0}(k_{\mathrm{x}},k_{\mathrm{y}}) + \tilde I_{{\mathrm{q}} = 1}(k_{\mathrm{x}},k_{\mathrm{y}})\).
Hence, in the object plane at z = 0, the electric field cross-sections \(E_{{\mathrm{q}} = 0,1}(x,y,z = 0)\) in the center of the illumination beams at planes [P2] and [P4] are
with \(r = \sqrt {x^2 + y^2}\) and \({\mathop{\rm{FT}}\nolimits} [ {1 - 2q \cdot {\Theta}(k_{\mathrm{y}})} ] =( {2\pi (1 - q)\delta (x,y) \,+ q \cdot {\textstyle{{2i} \over y}}} )\) as the Fourier transform of the step function. A one-dimensional (1D) convolution along y (symbol *) of a rotationally-symmetric Bessel beam \(J_0\left( {k_0{\mathrm{NA}}\,r} \right)\) with a 1D \({\mathop{\rm{sinc}}\nolimits} ( {2{\Delta}k_y \cdot y} )\) function leads to a smear-out of the Bessel ring system in this direction. The additional 1D convolution with a hyperbola function \({\textstyle{{2i} \over y}}\) in vertical y-direction, results in a sign flipping of the (imaginary) field of the Bessel beam and hence a destructive interference along the line (plane) where y = 0. This destructive interference ensures minimal depletion in the center of the STED sectioned Bessel beam. The corresponding beam intensities \(I_{{\mathrm{EX}}}(x,y,0,\beta _{{\mathrm{EX}}}) = \left| {E_{{\mathrm{EX}}}(x,y,0,\beta _{{\mathrm{EX}}})} \right|^2\) and \(I_{{\mathrm{ST}}}(x,y,0,\beta _{{\mathrm{ST}}}) = | {E_{{\mathrm{ST}}}(x,y,0,\beta _{{\mathrm{ST}}})} |^2\) are shown in plane [P2] in Fig. 1 and, for different sectioning angles β, in Fig. 2.
a Simulated and b experimental excitation beam cross-section in the xy-plane for three different sectioning angles β = 0°, 120°, 90°. The overlaid sketch defines the coordinate system. c, d The corresponding simulated and measured beam cross-sections for the stimulated emission depletion (STED) beam. The line of zero intensity along the x-axis results from the π-phase step in the STED hologram. The scale bar is 3 µm.
The 3D fluorescence distribution \(F_{{\mathrm{SB}}}({\mathbf{r}})\) with r = (x,y,z) in plane [P4] around z = 0 is defined by the excitation with the 3D beam intensity \(I_{{\mathrm{EX}}}({\mathbf{r}})\) and parallel depletion with the STED intensity \(I_{{\mathrm{ST}}}({\mathbf{r}})\) and hence by a space-variant probability for spontaneous emission \(\eta ({\mathbf{r}}) = I_{{\mathrm{sat}}}/\left( {I_{{\mathrm{sat}}} + I_{{\mathrm{ST}}}({\mathbf{r}})} \right)\)24. The remaining fluorescence along a single beam with sectioning angle ratio β1/2 = β1/β2 reads
with extinction cross-section Cext(r), quantum efficiency Qfl of the fluorophores and the saturation intensity \(I_{{\mathrm{sat}}} = \left( {hc \cdot k_{{\mathrm{fl}}}} \right)/\left( {\sigma _{{\mathrm{ST}}}\lambda _{{\mathrm{ST}}}} \right)\) (typically \(I_{{\mathrm{sat}}} \approx\) 10–20 mW/µm²), at which the rates of depletion \(\kappa _{{\mathrm{ST}}}\) and fluorescence \(\kappa _{{\mathrm{FL}}}\) equal each other (see inset of Fig. 1). \(\sigma _{{\mathrm{ST}}}\) is the fluorophore specific STED emission cross-section. For simplification, we set the quantum efficiency to \(Q_{{\mathrm{fl}}} = 1.\)
The simulated, remaining fluorescence of non-scanned beams is shown by one cross-section in \(F_{{\mathrm{SB}}}(x - x_{\mathrm{s}},y)\) in Fig. 1 center as well as by the three orthogonal cross-sections in Fig. 3 and Supplementary Fig. 3.
Center-slices through a simulated 3D fluorescence distribution of the excitation and STED beam as well as the resulting 3D fluorescence distribution for a STED power of 1 W. a Orthogonal center-slices through the excited fluorescence distribution F(x, y, 0), F(x, 0, z), and F(0, y, z) which represents the spatial intensity distribution of the excitation beam. b Schematic illustrating how the excitation and STED beams are superimposed to generate an effectively thinner fluorescence distribution in the xy-plane. c Center-slices through the yz-plane of the excitation beam, STED beam, and the resulting fluorescence distribution. The resulting fluorescence is significantly reduced in width along the detection y-direction. d xy-cross-sections of the light-sheets, where the green arrow indicates the beam scanning direction x.
3D imaging simulations
Three-dimensional imaging simulations were performed for a distribution c(r) of 250 nm small fluorescing spheres with refractive indices ns = nm + δn = 1.41 in a medium with nm = 1.33. Coherent scattering of the illumination light during beam propagation in z-direction was approximated by the beam propagation method. Here, the intensity \(| {E_{\mathrm{q}}(x,y,z + {\mathrm{d}}z)} |^2\) for both the excitation beam (q = 0) and the STED beam (q = 1) were calculated from
Images of spheres along a single beam at position \({\mathbf{r}}_{\mathrm{s}} = (x_{\mathrm{s}},y_{\mathrm{s}})\) were obtained by multiplying the effective intensity distribution \(\eta ({\boldsymbol{r - x}}_{\mathrm{s}}) \cdot I_{{\mathrm{EX}}}({\boldsymbol{r - x}}_{\mathrm{s}})\) at lateral beam position \({\boldsymbol{x}}_{\mathrm{s}} = x_{\mathrm{s}} \cdot {\mathbf{e}}_{\mathbf{s}}\) with a distribution of fluorescence spheres \(C_{{\mathrm{ext}}}({\boldsymbol{r}} - {\boldsymbol{y}}_{\boldsymbol{s}})\) vertically displaced by \({\boldsymbol{y}}_{\boldsymbol{s}} = y_s \cdot {\mathbf{e}}_{\mathbf{s}}\) (realized by the sample holder in the experiment).
A 3D single beam image \(p_{{\mathrm{SB}}}({\mathbf{r}})\) is obtained by a convolution with the perpendicularly oriented detection point spread function \(h_{\det }({\mathbf{r}})\) simulated for a detection lens with NA = 0.8:
In line-confocal detection mode12, a slit, i.e., an active camera area of width dslit is running in lateral x-direction parallel to the beam such that the effective illumination beam can be written as8
For a very thin slit width dslit → 0 the resulting line-confocal scanning mode leads to a multiplication of the point spread functions for illumination and detection, \(h_{{\mathrm{ill}}}(x,y) \cdot h_{\det }(x,y)\), which are approximately z-independent. Hence, by line confocal scanning, fluorescence is only detected in the central part of the 3D fluorescence distribution \(F_{{\mathrm{SB}}}({\boldsymbol{r}})\) described in Eq. (5). The confocal slit blocks the remaining fluorescence, which was excited by the (vertically reduced) ring system of the first SBB and not depleted by the STED SBB.
In the last simulation step, \(h_{{\mathrm{ill}}}({\mathbf{r}} - {\mathbf{r}}_s)\) is scanned laterally within the range [−xm; xm] through the object volume V to form a 2D line-confocal image of the object distribution c(r) at position yn and camera position y0:
Images are analyzed both in real space and in Fourier space. To ensure a sufficiently good signal-to-noise ratio, usually n = 120 cross-sections of Fourier image spectra in either the xy-plane or xz-plane, \(\left| {FT_{{\mathrm{xz}}}\left[ {p(x,y_{{n}},z)} \right]} \right|\) or \(| {FT_{{\mathrm{xy}}}[ {p(x,y,z_{{n}})} ]} |\), are averaged according to
For small beads the image spectra can be regarded as an approximation to the modulation transfer function (MTF) i.e., \(P(k_{\mathrm{x}},k_{\mathrm{y}}) \approx {\mathrm{MTF}}(k_{\mathrm{x}},k_{\mathrm{y}})\) and \(P(k_{\mathrm{x}},k_{\mathrm{z}}) \approx {\mathrm{MTF}}(k_{\mathrm{x}},k_{\mathrm{z}})\).
Beam design by computer simulations
Figure 2 shows a comparison between measured and simulated beam cross-sections for the excitation (a), (b) and depletion (c), (d) beam with different sectioning angles β at NA = 0.5 and λEX = 491 nm. The cross-sections in the centers of the beams were experimentally obtained by placing a 45° mirror at z = 0 to deflect the beams towards the main camera usually used for fluorescence. Therefore, the emission filter in the detection path was removed and beam profiles (b) and (d) were generated by applying the corresponding hologram to the excitation beam (λEX = 491 nm). It is worth mentioning that Fig. 2 shows beam cross-sections generated with the excitation laser. The hologram displayed in the depletion path during experiments, in contrast, was computed for the STED wavelength and featured a compensation factor (α = 1.1) to match beam sizes. In all six examples, the agreement between simulations and measurements is very good. It is clearly visible how a decrease of the sectioning angle β suppresses the ring system in the vertical y-direction, but amplifies the side lobes in the horizontal x-direction. The slight increase of the central main lobe’s width along y is hardly noticeable. The corresponding scanned profiles of these beams are shown in Supplementary Fig. 4 and further information is collected in Supplementary Note 1. An evaluation of the influence of the sectioning angle on the intensity minima in the STED beam is provided in Supplementary Fig. 5.
Feasibility study by imaging simulations
Figure 4 (Supplementary Fig. 6 with Supplementary Note 2) demonstrates by the results of computer simulations what can be experimentally expected from 3D imaging using the same wavelengths and numerical apertures as in the experiment. Beam parameters were q = 0, α = 1, β = 90° for the excitation beam and q = 1, α = 1.1, β = 60° for the STED beam (λST = 560 nm) with an optical CW power of 1 W over the whole cross-section of the SBB. The effect of line-confocal detection of fluorescence (λFL = 515 nm) relative to conventional detection is clearly visible in the y-direction and less pronounced in the x-direction as theoretically expected. The horizontal dashed lines in the bottom row displaying the image spectra (see Eq. (10)) serve as a guide to the eye to estimate the increase in spectral width (spatial frequencies) corresponding to an improved resolution and sectioning25. Switching on the STED beam (at 1 W beam power) leads to isotropic optical resolution along all three dimensions, e.g., inside the region of interest indicated by the white dashed ellipse. The red ellipses demonstrate how bead images in the background disappear due to the improved sectioning.
Image cross-sections of fluorescent 250 nm polystyrene beads (top row) and corresponding Fourier spectra (bottom row). a–f Display image cross-sections in the xz-plane and xy-plane and g–l the corresponding spectra. The left block of images shows the results for a sectioned Bessel beam (SBB) light-sheet with wide field for detection and in the center block the results for a line-confocal detection. The block of images on the right shows the results for a light-sheet with line-confocal detection and additional stimulated emission depletion (STED) (1 W). The two horizontal dashed lines serve as a guide to the eye to better compare the width of the image spectra. The scale bar is 1 µm for a–f and 15 µm−1 for g–l.
Resolution enhancement by STED
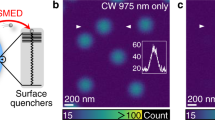
Figure 5 displays the analysis of the experimentally obtained imaging results from 200 nm fluorescence latex spheres (0.06% volume density). In a volume of dx × dy × dz = 140 × 5 × 40 µm³, bead images were automatically analyzed in all three directions by their full width half maximum (FWHM, Gauss fitting) after intensity classification and image selection of potential single beads. The beads were selected manually in subvolumes and inspected visually to preempt potential misinterpretation. Beam parameters were q = 0, α = 1, β = 90° for the excitation beam and q = 1, α = 1.1, β = 60° for the STED beam with an optical power of 300 mW over the whole cross-section of the SBB. As expected, no increase in lateral resolution is visible through STED, i.e., the FWHM(x) remains approximately constant over a propagation distance of dz = 40 µm for both sectioned Bessel beams. It needs to be remarked that the beams have propagated over 100 µm through the gel cylinder. Beam spreading and scattering are more visible for the FWHM(y) in detection direction by about 30% (Fig. 5a). With the STED beam switched on, the mean FWHM(y) is decreased by up to 34%, corresponding to about 0.3 µm resolution increase in the central field of view (see green markers). The effect of the STED beam leads to a thin light-sheet and thereby to a nearly isotropic resolution with FWHM (red markers) only slightly broader than that in the lateral direction. This is further illustrated by three exemplary, but representative frames selected from a 3D image stack shown in Fig. 5b. Adjacent beads, which cannot be resolved in detection direction, can be clearly separated with the STED beam switched on. An exemplary line scan reveals a distance of 510 nm between adjacent beads. The analysis of the averaged image spectra \(P(k_{\mathrm{x}},k_{\mathrm{y}}) \approx {\mathrm{MTF}}(k_{\mathrm{x}},k_{\mathrm{y}})\) shows significant broadening with the STED beam switched on, which is well visible at a 50% amplitude of optical transfer (Fig. 5c). A complete frequency-resolved increase in contrast is displayed in Fig. 5d, where line scans through the MTF in direction ky are displayed logarithmically for the cases STED off (blue) and STED on (red). The green curve displays the frequency-resolved amplification \(Q(k_{\mathrm{y}}) = {\mathrm{MTF}}_{{\mathrm{on}}}(k_{\mathrm{y}})/{\mathrm{MTF}}_{{\mathrm{off}}}(k_{\mathrm{y}}) - 1\) through the STED effect. The increase in contrast (optical transfer) reaches a maximum of 68% at the spatial frequency of 1.4 µm−1, which corresponds to a frequently occurring and relevant structure size in biological specimens.
a The full width at half maximum (FWHM) in lateral x-direction (left) and axial (right) y-direction for 200 nm bead images acquired with and without STED light-sheet. The blue circular markers show the FWHM along illumination beam propagation z-direction, the red triangular markers the corresponding point spread function (PSF) size with the STED laser turned on. The green diamond markers depict the relative decrease of the FWHM with STED switched on. The shaded areas behind the data points show the standard deviation of the measurements computed from a moving average windowed over a distance of 9.7 µm. b Three representative xy fluorescence cross-sections from a 3D image stack without (top row) and with (bottom row) STED applied. The red dotted regions of interest (ROI), demonstrate the improved axial resolution (y-axis) with STED beam on, enabling to clearly separate beads in close distance. The scale bar in all images is 1 µm. c Averaged spectra of bead images recorded for STED turned off (left) and on (right). With STED switched on, the frequency spectrum is clearly broadened in detection direction as illustrated by the 50% signal level. The scale bar in both images is 5 µm−1. d Line scans through the image spectra (MTF) along ky. The amplification factor Q(ky) is the relative frequency resolved increase in optical transfer when STED is turned on. The maximum amplification Qmax(ky) = 68% is at ky/2π = 1.4/µm.
3D imaging of cells
Figure 6 summarizes the results from a 3D imaging series of fixed HeLa cells labeled with Alexa Fluor® 488 Phalloidin in different imaging modes for single cells (a–c) and a 500 µm large cell cluster (d), (e). For these experiments, the additional STED mode was not used because of too strong fluorescence bleaching. Figure 6a compares the xy-fluorescence and xz-fluorescence cross-sections recorded with confocal Bessel light-sheet illumination to those obtained by confocal sectioned Bessel light-sheet illumination in Fig. 6b, revealing nearly isotropic resolution and minimal background blur. Figure 6c shows a rendered view of the maximum projections in the corresponding directions of Fig. 6b. Each xz-plane of the 3D image stack was recorded in 0.05 µm steps with two different phase-holograms (BB and SBB, see Fig. 1a) for fluorescence excitation.
Image stacks were acquired with (sectioned) Bessel beams in confocal line detection mode, but without stimulated emission depletion (STED). Fluorescence xy-cross-sections and xz-cross-sections of single cells imaged with a a confocal Bessel light-sheet (scale bar 10 µm) b confocal sectioned Bessel light-sheet illumination (scale bar 10 µm). c Maximum projected, rendered views of the image stack acquired in confocal sectioned Bessel mode as shown in b with thin membrane ruffles. d Single xz-cross-section of the of a 500 µm large Neuroblastoma cell cluster recorded in 80 µm detection depth. Line scans with exponential fits reveal enhanced 1/e penetration depth of the sectioned Bessel light-sheet versus the conventional (round) Bessel light-sheet. The green marked inset shows an intensity rescaled regions of interest (ROI) 4× the penetration depth. e Five micrometer maximum projection of the cell cluster acquired with confocal SBB illumination, revealing fine actin structures in three ROIs. The image spectrum P(kx, kz) is the Fourier transform of the ROI p(x, z).
The neuroblastoma cell clusters were grown from 1000 cells over a period of 5 days reaching a diameter of about 500 µm. Two hundred image slices were recorded at a distance of 1 µm to each other alternating for SBB and Bessel beam (BB) holograms to allow direct comparison and to minimize drift effects. Both beams reveal about the same image quality, although the SBB reveals a 35% enhanced penetration depth in the image at a detection depth y = 80 µm in this type of cell cluster as displayed by the fluorescence cross-section in Fig. 6d. The intensity line scans shown at the bottom were averaged over ten images and over a x-range of 90 µm as shown by the dashed white rectangle. Exponential line-fits reveal 1/e penetration depths of d = 48 µm and d = 65 µm for the BB and SBB, respectively. Figure 6e illustrates the achieved high resolution and contrast through maximum projections of the cell cluster, revealing fine actin structures even in SBB penetration depths of Δz > 180 µm as shown by the two regions of interest (ROI) (indicated by white squares). The image spectrum P(kx, kz) of the lower ROI indicates a corner frequency of (0.37 µm)−1 above the noise level, averaged over the whole 50 µm × 50 µm large ROI. The small ROI marked in light blue magnifies to parallel fibers with a gap width of only 0.32 µm.
Discussion
The ring system of Bessel beams consisting of “self-healing” photons is necessary for efficient beam reconstruction and propagation stability but excites fluorescence above and below the focal plane, which is detrimental for good optical sectioning. Since, on the one hand, confocal slit detection is not always able to block the fluorescence from the first ring of the Bessel ring system efficiently, and on the other hand the CW-STED efficiency is too low to deplete the fluorescence of the complete Bessel ring system, our approach aims to combine the advantages of those methods.
The goal of the shape-switch-block concept is to concentrate the optical depletion power only to the central part of the sectioned Bessel beam, i.e., to narrow the three central lobes in detection direction (see sketch of Fig. 1b) and block most of the fluorescence from the ring system by a confocal slit. First experiments with conventional, rotationally symmetric Bessel beams revealed that the depletion power of a higher-order Bessel beam19,20 was not strong enough to provide a significant resolution gain. This led to the idea not to deplete the fluorescence in the scanning direction, but to concentrate the STED power only in the detection direction.
Since the limited resolution in detection direction is still the bottleneck in light-sheet microscopy, we aimed to achieve nearly isotropic resolution even in scattering media by using the concept of SBB, which are characterized by a minimal overlap with the orthogonal oriented detection PSF15. Similar to lattice light-sheet microscopy16, we exploit the multiplication with the orthogonal detection PSF and that lateral scanning (dithering with the lattice) hardly increases the width of the resulting light-sheet. In addition to the small overlap of the SBB illumination PSF and the detection PSF, we used the STED effect to deplete only the fluorescence close to the beam center, which could not be blocked by (line-) confocal detection.
We used theoretical considerations and computer simulations to optimize the overlap between the SBB fluorescence excitation beam and the SBB fluorescence depletion beam (see Fig. 3 and Supplementary Figs. 3, 4), to find the optimal experimental configuration through the beam parameters α (focusing NA), sectioning angle β and q (diametrical π-phase step). The effect of these parameters is described by a mathematical model, giving room for future optimization processes and technical modifications. The agreement between simulations and experiments in the nonscattering case is qualitatively and quantitatively convincing (Fig. 2). In the next step, we considered the scattering of both laser beams and line-confocal light-sheet imaging in our simulations (Fig. 4), to investigate a possible increase in resolution and contrast. According to the simulations, the resolution in detection direction could be reduced to 0.5 µm at a power of 1 W.
Switching off fluorophores by STED increases the axial resolution significantly. However, with the CW-STED laser available in our lab, higher laser powers and depletion efficiencies were not possible (and would cause too much damage to the object). The illumination volume of our SBB STED beam (dark area at y = 0) can be estimated by the FWHMs of the two half-beams according to 2 × dx × dy × dz = 2 × 3 µm × 0.5 µm × 50 µm = 150 µm³, which is about 100 times larger than the volume of a typical point STED beam. Hence, our CW-power of 300 mW would correspond to 3 mW CW-power of a point STED focus. A pulsed laser optimized for STED, which we do not have, would achieve sufficiently high laser intensities with much less bleaching and phototoxicity. The fluorophore switching processes used with RESOLFT22 operates at low laser powers but is still much too slow. Modern sCMOS cameras with rolling shutters (e.g., 4 pixel or 650 nm slit width) achieve full frame image acquisition rates of 50 Hz. Aiming at 20 ms (or 100 ms) and 500 beam positions per image, an efficient fluorophore off-switching within 20 ms/500 = 40 µs (or 200 µs) per beam position is currently not possible. However, with a hopefully significantly increased fluorophore switching efficiency in the future, the RESOLFT concept would provide our shape-switch-block concept of line-scanning microscopy the optimal basis.
Nonetheless, we have demonstrated in Fig. 5 that, even with the simplest and non-optimal CW-STED mode, efficient fluorophore depletion in detection direction is possible, leading to a strongly reduced effective thickness of the light-sheet. The reduction of the FWHM by 34% to only about 0.5 µm represents a significant improvement in axial resolution and thereby a nearly isotropic resolution of only 0.47 µm × 0.47 µm × 0.53 µm, which is excellent for a light-sheet operating at up to 50 Hz confocal mode (maximum camera acquisition rate) and in a volume of 300 × 70 × 50 μm³. Although both beams propagated through a scattering medium, the beam overlap and the STED effect along a beam length of 40 µm are remarkable.
How does our approach compare to existing techniques? Published superior-resolution light-sheet microscopy techniques are either rather slow or can image only relatively small volumes and require post-processing16,17,22,26. Although these approaches achieve a higher optical resolution, they are limited by scattering and phase perturbation of the illumination beams propagating through the specimen and hence to smaller observation volumes. The current study aims at addressing a compromise between object size and scattering strength and the possible optical resolution and contrast connected with that. As shown by several of our studies, single scanned Bessel beams for light-sheet illumination are most robust against refractive index inhomogeneities causing typical beam deflections, which are detrimental for confocal-line detection.
Although phase shaping and fluorophore blocking works excellently for cells, additional fluorophore switching by STED bleaches the sample too strongly. The propagation stability of the SLM controlled illumination beams was demonstrated in the results of Fig. 6, revealing high contrast and a nearly isotropic resolution for images of five single cells and a 0.5 mm large cell cluster, even without the STED effect. Even after laser beam propagation through the cluster by about 200 µm, very small and thin actin structures are visible inside the cluster using scanned SBB and confocal line detection (Fig. 6b). Through the analysis of averaged fluorescence line scans along the propagation direction about 80 µm inside the object (Fig. 6d), an increase of 35% in 1/e propagation depth is apparent. A possible explanation is that even propagation-stable Bessel beams deviate laterally from the only 0.65 µm wide confocal slit during propagation, suppressing the detection of the fluorescence signal. It is well possible that the pronounced and dense side-lobes of the SBB (see Fig. 2) prevent this effect in the case of beam scattering and deflection.
The phase hologram of the SBB covers only half the illuminated SLM area and transports only half the energy into the specimen, relative to a rotationally symmetric BB. Although blocked by the confocal slit, the BB excites unnecessary fluorescence above and below the light-sheet. On the other hand, a non-negligible amount of energy of the SBB is stored in the lateral side lobes, which is blocked by the confocal slit and does not contribute to relevant signal information. Hence, while for the used cell cluster no improvement in contrast and signal-to-noise was visible, the image quality for single cells was significantly increased, revealing a nearly isotropic resolution, as displayed by the two orthogonal cross-sections of Fig. 6b, c and by Supplementary Movie 1.
Modern 3D imaging at the highest temporal and spatial resolution, especially in thick scattering media, is too complex to be performed with a single microscopy technique. Following a three-fold approach of beam shaping, photon blocking and fluorescence switching, we have demonstrated that the usage of spatial light modulators in modern light-sheet microscopes allows not only additional flexibility in object adapted illumination25,27, but also to compensate restrictions or to complement advantages of other established super-resolution microscopy methods such as STED and RESOLFT — despite our lack of pulsed lasers. We think that the principles and concepts presented in this paper will serve as a valuable basis for future technical improvements in light-sheet microscopy, especially in combination with SLMs and improved fluorophore switching approaches.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code used in this study is available from the corresponding author upon reasonable request.
References
Keller, P. J., Schmidt, A. D., Wittbrodt, J. & Stelzer, E. H. K. Reconstruction of zebrafish early embryonic development by scanned light sheet microscopy. Science 322, 1065–1069 (2008).
Fahrbach, F. O., Simon, P. & Rohrbach, A. Microscopy with self-reconstructing beams. Nat. Photon. 4, 780–785 (2010).
Vettenburg, T. et al. Light-sheet microscopy using an airy beam. Nat. Methods 11, 541 (2014).
Dean, K. M., Roudot, P., Welf, E. S., Danuser, G. & Fiolka, R. Deconvolution-free subcellular imaging with axially swept light sheet microscopy. Biophys. J. 108, 2807–2815 (2015).
Chang, B.-J., Perez Meza, V. D. & Stelzer, E. H. K. csiLSFM combines light-sheet fluorescence microscopy and coherent structured illumination for a lateral resolution below 100 nm. Proc. Natl Acad. Sci. 114, 4869–4874 (2017).
Method of the Year 2014. Nat. Methods 12, 1 https://doi.org/10.1038/nmeth.3251 (2014).
Sheppard, C. The use of lenses with annular aperture in scanning optical microscopy. Optik 48, 329–334 (1977).
Meinert, T., Tietz, O., Palme, K. J. & Rohrbach, A. Separation of ballistic and diffusive fluorescence photons in confocal Light-Sheet Microscopy of Arabidopsis roots. Sci. Rep. 6, 30378 (2016).
Planchon, T. A. et al. Rapid three-dimensional isotropic imaging of living cells using Bessel beam plane illumination. Nat. Methods 8, 417–423 (2011).
Olarte, O. E. et al. Image formation by linear and nonlinear digital scanned light-sheet fluorescence microscopy with Gaussian and Bessel beam profiles. Biomed. Opt. Express 3, 1492–1505 (2012).
Fahrbach, F. O., Gurchenkov, V., Alessandri, K., Nassoy, P. & Rohrbach, A. Light-sheet microscopy in thick media using scanned Bessel beams and two-photon fluorescence excitation. Opt. Express 21, 13824–13839 (2013a).
Fahrbach, F. O. & Rohrbach, A. Propagation stability of self-reconstructing Bessel beams enables contrast-enhanced imaging in thick media. Nat. Commun. 3, 632 (2012).
Baumgart, E. & Kubitscheck, U. Scanned light sheet microscopy with confocal slit detection. Opt. Express 20, 21805–21814 (2012).
Meinert, T., Gutwein, B.-A. & Rohrbach, A. Light-sheet microscopy in a glass capillary—feedback holographic control for illumination beam correction. Opt. Lett. 42, 350–353 (2016).
Fahrbach, F. O., Gurchenkov, V., Alessandri, K., Nassoy, P. & Rohrbach, A. Self-reconstructing sectioned Bessel beams offer submicron optical sectioning for large fields of view in light-sheet microscopy. Opt. Express 21, 11425–11440 (2013b).
Chen, B. -C. et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, 6208 (2014).
Zhao, T. et al. Multicolor 4D fluorescence microscopy using ultrathin Bessel light sheets. Sci. Rep. 6, 26159 (2016).
Zhang, P., Goodwin, P. M. & Werner, J. H. Fast, super resolution imaging via Bessel-beam stimulated emission depletion microscopy. Opt. Express 22, 12398–12409 (2014).
Gohn-Kreuz, C. & Rohrbach, A. Light-sheet generation in inhomogeneous media using self-reconstructing beams and the STED-principle. Opt. Express 24, 5855–5865 (2015).
Gohn-Kreuz, C. & Rohrbach, A. Light needles in scattering media using self-reconstructing beams and the STED principle. Optica 4, 1134–1142 (2017).
Friedrich, M. & Harms, G. S. Axial resolution beyond the diffraction limit of a sheet illumination microscope with stimulated emission depletion. J. Biomed. Opt. 20, 106006 (2015).
Hoyer, P. et al. Breaking the diffraction limit of light-sheet fluorescence microscopy by RESOLFT. Proc. Natl Acad. Sci. 113, 3442 (2016).
Gutierrez-Vega, J. C. et al. Experimental demonstration of optical Mathieu beams. Opt. Commun. 195, 35–40 (2001).
Leutenegger, M., Eggeling, C. & Hell, S. W. Analytical description of STED microscopy performance. Opt. Express 18, 26417–26429 (2010).
Kashekodi, A. B., Meinert, T., Michiels, R. & Rohrbach, A. Miniature scanning light-sheet illumination implemented in a conventional microscope. Biomed. Opt. Express 9, 4263–4274 (2018).
Cella Zanacchi, F. et al. Live-cell 3D super-resolution imaging in thick biological samples. Nat. Methods 8, 1047–1049 (2011).
Betzig, E. Excitation strategies for optical lattice microscopy. Opt. Express 13, 3021–3036 (2005).
Acknowledgements
The authors are thankful to Dr. Florian Fahrbach, Dr. Tobias Meinert and Dr. Cristian Gohn-Kreuz for helpful discussions and comments on the manuscript. The research was funded by the German Research foundation (grant RO3615/8-1).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
L.K. performed the simulations, experiments and data analysis. A.R. contributed to the data analysis and provided interpretations of the results. A.R. wrote the manuscript and L.K. contributed with figures and information. Both authors proofread the manuscript, made comments, and contributed to the manuscript revision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Köbele, L., Rohrbach, A. A shape-switch-block method for confocal light-sheet microscopy with sectioned Bessel beams and stimulated emission depletion. Commun Phys 3, 201 (2020). https://doi.org/10.1038/s42005-020-00458-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00458-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.