Abstract
Within linear continuum theory, no magnetic texture can propagate faster than the maximum group velocity of the spin waves. Here, by atomistic spin dynamics simulations and supported by analytical theory, we report that a strongly non-linear transient regime due to the appearance of additional magnetic textures results in the breaking of the Lorentz translational invariance. This dynamical regime is akin to domain wall Walker-breakdown in ferromagnets and involves the nucleation of an antiferromagnetic domain wall pair. While one of the nucleated domain walls is accelerated beyond the magnonic limit, the remaining pair remains static. Under large spin–orbit fields, a cascade of multiple generation and recombination of domain walls are obtained. This result may clarify recent experiments on current pulse induced shattering of large domain structures into small fragmented domains and the subsequent slow recreation of large-scale domains.
Similar content being viewed by others
Introduction
Within a general physical context, a topological defect is characterised by a local/core region where order is highly altered whereas far from that core region the order parameter varies smoothly in space1. Topological defects can be found in a variety of fields such as in superfluid helium2 named vortices, in periodic crystal structures, they are called dislocations3,4,5 and in magnetism, magnetic domain walls (DWs)6,7, vortices8,9 and skyrmions10. In elementary dislocations, the underlying reason why these defects are called topological is because they cannot be made to disappear by a continuous deformation of the order parameter in infinite extended films. The measure of the distortion is associated to the so-called Burgers vector whose magnitude expresses the strength of the dislocation which is quantised to integer multiples of the atomic spacing of the lattice vectors11. Continuum-based textures such as magnetic textures like DWs, vortices and skyrmions are often characterised by the so-called winding number (a topological charge) whose value stands in direct relation to the magnitude of the normalised Burgers vector. However, topology is not at odds with instability. A relevant example of the previous is the plastic deformation and its role in dislocation dynamics12. Under low applied stresses, there is a quasilinear dependence between the dislocation velocity and the applied stress described by linear elasticity theory13. However, dislocation mobility is not restricted to subsonic regime under high strain rates. Surpassing of the sonic barrier was first postulated theoretically14,15,16 and then confirmed by atomistic simulations in bcc tungsten17,18 and in iron screw dislocations19 by means of introducing secondary kinks via mother–daughter nucleation process with opposite Burgers vector20.
Within the micromagnetic approximation, in a two-dimensional infinite magnetic system, the order parameter that breaks the symmetry is reflected by an average quantity: the magnetisation \(\overrightarrow{m}(x,y)\) at each site in a given lattice. The connection between topology and magnetic media and its role in dynamics became apparent by the pioneering work of several authors21,22,23, when studying the dynamics of magnetic topological defects. The analytical approach consists of assuming the centre of the texture as a dynamical variable where the equation of motion can be derived using the Lagrangian formalism. Concretely, in ferromagnets, DWs are defined by the transition region that separates two homogeneously and opposite magnetised regions. In a similar fashion as for dislocations, a quantised topological invariant is defined for the magnetisation field24. By framing the magnetic texture on a closed path, it allows to define a map of the magnetisation configuration. Distinct topological textures are characterised by different winding number, w, which counts the number of times the magnetisation is wrapped onto itself25. The winding number density along the line at each point in time t, is \(w\left(x,t\right)=-{\nabla }_{x}\phi \left(x,t\right)\) (with the total winding number, W, being \(\frac{1}{2\pi }\int\ w\left(x,t\right){ {d}}x\), which for a 180° domain wall takes values \(\pm \frac{1}{2}\)). Here \(\phi \left(x,t\right)\) is the in-plane angle of the spin at location x at time t of the spin-configuration along the 1D-line. In the case of Bloch walls separating magnetic domains in ferromagnets topological defects arise in the form of Néel lines26. Since the 1990s, the study of DW mobility in ferromagnets has been the flagship in Spintronics because of its potential in data storage27,28 and logic devices29. However, a major difficulty to implement such technological proposals arise as a result of the intrinsic instability the DW structure presents when it overcomes a certain threshold velocity. In this Article we show that this interesting feature of DW is present irrespective of whether the magnetic material is a ferromagnet or antiferromagnet. In ferromagnets, this regime is known as the Walker limit30 and it is characterised by a DW mobility that is the result of the combination of translational and oscillatory dynamics31 leading to periodic alteration of the DW chirality. Unfortunately, the Walker breakdown (WB) occurs at low domain wall velocities and imposes a limit on a reliable control of the DW motion. An alternative to prevent the WB consists of using nanotubes or nanocylinders32,33. These particular geometries have unveiled the spin analogue of the Cherenkov effect which involves the emission of electromagnetic waves by charge particles moving at speeds faster than the speed of light in the given medium34. In the case of antiferromagnets, several studies have provided significant insights on DW motion in antiferromagnets where high speeds have been predicted thanks to prevention of the WB35,36, yet there is an upper theoretical limit which cannot be surpassed. Interestingly, the manner in which the spin-space is conformed in antiferromagnets obeys the relativistic kinematics of special relativity where the analogue role played by the photons in conventional space is played by the magnons in a magnetic system. Consequently, by comparison, the ultimate limiting velocity of any texture is given by the maximum group velocity of the magnons, vg. In this work, we reveal that in analogue fashion as it occurs for dislocations under plastic deformation where the dislocations propagate at supersonic speeds, super-magnonic regime of motion can occur through a sequence of multiple nucleated textures mimicking the so-called WB.
Results and discussion
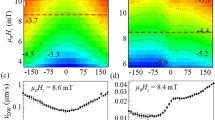
To elucidate the existence of such type of magnetisation dynamics, we combined one-dimensional atomistic spin dynamics simulations of a layered antiferromagnet, Mn2Au37, with one-dimensional analytical theory. In order to induce magnetisation dynamics in Mn2Au (see Fig. 1a), we make use of the predicted staggered field-like torque in such crystal structures38, where the effective magnetic field resulting from a staggered-induced spin-density, \({\overrightarrow{H}}_{\text{so}} \), possesses opposite signs at each sub-lattice and gives rise to a spin–orbit torque (see Fig. 1b). Some representative dynamics of the temporal evolution of DW position is obtained by extracting the spatiotemporal evolution of the winding number density shown in Fig. 1c, d. These spatiotemporal evolutions were obtained by firstly ramping the spin–orbit field (SO-field) from 0 to its maximum in a time interval of 10 ps and then it is kept constant till the end of the simulation Fig. 1e, f. The intrinsic inertial character of the translational motion of the DW is revealed by a non-linear trend that appears within the first 4–5 ps. The ballistic nature of the DW motion is revealed by the narrowing of the DW as it approaches vg according to the relativistic kinematics framework. The DW width at a given velocity is given by: \(\Delta (v)={(1-{v}^{2}/{v}_{\text{g}}^{2})}^{1/2}{\Delta }_{0}\), where Δ0 = 19.8 nm is the DW width at rest. This contraction translates into an increase of the DW exchange energy. It is noteworthy to comment that in conventional special relativity theory, the contraction observed from non-inertial reference frame does not result in any incremental (or detrimental) interaction among the constituents of the object. First, the DW is accelerated to a speed that approaches to vg. After these transient dynamics, two distinct behaviours are obtained depending on the applied SO-field. For low values of SO-fields (see Fig. 1c), a saturation effect of the DW speed is observed, characterised by the slope of the maximum winding number density position (DW position), q, with respect to time, t with v = ∂tq. A linear variation of the DW speed as a function of the SO-field is consistent with previous reports36. In such a case, the energy dissipation induced by the viscous damping inhibits the DW to move faster as reported in previous work35. In contrast, at an onset of 65 mT, a different dynamical behaviour is observed (see Fig. 1d) which can be defined as the critical stress at which the DW suffers a threshold deformation which leads to the breeding of a DW-pair with trivial composite winding number, w, preserving the overall winding number (see Fig. 1f) . This strongly nonlinear regime which involves the generation of additional particles has been reported under several conditions in ferromagnets, for instance, domain wall WB mediated by the vortex–antivortex generation33, vortex-core reversal in spin-torque oscillators in nanodots39 and nanocontacts40. However, its occurrence in antiferromagnets has never been reported nor proposed. In ferromagnets, the physical origin for the appearance of new magnetic textures, concretely in the case of vortex-core reversal has been associated to the emergence of a effective magnetic field whose origin is purely dynamical and can be derived from the kinetic part of the Lagrangian density, \({\mathcal{L}}={{\mathcal{L}}}_{\text{kin}}-V\). In our system, as the DWs are located in the ferromagnetic basal atomic planes where the coupling between the adjacent planes is antiferromagnetic one can derive the temporal evolution of the kinetic field using the Lagrangian formalism
where Ms is the sub-lattice magnetisation and is given by 4μB/2V where μB is the Bohr magneton and V is the unit cell volume. Although this emergent field has already been proposed to explain the reversal of the vortex core polarity in ferromagnets where the dynamics are gyrotropic, we use this formalism also to translational motion of DWs in layered antiferromagnets. In antiferromagnets due to the relativistic nature of the dynamics, the DW suffers a substantial deformation due to its translational velocity. The extension and the kinetic field profile with respect to the moving DW depends upon the dynamical regime the DW is at a given instant (see Fig. 2a–d). During the first 4–5 ps of ultra-fast acceleration, the kinetic field is located behind the DW and smoothly transitions from the back to the centre and then to the forefront of the DW while mimicking the DW profile. The maximum component of the kinetic field is found to be along the \(\hat{z}\)-direction and can reach values up ~35 T in absolute value (see Supplementary Note 1). Contrary to ferromagnets where the magnetic texture absorbs energy from the kinetic field, we attribute the nucleation of DW pairs to the torque exerted by the kinetic field onto the local magnetisation promoting a reverse magnetic domain along the −x with an approximate extension just before the DW-pair nucleation of the exchange length, lex = \({(A/{K}_{2\parallel })}^{1/2}\), where A is the effective exchange stiffness per unit area and K2∥ is the uniaxial anisotropy (see Table 1). The evolution of this reverse magnetic domain is governed by the competition between the exchange and anisotropy energies which results into breaking the reverse magnetic domain into a DW-pair with each of its constituents holding an opposite winding number (thus the sum of their windings is zero). We identify the time involved in the nucleation to be around 1 ps. Different types of magnetic distribution could in principle appear obeying the boundary conditions over the generated magnetic domain, however, we observed that the initially moving DW and the nucleated DW located just in front share the same winding number. The origin of this arrangement can be attributed to the minimisation of the total Zeeman energy now comprised of the SO-field and the kinetic field (see Supplementary Note 1). Therefore, while the torque provided by the kinetic field leads to a reverse magnetic domain in front of the moving DW with the appropriate extension to accommodate two DWs, the competition between the magnetic energies and the Zeeman energy gives rise to the generation of a DW-pair with a specific ordering.
a Crystal and spin structure of Mn2Au with a basal plane crystal lattice a0 = 0.3228 nm. Yellow arrow represents the current density injection, \(\overrightarrow{j}\), direction (\(\hat{x}\)-axis). b Schematic illustration of each basal plane magnetisation, \(\overrightarrow{m}\), containing a Néel type of domain wall (DW) under the action of the spin–orbit field, \({\overrightarrow{H}}_{\text{so}}\). c Spatiotemporal evolution of the winding number density, w, showing that after an initial inertial regime of motion, DW reaches a quasi-steady motion. d Spatiotemporal evolution of w showing the nucleation of a DW-pair, appearance of spin-waves and supermagnonic regime of motion of one of the nucleated DWs. e Excitation protocol corresponding to panel c where \({\overrightarrow{H}}_{\text{so}}\) is increased up to its maximum value of 40 mT in 10 ps and temporal evolution of numerically extracted total winding number, W. f Excitation protocol corresponding to panel d where \({\overrightarrow{H}}_{\text{so}}\) is ramped up to its maximum value of 65 mT in 10 ps and temporal evolution of W.
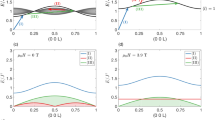
Snapshots of the x and y-components of the magnetisation, mx and my, kinetic field z-component, hkin,z, and x-component of the torque, Tx, exerted by the kinetic field at different instances during the domain wall one (DW1) motion. Panel a–d corresponds to physical times of 10, 90, 110 and 145 ps. At all times, during the atomistic spin dynamics simulations the \(\hat{x}\) and \(\hat{y}\)-components of the kinetic field reach values of the order of mT while hkin,z can reach absolute values circa 35 T. When the kinetic field is not centred at the DW central position, it induces a DW deformation thanks to the additional torque it exerts onto the local magnetisation.
The temporal evolution of the system after the DW-pair is present in the system is dramatically affected. Hereafter, we call the initially moving DW, DW1 and the nucleated DWs, DW2 and DW3 with DW2 always being the one closest to DW1 and DW3 located in front of DW2. As can be seen in Fig. 3a, immediately after the nucleation, DW1 and DW2 perform a few oscillations and then get stuck evolving in time but not in space. As DW1 and DW2 have the same winding number, they repel each other due to the ferromagnetic exchange interaction (see Fig. 3a). However, the region in between the pair (DW1 and DW2) has opposite orientation with respect to Hso and therefore, in order to reduce the Zeeman energy provided by the SO-field (note that the kinetic field is zero as the DWs are static), the distance between DW1 and DW2 has to be minimised. Consequently, as a result of the competition between the two forces, a local minimum appears that corresponds to a certain distance between the DW-pair. We verified this interpretation by calculating the energy barrier related to the distance among DW1 and DW2 (see Fig. 3b). The energy minimum corresponds to a given separation between the DWs’ centres, which depends on the magnitude of the SO-field (see Supplementary Note 2). From numerical simulations, we obtain a stable distance of 32 nm, whereas from analytical calculation the distance is 29 nm for Hso = 65 mT. Recent estimations of the effect of the current to produce a staggered local spin accumulations with opposite polarities are 2 mT per 107 A/cm2.
a Spatiotemporal evolution of the magnetisation. Inset represents the domain walls, DW1 and DW2 initial oscillations before reaching a stable distance between them. The separation is due to the competition between the Zeeman energy, EZee, provided by the spin–orbit field, \({\overrightarrow{H}}_{\text{so}}\), which tries to pull them closer while the exchange energy, Eexc, tries to separate them as both DWs have the same winding number. b Stable distance between DW1 and DW2 of 29 nm calculated for an applied \({\overrightarrow{H}}_{\text{so}}\) = 65 mT. c DW1, DW2 and DW3 velocity as a function of time. At the moment the nucleation starts, the maximum registered speed of DW3 travelling at supermagnonic speeds is 177 km/s. When DW1 and DW2 are fully formed, DW3 propagates at 133 km/s. A smooth recovery of DW3 towards submagnonic speeds is observed and lasts for about 100 ps. d Phase, vph, and group velocity, vg, of the magnons as a function of the wave-vector, k, for an applied \({\overrightarrow{H}}_{\text{so}}\) = 65 mT extracted from the dispersion relation. Notice that once DW3 enters into the supermagnonic regime of motion it also surpasses the phase velocity of the magnons which is manifested by the spin-Cherenkov radiation.
Another observation is that DW3 propagates forward by undergoing a velocity boost that surpasses the maximum group velocity of the magnons. This regime is transient and lasts for several tens of picoseconds which is sufficient for DW3 to cover over three microns. This mobility regime can be explained as follows. While the DW-pair is nucleated, DW1 and DW2 repel each other thanks to the ferromagnetic exchange interaction between them leading to a potential motion in opposite directions for each DW. Despite this fact, they barely move (see inset Fig. 3a) and therefore, all this stored energy is transferred from DW1 to DW3 in a similar fashion as reported by Tveten et al.41, where spin waves were able to transfer linear momentum to a given domain wall. Hence, the DW3 mobility at the moment of the nucleation consist of the velocity provided by the DW1, in addition to the boost coming from the momentum transfer due to the repulsion between DW1 and DW2. Using a collective coordinates approach combined with the Rayleigh dissipation function and the Euler–Lagrange equation of motion (see Supplementary Note 3), we obtain the DW3 velocity as a function of its distance with respect to the DW-pair to be
where α is the Gilbert damping, \({\Delta }_{{\text{DW}}_{1}}\) and \({\Delta }_{{\text{DW}}_{3}}\) are the DWs’ width for DW1 and DW3 at the nucleation extracted from the atomistic simulations, respectively, and x(t) is the distance between DW1 and DW3. From numerical simulations, the extracted distance between DW1 and DW3 is 17 nm when the nucleation starts occurring and the extracted speed value for DW3 is around 177 km/s (see Fig. 3c) which is circa 4 times the maximum group velocity that magnons can theoretically attain in Mn2Au (see Supplementary Note 4). The maximum speed according to Eq. (2) is circa 133 km/s which corresponds to a distance of 16.1 nm between the DW1 and DW3. It is appealing to think that the special theory of relativity is being violated as no magnetic texture is by principle allowed to propagate faster than the maximum velocity of the magnons in the spin space. However, as soon as the DW-pair (DW2 and DW3) is present in the system additional interactions need to be taken into account which result into a Lagrangian that is not Lorentz invariant and therefore, the constraint on the maximum speed must be lifted up. Besides, when DW3 enters into a super-magnonic regime of motion, there is a sudden emission of spin-waves propagating together but never surpassing DW3 (see Fig. 2d). Analogous effect has been reported in mechanical systems such as in edge dislocation dynamics under shear stress where spontaneous emission of radiation has also been observed42,43. We attribute the origin of the emitted spin-waves to a mixture of the so-called Bremsstrahlung effect44 (or breaking radiation) and the spin-Cherenkov effect45. The Bremsstrahlung effect arises due to the deceleration of a charge particle. Therefore, one could speculate that such staggering deceleration could lead to excitations of the spin medium. As shown in Fig. 3d, DW3 not only surpass the maximum group velocity of the magnons but it also enters in a mobility regime where it moves faster than the phase velocity of the magnons. It is difficult in our case to clearly separate the existence of Bremsstrahlung and spin Cherenkov radiation. We note in Figs. 1d and 3a that the number of oscillations of DW1 and DW2 equals the number of spin-wave ripples travelling with DW3 and further, that the decay of these ripples appear to stretch over a rather long time. Therefore, one possibility for co-existence of both types of radiation could be that the spin-Cherenkov-originated spin waves acts in an anti-damping fashion onto the Bremsstrahlung in conjunction with the observation that the radiative ripples do not propagate in opposite direction to DW3. It is pertinent to explore how the system reacts when it has at its disposal additional pumped energy. We start by injecting an electric current with the time profile illustrated in Fig. 4a. The electric current has a rising time of 5 ps up to a peak value of Hso = 100 mT. The value of Hso is kept constant for the following 50 ps before reducing it to zero, with a falling time of 5 ps. The SO-field is set to zero for 50 ps before starting this pattern again three times in succession. The closed blue circles in Fig. 4a represents the maximum π/2-windings, i.e. the number of DWs in each pulse. In each cycle, we can observe an avalanche of DW-pairs. Once the primal DW nucleates the first DW-pair, the DW that propagates from the DW-pair (DW1 and DW2) at supermagnonic speeds becomes a new breeder and gives rise to new DW-pair. This phenomenon repeats for a 13 times leading to the appearance of 26 additional DWs in the system preserving at all times the overall topological charge. It is worth noticing that the DWs once nucleated do not reorganise into a more stable configuration while the SO-field is maximum giving rise to DW-lattice-like structure whose inter-DW distance depends upon the SO-field pulse pattern. The average DW density per pulse is 0.013 DW/nm and it takes ~20 ps to generate the whole DW lattice. Here closed orange circles denotes the number of DWs when the SO-field starts decreasing. Once this occurs, the lattice decompresses which, in combination to the attractive exchange interaction among DWs with opposite winding number, leads to recombination of some DWs. We observed a similar value for closed orange circles with pulse number meaning that the same number of DWs recombine once the SO-field reaches 0 mT. The closed green circles represent the number of DWs extracted once the SO-field is about to rise up again. It can be seen from Fig. 4a that only spatially close situated DWs of opposite winding numbers annihilate increasing closed green circles in each pulse. This implies that the accumulated number of remnant DWs in the system after each pulse increases meaning that not all the generated DWs annihilate. After the fourth pulse, the number of DWs in the system is 8 with a spacing among the DWs that ranges from hundreds of nanometres to few micrometers. Initially the system contained two magnetic domains (separate by a single DW) and after four pulses the number of magnetic domains Nm, has increased by Nm = Ndws + 1, where, Ndws, accounts for the number of DWs in the system. More complex DW-crystal lattices can be obtained by varying the pulse duration and the sign of the SO-field (see Supplementary Note 5) showing the rich magnetisation dynamics in these type of systems. We wish at this point to also stress some observations (not shown here), that there appears to be no clear correlation between the strength of Hso and the number of DWs nucleated as well as the point in time and space where they are nucleated. This opens up the possibility that this system under the current excitation circumstances could potentially exhibit chaotic behaviour. This will be the topic of future work however. We note at this stage, that recent work on current-induced resistance changes in the antiferromagnet CuMnAs was, in conjunction with imaging attributed to the fragmentation and recovery of the domain structure46,47. In particular they observed a gradual increase in the resistance with repeated pulsing and a slow relaxation of the resistance towards lower values than after the last pulse when turning off the excitation completely. However, provided that finite size-effects can be excluded and that such a system observes global conservation of the total winding number, it should be possible to return to the original state by applying a reverse field below the AFM Walker-breakdown field, in order to recover completely the initial state of resistance, in other words, a complete reset of the system. Further, it is noteworthy that the relaxed resistance value after a long waiting time was higher than the original starting resistance. This could mean that residual DW are present. If the interpretation that the observed resistance changes is due to domain fragmentation and recovery/recombination is correct we cannot help but to speculate about possible measurements of our system under study. Although the mechanism of domain fragmentation in our case is due to the AFM WB in a perfect crystal and the results in the reported experimental work likely has heat as the main cause of fragmentation, this means that that such resistance variations in analogous systems where pinning and heating effects can be ruled out could be used as an indirect detection method for the occurrence of the AFM WB process and its associated generation of supermagnonic textures. It must be pointed out that for this particular pulse ramp-time no signature of DW-pair nucleation is obtained well after the SO-field has reached Hcrit = 65 mT, meaning that the critical feld depends upon the ramping time conditions rather than the absolute value of the energy pumped into the system. Figure 4b shows the transition from a system with a DW-lattice with 13 DW-pairs towards a system with only one DW-pair due to the multiple recombination when the SO-field is zero. It is noted that there is a distribution of distances that separate consecutive DWs with opposite winding number. This gives rise to a manifold of recombination times as shown in Fig. 4c. Analytically, it is possible to obtain the recombination time as a function of the distance by assuming that the decompression introduced by the absence of SO-field results in a transition phase from a DW-lattice to a DW-gas for a transient time. Therefore, the recombination time of a given DW-pair is only governed by intrinsic parameters such as, the exchange interaction, the damping and the distance between the DWs ruling out the effect of the presence of the rest of DW-pairs in the system. We can derive the recombination time from a general expression of the exchange interaction between two domain wall pairs with opposite winding number as
where Δ is the DW-width of each DW, l represents the distance each DW needs to travel before the recombination occurs at t0, l0 = 1 nm and tr represents the recombination time. We note that the predicted recombination time reproduce quantitatively the recombination time values extracted from the atomistic spin dynamic simulations which validates the hypothesis of 1D DW-pairwise gas approximation. For distances in the range of few hundreds of nanometres the recombination time is in the range of few picoseconds as the exchange interaction is a short-range interaction. However, we can see from Fig. 4b that there are DWs remaining in the system whose separation is in the range of few microns. For a given distance of 1.8 μm, the expected recombination time lies in the range of ~6 days. This suggests that in an ideal scenario where pinning effects, thermal fluctuation effects are not present, the stability of such a configuration is granted thanks to the absence of long-range interaction. We can observe in Fig. 4b that once the SO-field is set to zero, each of the recombination processes produces an excitation in the continuum spectrum. This highly nonlinear process yields to a deformation amplitude that oscillates in time with a very precise frequency. The emergence of this breather-like excitation is due to the excess of kinetic energy carried by each DW involved in the collision whose value is not large enough to escape the attractive potential provided by its anti-particle. By mapping the breather into a simple damped harmonic oscillator, we obtained a good quantitative agreement on the breather lifetime (see Supplementary Note 6). The breather decay occurs in 20–30 ps and it is governed by the Gilbert damping. Moreover, the characteristic frequency of the breather is determined to be 544 GHz frequency, which lies within the linewidth of the calculated spin-wave band gap at Hso = 100 mT, i.e. the frequency at zero wave vector, k = 0. We are thus compelled to assign the breather frequency to that of the band-gap.
a Schematic illustration of the excitation protocol and spatiotemporal evolution of the winding number density, w. Each of the pulses are characterised by a ramp and fall times of 5 ps and constant spin–orbit field (Hso) values of 100 mT and 0 T for 50 ps. Multiple domain wall avalanches can be observed at each Hso which translates into an increase in the number of DWs. b Time evolution of the x-component of the magnetisation, mx, which illustrates the recombination events between DWs with opposite winding number occurring predominantly when Hso is turned off. c Comparison of the recombination time, tr, extracted from the simulation and analytically from Eq. (3) as a function of the distance travelled by each DW with opposite winding number before recombination event occurs corresponding to panel a.
In summary, we have studied by atomistic spin dynamics and theory, the dynamical properties of staggered field-driven DWs in an AFM. A Walker-breakdown-like process has been identified whereby the DW nucleates an additional DW pair with a total trivial winding number. One of these nucleated DW forms a π DW together with the original one, whereas the other nucleated DW travels away from the breakdown site at speeds far exceeding the maximum group velocity of spin-waves in the medium, thus achieving supermagnonic speeds. At such high speeds we observe a radiative tail travelling together with the supermagnonic texture. According to the computed dispersion relation, for this system, it is only at supermagnonic speeds where the conditions for spin-Cherenkov radiation is met. Thus one contributing source to the observed radiation, we attribute to spin-Cherenkov radiation. At the same time, we would expect a breaking radiation to be present due to a rapid deceleration of DW1 and DW2. We observe associated oscillations in position of the said DWs as they come to a halt, with the number of oscillations equalling that of the number of radiative ripples travelling with DW3, opening the possibility of co-existence of the two types of radiation with the spin-Cherenkov radiation acting in an antidamping manner onto the breaking radiation, which could explain the rather slow decay of the radiative ripples. At higher spin–orbit field magnitudes, both multiple DW nucleations and DW recombinations occur, in order to keep conservation of the global winding number. Provided that the separation between nucleated magnetisation textures is sufficiently large, residual DWs can remain in the system after the pulse-excitation is turned off. Provided that the measured resistance in CuMnAs is of magnetic origin, in particular due to magnetic domain fragmentation46,47, our results imply that no Joule heating or temperatures approaching the Néel temperature are required in order to observe such resistance characteristics.
Methods
We perform numerical simulations via atomistic spin dynamics simulations. For this, the full Mn2Au crystal structure is taken into consideration. Two formula units as that in Fig. 1a in the main text is stacked on top of each and then replicated along the x-direction 60,000 times. The system has open boundaries along x and z while periodic boundary conditions are imposed along y. The time evolution of a unit vector spin at site i, Si, is simulated by solving the Landau–Lifshitz–Gilbert equation:
where γ is the gyromagnetic ratio of a free electron (2.21 × 105 m/A s), α is the Gilbert damping set here to 0.001 and \({{\bf{H}}}_{i}^{\,\text{eff}\,}\) is the effective field resulting from all of the interaction energies. The energies taken into account are the three exchange interactions (two antiferromagnetic and one ferromagnetic), magneto crystalline energy contributions and the spin–orbit field. The total energy, E, considered is
The first term on the right-hand side is the exchange energy where Jij is the exchange coefficient along the considered bonds (see Supplementary Note 4). The second and third terms are the uniaxial hard and easy anisotropies of strengths K2⊥ and K2∥, respectively, while the fourth and fifth terms collectively describes tetragonal anisotropy. For the in-plane part of the tetragonal anisotropy, u1 = \(\left[110\right]\) and u2 = \(\left[1\bar{1}0\right]\). Finally, μ0 and μs are the magnetic permeability in vacuum and the magnetic moment, respectively. We have used μs = 4μB, with μB being the Bohr magneton. It is to be noted that the tetragonal anisotropy was included for sake of completeness as it is present in this material but its role in the high speed dynamics is negligible due to the weak magnitude of its anisotropy constants. The effective field is then subsequently evaluated at each point in time using Eq. (5) as \({{\bf{H}}}_{i}^{\,\text{eff}\,}=\frac{-1}{{\mu }_{0}{\mu }_{\rm{{{s}}}}}\frac{\delta E}{\delta {{\bf{S}}}_{i}}\). The system of equations, Eq. (4) are solved by a fifth-order Runge–Kutta Method. Spatio-temporal data is analysed on an extracted 1-dimensional line of the computational domain (see Supplementary Note 4). Material constants used are summarised in Table 1.
Data availability
The data generated for the current study are available from the corresponding author upon reasonable request.
References
Chaikin, P. M. & Lubensky, T. C. Principles of Condensed Matter Physics (Cambridge University Press, 2000).
Anderson, P. W. & Brinkman, W. F. Anisotropic superfluidity in 3He: a possible interpretation of its stability as a spin-fluctuation effect. Phys. Rev. Lett. 30, 1108 (1973).
Levine, D. et al. Elasticity and dislocations in pentagonal and icosahedral quasicrystals. Phys. Rev. Lett. 54, 1520 (1985).
Socolar, J. E. S., Lubensky, T. C. & Steinhardt, P. J. Phonons, phasons, and dislocations in quasicrystals. Phys. Rev. B 34, 3345 (1986).
Kosterlitz, J. M. & Thouless, D. J. Long range order and metastability in two dimensional solids and superfluids. (Application of dislocation theory). J. Phys. C 5, L124–L126 (1972).
Bloch, F. Zur Theorie der Austauschproblems und der Remanenzerscheinung. Z. Physik. 74, p. 295 (1932).
Néel, L. The surface anisotropy of ferromagnetic substances. CR Acad. Sci. Paris 237, 1468 (1953).
Feldtkeller, E. Mikromagnetisch stetige und unstetige magnetisierungskonfigurationen. Z. Angew. Phys. 19, 530–536 (1965).
Bogdanov, A. N. & Rößler, U. K. Chiral symmetry breaking in magnetic thin films and multilayers. Phys. Rev. Lett. 87, 037203 (2001).
Rößler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 442, 797 (2006).
Weertman, J. et al. Elementary dislocation theory, dislocations and imperfections and active centers in semiconductors. Am. J. Phys. 33, 1091–1093 (1965).
Nadgorny, E. Dislocation dynamics and mechanical properties of crystals. Prog. Mater. Sci. 31, 1–530 (1988).
Hirth, J. P. & Loethe, J. Theory of Dislocations (Krieger Publishing Company, Malabar, 1982).
Eshelby, J. D. Uniformly moving dislocations. Proc. Phys. Soc. Sect. A 62, 307 (1949).
Stroh, A. N. Steady state problems in anisotropic elasticity. Stud. Appl. Math. 41, 77–103 (1962).
Frank, F. C. & van der Merwe, J. H. One-dimensional dislocations. I. Static theory. Proc. R. Soc. Lond. A 198, 205–216 (1949).
Gumbsch, P. & Huajian, G. Dislocations faster than the speed of sound. Science 283, 965–968 (1999).
Li, Q. & Shi, S.-Q. Dislocations faster than the speed of sound. Appl. Phys. Lett. 80, 3069 (2002).
Marian, J., Cai, W. & Bulatov, V. Dynamic transitions from smooth to rough to twinning in dislocation motion. Nat. Mater. 3, 158 (2004).
Vandersall, J. A., Young, J. A. & Wirth, B. D. Supersonic dislocation stability and nano-twin formation at high strain rate. Philos. Mag. 84, 3755–3769 (2004).
Thiele, A. A. Steady-state motion of magnetic domains. Phys. Rev. Lett. 30, 230 (1973).
Malozemoff, A. P. & Slonczewski, J. C. Magnetic Domain Walls in Bubble Materials: Advances in Materials and Device Research, Vol. 1 (Academic Press, 2016).
Odell, T. H. Ferromagnetodynamics—The Dynamics of Magnetic Bubbles, Domains and Domain Walls, 237 (New York Halsted Press, 1981).
Belavin, A. A. & Plyakov, A. M. Metastable states of two-dimensional isotropic ferromagnets. JETP Lett. 22, 245 (1975).
Braun, H. B. Topological effects in nanomagnetism: from superparamagnetism to chiral quantum solitons. Adv. Phys. 61, 1–1116 (2012).
Thiaville, A. & Miltat, J. Néel lines in the Bloch walls of bubble garnets and their dark-field observation. J. Appl. Phys. 68, 2883–2891 (1990).
Parkin, S. S., Hayashi, M. & Thomas, L. Magnetic domain-wall racetrack memory. Science 320, 190–194 (2008).
Tatara, G., Kohno, H. & Shibata, J. Microscopic approach to current-driven domain wall dynamics. Phys. Rep. 468, 213–301 (2008).
Allwood, D. et al. Magnetic domain-wall logic. Science 309, 1688–1692 (2005).
Schryer, N. L. & Walker, L. R. The motion of 180 domain walls in uniform dc magnetic fields. J. Appl. Phys. 45, 5406–5421 (1974).
Mougin, A. et al. Domain wall mobility, stability and Walker breakdown in magnetic nanowires. Europhys. Lett. 78, 57007 (2007).
Hertel, R. & Kirschner, J. Magnetization reversal dynamics in nickel nanowires. Physica B 343, 206–210 (2004).
Yang, M. et al. Magnetization reversal dynamics in nickel nanowires. Appl. Phys. Lett. 99, 122505 (2011).
Čerenkov, P. A. Visible radiation produced by electrons moving in a medium with velocities exceeding that of light. Phys. Rev. 52, 378 (1937).
Shiino, T. et al. Antiferromagnetic domain wall motion driven by spin–orbit torques. Phys. Rev. Lett. 117, 087203 (2016).
Gomonay, O., Jungwirth, T. & Sinova, J. High antiferromagnetic domain wall velocity induced by Néel spin–orbit torques. Phys. Rev. Lett. 117, 017202 (2016).
Roy, P. E., Otxoa, R. M. & Wunderlich, J. Robust picosecond writing of a layered antiferromagnet by staggered spin–orbit fields. Phys. Rev. B 94, 014439 (2016).
Železný, J. et al. Relativistic Néel-order fields induced by electrical current in antiferromagnets. Phys. Rev. Lett. 113, 157201 (2014).
Guslienko, K. et al. Dynamic origin of vortex core switching in soft magnetic nanodots. Phys. Rev. Lett. 100, 027203 (2008).
Watelot, S. P. et al. Commensurability and chaos in magnetic vortex oscillations. Nat. Phys. 8, 682 (2012).
Tveten, E. G., Qaiumzade, A. & Brataas, A. Antiferromagnetic domain wall motion induced by spin waves. Phys. Rev. Lett. 112, 147204 (2014).
Peng, S. et al. Supersonic screw dislocations gliding at the shear wave speed. Phys. Rev. Lett. 122, 045501 (2019).
Nosenko, V., Zhdanov, S. & Morfill, G. Supersonic dislocations observed in a plasma crystal. Phys. Rev. Lett. 99, 025002 (2007).
Tesla, N. An interesting feature of X-ray radiations. Electron. Rev. 29, 13–14 (1896).
Yang, M. Spin-Cherenkov effect and magnonic Mach cones. Phys. Rev. B 88, 220412 (2013).
Wörnle, M. S. et al. Current-induced fragmentation of antiferromagnetic domains. arxiv: 1912.05287 (2019).
Kăspar, Z. et al. High electrical and optical resistive switching in a thin film antiferromagnet. arxiv: 1909.09071 (2019).
Acknowledgements
The work of R.M.O. and K.Y.G. was partially supported by the STSM Grants from the COST Action CA17123 “Ultrafast opto-magneto-electronics for non-dissipative information technology”. K.Y.G. acknowledges support by IKERBASQUE (the Basque Foundation for Science) and Spanish MINECO project FIS2016-78591-C3-3-R.
Author information
Authors and Affiliations
Contributions
J.W., P.E.R. and R.M.O. initiated the project. P.E.R. developed the atomistic code. R.M.O. and P.E.R. analysed the data and interpreted the simulations result. R.M.O., K.Y.G. and R.R.-E. developed the analytical model. R.M.O., P.E.R., R.R.-E., J.G., K.Y.G. and J.W. discussed the data. R.M.O. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Otxoa, R.M., Roy, P.E., Rama-Eiroa, R. et al. Walker-like domain wall breakdown in layered antiferromagnets driven by staggered spin–orbit fields. Commun Phys 3, 190 (2020). https://doi.org/10.1038/s42005-020-00456-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00456-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.