Abstract
Spin-orbit torque nano-oscillators based on bilayers of ferromagnetic and nonmagnetic metals are ultra-compact current-controlled microwave signal sources. They are attractive for practical applications such as microwave assisted magnetic recording, neuromorphic computing, and chip-to-chip wireless communications. However, a major drawback of these devices is low output microwave power arising from the relatively small anisotropic magnetoresistance of the ferromagnetic layer. Here we experimentally show that the output power of a spin-orbit torque nano-oscillator can be significantly enhanced without compromising its structural simplicity. Addition of a ferromagnetic reference layer to the oscillator allows us to employ current-in-plane giant magnetoresistance to boost the output power of the device. This enhancement of the output power is a result of both large magnitude of giant magnetoresistance compared to that of anisotropic magnetoresistance and their different angular dependencies. Our results hold promise for practical applications of spin-orbit torque nano-oscillators.
Similar content being viewed by others
Introduction
Electric current flowing in the plane of a ferromagnetic (FM)/nonmagnetic (NM) bilayer can apply spin–orbit torque (SOT) to magnetization of the FM1,2,3,4,5,6,7,8. The simplest example of such a SOT is spin Hall torque (SHT) arising from pure spin current in the NM layer that flows in the direction orthogonal to both the charge current and the FM/NM interface9,10,11,12,13. When injected into the FM layer, this pure spin current applies SHT that can act as negative magnetic damping and thereby excite auto-oscillations of the FM magnetization14,15,16,17,18,19,20,21. The current-driven auto-oscillations of magnetization result in a microwave voltage generation by the FM/NM bilayer due to anisotropic magnetoresistance (AMR) of the FM15,22. Since AMR in thin films of FM metals is relatively small, the output microwave signal generated by the FM/NM bilayer spin Hall oscillators (SHOs) typically does not exceed several pW15,21.
The main advantage of SOT oscillators over spin-transfer torque oscillators based on magnetic tunnel junctions (MTJs)23,24,25,26,27,28 is their structural simplicity and ease of fabrication. Indeed, a FM/NM bilayer SOT oscillator device is powered by electric current flowing in the plane of the bilayer. Such a current-in-plane (CIP) nano-device can be produced by means of a single e-beam lithography step followed by a single etching step29. In contrast, MTJ-based oscillators are powered by electric current flowing perpendicular to the plane of the MTJ layers. Fabrication of such devices is a formidable task involving multiple lithography, etching, and deposition steps. Given the ease of fabrication of SOT oscillators, they find use in fundamental studies of SOTs30, as well as nonlinear magnetization dynamics31,32 and hold promise for practical applications, such as microwave-assisted magnetic recording33 and neuromorphic computing34. However, a major drawback of SOT oscillators devices is low efficiency of converting direct bias current into microwave output signal. This poor conversion efficiency arises from the small value of AMR employed for converting current-driven magnetization auto-oscillations into electromagnetic microwave signal. In the case of SHOs, efficiency is further reduced because the direction of magnetization maximizing antidamping SHT differs from that maximizing conversion of magnetization auto-oscillations into microwave signal by AMR.
Here, we report a new type of SHO with additional FM reference layer in which the microwave power generation relies on current-in-plane giant magnetoresistance (CIP GMR)35,36,37. Since the magnitude of GMR significantly exceeds that of AMR, this new type of SHO generates significantly higher microwave power than the AMR-based SHOs. The maximum measured microwave power generated by the GMR SHO device exceeds 1 nW, which is strongly enhanced compared to the maximum microwave power produced by AMR SHO devices. We use magnetoresistance and angular-dependent SHO emission measurements to show that the significant improvement the conversion efficiency is not only due to the increase of magnetoresistance, but also due to the matching of the angular dependence of magnetoresistance to that of SHT.
Results
Sample geometry and magnetoresistance
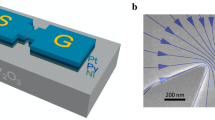
Figure 1a shows a schematic of the GMR SHO device. The device is a nanowire made from antiferromagnetic (AFM)/FM/NM/FM/Pt exchange biased spin valve multilayer, where the direction of magnetization of the bottom FM layer is pinned by exchange bias field from the AFM layer38,39,40. Direct electric current flowing along the nanowire in the heavy metal Pt layer applies SHT to magnetization of the adjacent free FM layer and excites its auto-oscillations15. CIP GMR in the FM/NM/FM spin valve serves as efficient converter of the FM magnetization auto-oscillations into resistance oscillations and microwave voltage, resulting from these resistance oscillations41,42,43.
a Schematic of a nanowire giant magnetoresistance spin Hall oscillator (GMR SHO) that consists of exchange biased current-in-plane giant magnetoresistance (CIP GMR) spin valve, in which the free layer is interfaced with a heavy metal layer (Pt). Here M is magnetization of the pinned layer (Co), m is magnetization of the free layer (Co/Py), NM is the nonmagnetic spacer layer (Cu), and ϕH is the angle between electric current and direction of in-plane magnetic field H. Exchange bias field from the antiferromagnetic (AFM) layer is set in the direction of the electric current (along the nanowire axis). Direct electric current density JHM flowing in the Pt layer injects pure spin Hall current density JS into FM free layer. This spin current applies antidamping spin–orbit torque to m and excites magnetization auto-oscillations. b Scanning electron micrograph of the GMR SHO nanowire device with 500 nm scale bar. c Magnetoresistance of the nanowire GMR SHO device measured at T = 4.2 K with magnetic field applied parallel to the nanowire axis and applied direct electric current Idc = 0.5 mA.
The GMR SHO nanowire devices studied here were patterned from a (sapphire substrate)/Ir25Mn75 (4 nm)/Co (2 nm)/Cu (4 nm)/Co (0.5 nm)/Py (3.5 nm)/Pt (5 nm) multilayer deposited by magnetron sputtering. The 0.5-nm-thick Co dusting layer was inserted between Cu and Py ≡ Ni80Fe20 layers to enhance CIP GMR of the spin valve44. This metallic spin valve multilayer was post-annealed at 523 K for 1 h to set the direction of the exchange bias field parallel to the nanowire axis. A 65 nm wide by 40 μm long nanowire was patterned from the multilayer by using e-beam lithography and Ar ion milling. Two Ti (5 nm)/Au (40 nm) contact pads separated by a 740 nm wide gap were attached to the nanowire, in order to apply in-plane electric bias current Idc to the wire. The 740 nm wide part of the nanowire between the contact pads forms the active region of the SHO, where electric current density and resulting antidamping SHT can reach sufficiently high values to cancel the natural magnetic damping of the FM layer and induce magnetization auto-oscillations15. Figure 1b shows the scanning electron micrograph of the GMR SHO device.
In order to compare performance of the GMR SHO to that of the conventional AMR SHO, we also fabricated and studied an AMR-based SHO with nominal lateral dimensions identical to those of the GMR SHO in Fig. 1b. This reference AMR SHO was patterned from (sapphire substrate)/Cu (4 nm)/Co (0.5 nm)/Py (3.5 nm)/Pt (5 nm) magnetic multilayer. The 4 nm Cu underlayer is added to the standard AMR SHO design15 to produce Oersted field acting on the free layer due to electric current in the Cu layer similar to that in the GMR SHO.
All measurements reported in this paper are performed in a continuous flow 4He cryostat at the bath temperature T = 4.2 K. Figure 1c shows resistance of the nanowire GMR SHO measured for magnetic field applied parallel to the wire axis at a small probe current Idc = 0.5 mA. The data reveal switching of the free layer magnetization between parallel (low resistance, RP = 117.8 Ω) and antiparallel (high resistance, RAP = 124.3 Ω) orientations with respect to magnetization of the pinned layer. The GMR ratio of the device ΔRGMR/RP, where ΔRGMR = RAP − RP, is measured to be 0.055. We also measured AMR ratio in the reference AMR SHO device and found it to be 0.004.
Microwave emission measurements
We next perform measurements of microwave signal generation by the GMR SHO and AMR SHO driven by application of a sufficiently large Idc to the nanowire. For these measurements, we applied magnetic field H = 800 Oe in the plane of the sample at angle ϕH with respect to the nanowire axis as shown in Fig. 1a. This field is sufficiently high to rotate the free layer magnetization, while the pinned layer magnetization in the GMR SHO still has a large component parallel to the nanowire axis. For ϕH near 90°, the antidamping action of SHT is maximized because spin Hall current polarization is nearly opposite to the free layer magnetization20.
The data in Fig. 2 shows measured power spectral density (PSD) of the microwave signal generated by the devices as a function of Idc. These measurements were made using a microwave spectrum analyzer and a low noise microwave amplifier15. The data in Fig. 2b reveal that auto-oscillations of magnetization in the AMR SHO turn on for Idc exceeding the critical value of ~3.0 mA, corresponding to estimated current density of ~2 × 108 A/cm2 in the Pt layer. For these measurements, we misalign the applied field direction from that perpendicular to the nanowire by a small angle of 5°(ϕH = 85°), in order to boost conversion efficiency of auto-oscillations of magnetization into a microwave signal due to AMR15,21. The auto-oscillatory mode frequency exhibits a small shift to higher values with increasing bias current. This blue frequency shift is to be contrasted to the red frequency shift observed for bulk spin-wave auto-oscillatory modes in Py/Pt SHOs15. We attribute this blue frequency shift in our Cu/Co/Py/Pt SHO to the Oersted field in the highly conductive Cu layer. This Oersted field points in nearly the same direction as the external applied field, and thus increases the FM resonance frequency45 of the free layer with increasing Idc.
Power spectral density (PSD, color scale on the right) of microwave signal generated by giant magnetoresistance spin Hall oscillator (GMR SHO) (a) and anisotropic magnetoresistance spin Hall oscillator (AMR SHO) (b), measured as a function of direct current Idc applied to the nanowire. For these measurements, in-plane magnetic field H = 800 Oe was applied at angle ϕH with respect to the nanowire axis. PSD versus frequency for GMR SHO (c) and AMR SHO (d) measured at H = 800 Oe (Idc = 6.0 mA and ϕH = 90° for the GMR SHO, Idc = 3.65 mA and ϕH = 85° for the AMR SHO).
Figure 2a reveals that the GMR SHO device exhibits two auto-oscillatory modes above the critical current of ~4.0 mA. The higher frequency mode has nearly the same frequency as that of the AMR SHO and exhibits nearly the same blue frequency shift as the single auto-oscillatory mode of the AMR SHO. We thus identify this mode as the auto-oscillatory bulk spin-wave mode of the free layer. As was shown in previous studies of AMR SHO, the amplitude of the auto-oscillatory bulk spin-wave mode is maximized in the middle of the nanowire15. The other auto-oscillatory mode of GMR SHO appears at a lower frequency and exhibits a much larger blue frequency shift, with increasing current compared to the higher frequency mode. This strong blue frequency shift cannot be explained by the Oersted field from Idc. Such a high blue shift has been previously observed for auto-oscillatory edge spin-wave modes in AMR SHOs15. The edge spin-wave mode results from spatially inhomogeneous demagnetizing field at the nanowire edges that produces a magnetic potential well for spin-wave excitations46,47. The edge mode in nanowires exhibits maximum amplitude at the wire edge. Recent theoretical work demonstrated that this blue frequency shift of the edge mode can result from nonlinearity of the confinement potential leading to magnon repulsion48. We therefore identify the lower frequency mode as the edge mode of the free layer. We rule out the possibility of the lower frequency mode being the pinned layer auto-oscillatory mode driven by SHT from the Ir25Mn75 layer49,50,51,52 because strong exchange bias field acting on the pinned Co layer requires its auto-oscillatory frequency to be much higher than 2 GHz seen in Fig. 2a at the onset of auto-oscillations.
The microwave power emitted by the edge mode rapidly increases with increasing current bias, and the overall microwave power emitted by the GMR SHO device is dominated by the edge mode. The dominant character of the edge mode auto-oscillations in the GMR SHO compared to the AMR SHO is likely a result of spatially inhomogeneous stray field from the pinned FM layer. Indeed, application of external magnetic field perpendicular to the nanowire axis (ϕH = 90°) rotates the pinned layer magnetization toward the applied field direction. This gives rise to a stray field from the pinned layer that is opposite to the applied field near the edge of the free layer. This spatially inhomogeneous stray field enhances the localizing spin-wave potential for the free layer edge mode. This, in turn, increases the spatial extent of the edge mode, which boosts the microwave power generated by the mode. Further theoretical studies are needed to test this proposed mechanism of the edge mode amplitude enhancement in GMR SHOs.
Figure 2c, d shows constant-current cuts of the data in Fig. 2a, b. These data reveal that the microwave power generated by the GMR SHO is much higher than that emitted by the AMR SHO. It is also clear that the spectral linewidth of the signal emitted by the AMR SHO (full-width at half-maximum Δf = 8 MHz) is much smaller than that of both the higher frequency and lower frequency modes in the GMR SHO (Δf = 120 MHz for the dominant lower frequency mode). The higher spectral linewidth in the GMR SHO can be explained by three dominant factors. First, since the critical current in the GMR SHO is higher, higher ohmic heating in GMR SHO leads to temperature-induced broadening of the spectral linewidth53,54,55. Second, since two auto-oscillatory modes are simultaneously exited in the GMR SHO, interaction between these modes leads to spectral broadening of both modes56,57. Third, strong nonlinear frequency shift of the edge mode gives rise to nonlinear enhancement of the linewidth53. In addition to the above mechanisms, the enhanced spin pumping58,59 and damping in the GMR SHO stack can contribute to a modest increase in the SHO linewidth and critical current53.
Bias dependence of SHO emission
Figure 3a shows integrated microwave power emitted by the GMR SHO (ϕH = 90°) and AMR SHO (ϕH = 85°) devices measured at H = 800 Oe as a function of current bias Idc. The data in Fig. 3 are obtained via integration of the spectra such as those in Fig. 2c, d. It is clear from Fig. 3 that the output power of the GMR SHO is much higher than that of the AMR SHO for this magnetic field direction maximizing antidamping efficiency of SHT. Figure 3b shows the AMR SHO data from Fig. 3a with rescaled axes. Consistent with previous studies15, integrated power of the AMR SHO first increases and then decreases with increasing Idc. The decrease of the integrated power at high currents can be attributed to enhanced magnon population, and resulting strong nonlinear magnon scattering at high current densities60. The integrated power of the GMR SHO monotonically increases with current up to the highest bias current value employed in this study (Idc = 6 mA). This is likely due to the higher critical current of the GMR SHO compared to the AMR SHO so that decrease of power induced by nonlinear interactions is expected at Idc > 6 mA.
a Integral microwave power generated by giant magnetoresistance spin Hall oscillator (GMR SHO, blue spheres) and anisotropic magnetoresistance spin Hall oscillator (AMR SHO, red spheres), as a function of bias current Idc. b Rescaled axes of the AMR SHO data from a. Error bars are smaller than data points.
Angular dependence of SHO emission
We next study angular dependence of the microwave power generated by the GMR SHO and AMR SHO devices. Figure 4 shows the dependence of the integrated power emitted by GMR SHO (Fig. 4a) and AMR SHO (Fig. 4b) on the direction ϕH of a 500 Oe in-plane magnetic field. The measurements are made with constant bias current set to the maximum value used in the microwave emission experiment. The angular dependence of the SHO output power arises from a combination of the angular dependencies of the magnetoresistance and the efficiency of the antidamping SHT. The angular dependence of the antidamping SHT is the same for both devices, as it is determined by the charge current path in the Pt layer. In the wire geometry, the charge current flows along the length of the wire and the strength of the antidamping torque is proportional to \(\sin ({\phi }_{M}^{0})\)11, and is thus always maximized for \({\phi }_{M}^{0}=\pi /2\ (9{0}^{\circ })\).
The maximum power generated by the GMR SHO is observed for magnetization direction ϕM perpendicular to the nanowire axis (ϕM = 90°). This result can be explained by a combination of two factors: (i) maximized SHT antidamping efficiency at this angle and (ii) favorable angular dependence of CIP GMR36 in this structure: \(R={R}_{{\rm{P}}}+\Delta {R}_{{\rm{GMR}}}\cos ({\phi }_{M})\). Indeed, the output microwave power is proportional to square of the SHO current-driven resistance oscillation amplitude, \({\delta {{R}^{2}_{{\rm{ac}}}}}\), defined by \(R(t)={R}_{0}+\delta {R}_{{\rm{ac}}}\sin (\omega t)\). The maximum contribution to output power due to magnetoresistance effects is expected for the equilibrium direction of magnetization \({\phi }_{M}^{0}\), which maximizes the amplitude of resistance oscillations δRac. Substituting the expression for time dependence of the in-plane direction of magnetization \({\phi }_{M}(t)={\phi }_{M}^{0}+\delta {\phi }_{M}^{{\rm{ac}}}\sin (\omega t)\) into the expression for the angular dependence of CIP GMR and assuming \(\delta {\phi }_{M}^{{\rm{ac}}}\ll 1\ (5{7}^{\circ })\), we derive \(\delta {R}_{{\rm{ac}}}=-\Delta {R}_{{\rm{GMR}}}\sin ({\phi }_{M}^{0})\delta {\phi }_{M}^{{\rm{ac}}}\). It is thus clear that \({\delta {R}^{2}_{{\rm{ac}}}}\) is maximized for \({\phi }_{M}^{0}=\pi /2\ (9{0}^{\circ })\). Therefore in the GMR SHO device, both the SHT efficiency and \({\delta {R}^{2}_{{\rm{ac}}}}\) are maximized at \({\phi }_{M}^{0}=\pi /2\ (9{0}^{\circ })\), and thus the output power of GMR SHO is maximized, consistent with the experimental data in Fig. 4a.
In the case of AMR SHO, the angular dependence of resistance is given by \(R={R}_{{\rm{P}}}-\Delta {R}_{{\rm{AMR}}}{\cos }^{2}({\phi }_{M})\). Substituting the expression for ϕM(t) into the expression for the angular dependence of AMR and assuming \(\delta {\phi }_{M}^{{\rm{ac}}}\ll 1\), we derive \(\delta {R}_{{\rm{ac}}}=\Delta {R}_{{\rm{AMR}}}\sin (2{\phi }_{M}^{0})\delta {\phi }_{M}^{{\rm{ac}}}\). Therefore, the maximum contribution to microwave output power due to magnetoresistance effects of the AMR SHO can be expected at \({\phi }_{M}^{0}=\pi /4\ (4{5}^{\circ })\) and \({\phi }_{M}^{0}=3\pi /4\ (13{5}^{\circ })\). The data in Fig. 4b reveal that the maximum power is observed near ϕH = 70° and ϕH = 110°. These angles ϕH are consistent with an angular dependence due to AMR and spin Hall efficiency, as they fall between the angle \({\phi }_{M}^{0}=\pi /2\ (9{0}^{\circ })\) that maximizes the antidamping SHT and the angles \({\phi }_{M}^{0}=\pi /4\ (4{5}^{\circ })\) and \({\phi }_{M}^{0}=3\pi /4\ (13{5}^{\circ })\) that maximize δRac for the AMR SHO. We note the prediction of the precise field angles that maximize AMR SHO output is complicated by two considerations. First, the shape anisotropy field of the nanowire tends to pull magnetization of the free layer closer to the axis of the nanowire than the applied field direction \({\phi }_{M}^{0}\). Therefore, \({\phi }_{M}^{0}\,<\,7{0}^{\circ }\) for ϕH = 70° (\({\phi }_{M}^{0}\,> \, 11{0}^{\circ }\) for ϕH = 110°). Second, owing to the angular dependence of antidamping SHT efficiency, the critical current Ic for excitation of auto-oscillations by SHT depends on the direction of magnetization17,18. \(({I}_{{\rm{c}}} \sim 1/\sin ({\phi }_{M}^{0}))\) and Ic increases when magnetization rotates away from \({\phi }_{M}^{0}=9{0}^{\circ }\). Therefore, rotation of the applied field away from ϕH = 90° at a constant bias current Idc results in Idc < Ic when ∣ϕH − 90°∣ reaches a certain critical value. This observation is consistent with the data in Fig. 4b that reveal a precipitous drop of the emitted power down to the background value for ϕH < 60° and ϕH > 120°. From these observations, another advantage of the GMR SHO over the AMR SHO becomes clear; the output power from the GMR SHO is always maximized for ϕH = π/2 (90°), while the optimal external field angle for the AMR SHO depends on the external field strength.
Discussion
In addition to SHT from the Pt layer, the free layer of the GMR SHO may experience spin-transfer torque applied by spin current arising from the pinned Co layer61,62,63,64. However, we expect this torque to be relatively small in our nanowire system because magnetization of the pinned layer is nearly collinear with the electric current direction in the pinned Co layer. Anomalous SOT acting on the free layer is expected to be small for magnetization nearly perpendicular to the electric current direction and for the relatively small thickness of the free layer used in our studies, and thus can be neglected for our system as well. Recently evidence of a spin torque with out-of-plane effective field has been shown in CIP GMR devices65; however, this torque is absent when the fixed layer magnetization and charge current density are collinear, as in the GMR SHO.
In the case of GMR SHO, one particular direction of magnetization \(({\phi }_{M}^{0}=\pi /2\ (9{0}^{\circ }))\) simultaneously maximizes the output microwave power and minimizes the critical current for the excitation of auto-oscillations of magnetization. Therefore, GMR SHO offers good performance in terms of both the critical current and the output power. In the case of AMR SHO, the critical current is minimized at \(({\phi }_{M}^{0}=\pi /2\ (9{0}^{\circ }))\), while the amplitude of resistance oscillations is maximized at different angles \(({\phi }_{M}^{0}=\pi /4\ (4{5}^{\circ }))\) and (\({\phi }_{M}^{0}=3\pi /4\ (13{5}^{\circ })\). Therefore, AMR SHO design considerations necessarily include a trade-off between low critical current and high output power. Finally, the larger linewidth for the GMR SHO as compared to the AMR SHO is undesirable for certain applications, particularly for telecommunication applications. In this case, one potentially may use synchronization of multiple oscillators17,66 to decrease linewidth in GMR SHOs, while benefiting from larger microwave output power.
An alternative route to achieve large output microwave power is to use a three-terminal spin torque oscillator that consists of an MTJ embedded on top of a heavy metal nanowire15,20,67. An example schematic can be seen in Fig. 1a of ref. 15. In this device approach, the free layer of the MTJ is driven into the auto-oscillatory state via SHT from the adjacent heavy metal nanowire in the same manner as the devices in this article. However, the microwave voltage is output across the MTJ to use the much larger tunneling magnetoresistance (TMR), compared to GMR and AMR, as an amplifier. The nanowire and MTJ can share a common ground, but to read the voltage drop across the MTJ using current perpendicular-to-plane TMR requires an additional terminal and bias current. Liu et al.15 first demonstrated microwave output powers of 0.25 nW using the three-terminal MTJ SHO design. Recently, Tarequzzaman et al.20 demonstrated microwave output powers of up to 48 nW in a the three-terminal MTJ SHO driven by combination of SHT and spin-transfer torque. In this case, the bias current applied to the MTJ was not only used as a probe current, but was actually large enough to drive spin-transfer torque.
While the three-terminal MTJ SHO has so far been shown to achieve larger maximum output power, the GMR SHO has a number of important advantages. The GMR SHO is much easier to fabricate and can occupy a smaller wafer footprint. In addition, the GMR SHO can be better impedance matched to standard 50 Ω microwave electronics. The MTJs in the three-terminal MTJ SHO have impedances typically in the kΩ range, which leads to a large reduction in the power available to a 50 Ω load as described in the “Methods” section. For example, the MTJ resistance in the work by Liu et al.15 was 4.4 kΩ and therefore the output power available to a 50 Ω load is actually reduced by a factor of ~22.5 to ~1 pW. In the work by Tarequzzaman et al.20, an 800 Ω MTJ was used leading to reduction of deliverable power by a factor of ~4.5 to ~10.6 nW. Powers reported in this manuscript are those deliverable to a 50 Ohm load. The power deliverable to a matched load for our GMR SHO would be increased by 20% for a maximum output power of 1.4 nW. In the nanowire geometry, the width and length can easily be tuned to make 50 Ω devices, while maintaining GMR ratio and practical required applied currents. To achieve a 50 Ω MTJ SHO, the tunneling barrier thickness would need to be reduced or the lateral dimensions greatly increased. Reducing thickness of tunneling barriers is problematic due to the increased possibility of pinholes and dielectric breakdown. Increasing lateral dimensions of MTJ SHOs is not an effectual approach, as it decreases the amplitude of auto-oscillations due to nonlinear magnon scattering16,60.
The GMR SHO device presented in this article is a proof of concept and there are promising routes in which the GMR SHO performance can be improved. First, improving the GMR ratio would increase the power output for the same amplitude of oscillation. Egelhoff et al.68 have demonstrated CIP GMR spin valves with GMR ratio of up to 17% which is ≈3× greater than the 5.5% GMR ratio achieved in our devices. Assuming 50 Ω devices with similar oscillation amplitude, such a large CIP GMR would lead to nearly an order of magnitude increase in microwave power output compared to the GMR SHO device studied here (\(P\propto \delta {R}_{{\rm{ac}}}^{2}\)). Another possibility is to tune the free layer magnetization, and damping to allow larger cone angle of magnetization precession (thus increasing δRac) and lower critical current densities. This may be achieved by further optimizing the direct exchange coupled multilayers of the GMR SHO free layer69. Recent work has also shown that the spin Hall efficiency of heavy metals can be greatly enhanced by increasing scattering70 and alloying with other elements71, which can lead to lower critical currents. Finally, the CIP GMR amplification of magnetoresistance should be compatible with STOs based on recently discovered sources of novel SOTs30,72,73 in addition to SHT.
In conclusion, we experimentally demonstrated that CIP GMR can be used to strongly enhance the output microwave power of a SHO compared to SHOs that utilize AMR for generation of microwave signal. Our data reveal that SHOs with giant magnetoresistance signal enhancement can be designed to simultaneously minimize the critical current for excitation of auto-oscillations and maximize the output microwave power of the oscillator. This enhancement increases the viability of SHOs for emerging nanotechnology applications, such as neuromorphic and reservoir computing34,74,75, and chip-to-chip wireless communications76.
Methods
Sample description
The giant magnetoresistance SHO nanowire devices studied here were patterned from a (sapphire substrate)/Ir25Mn75 (4 nm)/Co (2 nm)/Cu (4 nm)/Co (0.5 nm)/ Py(3.5 nm)/Pt (5 nm) multilayer deposited by magnetron sputtering. The 0.5 nm thick Co dusting layer was inserted between Cu and Py ≡ Ni80Fe20 layers to enhance CIP GMR of the spin valve44. This metallic spin valve multilayer was post-annealed at 523 K for 1 h to set the direction of the exchange bias field parallel to the nanowire axis. A 65 nm wide by 40 μm long nanowire was patterned from the multilayer by using e-beam lithography and Ar ion milling. Two Ti (5 nm)/Au (40 nm) contact pads separated by a 740 nm wide gap were attached to the nanowire, in order to apply in-plane electric bias current Idc to the wire.
Microwave emission experiments
All microwave emission experiments reported in this paper are performed in a continuous flow 4He cryostat at the bath temperature T = 4.2 K. A direct current was applied to the sample through the d.c. port of a bias tee. The microwave emission signal was then recorded via spectrum analyzer. We apply microwave emission background signal subtraction by additionally measuring each trace as a function of Idc at the opposite current polarity. At the opposite current polarity, the antidamping action becomes additional damping and magnetization dynamics are suppressed.
In this article, we report microwave emission power as that available to a standard 50 Ω load. The power deliverable to a matched load Pmatched can be calculated as
where Pmeasured is the power measured using standard microwave equipment, Rload = 50 Ω, and Rdevice is the resistance of the device.
Data availability
All data generated or analyzed during this study are included in this published article and are available from the corresponding author on reasonable request.
References
Ando, K. et al. Electric manipulation of spin relaxation using the spin Hall effect. Phys. Rev. Lett. 101, 036601 (2008).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Hellman, F. et al. Interface-induced phenomena in magnetism. Rev. Mod. Phys. 89, 025006 (2017).
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for Rashba spin–orbit coupling. Nat. Mater. 14, 871–882 (2015).
Freimuth, F., Blügel, S. & Mokrousov, Y. Spin-orbit torques in Co/Pt(111) and Mn/W(001) magnetic bilayers from first principles. Phys. Rev. B 90, 174423 (2014).
Belashchenko, K. D., Kovalev, A. A. & van Schilfgaarde, M. First-principles calculation of spin-orbit torque in a Co/Pt bilayer. Phys. Rev. Mater. 3, 011401 (2019).
Solyom, A. et al. Probing a spin transfer controlled magnetic nanowire with a single nitrogen-vacancy spin in bulk diamond. Nano Lett. 18, 6494–6499 (2018).
Sinova, J., Valenzuela, S. O., Wunderlich, J., Back, C. H. & Jungwirth, T. Spin Hall effects. Rev. Mod. Phys. 87, 1213–1260 (2015).
Zhang, S. Spin Hall effect in the presence of spin diffusion. Phys. Rev. Lett. 85, 393–396 (2000).
Hoffmann, A. Spin Hall effects in metals. IEEE Trans. Magn. 49, 5172–5193 (2013).
Ou, Y. et al. Exceptionally high, strongly temperature dependent, spin Hall conductivity of SrRuO3. Nano Lett. 19, 3663–3670 (2019).
Alghamdi, M. et al. Highly efficient spin–orbit torque and switching of layered ferromagnet Fe3GeTe2. Nano Lett. 19, 4400–4405 (2019).
Demidov, V. E. et al. Magnetic nano-oscillator driven by pure spin current. Nat. Mater. 11, 1028–1031 (2012).
Liu, L., Pai, C.-F., Ralph, D. C. & Buhrman, R. A. Magnetic oscillations driven by the spin Hall effect in 3-terminal magnetic tunnel junction devices. Phys. Rev. Lett. 109, 186602 (2012).
Duan, Z. et al. Nanowire spin torque oscillator driven by spin orbit torques. Nat. Commun. 5, 5616 (2014).
Awad, A. A. et al. Long-range mutual synchronization of spin Hall nano-oscillators. Nat. Phys. 13, 292–299 (2017).
Collet, M. et al. Generation of coherent spin-wave modes in yttrium iron garnet microdiscs by spin–orbit torque. Nat. Commun. 7, 10377 (2016).
Safranski, C. et al. Spin caloritronic nano-oscillator. Nat. Commun. 8, 117 (2017).
Tarequzzaman, M. et al. Spin torque nano-oscillator driven by combined spin injection from tunneling and spin Hall current. Commun. Phys. 2, 20 (2019).
Chen, T. et al. Spin-torque and spin-Hall nano-oscillators. Proc. IEEE 104, 1919–1945 (2016).
Liu, R. H., Lim, W. L. & Urazhdin, S. Spectral characteristics of the microwave emission by the spin hall nano-oscillator. Phys. Rev. Lett. 110, 147601 (2013).
Deac, A. M. et al. Bias-driven high-power microwave emission from MgO-based tunnel magnetoresistance devices. Nat. Phys. 4, 803–809 (2008).
Dussaux, A. et al. Large microwave generation from current-driven magnetic vortex oscillators in magnetic tunnel junctions. Nat. Commun. 1, 1–6 (2010).
Houssameddine, D. et al. Spin transfer induced coherent microwave emission with large power from nanoscale MgO tunnel junctions. Appl. Phys. Lett. 93, 022505 (2008).
Zeng, Z. et al. Ultralow-current-density and bias-field-free spin-transfer nano-oscillator. Sci. Rep. 3, 1426 (2013).
Zeng, Z. et al. High-power coherent microwave emission from magnetic tunnel junction nano-oscillators with perpendicular anisotropy. ACS Nano 6, 6115–6121 (2012).
Skowroński, W., Stobiecki, T., Wrona, J., Reiss, G. & van Dijken, S. Zero-field spin torque oscillator based on magnetic tunnel junctions with a tilted CoFeB free layer. Appl. Phys. Express 5, 063005 (2012).
Evelt, M. et al. Spin Hall-induced auto-oscillations in ultrathin YIG grown on Pt. Sci. Rep. 8, 1269 (2018).
Safranski, C., Montoya, E. A. & Krivorotov, I. N. Spin–orbit torque driven by a planar Hall current. Nat. Nanotechnol. 14, 27–30 (2019).
Yang, L. et al. Reduction of phase noise in nanowire spin orbit torque oscillators. Sci. Rep. 5, 16942 (2015).
Wagner, K. et al. Injection locking of multiple auto-oscillation modes in a tapered nanowire spin Hall oscillator. Sci. Rep. 8, 16040 (2018).
Braganca, P. M. et al. Nanoscale magnetic field detection using a spin torque oscillator. Nanotechnology 21, 235202 (2010).
Torrejon, J. et al. Neuromorphic computing with nanoscale spintronic oscillators. Nature 547, 428–431 (2017).
Baibich, M. N. et al. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 61, 2472–2475 (1988).
Binasch, G., Grünberg, P., Saurenbach, F. & Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828–4830 (1989).
Camley, R. E. & Barnaś, J. Theory of giant magnetoresistance effects in magnetic layered structures with antiferromagnetic coupling. Phys. Rev. Lett. 63, 664–667 (1989).
Khanal, S. et al. Exchange bias in (FeNi/IrMn)n multilayer films evaluated by static and dynamic techniques. J. Phys. D Appl. Phys. 47, 255002 (2014).
Ali, M. et al. Antiferromagnetic layer thickness dependence of the IrMn/Co exchange-bias system. Phys. Rev. B 68, 214420 (2003).
Krivorotov, I. N., Leighton, C., Nogués, J., Schuller, I. K. & Dan Dahlberg, E. Origin of complex exchange anisotropy in Fe/MnF2 bilayers. Phys. Rev. B 68, 054430 (2003).
Kiselev, S. I. et al. Microwave oscillations of a nanomagnet driven by a spin-polarized current. Nature 425, 380–383 (2003).
Rippard, W. H., Pufall, M. R., Kaka, S., Russek, S. E. & Silva, T. J. Direct-current induced dynamics in Co90Fe10/Ni80Fe20 point contacts. Phys. Rev. Lett. 92, 027201 (2004).
Krivorotov, I. N. et al. Time-domain measurements of nanomagnet dynamics driven by spin-transfer torques. Science 307, 228–231 (2005).
Parkin, S. S. P. Origin of enhanced magnetoresistance of magnetic multilayers: spin-dependent scattering from magnetic interface states. Phys. Rev. Lett. 71, 1641–1644 (1993).
Montoya, E., McKinnon, T., Zamani, A., Girt, E. & Heinrich, B. Broadband ferromagnetic resonance system and methods for ultrathin magnetic films. J. Magn. Magn. Mater. 356, 12–20 (2014).
Jorzick, J. et al. Spin wave wells in nonellipsoidal micrometer size magnetic elements. Phys. Rev. Lett. 88, 047204 (2002).
Duan, Z. et al. Spin wave eigenmodes in transversely magnetized thin film ferromagnetic wires. Phys. Rev. B 92, 104424 (2015).
Dvornik, M. & Åkerman, J. Anomalous nonlinearity of the magnonic edge mode. Preprint at https://arxiv.org/abs/1804.01585 (2018).
Tshitoyan, V. et al. Electrical manipulation of ferromagnetic NiFe by antiferromagnetic IrMn. Phys. Rev. B 92, 214406 (2015).
Zhang, W. et al. Giant facet-dependent spin-orbit torque and spin Hall conductivity in the triangular antiferromagnet IrMn3. Sci. Adv. 2, e1600759 (2016).
Saglam, H. et al. Independence of spin-orbit torques from the exchange bias direction in Ni81Fe19/IrMn bilayers. Phys. Rev. B 98, 094407 (2018).
Zhou, J. et al. Large spin-orbit torque efficiency enhanced by magnetic structure of collinear antiferromagnet IrMn. Sci. Adv. 5, eaau6696 (2019).
Slavin, A. & Tiberkevich, V. Nonlinear auto-oscillator theory of microwave generation by spin-polarized current. IEEE Trans. Magn. 45, 1875–1918 (2009).
Sankey, J. C. et al. Mechanisms limiting the coherence time of spontaneous magnetic oscillations driven by dc spin-polarized currents. Phys. Rev. B 72, 224427 (2005).
Boone, C. et al. Experimental test of an analytical theory of spin-torque-oscillator dynamics. Phys. Rev. B 79, 140404(R) (2009).
Krivorotov, I. N., Emley, N. C., Buhrman, R. A. & Ralph, D. C. Time-domain studies of very-large-angle magnetization dynamics excited by spin transfer torques. Phys. Rev. B 77, 054440 (2008).
Iacocca, E., Heinonen, O., Muduli, P. K. & Åkerman, J. Generation linewidth of mode-hopping spin torque oscillators. Phys. Rev. B 89, 054402 (2014).
Urban, R., Woltersdorf, G. & Heinrich, B. Gilbert damping in single and multilayer ultrathin films: role of interfaces in nonlocal spin dynamics. Phys. Rev. Lett. 87, 217204 (2001).
Šimánek, E. & Heinrich, B. Gilbert damping in magnetic multilayers. Phys. Rev. B 67, 144418 (2003).
Demidov, V. E. et al. Control of magnetic fluctuations by spin current. Phys. Rev. Lett. 107, 107204 (2011).
Taniguchi, T., Grollier, J. & Stiles, M. D. Spin-transfer torques generated by the anomalous hall effect and anisotropic magnetoresistance. Phys. Rev. Appl. 3, 044001 (2015).
Gibbons, J. D., MacNeill, D., Buhrman, R. A. & Ralph, D. C. Reorientable spin direction for spin current produced by the anomalous Hall effect. Phys. Rev. Appl. 9, 064033 (2018).
Baek, S.-hC. et al. Spin currents and spin–orbit torques in ferromagnetic trilayers. Nat. Mater. 17, 509–513 (2018).
Amin, V. P. & Stiles, M. D. Spin transport at interfaces with spin-orbit coupling: phenomenology. Phys. Rev. B 94, 104420 (2016).
Bose, A. et al. Observation of anomalous spin torque generated by a ferromagnet. Phys. Rev. Appl. 9, 064026 (2018).
Zahedinejad, M. et al. Two-dimensional mutually synchronized spin Hall nano-oscillator arrays for neuromorphic computing. Nat. Nanotechnol. 15, 47–52 (2020).
Jué, E., Rippard, W. H. & Pufall, M. R. Comparison of the spin-transfer torque mechanisms in a three-terminal spin-torque oscillator. J. Appl. Phys. 124, 043904 (2018).
Egelhoff, W. et al. Specular electron scattering in giant magnetoresistance spin valves. IEEE Trans. Magn. 33, 3580–3582 (1997).
Omelchenko, P., Montoya, E. A., Coutts, C., Heinrich, B. & Girt, E. Tunable magnetization and damping of sputter-deposited, exchange coupled Py∣Fe bilayers. Sci. Rep. 7, 4861 (2017).
Sagasta, E. et al. Tuning the spin Hall effect of Pt from the moderately dirty to the superclean regime. Phys. Rev. B 94, 060412 (2016).
Obstbaum, M. et al. Tuning spin Hall angles by alloying. Phys. Rev. Lett. 117, 167204 (2016).
Mellnik, A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Amin, V. P., Zemen, J. & Stiles, M. D. Interface-generated spin currents. Phys. Rev. Lett. 121, 136805 (2018).
Romera, M. et al. Vowel recognition with four coupled spin-torque nano-oscillators. Nature 563, 230–234 (2018).
Marković, D. et al. Reservoir computing with the frequency, phase, and amplitude of spin-torque nano-oscillators. Appl. Phys. Lett. 114, 012409 (2019).
Lee, H. S. et al. Power-efficient spin-torque nano-oscillator-based wireless communication with CMOS high-gain low-noise transmitter and receiver. IEEE Trans. Magn. 55, 1–10 (2019).
Acknowledgements
This work was supported by the National Science Foundation through Grants No. DMR-1610146, No. EFMA-1641989, and No. ECCS-1708885. We also acknowledge support by the Army Research Office through Grant No. W911NF-16-1-0472, Defense Threat Reduction Agency through Grant No. HDTRA1-16-1-0025, and the Beall Innovation Award at the University of California, Irvine.
Author information
Authors and Affiliations
Contributions
J.-R.C. made magnetoresistance and microwave emission measurements. J.-R.C. and A.S. developed sample nanofabrication techniques and made the samples. J.-R.C. and E.A.M. analyzed the data. I.N.K., J.G.L., and E.A.M. wrote the manuscript. I.N.K. and J.G.L. planned the study. I.N.K. managed the project. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, JR., Smith, A., Montoya, E.A. et al. Spin–orbit torque nano-oscillator with giant magnetoresistance readout. Commun Phys 3, 187 (2020). https://doi.org/10.1038/s42005-020-00454-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00454-7
This article is cited by
-
Easy-plane spin Hall oscillator
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.