Abstract
Today almost all refrigeration systems are based on compressors, which often require harmful refrigerants and typically reach 50% of the Carnot efficiency. Caloric cooling systems do not need any detrimental fluids and are expected to reach 60–70% of the Carnot limit. Current caloric systems utilise the active magnetocaloric regeneration principle and are quite cost-intensive, as it is challenging to achieve large cycle frequencies and thus high specific cooling powers with this principle. In this work, we present an alternative solution where the heat transfer from the heat exchangers to the caloric material is predicated on condensation and evaporation of a heat transfer fluid. Using thermal diodes, a directed heat flow is generated. Thereby we were able to build a cooling unit achieving a specific cooling power of 12.5 W g−1 at a cycle frequency of 20 Hz, which is one order of magnitude larger than the state-of-the-art.
Similar content being viewed by others
Introduction
The global demand for cooling and air conditioning is growing enormously1. In the effort to achieve the climate targets, the requirements on the efficiency of these systems are increasing. The state-of-the-art technology for cooling units is vapour-compression refrigeration, whereby most of these systems just reach 50% of the thermodynamically possible efficiency2. Furthermore, frequently used hydrofluorocarbons have a strong greenhouse potential3, which contribute with 7.8% to global warming4. Since 2014, they are regulated by the European Union, in which the amount of hydrofluorocarbons is gradually being reduced to fulfil the obligations of the Kigali amendments to the Montreal Protocol, which limited the production and consumption of hydrochlorofluorocarbons because of their negative impact on the ozone layer. Besides synthetic refrigerants, also natural refrigerants, such as ammonia, butane, or carbon dioxide, do have disadvantages: either they are toxic, flammable, or high-pressure fluids.
An alternative to vapour-compression omitting hydrofluorocarbons is solid-state cooling, i.e., thermoelectric5 and caloric cooling6. Thermoelectric cooling systems are based on the Peltier effect and are especially suited for exact temperature control and hot spot cooling; however, attain a comparably low efficiency of only ~10% (ref. 7) of Carnot. Caloric cooling systems on the other hand are based on the caloric effect of magnetocaloric8,9, electrocaloric10, elastocaloric11, or barocaloric12. These materials exhibit a reversible adiabatic temperature change when exposed to their corresponding fields (magnetic, electric, or mechanical). Cooling systems working with these materials can attain very large efficiencies, e.g., in case of magnetocaloric materials (MCMs) up to 60% (ref. 13) without requiring any harmful fluids. In general, a magnetocaloric cooling system utilises cyclical magnetisation and demagnetisation of the MCM: while the MCM is exposed to a magnetic field, thermal energy of the MCM is transferred to a heat sink. Once the magnetic field is removed, the temperature of the MCM drops and thermal energy from a heat source can be absorbed. By cyclic repetition of this reversible process, thermal energy can be transferred from cold to hot reservoir. Thereby, the cooling power of magnetocaloric cooling systems is proportional to the amount of MCM and to the cycle frequency.
For all magnetocaloric cooling units strong magnetic fields and thus magnet systems are required. The more MCM has to be magnetised, the larger the magnet system has to be14. These are the main cost driver for magnetocaloric cooling systems15. To save costs, either the magnet costs can be reduced by using recycled magnets16 or the cycle frequency can be increased to enhance the specific cooling power. The larger the cycle frequency, the less MCM and permanent magnets are required to reach a certain cooling power15. For cost-competitive magnetocaloric cooling systems, a cycle frequency of 10 Hz is estimated to be the break-through threshold17.
Since the discovery of the giant magnetocaloric effect in 1997 by Pecharsky and Gschneidner18, Gd or Gd alloys are widely used as MCMs. Their favourable magnetocaloric properties (a high adiabatic temperature change over a wide temperature span, a high isothermal entropy change and a small or no hysteresis) are in contrast to the high costs due to low availability. For this reason, Gauß et al. suggest (MnFe)2P- and La(FeSi)13-based MCMs as cost-efficient alternative, since they have similar magnetocaloric properties like Gd and are uncritical due to their good availability19.
Several magnetocaloric prototypes based on the ‘active magnetic regenerator (AMR)’ concept have been developed20. In these systems, a fluid (liquid or gaseous) is pumped through a bed of powdered or structured MCM. Thereby thermal energy is gradually transported from the cold-side heat exchanger through the MCM to the hot-side heat exchanger. The MCM bed thus operates as a sort of regenerator, in which thermal energy is periodically stored. This results in the major advantage of AMR systems: temperature spans between the heat exchangers can be achieved that are significantly higher than the adiabatic temperature change of the MCM.
Using this concept, Rowe and Tura approached a temperature span of 50 K at a magnetic flux density of 1.5 T and a cycle frequency of 1 Hz with their magnetocaloric cooling unit in 2006 (ref. 21). Russek et al. demonstrated in 2010 with a rotating magnet system at 1.4 T flux density a maximum specific cooling power of 0.95 W g−1 at zero temperature span and a specific cooling power of 0.45 W g−1 at a temperature span of 10 K, and a cycle frequency of 4.7 Hz (ref. 22). In 2014, Jacobs et al. achieved a specific cooling power of >2 W g−1 using 1.52 kg of MCM with an optimal cycle frequency of 4 Hz (ref. 23). Four years later, in 2018, Chaudron et al. built an impressive magnetocaloric cooling unit with an experimentally quantified total efficiency of 60% of Carnot limit, the highest ever measured value for these systems13. The cooling unit has a cooling power of 900 W and temperature span of 23.5 K with a cycle frequency of 1.12 Hz. Fortkamp et al. achieved an efficiency of 19% in 2018 with their AMR system, at a cooling power of 80 W, a cycle frequency of 1 Hz and a temperature span of 10.5 K (ref. 24).
For all AMR systems, a fundamental trade-off is given: to facilitate the heat exchange and thereby increase the systems frequency and specific power, finer structures with a larger surface-to-volume-ratio are needed25. This, however, makes it more difficult to pump the heat transfer fluid through the material, the pressure drop increases at the expense of efficiency.
In this work, we present a system concept, which we call ‘active magnetocaloric heat pipe (AMH)’, reaching cycle frequencies and specific cooling powers one order of magnitude larger than those shown in the literature. In this concept26, the heat transfer is realised by evaporation and condensation of a heat transfer fluid.
Results and discussion
Active magnetocaloric heat pipe
The concept of transferring thermal energy using latent heat via evaporation and condensation of a heat transfer fluid is already commonly used in heat pipes, as well as in thermosiphons for, e.g., heat spreaders27. Here, a fluid is enclosed in a hermetically sealed container with all non-condensable gases being extracted. The fluid is present in the two phases, liquid and gas. In this two-phase region, the pressure is only a function of the temperature, independently of the fraction of liquid and gas. As the container presents a thermodynamically closed system, any increase in temperature results directly in an evaporation of liquid and an increase in pressure, while a temperature decrease results in condensation of gaseous fluid and a decrease in pressure. Thus, if the temperature on the hot side of the container rises, liquid evaporates, increasing the systems pressure, followed by an immediate condensation on the cold side, accompanied by a very efficient and fast heat transfer.
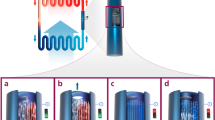
The basic unit of a magnetocaloric cooling system based on the AMH concept is the magnetocaloric segment (Fig. 1). This segment consists of a heat pipe container, a heat transfer fluid, the MCM (1) and passive check valves (2), which act as thermal diodes. The check valves themselves are spring loaded elements that open and close due to the pressure changes caused by the temperature changes induced in the MCM by the magnetic field (3). Thus by alternating the magnetisation of the segment, a unidirectional gas flow from the cold side to the hot side occurs, whereby heat is pumped. The liquid fluid, which accumulates in the condenser, is transferred to the evaporator through a throttle, in analogy to classical refrigeration systems.
a The magnetic field (3) is applied. Thereby, the magnetocaloric material (MCM) (1) is heated and condensed liquid evaporates. b The pressure increases due to the evaporation of the liquid. The check valve (2) to the right side opens; fluid in the gas phase transmits latent heat into the adjoining segment. c Once the magnetic field is switched off by rotating the magnet to the next segment, the MCM cools down below the starting temperature due to the removed heat. d Fluid from the gas phase condensates on the MCM, the vapour pressure decreases below the value in the previous segment. The check valve to the left opens, gaseous fluid from the left enters and heat is absorbed from the previous segment.
A single segment described in the section above was installed into a 1.2 T magnet system. The MCM used is spherical La(FeMnSi)13 with a diameter of 200–400 µm (Calorivac-H from Vacuumschmelze GmbH), and a first-order magnetic phase transition. The adiabatic temperature change ΔTad is (2.8 ± 0.1) K at a magnetic flux density of 1.2 T with a peak temperature at 20.7 °C. The segment consists of 3.5 g MCM, methanol with its high vapour pressure gradient working as heat transfer fluid, two check valves28, an evaporator wrapped with heating wire being thermally insulated to the environment and a condenser connected to a thermal bath at an adjustable temperature (see “Methods” for details).
Specific cooling power and cut-off frequency
This system was characterised by measuring the temperature span between condenser and evaporator for different heat loads and magnetisation frequencies. A maximum specific cooling power \(\dot q\) of 12.5 W g−1 at a frequency of 20 Hz was measured. Figure 2 shows the dependence of the experimentally determined specific cooling power at zero temperature span \(\dot q\left( {f,{\mathrm{{\Delta} }}T = 0} \right)\) on the magnetisation frequency f. The specific cooling power \(\dot q\left( {f,{\mathrm{{\Delta} }}T = 0} \right)\) can be described theoretically by the work of Hess et al.29:
Measured maximum specific cooling power for zero temperature span \(\dot q\left( {f,{\mathrm{{\Delta} }}T = 0} \right)\) with the Gaussian error propagation (green squares), as a function of the cycle frequency f with an uncertainty of 0.1%. Equation (1) was fitted to the data (black line) to determine the maximum achievable specific cooling power \(\dot q\)max for \(f \to \infty\) (grey dashed line) and the cut-off frequency fc (blue dotted line)29. Here, \(\dot q\)max as well as fc depend on the total thermal system resistance. Above fc, an increase of the cycle frequency leads only to a sublinear increase of \(\dot q\)max and is no longer efficient. The specific cooling power \(q_{{\mathrm{MCM}}}f\) (orange dash-dot line) can be obtained theoretically with the MCM without any system losses.
Fitting Eq. (1) to the experimental data gives the cut-off frequency fc = 10.9 Hz and the maximum specific cooling power \(\dot q_{{\mathrm{max}}} = 13.2\) W g−1. The cut-off frequency \(f_{\mathrm{c}}\) indicates the frequency up to which an increase in cycle frequency theoretically results in a linear increase of the specific cooling power. For magnetisation frequencies above this cut-off frequency, the specific cooling power approaches an asymptotic value \(\dot q_{{\mathrm{max}}}\) with the MCM mass m:
Here, R is the total thermal resistance of the caloric cooling unit and can be calculated from Eq. (2), yielding R = 0.01 K W−1 in our case. This resistance includes the pressure drop across the valve and the tubing, as well as the heat transfer from the MCM to the heat transfer fluid, which is limited by the heat transfer coefficient, the evaporator surface of the MCM, the pressure drop in the packing of caloric spheres and the thermal diffusion length of the MCM.
The thermal diffusion length depends on the cycle frequency and defines the path length (the radius of the MCM sphere) up to which the heat can be dissipated from the inside of the MCM to the surface within a magnetisation cycle. The thermal diffusion length for the MCM used in this AMH for a frequency of 20 Hz is l ≈ 182 μm (see Eq. (4)). The radius of the MCM spheres is 100–200 µm, and the thermal diffusion length for a cycle frequency of 20 Hz is also in this range. Thus, for higher frequencies the specific power is limited by this length. To prevent this, the diameter of the MCM spheres must be reduced.
MCM’s energy amount
The energy amount released or absorbed during the caloric cycle is given by
Here, \(q_{\mathrm{{MCM}}}f\) indicates the theoretical specific cooling power as a function of frequency, which is defined only by the properties of the MCM, without any system losses.
The specific cooling power and the optimum cycle frequency of the AMH system are compared to magnetocaloric cooling systems defining the state-of-the-art (Fig. 3). The systems are classified with respect to the MCM used, and the temperature span\({\mathrm{{\Delta} }}T\) at which the maximum specific cooling power \(\dot q\) was achieved. It can be seen that the AMH concept exhibits a cycle frequency and a specific cooling power that are one order of magnitude larger than previously published values for AMR systems. The main reason for the enhanced performance is the significant reduction of the thermal resistance of the heat transfer between caloric material and heat source/heat sink, facilitated by using latent heat, i.e., evaporation and condensation.
The magnetocaloric devices are operated at their maximum specific (cooling or heating) power \(\dot q\) and at their optimum cycle frequency f (refs. 13,22,23,24,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61). The higher the frequency and the higher the specific power, the more competitive the caloric device. The circles refer to all systems with Gd or Gd alloys, the stars to the use of LaFeSi, the upward-pointing triangle to Gd in combination with LaFeSiCo and the downward-pointing triangle to MnFePAs. The colours indicate the temperature span \({\mathrm{{\Delta} }}T\) at which \(\dot q\) was measured.
Furthermore, the AMH concept offers the potential to increase the energy efficiency of caloric cooling systems. For the heat flow from the cold side via the MCM to the hot side, no active pumps are required, in contrast to AMR systems. In addition, the required mass flow of the gaseous fluid in an AMH system is orders of magnitudes smaller than of liquid fluids in AMR systems, because of the large latent heat of condensation and evaporation processes. This results in very small pressure drops across the valves (~0.3 mbar; ref. 28) and the MCM, leading to an almost isothermal heat transfer, allowing nearly perfect Carnot-like cooling cycles.
Besides the application to MCMs, it is straightforward to transfer the concept also to elastocaloric, barocaloric and electrocaloric materials. In order to achieve an adequate temperature span, several caloric segments must be connected in series, which inevitably leads to a higher amount of MCM. Nevertheless, the achieved specific power shows that it seems to be possible to build cost-efficient caloric cooling and heating systems, and therefore become a standard solution, replacing step by step the >100-year-old compressor technology.
Methods
Magnet system
The magnet system was kindly provided by Bahl et al. from the Technical University of Denmark and has already been described in detail30. The magnet system consists of two magnetic cylinders with an air gap in the centre for the caloric system. Furthermore, the individual magnet segments are arranged in such a way that there are four areas with maximum flux density (1.24 T) and four areas with a flux density approaching zero. The magnet system has been modified such that a cycle frequency of 2–20 Hz can be set.
Magnetocaloric material
The MCM is a La(FeMnSi)13-based alloy (Calorivac-H) provided and optimised by Vacuumschmelze. Spherical granules were produced using an extrusion–spheronisation process. The brown parts are debinded to remove the organic additives, sintered to achieve full-density parts and finally hydrogenated to set the magnetocaloric properties around room temperature. In the experiment, 3.5 g spherical MCM with a diameter of 200–400 µm and a temperature peak at 20.7 °C was used. The MCM was characterised for a magnetic flux density of 1.2 T. The adiabatic temperature change ΔTad was measured as a function of temperature Τ (Supplementary Fig. 1). The dashed line indicates \({\mathrm{{\Delta} }}T_{{\mathrm{ad}}} = (2.8 \pm 0.1)\) K at the systems temperature of 21 °C. The zero-field heat capacity \(c_0 = (468 \pm 14)\) J kg−1 K−1 was measured by Ingpuls GmbH. From this, the amount of specific energy of the MCM \(q_{\mathrm{MCM}} = (1.3 \pm 0.1)\) J g−1 is obtained (see Eq. (3)). The product qMCMf is shown in Fig. 2. The thermal diffusion length l of the MCM can be calculated from the thermal conductivity λ = (7 ± 1) W m−1 K−1, the density ρ = 7.2 g cm−3 and specific heat capacity c0 (these parameters were determined by Vacuumschmelze) and is given by:
Check valves
The check valve consists of a valve disk made of copper–beryllium with a thickness of 50 µm, to which three meander-shaped spring arms are radially attached (Supplementary Fig. 2). The spring arms are fixed to an orifice-like valve seat made of polyether ether ketone (PEEK). The stroke catcher, which is also made of PEEK, is designed to prevent plastic deformation of the valve disk. When a pressure surge occurs in forward direction, the valve disk is deflected up to the stroke catcher. In the opposite direction, the valve disk closes the valve seat via the sealing ring. The heat flux through the check valve in forward direction is 547 W for methanol at a temperature difference of 1 K. In reverse direction, the heat flow is 0.03 W at a temperature difference of −1 K (ref. 28).
Set up and measurement method of the magnetocaloric cooling unit
In Supplementary Fig. 3, the whole caloric cooling system for one segment is shown. The heat pipe container is mounted in the rotating magnet system. The container part inside the magnet up to the pressure sensors is made of PEEK, the remaining part of stainless steel.
The heat pipe container holds a single segment consisting of the MCM and two check valves. The evaporator and the condenser are coupled via a control valve, which is closed during the measurement. A turbo vacuum pump CDK 240 from Ilmvac first evacuates the heat pipe container, including the whole pipe system. Afterwards, the evaporator is filled with degassed methanol. The entire system now contains a saturated methanol steam atmosphere. The saturated steam atmosphere leads to corresponding temperature and pressure conditions, i.e., every change in temperature leads to a change in pressure. Therefore, using fluid parameters from the database of the National Institute of Standards and Technology31, the temperatures are calculated from the experimentally quantified pressure values, using two CMR371 pressure sensors from Pfeiffer. The condenser is permanently tempered to 21 °C by a chiller. The specific cooling power is obtained by applying an electrical load using a heating wire wrapped around the evaporator. The cycle frequency is measured by a photoelectric sensor BOS 12M-PS-RD10-02 from BALLUFF. The signal is converted into a voltage by a Motrona SD 340 frequency converter. The applied load of the heating wire, the cycle frequency and the pressures are recorded by a Keithley 2700E multimeter.
Calculation of specific cooling power
The maximum specific cooling power for a zero temperature span \(\dot q\left( {f,{\mathrm{{\Delta} }}T = 0} \right)\) shown in Fig. 2 is calculated, using a linear fit to the measured raw data of the temperature span ΔT. Supplementary Table 1 shows an example of the measured temperature spans between evaporator and condenser for different specific cooling powers \(\dot q\) and cycle frequencies f.
Quantification of measurement uncertainties
Temperature span σΔT
The uncertainty σΔT of ΔT results from the uncertainty of the pressure sensors, which is 0.3 mbar according the manufacturer. Applying Gaussian error propagation this gives a total of 0.4 mbar for both sensors. With fluid parameters from the database of the National Institute of Standards and Technology31: 0.4 mbar ≈ 0.06 K. With an additional offset error of the pressure sensors (0.05 K), the total error of ΔT is ~0.11 K.
Specific cooling power \(\sigma_{\dot q}\)
The gradient of the linear fit in Supplementary Fig. 4 is \(m = \frac{{{\mathrm{{\Delta} }}T}}{{\dot q}}\) and the ΔT-axis intercept at \(\dot q = 0\) is c. From the standard deviation of the gradient σm and the standard deviation of the ΔT-axis intercept σc, the uncertainty \(\sigma _{{\dot{q}}}\) is obtained with Gaussian error propagation: \(\sigma _{\dot q} = \sqrt {\left( {\frac{{\sigma _c}}{m}} \right)^2 + \left( {\frac{{c\,\sigma _m}}{{m^2}}} \right)^2}\). For exact values see Supplementary Table 1.
Frequency \(σ_f\)
The uncertainty of the frequency sensor is given as 0.1%, according to the manufacturer.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
International Energy Agency. The future of cooling. Technology Report https://www.iea.org/reports/the-future-of-cooling (2018).
Raveendran, P. S. & Joseph Sekhar, S. Exergy analysis of a domestic refrigerator with brazed plate heat exchanger as condenser. J. Therm. Anal. Calorim. 127, 2439–2446 (2017).
McLinden, M. O., Brown, J. S., Brignoli, R., Kazakov, A. F. & Domanski, P. A. Limited options for low-global-warming-potential refrigerants. Nat. Commun. 8, 14476 (2017).
Kitanovski, A. Energy applications of magnetocaloric materials. Adv. Energy Mater. 10, 1903741 (2020).
Zhao, D. & Tan, G. A review of thermoelectric cooling: materials, modeling and applications. Appl. Therm. Eng. 66, 15–24 (2014).
Moya, X., Kar-Narayan, S. & Mathur, N. D. Caloric materials near ferroic phase transitions. Nat. Mater. 13, 439–450 (2014).
Vining, C. B. An inconvenient truth about thermoelectrics. Nat. Mater. 8, 83–85 (2009).
Waske, A., Gruner, M. E., Gottschall, T. & Gutfleisch, O. Magnetocaloric materials for refrigeration near room temperature. MRS Bull. 43, 269–273 (2018).
Franco, V. et al. Magnetocaloric effect: from materials research to refrigeration devices. Prog. Mater. Sci. 93, 112–232 (2018).
Ma, R. et al. Highly efficient electrocaloric cooling with electrostatic actuation. Science 357, 1130–1134 (2017).
Tušek, J. et al. A regenerative elastocaloric heat pump. Nat. Energy 1, 10 (2016).
Li, B. et al. Colossal barocaloric effects in plastic crystals. Nature 567, 506–510 (2019).
Chaudron, J. B., Muller, C., Hittinger, M., Risser, M. & Lionte, S. Performance measurements on a large-scale magnetocaloric cooling application at room temperature. In Proceedings of the Thermag VIII International Conference on Caloric Cooling (Darmstadt, Germany, 2018).
Russek, S. L. & Zimm, C. B. Potential for cost effective magnetocaloric air conditioning systems. Int. J. Refrig. 29, 1366–1373 (2006).
Kitanovski, A. et al. Magnetocaloric Energy Conversion (Springer International Publishing, 2015).
Benke, D. et al. Magnetic refrigeration with recycled permanent magnets and free rare‐earth magnetocaloric La–Fe–Si. Energy Technol. 8, 1901025 (2020).
Kitanovski, A. & Egolf, P. W. Application of magnetic refrigeration and its assessment. J. Magn. Mater. 321, 777–781 (2009).
Pecharsky, V. K. & Gschneidner, J. K. A. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 78, 4494–4497 (1997).
Gauß, R., Homm, G. & Gutfleisch, O. The resource basis of magnetic refrigeration. J. Ind. Ecol. 21, 1291–1300 (2017).
Greco, A., Aprea, C., Maiorino, A. & Masselli, C. A review of the state of the art of solid-state caloric cooling processes at room-temperature before 2019. Int. J. Refrig. 106, 66–88 (2019).
Rowe, A. & Tura, A. Experimental investigation of a three-material layered active magnetic regenerator. Int. J. Refrig. 29, 1286–1293 (2006).
Russek, S. et al. The performance of a rotary magnet magnetic refrigerator with layered beds. In Proc. 4th Int. Conference on Magnetic Refrigeration at Room Temperature, 339–349 (Baotou, China, 2010).
Jacobs, S. et al. The performance of a large-scale rotary magnetic refrigerator. Int. J. Refrig. 37, 84–91 (2014).
Fortkamp, F. P. et al. Experimental investigation of different fluid flow profiles in a rotary multi-bed active magnetic regenerator device. Int. J. Refrig. 91, 46–54 (2018).
Wieland, S. & Petzoldt, F. Powder-extrusion and sintering of magnetocaloric LaCe(FeMnSi) 13 alloy. J. Alloy. Compd. 719, 182–188 (2017).
Bartholomé, K. & König, J. D. Air conditioning device having at least one heat pipe, in particular thermosiphon. U.S. patent application no. 15/326,260 (2017).
Eastman, G. Y. The heat pipe. Sci. Am. 5, 38–47 (1968).
Maier, L. M. et al. Method to characterize a thermal diode in saturated steam atmosphere. Rev. Sci. Instrum. 91, 65104 (2020).
Hess, T. et al. Modelling cascaded caloric refrigeration systems that are based on thermal diodes or switches. Int. J. Refrig. 103, 215–222 (2019).
Engelbrecht, K. et al. Experimental results for a novel rotary active magnetic regenerator. Int. J. Refrig. 35, 1498–1505 (2012).
National Institute of Standards and Technology. Reference fluid thermodynamic and transport properties database. REFPROP https://www.nist.gov/srd/refprop (2019).
Huang, B. et al. Development of an experimental rotary magnetic refrigerator prototype. Int. J. Refrig. 104, 42–50 (2019).
Govindappa, P. et al. Experimental investigation of MnFeP 1− x As x multilayer active magnetic regenerators. J. Appl. Phys. 50, 315001 (2017).
Teyber, R. et al. Experimental performance investigation of an active magnetic regenerator subject to different fluid flow waveforms. Int. J. Refrig. 74, 38–46 (2017).
Aprea, C., Cardillo, G., Greco, A., Maiorino, A. & Masselli, C. A rotary permanent magnet magnetic refrigerator based on AMR cycle. Appl. Therm. Eng. 101, 699–703 (2016).
Capovilla, M. S., Lozano, J. A., Trevizoli, P. V. & Barbosa, J. R. Performance evaluation of a magnetic refrigeration system. Sci. Technol. Built Environ. 22, 534–543 (2016).
Gao, X. Q. et al. Improvements of a room-temperature magnetic refrigerator combined with Stirling cycle refrigeration effect. Int. J. Refrig. 67, 330–335 (2016).
Lozano, J. A. et al. Development of a novel rotary magnetic refrigerator. Int. J. Refrig. 68, 187–197 (2016).
Teyber, R. et al. Performance evaluation of two-layer active magnetic regenerators with second-order magnetocaloric materials. Appl. Therm. Eng. 106, 405–414 (2016).
Trevizoli, P. V. et al. Magnetic heat pumps: an overview of design principles and challenges. Sci. Technol. Built Environ. 22, 507–519 (2016).
Eriksen, D. et al. Design and experimental tests of a rotary active magnetic regenerator prototype. Int. J. Refrig. 58, 14–21 (2015).
Arnold, D. S., Tura, A., Ruebsaat-Trott, A. & Rowe, A. Design improvements of a permanent magnet active magnetic refrigerator. Int. J. Refrig. 37, 99–105 (2014).
Bahl, C. R. H. et al. Development and experimental results from a 1 kW prototype AMR. Int. J. Refrig. 37, 78–83 (2014).
Lozano, J. A. et al. Experimental and numerical results of a high frequency rotating active magnetic refrigerator. Int. J. Refrig. 37, 92–98 (2014).
Tušek, J., Kitanovski, A., Tomc, U., Favero, C. & Poredoš, A. Experimental comparison of multi-layered La–Fe–Co–Si and single-layered Gd active magnetic regenerators for use in a room-temperature magnetic refrigerator. Int. J. Refrig. 37, 117–126 (2014).
He, X. N. et al. Design and performance of a room-temperature hybrid magnetic refrigerator combined with Stirling gas refrigeration effect. Int. J. Refrig. 36, 1465–1471 (2013).
Tušek, J., Kitanovski, A., Zupan, S., Prebil, I. & Poredoš, A. A comprehensive experimental analysis of gadolinium active magnetic regenerators. Appl. Therm. Eng. 53, 57–66 (2013).
Shassere, B., Abdelaziz, O., West, D. & Evans, B. Thermal imaging of active magnetic regenerator MCE materials during operation. In Proceedings of the Fifth IIF-IIR International Conference On Magnetic Refrigeration At Room Temperature, Thermag V, 565–572 (Grenoble, France, 2012).
Arnold, D. S., Tura, A. & Rowe, A. Experimental analysis of a two-material active magnetic regenerator. Int. J. Refrig. 34, 178–191 (2011).
Trevizoli, P. V., Barbosa, J. R. & Ferreira, R. T. S. Experimental evaluation of a Gd-based linear reciprocating active magnetic regenerator test apparatus. Int. J. Refrig. 34, 1518–1526 (2011).
Tura, A. & Rowe, A. Permanent magnet magnetic refrigerator design and experimental characterization. Int. J. Refrig. 34, 628–639 (2011).
Okamura, T., Rachi, R., Hirano, N. & Nagaya, S. Improvement of 100 W class room temperature magnetic refrigerator. In Proc. 2nd Thermag International Conference of Magnetic Refrigeration at Room Temperature, 377–382 (Portoroz, Slovenia).
Zimm, C. et al. Design and initial performance of a magnetic refrigerator with a rotating permanent magnet. In Proc. 2nd International Conference of Magnetic Refrigeration at Room Temperature, 341–347 (Portoroz, Slovenia).
Huang, Jiaohong et al. Development of permanent magnetic refrigerator at room temperature. Rare Met. 25, 641–644 (2006).
Okamura, T., Yamada, K., Hirano, N. & Nagaya, S. Performance of a room-temperature rotary magnetic refrigerator. Int. J. Refrig. 29, 1327–1331 (2006).
Yao, G. H., Gong, M. Q. & Wu, J. F. Experimental study on the performance of a room temperature magnetic refrigerator using permanent magnets. Int. J. Refrig. 29, 1267–1273 (2006).
Richard, M.-A., Rowe, A. M. & Chahine, R. Magnetic refrigeration: single and multimaterial active magnetic regenerator experiments. J. Appl. Phys. 95, 2146–2150 (2004).
Clot, P. et al. A magnet-based device for active magnetic regenerative refrigeration. IEEE Trans. Magn. 39, 3349–3351 (2003).
Blumenfeld, P. E., Prenger, F. C., Sternberg, A. & Zimm, C. High temperature superconducting magnetic refrigeration. AIP Conf. Proc. 613, 1019–1026 (2002).
Hirano, N. et al. Develpment of magnetic refrigerator for room temperature application. AIP Conf. Proc. 613, 1027–1034 (2002).
Green G., Chafe J., Stevens J., Humphrey J. A Gadolinium-Terbium Active Regenerator (Springer US, Boston, MA, 1990).
Acknowledgements
This work is funded by the Fraunhofer internal projects Talenta and MagCon and by the Federal Ministry of Economics and Energy (BMWi) of Germany within the project MagMed (FKZ 03ET1478).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
P.C. and L.M.M. performed the experiments; L.M.M., P.C. and K.B. analysed the data, L.M.M., P.C., K.B, C.V., O.S.-W. and J.W. interpreted the data; L.M.M. and K.B. performed the modelling; J.D.K. and K.B. developed the AMH concept; A.B. and H.V. optimised and provided the magnetocaloric material; and L.M.M., K.B., J.W., C.V. and O.S.-W. wrote the manuscript. All authors contributed to the interpretation of the data and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maier, L.M., Corhan, P., Barcza, A. et al. Active magnetocaloric heat pipes provide enhanced specific power of caloric refrigeration. Commun Phys 3, 186 (2020). https://doi.org/10.1038/s42005-020-00450-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00450-x
This article is cited by
-
Electrocaloric cooling system utilizing latent heat transfer for high power density
Communications Engineering (2024)
-
Scaling Laws of Elastocaloric Regenerators
Shape Memory and Superelasticity (2024)
-
Ultrasensitive barocaloric material for room-temperature solid-state refrigeration
Nature Communications (2022)
-
Materials, physics and systems for multicaloric cooling
Nature Reviews Materials (2022)
-
Long-term stable compressive elastocaloric cooling system with latent heat transfer
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.