Abstract
The application of optical methods for tissue diagnosis, activation, and treatment suffers dramatically from the low accessible depths due to strong light scattering in tissues. Here we demonstrate a method to address this issue by utilizing transient ultrasound waves, travelling transversally to the light propagation direction, to guide light into deeper tissue regions. We study the formation of the ultrasound-induced refractive index structures and waveguides using simple ultrasound field configurations and analyze their effects on the propagation of short light pulses. As a proof of concept, we demonstrate using 5 ns pulses of 532 nm light and Intralipid-20%-based phantoms with \(\mu _{\mathrm{s}}^\prime\) up to 4.5 cm−1 a waveguide supported light intensity increase up to the depths of at least 90 mean free paths.
Similar content being viewed by others
Introduction
Optical methods are safe for biomedical applications and provide high speed, high resolution, and selectivity1. By virtue of these advantages, various optical concepts are currently used for light-based tissue imaging2, activation3, and treatment4. Their practical applicability, however, is severely impeded by light scattering, hindering the ability to deliver light into regions deeper than a few millimeters2,5. Therefore, the applicability of light-based methods to image, activate, and cure deep tissue remains limited.
Over time, numerous ways to mitigate or circumvent these difficulties were developed. Passive methods include the use of near-infrared instead of visible light to access the biomedical transparency window(s), or the use of sophisticated filtering concepts for imaging, as is done in ballistic imaging, optical coherence tomography, and diffuse optical tomography2,6.
Additionally, several active strategies to handle light scattering and its effects by influencing light propagation were introduced. For instance, the amount of scattering events can be diminished using invasive solutions3,7 and optical clearing8,9, or affecting the distribution of scatterers10.
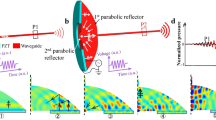
Among the most successful recent active approaches used to counteract light scattering and to improve light delivery is light wavefront shaping (LWS)11,12. This technique requires the knowledge of the light intensity at some point in-depth as a feedback signal to optimize the incident light field and to improve light delivery to the given position. Hence, it is possible to employ photoacoustic (PA) and acoustooptic (AO) interactions to recover light intensity information from the deep tissue. Subjected to lower propagation losses of ultrasound (US) as compared to light, both modalities are able to increase the sensing range and thus are able to extend the depths where the LWS methods may be used13,14,15. However, even PA- and AO-aided LWS (PA/AO-LWS) require that threshold illumination levels are achieved first. Therefore, their application towards deeper tissue regions is also dependent on achievements in light delivery (Fig. 1a).
a Collimated laser light beam impinging on the highly scattering tissue forms a typical forward-scattering pattern: the straight line propagation is broken, and light penetration depth is limited. b Light can be guided deeper into the tissue by a carefully crafted ultrasound field, emitted by an ultrasound transducer (UST), and detrimental effects of scattering are reduced. c As the ultrasound pulse propagates along the scattering medium (bottom-up), the associated refractive index pattern creates a waveguide, which could support the propagation of a synchronous short light pulse into the depth of the medium. d At a rather shallow depth or in low scattering samples light could be focused in the point of observation o by an external lens, however, as scattering is increased such focusing is destroyed. e In the absence of the ultrasound-induced waveguide, the light from a coupling lens is scattered close to the surface of the sample. f A fraction of light, scattered within a small angle close to the beam axis, that would be scattered away otherwise, is coupled into the ultrasound-induced waveguide and its propagation into depth is promoted. Although the induced refractive index contrast is small, and the induced waveguide would accept only a small fraction of scattered photons, it is sufficient to provide an advantage over the reference case e in the point of observation o.
It is known that refractive index gradients formed in a layered fashion16,17,18 or liquid core–liquid cladding elements, known in the transformation optics domain19,20,21,22, possess interesting light manipulation capabilities, including light focusing and waveguiding.
As US is locally changing the refractive index of the medium upon propagation23,24, several concepts of US-induced light waveguiding have been proposed recently to aid light delivery in depth. So far, they are based on US waves in a cylindrical cavity, either formed by a cylinder-shaped ultrasound transducer (UST)25,26,27, or by an absorber, acting as a cylindrical source of nonlinear PA waves28. These studies demonstrate that the US-induced variations in a scattering medium could provide sufficient AO-interaction to aid light delivery in-depth.
However, the difficulties of upscaling the cylindrical sources and application of the acoustic load to the entire volume of the sample might limit the applicability of the proposed concepts25,26,27,28 in vivo. These constraints could be eased by the use of transient US waves for light guiding into scattering media29. Utilizing transient US waves, transversal to the light propagation direction (Fig. 1b, c), allows the usage of US beamforming to tailor the required US field distribution in space and time. Formed without an enclosure and in transient fashion, they provide an opportunity to increase the source-waveguide distance while reducing the acoustic load on the sample both per area and per time unit.
Our concept builds up on the following blocks: (A) transversal gradients of refractive index can guide the light19,20, (B) an US wave can change the refractive index of the medium23,24, (C) arbitrary US patterns can be created using wave interference30, (D) the phase front of a single-frequency US burst is not substantially distorted by its propagation in a homogeneous scattering medium31,32. Consequently, tailored transient US fields could be used to manipulate light propagation, including light waveguiding as we report below.
While in a clear medium, this enables the formation of US-controlled optical elements like lenses and phase masks, US influence on light propagation in scattering media is different. Thus, in contrast to media with low scattering, or to areas close to the sample surface (Fig. 1d), light cannot be focused in strongly scattering media with an external lens. The photons that are injected into the sample and initially propagate near the beam axis would get lost from the axial region due to scattering (Fig. 1e). But the presence of the US-induced waveguide promotes their propagation to the observation point, as shown in Fig. 1f. Such collection of the scattered photons is aided by the dominating forward scattering in biomedical tissues as the amount of the photons available for collection is increased. Therefore, the desired effect of the US-induced refractive index structures (US-IRISs) in the scattering media is based on a combination of waveguiding and forward scattering.
Here we investigate the formation of US-IRISs and waveguides by transient transversal US waves, present the idea of transient US light waveguiding (TULW), and prove its validity in experiments with homogeneous scattering media. To do so, we use Intralipid-20% (IL)-based phantoms with estimated reduced scattering coefficient up to \(\mu _{\mathrm{s}}^\prime\) ≈ 4.5 cm−1, 532 nm laser pulses of 5 ns pulse width, and a few simple US beamforming configurations. Although optical properties of tissues vary significantly4,5,30, this value for \(\mu _{\mathrm{s}}^\prime\) is in the range of weakly scattering tissues (i.e. bladder wall4 with \(\mu _{\mathrm{s}}^\prime\) = 1.28–3.30 cm−1). Thus, by showing the needle-like waveguide support by low-pressure transient US in scattering media, we suggest a versatile way to non-invasive, biocompatible, and adaptable low-loss light delivery, and highly customized light manipulation deep in biological tissues.
Results
Formation of dynamic US-IRISs
As US is propagating in the medium as a longitudinal wave, areas of local compression and rarefaction of the material follow each other. These zones of local density change are altering the refractive index of the medium24 upon US propagation, which forms a dynamic US-IRIS in the medium (Fig. 1c). When a planar transducer is excited with a typical few-cycle single-frequency sine signal, one-dimensional-layered sinusoidal refractive index gradients, traveling across the medium with US speed, are created.
Since the speed of light is much higher than that of the US, the resulting movement of the US-IRIS during the propagation of a short light pulse through it is negligible. Then a sufficiently short light pulse, sent sideways, is impinging on a quasi-static transversal refractive index distribution (Fig. 1c).
In a linear approximation24, the local change of the refractive index Δn is proportional to the local US pressure p, which is proportional to the driving voltage V within linear US emission and propagation31. Then, the refractive index distribution, observed by the light pulse. is determined by the transducers’ excitation signal. Hence, for the US emission along y direction, at the moment t = tp of light pulse arrival on the boundary of the medium, the refractive index modulation is given as \(\Delta n(y)|_{t = t_{\mathrm{p}}} \propto {\mathrm{sin}}(2{\uppi}y/\lambda _{\mathrm{a}} + \phi )\), where λa = va/fa is the acoustic wavelength, determined by US speed in the medium va and its frequency fa, and the phase ϕ is dependent on the synchronization between the light pulse and the US burst (Δt). The amplitude of this modulation is given as Δn ∝ γp, where the piezo-optic coefficient of water is γ = 1.2…1.5 × 10−10 Pa−1 (refs. 23,24,32). With the given values of γ, and within a range of US pressures considered safe31, a Δn in the order of 10−4–10−5 can be achieved. We verified that even refractive index gradients in the order of Δn = 10−5 achieved with pressure levels below 100 kPa are capable of light focusing in clear media, and hence may promote light manipulation and waveguiding, which we confirm experimentally below.
A single period of such US-IRIS forms a refractive index variation comparable to a gradient refractive index medium lens and its function could be described respectively16,17,18. Then the effect, introduced by a plane-wave US-IRIS, is dependent on its current location (Δt), the amplitude of the refractive index change (Δn), given by the local pressure of the US wave (p ∝ V), and the extent of the US-IRIS (L) in the direction of the light propagation (z-axis in Fig. 1b). The optical properties of the US-IRIS are then given by the combination of these parameters, determining the refractive index profile in the plane transversal to the light propagation direction (xy plane). Therefore, an alteration of the US pressure leads to a respective change of the refractive power of the US-IRIS, similar to liquid core–liquid cladding systems, whose optical properties are tuned by adjustment of the interdiffusion of the used liquids19,20,21,22. Thus, a plane-wave US-IRIS is capable of one-dimensional light manipulation and even focusing, where the position of the focal plane is tunable via the US pressure, controlled by the driving voltage. Moreover, US wave interference could be used to shape the US field as required as discussed further below.
Planar US-IRISs in clear water
To demonstrate US pressure-dependent light manipulation, two experimental arrangements are used for clear water (Fig. 2a) and scattering media (Fig. 2b), respectively. Hereafter control voltage refers to the function generator output (see “Methods”). Investigation of the US effects on light propagation is first performed in clear water with plane US waves, with a transmission experiment (Fig. 2a). A pulsed frequency-doubled Nd:YAG laser (532 nm, 5 ns pulse width) is used as a light source, and a planar UST is driven at its peak frequency with a 7-cycle sine burst (fa = 2.28 MHz). The US control voltage sweep is performed, while a gated camera is imaging the exit facet (z = 20 cm, xy plane) of the experimental volume to monitor the light intensity distribution behind the US-IRIS. The corresponding plane-wave pressure ppl is assessed using an end-calibrated hydrophone and is varied in the range up to about 33 kPa (see “Methods”). The cross-section of the respective US configuration is shown in Fig. 2c, d, and time delay adjustment is used to capture plane waves before they reach the reflector R2. Further US configurations used in the study are schematically shown in Fig. 2e, f and discussed further below. The subset of the acquired image sequence, illustrating the area, covered by a single cycle of the US wave is presented in Fig. 3a.
a Wide beam illumination and camera (CAM) detection employed in water-based experiments. b Long focal distance lens is used to aid light coupling-in into the ultrasound (US)-induced waveguide while fiber-based raster scanning acquisition of light intensity in the depth of Intralipid-based scattering phantoms is used for detection. c Cross-section of the experimental chamber, showing the placement of US reflectors R1 and R2, used to achieve required US configuration: d planar, e crossed, and f column-focused. Respective enlarged images show λa × λa region. UST ultrasound transducer, R1, R2 aluminum reflectors, CAM synchronized camera; MMF multimode fiber, LSA linear stage assembly for 3D raster scanning, PD photodetector. Exact time delays Δt are given by the separation of the UST and the light propagation volume and account for US wave propagation time.
a–c Light intensity distribution changes as the ultrasound (US) pressure is increased, as captured in a plane 16 cm behind the US-light interaction volume (at z = 20 cm), using respectively planar (a), crossed (b), and column-focused (c) ultrasound configurations, wide beam illumination and camera detection. Insets on the left show the schematic of the US configuration cross-section. d Focal plane light intensity distribution from c (Vpp = 0.08 V, pcf ≈ 9 kPa). e Focal plane light intensity distribution, obtained with the fiber-based probe and an external focusing lens, at the plane z = 2 cm, using Vpp = 0.7 V, pcf ≈ 80 kPa. Light transport medium: clear water, field-of-view corresponds to the single period of the US wave (fa = 2.28 MHz, λa × λa = 650 × 650 μm). Exact time delays Δt between US pulse and light pulse emission are Δt1 = Δt2 = 89.275 µs for planar (a), and crossed (b) US arrangements and adjacent US wave peaks and windowing are used for visualization. For the column-focused (c) arrangement, Δt3 = 96.735 µs. Individual panels are normalized before visualization; note that the light intensity distributions at Vpp = 0 correspond to the “US off” case.
It is notable that the maximum light intensity in the imaging plane changes along with voltage tuning, reaching the peak when the corresponding focal plane of the US-IRIS aligns with the imaging plane of the camera (highest light intensity in Fig. 3a, Vpp = 0.19 V, ppl ≈ 9 kPa). This observation is in accordance with light redistribution from the area of the clear aperture of the single period of the US-IRIS to its focal spot. Furthermore, the produced light intensity distribution is in agreement with the patterns produced by multimode interference19. Full dynamic illustration of the outcomes of the US pressure tuning through the control voltage sweep is presented in Supplementary Fig. 1a and in Supplementary Movie 1.
Thus, a single period of a transversal plane-wave (1D) US-IRIS can manipulate the light propagation and acts similarly to a pressure-tunable cylindrical lens. Accordingly, when a wide beam illuminates multiple periods of the US-IRIS, multiple focal lines are produced. Then, the line spacing is determined by the acoustic wavelength of the applied US in the medium λa, and the US-IRIS operation in the low-pressure regime is similar to that of a cylindrical microlens array, as illustrated in Fig. 2a.
Wave interference for US-IRIS shaping in clear water
After confirming one-dimensional light focusing by the planar US-IRIS, we now proceed with two-dimensional manipulation and focusing. Generally, it is possible to use the interference of two or more US waves to create more complex pressure profiles33 and corresponding refractive index distributions. Two simple US field configurations of practical interest are crossed and column-focused arrangements.
When a perpendicular combination of two planar transducers or, even better, sophisticated transducer arrays are used, 2D focusing of the light beam can be achieved within each period of such a 2D US-IRIS. As such transducer arrays were not available for our experiment, we realized this US configuration with a single UST by introducing a metallic reflector R2 in the US beam in such a way that the incident and the reflected acoustic beams overlay34, and produce the required crossed arrangement as schematically shown in Fig. 2e. A pressure-tuning experiment, similar to the one described above with a planar US-IRIS, is then repeated.
The corresponding change of the light intensity distribution at the exit facet of the experimental volume (z = 20 cm) is shown in Fig. 3b. Again, the produced light intensity reaches the maximum when the focus of the 2D US-IRIS is aligned with the imaging plane of the camera (Vpp = 0.19 V). The appearing side lobes suggest a square aperture function, which agrees with the US configuration used. Similarly, a full dynamic illustration of the US pressure tuning impact in Fig. 3b is presented in Supplementary Fig. 1b and in Supplementary Movie 2.
Likewise, as in the case of planar US-IRIS described above, when a wide beam illumination is used over multiple US-IRIS periods, such a crossed US arrangement creates a 2D grid of focal points, spaced by the acoustic wavelength λa in both x and y directions, similar to a microlens array35.
To further increase the refractive index gradient induced by the US and the US-IRIS action on the propagating light, a focused US field could be employed. For instance, a cylindrical acoustic lens might be used to focus a planar US wave into a short-lived high-pressure column in a propagation volume. This is achieved experimentally, using a parabolic mirror as depicted in Fig. 2f. As a short US burst is used to drive the UST, only the reflected waves interact in this configuration, forming the required transient US field configuration transversally to the beam propagation direction.
The respective pressure-dependent light intensity distributions are presented in Fig. 3c and in full in Supplementary Fig. 1c, d and in Supplementary Movie 3. The intensity patterns obtained (Fig. 3c) indicate an elliptical cross-section of the so formed waveguide36, which is in accordance with the US pressure distribution near the focus of the acoustic cylindrical lens37,38. It is notable that in the column-focused US configuration, lower control voltage (Vpp = 0.08 V, Fig. 3c, d) is required to focus the light in the imaging plane of the camera. We use the ratio between the control voltages required in the planar and column focusing configuration to estimate the pressure multiplication factor β provided by the parabolic reflector R2. We estimate β = 2.4, so the maximum pressure used in our experiments is in the column-focused configuration about 80 kPa (pcf, see Methods).
So far, we have demonstrated that transient US waves, traveling transversally to the light beam transit direction, can manipulate its propagation in water. In clear water, this can even provide light focusing. The effect of the US waves on the light propagation depends on the applied US pressure and the US configuration. Accordingly, changing the applied US pressure will affect the refractive power of the US-IRIS and its light manipulation capabilities.
Consequently, increase of the applied voltage as compared to Fig. 3d shifts the focal plane to lower z-values. As a result, the light intensity distribution, captured in a distant observation plane behind the focal plane, is becoming quite complex and increasingly difficult to interpret, as the outputs of the adjacent periods of the US-IRIS mix. This mixing is illustrated in Supplementary Fig. 1 and Supplementary Movies 1–3. To be able to use higher control voltage and unambiguously probe the region of lower z-values inside the light–US interaction region (z < 4 cm), a fiber-based point detector is used to perform 3D raster scanning39. The change of the detection schematic is motivated by the challenges that the determination of the light distribution in the scattering phantoms with complex geometry presents. In homogeneous and axially layered samples, simulation methods40, or recently developed non-invasive techniques of light fluence assessment, are available41,42. However, the transversal structuring of the medium, induced by the US, extends beyond their current applicability and would thus induce ambiguities.
Therefore, to perform unambiguous high-resolution 3D mapping of light intensity in the depth of a bulk scattering sample, we utilized raster scanning of the volume-of-interest by a fiber-based point detector39. It has been shown recently that this is an unambiguous minimally invasive approach to locally assess the light intensity distribution inside the scattering medium with required resolution39 (see “Methods”).
This approach is verified in clear water. For an applied voltage Vpp = 0.7 V the focal plane appears at z = 2 cm, and the obtained data as shown in Fig. 3e resemble well the focal plane distribution from Fig. 3d and thus further confirm our fiber-based probing approach.
As a short single-frequency US burst does not experience phase front distortion during propagation in a homogeneous medium31, we could expect the US-induced refractive index distributions to be qualitatively reproduced in a homogeneous scattering medium. However, the light propagation in the scattering medium is drastically changed. Due to the strongly reduced directivity of the light propagation, light focusing by external lenses or by the US-IRIS becomes inefficient. Nevertheless, as we will show in the following, the US-IRIS still can act as a waveguide supporting light delivery deeper into tissue. Then, targeting US light waveguiding, a high-pressure column-focused US, created with the configuration shown in Fig. 2f, is preferred, as it provides stronger refractive index gradients and thus could offer better light confinement within the US-induced waveguide.
US light manipulation in scattering phantoms
To further study the effects of an US-IRIS on light propagation in scattering media, the experimental layout is adjusted accordingly. The light intensity in the presence of strong scattering is monitored with our fiber-based probe as described above (see “Methods”). Further, to significantly increase the fraction of the photons, which propagate through the high-pressure US column and thus through the US-IRIS, the beam expander is removed and replaced with a long focal distance coupling lens (LA1484, Thorlabs, focal length f = 30 cm, focal plane z = 0 cm) as depicted in Fig. 2b. This lens is mounted on a three-axis translation stage and its position is optimized while the detector signal is monitored in order to ensure optimum coupling into the US-induced waveguide (see “Methods”). Exemplary US on/off beam cross-section acquired in clear water is presented in Supplementary Fig. 2.
Scattering phantoms for the investigation are created by volume-guided dilution of Intralipid-20%. These are common liquid scattering phantoms for light transport studies, proven to be long-time stable and to provide inter-comparable results43,44.
Results on the US-IRIS effect on light propagation in phantoms with Intralipid-20% volume concentration (VC) of 1.0 and 1.5% are reported below. These IL concentrations correspond to lower boundary estimated reduced scattering coefficients \(\mu _{\mathrm{s}}^\prime\) of 3 and 4.5 cm−1 for the 532 nm light used in the experiment. Then, assuming the scattering anisotropy factor of IL g = 0.9 (refs. 25,26), the optical thickness τ of the phantoms could be calculated as \(\tau = 10 \times \mu _{\mathrm{s}}^\prime \times z\), where the acquisition depth z (sample thickness) is measured from the boundary of the scattering phantom (see z = 0 in Fig. 2a, b). The optical thickness is then expressed in units of the mean free path (MFP), the average distance a photon could travel in the medium before the first scattering event is happening.
To illustrate the effects of the US field presence on the light propagation in the scattering medium, we further acquire via the mentioned raster scanning procedure pairwise datasets for each phantom investigated: with US burst present in the light propagation domain (“US on”) and with US beam being disabled (“US off”) as a reference measurement of the local light intensity. We then pointwise calculate the ratio of maximum light intensity in both cases (κ = max(Ion)/max(Ioff)) to identify, quantify, and analyze the effects of US-IRIS on light transport (see “Methods”).
First, the ratio of the maximum intensities κ in the light beam cross-section is investigated. Since the phase front of the US field is preserved well in low concentration water-based Intralipid-20% dilutions45, we expect the shape of the induced refractive index pattern in the beam cross-sectional plane to be maintained. The US attenuation, which could take place in the phantom, will only affect the magnitude of the refractive index modulation, and could be accounted for by adjusting the control voltage accordingly (see “Methods”).
The US on/off maximum light intensity acquisitions and their ratios (κ) for the mentioned phantom media with estimated reduced scattering coefficients \(\mu _{\mathrm{s}}^\prime\) of 3 and 4.5 cm−1 are presented in Fig. 4a–f. While no traces of external light focusing is present in reference acquisitions (Fig. 4b, e), US-IRIS provides prominent maximum light intensity increase in both cases, as visible directly from the acquisition data (Fig. 4a, d, respectively) and the US on/off maximum intensity ratio κ, presented in Fig. 4c, f accordingly. The imaging depth z = 2 cm corresponds then to optical thicknesses τ of 60 and 90 MFP, respectively. The expected similarity of the pattern in Figs. 4c to 3d–e is notable, while only the central part of the pattern is preserved in the case of higher scattering shown in Fig. 4f. These results confirm that the US pressure distribution and its effect on guiding the light are preserved up to the added amount of scatterers, and the mechanism of US-IRIS formation is not altered.
a–c In Intralipid-20% phantom with lower boundary estimated reduced scattering coefficient \(\mu _{\mathrm{s}}^\prime\) of 3.0 cm−1 over the beam cross-section at the depth z = 2 cm (optical thickness τ of 60 MFP), a maximum light intensity distribution in “US on” case, b reference maximum light intensity distribution, c maximum light intensity ratio κ (a/b). d–f In Intralipid-20% phantom with lower boundary estimated reduced scattering coefficient \(\mu _{\mathrm{s}}^\prime\) of 4.5 cm−1 over the beam cross-section at the depth z = 2 cm (optical thickness τ of 90 MFP), d maximum light intensity distribution in “US on” case, e reference maximum light intensity distribution, f maximum light intensity ratio κ (d/e). Panels a, b and d, e are sharing the colormaps. Control voltage used in a, d Vpp = 0.7 V, pcf ≈ 80 kPa, US frequency of fa = 2.09 MHz, λa = 710 µm. Note z = 2 cm is located within the light–ultrasound interaction volume. All images are acquired using a fiber-based point detector, and configuration with an external focusing lens, their field-of-view is 400 × 400 μm. Scan step size is 50 µm, and the scale bar shown in b is 50 µm and is valid for all panels. The dashed line in f shows the longitudinal cross-sectional direction.
The increasing light scattering leaves only a small core region, where the maximum light intensity is increased in the strongest scattering case studied (Fig. 4f). This result confirms that the area of a higher light intensity is restricted in the beam cross-sectional plane. Thus, the ability of the US-IRIS to locally increase the available light intensity in scattering medium is proved.
Deep light waveguiding by US-IRIS
Finally, to prove the waveguiding capabilities of the transient US-IRIS, the transversal confinement of the light propagation within the waveguide has to be confirmed. Therefore, it is necessary to evaluate the longitudinal light intensity distribution, following the US-IRIS axis.
Figure 5a shows the behavior of the US on/off maximum light intensity, and Fig. 5b shows the maximum intensity ratio κ over the longitudinal cross-section in the direction of the light propagation and column-focused US-IRIS extent (waveguide region from 0 to 2 cm on the z-axis in Fig. 2, scan region z = 1.5…2 cm). The central part of both panels features a prominent higher light intensity area, corresponding to the waveguide axis. This longitudinal intensity increase confirms the lateral restriction of the light propagation within the waveguide core, therefore proving the waveguiding capabilities of the US-IRIS in the scattering medium. The corresponding US on/off maximum light intensity comparison in the axial beam cross-sections at the beginning and at the end of the scanned region is presented in Supplementary Fig. 3. Figure 5a, b demonstrates a 4.9–12.3% light intensity increase achieved by the waveguiding as compared to the reference case.
a Longitudinal sections (yz plane) of the maximum light intensity in the direction of light propagation in the case of the ultrasound waveguiding (asterisks) and reference case (dots), as captured with the fiber-based probe (see “Methods”). b Maximum intensity ratio κ for the data shown in a, demonstrating maximum light intensity increase in the waveguide core region, confirming transverse light confinement. c Line scans performed for the waveguiding case (asterisks) and reference case (dots) at the end of the scanned region in the plane z = 2 cm, corresponding to optical thickness of 90 MFP. Mean values over Nacq = 100 acquisitions per scan point and shaded 95% confidence intervals are shown, demonstrating that the US on/off signals are clearly separated even in the most extreme condition studied.
To further illustrate significant separation of US on/off cases, Fig. 5c reports the data on the registered intensity variability, demonstrating mean maximum intensity values, obtained averaging 100 acquisitions per scanning point at z = 2 cm as well as shaded 95% confidence intervals. Clearly, the “US on” and “US off” cases are separated well even in the most extreme condition studied. This data further demonstrate the relation of the light intensity within the waveguide core to the diffused light background. We attribute the variation of the maximum intensity ratio values κ at z = 2 cm in the consecutive scans in Figs. 4f and 5b, c to pulse-to-pulse variations and the dynamic character of the induced waveguides.
As following from Figs. 4 and 5, a column-focused US-IRIS provides 2D localized point light delivery and supports light waveguiding up to the depth of at least 90 MFPs in a scattering phantom with lower boundary estimated \(\mu _{\mathrm{s}}^\prime\) ≈ 4.5 cm−1 for a laser wavelength of 532 nm. To this extent, these results demonstrate transient US-induced waveguide support by small US pressures of about 80 kPa (pcf) and to the farthest depth reported. It should be noted that by using appropriate transducer arrays for US-IRIS generation, there is no need to enclose the light propagation volume, and this flexibility enables to apply our approach in vivo and non-invasively. As the recent results suggest38, the depth, at which the US-induced waveguiding effects could be detected, can be significantly improved upon further improvement of employed filtering.
Discussion
We confirm both 2D light concentration and waveguiding into depths of 2 cm (90 MFP) in scattering phantoms with estimated reduced scattering coefficient up to \(\mu _{\mathrm{s}}^\prime\) ≈ 4.5 cm−1 by transversally traveling US waves with pressures of about 80 kPa (pcf). The maximum level of \(\mu _{\mathrm{s}}^\prime\) that we have tested experimentally approaches the range of that of weakly scattering real tissue parameters4,5,30. Of course, the in vivo usage of the concept proposed in even stronger scattering tissues introduces challenges, and higher US pressure than used in our proof of principle studies may be required to deal with it. Thus, in the following, the associated technical and biosafety aspects are briefly addressed.
First and foremost, the application of high-pressure US to biological tissues could lead to various acoustic and biomechanical effects, including cavitation, dependent on peak rarefactional (peak negative) pressure, and thermal and mechanical load on the tissue, dependent on the insonification parameters, primarily US amplitude and duty cycle31,46. We performed the US-light manipulation experiments with US fields at fa = 2.09 and 2.28 MHz using peak pressures of about 80 kPa (pcf, pressure measurements and estimates are detailed in “Methods”). This maximum pressure level is fivefold below the lower boundary of pressures used in clinical B-mode US of 0.54 MPa, considered safe31. Therefore, for in vivo applications in stronger scattering real tissue, the applied US amplitude could be increased by an order of magnitude without exceeding the safety limits. To realize this in practice, the driving voltage could be increased, optimized excitation signals can be employed, and US delivery and focusing could be significantly improved. These considerations outline strategies to address stronger light scattering and US attenuation in the tissues.
Our proof of concept is based on experiments in homogeneous scattering phantoms. However, in vivo application scenarios certainly require strategies to manage tissue heterogeneity. The most detrimental effect of tissue heterogeneity is the US phase front distortion due to variable US propagation speed in heterogeneous areas. This is a known problem in the reconstruction of PA computed tomography images. It has been shown that this challenge can be addressed well by acquisition of precise maps of speed of sound, using joined PA and US measurements47. As TULW is intrinsically PA/US compatible, such maps could be recorded and fed back to adapt the US phase fronts to the tissue heterogeneity.
Our proposed TULW/transient US-IRIS concept is related to similar approaches by Chamanzar and co-workers25,26,27 and Ishijima et al.28, where light waveguiding by transversal US application has been achieved by using either a cylinder-shaped UST array (radius 19 mm, height 30 mm)25 or a cylindrical absorber for generation of nonlinear PA waves (maximum sample size ~3 × 10 mm)28. In both cases, the sample size is restricted in both directions. Moreover, the US-induced light shaping is restricted by the US modes available within the cylinder’s cross-section.
In contrast to these approaches, our concept with transient US waves traveling transversally to the light propagation direction reduces the geometrical limitations. In our experimental realization, a simple reflector is used to provide the required spatial and temporal US pressure distribution in the light propagation domain. The use of state-of-the-art US beamforming methods, such as acoustic lenses or phased arrays, would further provide greater control of the US profile and its optical effects. Hence, the properties of the US-IRISs and TULW are fundamentally limited only by US propagation losses, whereby US attenuation could be corrected by an adjustment of the driving signals, and tissue heterogeneity could be addressed as described above. The presented method is readily available to samples where side access is possible to achieve the required transversal US field configuration. An extension of the method for single-sided access geometry is not straightforward but may be possible by development of effective transducer arrangements. The direct translation of the method requires an axially extended uniform positive instantaneous pressure region and provides a difficult challenge. However, utilizing annular arrays with coaxial opening48 and US Bessel beams49, an on-axis series of two-dimensional gradient refractive index medium lenses might be induced, that are potentially capable of light waveguiding or even relay imaging27. We suggest to investigate such arrangements further for possible in vivo applications with single-sided access.
In summary, we present optical waveguiding by transient transversally traveling US into deeper regions of scattering media. The concept has no geometrical constraints and could be straight forwardly transferred into non-invasive in vivo applications on scattering biomedical tissue. The high adaptability of our transient US-IRIS and TULW concepts might further benefit from the combination with PA/AO-LWS13,14,15,50 that could provide additional opportunities to increase light intensity in-depth.
It is important to note that the mechanisms used in our approach are not relying on light coherence51. While previously considered too weak for experiment51,52,53,54,55, this particular type of light–US interaction is regaining interest25,26,27,28,38,56,57,58 and our approach presents a different viewpoint to enrich the understanding of the complex processes involved. Complete uncovering the mechanism of the waveguiding at low pressures requires further investigation and the development of an appropriate theoretical model.
To conclude, by presenting and examining the US-IRIS and TULW, we show a proof of the concept and its applicability towards real tissues. We showed isolated light guiding observation with little to no beam pre-shaping. We have successfully demonstrated its applicability up to depths of 2 cm (90 MFP) in scattering medium with an estimated reduced scattering coefficient of \(\mu _{\mathrm{s}}^\prime\) ≈ 4.5 cm−1 and an incident laser wavelength of 532 nm using column-focused US pressures pcf of about 80 kPa.
Methods
Experimental arrangements
An extra-cavity frequency-doubled Q-switched Nd:YAG laser is used as a light source (Minilite II, Continuum, pulse width 5 ns, repetition rate 14 Hz, wavelength of 532 nm). In the experiments with wide field-of-view (Fig. 3), the light beam is expanded with a 10× beam expander (BE10M-B, Thorlabs), while for the experiments with scattering phantoms (Figs. 4b, c and 5), a low numerical aperture (NA) focusing lens is used (LA1484, focal length f = 30 cm, Thorlabs) to aid coupling-in. The NA of the lens is estimated as 0.0050 while NA of the US-induced waveguide (Vpp = 0.7 V, pcf ≈ 80 kPa) is in the range of 0.0072–0.0080. The lens focuses the light in the entrance plane of the US-induced waveguide at z = 0, and is mounted on a three-axis mechanical translation stage to optimize the position while the detector signal is monitored. The light is propagating through the frontal and main chambers of a tri-section 3-mm-thick float glass container.
To create planar, crossed, and column-focus US-IRISs adjacent to the entrance facet of the transport medium in the main chamber, aluminum reflectors (R1, R2, Fig. 2) are used to fold and profile the US beam. A planar single element UST (model A395S-SU, Olympus Panametrics-NDT, element diameter 38 mm) is placed in the auxiliary (Aux) chamber facing downwards. The UST, emitting in +x direction, is offset in −z direction against the boundary between the frontal and the main chambers, a planar reflector R1 is redirecting the US beam into the main chamber, and a parabolic US reflector R2 is used to produce a crossed or column-focused US field as required (Fig. 2c). Note all three discussed US configurations could be created using a parabolic US reflector and respective delay time adjustment as shown in Fig. 2d–f. All reflectors are placed in such a way that the normal to their surface is perpendicular to the light propagation direction. In this way, the required US beam profile is created in the plane transversal to the light propagation.
The UST is excited at its peak frequency (fa), which was 2.28 MHz for experiments with clear water and 2.09 MHz for experiments in scattering media. This difference is due to variation of properties of different transducers of the same type. The UST is driven with a seven-cycle sine burst using a combination of a waveform generator (K3390, Keithley) and a linear 55 dB RF amplifier (A150, ENI), while a delay generator (DG535, Stanford Research Systems) ensures synchronization between the system components. Usage of short US bursts prevents standing wave formation and reduces the acoustic load onto the sample. The waveform generator peak-to-peak voltages are reported in the text as control voltages Vpp. After amplification, the driving voltage applied to the transducer is the control voltage Vpp, multiplied by the gain factor of about 540.
In water-based experiments (Figs. 2a and 3), the frontal and main chambers are filled with purified water, while the light intensity distribution at the rear wall of the main chamber is picked up with an inline gated camera (CAM, 1300 Solar, PCO), and a set of neutral density filters is used to avoid saturation.
In scattering phantom experiments (Figs. 2b, 4 and 5), the main chamber is filled with volume-guided Intralipid-20% dilutions (see “Scattering phantoms” and Supplementary Table 1), while the frontal chamber is kept empty. To perform high-resolution 3D raster scanning of the light intensity distribution inside the scattering phantom, a fiber-based probe is used. The probe is a cleaved GIF625 fiber (Thorlabs), the distal end of which is affixed in a metallic needle (MS110, Thorlabs), connected to a linear stage assembly (LSA, a combination of linear stages M-403.42S, M-405.2S, M-403.82S, Physik Instrumente)39. The light picked up by the fiber probe in the medium is guided towards a fast photodetector (PD10A/M, Thorlabs), while another fast photodetector (DET210, Thorlabs) is used to monitor pulse-to-pulse variations. Both signals are fed to a digital sampling oscilloscope (DSO, WaveSurfer 104Mx, LeCroy, 5 GHz sampling frequency). The data acquired with fiber probe are used to produce Figs. 4 and 5.
Given the applied US frequency fa of 2.09 MHz and the speed of sound va of 1482 ms−1 (ref. 31), the acoustic wavelength λa is estimated to be 710 µm. Therefore, for the 62.5 µm fiber core, the detector area is well below the US wavelength, and a fiber is used as point detector to obtain the 3D light intensity distribution within the US-IRIS39. Through the measurement design, the fiber probe is sampling the light intensity at a plane behind a given US–light interaction volume. No effects of the fiber probe presence in the waveguiding region on the US propagation were observed. We anticipate that distortions of the US wave in the vicinity of the fiber probe due to its finite size are negligible due to their de-magnification in the column-focused US configuration (Figs. 4 and 5). As such distortions could only have a negative impact on the induced US field and the corresponding measured light distribution, a better light confinement and higher maximum light intensity ratios κ shall be achieved in the absence of a fiber probe. System operation control, data acquisition, processing, and analysis are performed using a PC running MATLAB (Mathworks).
Scattering phantoms
Volume-guided dilutions of Intralipid-20% (IL, I141, Sigma-Aldrich) are used as phantom media. A calculated volume of IL is mixed with purified water with the aid of a magnetic stirrer to obtain a dilution of required volume and estimated reduced scattering coefficient \(\mu _{\mathrm{s}}^\prime\). The parameters of the IL dilutions used in the experiments are listed in Supplementary Table 1.
Lower boundary estimates of the reduced scattering coefficients of the IL dilutions provided in Supplementary Table 1 are based on the available literature data on IL intrinsic optical properties43,44,59,60 and a linear dependence of the reduced scattering coefficient \(\mu _{\mathrm{s}}^\prime\) of a dilution on the IL VC43: \(\mu _{\mathrm{s}}^\prime = {\mathrm{VC}} \, \times \, \mu _{{\mathrm{sIL}}}^\prime\). The used value \(\mu _{{\mathrm{sIL}}}^\prime\) ≈ 300 cm−1 is the reduced scattering coefficient attributed to Intralipid-20%, measured at a laser wavelength of 543 nm59, which is sufficiently close to the wavelength of 532 nm used in our experiments. Such estimation ignores the effects of dependent scattering43,59,61 on scattering strength, and based on the spectral dependency of \(\mu _{{\mathrm{sIL}}}^\prime\) and available near-infrared measurements43,60, real values of the reduced scattering coefficient of the IL dilutions used are expected to be within a factor of 1 to 1.5 higher than the values presented in Supplementary Table 1.
Data acquisition and processing
Ensemble averaging of raw signals is used to decrease the effects of fluctuations and noise for both camera and fiber-based experiments.
In water-based experiments (Fig. 3a–d), Nacq = 30 camera images are recorded and averaged for each UST control voltage level Vpp, proportional to the US peak pressure level p. A subset of the frames is used for Fig. 3a–d, while the full data are included in Supplementary Movies 1–3. Supplementary Figure 1 demonstrates an alternative cross-section of the full dataset in the y–Vpp plane. For the fiber-based detector data in Fig. 3e, Nacq = 14 pulses per raster scanning point are ensemble averaged at the DSO and stored, and the temporal peak values of the averaged traces (max(I)) are extracted.
Pairs of raster scanning acquisitions with fiber-based probe are further employed to produce the US on/off comparisons. For Figs. 4 and 5a, b, Nacq = 98 acquisitions for each raster scanning point are used to adapt to significantly decreased signal intensities. First, the maximum light intensity distribution is acquired with the US burst synchronized to the respective position in the volume of interest (“US on,” max(Ion)). Second, the waveform generator driving the US transducer is disabled and the acquisition process is repeated (“US off,” max(Ioff)), and the data processed in the same way. Finally, point-by-point ratios of respective US on/off acquisitions κ = max(Ion)/max(Ioff) are computed and displayed.
To ensure that US on/off maximum intensity values are significantly separated, additional Nacq = 100 sequential single trace acquisitions per raster scanning point are obtained in a line scan at the end of the measurement region, marked by a dashed line in Fig. 5b. Then, the respective temporal peak values max(I) are extracted to calculate mean values and 95% confidence intervals, which are presented in Fig. 5c.
The reference photodetector data were monitored to ensure that the respective US on/off acquisition pairs are obtained under comparable conditions. No incongruence of the incident light intensity was identified within any of the acquisition pairs.
Hydrophone measurements and pressure multiplication factor
As the direct measurement of US pressure within the waveguiding region without its distortion is not available, a two-step process is used to estimate it.
First, hydrophone measurements are performed with fa = 2.09 MHz in a plane-wave configuration, using an end-cable calibrated system of a 1-mm needle PVDF hydrophone (PA1272, frequency band 0.1–20 MHz) with preamplifier (PA07084) and coupler (DC2/686, all Precision Acoustics). The hydrophone is placed on the height of the laser beam consecutively in the main and auxiliary chamber along with a planar aluminum reflector, similar to R1 above, used to fold the US beam to ensure its perpendicular incidence onto the hydrophone membrane in the y–z plane. The hydrophone output is recorded using the same DSO as described above and ensemble averaging of Nacq = 100 acquisitions is performed. In this way, the linearity of the transducer output against the input waveform is assured, and the pressure levels in the main and auxiliary chamber are quantified. Through the ratio between the peak negative plane-wave US pressure ppl at Vpp = 0.7 V in the main (<33 kPa) and auxiliary (160 kPa) chambers, a chamber wall transmission coefficient of 20% is estimated, in agreement with the literature62. As the water-soft tissue boundary provides lower US losses31,63, a fivefold increase of US amplitude could be provided by better US delivery. Assuming an upper limit of 20% measurement uncertainty, the maximum plane-wave pressure ppl in the main chamber is certainly below 40 kPa.
Second, for the column-focused US configuration, a pressure enhancement by the parabolic reflector R2 (Fig. 2c) may be expected. However, we cannot directly measure the corresponding pressure enhancement factor β with a hydrophone. Therefore, β is derived from the camera-based data (Fig. 3a/c) as following. In general, the refractive power of the US-IRIS is proportional to the US pressure24,25, and the US pressure is proportional to the control voltage level Vpp. For a certain beam profile, the refractive power of the US-IRIS required to achieve beam focusing in the camera imaging plane is independent on the US configuration and thus equal for plane wave and column-focused configurations. Thus, we determine the respective control voltages Vpp required for beam focusing in the imaging plane for the column-focused (Vpp = 0.08 V) and plane-wave configurations (Vpp = 0.19 V). The ratio of the determined control voltages provides then the pressure gain β. For the parabolic configuration (Fig. 2f), we achieve β = 2.4, compared to the plane-wave case (Fig. 2d). Therefore, the maximum peak negative pressure in the main chamber used in our experiment is in column-focused configuration and is about 33 kPa × 2.4 = 80 kPa (pcf). Again assuming an upper limit of 20% measurement uncertainty, the maximum pressure in the main chamber in parabolic reflector configuration is certainly below 96 kPa.
US safety concerns
In the US dosimetry, two criteria are employed to ensure safe biomedical application of the US: the peak negative (peak rarefactional) pressure and the spatial-peak temporal average intensity ISPTA. From the hydrophone measurements of the plane-wave pressure and our estimate of the pressure multiplication factor β above, we conclude that the maximum peak rarefactional pressure in our experiments does not exceed 96 kPa. This pressure level is fivefold below the lower boundary of the range of widely used B-mode diagnostic US, where for the frequency range 1–15 MHz, a peak rarefactional pressure range from 0.54 to 5.4 MPa is considered safe31.
Second US dosimetry parameter, spatial-peak temporal average intensity ISPTA, could be evaluated based on the above considerations of the peak rarefactional pressure. As our method relies on transient US waves, the same tissue volume only has to be exposed to the US wave during its propagation, and ISPTA could be kept low by a low duty cycle. For the conditions of our experiments in scattering phantoms, with a seven-cycle 2.09 MHz sine burst at 14 Hz repetition rate and the maximum peak rarefactional pressure of 96 kPa, the spatial-peak temporal average intensity value ISPTA = 0.014 mW cm−2 is orders of magnitude below the allowed maximum value of 720 mW cm−2 (refs. 31,46,64).
Therefore, with respect to both peak rarefactional pressure and spatial-peak temporal average US intensity ISPTA, transient US-IRIS and TULW possess a large headroom for increasing the pressure within safe US margins31.
Data availability
The data supporting the study is available from the corresponding author upon reasonable request.
Code availability
The code supporting the study is available from the corresponding author upon reasonable request.
References
Baker, M. Whole-animal imaging: the whole picture. Nature 463, 977–980 (2010).
Ntziachristos, V. Going deeper than microscopy: the optical imaging frontier in biology. Nat. Methods 7, 603–614 (2010).
Park, S. et al. One-step optogenetics with multifunctional flexible polymer fibers. Nat. Neurosci. 20, 612–619 (2017).
Sandell, J. L. & Zhu, T. C. A review of in-vivo optical properties of human tissues and its impact on PDT. J. Biophotonics 4, 773–787 (2011).
Jacques, S. L. Optical properties of biological tissues: a review. Phys. Med. Biol. 58, R37–R61 (2013).
Haisch, C. Optical tomography. Annu. Rev. Anal. Chem. 5, 57–77 (2012).
Simandoux, O. et al. Optical-resolution photoacoustic imaging through thick tissue with a thin capillary as a dual optical-in acoustic-out waveguide. Appl. Phys. Lett. 106, 094102 (2015).
Tuchin, V. V. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis, 2nd edn (SPIE Press, 2007).
Genina, E. A., Bashkatov, A. N. & Tuchin, V. V. Tissue optical immersion clearing. Expert Rev. Med. Devices 7, 825–842 (2010).
Chan, E. K. et al. Effects of compression on soft tissue optical properties. IEEE J. Sel. Top. Quantum Electron. 2, 943–950 (1996).
Vellekoop, I. M. & Mosk, A. P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 32, 2309–2311 (2007).
Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photonics 6, 283–292 (2012).
Xu, X., Liu, H. & Wang, L. V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat. Photonics 5, 154–157 (2011).
Chaigne, T. et al. Controlling light in scattering media non-invasively using the photoacoustic transmission matrix. Nat. Photonics 8, 58–64 (2014).
Lai, P., Wang, L. V. L., Tay, J. W. & Wang, L. V. L. Photoacoustically guided wavefront shaping for enhanced optical focusing in scattering media. Nat. Photonics 9, 126–132 (2015).
Gross, H. Gradient-index Lenses in Handbook of Optical Systems, Volume 1: Fundamentals of Technical Optics (ed. Gross, H.) 705–714 (Wiley-VCH Verlag GmbH & Co. KGaA, 2005).
Gross, H., Zügge, H., Peschka, M. & Blechinger, F. Gradient Index Media in Handbook of Optical Systems, Volume 3: Aberration Theory and Correction of Optical Systems (ed. Gross, H.) 463–495 (Wiley-VCH Verlag GmbH & Co. KGaA, 2007).
Greisukh, G. I., Bobrov, S. T. & Stepanov, S. A. Introduction to Theory of Gradient-Index Elements in Optics of Diffractive and Gradient-index Elements and Systems 36–54 (SPIE Optical Engineering Press, 1997).
Yang, Y. et al. Optofluidic waveguide as a transformation optics device for lightwave bending and manipulation. Nat. Commun. 3, 651 (2012).
Shi, Y., Liang, L., Zhu, X. Q., Zhang, X. M. & Yang, Y. Tunable self-imaging effect using hybrid optofluidic waveguides. Lab Chip 15, 4398–4403 (2015).
Wolfe, D. B. et al. Dynamic control of liquid-core/liquid-cladding optical waveguides. Proc. Natl Acad. Sci. USA 101, 12434–12438 (2004).
Liu, H. L., Zhu, X. Q., Liang, L., Zhang, X. M. & Yang, Y. Tunable transformation optical waveguide bends in liquid. Optica 4, 839–846 (2017).
Pitts, T. A. & Greenleaf, J. F. Three-dimensional optical measurement of instantaneous pressure. J. Acoust. Soc. Am. 108, 2873–2883 (2000).
Pitts, T. A., Sagers, A. & Greenleaf, J. F. Optical phase contrast measurement of ultrasonic fields. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 48, 1686–1694 (2001).
Chamanzar, M. et al. Ultrasonic sculpting of virtual optical waveguides in tissue. Nat. Commun. 10, 92 (2019).
Karimi, Y., Scopelliti, M. G., Do, N., Alam, M.-R. & Chamanzar, M. In situ 3D reconfigurable ultrasonically sculpted optical beam paths. Opt. Express 27, 7249–7265 (2019).
Scopelliti, M. G. & Chamanzar, M. Ultrasonically sculpted virtual relay lens for in situ microimaging. Light Sci. Appl. 8, 65 (2019).
Ishijima, A. et al. Nonlinear photoacoustic waves for light guiding to deep tissue sites. Opt. Lett. 44, 3006–3009 (2019).
Cherkashin, M. N., Brenner, C., Schmitz, G. & Hofmann, M. R. Transient light waveguides deep into scattering media by transversal ultrasound. In Biophotonics Congress: Biomedical Optics 2020 (Translational, Microscopy, OCT, OTS, BRAIN). JTh2A.15 (OSA, 2020).
Bashkatov, A. N., Genina, E. A. & Tuchin, V. V. Optical properties of skin, subcutaneous, and muscle tissues: a review. J. Innov. Opt. Health Sci. 04, 9–38 (2011).
Szabo, T. L. Diagnostic Ultrasound Imaging: Inside Out 2nd edn (Academic Press, 2014).
Pitts, T. A., Kinnick, R. R. & Greenleaf, J. F. Optical measurement of wideband ultrasound fields via Gabor holography. In 1997 IEEE Ultrasonics Symposium Proceedings. An International Symposium Vol. 1, 761–764 (IEEE, 1997).
Melde, K., Mark, A. G., Qiu, T. & Fischer, P. Holograms for acoustics. Nature 537, 518–522 (2016).
Malkin, R., Todd, T. & Robert, D. Quantitative imaging of acoustic reflection and interference. J. Phys. Conf. Ser. 581, 012007 (2015).
Dörband, B., Müller, H. & Gross, H. Hartmann-Shack Sensor in Handbook of Optical Systems, Volume 5: Metrology of Optical Components and Systems (ed. Gross, H.) 183–208 (Wiley-VCH Verlag GmbH & Co. KGaA, 2012).
Kapany, N. S. & Burke, J. J. Waveguide Mode Launching in Optical Waveguides 159–179 (Academic Press, 1972).
Zemp, R. J., Abbey, C. K. & Insana, M. F. Linear system models for ultrasonic imaging: application to signal statistics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 50, 642–654 (2003).
Bengtsson, A. et al. Characterization and modeling of acousto-optic signal strengths in highly scattering media. Biomed. Opt. Express 10, 5565–5584 (2019).
Cherkashin, M. N., Brenner, C. & Hofmann, M. R. High-resolution 3D light fluence mapping for heterogeneous scattering media by localized sampling. Appl. Opt. 57, 10441–10448 (2018).
Wang, L., Jacques, S. L. & Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Prog. Biomed. 47, 131–146 (1995).
Hussain, A., Daoudi, K., Hondebrink, E. & Steenbergen, W. Mapping optical fluence variations in highly scattering media by measuring ultrasonically modulated backscattered light. J. Biomed. Opt. 19, 66002 (2014).
Schreurs, T. J. L. et al. Noninvasive fluence rate mapping in living tissues using magnetic resonance thermometry. J. Biomed. Opt. 22, 036001 (2017).
Di Ninni, P., Martelli, F. & Zaccanti, G. Effect of dependent scattering on the optical properties of intralipid tissue phantoms. Biomed. Opt. Express 2, 2265–2278 (2011).
Spinelli, L. et al. Determination of reference values for optical properties of liquid phantoms based on Intralipid and India ink. Biomed. Opt. Express 5, 2037–2053 (2014).
Cook, J. R., Bouchard, R. R. & Emelianov, S. Y. Tissue-mimicking phantoms for photoacoustic and ultrasonic imaging. Biomed. Opt. Express 2, 3193–3206 (2011).
Shaw, A. & Martin, K. The acoustic output of diagnostic ultrasound scanners in The Safe Use of Ultrasound in Medical Diagnosis 3rd edn (ed. Ter Haar, G. R.) 18–45 (The British Institute of Radiology, 2012).
Matthews, T. P. & Anastasio, M. A. Joint reconstruction of the sound speed and initial pressure distributions for ultrasound computed tomography and photoacoustic computed tomography. In Medical Imaging 2017: Ultrasonic Imaging and Tomography (eds. Duric, N. & Heyde, B.) 101390B (SPIE, 2017).
Filoux, E., Sampathkumar, A., Chitnis, P. V., Aristizábal, O. & Ketterling, J. A. High-frequency annular array with coaxial illumination for dual-modality ultrasonic and photoacoustic imaging. Rev. Sci. Instrum. 84, 053705 (2013).
Jiménez-Gambín, S., Jiménez, N., Benlloch, J. M. & Camarena, F. Generating Bessel beams with broad depth-of-field by using phase-only acoustic holograms. Sci. Rep. 9, 20104 (2019).
Tay, J. W., Lai, P., Suzuki, Y. & Wang, L. V. Ultrasonically encoded wavefront shaping for focusing into random media. Sci. Rep. 4, 3918 (2015).
Wang, L. V. Mechanisms of ultrasonic modulation of multiply scattered coherent light: an analytic model. Phys. Rev. Lett. 87, 43903 (2001).
Wang, L. V. Ultrasound-mediated biophotonic imaging: a review of acousto-optical tomography and photo-acoustic tomography. Dis. Markers 19, 123–138 (2004).
Elson, D. S., Li, R., Dunsby, C., Eckersley, R. & Tang, M.-X. Ultrasound-mediated optical tomography: a review of current methods. Interface Focus 1, 632–648 (2011).
Resink, S. G. State-of-the art of acousto-optic sensing and imaging of turbid media. J. Biomed. Opt. 17, 040901 (2012).
Gunther, J. & Andersson-Engels, S. Review of current methods of acousto-optical tomography for biomedical applications. Front. Optoelectron 10, 211–238 (2017).
Kobayashi, M., Mizumoto, T., Shibuya, Y., Enomoto, M. & Takeda, M. Fluorescence tomography in turbid media based on acousto-optic modulation imaging. Appl. Phys. Lett. 89, 181102 (2006).
Resink, S. G., Hondebrink, E. & Steenbergen, W. Towards acousto-optic tissue imaging with nanosecond laser pulses. Opt. Express 22, 3564–3571 (2014).
Jarrett, C. W., Caskey, C. F. & Gore, J. C. Detection of a novel mechanism of acousto-optic modulation of incoherent light. PLoS ONE 9, e104268 (2014).
Michels, R., Foschum, F. & Kienle, A. Optical properties of fat emulsions. Opt. Express 16, 5907–5925 (2008).
Di Ninni, P., Bérubé-Lauzière, Y., Mercatelli, L., Sani, E. & Martelli, F. Fat emulsions as diffusive reference standards for tissue simulating phantoms? Appl. Opt. 51, 7176–7182 (2012).
Raju, M. & Unni, S. N. Concentration-dependent correlated scattering properties of intralipid 20% dilutions. Appl. Opt. 56, 1157–1166 (2017).
Viennet, R., Hihn, J.-Y., Jeannot, M. & Berriet, R. Study of ultrasound transmission through an immersed glass plate in view of sonochemical reactor design optimisation. Adv. Acoust. Vib. 2009, 1–9 (2009).
Selfridge, A. R. Approximate material properties in isotropic materials. IEEE Trans. Sonics Ultrason. 32, 381–394 (1985).
Nelson, T. R., Fowlkes, J. B., Abramowicz, J. S. & Church, C. C. Ultrasound biosafety considerations for the practicing sonographer and sonologist. J. Ultrasound Med. 28, 139–150 (2009).
Acknowledgements
The authors acknowledge the help of W. D. Putro through early stage of the project, support of N. Surkamp with CAD models and workshops with manufacturing of the parabolic mirror and the three-section experimental container, support of T. Kranemann and T. Ersepke with hydrophone measurements, discussions with H. Estrada and J. Guggenheim, and manuscript proofreading by C. Saraceno. This project was partly funded by EU FP7 People: Marie Curie Actions Programme, Award No. 317526 (OILTEBIA). Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
M.N.C. and M.R.H. conceived the idea. M.N.C. and C.B. designed the experiments and analyzed the data. M.N.C. performed the experimental work. G.S. supervised the ultrasound part of the work. M.R.H. performed general supervision of the project. M.N.C., C.B., and M.R.H. wrote the manuscript. All authors discussed the results and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cherkashin, M.N., Brenner, C., Schmitz, G. et al. Transversally travelling ultrasound for light guiding deep into scattering media. Commun Phys 3, 180 (2020). https://doi.org/10.1038/s42005-020-00443-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00443-w
This article is cited by
-
Enhanced light focusing inside scattering media with shaped ultrasound
Scientific Reports (2023)
-
Optimized virtual optical waveguides enhance light throughput in scattering media
Nature Communications (2023)
-
Reply to: The overwhelming role of ballistic photons in ultrasonically guided light through tissue
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.