Introduction

Optical frequency metrology requires the capability to measure optical frequencies with high precision and accuracy. A traditional approach to this kind of measurements is the combination of a narrow-linewidth continuous-wave (cw) laser probing a molecular transition at high resolution and a second stable laser acting as a frequency reference for the probe laser. Since their invention almost 20 years ago1, optical frequency combs have become the primary choice for the reference laser, as their discrete regularly spaced spectrum ensures at once repeatability and calibration of the frequency axis of the probe laser to a primary time reference.

The lack of continuously tunable single-mode lasers in the region from 13 to 20 μm2 (770–500 cm−1) has been a stumbling block for optical metrology and high-resolution spectroscopy in the region of vibrational bending modes3, which offers intense and unique spectroscopic fingerprints of a large variety of molecules, including volatile organic compounds of environmental4, biomedical5 and astrophysical interest6. Cryogenically cooled lead-salt diode lasers have almost disappeared in recent years7. They have been replaced by room-temperature distributed feedback quantum cascade lasers (DFB-QCLs) that offer portability, stable operation and mode-hop-free tuning8. However, they are commercially available only below 13 μm9, whereas the emerging technology of InAs-based long-wavelength QCLs is still under development and not available for applications10. An alternative approach is difference frequency generation (DFG) from cw Ti:sapphire11,12 or diode13 lasers, but this is accompanied by extremely low optical powers (10–100 nW range) that impair the acquisition of absorption spectra at a high signal-to-noise ratio (SNR). The limitations of laser technology have established Fourier-transform spectroscopy driven by incoherent light sources as a gold standard for the long-wavelength infrared (LWIR) region, yet not for optical metrology14,15 and precision spectroscopy studies16 because of the low resolution (0.0007 cm−1 or 21 MHz in the best cases17) and the lack of absolute calibration for the frequency axis18. A powerful solution to both issues is direct comb spectroscopy19,20, which exploits millions of laser modes that compose the comb spectrum to directly probe molecular absorption over extremely large bands and with absolute frequency calibration21. Thanks to a time-domain counterpart formed by a coherent train of femtosecond laser pulse20, frequency combs are ideal sources for efficient nonlinear frequency conversion deep into the mid-infrared (MIR)22, also fostered by innovative solutions for laser gain media23, nonlinear materials24 and frequency conversion schemes25,26,27. However, it has only been recently that snapshots of entire bands have been acquired by a dual-comb approach28 at high temporal and spectral resolution in the LWIR, from 6.7 to 16.7 µm (1500–600 cm−1)29,30. This achievement does not remove, however, the need for cw probe lasers to observe single lines with high accuracy3,14,15 and extreme speed31 in a region where the Doppler width and the typical line densities are consistently below the spacing between adjacent comb modes. Furthermore, to the best of our knowledge, no frequency data of metrological quality have been provided so far in the LWIR region.

In this paper, we introduce a spectrometer that enables metrological studies in the bending modes region of two symmetric molecules, namely carbon dioxide and benzene. The spectrometer includes a nonlinear laser source, based on DFG between a quantum cascade and a CO2 laser, covering the 12–15 μm region almost continuously with optical power up to 110 μW, 2.2 MHz linewidth and frequency calibration against a thulium (Tm) comb. We assess several frequency standards as accurate as 30 kHz between 14 and 15 μm based on CO2 transitions. We also apply the spectrometer to the rich and congested absorption spectrum of the ν11 bending band of benzene, resolving 729 lines and retrieving the rotational parameters of the excited state with increased accuracy over the state-of-the-art. These outcomes attest to the value of our approach for extending high-resolution spectroscopy and optical metrology to the yet unexplored long-wavelength part of the mid-infrared spectrum.

Results

Technical approach

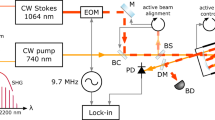
The spectrometer is schematically shown in Fig. 1a. The laser source is based on the DFG process between two MIR sources, namely a cw DFB-QCL and a CO2 laser, in an orientation-patterned gallium arsenide (OP-GaAs) crystal24. The DFG laser provides highly coherent radiation between 12.1 and 14.8 μm (826 and 675 cm−1) with optical power up to 110 μW and 2.2 MHz linewidth. The broad spectral range comes from the coarse wavelength adjustment of the CO2 laser (from 9.23 to 10.71 μm) combined with the fine temperature-based tuning of the QCL (over ~4 cm−1 around 5.69 μm) and the fan-out structure of the poling periods of the OP-GaAs crystal (see “Methods” for details). The optical power is 2–3 orders of magnitude higher than previous DFG sources starting from cw Ti:sapphire lasers with GaSe crystals11,12. The obtained power agrees within 15% with our calculations using 63 pm V−1 as the effective nonlinear coefficient. Such an excellent agreement reflects the quality of the crystal and a very favourable MIR–MIR interaction that ensures similar diffraction conditions for the interacting beams and thus optimal spatial overlap over a long crystal. The absolute frequency calibration of the DFG radiation comes from the referencing of both QCL and CO2 lasers to a 100 MHz comb via sum frequency generation (SFG)32 (see “Methods” for details). As sketched in Fig. 1b, the CO2 laser remains offset-locked to the nearest comb mode during the measurements, whereas the frequency of the temperature-tuned DFB-QCL is tracked against the comb by real-time fast Fourier-transform (FFT) analysis and barycentre calculation of its beat note. Synchronous acquisition of the beat note and gas transmission allow spectra to be straightforwardly calibrated.

Fig. 1: Nonlinear laser source and detection scheme.
figure 1

a Experimental lay-out of the comb-referenced nonlinear laser source for long-wavelength mid-infrared. QCL quantum cascade laser; BC beam combiner; PM parabolic mirror; OP-GaAs orientation-patterned Gallium Arsenide nonlinear crystal; F low-pass filter; PD liquid nitrogen cooled photodetector; SFG: sum frequency generation. b Pictorial view of the difference frequency generation (DFG) process between the comb-locked CO2 laser and the quantum cascade laser (QCL). The optical frequency of the QCL beam (pump, orange line) is swept while keeping the CO2 beam (signal, red line) locked to the comb. The frequency of the DFG beam (idler, brown line) is correspondingly swept over a range that contains the long-wavelength mid-infrared (LWIR) absorption signatures (blue line). The acquisition of the QCL-comb radiofrequency (RF) beat note (fbeat, black line) permits the absolute calibration of the DFG frequency during the scan, synchronously with the acquisition of the idler transmission through the molecular sample (IPD). Pump and signal are shown to beat directly with a MIR comb, yet this happens through the interposition of a sum frequency generation process (see “Methods” for details).

Full size image

Carbon dioxide metrology

Figure 2a shows an example of a comb-calibrated transmission spectrum for some intense lines of the v2 band of CO2 in the 675–689 cm−1 (14.5–14.8 µm) range. Lines are well isolated and in excellent qualitative agreement with the high-resolution transmission molecular absorption database (HITRAN33) simulations.

Fig. 2: Carbon dioxide spectroscopy.
figure 2

a Absorption spectrum of the ν2 band of CO2 (blue) as compared to the high-resolution transmission molecular absorption database (HITRAN) simulations (red). Experimental conditions: interaction length = 0.67 m, pressure = 0.93 Pa, room temperature. The scattering of baseline points is due to etalons that have been fitted out in the proximity of lines. b Zoomed-in view of the R(14) line, with three independent measurements of the same line (coloured dots) and fit with a Voigt profile (black line). Each measurement is composed of 170 points acquired over 2 s. c Residuals from the Voigt fitting of each individual measurement, showing the presence of a periodic structure due to parasitic etalons in the setup. The black lines delimit the region of ±1 standard deviation of the residuals (0.3% of the line amplitude).

Full size image

Figure 2b shows three independent experimental traces of the R(14) line, reported in different colours to highlight their reproducibility over the two measurement axes. The presence of spectral gaps is due to the missed calibration that occurs when the comb-QCL beat note approaches either direct current or half the spacing between neighbouring comb modes (50 MHz, see “Methods” for details). With an additional spectral acquisition at a slightly different comb repetition rate, interleaved spectral points could be added to fill the gaps (more details can be found elsewhere34). They do not, however, represent an issue when fitting the data (black line in Fig. 2b): the residuals in Fig. 2c refer to a Voigt model and give an SNR of approximately 300 with a measurement time of 2 s. This translates into a statistical uncertainty of about 140 kHz (4.7 × 10−6 cm−1) on the inferred line-centre frequency, mostly due to the reduced Doppler broadening (30 MHz or 10−3 cm−1 level) given by the LWIR range and to the negligible collisional broadening at the low pressure used here.

For each measured line, Fig. 3a (for lines pertaining to the R branch of the v2 band) and Fig. 3b (for lines pertaining to the Q branch of the v1 ← v2 band) show the difference between its absolute line-centre frequency and the value in HITRAN, together with an error bar dominated by statistical uncertainties (see “Methods” for details). Some lines have been intentionally measured several times to improve their line-centre uncertainty, which is below 30 kHz for three lines (see Supplementary Table 1), and to provide frequency standards in a region where absolute calibration has not been reported so far, to the best of our knowledge. The weighted deviation from HITRAN, averaged over 24 transitions, amounts to a remarkably low 0.34 MHz (1.1 × 10−5 cm−1), which is consistent with the declared HITRAN uncertainty (0.3–3 MHz or 10−3–10−4 cm−1). The line centres reported for each line in the Supplementary Table 1 offer a metrological benchmark to calibrate past and future spectra in the 670–720 cm−1 (14–15 μm) region.

Fig. 3: Experimental line centres vs database values for carbon dioxide.
figure 3

a Difference between experimental and high-resolution transmission molecular absorption database (HITRAN33) line centres for several lines of the R branch of the v2 band and b of the Q branch of the v1 ← v2 band. Error bars represent standard errors of the mean (±1σ). The variation of error bars comes from a different number of measurements per line.

Full size image

Benzene precision spectroscopy

In Fig. 4, we report the experimental spectrum of the R branch of the v11 band of benzene over 675–688 cm−1 (14.5–14.8 µm). This intense, parallel band is an interesting testbed for the spectral resolution and frequency repeatability of the spectrometer because of the large density of rotational lines. Apart from transitions with quantum number K = 0, 1 and 2, whose separation is smaller than the Doppler width, all K lines are well resolved. This is shown in the insets in Fig. 4 and is particularly evident at large J. Lines from three hot bands, namely v11 + v16 − v16, v11 + v6 − v6, and 2v11 − v11, are also present in the recorded spectral region, but the analysis was restricted to the 729 ro-vibration transitions of the ν11 band, with J up to 38 and K up to 36, since these are mostly isolated, medium intensity lines. We adopted a weighted least-squares fitting procedure to determine highly accurate term values of the excited ro-vibration levels, according to the equation:

$$E_v(J,k) = \, E_v^0 + B_v[J(J + 1) - k^2] + C_vk^2 - D_{v,J}[J(J + 1)]^2 \\ - D_{v,JK}J(J + 1)k^2 - D_{v,K}k^4\\ + H_{v,J}[J(J + 1)]^3 + H_{v,JK}[J(J + 1)]^2k^2 \\ + H_{v,KJ}[J(J + 1)]k^4 + H_{v,K}k^6,$$
(1)

where Ev(J,k) is the sum of the vibration and rotation contributions to the energy level with rotational quantum number J and signed quantum number k = ±K (k = 0, ±1, …, ±J). \(E_v^0\) represents the vibration contribution, while B and C represent the rotational constants. DJ, DJK, DK are the centrifugal distortion constants in the 4th order of the angular momentum, while HJ, HJK, HKJ, HK are the centrifugal distortion constants in the 6th order of the angular momentum. All rotational and centrifugal distortion constants depend on the vibration state v in the subscripts (in our case v = v11 = 1). The ground state term values were derived from Doi et al.35 and Eq. (1) with v = 0, \(E_v^0 = 0\) and keeping all H centrifugal distortion parameters fixed to zero. A unitary weight was attributed to the isolated lines, whose wavenumber precision is estimated to be 10−5 cm−1 (300 kHz). The weights of blended or weak lines were reduced to 0.01, and, in addition, for lines with multiple assignments, the weight was further reduced by a factor equal to the number of overlapped transitions. Observed and calculated linecenter values, along with the weighting factors, of the benzene v11 band are provided as Supplementary Data.

Fig. 4: Absorption spectrum of the R branch of the v11 band of benzene.
figure 4

Experimentally measured transmission at the output of a 0.67 m long cell at a pressure of 13.3 Pa and room temperature. The spectral features have a typical shape, with the K-structure degrading regularly towards higher wavenumbers and an apparent intensity alternation of subsequent lines. The insets show zoomed-in views of RK(6) and RK(33) features (left and right inset, respectively): for the latter, the K-splitting is much more manifest together with intensity alternation of K components, owing to spin statistics, that varies as 10:11:9:14, for K = 6p, 6p ± 1, 6p ± 2, 6p ± 3, respectively, (p = 0, 1, 2, 3…)41.

Full size image

The parameters obtained from the best fit are listed in Table 1, and compared with those of the ground state. All parameters reported in Table 1 are statistically well determined. The uncertainty of the band origin (\(E_v^0\)) has been reduced by about one third with respect to its value in Hollenstein et al.36. The B, C, DJ, DJK and DK constants are consistent and close to those of the ground state35. The values of B, DJ and DJK are more accurate than those in Hollenstein et al.36 by one order of magnitude. The values of C, DK and HJ constants of v11 = 1 are determined here for the first time. The standard deviation of the fit, 5.1 × 10−5 cm−1 (1.5 MHz), is one order of magnitude smaller than in the past literature for the same band36. At the same time, it is about 10 times higher than for single CO2 lines due to a combination of factors, namely, the many partially overlapped lines and the difficulty to access the intensity baseline due to the congested spectrum. The absolute calibration of the frequency axis allows, for the first time, the stacking of repeated measurements and the determination of absolute line positions at these wavelengths.

Table 1 Spectroscopic parameters of benzene.
Full size table

Discussion

Overall, the metrological approach presented here considerably expands the portfolio of laser tools to probe molecules in the gas phase with high resolution and accuracy. This is proactive for the study of large molecules through the unique fingerprint features offered by the LWIR spectral region, for example molecules of the BTEX (benzene, toluene, ethylbenzene, xylenes) family that are of high interest for environmental modelling applications. In the case of benzene, which lacks a permanent dipole moment and, therefore, cannot be detected by pure rotational spectroscopy, infrared bands such as the ν11 explored here represent the clue to assess their presence in remote spatial environments, such as planetary atmospheres6,37,38. On another front, by the use of a sub-hertz linewidth comb and phase-locking loops for pump and signal lasers, the spectrometer could reach the level of stability and spectral purity needed for tests of fundamental physics on molecular samples39,40 in a spectral region not explored so far.

Methods

Difference frequency generation

The pump radiation in the DFG process is provided by a DFB-QCL from Alpes Lasers, emitting at around 5.69 μm. Tuning its temperature from 20 °C to −10 °C results in continuous spectral coverage from 1757 to 1761 cm−1 (i.e., over 4 cm−1) with an optical power from 17 to 48 mW, respectively. The signal radiation is generated by a CO2 laser (L20GD, Access Laser) operating in a pulse modulation mode (“super-pulse mode”) with a duty cycle of 20% and a modulation frequency of 10 kHz. Its emission can be finely piezo-tuned over few tens of megahertz and coarsely tuned by grating over ~80 lines, from 9.23 to 10.71 μm, with peak powers varying from 3 to 27 W depending on the line. The wavelength combination of the two lasers provides access to a 12.1–14.8 μm (675–826 cm−1) wavelength range for the idler beam, apart from 10 cm−1 gaps at 12.6 and 14.4 μm (794 and 694 cm−1) and a 30 cm−1 gap at 13.3 μm (752 cm−1) due to the discontinuities between adjacent CO2 lasing bands. The OP-GaAs crystal used for DFG is 35 mm long and equipped with poling periods from 183 to 203 μm in a fan-out structure, which ensures phase matching over the entire tuning range available for the nonlinear laser source. The width of the crystal is 20 mm, which is sufficiently large to discard any efficiency drop due to non-uniform phase-matching conditions across the beams. In fact, the poling period changes by <0.2 μm, which is far below the phase matching bandwidth of 0.7 μm, over beam diameters of 120 and 200 μm for pump and signal, respectively. As expressed in terms of wavenumbers, the phase-matching bandwidth amounts to 4.2 cm−1, which implies that there is no need for adjustment of the crystal position while tuning the QCL. The optical power generated by the DFG considerably depends on both the QCL temperature and the CO2 lasing line, but it remains above 20 µW (peak power) if the CO2 emission is chosen among the 70% most intense lines, as it is the case for all measurements shown here.

Comb referencing and spectra acquisition

Pump (5.7 μm) and signal (9.2–10.7 μm) lasers are referenced to the same 1.9 μm Tm:fibre frequency comb through two independent SFG processes, in AgGaSe2 and ZnGeP2 (ZGP) crystals, respectively. The SFG processes shift the comb frequency vn = fceo + nfrep (fceo and frep being carrier-envelope-offset and repetition frequency of the comb, respectively) by the pump (vp) and signal (vs) frequency, thereby generating two replicas of the comb around 1.4 μm (vn,p = vn + vp) and 1.6 μm (vn,s = vn + vs) for pump and signal, respectively. When these replicas are superimposed with a coherent continuum (vm = fceo + mfrep) generated from the original comb and extending down to 1.4 μm, a beat note is extracted, \(f_{{\mathrm{beat}}} = \pm ( {\nu_{n{\mathrm{,p/s}}} - \nu _m} ) = \pm ( {\nu _{{\mathrm{p/s}}} - \left( {m - n} \right)f_{{\mathrm{rep}}}} )\) that straightforwardly links the unknown pump/signal frequency to an integer number of frep, independently of fceo. In our case, frep is stabilized to a global positioning system (GPS)-tracked low-noise radiofrequency (RF) signal at 100 MHz while fceo is left free running. From an analysis of their beat notes (Supplementary Figs. 1 and 2), QCL and CO2 lasers give an almost Gaussian instrumental line shape full width at half maximum (FWHM) of 1.6 and 1.5 MHz, respectively, which overall determine a spectral resolution limited to 2.2 MHz (see Supplementary Note 1). The relatively large contribution from the CO2 laser comes from the adopted super-pulse mode, and it could be suppressed by choosing a cw emission followed by external modulation, at the expense of DFG power. The CO2 beat note is locked to an RF local oscillator via piezo-feedback to the grating position, whereas the QCL beat note is measured in real time by a 100 MS s−1 digital acquisition board, followed by an FFT conversion at every 1024 samples and a barycentre calculation via field-programmable gate array (FPGA, PXIe-7961 FPGA board and NI-5781 add-on, National Instruments). The same board digitizes the lock-in output in order to synchronize horizontal and vertical axis of the measurement. An example of raw data for QCL beat note and gas absorption is given in Supplementary Fig. 3. The acquisition of a 4 cm−1 large spectrum is typically accomplished in 12 min (tuning rate of 180 MHz s−1) to prevent laser frequency changes by more than its linewidth over the integration time of 10 ms set for the lock-in. A higher speed would be possible with a faster modulation of the CO2 laser and a correspondingly smaller integration time. Spectra larger than 4 cm−1, as those in Figs. 2 and  4, are acquired piecewise, due to the need of changing the CO2 laser frequency and correspondingly adjusting the phase-matching condition for DFG. No tuning of the phase-matching angle is necessary for the SFG processes because of the much larger phase-matching bandwidths given by the shorter interaction length (6 mm) and the type of phase matching (birefringence rather than quasi-phase matching). The assignment of the comb mode order for correct calibration of the frequency axis is straightforward because of the low uncertainty of both CO2 and C6H6 tabulated lines, well below the comb mode spacing (100 MHz).

Uncertainty budget

A 240 MHz-broad spectrum of a single isolated line, such as that shown in Fig. 2b, is typically acquired in 2 s and encompasses 170 spectral points: these are almost evenly distributed in 5 groups separated at every 50 MHz, namely at every half frep, by 18 MHz blanks due to the missed tracking of the comb-QCL beat note. In these conditions, the absorption noise (3 × 10−3 on the most intense lines) and the frequency uncertainty on each spectral point (29 kHz) account for about 70% and 5%, respectively, of the observed 140 kHz root mean square (rms) deviation of the line centre for repeated measurements. The missing contribution comes from distortions of the spectral baseline that change from measurement to measurement and are not properly fit out. Repeated measurements were performed on most lines to reduce the statistical uncertainty on the line frequency. A Gaussian-like distribution was found, justifying an inverse square law between statistical uncertainty and number of independent measurements. This number is specified in the last column of Supplementary Table 1 for each line. The statistical uncertainty dominates over systematic effects, due to the negligible impact from the instability of the GPS-based frequency standard (2 kHz over 2 s), the inaccuracy of the absolute pressure gauge and of the pressure shift coefficients used to extrapolate line centres to zero pressure (<2 kHz, thanks to the low pressure), and the inappropriateness of the Voigt fitting model (<3 kHz, due to the negligible asymmetry of line profiles in the low-pressure collisional regime).