Abstract
Understanding the evolution of extreme states of matter driven by relativistic laser-plasma interactions is a fundamental problem in high-field physics. This is especially true for nanostructured targets, where hydrodynamic effects play a key role within the ultra-fast time scale of laser absorption. Nanowire array targets are of particular interest as they provide an efficient means to access the ultra-high-energy-density regime due to their increased optical absorption, and have been shown to act as very efficient x-ray emission sources. Here we present analysis of time-resolved x-ray emission spectroscopy from petawatt-irradiated Nickel nanowire arrays, used to characterise the conditions achieved when scaling the performance of nanowire targets to relativistic intensities. A full time evolution of the plasma conditions is extracted from the experimental data, and shows good agreement with the physical interaction picture developed by prior computational studies.
Similar content being viewed by others
Introduction
Understanding the response of matter irradiated by high-power lasers at relativistic intensities is a key challenge in high-field physics1,2, of broad importance to the study of extreme astrophysical objects3,4, of particle acceleration mechanisms5,6 and of exotic phenomena such as radiation reaction7 and vacuum polarization8. Because of the complexity of the interactions and the ultrafast times scales on which they occur, much of our fundamental understanding of plasma dynamics in strong laser fields is driven by detailed modelling using particle-in-cell (PIC) simulations9,10,11,12. In contrast, there are a very limited number of studies detailing time-resolved plasma dynamics of solid targets resulting from ultrashort relativistic laser interaction13,14,15, and the evolution of these systems at kilojoule-scale facilities has been unexplored experimentally16.
From an applications viewpoint, intense laser–matter interactions are also important because they provide a mechanism to create bright X-ray sources for high-energy-density (HED) physics experiments, supporting research in laboratory plasmas and in inertial confinement fusion (ICF)17,18. These applications have been the driving force behind the continued development of brighter, more uniform and more repeatable X-ray sources18,19, the careful characterization of which has been shown to be of high importance19,20. In this context, nanowire array targets were proposed as a route forward for X-ray radiography studies21, as their geometry allows increased laser absorption21,22,23,24 as well as volumetric heating of the target9,25 to reduce the strong plasma parameter gradients present in flat targets. Nanowire array targets have demonstrated increases in X-ray emission intensity of up to 50× when compared to flat foils9,24,25, and the improved laser-target energy coupling can lead to energy densities of 2 GJ cm−3 (ref. 9), comparable to those reached in ICF implosions. Scaling the performance of these targets for use at high-energy laser facilities has been challenging due to the extreme contrast requirements on laser systems to avoid damaging the highly optically absorbent targets before the main drive pulse arrives24,26. In addition to serving as bright X-ray sources, nanowire arrays show great potential as platforms for ultra-HED studies25,27 if their complex hydrodynamic evolution can be accurately diagnosed9,16,25.
Here we present analysis of time-resolved X-ray spectra from nanowires driven by relativistic laser intensities16, providing insight into the dynamics and evolution of these HED systems on picosecond timescales. We detail how the time- and spectrally-resolved X-ray emission bounds the conditions of transient plasma states, and demonstrate good agreement of the observed data with the understanding of these systems gained from PIC simulations.
Results
Experimental details
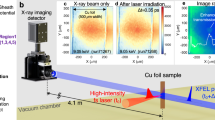
An experimental campaign investigating the potential to scale nanowire targets to kilojoule-scale laser facilities was undertaken using the high-contrast Orion petawatt laser at AWE, UK28. Full details of the experimental setup are provided in Hill et al.16 and a schematic of the experimental setup is reproduced in Fig. 1. Arrays of Ni nanowires were shot with the frequency-doubled Nd:glass short-pulse laser (100 J, 600 fs, 10 μm full-width half-max focal spot), at intensities of ~1020 W cm−2 of 532 nm wavelength light, normalized vector potential a0 ≈ 6. A contrast of 1018 at 100 ps was maintained to avoid damaging the highly optically absorbent nanowires before the main pulse arrived28. The nanowires had ~15% fill fraction, and were 12.5 μm in length, with diameters of 400 or 1000 nm. The laser was incident at 25∘ from normal, and spectra were collected on a curved germanium crystal spectrometer coupled to an ultrafast X-ray streak camera for an ultrafast X-ray streaked spectrometer (XRSS) diagnostic observing the front of the target 55∘ off-normal.
Experimental layout showing the incident frequency-doubled (2ω) Orion short-pulse drive, the primary diagnostic, the ultrafast X-ray streaked spectrometer (XRSS) and the Kirkpatrick-Baez (KB) X-ray microscope to monitor the quality of the focal spot. A scanning electron microscope image of the 400 nm diameter (dia.) nickel nanowire target is also shown.
The emission collected on the XRSS has a time resolution of ~1 ps, and an energy resolution E/ΔE ~ 500 for the energy range observed (7.4–8.4 keV). The energy range collected captures emission of the cold Kα, as well as the Heα and Lyα from high ionization states, including the associated satellite peaks as seen in Fig. 2a. By observing the time-resolved satellite emission and comparing to a collisional radiative code such as FLYCHK29, it is possible to infer the evolving ionization balance and associated temperature and density of the plasma.
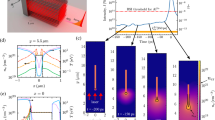
a Spectral emission data and fits from the 400 nm Ni nanowire target showing the key K-shell emission features, with emission from distinct phases of evolution indexed I–VI. b Track of the centroid of the fitted emitting plasma distribution on T–ρ showing the evolution of the system in time (as colour). Half of the standard deviation of the distribution is plotted as an ellipse for each time step, which are then connected along the time evolution with their common tangents to represent our uncertainty in the dynamical path. c Normalized distributions of the plasma conditions as a function of temperature and density at times indexed I–VI.
The nanowires, similar to previous high intensity studies, exhibit brighter and prolonged emission compared to a flat foil target9,16,21. The increase in intensity comes primarily from the high-lying charge states, with a 2× increase in He-like emission brightness, yielding a 3× increase in the time-integrated emission across the full energy range.
Modelling the experimental spectra
In order to identify the conditions present within the plasma, the FLYCHK collisional radiative code29 was used to produce spectra over a wide range of temperature and density conditions that would be present in the plasma. The FLYCHK code uses a screened hydrogenic model with relativistic corrections, which when simulating an Ni plasma includes all detailed term levels for Li-like satellite states up to n = 4 from the HULLAC database. Spectra resulting from H-, He- and Li-like ions have good line positions as a result of the detailed level structure which is beneficial for our study of high-lying charge states. As expected, a single temperature–density condition was insufficient to model the emission due to the range of conditions present in the target, so a combination of steady-state emission profiles had to be used. A grid of 10 temperatures, 0–4 keV and 10 densities, exponentially sampled between 0.1 and 10 g cm−3, was used to produce simulated emission spectra. The limits on the T–ρ grid were chosen to correspond to the estimated conditions of the plasma based on PIC and radiation-hydrodynamic simulations16, while still having observable emission in the energy range collected by the spectrometer. The functional form of the spectrum is reliably reconstructed using a linear combination of these steady-state emission profiles over the duration of the emission, as seen in Fig. 2a.
In the interest of avoiding over-parameterizing our dataset, a subset of weighting points within this 10 × 10 sample grid was chosen as the set of fitting parameters, with the remaining spectral weightings being interpolated between them. This interpolation scheme allows a reduced number of free parameters to converge on a well conditioned fit to the data over the full temperature–density parameter space, and can be seen as fitting a generalized functional form to the T–ρ profile of the plasma with a resolution determined by the number of fitted points. Weightings were log-interpolated for density, due to the expected properties of the ablating plasma, and the exponentially sampled density grid. The fitted spectral weightings were found by minimizing a weighted least-squares cost function, with weightings taken from the combined absolute and relative noise on the level of retrieved signal from the XRSS.
In order to remain sensitive to all spectral emission distributions, the points chosen as the subset of fitting parameters was sampled over all possible subsets. The resulting ensemble fit to the data was then averaged for each time step in the emission, with uncertainty due to the sampling and interpolation estimated by taking the deviation of the fitted spectral weightings obtained from the weighted least-squares spectrum. In order to fit our data, five points were taken in both temperature and density, retaining end points to construct a valid interpolant. The centroid of fitted emitting plasma distributions through time is shown in Fig. 2b, with a selection of full distributions for 400 nm diameter nanowires is shown in Fig. 2c, showing key points in the evolution of the plasma. An example distribution for a flat foil target is shown in Fig. 3a, 7 ps after drive.
The fitted evolution of a flat foil target irradiated by the Orion short-pulse drive is shown to identify the dynamics present. a, b Plasma conditions and spectral emission 7 ps after drive, showing the denser parts of the target beginning to expand, after being moderately heated by the highly energetic particles driven into the target, redistributing the energy. c The time evolution of the centroid of the emitting plasma distribution, with a band representing half the standard deviation connected along the dynamical path. Annotated parts of the dynamics of the flat foil targets can be understood similarly to the evolution of the nanowire targets, but the evolution is not as rich and points III–V do not feature.
At late times the collected emission can be seen to exhibit sharp features not captured by the fitted spectrum as in Fig. 3b—this is most likely as a result of low signal levels giving large, Poisson-like noise on the detector below the energy resolution of the XRSS, which can be seen across the full spectral range. Another possible source of the discrepancy is due to the form of the fit yielding a parameter-number limited resolution of the T–ρ profile. At this late time it is possible that the emitting plasma would be better modelled by a narrower distribution than the model supports—or similarly, for a narrower range of conditions than is captured on the 10 × 10 sample grid—however, the form of the distribution in Fig. 3a does not support this. A final possibility is that the emission is due to significant high-lying satellite state populations not included in the FLYCHK model, which is a limitation of the choice of collisional radiative code.
In order to visualize the full time evolution of the fitted plasma distribution, we track the centroid of the ensemble-averaged weights on the T–ρ grid, shown in Fig. 2b for 400 nm diameter nanowires, and Fig. 3c for flat foil. The plasma distribution is calculated in 500 fs time steps; however, broadening in the detector limits time resolution to ~1 ps. The temporal blurring affects the rise time on the detector, and therefore the timescale of features due to laser heating and reflection may be extended relative to t0, which is based on the onset of collected emission. The width of the plasma distribution in temperature and density is shown as an ellipse around each data point, connected along the time evolution, while the fitted volume of emitting plasma and the uncertainty in the distribution is not shown along the evolution, and will also vary along the dynamical path according to the level of signal (Fig. 4a). Key aspects of the plasma evolution in time are labelled I–VI, which can be understood with the aid of simulations and theory16,25.
a The spectrally integrated emission from the primary emission complexes for 400 and 1000 nm diameter nanowire, and flat Ni targets. b Extracted FLYCHK ion populations for high-lying charge states, showing a late-time jump in highly charged ions for the nanowire targets when neighbouring wires collide—a feature not seen in the raw time-resolved emission. Bands on the data represent the ion-population-weighted standard deviation of the ensemble fit to the time-resolved spectral data.
Plasma evolution
The formation of a uniform plasma from nanowires and flat foil targets under the extreme intensities present at the Orion laser is a complex and dynamic process, as illustrated by the vermiform path of plasma conditions in Figs. 2b and 3c. The key features of the emitting plasma profile, indexed I–VI, can be understood to result from the plasma dynamics as
-
I.
Initial laser heating—The temperature of the emitting plasma rises to keV levels within the temporal resolution of the camera as the laser pulse is absorbed.
-
II.
Laser reflection and energy redistribution—The target forms a plasma mirror and reflects the remainder of the laser pulse. Hot electrons redistribute energy in the target.
-
III.
Heating dense wire cores—The dense cores of the nanowires are heated by massive return currents.
-
IV.
Nanowire recollision—The nanowires explode and collide with neighbouring wires within the irradiated area, heating the system.
-
V.
High-temperature inertially confined stagnation—The high-temperature plasma emits while inertially confined by its volume.
-
VI.
Expansion and cooling—The plasma expands and cools to the signal/noise limit of the XRSS.
During the initial heating of the system, the emission is broadened by the time resolution of the XRSS. The temporal broadening results in the initial observed density lower than 8.91 g cm−3 solid density; however, this could also be in part due to the inter-wire channel filling before the onset of emission above the noise floor of the detector, as the bulk of the wire is not yet heated.
In the case of flat foil laser targets, the uniform surface will rapidly form a plasma mirror limiting heating past the critical density, and in addition to the time broadening this would result in the density of the average emitting plasma being lowered due to contribution of the ablator layer at early time. Without the laser energy being absorbed deeper into the target, a lower volume of plasma is produced, preventing the long, inertially confined, timescales seen in nanowire systems, and shown by the duration of emission in Fig. 4b. The limited key dynamics responsible for the time-resolved emission in foils can be understood using only points I, II and VI, in contrast to the rich nanowire dynamics.
The reflection of the laser pulse will occur during the first few time steps of the extracted evolution, as the temporal resolution of streak camera cannot resolve effects that occur during the pulse. The timescale of void closure for nanowire targets at these intensities is estimated as between 100 fs and 1 ps at the tips of the wires24,25; however, this will vary over the range of intensities in the focal spot. Energetic particles from the laser-plasma interaction are able to penetrate and heat denser parts of the target, although lowering the average temperature of the emitting plasma as energy is redistributed within the interaction volume.
While in bulk targets a return current is generated to be approximately locally balanced with the current of hot electrons, in nanowire targets electrons are stripped and mainly driven by the laser in the inter-wire voids, where there are no conduction electrons to locally offset the currents and fields generated. The geometrically constrained current is recirculated at the base of the nanowires to neutralize the space charge at the tips due to the depletion of electrons16, drawing megaampere-scale return current along the length of the wires, generating gigagauss magnetic fields. The return current, along with radially propagating shock fronts from the ablating wire edges forms a Z-pinch, which compresses and heats the dense wire cores. The nanowires then explode and collide, stimulating significant secondary heating in the target. The overall density of the emitting plasma plateaus at ~1 g cm−3, or ~11% solid density, corresponding to the initial ~15% nanowire fill fraction. The width of the plasma distribution narrows in density as the system homogenizes along the length of the wires, seen in Fig. 2b as the height of the shaded region around the dynamical path. Transverse temperature gradients will still exist in the target due to the focal spot intensity profile, so we do not see the distribution collapse around a single T–ρ point within the resolution of our generalized functional form.
The large volume of high-temperature plasma undergoes a relatively prolonged period of stagnation and homogenization, along the full length of the heated wires. As the plasma fully thermalizes it begins to expand out of the plane of the target to lower densities, the larger volume of nanowire plasma cools more slowly than the relatively thin layer in the foil target. This manifests as a slight increase in apparent density at late times, as emission from the cooler low-density regions drops below the dynamic range of the XRSS.
Discussion
The ability to probe the complete evolution of complex plasma conditions using time-resolved emission from single-shot XRSS data is vital in benchmarking and improving physical models. The sustained high temperatures and densities in the nanowire plasma offer a unique platform bridging the regimes typically associated with PIC and radiation-hydrocodes. High computational expense and physical complexity from the wide-ranging spatio-temporal scales in this environment force any simulation to make approximations; without experimental data there is no way of identifying which of these are reasonable.
Analysing the plasma evolution with FLYCHK also offers insights into the time-resolved ion populations from the ensemble fit to the data, including the predicted population of fully stripped Ni28+ ions, which are not spectroscopically observable. While the FLYCHK code is zero dimensional, the spectral module produces the expected observations of an infinite 1-μm-thick slab in units of J cm−2 Hz−1 sr−1, and is therefore an effective spectrum for a defined volume at the ion density used as an input. Using the set of fitted weights, input atomic densities and output relative contributions of ion constituents from each point in the distribution, the time-resolved ion populations can be plotted, including the uncertainty from the ensemble-averaged distribution. As the experimental spectrum is not absolutely calibrated, the extracted ion populations represent only the relative proportions of ion species. The fitted evolution of ion populations for both nanowire and flat Ni targets are plotted in Fig. 4a, where collisional heating can clearly be seen to generate a late-time jump in highly charged ion stages for nanowires, not visible from the spectrally integrated line emission (Fig. 4b).
The volumetric heating effects in the nanowire targets result in a larger quantity of slightly lower temperature plasma when compared to the conditions identified for a flat foil target, homogenized along the wire length. Effects of the increased volume of emitting plasma can be seen in the enhanced Ni27+ population from early time, as well as the prolonged high-temperature stagnation seen in Fig. 2b. In contrast, the flat foils reach maximum ionization almost immediately before rapidly cooling and expanding.
The 1000 nm diameter nanowire target exhibits some of the behaviour of both bulk and nanowire interaction, with notable early- and late-time heating events in the highly charged ion populations seen in Fig. 4a. This dichotomous nature results in significant bimodal distributions in temperature and density which cannot be sufficiently resolved based on the limited resolution of the generalized functional form of the distribution, nor is tracking the centroid of a bimodal distribution a useful exercise. Nevertheless, the irregular wire spacing in both the 1000 and 400 nm arrays manifests as multiple ionization peaks in the time history; it is expected that a regularly spaced array with a larger number of wires contained within the focal spot would exhibit a more clearly defined evolution.
We have presented a method for determining plasma conditions in rapidly evolving samples containing significant density and temperature gradients, applicable to many datasets whether time-resolved or time-integrated. While not an exact inversion, this technique is capable of producing meaningful results which correspond well to our developing understanding of nanowire dynamics at these incident intensities. The ability to understand the complex plasma evolution in near-solid-density, high-temperature conditions, from single-shot emission, has significant potential utility across a range of warm dense matter and HED studies. The main limitations in the reconstruction of the emitting plasma profile are due to a combination of the signal:noise ratio present in the data (limited by the desired time resolution), the energy resolution of the collected spectrum and intensity broadening effects during electron time of flight in the XRSS.
Our results demonstrate the importance of understanding the unique and complex dynamics of nanostructured laser targets. With continued optimization of nanostructure design and analysis techniques it will be possible to unlock their potential as extremely bright short-pulse probes, and as a platform for routine laboratory experiments in the ultra-HED plasma regime.
Data availability
Data are British Crown Owned Copyright 2020/AWE. The data that support the findings of this study will be made available upon reasonable request to the corresponding author.
References
Ditmire, T. et al. Overview of future directions in high energy-density and high-field science using ultra-intense lasers. Radiat. Phys. Chem. 70, 535–552 (2004).
Danson, C. N. et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 7, e54 (2019).
Meinecke, J. et al. Turbulent amplification of magnetic fields in laboratory laser-produced shock waves. Nat. Phys. 10, 520 (2014).
Bailey, J. E. et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 517, 56–59 (2015).
Bulanov, S., Esirkepov, T. Z., Habs, D., Pegoraro, F. & Tajima, T. Relativistic laser-matter interaction and relativistic laboratory astrophysics. Eur. Phys. J. D 55, 483 (2009).
Roth, M. et al. Laser accelerated ions and electron transport in ultra-intense laser matter interaction. Laser Part. Beams 23, 95–100 (2005).
Blackburn, T., Ridgers, C. P., Kirk, J. G. & Bell, A. Quantum radiation reaction in laser–electron-beam collisions. Phys. Rev. Lett. 112, 015001 (2014).
King, B. & Heinzl, T. Measuring vacuum polarization with high-power lasers. High Power Laser Sci. Eng. 4, e5 (2016).
Bargsten, C. et al. Energy penetration into arrays of aligned nanowires irradiated with relativistic intensities: scaling to terabar pressures. Sci. Adv. 3, 3–11 (2017).
Ceccotti, T. et al. Proton acceleration with high-intensity ultrahigh-contrast laser pulses. Phys. Rev. Lett. 99, 185002 (2007).
Decker, C., Mori, W. & Katsouleas, T. Particle-in-cell simulations of raman forward scattering from short-pulse high-intensity lasers. Phys. Rev. E 50, R3338 (1994).
Thaury, C. et al. Plasma mirrors for ultrahigh-intensity optics. Nat. Phys. 3, 424–429 (2007).
Audebert, P. et al. Time-resolved plasma spectroscopy of thin foils heated by a relativistic-intensity short-pulse laser. Phys. Rev. E 66, 066412 (2002).
Palaniyappan, S. et al. Dynamics of relativistic transparency and optical shuttering in expanding overdense plasmas. Nat. Phys. 8, 763–769 (2012).
Nilson, P. et al. Time-resolved measurements of hot-electron equilibration dynamics in high-intensity laser interactions with thin-foil solid targets. Phys. Rev. Lett. 108, 085002 (2012).
Hill, M. P. et al. Volumetric heating of nanowire arrays to keV temperatures using kilojoule-scale petawatt laser interactions. Preprint at https://arxiv.org/abs/2007.10410 (2020).
Uschmann, I. et al. Time-resolved ten-channel monochromatic imaging of inertial confinement fusion plasmas. Appl. Opt. 39, 5865–5871 (2000).
Kritcher, A. et al. Probing matter at gbar pressures at the nif. High. Energy Density Phys. 10, 27–34 (2014).
Tommasini, R. et al. Short pulse, high resolution, backlighters for point projection high-energy radiography at the national ignition facility. Phys. Plasmas 24, 053104 (2017).
Marshall, F. et al. Plasma-density determination from x-ray radiography of laser-driven spherical implosions. Phys. Rev. Lett. 102, 185004 (2009).
Kulcsar, G. et al. Intense picosecond X-Ray pulses from laser plasmas by use of nanostructured "Velvet" targets. Phys. Rev. Lett. 84, 5149–52 (2000).
Kahaly, S. et al. Near-complete absorption of intense, ultrashort laser light by sub-λ gratings. Phys. Rev. Lett. 101, 145001 (2008).
Cao, L. et al. Enhanced absorption of intense short-pulse laser light by subwavelength nanolayered target. Phys. Plasmas 17, 043103 (2010).
Marjoribanks, R. S. et al. Ultrafast laser-matter interaction with nanostructured targets. In X-Ray Lasers and Coherent X-Ray Sources: Development and Applications XIII, Vol. 11111, 111110L (ed. Klisnick, A.) (International Society for Optics and Photonics, 2019).
Purvis, M. A. et al. Relativistic plasma nanophotonics for ultrahigh energy density physics. Nat. Photonics 7, 796 (2013).
Cristoforetti, G. et al. Investigation on laser–plasma coupling in intense, ultrashort irradiation of a nanostructured silicon target. Plasma Phys. Controlled Fusion 56, 095001 (2014).
Curtis, A. et al. Micro-scale fusion in dense relativistic nanowire array plasmas. Nat. Commun. 9, 1077 (2018).
Hillier, D. et al. Contrast enhancements to petawatt lasers using picosecond optical parametric amplification and frequency doubling. In 2014 Conference on Lasers and Electro-Optics (CLEO)-Laser Science to Photonic Applications, 1–2 (IEEE, 2014).
Chung, H.-K., Chen, M., Morgan, W., Ralchenko, Y. & Lee, R. Flychk: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements. High Energy Density Phys. 1, 3–12 (2005).
Acknowledgements
The authors wish to thank J. J. Roccaʼs group at Colorado State University for target fabrication and insightful discussion. O.S.H. and S.M.V. acknowledge support from the U.K. EPSRC (EP/P015794/1), the Oxford University Centre for High Energy Density Physics (OxCHEDS) and the Royal Society. S.M.V. is a University Research Fellow of the Royal Society.
Author information
Authors and Affiliations
Contributions
The experimental data was collected by P.A., C.R.D.B., L.M.R.H., S.F.J., M.G.R., B.W., D.J.H. and M.P.H. Analysis was performed by O.S.H. The manuscript was prepared by O.S.H. and S.M.V.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Humphries, O.S., Allan, P., Brown, C.R.D. et al. Time evolution of transient plasma states from nanowire arrays irradiated at relativistic intensities. Commun Phys 3, 170 (2020). https://doi.org/10.1038/s42005-020-00438-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00438-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.