Abstract
The potential of photon-magnon hybrid systems as building blocks for quantum information science has been widely demonstrated, and it is still the focus of much research. We leverage the strengths of this unique heterogeneous physical system in the field of precision physics beyond the standard model, where the sensitivity to the so-called “invisibles” is currently being boosted by quantum technologies. Here, we demonstrate that quanta of spin waves, induced by effective magnetic fields, can be detected in a large frequency band using a hybrid system as transducer. This result can be applied to the search of cosmological signals related, for example, to cold Dark Matter, which may directly interact with magnons. Our model of the transducer is based on a second-quantisation two-oscillators hybrid system, it matches the observations, and can be easily extended to thoroughly describe future large-scale ferromagnetic haloscopes.
Similar content being viewed by others
Introduction
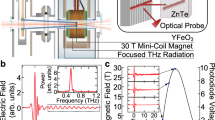
In the last decades, precision magnetometry emerged as a promising probe of physics beyond the standard model1,2. Amongst all, GHz-frequency magnetometers can probe spin-related effects through the use of the electron spin resonance techniques. Recent advances in the field are due to quantum computing research3, which allowed to reach the sensitivity to detect single quanta of magnetisation in macroscopic samples using photon-magnon hybrid systems (HSs)4,5. In these devices, the coherent interaction between photons and magnons is increased to such an extent that they can no longer be considered as separate entities, and the HS is described within the cavity quantum electrodynamics framework. Photons are confined within a microwave cavity hosting a magnetised sample, whose Larmor frequency ωm is adjusted close to the one of a suitable cavity mode ωc. In the strong coupling regime, in which the coupling strength is much larger than the related linewidths, photons and magnons are in a hybrid magnon-polariton state induced by magnon Rabi oscillation. Such a cooperative spin dynamics is governed by the physics of coupled harmonic oscillators with beating periods much shorter than dissipation times6. As under these conditions the two-oscillators exchange energy, the dispersion plot of the system displays the quantum phenomenon of avoided crossing: when ωc ≃ ωm, instead of two intersecting lines, the system dispersion relation exhibits an anticrossing curve7,8 as shown in Fig. 1a. A scheme of the HS used in this work is reported in Fig. 1b, and its conceptual representation is in Fig. 1c.
a Avoided level crossing of a photon-magnon hybrid system. The curve is typically obtained by recording the cavity transmission spectrum at several values of the static magnetic field, which determines the ferrimagnetic resonance ωm according to ωm = γB0 ≃ (2π × 28 GHz/T) × B0, with γ gyromagnetic ratio of the electron. b Scheme of the apparatus used in this work. The magnetic material (black) is hosted inside a microwave cavity (orange), and polarised with the field generated by an electromagnet (grey, with N and S labels standing for north and south poles). A laser pulse (red) excites the magnetostatic modes of a yttrium iron garnet sphere, including the Kittel mode, allowing for investigating the hybrid system dynamic response to a direct excitation of its magnetic component. c Coupled oscillators representation of the ferromagnetic haloscope, in which the strong coupling is realised between an rf cavity mode c (frequency ωc) with the Kittel mode m (ωm) to improve the setup sensitivity. The axion–Dark Matter field acts as a tiniest classical rf field on the hybrid system, and it is thus represented by a weakly coupled oscillator a.
These HSs have been realised and extensively studied in the last decade9,10,11,12,13,14, and applied to the development of quantum memories15,16, microwave to optical photon conversion17,18,19,20,21, detection of single magnons5, or in spintronics22. Furthermore, the investigation of non-Hermitian quantum mechanics23 is currently pursued with photon-magnon HSs. Here we focus on an HS devised to probe weak and persistent effective rf fields, which is the physics case of dark matter (DM) axions24.
The axion is a hypothetical particle introduced as a consequence of the strong CP problem solution found by Peccei and Quinn25,26,27. It is a light pseudo-Goldstone boson arising from the breaking of the Peccei–Quinn symmetry at extremely high energies fa ≃ 1012 GeV. Since its mass and couplings are proportional to 1/fa the axion is extremely light and weakly interacting28,29,30,31. Relevant quantities of them may have been produced in the early universe, qualifying the axion as a viable candidate of cold DM that would account for the whole density ρDM = 0.45 GeV/cm3 of the Milky Way’s halo32,33,34,35,36. A suitable mass range for the axion is ma = 10−(3/5) eV37,38,39,40,41, hence its de Broglie wavelength is of the order of metres and allows a coherent interaction with macroscopic systems. Together with the high occupation number ρDM/ma, this allows to treat the axion DM field as a classical rf field. The presence of axions can be tested with earth-based precision measurements42,43,44 probing observables sensitive to the presence of DM axions, i.e., the rf-power in a microwave cavity under a static magnetic field45,46,47,48,49,50,51 or the magnetisation of a sample24,52,53,54,55; we focus on this last case. The described HSs emerge as a natural choice to detect the axion effective field as the variation of a sample magnetisation, and an apparatus measuring the power deposited in an HS by DM axions, and hereafter called Pac, is therefore called ferromagnetic haloscope. As the underlying interaction is tiniest, the ferromagnetic haloscope relies on maximising signal power Pac, which translates to hosting in the limited volume of GHz-frequency cavities a sample with the highest possible electron spin density. In addition, the hybrid modes Q-factor should not be much lower than the axion figure of merit (2 × 106). By using yttrium iron garnet (YIG) as magnetic sample, these two requirements are well satisfied, owing to its high spin density (2 × 1028 spins/m3) and small damping constant (~10−5).
In this work we theoretically analyse the response of a photon-magnon HS to a direct excitation of the magnetic component using a second-quantisation model, and experimentally test the model results with an apparatus involving an optical excitation of the magnetic material. We obtain the first experimental demonstration of the broad frequency tunability of the ferromagnetic haloscope, a crucial property that previously had only been theoretically analysed54. This precision detector at the low energy frontier of particle physics can probe the axion coupling with electron spins in mass ranges of few μeV, as large as that probed by Primakoff haloscopes45,50,51,56, with the advantage of a much simpler frequency scan system. The latter is, in this case, accomplished by varying the amplitude of the external magnetic field, instead of moving tuning rods in ultra-cryogenic environments. While Primakoff haloscopes are based o the coupling of axions to photons, ferromagnetic haloscopes search for axions through their electron interaction. Since testing both these couplings is a way to distinguish between different axions, the two detectors provide a complementary insight into the different models.
In addition, the knowledge we gain on the dynamic response of this photon-magnon HS, allows for the optimising the spin magnetometer, as we can maximise the collected axion power with different magnetising fields.
Results
Theoretical model
To understand the dynamics of a ferromagnetic haloscope and optimise its operation, it is useful to model it. The system parameters are the resonant frequencies of the cavity mode ωc, the one of the Kittel mode ωm, and their linewidths γc and γm, respectively. We use a second-quantisation formalism57,58,59,60,61 in natural units to write the Hamiltonian of this system as the one of two coupled oscillators, photon and magnon, and an external axion field a that interacts only with the magnon. In the rotating-wave approximation it results
where m (m+), c (c+) are the destruction (creation) operators of magnons and photons respectively, and gcm and gam are the magnon-photon and axion-magnon couplings. A scheme of the considered system is shown in Fig. 1c. The last term in Eq. 1 represent the interaction of the axion with the magnon, Na is the axion number Na = 〈a+a〉 and its mass fixes the frequency ωa. We are assuming Na > > 1 and treating axions as a classical external field perturbing the photon-magnon system. The effect of the axion field is to deposit energy in the form of spin-flips (i.e. magnons), which, with the rate gcm, are converted into photons that can be collected as rf power.
Starting from the Hamiltonian in Eq. 1, the evolution of the system can be derived with the Heisenberg–Langevin equations57,58 for the mean values of magnon 〈m〉
and cavity photon 〈c〉 state
where γc,m accounts for dissipations to the thermal reservoir. Given the high occupation number of the magnon and photon states, we solve the equations in a semiclassical approach, and neglect quantum correlations. Eqs. 2 and 3 can be recast as a matrix differential equation
where M is the two-component vector M = (〈m〉, 〈c〉). If we rewrite M as a plane wave \(M=A\exp (-i{\omega }_{a}t)\), Eq. 4 can be recast as
yielding the amplitude of M
from which it is possible to extract the (2, 1) component describing the coupling between the axion field and the cavity
The observable of our apparatus is the power deposited in the resonant cavity by the axion field, which can be calculated through the quadrature operator \(z\equiv ({c}^{+}+c)/\sqrt{2{\omega }_{c}}\), and results
The obtained expression of Pac fully describes the dynamics of the system and can be used to maximise the ferromagnetic haloscope sensitivity. It is interesting to consider the case of the power deposited by an axion field on resonance with one of the two hybrid modes of the system at frequencies
Since the system collects power at the hybrid modes frequencies, to infer the bandwidth of the apparatus one needs to recast ωm in terms of ω± by inverting Eq. 9. Substituting the expression into Eq. 8, Pac results
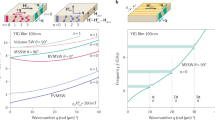
The deposited power is plotted in Fig. 2 for the parameters of our experimental apparatus, and is in agreement with previously reported results54,62. The haloscope collects power on two separated axion-mass intervals, each being one order of magnitude broader than the resonance linewidth, demonstrating a wideband tunability of the haloscope. Hereafter, we call dynamical bandwidth the frequency interval that can be scanned by changing the Larmor frequency, highlighted in red in Fig. 2 for the lower frequency hybrid mode.
a The main figure is the anticrossing plot Pac(ω±, ωm) given by Eq. 8, while the upper and right plots are the projection of the deposited power as function of ω± and ωm, respectively. The upper plot, representing Pac(ω±), shows the apparatus bandwidth in blue for ω− and in orange for ω+. The bandwidth is calculated as the full width half maximum of the ω− curve of Pac(ω±), and its experimentally measured value is reported in red. b In the grey box, the experimental parameters used for the calculation are reported in black, gam and Na (values in blue) have been arbitrarily chosen, and the dynamical bandwidth is shown in red.
The parameters used for this calculation are arbitrarily chosen as they do not influence the experimental results, but we mention that they are related to the axion model and to some cosmological parameters. In particular, the axion number Na depends on the axion number density and on the volume of magnetic material; under the assumption that DM is entirely composed of axions, at the considered frequency we have ρDM/ma ≃ 2 × 1013 axions/cm3. The axions figure of merit depends on their thermal distribution and, as they are cold DM, the energy dispersion is smaller than its mean by a factor 2 × 106. The coupling gam is proportional to the axion–electron coupling constant gaee ≃ 3 × 10−11(ma/1 eV), which slightly depends on the considered axion model, and is a number inversely proportional to the axion mass. For more details on the axion-to-magnon conversion scheme see refs. 24,53,63.
Experimental validation
To study the system frequency response to a direct excitation of the material like that related to the searched particle in ferromagnetic haloscopes, we photoexcite the material with 1064-nm wavelength, 11-ps duration laser pulses and measure the power stored in the HS modes for several values of applied magnetic field. At 1064 nm, the absorption coefficient of YIG is ~10 cm−1 64,65,66, corresponding to the transition 6A1g(6S) → 4T1g(4G) between electronic levels in the octaedral crystal field configuration67. In addition, the laser beam is focused within the sphere and we can thus reasonably assume that the 0.1 mJ energy of the pulse is almost entirely absorbed in the material. A fraction of this energy is transferred from the excited electrons to magnetic oscillations of the material, including the uniform precession mode used in the ferromagnetic haloscope. The optical pulse corresponds to a broadband excitation on the HS, allowing to study the system dynamics by considering the stimulus as frequency-independent. Therefore, this optical excitation is well represented by the last term in Eq. 1, mimicking the axion interaction for the present purpose of demonstrating the spin magnetometer dynamical bandwidth.
We accomplish the strong cavity regime by coupling the Kittel mode, i.e., the uniform precession ferromagnetic resonance8,68, to the TE102 mode of a rectangular cavity, whose resonance frequency is ωc ≃ (2π) 4.7 GHz and the linewidth is γc ≃ (2π) 1.1 MHz. This magnetic dipole coupling is strengthened when the magnetic field amplitude of the chosen cavity mode is maximum at the location of the spin ensemble. By setting a static field B0 such that ωm = γB0 = ωc, we measure the coupling coefficient 2gcm ≃ (2π) 57 MHz, and γm through the linewidth of the hybrid mode γh as γm = 2γh − γc ≃ (2π) 3.5 MHz (see Fig. 3a).
a Transmission spectrum of the cavity (B0 = 0) and of the hybrid system (B0 = 168 mT). The frequency band where the signal is down-converted is evidenced in green. The frequency separation between the hybrid modes is related to the coupling strength between cavity photons and magnons. b Oscilloscope traces of the relevant signals. The laser pulse acts as acquisition trigger (orange) for the down-converted microwave pulse r(t) (blue).
The laser pulses deposit energy in the YIG sphere, which is electromagnetically transduced to cavity excitations. The power deposited in the hybrid mode is dissipated in a time 1/γh = τh, and is measured through an antenna coupled to the cavity. Hence, when the infrared laser pulse excites the YIG sphere, the representative signal r(t) shown in Fig. 3b is detected with the heterodyne microwave receiver detailed in the Methods section. The amplitude of the down-converted r(t) signal is comparable with the receiver noise when B0 is such that the system is far from the anticrossing point, ruling out a direct cavity excitation.
To obtain the transduction coefficient from magnons to photons realised by the strong coupling, we record r(t) for several values of the hybrid frequency ω−, which is varied through the B0 field. The experimental results are compared to the theoretical prediction in Fig. 4. The transduction curve \(q({\omega }_{-})={P}_{ac}({\omega }_{-})/\max ({P}_{ac}({\omega }_{-}))\) has been derived from Eq. 10, and is the normalised top-left projection of the dispersion plot reported in Fig. 2.
The blue curve has been calculated with the parameters reported in Fig. 2. The maximum measured signal was taken to be unitary and the other points were scaled consequently. The grey points were collected with a fixed antenna optimised for measurements around 4.67 GHz, while for the red ones its coupling was, to some extent, adapted for the respective frequency. The data points and relative errorbars are obtained as mean and standard deviation of repeated measurements.
Each measured value is instead obtained with the integral:
where t0 is given by the laser pulse (orange curve in Fig. 3b). As the laser system exhibits shot-to-shot intensity fluctuation of the output pulses, for each ω− the mean and standard deviation of the data is obtained by averaging hundreds of qr(ω−). In Fig. 4 data points are plotted normalised with respect to the one with larger amplitude at 4.67 GHz. It is important to note that no additional elaboration has been carried out on the data, nor fitting procedure on the curve reported in Fig. 4. They indeed display a good agreement for ω− > 4.65 GHz, with a slight discrepancy at lower frequencies that can be explained in terms of mismatched transmission line. In fact, in the model we implicitly assume a condition of critical coupling (i.e. the extracted power is maximum), whereas the coupling between the receiver antenna and the cavity mode changes for different values of ω−. When the coupling is optimised (red data points in Fig. 4), the agreement between experiment and theory significantly improves. The system, see Fig. 2, should behave symmetrically for the resonance ω+.
Discussion
Devising a simple and yet predictive model of an HS-based transducer is a key ingredient to understand the behaviour of a ferromagnetic haloscope. We used a simple second-quantisation model based on a system of two strongly coupled oscillators, a microwave cavity mode and a magnetostatic mode, to describe the transduction of pure magnetic excitations to microwave photons. The modelled physical system includes an external power injection through the magnetostatic mode. This magnetisation oscillation can be given e.g. by DM axions, which, interacting coherently with magnons, would resonantly deposit power in the HS. The transducer converts magnons into photons which can be collected by an antenna. From this model we derive the HS transduction coefficient as a function of the external magnetic field, an easily tunable parameter which changes the resonant frequencies of the HS, and thus the transduction frequency.
To validate the model and to measure the dynamical bandwidth of a photon-magnon HS transducer, we introduce a new optical method to realise a selective excitation of the HS magnetic component, as is the case for axion–DM interactions in the haloscope. This is fundamentally different from the calibration procedure used in Primakoff haloscopes50,51, wherein rf power injection is accomplished through an antenna coupled to the cavity mode. The axion-field sensitivity of this setup is not discussed as the apparatus was not optimised to this aim. The sensitivity of a similar apparatus, and the one of an optimised haloscope, are reported in refs. 63,69, respectively. We note that the magnetic field tuning of the apparatus can be combined with the variation of the cavity resonant frequency50,51,70 to further increase the total bandwidth of the apparatus.
In a ferromagnetic haloscope, a spectroscopic characterisation provides the HS parameters, namely its resonant frequencies, linewidths and couplings, that we insert in our analytical model. By varying the static magnetic field, we change the transduction frequency and experimentally reconstruct the dynamical bandwidth, that is found to be in agreement with the function obtained by the model. Our findings represent the first confirmation of the wide frequency tunability of ferromagnetic haloscopes. Axion masses can in principle be probed by an optimised haloscope in a range up to a few GHz, provided that large bandwidth quantum-limited amplifiers, like travelling-wave Josephson parametric amplifiers71,72, are employed as a first stage of amplification.
The present model can thus be extended to describe more sophisticated ferromagnetic haloscope configurations, namely including ten YIG spheres, as reported in ref. 69, where the transduction efficiency has been used to calculate the upper limit on the axion–electron coupling constant. Whilst we envision the upgrade of the ferromagnetic haloscope to even larger scales to boost the axion signal, we are aware of limitations that might arise in the HS due to the consequent large hybridisation and the corresponding broader dynamical bandwidth. The use of larger spheres54, multiple samples53 or both69, leads to higher order modes, size-effects or multi-spheres disturbances that are not taken into account in the modelled two oscillator HS. A consistent description of such complex apparatus can be obtained by adding additional modes in our model, that can be easily extended to an arbitrary number of coupled oscillators.
These optical tests will be fundamental to get end-to-end calibration in precision measurement apparatuses as those previously mentioned, provided the conversion factor of the underlying process is precisely known. For instance, a cw laser whose intensity is modulated at the relevant frequency might be used to mimic the effective AC magnetic field via the inverse Faraday effect18. Moreover, similar phenomena are studied for optical manipulation of magnons17,18, hence setups like the one presented in this work could be useful to understand the conversion capabilities of HSs.
The study of HSs is continuously growing and cross-fertilise multiple physical topics. In the last years non-Hermitian physics phenomena are tackled by coupling photons and magnons, and exceptional points and surfaces were experimentally demonstrated73,74,75,76,77. In general, our scheme allows for a selective power injection in HSs, feature which can be used to study them on a fundamental level78.
Methods
Ultrafast laser
The laser system in Fig. 5 consists of a passively mode-locked oscillator, followed by a quasi-CW, two-stage Nd:YVO4 slabs amplifier. From a stable train of 8-ps duration, 1064-nm wavelength pulses at 60 MHz repetition rate, an extra-cavity acousto-optic (AO) pulse-picker selects, with adjustable repetition rate, nJ energy pulses that are amplified up to an energy of 100 μJ. The amplifier slabs are pumped by a 150 W peak power quasi-CW laser diode array, synchronised with the oscillator pulses sampled by the AO pulse picker. This has been accomplished by clocking the laser electronics with a secondary output beam of the oscillator by means of a photodiode. The amplified pulses duration is 11 ps, and their repetition rate is 30 Hz.
The 2-mm diameter yttrium iron garnet (YIG) sphere is hosted inside a 98 × 12.6 × 42.5 mm rectangular microwave cavity resonator, at the position of maximum magnetic field intensity for the TE102 mode (as indicated by the colour map filling the cavity) to allow for maximising the coupling between cavity photons and magnons. An electromagnet, represented by its north (N, blue) ad south (S, red) poles, provides the static magnetic field. Picosecond-duration, 1064-nm wavelength laser pulses are used to excite the magnetostatic modes in the YIG sphere, and are monitored thanks to a beam splitter (BS) and a photodiode. The hybrid system dynamics is investigated through a heterodyne receiver coupled to the cavity mode through the antenna θ1, where A1, A2, and A3 are its amplifiers. The signal is amplified before mixing with the output of a local oscillator (LO), further amplified and recorded at the oscilloscope for several values of the external magnetic field. A signal generator (SG), which is weakly coupled to the cavity mode through an inductive loop (θ2), combined with the power splitter (PS) and the spectrum analyser are used to obtain cavity and hybrid system transmission spectra.
Hybrid system
The magnetic material is a 2-mm diameter spherical YIG single crystal. The sphere is glued to a ceramic rod to suspend it in its position, with the easy axis aligned to the static magnetic field. The B0 field is supplied by a small electromagnet. The cavity is a rectangular copper cavity, whose dimensions are 98 × 12.6 × 42.5 mm. The TE102 mode resonates at 4.7 GHz and the quality factor is 4300, estimated with an S21 measurement. The sphere is located at the centre of the cavity, where the rf magnetic field is maximum, and perpendicular to the direction of B0.
Readout and heterodyne
Two antennas, θ1 and θ2, are coupled to the rectangular cavity as sketched in Fig. 5. The coupling of θ2, connected to the microwave oscillator SG, is fixed, while the coupling of θ1 can be varied by changing its position. The weakly coupled θ2 is used to inject microwave power, and thus perform spectroscopic measurements of the HS. The position of θ1 is chosen by doubling the hybrid uncoupled linewidth when ωc = ωm, so that the coupling is close to critical, and remains the same within the measurement. The signal collected by θ1 is amplified by A1 and A2, two high electron mobility field effect transistors low-noise amplifiers. It is then split between a spectrum analyser, useful to acquire the transmission measurements of the HS, and a heterodyne that down-converts the signal to lower frequencies using a mixer and a local oscillator (LO). The down-converted signal, whose band is shown in green in Fig. 3a, is further amplified by A3 and acquired by an oscilloscope triggered by the signal of a photodiode, as shown in Fig. 3b. The frequency of the LO is adjusted whenever the B0 field is changed, in order to keep the hybrid mode frequency ω− within in the down-converted band. The frequency of r(t) in Fig. 3b is the difference between the ones of the LO and of the hybrid mode. The total gain of the amplification chain is of order 71 dB, and the noise temperature of A1 is about 40 K, thus the noise of the apparatus is essentially due to room temperature thermodynamical fluctuations.
Data availability
The data collected during this study are available from the corresponding author upon reasonable request.
References
Jaeckel, J. & Ringwald, A. The low-energy frontier of particle physics. Annu. Rev. Nucl. Part. Sci. 60, 405–437 (2010).
Kirch, K. Symmetries and fundamental interactions: precision experiments at low energies. Eur. Phys. J. 133, 414 (2018).
Lachance-Quirion, D., Tabuchi, Y., Gloppe, A., Usami, K. & Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 12, 070101 (2019).
Lachance-Quirion, D. et al. Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet. Sci. Adv. 3, e1603150 (2017).
Lachance-Quirion, D. et al. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 367, 425–428 (2020).
Schuster, D. I. et al. High-cooperativity coupling of electron-spin ensembles to superconducting cavities. Phys. Rev. Lett. 105, 140501 (2010).
Landau, L. & Lifshitz, E. Quantum Mechanics: Non-Relativistic Theory. Course of Theoretical Physics (Elsevier Science, 1981).
Kittel, C. Introduction to Solid State Physics 8 edn, (Wiley, 2004).
Clerk, A. A., Lehnert, K. W., Bertet, P., Petta, J. R. & Nakamura, Y. Hybrid quantum systems with circuit quantum electrodynamics. Nat. Phys. 16, 257–267 (2020).
Huebl, H. et al. High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids. Phys. Rev. Lett. 111, 127003 (2013).
Tabuchi, Y. et al. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 113, 083603 (2014).
Zhang, X., Zou, C.-L., Jiang, L. & Tang, H. X. Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113, 156401 (2014).
Goryachev, M. et al. High-cooperativity cavity qed with magnons at microwave frequencies. Phys. Rev. Appl. 2, 054002 (2014).
Zhang, D. et al. Cavity quantum electrodynamics with ferromagnetic magnons in a small yttrium-iron-garnet sphere. npj Quantum Inf. 1, 15014 (2015).
Heshami, K. et al. Quantum memories: emerging applications and recent advances. J. Mod. Opt. 63, 2005–2028 (2016).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proc. Natl Acad. Sci. 112, 3866–3873 (2015).
Braggio, C., Carugno, G., Guarise, M., Ortolan, A. & Ruoso, G. Optical manipulation of a magnon-photon hybrid system. Phys. Rev. Lett. 118, 107205 (2017).
Hisatomi, R. et al. Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93, 174427 (2016).
Fernandez-Gonzalvo, X., Chen, Y.-H., Yin, C., Rogge, S. & Longdell, J. J. Coherent frequency up-conversion of microwaves to the optical telecommunications band in an er:yso crystal. Phys. Rev. A 92, 062313 (2015).
Williamson, L. A., Chen, Y.-H. & Longdell, J. J. Magneto-optic modulator with unit quantum efficiency. Phys. Rev. Lett. 113, 203601 (2014).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Moiseyev, N. Non-Hermitian Quantum Mechanics (Cambridge University Press, 2011).
Barbieri, R. et al. Searching for galactic axions through magnetized media: the quax proposal. Phys. Dark Universe 15, 135 – 141 (2017).
Peccei, R. D. & Quinn, H. R. CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 38, 1440–1443 (1977).
Weinberg, S. A new light boson? Phys. Rev. Lett. 40, 223 (1978).
Wilczek, F. Problem of strong p and t invariance in the presence of instantons. Phys. Rev. Lett. 40, 279 (1978).
Dine, M. & Fischler, W. The not-so-harmless axion. Phys. Lett. B 120, 137 – 141 (1983).
Kim, J. E. Weak-interaction singlet and strong CP invariance. Phys. Rev. Lett. 43, 103–107 (1979).
Shifman, M., Vainshtein, A. & Zakharov, V. Can confinement ensure natural cp invariance of strong interactions? Nucl. Phys. B 166, 493 – 506 (1980).
Dine, M., Fischler, W. & Srednicki, M. A simple solution to the strong cp problem with a harmless axion. Phys. Lett. B 104, 199 – 202 (1981).
Spergel, D. et al. Wilkinson microwave anisotropy probe (wmap) three year results: implications for cosmology, 2007. Astrophys. J. Suppl. 170, 377 (2007).
Abbott, L. F. & Sikivie, P. A cosmological bound on the invisible axion. Phys. Lett. B 120, 133–136 (1983).
Turner, M. S. Windows on the axion. Phys. Rep. 197, 67–97 (1990).
Raffelt, G. G. Stars as laboratories for fundamental physics: The astrophysics of neutrinos, axions, and other weakly interacting particles (University of Chicago press, 1996).
Preskill, J., Wise, M. B. & Wilczek, F. Cosmology of the invisible axion. Phys. Lett. B 120, 127 – 132 (1983).
Claudio, B. et al. Recent progress on qcd inputs for axion phenomenology. EPJ Web Conf. 137, 08004 (2017).
Berkowitz, E., Buchoff, M. I. & Rinaldi, E. Lattice qcd input for axion cosmology. Phys. Rev. D. 92, 034507 (2015).
Borsányi, S. et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 539, 69 (2016).
Petreczky, P., Schadler, H.-P. & Sharma, S. The topological susceptibility in finite temperature qcd and axion cosmology. Phys. Lett. B 762, 498–505 (2016).
di Cortona, G. G., Hardy, E., Vega, J. P. & Villadoro, G. The qcd axion, precisely. J. High. Energy Phys. 2016, 34 (2016).
Sikivie, P. Experimental tests of the "invisible" axion. Phys. Rev. Lett. 51, 1415–1417 (1983).
Irastorza, I. G. & Redondo, J. New experimental approaches in the search for axion-like particles. Prog. Part. Nucl. Phys. 102, 89–159 (2018).
Graham, P. W., Irastorza, I. G., Lamoreaux, S. K., Lindner, A. & van Bibber, K. A. Experimental searches for the axion and axion-like particles. Annu. Rev. Nucl. Part. Sci. 65, 485–514 (2015).
Brubaker, B. M. et al. First results from a microwave cavity axion search at 24 μeV. Phys. Rev. Lett. 118, 061302 (2017).
Petrakou, Eleni & for CAPP/IBS. Haloscope searches for dark matter axions at the center for axion and precision physics research. EPJ Web Conf. 164, 01012 (2017).
McAllister, B. T. et al. The organ experiment: An axion haloscope above 15 ghz. Phys. Dark Universe 18, 67–72 (2017).
Asztalos, S. J. et al. Squid-based microwave cavity search for dark-matter axions. Phys. Rev. Lett. 104, 041301 (2010).
Caldwell, A. et al. Dielectric haloscopes: a new way to detect axion dark matter. Phys. Rev. Lett. 118, 091801 (2017).
Du, N. et al. Search for invisible axion dark matter with the axion dark matter experiment. Phys. Rev. Lett. 120, 151301 (2018).
Braine, T. et al. Extended search for the invisible axion with the axion dark matter experiment. Phys. Rev. Lett. 124, 101303 (2020).
Budker, D., Graham, P. W., Ledbetter, M., Rajendran, S. & Sushkov, A. O. Proposal for a cosmic axion spin precession experiment (casper). Phys. Rev. X 4, 021030 (2014).
Crescini, N. et al. Operation of a ferromagnetic axion haloscope at ma = 58 μeV. Eur. Phys. J. C. 78, 703 (2018).
Flower, G., Bourhill, J., Goryachev, M. & Tobar, M. E. Broadening frequency range of a ferromagnetic axion haloscope with strongly coupled cavity-magnon polaritons. Phys Dark Universe 100306, 67–72 (2019).
Garcon, A. et al. The cosmic axion spin precession experiment (CASPEr): a dark-matter search with nuclear magnetic resonance. Quantum Sci. Technol. 3, 014008 (2017).
Stern, I. et al. Cavity design for high-frequency axion dark matter detectors. Rev. Sci. Instrum. 86, 123305 (2015).
Walls, D. F. & Milburn, G. J.Quantum optics (Springer Science & Business Media, 2007).
Scully, M. O. & Zubairy, M. S.Quantum optics (American Association of Physics Teachers, 1999).
Dutra, S. M.Cavity quantum electrodynamics: the strange theory of light in a box (John Wiley & Sons, 2005).
Walther, H., Varcoe, B. T., Englert, B.-G. & Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 69, 1325 (2006).
Bhattacharya, M., Shi, H. & Preble, S. Coupled second-quantized oscillators. Am. J. Phys. 81, 267–273 (2013).
Flower, G., Goryachev, M., Bourhill, J. & Tobar, M. E. Experimental implementations of cavity-magnon systems: from ultra strong coupling to applications in precision measurement. N. J. Phys. 21, 095004 (2019).
Barbieri, R., Cerdonio, M., Fiorentini, G. & Vitale, S. Axion to magnon conversion. a scheme for the detection of galactic axions. Phys. Lett. B 226, 357–360 (1989).
Wemple, S. H., Blank, S. L., Seman, J. A. & Biolsi, W. A. Optical properties of epitaxial iron garnet thin films. Phys. Rev. B 9, 2134–2144 (1974).
Scott, G. B., Lacklison, D. E. & Page, J. L. Absorption spectra of Y3Fe5O12 (yig) and Y3Ga5O12: Fe3+. Phys. Rev. B 10, 971–986 (1974).
Zheng-Wu, Z., Ping-Feng, W., Jian-Hua, Y. & Kang-Wei, Z. Absorption spectrum and zero-field splitting of y3fe5o12. Phys. Rev. B 48, 16407–16409 (1993).
Wang, S. H. et al. Strongly extended diffusion length for the nonequilibrium magnons in Y3Fe5O12 by photoexcitation. Phys. Rev. Mater. 2, 051401 (2018).
Shen, Y. R. & Bloembergen, N. Interaction between light waves and spin waves. Phys. Rev. 143, 372–384 (1966).
Crescini, N. et al. Axion search with a quantum-limited ferromagnetic haloscope. Phys. Rev. Lett. 124, 171801 (2020).
Potts, C. A. & Davis, J. P. Strong magnon-photon coupling within a tunable cryogenic microwave cavity. Appl. Phys. Lett. 116, 263503 (2020).
Macklin, C. et al. A near–quantum-limited josephson traveling-wave parametric amplifier. Science 350, 307–310 (2015).
Planat, L. et al. Photonic-crystal josephson traveling-wave parametric amplifier. Phys. Rev. X 10, 021021 (2020).
Yuan, H. Y. et al. Steady bell state generation via magnon-photon coupling. Phys. Rev. Lett. 124, 053602 (2020).
Zhang, D., Luo, X.-Q., Wang, Y.-P., Li, T.-F. & You, J. Q. Observation of the exceptional point in cavity magnon-polaritons. Nat. Commun. 8, 1368–1368 (2017).
Zhang, X., Ding, K., Zhou, X., Xu, J. & Jin, D. Experimental observation of an exceptional surface in synthetic dimensions with magnon polaritons. Phys. Rev. Lett. 123, 237202 (2019).
Wang, Y.-P. & Hu, C.-M. Dissipative couplings in cavity magnonics. J. Appl. Phys. 127, 130901 (2020).
Cao, Y. & Yan, P. Exceptional magnetic sensitivity of \({\mathcal{PT}}\)-symmetric cavity magnon polaritons. Phys. Rev. B 99, 214415 (2019).
Wolz, T. et al. Introducing coherent time control to cavity magnon-polariton modes. Commun. Phys. 3, 3 (2020).
Acknowledgements
The authors would like to thank Riccardo Barbieri for the help in the development of the theoretical model and Federico Pirzio for the advice on the laser system. We acknowledge the work of Enrico Berto, Mario Tessaro, and Fulvio Calaon, which contributed in the realisation of the mechanics and electronics of the experiment, and INFN-Laboratori Nazionali di Legnaro for hosting the experiment.
Author information
Authors and Affiliations
Contributions
N.C. conceived the experiment and performed the measurements with the help of R.D.V., C.B. G.C. G.R. contributed to the construction of the setup, and N.C., R.D.V., A.O. analysed the data. N.C., C.B. wrote the manuscript. All the author discussed the results and the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Crescini, N., Braggio, C., Carugno, G. et al. Magnon-driven dynamics of a hybrid system excited with ultrafast optical pulses. Commun Phys 3, 164 (2020). https://doi.org/10.1038/s42005-020-00435-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00435-w
This article is cited by
-
Tunable interaction between excitons and hybridized magnons in a layered semiconductor
Nature Nanotechnology (2023)
-
Recent progress on optomagnetic coupling and optical manipulation based on cavity-optomagnonics
Frontiers of Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.