Abstract
The use of structured ultrashort pulses with coupled spatiotemporal properties is emerging as a key tool for ultrafast manipulation. Ultrafast vector beams are opening exciting opportunities in different fields such as microscopy, time-resolved imaging, nonlinear optics, particle acceleration or attosecond science. Here, we implement a technique for the full characterization of structured time-dependent polarization light waveforms with spatiotemporal resolution, using a compact twofold spectral interferometer, based on in-line bulk interferometry and fibre-optic coupler assisted interferometry. We measure structured infrared femtosecond vector beams, including radially polarized beams and complex-shaped beams exhibiting both temporal and spatial evolving polarization. Our measurements confirm that light waveforms with polarization evolving at the micrometer and femtosecond scales can be achieved through the use of structured waveplates and polarization gates. This new scale of measurement achieved will open the way to predict, check and optimize applications of structured vector beams at the femtosecond and micrometer scales.
Similar content being viewed by others
Introduction
During the last decades, the development of laser technology has boosted our ability to control the properties of ultrafast light pulses. Nowadays it is possible to routinely generate coherent radiation from the near-infrared to the soft X-rays1, which can be emitted in the form of few-cycle femtosecond laser pulses2,3,4, or even attosecond pulses5. Furthermore, it is possible not only to tailor their spatiotemporal properties6,7,8, but also to structure ultrafast light fields in their angular momentum properties, including both polarization and orbital angular momentum9,10,11. The ultimate control of the angular momentum properties of ultrafast laser pulses has opened new routes for the study of chiral structures12,13,14, topological systems15,16,17 or magnetic materials18,19 at the ultrafast timescales.
One example of structured ultrafast light fields with tailored spatiotemporal and angular momentum properties are the so-called vector beams20. The paradigm of vector beams is constituted by radially (RP) and azimuthally (AP) polarized beams. In RP and AP beams, the polarization at each point of the beam transverse plane is linear, directed in the radial and tangential directions, respectively. Interestingly, RP beams allow to focus light below the diffraction limit21, which enables applications in different fields such as laser machining22,23 or particle acceleration24,25, among others. AP beams can induce longitudinal magnetic fields at the singularity of the electric field26, which offers potential applications in spectroscopy and microscopy27. Recently, it has been shown that they can be used to produce collinear vortices28.
Nowadays vector beams can be routinely produced as continuum waves in the infrared (IR) and visible regimes through the use of uniaxial and biaxial crystals29,30,31, spatial light modulators32, optical fibres33, electrically-tuned q-plates34 or azimuthally dependent half-waveplates fabricated by ultrafast laser nanostructuring of silica glass, also known as s-waveplates35, among others. Recently, the generation of short pulsed, femtosecond vector beams36,37 has gained interest due to their application in high harmonic generation and attosecond science38,39,40 or particle acceleration41. However, the advances of new laser sources and their applications are tied up to the development of characterization techniques. Since the 1990s, different techniques have been used for the temporal characterization of scalar—i.e., with constant linear polarization (LP)—ultrashort laser pulses42. In the last two decades, the problem of measuring spatiotemporal couplings in scalar beams has been tackled with new strategies43,44,45,46,47. In parallel, the reconstruction of time-evolving polarization pulses has also been addressed48,49,50,51,52,53. However, the necessity for the full spatiotemporal characterization of structured ultrafast laser pulses, which simultaneously includes both spatiotemporal and polarization properties, remained a challenge up to now.
In this work we implement a technique to characterize the arbitrarily space-time (and the space-frequency) polarization dependence of structured ultrafast fully polarized light pulses. In particular we perform the full characterization of infrared femtosecond vector beams generated through an s-waveplate, which allow us: (i) to measure the spatiotemporal quality of RP pulses; (ii) to shape and characterize time-dependent vector beams, structured through the use of polarization gates, and (iii) to monitor the focusing properties of structured vector beams. Our technique is based on two-fold spectral interferometry, both for the spatiotemporal reconstruction through spatially resolved spectral interferometry assisted by a fibre-optic coupler44, and for the polarization analysis through in-line bulk interferometry with a thick birefringent plate53. The complete knowledge of the vector beam amplitude and phase allows to reconstruct the polarization state of the beam profile (including intensity, polarization azimuth and relative phase between the polarization components) both in the space-frequency and space-time domains. We demonstrate that spectral interferometry is a powerful technique for the characterization of ultrafast vector beams, opening the route for a new set of characterization techniques of structured light waveforms, to be used in a diverse range of applications50,54,55 that make use of spatial and temporal polarization shaping.
Results
Technique for full spatiotemporal polarization measurement
An ultrafast vector beam can be either expressed in the space-frequency domain or in the space-time domain, being the representation equivalent as they are connected by the Fourier-transform. In the paraxial approximation, the vector beam propagating in the z-axis will be characterized by the polarization components in the xy plane, this is to say, \({\mathbf{E}} = ( {E_x,E_y})\). In the spatiospectral domain (depending on the angular frequency \(\omega\) and the transverse coordinates x and y), the electric-field components at a certain propagation distance z (observation plane) can be expressed as a function of their amplitudes (\(A_x\) and \(A_y\)) and phases (\(\phi _x\) and \(\phi _y\)), as given by
As we will discuss later, the amplitudes can be directly obtained from the corresponding measured spectra \(S\) of the beam, i.e. \(A = \sqrt S\), while the measurement of the phases conforms the core of the technique.
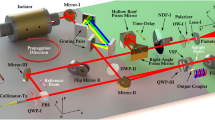
The technique that we have used to perform the complete spatiotemporal and polarization characterization is based on two-fold spectral interferometry. A scheme of the experimental setup is shown in Fig. 1. The laser output is divided into two replicas, one of them is used as a reference (known), while the other beam is shaped in its polarization components—using an s-waveplate optionally with retarder waveplates (in the case of the multiple-order plate, it introduces a delay \(\tau _{{\mathrm{PG}}}\) between the fast and slow axes of the plate, due to the difference of dispersion as a result of the birefringence)—, conforming the unknown beam to be characterized. In the unknown beam arm, a thick birefringent plate is placed to introduce a delay \(\tau _{{\mathrm{YX}}}\) between the horizontal and vertical polarization components of the beam. Afterwards, a linear polarizer is used to sample different polarization projections of the beam (0°, 45° and 90° with respect to the x-axis polarization direction). While the reference beam is collected by a fixed position fibre port (therefore not being scanned), the unknown beam is spatially scanned (in the transverse xy plane) with the optical fibre port in a motorized two-dimensional (2D) translation stage. Notice that it is needed to spatially scan the three projections (0°, 45° and 90°), as well as to scan the x-component interference with the fixed reference beam. In the present work, depending on the symmetry of the beam, we have performed in a general case the said scan forming a 2D grid (see Supplementary Note 7) or, when the polarization state does not depend on the radial coordinate, just varying the azimuthal coordinate θ (i.e. describing a circumference as shown in Supplementary Fig. 3). Both single-mode fibres are combined in a broadband fibre-optic coupler. The delay between the reference and the unknown beam, \(\tau _{{\mathrm{XR}}}\), is adjusted and fixed with the longitudinal position of the reference fibre. The known reference phase is measured with a standard temporal characterization technique42 (e.g. in the present case, the spectral phase interferometry for direct electric-field reconstruction (SPIDER) technique56).
An input beam (in our case, a Gaussian pulsed beam presenting horizontal linear polarization and a time duration of 100 fs at full width half maximum, FWHM) is divided into two arms by a beam splitter. The reference pulse is calibrated by a standard method and collected by one of the two single-mode optical fibre port. This port can be moved in the propagation direction in order to adjust a certain delay \(\tau _{{\mathrm{XR}}}\) between the arms of the reference and the unknown beam (x projection), needed for the implementation of the spatiotemporal measurements. The beam in the other arm (unknown beam arm) is shaped by a beam shaper made of an s-waveplate, a multiple-order quarter-waveplate introducing a certain delay \(\tau _{{\mathrm{PG}}}\) between the horizontal and vertical polarization components, and a zero-order quarter waveplate (the last two to create the polarization gate). The x and \(y\) components of the polarization shaped (unknown) beam are delayed with a birefringent plate, introducing a delay \(\tau _{{\mathrm{YX}}}\) for the polarization resolved measurements. The unknown beam is spatially scanned with an optical fibre port, that is recombined with the reference beam by means of a fibre coupler. The x projection spectrally interferes with a known reference pulse, while the \(y\) and x components spectrally interfere after a 45° linear polarizer. Inset polarization ellipse: scheme of the polarization ellipse defined through the polarization azimuth angle \(\chi\) and the ellipticity \(\varepsilon' = b/a\). Inset coordinate axes: the unknown beam propagates in the z-axis, the x- and y-axes are defined in the transverse plane, where the azimuthal coordinate \(\theta\) is measured with respect to the x-axis.
In order to perform the complete characterization, first we measure the spatially resolved spectral interferometry between the 0°-projection (x-component) of the unknown beam and the reference pulse, \(S_{x + {\mathrm{Ref}}}(\omega ,x,y)\), by setting the linear polarizer horizontal. Then we obtain their relative phase using Fourier analysis57 (see details in Methods). Afterwards, we measure the spectrum profile of the same beam projection, \(S_x(\omega ,x,y)\). As the reference phase is known, we obtain the spatiospectral (and spatiotemporal) amplitude and phase of the x-component of the unknown beam. This strategy44 has been shown to be very versatile by use in the measurement of diffractive focusing, nonlinear processes and few-cycle pulse characterization8,58,59,60, among others.
Second, we acquire the 90°-projection of the unknown beam, \(S_y(\omega ;x,y)\), by placing the linear polarizer vertically. Finally, with the linear polarizer at 45°, we measure an intermediate projection of the x and y components, \(S_{x + y}(\omega ;x,y)\), which encodes their relative phase (see details in Methods). This allows us to accurately retrieve the phase of the y component, and thus, the frequency-dependent and time-dependent polarization53. The phase introduced by the birefringent plate is calibrated as described in the Methods Section. Since the fibre scans the transverse profile of the unknown beam, we retrieve the full spatiotemporal (and spatiospectral) polarization dependence of the beam. The measured polarization ellipses are fully characterized in terms of their ellipticity, \(\varepsilon' = b/a\), and polarization azimuth angle χ (see inset polarization ellipse in Fig. 1), together with the measured dephase, \(\delta = \phi _y - \phi _x\), that is related to the ellipticity and provides the handedness of the polarization (positive and negative values of the dephase \(\delta\) stand for right- and left-handed polarization, respectively). We redefine the ellipticity as \(\varepsilon = {\mathrm{sign}}(\delta )\cdot b/a\), so it provides the ellipticity and the handedness in a single parameter. A detailed explanation of polarization states and the calculation of \(\varepsilon\), χ can be found in the Supplementary Note 1.
Characterization of radially polarized laser pulses
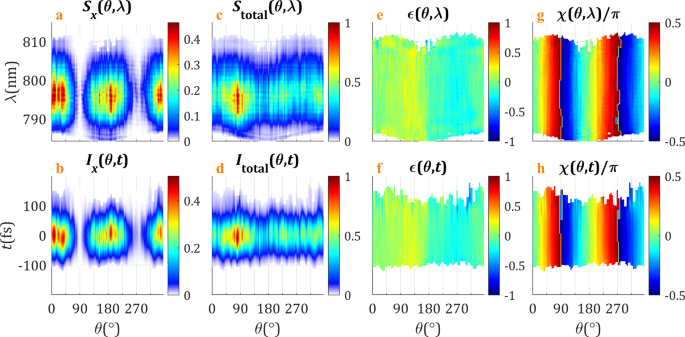
First, we have characterized a femtosecond RP beam created through an s-waveplate placed after the output of a chirped pulse amplification Ti:sapphire laser (see Methods for further details). In the present case, the radial r and the azimuthal coordinate \(\theta\) in the \(xy\) plane are uncoupled in the detection plane, provided that the dependence on r is related to the transverse profile of the input beam, which can be considered Gaussian. In order to explore the polarization distribution of the beam along the azimuthal coordinate \(\theta\), we scanned the xy plane through a circumference of radius R = 3 mm (corresponding to the half maximum of the beam intensity, see Supplementary Fig. 3) around the optical axis. In Fig. 2 we show the ellipticity (ε), polarization azimuth (χ) and intensity profiles (x-projection, and total) of the vector beam in the space-frequency (first row) and space-time (second row) domains. The x-projection of the spectrum or intensity (Fig. 2a, b) describes the expected lobes found when a RP beam passes through a linear polarizer horizontally oriented. The y-component is complementary so that the total spectrum and intensity (Fig. 2c, d) are almost constant across the circular scan. This spatial dependence is inherent to the spatial profile of our laser beam (as shown in Supplementary Note 3). Whereas the ellipticity \(\varepsilon\) is found to be close to zero (Fig. 2e, f), the polarization azimuth \(\chi\)—which reflects the orientation angle of the LP field—describes the RP behaviour of the beam (Fig. 2g, h), corresponding to the \(\chi\)-varying LP beam created by the s-waveplate (i.e. the polarization at each point of the beam transverse plane is linear, directed in the radial direction). We find that the operation of the s-waveplate to imprint a RP profile can be considered homogeneous both in the spectral and temporal domains, despite the polychromatic nature of the pulse (notice that the whole spectral bandwidth extends over 25 nm). The full results are shown in Supplementary Note 4. Although in this work we opted to use a radially polarized beam, equivalent results (shifted 90° in the azimuthal coordinate) would be found if using an azimuthally polarized beam (Supplementary Note 5).
a, b x-projection of the spectrum \(S_x\)/intensity \(I_x\); c, d total spectrum \(S_{{\mathrm{total}}}\)/intensity \(I_{{\mathrm{total}}}\); e, f ellipticity \(\varepsilon\); and g, h polarization azimuth \(\chi\). a, c, e, g spatiospectral dependence; b, d, f, h spatiotemporal dependence. Results in the spectral domain are represented as a function of the wavelength \(\lambda\), and the time is denoted by \(t\). The azimuthal coordinate \(\theta\) was sampled in 90 points with a radius of 3 mm. The input laser pulses had a 10 nm (full width at half maximum) spectral bandwidth and 100 fs duration. The results presented in this and following figures are cut below the 1% of the spectral/temporal peak signal. The total spectrum and intensity are normalized to 1.
Measuring shaped time-dependent ultrafast vector beams
In order to show the ability of our technique to characterize vector beams whose polarization distribution varies temporally in the femtosecond timescale, we structure a laser pulse through the use of polarization gates61. When combining an s-waveplate with different types and sets of waveplates, the resulting beam presents a strong spatiospectral and spatiotemporal coupling in its intensity and polarization parameters. One set of waveplates that is particularly interesting is the so-called narrow polarization gate, which is used to effectively generate shorter pulses in certain applications as e.g. isolated attosecond pulse generation61,62,63. In the Methods Section we detail the operation of the narrow gate using a multiple-order quarter-waveplate (QWM) and a zero-order quarter-waveplate (QW0).
In this experiment, we used the RP beam described in the previous Section (created with the s-waveplate), to illuminate the narrow gate elements (i.e. the two waveplates, first the QWM with fast axes at 0° and second the QW0 at 45°). The narrow gate setup is depicted in the Methods Section. The global effect of the narrow gate is that of producing two circular polarization (CP) pulses delayed 100 fs (similar to the pulse duration) with opposite helicity. When using a RP vector beam, the constant orientation angle (polarization azimuth \(\chi\)) of the LP light entering the narrow gate depends on the azimuthal coordinate \(\theta\), and thus the relative amplitude of both CP pulses depends on \(\theta\). When both amplitudes are equal, this is for \(\theta = \pi /4 + m\pi /2\) (being \(m\) an integer), the narrow gate operates normally (see in Methods), producing LP in the centre and CP in the edges of the pulse in the time domain (Fig. 3a, b), whereas the spectral domain ellipticity (Fig. 3c, d) is close to \(\varepsilon \approx 0\) (as measured in ref. 53). For the azimuthal coordinates \(\theta\) in the RP beam where the linear polarization is parallel to the axes of the QWM (see example in Methods), i.e. \(\theta = m\pi /2\), there is only one of the two CP pulses, either being the first (fast axis) or second (slow axis) pulse, which is seen in the temporal intensity (Fig. 3e, f), while both, the temporal and spectral ellipticities are \(\left| \varepsilon \right| = 1\) (constant CP) with the corresponding handedness (left- and right-handed for the pre and postpulse respectively), as shown in Fig. 3a–d. For intermediate azimuthal coordinates \(\theta ,\) the temporal ellipticity minimum (\(\varepsilon = 0\)) is shifted towards the less intense pulse, placed where the two overlapping pulses have the same amplitude (Fig. 3a, b). In the spectral domain, the x-projection of the spectrum is modulated presenting minima/maxima for \(\theta = \pi /4 + m\pi /2\) for the wavelengths where the QWM introduces a dephase \(\pm \!\pi /2\) (exact quarter-wave operation), so its combination with the QW0 results in a vertical/horizontal LP (Fig. 3g, h). Therefore, the whole evolution of the polarization shows a strong dependence in the space and time coordinates as seen in the polarization ellipses (Fig. 3i, j, and Supplementary Note 6). The effect of the combination of radial polarization and the polarization gate is also manifested in the spatiospectral dependence of the polarization azimuth (Fig. 3k, l). The comparison of the experimental results and our numerical simulations performed as described in the Methods Section is shown in Fig. 3. The good agreement between the experimental and theoretical results serves as a validation of our characterization technique. As found in the previous Section, here the small deviations of the experimental results are also due to the spatial profile of the laser beam.
a, b spatiotemporal ellipticity \(\varepsilon\), c, d spatiospectral ellipticity \(\varepsilon\), e, f spatiotemporal total intensity \(I_{{\mathrm{total}}}\), g, h x-projection of the spatially resolved spectrum \(S_x\), i, j selection of spatiotemporal polarization ellipses (\(E_x\) and \(E_y\) are the x and y projections of the electric field) for different scanning positions coloured by their time-dependent ellipticity, and k, l spatiospectral polarization azimuth \(\chi\). a, c, e, g, i, k experiment, b, d, f, h, j, l: simulation. The wavelength and the time are denoted by \(\lambda\) and \(t\), respectively. The azimuthal coordinate \(\theta\) is scanned in 90 points with a radius R = 3 mm. In the ellipticity, the colour scale varies from left-handed circular polarization (\(\varepsilon = - 1\), blue), to linear polarization (\(\varepsilon = 0\), green) and to right-handed circular polarization (\(\varepsilon = + 1\), red). The x projection of the spectrum and the total intensity are normalized to 1.
Focusing monitorization of time-dependent vector beam pulses
Many applications of vector beams, e.g. particle trapping, microprocessing, particle acceleration or nonlinear optics, are carried out at their focus position. Our characterization technique allows us to perform the full characterization both at the far-field and at the near-field. Here we analyse and compare the spatiotemporal polarization dynamics at the focus of the two previously presented vector beams, i.e. the RP vector beam (Fig. 4a–e) and the RP beam followed by the narrow polarization gate (Fig. 4f–t). In both cases, the beam was focused using an achromatic lens with a focal length of 50 cm. In these experiments the ultrafast vector beam presents a rich evolution both in the radial and azimuthal coordinates (r and \(\theta\)). Therefore, we did a 2D spatial scan along the transverse xy plane.
a–e comparison with the focus for the radially polarized beam at the pulse centre (at time \(t\) = 20 fs). f–t selections for three different times, respectively, f–j −100, k–o 20 and p–t 120 fs, for the radially polarized beam followed by a narrow gate. a, f, k, p Horizontal projection of the intensity \(I_x\), b, g, l, q vertical projection of the intensity \(I_y\), c, h, m, r total intensity \(I_{{\mathrm{total}}}\), d, i, n, s ellipticity \(\varepsilon\), e, j, o, t polarization azimuth \(\chi\). The spatial scan was performed in a square grid with 21 × 21 points using a step of 18 μm. All individual intensity maps are normalized to 1.
First, when using a purely RP beam, the ellipticity \(\varepsilon \left( {x,y,t} \right)\) is ideally zero for every position x, y and time t. As shown before, although there is a spatiotemporal intensity modulation, there is no substantial temporal dependence of the polarization parameters of the beam. In Fig. 4c, we show the spatial profile at the focus position for a temporal instant that corresponds to the peak of the pulse. We notice that, instead of an ideally homogeneous ring shape of a RP, the measured beam presents spatial intensity modulations due to the above-mentioned inhomogeneities of the input spatial profile. On the other hand, the spatial distributions of the x and y polarization projections (Fig. 4a, b, respectively) correspond to that of a RP with the singularity at the centre (see the polarization azimuth \(\chi\) profile in Fig. 4e). In the Supplementary Movie 1 we show that the structure of these magnitudes of the focused RP beam is preserved in time.
Contrarily to this case, when focusing the RP beam after passing through the narrow gate, the beam exhibits a temporal/spectral polarization evolution together with the spatial dependence. In this second case the intensity ring is split into two lobes with time-dependent orientations, except for the centre of the pulse at t = 20 fs (the mean propagating time of the beam components passing through the fast and slow axes of the QWM), where the ring is recovered (Fig. 4m), as in the case of a focused RP beam (Fig. 4c). The x and y projections of this temporal snapshot of the intensity corresponds to two lobes oriented at ±45° (Fig. 4k, l). In the temporal leading edge of the beam—corresponding to the fast axis component at QWM—the two lobes are oriented in the x-axis for the total intensity as well as for the x and y projections (Fig. 4f–h). On the opposite, in the temporal trailing edge, the two lobes are oriented in the y-axis (Fig. 4p–r), as the slow axis of the QWM is oriented vertically. The complete temporal evolution is shown in Supplementary Movie 2, where the total intensity evolves from two vertical lobes until they completely fill the ring and then they split into two horizontal lobes. Thus, the x and y intensity projections consist in two spatial lobes evolving from vertical to horizontal but rotating in opposite direction. Regarding the ellipticity (Fig. 4i, n, s), the beam evolves from two dominating left-handed CP horizontal lobes (prepulse) to two dominating right-handed CP vertical lobes (postpulse), with a gradual growing of the latter in detriment of the initial lobes. In between the opposite handedness CP lobes there is LP with a gradual transition. For the temporal maximum (where the total intensity forms a ring), the polarization azimuth \(\chi\) (Fig. 4o) of the LP contributions mentioned before is oriented at 0° (horizontal) at the azimuthal coordinate \(\theta = 45^\circ\) and \(\theta = 225^\circ\) (notice that for those positions the signal is zero for the y-projection of the intensity in Fig. 4l), and the LP oriented at 90° (vertical) at the azimuthal coordinate \(\theta = 135^\circ\) and \(\theta = 315^\circ\) (where the x-projection of the intensity in Fig. 4k is zero). The polarization azimuth \(\chi\) also evolves gradually from the prepulse (Fig. 4j) to the postpulse (Fig. 4t), alternating the orientation of the LP regions described in Fig. 4i, n, s (see Supplementary Movie 2).
In the spatiospectral domain, the frequency dependence presents some similarities related to the time domain evolution. First, for the focused radially polarized beam, as the behaviour is achromatic, the results are constant in the spectral domain (as shown in Fig. 5a–e for 800 nm, and in the Supplementary Movie 3). For the radially polarized beam followed by a narrow gate (Fig. 5f–t), for some wavelengths (e.g. 795 nm) the x and y projections of the spatially resolved spectrum corresponds to two lobes with opposite orientations at ±45° in the xy-plane (Fig. 5f, g). Observing the spectral evolution (Supplementary Movie 4), for some wavelengths (e.g. 800 nm) the spatial profile of the x and y projections forms a ring (Fig. 5k, l), while for other wavelengths (e.g. 803 nm) the two lobes are crossed at \(\mp\)45° with respect to the 795 nm case (Fig. 5p, q). The total spectrum forms a ring for every wavelength (Fig. 5h, m, r). Also, the ellipticity pattern is frequency-independent (Fig. 5i, n, s), with two horizontal left-handed CP lobes and two vertical right-handed CP lobes and a gradual transition in between (LP at ±45° axes in the xy plane), similarly as described for Fig. 4n (temporal centre of the beam). As expected from the frequency-dependent x- and y-projections of the spectrum, the polarization azimuth also varies with the wavelength (Fig. 5j, o, t), being, e.g. for 795 nm (Fig. 5j), \(\chi = 0\) in the \(+ 45^\circ\) axis of the xy plane and \(\chi = \pm \!\pi /2\) in the \(- 45^\circ\) axis of the xy plane. For 803 nm (Fig. 5t) the polarization azimuth is oriented opposite to the 795 nm case.
a–e comparison with the focus for the radially polarized beam at the wavelength \({\uplambda}\) = 800 nm. f–t selections for three different wavelengths, respectively, f–j 795, k–o 800 and p–t 803 nm, for the radially polarized beam followed by a narrow gate. a, f, k, p Horizontal projection of the spectrum \(S_x\), b, g, l, q vertical projection of the spectrum \(S_y\), c, h, m, r total spectrum \(S_{{\mathrm{total}}}\), d, i, n, s ellipticity \(\varepsilon\), e, j, o, t polarization azimuth \(\chi\). All individual spectrum maps are normalized to 1.
Discussion
Tailoring light beams in full dimensionality, i.e. both spatial and temporal shaping of the individual light waveforms on a femtosecond timescale, is nowadays possible. Our results demonstrate spectral interferometry as a suitable technique for performing a complete spatiotemporal and spatiospectral characterization of such ultrafast beams, whose polarization changes in time and space. The use of spectral interferometry is advantageous as the detection is fully linear (except for the reference measurement) and the data processing is fast, direct and univocal, as well as the acquired data being minimal for this level of measurements. The use of a birefringent plate and a fibre-optic coupler to implement a two-fold interferometer avoids using multiple standard interferometers and alignment of beam recombination.
Regarding the vector beam shaping, we show that the combination of spatially varying polarization with temporal polarization shaping can produce singular spatiotemporal polarization dependences. By using a radially polarized beam followed by a narrow polarization gate, we create a complex vector beam with different orientations of the polarization gate or constant circular polarization, depending on the azimuthal coordinate \(\theta\) in the transverse plane. We show experimentally that the temporal evolution at the focus of such a beam presents rich dynamics in contrast to focused radially polarized beams. The typical ring mode of focusing is effectively shortened in time because of the narrow polarization gate, which could be used for example to manipulate or trap nanoparticles during shorter times. This can be advantageous when using few-cycle pulses, due to the dispersion in media for ultrabroadband pulses.
In conclusion, the technique presented here constitutes the full spatiotemporally resolved polarization measurements at the femtosecond scale. It can be applied for far-field and near-field measurements, allowing in situ diagnostics within the region of interest in most experiments. As a consequence, a complete characterization of ultrashort vector beams can now be performed, allowing, for example, for quantitative measurements of imperfections and small deviations of spatiotemporal polarization distributions from ideal vector beams (as shown in this work). Such accurate measurements can be of capital relevance in applications in particle trapping, extreme ultraviolet pulse generation through high harmonic generation, or particle acceleration, where the quality of the beam mode is fundamental.
Our results pave the way for the full characterization of the most complex waves created up to now. Some examples include ultrafast beams carrying both spin and orbital angular momentum, whose quality is very important if applied to high nonlinear processes such as high harmonic generation9, light beams with time-dependent orbital angular momentum properties10, synthetic chiral fields14 or bicircular fields composed of counter rotating fields of different frequencies19,64,65. The emergence of these complex beams has opened opportunities, for example, to resolve the enantiomeric response of chiral molecules or to perform ultrafast studies of magnetic materials. Further advances in these new directions of ultrafast science are ultimately related to the ability to develop characterization techniques of these new laser sources.
Methods
Experimental details
The laser beam employed to perform the measurements was delivered by a chirped pulse amplification Ti:sapphire laser system (Spectra Physics Inc.), with central wavelength at 797 nm and spectral bandwidth of 10 nm FWHM (full width at half maximum) at a repetition rate of 1 kHz. When compressed, the laser pulses have a duration of 100 fs FWHM.
The fibre coupler is made of broadband single-mode fibres centred at 800 nm, being both input arms almost equal-length so that their dispersion is compensated. The relative dispersion due to small difference (~1 mm) between both input arms is calibrated with spectral interferometry.
The thick birefringent plate used was a 3-mm calcite plate (Altechna) with the fast axis oriented vertically. The multiple-order waveplate QWM is a 3-mm quartz plate operating as quarter-wave for 806 nm. The zero-order waveplate QW0 is a 1.3-mm quartz plate designed for quarter-wave operation at 800 nm.
The spectra were acquired with a fibre-coupled spectrometer (Avantes). The spatial scan in the xy plane was done with a two-axes motorized stage (Thorlabs). The reference pulse was characterized with a home-made SPIDER measurement56.
The s-waveplate for 800 nm wavelength was fabricated by ultrafast laser nanostructuring of silica glass.
Spectral interferometry and data analysis
In spectral interferometry, two delayed collinear pulses interfere in the spectral domain and their spectral fringes encode their relative phase as given in
The relative phase can be extracted by Fourier-transform Spectral Interferometry (FTSI) analysis of the fringes57, which is detailed in Supplementary Note 2. The pulse delay \(\tau\) must be high enough to separate the signals in the time domain after Fourier-transform, as well as small enough to yield spectral interferences within the spectrometer resolution. Note that we perform a two-fold interferometer. On one hand, the delay introduced by the birefringent plate between the x- and y-component of the unknown beam is 1.8 ps, determined by the plate thickness and material (3-mm calcite). In the spectral interferometry between the reference pulse and the x-component of the beam, we manually introduced a 2 ps delay. The spectral bandwidth of the unknown pulse must be less or equal than the reference spectrum that interfere, and their relative amplitude must be of the same order to obtain better contrasted fringes. Note that we subtract the individual spectra \(S_1\left( \omega \right)\) and \(S_2\left( \omega \right)\) before applying the FTSI algorithm to improve the reconstruction for lower contrasts (details in Supplementary Note 2). The spatial resolution of the technique is related to the mode-field diameter of the single-mode optical fibre, being in the present case 4 μm. The resolution of the motorized 2D translation stage is 1 μm.
As the reference pulse is characterized—and hence, the phase \(\phi _{{\mathrm{Ref}}}\left( \omega \right)\) is known—the phase of the horizontal projection of the unknown vector beam, \(\phi _x\left( {\omega ;x,y} \right)\), is obtained from the spatially resolved spectral interferences with the reference pulse, given by
Then, from the interference between the projections at 45° of the \(x\) and y components of the unknown beam, the phase of the vertical projection of the unknown vector beam, \(\phi _Y\left( {\omega ;x,y} \right)\), is obtained as
where \(\phi _{yx,{\mathrm{BP}}}\) is the relative phase of the birefringent plate eigenaxes. The calibration of this phase is described in the following subsection. Notice that this relative phase is directly responsible for the introduction of the delay \(\tau _{{\mathrm{YX}}}\) used for the interferometry.
In general, the delay \(\tau\) introduced by a birefringent plate with thickness \(d\) and with extraordinary and ordinary refractive indices \(n_{\mathrm{e}}\) and \(n_{\mathrm{o}}\), respectively, can be calculated as
where \(c\) is the speed of light and we have assumed that the refractive indices are not dispersive. The expression in Eq. (5) is applied to the thick birefringent plate used to introduce \(\tau _{{\mathrm{YX}}}\) for interferometry, as well as for the QWM introducing \(\tau _{{\mathrm{PG}}}\) in the polarization gate.
The spatial scans of the individual spectra, \(S_x\) and \(S_y\), are optional as they can be obtained with the FTSI algorithm from the measurement of \(S_{{\mathrm{Ref}}}\) and the spectral interferometry scans given above, i.e. the spatially resolved interferences \(S_{x + {\mathrm{Ref}}}\) and \(S_{x + y}\) of Eqs. (3) and (4), respectively. Nevertheless, as they can be directly measured, we acquired them, since the performance of the FTSI algorithm is improved when subtracting the individual spectra from the interferences before data processing.
Calibrations
The global dispersion of the birefringent plate can be calculated from the thickness and the refractive index using Sellmeier equations. However, the accurate knowledge of the relative phase between the fast and slow axes is critical for the correct retrieval of the beam polarization. This calibration depends on the thickness and alignment of the birefringent plate. In order to calibrate the system we used a linearly polarized pulse, with no time-evolving polarization, at 45° before the birefringent plate53. From its own interferences, with the projection \(S_{x + y}\), we retrieved accurately the relative dispersion of the birefringent plate. In our measurements, we repeated this calibration after any realignment. We also found that the calibration of the birefringent plate did not depend on the transverse spatial position. Furthermore, with the same calibrating pulse (linearly polarized at 45°), we measured \(S_x\) and \(S_y\) at the same sampling position, to calibrate the amplitude response of the system, which we used to correct the measurements of the individual spectra, \(S_x\) and \(S_y\), of the unknown beam.
Models for the simulations
To simulate the shaped vector beam shown in this work, we started from a homogeneous beam, plane wave, using the experimental spectral amplitude of the laser output. To model the zero-order and multiple-order quartz waveplates, we firstly calibrated their thickness and retardation (if previously unknown) using spectral interferometry in combination with our detection (birefringent plate, linear polarizer and spectrometer). In the simulations, we calculated the dispersion of their eigenaxes from Sellmeier equations and then we imposed the known retardation for the corresponding operation wavelength. Naturally, we applied every element considering the described orientations.
For the s-waveplate, we modelled it as a half-waveplate with the fast axis orientation depending on the azimuthal coordinate \(\theta\). As a reference, when the s-waveplate is oriented to create RP from input horizontal linear polarization, the fast axis orientation is \(\theta /2\). We operated in the space-frequency domain, and at the end we obtained the space-time dependence by Fourier transformation.
Generation of the narrow polarization gate
The experimental implementation for the narrow polarization gate61 consists of using two consecutive quarter-waveplates, the first multiple-order QWM and the second zero-order QW0, with relative eigenaxes at 45°. In the scheme of Fig. 6, the fast axes of QWM and QW0 are located at 0° and 45°, respectively. To operate as a narrow gate, the system is illuminated with LP pulses at 45° with respect to QWM (upper drawing). The thickness of the QWM introduces a delay (of the order of the pulse duration) between the \(x\) (fast) and \(y\) (slow) polarization projections. After the QWM, there is a superposition of both delayed pulse projections, producing LP at 0° and LP at 90° at the leading and trailing edges of the pulse, respectively. Due to the dephase of the QWM, there is CP in the centre of the pulse (same amplitude of the projections). When this pulse impinges on the second waveplate (QW0), the leading and trailing edges of the pulse switch to left- and right-handed CP, respectively, while the CP is converted to LP, producing a sharp minimum of ellipticity in the centre of the pulse, known as narrow polarization gate53,61,62,63. Contrarily, if the input light before the waveplates has LP at 0° (lower scheme in Fig. 6), this is preserved after QWM (having a neutral axis at 0°). The LP is converted to constant CP after QW0 because the 45°-angle between the LP pulse and the eigenaxes of the waveplate. For other input LP pulses, the narrow gate will operate differently, as we show and discuss in the corresponding Results Section when the input beam is radially polarized.
Firstly, a multiple-order quarter-waveplate (QWM) and, secondly, a zero-order quarter-waveplate (QW0) are oriented with their fast axes at 0° and 45°, respectively. When the input pulse has linear polarization (LP) at 45° (upper drawing), the narrow gate operates normally and produces a pulse with circular polarization (CP) at the edges and LP at the centre. If the input pulse has LP at 0° (lower drawing), the output pulse presents constant CP. The ellipticity \(\varepsilon\) is represented in the given colour scale.
Data availability
The raw data that support the findings of this article are available from the corresponding author upon reasonable request.
References
Popmintchev, T. et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. Science 336, 1287–1291 (2012).
Wirth, A. et al. Synthesized light transients. Science 334, 195–200 (2011).
Silva, F. et al. Strategies for achieving intense single-cycle pulses with in-line post-compression setups. Opt. Lett. 43, 337–340 (2018).
Butler, T. P. et al. Watt-scale 50-MHz source of single-cycle waveform-stable pulses in the molecular fingerprint region. Opt. Lett. 44, 1730–1733 (2019).
Brabec, T. & Krausz, F. Intense few-cycle laser fields: frontiers of nonlinear optics. Rev. Mod. Phys. 72, 545–591 (2000).
Li, Y. & Lewellen, J. W. Generating a quasiellipsoidal electron beam by 3D laser-pulse shaping. Phys. Rev. Lett. 100, 74801 (2008).
Vincenti, H. & Quéré, F. Attosecond lighthouses: how to use spatiotemporally coupled light fields to generate isolated attosecond pulses. Phys. Rev. Lett. 108, 113904 (2012).
Alonso, B., Pérez-Vizcaíno, J., Mínguez-Vega, G. & Sola, Í. J. Tailoring the spatio-temporal distribution of diffractive focused ultrashort pulses through pulse shaping. Opt. Express 26, 10762–10772 (2018).
Dorney, K. M. et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin–orbit momentum conservation. Nat. Photonics 13, 123–130 (2019).
Rego, L. et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 364, eaaw9486 (2019).
Ghadimi Nassiri, M. & Brasselet, E. Multispectral management of the photon orbital angular momentum. Phys. Rev. Lett. 121, 213901 (2018).
Cireasa, R. et al. Probing molecular chirality on a sub-femtosecond timescale. Nat. Phys. 11, 654–658 (2015).
Neufeld, O. et al. Ultrasensitive chiral spectroscopy by dynamical symmetry breaking in high harmonic generation. Phys. Rev. X 9, 31002 (2019).
Ayuso, D. et al. Synthetic chiral light for efficient control of chiral light–matter interaction. Nat. Photonics 13, 866–871 (2019).
Spektor, G. et al. Revealing the subfemtosecond dynamics of orbital angular momentum in nanoplasmonic vortices. Science 355, 1187–1191 (2017).
Shen, Y. et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 8, 90 (2019).
Silva, R. E. F., Jiménez-Galán, Á., Amorim, B., Smirnova, O. & Ivanov, M. Topological strong-field physics on sub-laser-cycle timescale. Nat. Photonics 13, 849–854 (2019).
Kimel, A. V. et al. Ultrafast non-thermal control of magnetization by instantaneous photomagnetic pulses. Nature 435, 655–657 (2005).
Fan, T. et al. Bright circularly polarized soft X-ray high harmonics for X-ray magnetic circular dichroism. Proc. Natl Acad. Sci. USA 112, 14206–14211 (2015).
Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photonics 1, 1–57 (2009).
Dorn, R., Quabis, S. & Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 91, 233901 (2003).
Meier, M., Romano, V. & Feurer, T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl. Phys. A 86, 329–334 (2007).
Hnatovsky, C., Shvedov, V., Krolikowski, W. & Rode, A. Revealing local field structure of focused ultrashort pulses. Phys. Rev. Lett. 106, 123901 (2011).
Salamin, Y. I., Harman, Z. & Keitel, C. H. Direct high-power laser acceleration of ions for medical applications. Phys. Rev. Lett. 100, 155004 (2008).
Marceau, V., Varin, C., Brabec, T. & Piché, M. Femtosecond 240-keV electron pulses from direct laser acceleration in a low-density gas. Phys. Rev. Lett. 111, 224801 (2013).
Blanco, M. et al. Ultraintense femtosecond magnetic nanoprobes induced by azimuthally polarized laser beams. ACS Photonics 6, 38–42 (2019).
Guclu, C., Veysi, M. & Capolino, F. Photoinduced magnetic nanoprobe excited by an azimuthally polarized vector beam. ACS Photonics 3, 2049–2058 (2016).
Lopez-Quintas, I. et al. Optical vortex production mediated by azimuthal index of radial polarization. J. Opt. 22, 095402 (2020).
Shvedov, V. G., Hnatovsky, C., Shostka, N. & Krolikowski, W. Generation of vector bottle beams with a uniaxial crystal. J. Opt. Soc. Am. B 30, 1–6 (2013).
Phelan, C. F., Donegan, J. F. & Lunney, J. G. Generation of a radially polarized light beam using internal conical diffraction. Opt. Express 19, 21793–21802 (2011).
Turpin, A. et al. Polarization tailored novel vector beams based on conical refraction. Opt. Express 23, 5704–5715 (2015).
Beversluis, M. R., Novotny, L. & Stranick, S. J. Programmable vector point-spread function engineering. Opt. Express 14, 2650–2656 (2006).
Hirayama, T., Kozawa, Y., Nakamura, T. & Sato, S. Generation of a cylindrically symmetric, polarized laser beam with narrow linewidth and fine tunability. Opt. Express 14, 12839–12845 (2006).
D’Ambrosio, V., Baccari, F., Slussarenko, S., Marrucci, L. & Sciarrino, F. Arbitrary, direct and deterministic manipulation of vector beams via electrically-tuned q-plates. Sci. Rep. 5, 7840 (2015).
Beresna, M., Gecevičius, M., Kazansky, P. G. & Gertus, T. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass. Appl. Phys. Lett. 98, 201101 (2011).
Carbajo, S. et al. Efficient generation of ultra-intense few-cycle radially polarized laser pulses. Opt. Lett. 39, 2487–2490 (2014).
Kong, F., Larocque, H., Karimi, E., Corkum, P. B. & Zhang, C. Generating few-cycle radially polarized pulses. Optica 6, 160–164 (2019).
Hernández-García, C. et al. Extreme ultraviolet vector beams driven by infrared lasers. Optica 4, 520–526 (2017).
Turpin, A., Rego, L., Picón, A., San Román, J. & Hernández-García, C. Extreme ultraviolet fractional orbital angular momentum beams from high harmonic generation. Sci. Rep. 7, 43888 (2017).
Kong, F. et al. Vectorizing the spatial structure of high-harmonic radiation from gas. Nat. Commun. 10, 2020 (2019).
Varin, C. et al. Direct electron acceleration with radially polarized laser beams. Appl. Sci. 3, 70–93 (2013).
Walmsley, I. A. & Dorrer, C. Characterization of ultrashort electromagnetic pulses. Adv. Opt. Photonics 1, 308–437 (2009).
Bowlan, P., Gabolde, P. & Trebino, R. Directly measuring the spatio-temporal electric field of focusing ultrashort pulses. Opt. Express 15, 10219–10230 (2007).
Alonso, B. et al. Spatiotemporal amplitude-and-phase reconstruction by Fourier-transform of interference spectra of high-complex-beams. J. Opt. Soc. Am. B 27, 933–940 (2010).
Miranda, M. et al. Spatiotemporal characterization of ultrashort laser pulses using spatially resolved Fourier transform spectrometry. Opt. Lett. 39, 5142–5145 (2014).
Pariente, G., Gallet, V., Borot, A., Gobert, O. & Quéré, F. Space-time characterization of ultra-intense femtosecond laser beams. Nat. Photonics 10, 547–553 (2016).
Dorrer, C. Spatiotemporal metrology of broadband optical pulses. IEEE J. Sel. Top. Quantum Electron. 25, 1–16 (2019).
Walecki, W. J., Fittinghoff, D. N., Smirl, A. L. & Trebino, R. Characterization of the polarization state of weak ultrashort coherent signals by dual-channel spectral interferometry. Opt. Lett. 22, 81–83 (1997).
Schlup, P., Masihzadeh, O., Xu, L., Trebino, R. & Bartels, R. A. Tomographic retrieval of the polarization state of an ultrafast laser pulse. Opt. Lett. 33, 267–269 (2008).
Rhee, H. et al. Femtosecond characterization of vibrational optical activity of chiral molecules. Nature 458, 310–313 (2009).
Sato, M. et al. Terahertz polarization pulse shaping with arbitrary field control. Nat. Photonics 7, 724–731 (2013).
Lin, M.-W. & Jovanovic, I. Single-shot measurement of temporally-dependent polarization state of femtosecond pulses by angle-multiplexed spectral-spatial interferometry. Sci. Rep. 6, 32839 (2016).
Alonso, B. & Sola, Í. Measurement of ultrashort vector pulses from polarization gates by in-line, single-channel spectral interferometry. IEEE J. Sel. Top. Quantum Electron. 25, 8900307 (2019).
Misawa, K. Applications of polarization-shaped femtosecond laser pulses. Adv. Phys. X 1, 544–569 (2016).
Chen, J., Wan, C. & Zhan, Q. Vectorial optical fields: recent advances and future prospects. Sci. Bull. 63, 54–74 (2018).
Iaconis, C. & Walmsley, I. A. Spectral phase interferometry for direct electric-field reconstruction of ultrashort optical pulses. Opt. Lett. 23, 792–794 (1998).
Lepetit, L., Chériaux, G. & Joffre, M. Linear techniques of phase measurement by femtosecond spectral interferometry for applications in spectroscopy. J. Opt. Soc. Am. B 12, 2467–2474 (1995).
Mendoza-Yero, O. et al. Spatio-temporal characterization of ultrashort pulses diffracted by circularly symmetric hard-edge apertures: theory and experiment. Opt. Express 18, 20900–20911 (2010).
Alonso, B., Miranda, M., Sola, I. J. & Crespo, H. Spatiotemporal characterization of few-cycle laser pulses. Opt. Express 20, 17880–17893 (2012).
Alonso, B. et al. Characterization of sub-two-cycle pulses from a hollow-core fiber compressor in the spatiotemporal and spatiospectral domains. Appl. Phys. B 112, 105–114 (2013).
Tcherbakoff, O., Mevel, E., Descamps, D., Plumridge, J. & Constant, E. Time-gated high-order harmonic generation. Phys. Rev. A 68, 043804 (2003).
Sansone, G. et al. Isolated single-cycle attosecond pulses. Science 314, 443–446 (2006).
Sola, I. J. et al. Controlling attosecond electron dynamics by phase-stabilized polarization gating. Nat. Phys. 2, 319–322 (2006).
Chen, C. et al. Tomographic reconstruction of circularly polarized high-harmonic fields: 3D attosecond metrology. Sci. Adv. 2, e1501333 (2016).
Jiménez-Galán, Á. et al. Attosecond recorder of the polarization state of light. Nat. Commun. 9, 850 (2018).
Acknowledgements
We acknowledge funding from Junta de Castilla y León (SA287P18), cofunded by the FEDER Funds, and from Spanish Ministerio de Economía y Competitividad (FIS2016-75652-P, FIS2017-87970-R, EQC2018-004117-P). C.H.G. acknowledges support from Ministerio de Ciencia, Innovación y Universidades for a Ramón y Cajal contract (RYC-2017-22745), cofunded by the European Social Fund, and support from Ministerio de Ciencia e Innovación (PID2019-106910GB-I00). B.A. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Individual Fellowship grant agreement No. 798264. P.G.K. acknowledges support of ERC project ENIGMA. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 851201).
Author information
Authors and Affiliations
Contributions
I.J.S. and B.A. conceived the idea and designed the experiments. B.A. conducted the experiments. I.J.S. and I.L.Q. participated in the experiments. W.H. collaborated in the experimental setup. P.G.K. and R.D. fabricated and provided the s-waveplate. B.A. analysed the experimental results and performed the simulations and the graphics. I.J.S., B.A. and C.H.G. discussed the results and wrote the first manuscript. All authors revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alonso, B., Lopez-Quintas, I., Holgado, W. et al. Complete spatiotemporal and polarization characterization of ultrafast vector beams. Commun Phys 3, 151 (2020). https://doi.org/10.1038/s42005-020-00419-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00419-w
This article is cited by
-
Optical spatiotemporal vortices
eLight (2023)
-
Broadband control of topological–spectral correlations in space–time beams
Nature Photonics (2023)
-
Supertoroidal light pulses as electromagnetic skyrmions propagating in free space
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.