Abstract
The nature of hadrons is one of the most fundamental mysteries of physics. It is generally agreed that they are made of “colored” quarks, which move nearly free at short scales but are confined inside hadrons by strong interactions at large distances. Because of confinement, quarks are never directly observable and, experimentally, their properties can be tested only indirectly, via high energy collisions. Here we show that superinsulating films realize a complete, one-color model system of hadron physics with Cooper pairs playing the role of quarks. We report measurements on highly controlled NbTiN films that provide a window into the interior of "Cooper pair mesons" and present the first direct evidence of asymptotic freedom, ‘t Hooft’s dual superconductivity confinement mechanism, and magnetic monopoles.
Similar content being viewed by others
Introduction
Quark interactions are described by quantum chromodynamics (QCD), a non-Abelian gauge theory. A salient feature of QCD is asymptotic freedom1,2, the weakening of the interaction coupling strength at short distances (ultraviolet (UV) limit). At large distances (infrared (IR) limit), the quarks are thought to be confined within hadrons, which are physical observable excitations, by strings. Quarks themselves cannot be extracted from hadrons and be seen in isolation. The mechanism for the transition from weak quark interactions in the UV regime to confinement and strings in the IR regime remains an open issue.
‘t Hooft3 put forth an appealing confinement mechanism, the dual superconductivity where the condensate of magnetic monopoles4 constricts the chromoelectric field into thin flux tubes binding quarks into mesons. He coined the term “superinsulator”, as opposite to superconductor, for the confined quark matter with infinite (chromo)-electric resistance. Polyakov showed that this confinement mechanism occurs also in Abelian gauge theories, provided they are compact and hence support topological excitations, magnetic monopoles, which are instantons in 2D and solitons in 3D5,6. The fact that the compact QED in the confinement regime maps onto a confining string theory7,8 makes it a perfect model for ’t Hooft’s dual superconductivity mechanism.
Remarkably, Abelian confinement emerged in a condensed matter realization of superinsulators, predicted first for Josephson junction arrays (JJA) in ref. 9 and rediscovered in ref. 10 in films experiencing the superconductor-insulator transition (SIT). These electric superinsulators constitute a new state of matter with infinite resistance at finite temperatures due to electric strings binding Cooper pairs into “electric mesons”11. Transport measurements revealed superinsulation in titanium nitride (TiN) films10,12, niobium titanium nitride (NbTiN) films13, and, albeit under a different name, InO films14,15. The long-distance electromagnetic response of superinsulators is exactly Polyakov’s compact QED11 with the effective coupling constant
Here α = e2/(ℏc) is the fine structure constant, κ = λ/ξ is the Ginzburg-Landau parameter of the superconducting material, with λ its London penetration depth and ξ its coherence length and ε is the dielectric permittivity of the normal insulating state. Finally, g is the tuning parameter driving the system across the SIT, so that g ≃ 1 near the transition. The function f(κ) is smooth and is \({\mathcal{O}}(1/\kappa )\) for κ ≫ 111. Pure gauge compact QED in 2D is not renormalizable. However, coupling the action to dynamical matter results in a non-trivial fixed point16,17. The same occurs in our case: compact QED is induced by an underlying matter dynamics from which it inherits the corresponding fixed point structure encoded in g. One can show18,19 that g, and hence also the effective coupling \({e}_{{\rm{eff}}}^{2}\), have a Berezinskii–Kosterlitz–Thouless (BKT) (see ref. 20 for a review) infrared (IR) fixed point at the critical value gc, at which the string tension diverges. The tension, and thus the interaction strength, flow to smaller values in the UV limit and, as a result, the induced compact QED2 becomes asymptotically free, albeit this applies near the confining IR fixed point, instead of near the UV-free fixed point, as in QCD.
Confinement by strong interactions prevents a direct view on quarks despite that they move nearly free at small scales. Since electric Cooper pair mesons are generated by much weaker Coulomb interactions, they have a macroscopic dimension and are accessible to direct experimental study. Here we investigate superinsulators, which allow for a direct observation of the interior of electric mesons made of Cooper pairs by standard transport measurements. We reveal the transition from the confined to the asymptotic free Cooper pair motion upon decreasing the distance between electrodes, realizing the observation spatial scale. Using the compact QED mapping we demonstrate the electric Meissner effect and calculate the I–V-characteristics in the confinement regime. Comparing our experimental results with theoretical predictions yields the string tension and constitutes the first ever “look inside a meson”, directly confirming asymptotic freedom and ’t Hoofts confinement mechanism by magnetic monopoles.
Results
Strings and the Meissner and mixed states of a superinsulator
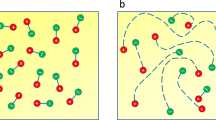
A quantitative theory of the response of a superinsulator to a dc electric field rests on the fact that in a superinsulator the fundamental excitations are electric strings with linear tension σ11. The electric Meissner state is obtained from the dual analog of the London equations7,8,21, describing the electrodynamics of strings connecting charged particles. Deferring the technical derivation of the Meissner state and its vanishing static electric permittivity, εSI = 0, to the end of the paper, we note here that the strings can be either closed, describing pure gauge excitations (the analogs of glueballs in QCD)22 or open, representing Cooper pairs–anti-Cooper pair dipoles (the analogs of mesons in QCD). The presence of such Cooper pair dipoles follows from either self-induced or imposed electronic granular structure of a system supporting superinsulation. When a Cooper pair tunnels from one granule to another it leaves behind a +2e charge excess representing a Cooper pair “hole”. This picture is fully supported by the experimental observation of the charge BKT transition in such materials13. The energy to create pure gauge excitations is ΔG = mv2, with m being the gauge-field mass and v = c/(εμ)1/2 (μ ≈ 1 is the magnetic permeability) being the light velocity in the medium. Open strings have the typical length \({d}_{{\rm{s}}}={\mathcal{O}}(\sqrt{\hslash v/\sigma })\) and a gap of the order \({\mathcal{O}}(\sqrt{\hslash v\sigma })\). The width of the strings is defined by the screening length λel = ℏ/mv22. Both ΔG and the string tension σ are expressed via the ultraviolet (UV) cutoff Λ0 = ℏv/r0, where r0 ≃ ξ in films and is of order of the plaquette size in JJA, as functions of the effective coupling (Eq. (1)) and v23,
For samples with linear dimension L ≫ ds, small electric fields below a critical value Ec1 are sufficient only to excite isolated strings of typical length ds much smaller than the sample size. In this regime, the applied electric field does not penetrate the sample, only neutral “pion-like” dipole excitations made of a Cooper pair and a Cooper “hole” can be created. This is the Meissner state of the superinsulator. When the applied electric field reaches the critical value Ec1, enough electric pions can be created such that a chain of them reaches from one end of the sample to the other. At this point, a single electric flux tube can traverse the sample end-to-end and the Meissner state is destroyed. For E > Ec1 electric fields penetrate the superinsulator in form of flux tubes of typical width λel and the mixed state of the superinsulator sets in. This is the dual state of the Abrikosov lattice in superconductors. Finally, at the critical field Ec2, superinsulation breaks down.
Current-voltage characteristics
We start the derivation of the I(V) response by writing down the compact QED potential for the interaction between Cooper pairs
where the second term is the so-called Lüscher term24. The third term is the screened 2D Coulomb potential (K0 is the MacDonald function) that reduces to \(a\,{\mathrm{ln}}\,(r/{r}_{0})\) at r ≪ λel and decays exponentially at r ≫ λel. At r > r0, the Lüscher term is negligible, so that U(r0) ≃ 0. Near the SIT, the strength of the Coulomb potential becomes11
In the samples with sizes λel < L < ds, Cooper pairs feel neither the string tension nor the Coulomb interaction screened on the scale λel. As we show below this is the asymptotically free regime.
To relate superinsulating parameters to observable quantities, note that strings of length ds have energy \(\sqrt{\hslash v\sigma }\). Hence the energy to form a string chain spanning the entire system is 2eVc1 = σL. Accordingly, one can introduce the lower critical electric field for first string penetration the superinsulating sample
which corresponds to the lower critical field Bc1 in superconductors. For E < Ec1 the Meissner state of superinsulators is realized: electric fields are completely expelled from the superinsulator by the electric dual of the Meissner effect. For E > Ec1, instead, the mixed state of a superinsulator forms. Next, we introduce the deconfinement temperature Tdec that marks the transition between linearly bound charges and unbound charges at T > Tdec. This transition belongs in the BKT universality class and occurs via instanton condensation6. According to ref. 25
where \({{\mathcal{E}}}_{{\rm{C}}}=4{e}^{2}/2\pi \varepsilon {\varepsilon }_{0}{r}_{0}\) is the characteristic bare Coulomb energy of the Cooper pair and a is defined by Eq. (4).
We calculate the current as I ∝ 2enfV, where nf is the equlibrium density of free charges. For the external field Eext < Ec1 ≡ σ/2e the maximum of the potential lies always at the distance L corresponding to the sample size and, thus, the current is simply proportional to the number of charges activated over the barrier (σ − 2eEext)L,
which, in the thermodynamic limit L → ∞, implies an infinite resistance.
For Ec1 < Eext, the potential has a maximum at r = r* determined by the equation \({K}_{1}\left({r}^{* }/{\lambda }_{{\rm{el}}}\right)=\left(2e{E}_{{\rm{ext}}}-\sigma \right){\lambda }_{{\rm{el}}}/a\). Two distinct regimes become possible. The first is realized in small samples such that
where ΔV = V − Vc1, and we have used ds = ℏv/kBTdec. Then the potential for λel < r < L is essentially flat, implying the asymptotic free regime, where charges effectively do not interact, and we expect thus a metallic saturation of the resistance at the lowest temperatures. The ratio ds/λel > 1 but not typically extremely large11. Also, the function K1(x) ≃ \(\exp (-x)\)/\(\sqrt{x}\) at x ≫ 1. Thus, the typical sample size for which this metallic behavior emerges is O(ds), although it can become larger if measurements are taken just above Vc1.
In the limit opposite to Eq. (8), the total energy \({U}_{{{\rm{E}}}_{{\rm{ext}}}}\) of the charge-anticharge pair following from Eq. (3) is
where F = 2eEext − σ is the effective force pulling the charge-anticharge pair apart. The saddle point r* of this potential, controlling the activated current, is r* = a/F, so that the energy barrier is U* ≡ \({U}_{{{\rm{E}}}_{{\rm{ext}}}}({r}^{* })\) = \(a\left[\mathrm{ln}\,(a/F{r}_{0})-1\right]\). In equilibrium, the ionization rate \({\mathcal{R}}\) ∝ \(\exp (-{U}^{* }/{k}_{{\rm{B}}}T)\) and the recombination rate, \({{\mathcal{R}}}_{{\rm{r}}}\), of the ± charges, are equal. Since \({{\mathcal{R}}}_{{\rm{r}}}\) ∝ n+n− = \({n}_{{\rm{f}}}^{2}\), then with logarithmic accuracy nf = \(\sqrt{{\mathcal{R}}}\) ∝ \(\exp (-{U}^{* }/2{k}_{{\rm{B}}}T)\) ∝ \({(F{r}_{0}/a)}^{a/(2{k}_{{\rm{B}}}T)}\), and Eq. (6) yields
where the upper critical voltage V = Vc2 is the voltage where the energy barrier U* vanishes, the I–V curve experiences a jump and the system switches from superinsulation into a normal insulating state. In the field interval such that Vc1 < V < Vc2, the superinsulator is in the mixed state, where an ensemble of electric strings penetrates the system. This is the analog to the mixed, or Abrikosov state in superconductors.
Experiment
The measurements are taken on a polycrystalline 10 nm thin NbTiN film obtained by atomic layer deposition (ALD)13 at temperature 350 ∘C. The temperature dependencies of the resistances are measured on a sample patterned by photolithography into the Hall bar with the width 50 μm, see inset in Fig. 1a. The chosen geometry enables measurements on bridges of different lengths. The experiment is carried out in a 3He/4He dilution refrigerator. The resistance is measured by two-terminal circuit under the low-frequency, f ~ 1 Hz, ac voltage, V ~ 100 μV, in the linear regime as verified by the direct measurements of the films’ I–Vs.
a The Arrhenius plot of sheet resistance R□ vs. reversed temperature 1/T for fridges of various length L. Dashed line shows \(R\propto \exp (1/T)\). Inset: Experimental setup. The Si substrate with AlN buffer layer is shown with light gray and Hall bridge of NbTiN is dark gray. The square gold contacts are given in yellow. All lateral sizes are given in millimeters. The bridges lengths (i.e., distances between measuring electrodes) shown in the legend in panel b. b Same data as in a but replotted as conductance G = 1/R□ vs. T in log-line scale. A few curves are omitted to avoid overcrowding. Dotted lines are fits using a two dimensional Coulomb gas model20 that generalizes the Berezinskii–Kosterlitz–Thouless (BKT) formula for conductance \(G\propto \exp [-{(T/{T}_{{\rm{dec}}}-1)}^{1/2}]\) by incorporating a self-consistent solution to the effects of electrostatic screening13, where the screening length λc and Tdec enter as fitting parameters. For all bridges we find Tdec ≈ 400 mK. c Same data as in b but for temperature renormalized as \({(T/{T}_{{\rm{dec}}}-1)}^{1/2}\). Solid line corresponds to the case of an infinite electrostatic screening length λc → ∞. Inset: Screening length as function of the bridge length L. Symbols correspond to BKT-fits of G(T) (dotted lines in b and c) and dashed line is the eye guide. The error bars are obtained from variations of parameters leaving self-consistent solutions of electrostatic equations of ref. 13 unchanged and are much less than the size of symbols.
The Arrhenius plots of the resistances per square R□(T) vs. inverse temperature 1/T for bridges of different lengths of the same NbTiN film are shown in Fig. 1a. At T > 0.8 K, R□(T) all curves collapse on top of each other. For temperatures below Tdec = 400 mK the long bridges show the hyperactivated behaviors characteristic of superinsulators10,12. The smallest bridge 0.2 mm short, however, clearly shows a metallic-like saturation at very low temperatures. Using the measured critical temperature of 400 mK, the known dielectric constant ε = 800, and the coherence length r0 = ξ = 10 nm in NbTiN13, one can estimate the string size as ds ≃ ℏv/kBTdec, obtaining ds ≃ 0.13 mm in a remarkable quantitative agreement with the experimental result shown in Fig. 1a.
Displayed in Fig. 1b, are the same resistive curves plotted as G = 1/R□ vs. temperature. Fitting them by the standard BKT critical formula \(G={G}_{0}\exp (-{\rm{const}}/\sqrt{T/{T}_{{\rm{dec}}}-1})\), yields indeed Tdec ≈ 400 mK. Deviations from the BKT criticality at lowest temperatures in Fig. 1b, c indicate the point where the typical size of the dissolving dipole matches the size of the finite electrostatic screening length λc which appears in the normal insulator due to screening effect mediated by the free charges (at the BKT transition λc → ∞, and as a practical matter, the perfect criticality would have been observed for λc > 105 13). Following13 and recalling that G ∝ nf, where nf is the density of free charge carriers, one obtains λc using it as an adjusting parameter to fit the curves in Fig. 1c. When doing that, one has to account for the image forces in the Poisson equation that lead to λc = βLL, where βL is a numerical coefficient that serves as an adjusting parameter and L is the length of the bridge. The result in the inset in Fig. 1c perfectly confirms that λc ∝ L.
Comparison of experimental data with theoretical predictions
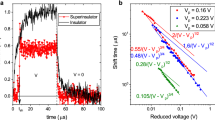
Figure 2 presents the threshold behaviors of the I–V curves corresponding to bridges of different length for two samples having the resistances R□ = 0.2 and 2 MΩ, respectively at T = 2 K. The current jumps span a range of a few orders of magnitude and become less sharp upon shortening the distance between electrodes. The threshold voltage Vc2 exhibits a linear dependence upon L, see in Fig. 2c, d, implying that the threshold electric field Ec2 = Vc2/L is independent on the distance between electrodes in full accordance with Eq. (10). For the low-resistance sample, shown in Fig. 2a, the string tension can be estimated from ds ≃ 0.13 mm as σ ≃ 4.15 × 10−21 J/m = 26 meV/m, which leads to a contribution σ/2e = 1.3 × 10−5 V/mm to the slope. This is negligible with respect to the Coulomb contribution (second term in Eq. (10)), which amounts to a predicted slope of 0.63 V/mm, again in remarkable quantitative agreement with the measured slope of 0.78 V/mm. The I–V characteristics below the threshold, measured at 50 mK, are linear, which agrees reasonably well with the theoretically predicted power-law exponent 1 + (Tdec/16T) = 1 + (400 mK/16 × 50 mK) = 1.5.
The I–V curves of two different NbTiN samples with (a) R□(T = 2 K) = 0.2 MΩ and (b) R□(T = 2 K) = 2 MΩ taken at the same temperature T = 50 mK. Different colors correspond to different bridge’s length L (distance between electrodes). c Dependence of the threshold voltage Vc2 on the bridge’s length for 0.2 MΩ sample. The dashed line depicts Vc2 = 0.78 ⋅ L dependence. The error bars are defined as the width of the jump and are less than the symbol sizes. d Threshold voltage Vc2 for the 2 MΩ sample; Vc2 = 2.1 ⋅ L (dashed line). Error bars are given by the width of the jump. e The dependence of the kink voltage marked by arrows in main panel, which we associate with the critical voltage Vc1 upon the bridge length. The error bars are determined from the errors in the slopes of the I–V curves and are much less than the symbol sizes.
The I–V characteristics of the high-resistance sample are shown in Fig. 2b. The three largest bridges exhibit two-kink I–V curves. The low-voltage kinks are identified as Vc1, and the upper ones represent Vc2. The two smallest bridges do not resolve Vc1. This is because their size is so small that the strings penetrate the entire sample in the whole experimentally accessible voltage range and, thus, the Meissner state is not visible. The linear dependence Vc2 ∝ L of the bridge length L has the slope 2.1 V/mm, see Fig. 2d. Three available values of Vc1 are apparently not sufficient for conclusive evidence of linearity, see Fig. 2e. Let us however assume that Vc1 ∝ L in accordance with (7). Then the mean square deviation estimate for the approximating straight line (shown in red) would give 1.02 V/mm for the slope. Making use Eq. (10), one would obtain the slope 2.1 − 1.02 ≈ 1.1 characterizing the pure Coulomb contribution. From Eq. (10), we then estimate the deconfinement temperature 692 mK for this sample, yielding the exponent 1 + (Tdec/16T) = 1 + (692 mK/16 × 50 mK) = 1.86 for the I–V characteristics in the mixed state, Vc1 < V < Vc2. Comparing this value with the measured ones for the three largest bridges, 1.6, 1.8 and 2, respectively, we conclude that the assumption Vc1 ∝ L results in a fair quantitative agreement between the predicted and measured exponents. Thus, the observation of Vc1 is the first ever direct measurement of Polyakov’s string tension.
Finally, let us discuss why the kink associated with Vc1 is not seen in the IV-curves of the low-resistance sample. Due to its lower resistance, this sample is closer to the SIT, where the deconfinement temperature decreases towards zero. Since measurements of both samples are made at the same temperature, this means that the low-resistance sample is closer to the deconfinement temperature, where the string tension vanishes and strings become infinitely long. As a consequence, strings in the lower-resistance sample are longer than in the high-resistance sample and penetrate the sample end-to-end for all accessible voltages, so that the lower kink Vc1 is not observable. In order to resolve the lower kink and access the Meissner state one needs larger samples, which are sufficiently far from the the SIT and have measurements carried out at low enough temperatures so that the kink was not fogged by the noise.
A theory of the electric Meissner state
Now we discuss the electric Meissner effect and formation of the electric Meissner state at electric fields E < Ec1 which is another spectacular manifestation of Cooper pair confinement. The action of the Abelian confining string, in its local formulation, is induced by the antisymmetric tensor gauge field of the second kind7,8. The vector current of point-like particles is replaced by the tensor current \({{\mathcal{J}}}^{\mu \nu }\) of strings (Greek letters denote space-time indices, Latin letters stand for spatial indices, and we use natural units c = ℏ = 1). Accordingly, the vector potential Aμ, related to the electromagnetic field via Fμν = ∂μAν − ∂νAμ, and coupling to the particle vector current, is replaced by the fundamental field tensor \({{\mathcal{F}}}_{\mu \nu }\) coupled directly to the string tensor current \({{\mathcal{J}}}^{\mu \nu }\). The equations for this field, see “Methods” section
with m = Λ/e, \(\Lambda ={\Lambda }_{0}\sqrt{z}/4\), can be viewed as the dual London equations. In a superinsulator with the light speed v they become, see “Methods” section
where \({\tilde{{\mathcal{J}}}}^{0i}=v{{\mathcal{J}}}^{0i}\), \({\tilde{{\mathcal{J}}}}^{ij}=(1/v){{\mathcal{J}}}^{ij}\), and time derivatives and factors \({{\mathcal{F}}}^{0i}\) in Eq. (12) must be substituted by (1/v)∂0 and \((1/v)\,{{\mathcal{F}}}^{0i}\), respectively. Equation (13) implies the electric Meissner effect for applied voltages below a critical value Vc1 where strings do not penetrate the sample. In the static situation with no strings, Eq. (13) reduces to
For a superinsulator occupying the z > 0 half-space and a uniform electric field Eext applied in the x direction with boundary condition \({{\mathcal{F}}}^{01}(z=0)={E}_{{\rm{ext}}}\) one finds
where λel = 1/(vm) is the electric analog of the London penetration length. Hence, in a bulk superinsulator in the electric Meissner state, the static dielectric permittivity εSI = 0.
To describe the electric Meissner effect in terms of magnetic monopoles, let us recall that the electrodynamics of the dual charge-monopole ensemble is governed by the Maxwell-Dirac equations4
where \({\tilde{F}}^{\mu \nu }=(1/2){\epsilon }^{\mu \nu \alpha \beta }{F}_{\alpha \beta }\) is the dual electromagnetic field tensor (ϵμναβ is the totally antisymmetric tensor), \({j}_{q}^{\mu }\) is the charge current and \({j}_{\phi }^{\mu }\) is the magnetic monopole current. Consider an infinite superinsulating slab harboring an ensemble of vortices aligned along the z axis perpendicular to the slab surfaces, with their magnetic monopole endpoints. The applied dc electric field E ≡ (Ex, 0, 0) generates a magnetic monopole current, according to the dual Ampère law ∇ × E = − jϕ, circulating around the slab in the ±y-direction, which, in turn, induces a shielding electric field opposite to the applied one. Since, in the condensate, monopole motion is dissipationless, the entire external applied electric field is screened. Hence the electric Meissner effect.
The above consideration captures the physics of bulk superinsulators, but the case of thin films is more subtle. The screening length \({\lambda }_{{\rm{el}}}\,\lesssim\, {d}_{{\rm{s}}}\simeq \sqrt{v/\sigma }\)11, increases with temperature and diverges at the deconfinement transition26. For TiN, ds ≃ 60 μm11. In typical experiments on TiN and NbTiN films, where the film thickness d = 3 − 20 nm ≪ λel, the concept of circular monopole currents does not apply literally, since the physical size of the “bulk” monopoles exceeds the film thickness. In this 2D case, monopoles become instantons6, describing tunneling events at which vortex “particles” appear and disappear in the condensate.
Discussion
The novel material presented here, a superinsulator based on an atomic layer deposition grown NbTiN film, opens a new route for further exploring the superinsulating state. Mapping the superinsulator onto compact QED enabled us to construct an electric analog of the superconducting London theory and to describe the electric response and the I–V characteristics of a superinsulator. The device geometry, a Hall bar pattern, allowed us to investigate the details of the electric behavior of a superinsulator as function of the system size and to reveal the linear dimension dependencies of both critical voltages, Vc1, at which the electric mixed state forms, and Vc2, at which superinsulation breaks down. These observations open the door for a direct observation of asymptotic freedom phenomena and allow first-ever measurements of the linear tension of Polyakov’s strings and investigations of the interior of an electric meson via desktop experiments.
Considering the crudeness of our long-wavelength model, the observed Vc2(L) dependencies demonstrate an amazingly good agreement with the theoretical predictions. At the same time, while the results for Vc1 are in an excellent concert with the theoretical estimates, provided the linear dependence Vc1 is assumed, more experimental research is required to establish a calibrated tool for measurements of the string tension.
Methods
Electric London equations
The tensor current describing the motion of strings replaces the vector current encoding the motion of point particles. Correspondingly, the vector potential Aμ related to the original electromagnetic field strength via Fμν = ∂μAν − ∂νAμ is replaced by a fundamental tensor field \({{\mathcal{F}}}_{\mu \nu }\) coupled to the tensor current \({{\mathcal{J}}}^{\mu \nu }\). The associated field strength is given by the three-tensor \({{\mathcal{H}}}_{\mu \nu \rho }={\partial }_{\mu }{{\mathcal{F}}}_{\nu \rho }+{\partial }_{\nu }{{\mathcal{F}}}_{\rho \mu }+{\partial }_{\rho }{{\mathcal{F}}}_{\mu \nu }\). The Euclidean action for electric and magnetic fields in the superinsulating vortex condensate8 acquires the form (we use natural units c = 1, ℏ = 1)
where \(\Lambda ={\Lambda }_{0}\sqrt{z}/4\), with Λ0 = 1/r0 the UV cutoff and z the magnetic monopole quantum fugacity. Varying with respect \({{\mathcal{F}}}_{\mu \nu }\) yields the equations of motion
which, in turn, reduce to Eqs. (11) and (12) of the main text.
For the sake of transparency, we now show how they reduce to the usual Maxwell equations in the limit of vanishing monopole fugacity, z → 0, when the vortex condensate disappears. In this limit we have Λ → 0 and finiteness of the partition function \(Z=\int\,{\mathcal{D}}{{\mathcal{F}}}_{\mu \nu }\,\exp (-S)\) requires that the 3-tensor field strength vanishes, \({{\mathcal{H}}}_{\mu \nu \rho }=0\). This is generically the case for “pure gauge configurations” \({{\mathcal{F}}}_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }={F}_{\mu \nu }\) so that, in this limit, the partition function of classical Maxwell electrodynamics is recovered,
with the current \({j}^{\mu }={\partial }_{\nu }{{\mathcal{J}}}^{\mu \nu }\) describing the now free charges at the end of the original strings. This shows what is the relation between electrodynamics within the vortex condensate and the familiar Maxwell theory. The latter is recovered as a “pure gauge” version of the former.
Electric field equations in materials with v = c/\(\sqrt{\varepsilon \mu }\)
The above “electric London equations” hold if the speed of light is c (=1 in our natural units), which is reflected in the Lorentz invariance of the action (Eq. 17) and the Lorentz covariance of the equations of motion (Eq. 11) of the main text. For real materials, however, this is surely not the case. The (Euclidean) action for electromagnetic fields in a linear material is given by
where, \(v=1/\sqrt{\mu \varepsilon }\) is the light velocity in the material, expressed in terms of the dielectric permittivity ε and the magnetic permeability μ. Due to v < 1, the symmetry of this action is now restricted to non-relativistic Galilean invariance. Correspondingly, the Galilean-invariant action for a superinsulating thin film of this material when vortices condense, is
where, v is the light velocity expressed in terms of material parameters of the normal insulating state. The equations of motion Eqs. (11) and (12) are modified to
where, ΔSI = mv2 represents the energy gap of the superinsulator, \({\tilde{{\mathcal{J}}}}^{0i}=v{{\mathcal{J}}}^{0i}\), \({\tilde{{\mathcal{J}}}}^{ij}=(1/v){{\mathcal{J}}}^{ij}\), and every time derivative and factor \({{\mathcal{F}}}^{0i}\) in the gauge condition, Eq. (12) of the main text, must be substituted by (1/v)∂0 and \((1/v)\,{{\mathcal{F}}}^{0i}\), respectively.
Sample preparation
The sample growths were carried out in a custom-made viscous flow ALD reactor in the self limiting regime. A constant flow of ultrahigh-purity nitrogen (UHP, 99.999%, Airgas) at ~350 sccm with a pressure of ~1.1 Torr was maintained by mass flow controllers. An inert gas purifier (Entegris GateKeeper) was used to further purify the N2 gas by reducing the contamination level of H2, CO, and CO2 to less than 1 ppb and O2 and H2O to less than 100 ppt. The thermal ALD growth of the AlN/NbTiN multilayer was performed using alternating exposures to the following gaseous reactants with the corresponding timing sequence (exposure-purge) in seconds: AlCl3 (anhydrous, 99.999%, Sigma-Aldrich) (1–10), NbCl5 (anhydrous, 99.995%, Sigma-Aldrich) (1–10), TiCl4 (99.995%, Sigma-Aldrich) (0.5–10) and NH3 (anhydrous, 99.9995%, Sigma-Aldrich) (1.5–10). The intrinsic silicon substrates were initially cleaned insitu using a 60 s exposure to 7.5 ± 0.5 nm was deposited at 450 ∘C with 200 ALD cycles. The chamber temperature was then lowered to 350 ∘C to synthesize the NbTiN layers. The growth cycle of the NbTiN is 2× (TiCl4 + NH3) and 1× (NbCl5 + NH3) that was repeated 80 times with the corresponding total ALD cycles 240 to produce the film thicknesses 10 nm as measured ex-istu by X-ray reflectivity (XRR). The chemical composition measured by X-ray Photoemission Spectroscopy (XPS) and Rutherford Backscattering Spectroscopy (RBS) show consistently for the AlN layer 5.5 ± 0.3% of Cl impurities and a Al/N ratio of 1 ± 0.05, whereas for the NbTiN films 3 ± 0.3% of Cl impurities, a Nb/Ti ratio of 2.3 ± 0.03 and a (Nb+Ti)/N ratio of 1 ± 0.03. The material densities measured by RBS and XRR are 2.5 ± 0.01 g/cm3 in AlN and 6 ± 0.05 g/cm3 in the NbTiN. After deposition films were stored at room conditions in ten years.
Samples parameters and measurements
The sample parameters are as follows: the diffusion constant D ~ 0.25 cm2s−1, the superconducting coherence length ξ(0) ~ 5 nm, the density of states as n ~ 4 ⋅ 1021 cm−3 27. NbTiN film was patterned using photolithography and plasma etching into resistivity bar 50 μm wide and with 100, 250 and 100 μm separation between additional perpendicular bars. On this additional bars were making gold contacts. The chosen design allows for two-probe resistivity measurements of regions with different length (2.4, 1.34, 0.55, 0.44, 0.32, 0.2 μm). Measurements of the temperature dependencies of the resistance were carried out in 3He/4He dilution refrigerator Triton400. Two-probe technique was used with the 100 μV and 1 Hz. The chosen values of applied voltage guaranteed that the resistance was obtained in the linear response regime by the direct measurements of current-voltage characteristics. Ac measurements were performed using SR830 lock-in amplifier, dc measurements were performed using nanovoltmeter Agilent 34420, current was transformed into voltage with using SR570 low-noise current preamplifier with filtration system.
Data availability
The authors declare that all relevant data supporting the findings of this study are available within the article.
References
Gross, D. J. & Wilczek, F. Ultraviolet behaviour on non-Abelain gauge theories. Phys. Rev. Lett. 30, 1343–1346 (1973).
Poolitzer, H. D. Reliable perturbative results for strong interactions. Phys. Rev. Lett. 30, 1346–1349 (1973).
t Hooft, G. On the phase transition towards permanent quark confinement. Nucl. Phys. B 138, 1–25 (1978).
Goddard, P. & Olive, D. I. Magnetic monopoles in gauge fields theories. Rep. Progr. Phys. 41, 1357–1437 (1978).
Polyakov, A. M. Compact gauge fields and the infrared catastrophe. Phys. Lett. 59, 82–84 (1975).
Polyakov, A. M. Gauge Fields and Strings. (Harwood Academic Publisher, Chur, Switzerland, 1987).
Polyakov, A. M. Confining strings. Nucl. Phys. B 486, 23–33 (1997).
Diamantini, M. C., Quevedo, F. & Trugenberger, C. A. Confining strings with topological term. Phys. Lett. B 396, 115–121 (1997).
Diamantini, M. C., Sodano, P. & Trugenberger, C. A. Gauge theories of Josephson junction arrays. Nucl. Phys. B 474, 641–677 (1996).
Vinokur, V. M. et al. Superinsulator and quantum synchronization. Nature 452, 613–615 (2008).
Diamantini, M. C., Trugenberger, C. A. & Vinokur, V. M. Confinement and asymptotic freedom with Cooper pairs. Comm. Phys. 1, 77 (2018).
Baturina, T. I., Mironov, A. Y., Vinokur, V. M., Baklanov, M. R. & Strunk, C. Localized superconductivity in the quantum-critical region of the disorder-driven superconductor-insulator transition in TiN thin films. Phys. Rev. Lett. 99, 257003 (2007).
Mironov, A. Y. et al. Charge Berezinskii-Kosterlitz-Thouless transition in superconducting NbTiN films. Sci. Rep. 8, 4082 (2018).
Sambandamurthy, G., Engel, L. M., Johansson, A., Peled, E. & Shahar, D. Experimental evidence for a collective insulating state in two-dimensional superconductors. Phys. Rev. Lett. 94, 017003 (2005).
Ovadia, M. et al. Evidence for a finite-temperature insulator. Scientific Reports 5, 13503 (2015).
Nogueira, F. S. & Kleinert, H. Compact quantum electrodynamics in 2.1 dimensions and spinon confinement: a renormalization group analysis. Phys. Rev. B 77, 045107 (2008).
Kleinert, H., Nogueira, F. S. & Sudbo, A. Kosterlitz-Thouless-like deconfinement mechanism in the (2.1)-dimensional Abelian Higgs model. Nucl. Phys. B 666, 361–395 (2003).
Diamantini, M. C. et al. Bosonic topological intermediate state in the superconductor-insulator transition. Phys. Lett A 384, 126570 (2020).
Diamantini, M. C. & Trugenberger, C. A. Superinsulators, a toy realization of QCD in condensed matter. Invited Contribution to R. Jackiwʼs 80ʼs Birthday Festschrift, pp. 275–286 (World Scientific, Singapore, 2020).
Minnhagen, P. The two-dimensional Coulomb gas, vortex unbinding, and superfluid-superconducting films. Rev. Mod. Phys. 59, 1001 (1987).
Quevedo, F. & Trugenberger, C. A. Phases of antisymmetric tensor field theories. Nucl. Phys. B 501, 143–172 (1997).
Caselle, M., Panero, M. & Vadacchino, D. Width of the flux tube in compact U(1) gauge theory in three dimensions. JHEP 02, 180 (2016).
Kogan, I. I. & Kovner, A. Compact QED3: a simple example of a variational calculation in a gauge theory. Phys. Rev. D 51, 1948–1955 (1995).
Lüscher, M. Symmetry-breaking aspects of the roughening transition in gauge theories. Nucl. Phys. B 180, 317–329 (1981).
Agasyan, N. O. & Zarembo, K. Phase structure and nonperturbative states in three-dimensional adjoint Higgs model. Phys. Rev. D 57, 2475 (1998).
Diamantini, M. C., Gammaitoni, L., Trugenberger, C. A. & Vinokur, V. M. Vogel-Fulcher-Tamman criticality of 3D superinsulators. Phys. Rep. 8, 15718 (2018).
Burdastyh, M. V. et al. Dimension effects in insulating NbTiN disordered films and asymptotic freedom of Cooper pairs. Pis'ma v ZhETF 109, 833–838 (2019).
Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division (V.M.V.). Experimental work (S.V.P. and A.Yu.M.) were supported by Russian Science Foundation project No. 18-72-10056. M.C.D. thanks CERN for hospitality during completion the work. We are grateful to Dr. T. I. Baturina for valuable contribution at the initial stage of research of superinsulator in NbTiN.
Author information
Authors and Affiliations
Contributions
C.M.D., C.A.T. and V.M.V. conceived the work and performed calculations; S.V.P. and A.Yu.M. carried out experiment and analyzed the data; L.G. and C.S. discussed an experiment; all authors discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Diamantini, M.C., Postolova, S.V., Mironov, A.Y. et al. Direct probe of the interior of an electric pion in a Cooper pair superinsulator. Commun Phys 3, 142 (2020). https://doi.org/10.1038/s42005-020-00410-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00410-5
This article is cited by
-
How planar superconductors cure their infrared divergences
Journal of High Energy Physics (2022)
-
Supercapacitance and superinductance of TiN and NbTiN films in the vicinity of superconductor-to-insulator transition
Scientific Reports (2021)
-
Quantum magnetic monopole condensate
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.