Abstract
Quantum computing and quantum communication, have been greatly developed in recent years and expected to contribute to quantum internet technologies, including cloud quantum computing and unconditionally secure communication. However, long-distance quantum communication is challenging mainly because of optical fiber losses; quantum repeaters are indispensable for fiber-based transmission because unknown quantum states cannot be amplified with certainty. In this study, we demonstrate a versatile entanglement source in the telecom band for fiber-based quantum internet, which has a narrow linewidth of sub-MHz range, entanglement fidelity of more than 95%, and Bell-state generation even with frequency multimode. Furthermore, after a total distribution length of 20-km in fiber, two-photon correlation is observed with an easily identifiable normalized correlation coefficient, despite the limited bandwidth of the wavelength converter. The presented implementation promises an efficient method for entanglement distribution that is compatible with quantum memory and frequency-multiplexed long-distance quantum communication applications.
Similar content being viewed by others
Introduction
Recently, quantum technologies have been intensively developed globally. For instance, a quantum processor with 53 qubits was demonstrated by Google1, and they reported that quantum supremacy was verified experimentally. If even larger numbers of qubits become controllable in the future, Rivest–Shamir–Adleman (RSA) cryptosystems could be decrypted using quantum computers2. Quantum communication needs to be developed for the purposes of unconditional security3,4 and of efficient quantum computing by connecting quantum computers through quantum communication network, or quantum internet5. Quantum internet connects remote nodes using quantum entanglement and can enable technologies such as quantum networks of clocks6, secure cloud quantum computing7, and distributed quantum computing. The key element of this technology is quantum entanglement, which is the basis of quantum internet and can be directly applied to quantum teleportation8, entanglement swapping9, and dense coding10.
However, long-distance quantum communication involves challenges due to losses in optical fibers, where unknown quantum states cannot be amplified with certainty, resulting in the need for a quantum repeater for fiber-based transmission. Satellite-based experiments (without a fiber network) have demonstrated 1200-km entanglement generation11, 7600-km BB84 with a decoy state containing a trusted relay12, and photon transmission over ~20,000 km from a medium-Earth orbit satellite13. Although atmospheric transmission can, in principle, facilitate long-distance communication relatively easily, it is significantly limited by air conditions and beam diffraction12. In this case, optical-fiber-based transmission can realize more stable operation not only because fibers are not highly dependent on weather conditions but also because a colossal network of fibers has already been installed around the world.
The solution to overcoming the distance limitations is to use quantum repeaters, which mainly consist of Bell-state operators with14 or without15 quantum memory (QM). The maximum distance of quantum key distribution (QKD) without using quantum repeaters was estimated to be approximately 550 km16; the maximum distance achieved experimentally to date is 421 km17. Aiming beyond secure communication of classical information by QKD, for instance, to combine quantum nodes such as quantum simulators and/or quantum computers, QM is required18 to assist the repeater and preserve quantum information with arbitrary operation timing for multipartite processing.
Based on the above discussion, QM-compatible versatile entanglement source (VES) is ardently desired to approach long-distance fiber-based quantum internet. The VES should emit telecom wavelength photons (~1.5 μm) to minimize fiber loss, have a sufficiently narrow linewidth for many types of QM (≪10 MHz), and achieve high-fidelity quantum entanglement. Each of these specifications, however, is very difficult to realize that there have been only a few reports19 about VES to date: It is still challenging to obtain all of high photon-count rate, narrow linewidth, and high entanglement fidelity in the telecom regime. In previous studies, cavity-enhanced spontaneous parametric down conversion (SPDC) photon sources were demonstrated for many applications20; for example, demonstrating theoretical/proof-of-principle models21,22,23,24,25,26, highly bright single modes27,28,29,30,31, and narrow linewidths32,33,34,35. On the other hand, for compatibility between telecom and QM absorption line, wavelength conversion (WC) is demonstrated using a laser36,37 and single photons38,39 for application to nitrogen-vacancy centers, rare-earth-doped crystals, quantum dots, and rubidium gas, among others. Wavelength conversion still has difficulty about conversion efficiency and noise photon to realize photonic interface.
In this study, we demonstrate a VES with wavelength conversion after 10-km fiber transmission. We utilize the two-photon comb (TPC) technique, which realizes a large number of frequency multimodes and entangled photon pairs with a narrow sub-MHz linewidth even in a telecom band. The WC is based on sum-frequency generation (SFG) and target Pr3+:YSO QM. We successfully realize two-photon 10-km transmission in an optical fiber or overall 20-km distribution and subsequent WC, resulting in a clear observation of comb structure of wavelength-converted TPC (WC-TPC), which is most suitable for use in frequency-multiplexed quantum communication. This technical development can be applied not only to quantum information science but also to experimental optics.
Results
TPC specifications
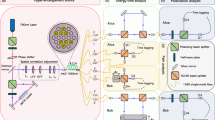
The TPC used herein consists of degenerate 1514-nm SPDC crystals and a surrounding cavity. Further, SPDC occurred in type-0 periodically poled lithium niobite (PPLN) with temperature stability on the order of a few millikelvins. As shown in Fig. 1, we used a mutually orthogonal arrangement to generate two-photon polarization entanglement α|HH〉 + β|VV〉, where α and β are the probability amplitudes including relative phase40. This type of entanglement generation method has three advantages: high brightness or photon-generation rate compared with other phase matching types based on overlapped SPDC cones40, low dependence on optics alignment, and path/phase compensation caused by birefringence in the crystal. However, this type of entanglement generation reduces the finesse of the surrounding cavity because of optical losses (e.g., via absorption, scattering, and reflection) in the crystal, which is a serious problem related to the absorption line of QM. For example, when two 1-cm-long PPLN crystals are placed inside a typical 0.5-m cavity, the theoretical linewidth of the cavity is ~5.3 MHz with a typical PPLN loss of 0.06 dB cm−1 41 in the impedance-matched case. Photons with such linewidth will be coupled to a 10-MHz-linewidth QM with an efficiency of ~70% (we assume Lorentzian photon profile and squarish QM absorption line). Furthermore, because this value can only be obtained in a perfectly aligned case, careful cavity alignment is always required, which requires an additional complicated maintenance procedure. To overcome this disadvantage, we developed a ~2.5-m-long bow-tie cavity with a free spectral range (FSR) of ~120 MHz, which enabled a sub-MHz linewidth along with an increase in the number of frequency modes. All frequency modes are entangled in each photon pair and have good compatibility with atomic-frequency-comb QM, which enables time- and frequency-multiplexed quantum communication42. Cavity locking was achieved using the Pound–Drever–Hall technique to target the absorption line of QM and stabilize the relative phase of entanglement.
The upper part shows two-photon comb (TPC), and the lower part shows a wavelength converter. SPDC pump light was produced by second harmonic generation (SHG) from a 1514-nm external cavity diode laser (ECDL). A half-wave plate (HWP) changes the polarization of the pump light to adjust the ratio of horizontal to vertical generation. SPDC occurs in two mutually orthogonal periodically poled lithium niobite (PPLN) crystals. After coupling to a single-mode optical fiber and transmitting through the 10-km fiber, two collimated photons are combined with a 1010-nm auxiliary laser using a dichroic mirror (DM) to convert the wavelength to 606 nm in the PPLN waveguide (WG). Spectral filters are composed of two dichroic mirrors and one bandpass filter. Detection is performed by two silicon avalanche photodiodes (SiAPDs) and a time-correlated single-photon counting module (TCSPC) with a fiber beam splitter (BS) to realize a Hanbury–Brown–Twiss-type interferometer. To perform two-photon state tomography, a long-pass filter and a 50:50 laser-line beam splitter are inserted before the 10-km fiber, and the two split photons pass through the set of a zero-order 1514-nm quarter-wave plate, a half-wave plate, a vertical-transmittance polarizer, and a fiber coupler to be detected by superconducting single-photon detector (SSPD) of superconducting single photon detector.
To evaluate the quality of the generated two photons, we measured two-photon statistics with a Hanbury–Brown–Twiss-type setup, which consists of a 50:50 beam splitter, two superconducting single photon detector (SSPDs), and a time-correlated single-photon counting module (TCSPC). We utilized SSPD and silicon avalanche photodiode (SiAPD) depending on whether the wavelength of photon was telecom or visible. The SSPDs have efficiencies of approximately 85% at telecom wavelength; Fig. 2a shows the raw data of two-photon correlation with 10-μW pump power. This type of Glauber’s correlation function, which is similar to a comb structure, indicates frequency multimodality as in the Fourier relation. The measured time interval, corresponding to the time taken for a round trip in the cavity, was 8.6 ns, and the FSR was 116 MHz. In general, the ratio between the time interval and the pulse width of each peak gives the number of frequency modes or comb range: if some fiber dispersion exists, the number of modes can be evaluated because the pulse width becomes substantially larger than the timing jitter and thus the timing jitter becomes ignorable. Then, we performed 10-km fiber transmission and evaluated the width of the frequency range by measuring the dispersion. We observed ~2 ns broadening per one channel of TCSPC, and we estimated that TPC had a comb range of approximately 1–2 THz from the fiber dispersion of 15 ps nm−1 km−1 (see Supplementary Note 3).
a Glauber’s two-photon correlation function. The time interval is a cavity round-trip time of 8.6 ns, and the free spectral range (FSR) can be reciprocally estimated as ~120 MHz. The exponential-envelope function had a cavity linewidth of 0.95 MHz, which showed a coherence time of up to 1 μs. Reconstructed density matrices showing the absolute value of b real part and c imaginary part. H horizontal, V vertical.
The exponential envelope with a long coherence time implies a narrow cavity linewidth ∆ν that is affected by the loss over the round trip. By approximating the envelope as e−2π(∆ν)t, we calculated ∆ν as 0.95 MHz (or, according to ref. 25, the degenerate photon linewidth will be 0.64 times this value, i.e., ~0.61 MHz). Whereas this is the case with an output mirror of 99% reflectivity, an output mirror of 95% reflectivity resulted in a broader cavity linewidth of 1.35 MHz and a higher brightness because the escape efficiency was approximately 2−3 times higher.
Photonic-state tomography was performed using the mirror of 95% reflectivity to obtain more precise counts in a shorter acquisition time; Fig. 2b, c shows the reconstructed density matrix of the absolute value after applying the maximum-likelihood method to 16 measurements43. The maximal fidelity to an arbitrary pure state was 96.1% and the concurrence was 93.0%, which were the highest values in the multimode regime (see Supplementary Note 6). Through 16 similar measurements, we further obtained a Clauser–Horne–Shimony–Holt parameter44 S of 2.47 (>2 implies nonlocality). Subsequently, we placed zero-order half-waveplates on the path after the beam splitter to adjust the relative phase of the entangled state and form a Bell state. Four Bell states were achieved (Fig. 3) by changing the angle of the horizontal plane, i.e., the yaw angle and slow axis in the vertical plane. The fidelity to |Φ+〉=|HH〉+|VV〉, |Φ− 〉= |HH〉−|VV〉, |Ψ+〉=|HV〉+|VH〉, and |Ψ−〉=|HV〉−|VH〉 was 90.0%, 90.2%, 89.4%, and 88.1%, respectively (we omitted the coefficients \(1/\sqrt 2\)). These results show that this technique is effective, even for frequency-multiplexed entanglement.
Only the real parts are shown because all the imaginary parts were nearly zero. The fidelity to \(|{{\Phi }}^ + \rangle= |{\mathrm{HH}}\rangle + |{\mathrm{VV}}\rangle\), \(|{{\Phi }}^ -\rangle = |{\mathrm{HH}}\rangle - |{\mathrm{VV}}\rangle\), \(|{{\Psi }}^ +\rangle = |{\mathrm{HV}}\rangle + |{\mathrm{VH}}\rangle\), and \(|{{\Psi }}^ -\rangle = |{\mathrm{HV}}\rangle - |{\mathrm{VH}}\rangle\) was 90.0%, 90.2%, 89.4%, and 88.1%, respectively (we omitted the coefficients \(1/\sqrt 2\)). The raw counts are presented in Supplementary Note 1.
Wavelength-converted two-photon comb
The principle of WC is sum frequency generation (SFG) in a PPLN waveguide with a strong auxiliary laser. Our target wavelength was ~606 nm, which is the center of the Pr3+:YSO absorption line 3H4(0)-1D2(0) 45. In the whole experiment, we used 1514-nm photons and a 1010-nm laser, which satisfy the following two conditions: their sum frequency must be 606 nm and they can be stabilized by molecular gases of acetylene and iodine, respectively. Our setup aimed at conversion of a time-bin state that is suitable for long-distance fiber transmission and would achieve proper quantum frequency conversion because the temporal/linewidth profile of input photons would be preserved. Figure 4a shows WC-TPC with a SPDC pump power of 10 mW and SFG laser power of 50 mW. The WC-TPC has two important parameters: noise floor level and signal-to-noise ratio (SNR). The noise floor level is influenced by many factors, including the presence of a residual laser, which can induce other nonlinear processes such as SPDC and Raman scattering36,37, dark counts in the detector, and stray light (related results are presented in Supplementary Note 5).
a WC-TPC without 10-km optical fiber. Measurement conditions: SPDC pump power of 10 mW; SFG auxiliary laser power of 50 mW; silicon avalanche photodiode (SiAPD) efficiency of ~60%. b Normalized correlation coefficient \({{g}}_{{{s}},{{i}}}^{\left( 2 \right)}\left( 0 \right)\) versus SPDC pump power. The blue circles connected by a line represent 1514-nm two-photon data (without wavelength conversion), and the orange squares represent the WC-TPC data. The error bars, which mean 1 standard deviation of \({{g}}_{{{s}},{{i}}}^{\left( 2 \right)}\left( 0 \right)\), are smaller than the points (or some can be seen in lower power range; see Supplementary Figure 2b and are therefore omitted. Although superconducting single photon detector (SSPD) and SiAPD have almost the same efficiency of 60% owing to the adjustment of applied current, the timing jitters were very different (~40 ps for SSPD, and ~300 ps for SiAPD). c WC-TPC with 10-km fiber. Measurement conditions are same as (a).
Two-photon correlation was characterized by the normalized second-order signal-idler correlation coefficient \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\), which is defined as the ratio of the highest count to the average noise count, similar to SNR (Fig. 4b). The blue circles connected by a line represent \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) before WC (1514-nm two-photon data without WC), and the orange squares represent the values after WC-TPC (the log scale one is in Supplementary Note 2). Some scattering was observed in the values after WC-TPC because the timing jitter increased by one order in the visible range compared with the telecom range. The variation in \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) clearly showed that the low SNR in the signal from the two photons in the telecom range can be increased by putting the two photons through the wavelength converter (see “Discussion” for details). When we tried to demonstrate only single-photon WC, which corresponds to a correlation between the telecom photon and the visible-range photon, we did not observe a clear correlation function, despite extensive adjustment of the SPDC/SFG pump power and spectral filters; we observed \({\mathrm{g}}_{s,i}^{\left( 2 \right)}\left( 0 \right)\,\approx\,1\), i.e., almost the noise floor (data not shown).
Wavelength conversion after fiber transmission
For achieving memory-assisted quantum communication, TPC and WC were combined in an attempt to achieve long-distance communication, assuming that each wavelength has a distinct advantage: telecom qubits can be transmitted across long distances through a fiber with an attenuation of 0.2 dB km−1, whereas the visible-range qubits can interact with highly efficient QM. It is very important to ensure that the whole system is applicable to fiber-based quantum communication because other problems such as the degree of polarization mixing and modulation by wavelength dispersion exist.
Figure 4c shows WC-TPC after telecom two-photon 10-km transmission; this result is comparable to Fig. 4a, which has the same experimental conditions, except for the fiber length. Even two photons with a total separation of 20 km and a long timing jitter of the detector can yield a \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) value of approximately 3. The factors decreasing \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) do not affect the noise floor (but only weaken the coincidence counts) and include fiber losses depending on its length (including a connection loss), polarization rotation induced by birefringence due to the polarization-sensitive WC, and pulse broadening by wavelength dispersion over the time-bin size of the TCSPC. The first factor can be reduced at telecom wavelengths, and our measured transmittance value was approximately 62% at 1514 nm. The second factor can be corrected only when the environmental conditions remain almost unchanged. The third factor is very small because the wavelength converter has a bandwidth of ~0.03 nm. The fiber dispersion of 15 ps nm−1 km−1 therefore induces a pulse spreading of 4.5 ps which is much smaller than the timing jitter. For further increase in \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) with or without a long fiber, the most effective approach is to develop a filter with a suitable frequency range to remove WC noise from the WC-TPC spectra; this technique is discussed in the following section.
Discussion
The TPC has a wide spectral range of ~1 THz, but a very narrow linewidth of ~1 MHz, and it shows polarization entanglement with a fidelity of ~90% to an arbitrary Bell state. In addition, it has a very long time interval and ensures high-speed modulation or time-bin state generation. A narrow linewidth is guaranteed by the long cavity length (or short FSR), even with low finesse. Therefore, the highest finesse in the current setup is not required because the linewidth will remain narrower than the absorption line of QM, even if the finesse reduces slightly due to either a shift in alignment or something else; in our case, the photon with 1-MHz linewidth has a redundancy and will couple to 4.6-MHz window of Pr3+:YSO QM even if finesse becomes less than a half of the present value. Accordingly, TPC is free of frequent cavity alignment, resulting in good compatibility with the troublesome Bell-state generation and connection to QM. At smaller finesse, it has been reported that the intensity of side (or additional) clusters of the main frequency comb increases28; however, because of their spectral separation, the side clusters can be removed using a spectral filter or can be used to increase the number of modes without filtering. The cavity condition is affected by the temperature and convection of air, which can be compensated for by ensuring that the temperature stability of the crystal is of the order of several millikelvins over a period of few days. The condition of the crystal is the main factor preventing high fidelity because many frequency and time modes exist. The relative phase and coherence will clearly deteriorate if the crystal position is changed. To approach the best condition, we used a polyethylene-terephthalate board to eliminate thermal interaction between the crystal holder and the positioning stage, and a wind shield to reduce the changes in air conditions and cavity length. For further improvement, an external compensation crystal, similar to that used for single-pass SPDC46, and separative adjustment of the signal/idler using a conjoint double cavity47 could be included.
To ensure good compatibility between QM and TPC, the QM requires an atomic frequency comb with a tailored absorption line composed of a finely arranged comb-like structure in the wide inhomogeneous-broadening of the rare-earth-ion ensemble (see Supplementary Note 7). This QM has many degrees of freedom of frequency where the absorption line is constructed, except in the case of an extremely small frequency difference (~10 MHz) because of the hyperfine structure. Some previous studies have investigated multifrequency modes48,49. In the case of Pr3+:YSO, the achievable atomic-frequency-comb range is <4.6 MHz, and the inhomogeneous bandwidth is of the order of several to tens of GHz (when the concentration of the dopant Pr3+ is 1%); however, we could not measure the largest bandwidth accurately. Such a wide inhomogeneous broadening can show good connectivity with the overall comb range of WC-TPC limited by the bandwidth of the wavelength converter. Further, assuming that the profile of a photon linewidth of ~1 MHz is pure Lorentzian and that one of the absorption range of 4.6 MHz is squarish, the coupling efficiency is >90%.
Based on the tomographic results, we consider that the dispersion or wavelength-dependent retardance of the waveplates affects the tomographic reconstruction. To realize desired states, additional waveplates unrelated to the tomography are utilized: one for |Φ±〉, and two for |Ψ±〉. Although estimating the magnitude of the effect is difficult due to complex system, the obtained fidelity does appear lower when this is taken into account.
The increase in \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) after the WC was attributed to the different sources of noise before and after the WC, and it also indicates a post-selective effect in which an inconsecutive photon of a pair can be chosen by a so-called “correlation filter”. In the process of WC, because SFG acts only as a spectral shift from telecom to visible wavelengths, it cannot exceed the original SNR with only shifting. Let us consider this effect from two perspectives: frequency and time domains. In the frequency domain, the degenerate-SPDC has a gain curve whose center of degenerate point shows the highest SNR per unit frequency. In this case, the wavelength converted range is positioned around the degenerate point, and it is possible to pick up the highly correlated two photons. In the time domain, in terms of noise, the main sources of noise before WC are the generation of new pairs of photons within the coherence time of another pair that has not yet completed its round trip in the cavity. Then, the decrease in \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) of telecom photons can be attributed to the probability of multipair generation in the cavity. After WC, although \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) depends on the SFG auxiliary laser power, resulting in WC efficiency and noise, the two photons that are separated in the time domain but are certainly correlated will be transferred to the visible range and their correlation will be enhanced within the spectral bandwidth of WC. This effect can also explain the result of very low SNR in one-photon WC: in the telecom range, there were many noise photons consisting of other pairs generated by next SPDC and, consequently, although the WC had high loss and additional noise, the correlation of the two photons reduced.
Although our WC crystal has a limited bandwidth of ~25 GHz that is restricted by the phase-matching condition, WC-TPC can achieve an adequate SNR despite attenuation by a dissonance between the bandwidths of WC and TPC. We demonstrated that the two-photon rate can be increased by controlling the SFG pump power owing to the correlation-filtering effect, which enables detection of photon pairs even if an uncorrelated photon exists within the coherence time of a pair. A trade-off exists between conversion efficiency and noise count depending on the auxiliary laser power. A lower noise count at an SPDC pump power <1 mW is appropriate despite the decrease in conversion efficiency. To achieve an optimal conversion efficiency and noise count, a dedicated filter focusing on the TPC spectrum is required. We propose a filter containing Pr3+:YSO with a high dopant concentration. Using rare-earth ions as a dynamical bandpass filter is not a new idea50,51; however, Pr3+:YSO with a high dopant concentration of ~1% has not been studied well, and is expected to absorb a broad noise spectrum. Although we consider that QM absorption also plays a role in decreasing the noise from outside the two-photon spectra, it degrades the atomic frequency comb because ions may transfer from other hyperfine states.
After developing a special filter, WC can be customized as a polarization-insensitive type39, which is difficult to achieve with the same efficiency as that of a single-polarization type. Polarization-insensitive WC is beneficial in the case of randomly rotating polarization when the conversion efficiency is more than half that of single-polarization WC. Irrespective of the type, the flying qubits should be in a time-bin state that is resistant to polarization changes along the transmission path52. Our single-polarization type WC can be directly applied to real quantum communication by using time-bin states because of the advantages of relative simplicity and higher efficiency: the polarization of time-bin photons will become unpolarized along with long-fiber transmission, and the condition will become the same as in this experiment, except for the quantum state.
In summary, we demonstrated VES with telecom TPC and wavelength conversion of two photons with a total fiber distribution length of 20 km. This technique renders a very narrow linewidth in the telecom range and high fidelity even with a long coherence time and multifrequency modes, thereby creating prospects for quantum applications such as quantum networks combined with WC and the correlation-filtering effect. For further improving the TPC, a new method for separating two degenerate photons is desired to increase the distribution rate and investigate photon statistics. In the case of WC, a specialized filter is required to increase the SNR and establish a good relationship with QM. In addition, Bell state measurements for multimodes are preferable for frequency-multiplexing quantum communication applications. Our future plan is to convert polarization basis to time-bin basis and to add the loss of basis-conversion system to the WC-TPC result, which will enable us to estimate the whole quantum-communication system performance.
Methods
Two-photon comb
Two photons were generated by the SPDC process in two PPLN crystals (manufactured by Jinan Institute of Quantum Technology) having the dimensions of 0.5 × 3 × 10 mm and 0.5 × 0.5 × 10 mm, arranged orthogonally in a bow-tie cavity. The small dimensions allowed the crystals to precisely align with the laser path. The temperatures of the crystals and their holders were stabilized to be within ~1 mK. An SPDC pump laser of 757 nm was obtained by second harmonic generation (SHG) of a 1514-nm external-cavity diode laser (Sacher, TEC420-1530-1000), whose wavelength was stabilized using acetylene molecules. The pump laser was focused to a waist size of ~25 μm using lenses and a plano–concave mirror to achieve strong parametric interaction53.
The optical cavity was stabilized using the Pound–Drever–Hall technique for this laser with an optical chopper with a duty cycle of 1/3. The two photons were separated using a 50:50 laser-line beam splitter, following which they entered a tomographic setup consisting of a zero-order 1514-nm quarter-wave plate, half-wave plate, and vertical-transmittance polarizer, similar to that in ref. 43. To generate a Bell state, two additional half-waveplates were placed in the path of one photon: one plate was used as a phase shifter by aligning the yaw angle, and the other was used as a bit flipper with a slow axis of 45°. The measurement time for one basis was 15 s, which was sufficient to converge the correlation function with a relatively strong pump power of 100 μW. The total testing time was ~10 min, including a rest time of 20 s. In almost all our experiments, the SSPDs were superconducting single-photon detectors with a detection efficiency of ~85%, which was the maximum value for our setup. However, a detection efficiency of ~60% was used in the experiments yielding the results shown in Fig. 4b (blue dots) because our SiAPDs had an efficiency of 60% for visible wavelengths (SPCM-AQRH-14-FC). The maximal input power was 10 mW, resulting in a detected count rate approaching the limit of ~107. We utilized HydraHarp 400 as a TCSPC module, whose resolution is 32 ps for that shown in Fig. 2a, and 16 ps for the others. The 32-ps resolution was used because it could record longer interval times, which was required for measuring the coincidences with an adequate margin.
Wavelength converter
By removing the beam splitter and the tomographic setup, telecom photons were coupled to a polarization-maintaining fiber to be transported to the wavelength converter. An output collimator, consisting of a triplet lens, was placed immediately after the fiber for producing a high-quality single-mode Gaussian beam of diameter ~3 mm. The PPLN for the wavelength converter was of the waveguide type with an area of 9.9 × 11 μm and length of 48 mm (NTT electronics) with a type-0 phase matching condition (all three interacting lights are vertically polarized). The auxiliary laser for SFG has a wavelength of 1010 nm (TOPTICA, TA pro), where the emitted SHG light was stabilized using iodine molecules. Telecom photons and an auxiliary laser were coupled to this waveguide with efficiencies of ~60%. The external conversion efficiency was calculated by multiplying the coupling efficiency and the internal conversion efficiency. The external conversion efficiency was ~60%, whereas the internal counterpart was ~96% (details are presented in Supplementary Note 4). To obtain higher efficiency, we examined a lot of experimental conditions like changes in the combination of lenses, careful observation of waveguides by using camera, and optimization of noise filters. We found the best setup and realized the wavelength conversion of both two photons. Two dichroic mirrors and one bandpass filter were installed as filters to remove WC noise, because using a spectrometer or numerous filters can cause optical loss, decreasing the two-photon coincidence count. In the process of obtaining WC-TPC, one-photon wavelength-converted coincidences were highly noisy that only the noise floor or an extremely low \({\mathrm{g}}_{s,i}^{\left( 2 \right)}(0)\) was observed because of an excessively high photon rate at the telecom detector (~10 Mcts s−1) due to pump-power-dependent uncorrelated photons.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Shor, P. W. Algorithms for quantum computation: discrete logarithms and factoring. In Proc. 35th IEEE FOCS (ed. Goldwasser, S.), pp.124−134 (IEEE Computer Society Press, 1994).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In Proc. IEEE International Conference on Computers Systems and Signal Processing (ed. Goldwasser, S.), pp. 175−179 (IEEE Computer Society Press, 1984).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Kimble, H. The quantum internet. Nature 453, 1023–1030 (2008).
Kómár, P. et al. A quantum network of clocks. Nat. Phys. 10, 582–587 (2014).
Broadbent, A., Fitzsimons, J. & Kashefi, E. Universal blind quantum computation. In 2009 50th Annual IEEE Symposium on Foundations of Computer Science, (ed. Spielman, D.), pp. 517−526 (IEEE Press, 2009).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein−Podolsky−Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Zukowski, M., Zeilinger, A., Horne, M. A. & Ekert, A. K. “Event-ready-detectors” Bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287–4290 (1993).
Bennet, C. H. & Wiesner, S. J. Communication via one- and two-particle operators on Einstein−Podolsky−Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992).
Yin, J. et al. Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144 (2017).
Liao, S.-K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Calderaro, L. et al. Towards quantum communication from global navigation satellite system. Quantum Sci. Technol. 4, 015012 (2018).
Panayi, C., Razavi, M., Ma, X. & Lütkenhaus, N. Memory-assisted measurement-device-independent quantum key distribution. N. J. Phys. 16, 043005 (2014).
Hasegawa, Y. et al. Experimental time-reversed adaptive Bell measurement towards all-photonic quantum repeaters. Nat. Commun. 10, 378 (2019).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 557, 400–403 (2018).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
DiVincenzo, D. P. The physical implementation of quantum computation. Fortschr. der Phys. 48, 9–11 (2000).
Kaiser, F. et al. A versatile source of polarisation entangled photons for quantum network applications. Laser Phys. Lett. 10, 045202 (2013).
Slattery, O., Ma, L., Zong, K. & Tang, X. Background and review of cavity-enhanced spontaneous parametric down-conversion. J. Res. Natl Inst. Stand. Technol. 124, 124019 (2019).
Collett, M. J. & Gardiner, C. W. Squeezing of intracavity and traveling-wave light fields produced in parametric amplification. Phys. Rev. A 30, 1386–1391 (1984).
Eckardt, R. C., Nabors, C. D., Kozlovsky, W. J. & Byer, R. L. Optical parametric oscillator frequency tuning and control. J. Opt. Soc. Am. B 8, 646–667 (1991).
Ou, Z. Y. & Lu, Y. J. Cavity enhanced spontaneous parametric down-conversion for the prolongation of correlation time between conjugate photons. Phys. Rev. Lett. 83, 2556–2559 (1999).
Lu, Y. J. & Ou, Z. Y. Optical parametric oscillator far below threshold: experiment versus theory. Phys. Rev. A 62, 033804 (2000).
Scholz, M., Koch, L. & Benson, O. Statistics of narrow-band single photons for quantum memories generated by ultrabright cavity-enhanced parametric down-conversion. Phys. Rev. Lett. 102, 063603 (2009).
Jeronimo-Moreno, Y., Rodriguez-Benavides, S. & U’Ren, A. B. Theory of cavity-enhanced spontaneous parametric down conversion. Laser Phys. 20, 1221–1233 (2010).
Chuu, C.-S. & Harris, S. E. Ultrabright backward-wave biphoton source. Phys. Rev. A 83, 061803(R) (2011).
Luo, K.-H. et al. Direct generation of genuine single-longitudinal-mode narrowband photon pairs. N. J. Phys. 17, 073039 (2015).
Ahlrichs, A. & Benson, O. Bright source of indistinguishable photons based on cavity-enhanced parametric down-conversion utilizing the cluster effect. Appl. Phys. Lett. 108, 021111 (2016).
Wu, C.-H. et al. Bright single photons for light-matter interaction. Phys. Rev. A 96, 023811 (2017).
Tsai, P.-J. & Chen, Y.-C. Ultrabright, narrow-band photon-pair source for atomic quantum memories. Quantum Sci. Tech. 3, 034005 (2018).
Goto, H., Yanagihara, Y., Wang, H., Horikiri, T. & Kobayashi, T. Observation of an oscillatory correlation function of multimode two-photon pairs. Phys. Rev. A 68, 015803 (2003).
Fekete, J., Rieländer, D., Cristiani, M. & de Riedmatten, H. Ultranarrow-band photon-pair source compatible with solid state quantum memories and telecommunication networks. Phys. Rev. Lett. 110, 220502 (2013).
Rieländer, D., Lenhard, A., Mazzera, M. & de Riedmatten, H. Cavity enhanced telecom heralded single photons for spin-wave solid state quantum memories. N. J. Phys. 18, 123013 (2016).
Rambach, M., Nikolova, A., Weinhold, T. J. & White, A. G. Sub-megahertz linewidth single photon source. APL Photonics 1, 096101 (2016).
Tamura, S. et al. Two-step frequency conversion for connecting distant quantum memories by transmission through an optical fiber. Jpn. J. Appl. Phys. 57, 062801 (2018).
Strassmann, P. C., Martin, A., Gisin, N. & Afzelius, M. Spectral noise in frequency conversion from the visible to the telecommunication C-band. Opt. Express 27, 14298–14307 (2019).
De Greve, K. et al. Quantum-dot spin–photon entanglement via frequency down conversion to telecom wavelength. Nature 491, 421–425 (2012).
Ikuta, R. et al. Polarization insensitive frequency conversion for an atom-photon entanglement distribution via a telecom network. Nat. Commun. 9, 1997 (2018).
Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 60, R773–R776 (1998).
Pomarico, E. et al. Waveguide-based OPO source of entangled photon pairs. N. J. Phys. 11, 113042 (2009).
Afzelius, M., Simon, C., de Riedmatten, H. & Gisin, N. Multimode quantum memory based on atomic frequency combs. Phys. Rev. A 79, 052329 (2009).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Holliday, K., Croci, M., Vauthey, E. & Wild, U. P. Spectral hole burning and holography in an Y2SiO5:Pr3+ crystal. Phys. Rev. B 47, 14741 (1993).
Steinlechner, F. et al. A high-brightness source of polarization-entangled photons optimized for applications in free space. Opt. Express 20, 9640–9649 (2012).
Wang, J. et al. Universal photonic quantum interface for a quantum network. Phys. Rev. Appl. 10, 054036 (2018).
Yang, T.-S. et al. Multiplexed storage and real-time manipulation based on a multiple degree-of-freedom quantum memory. Nat. Commun. 9, 3407 (2018).
Seri, A. et al. Quantum storage of frequency-multiplexed heralded single photons. Phys. Rev. Lett. 123, 080502 (2019).
Zhang, H. et al. Slow light for deep tissue imaging with ultrasound modulation. Appl. Phys. Lett. 100, 131102 (2012).
Beavan, S. E., Goldschmidt, E. A. & Sellars, M. J. Demonstration of a dynamic bandpass frequency filter in a rare-earth ion-doped crystal. J. Opt. Soc. Am. B 30, 1173–1177 (2013).
Brendel, J., Gisin, N., Tittel, W. & Zbinden, H. Pulsed energy-time entangled twin-photon source for quantum communication. Phys. Rev. Lett. 82, 2594–2597 (1999).
Boyd, G. D. & Kleinman, D. A. Parametric interaction of focused Gaussian light beams. J. Appl. Phys. 39, 3597–3639 (1968).
Acknowledgements
We thank H. Goto, Q. Zhang, Y. Yamamoto, S. Utsunomiya, T. Kobayashi, M. Fraser, I. Iwakura, S. Tamura, K. Ikeda, and F.-L. Hong for their support. This work was supported by the Toray Science Foundation, the Asahi Glass Foundation, the KDDI Foundation, the SECOM Foundation, Research Foundation for Opto-Science and Technology, JST PRESTO JPMJPR1769, JST START ST292008BN, and Kanagawa Institute of Industrial Science and Technology (KISTEC). T.H. also acknowledge members of Quantum Internet Task Force, which is a research consortium to realize the Quantum Internet, for comprehensive and interdisciplinary discussions of the Quantum Internet.
Author information
Authors and Affiliations
Contributions
K.N. and T.H. conceived this project. K.N., D.Y., I.N., N.T., K.O., and T.H. designed the experiments. M.-Y.Z. and X.-P.X. fabricated the SPDC crystals. K.N., D.Y., and K.I. performed the experiments. K.N. and T.H. analyzed the data and drafted the manuscript. K.N., N.T., X.-P. X., and T.H. revised the text. All the authors contributed to discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Niizeki, K., Yoshida, D., Ito, K. et al. Two-photon comb with wavelength conversion and 20-km distribution for quantum communication. Commun Phys 3, 138 (2020). https://doi.org/10.1038/s42005-020-00406-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00406-1
This article is cited by
-
Nonlinear improvement of measurement-device-independent quantum key distribution using multimode quantum memory
Applied Physics B (2023)
-
Design and Simulation of Physical Layer Security for Next Generation Intelligent Optical Networks
Wireless Personal Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.