Abstract
A most fundamental goal in spintronics is to electrically tune highly efficient spin injectors and detectors, preferably compatible with nanoscale electronics and superconducting elements. These functionalities can be obtained using semiconductor quantum dots, spin-polarized by a ferromagnetic split-gate, which we demonstrate in a double quantum dot spin valve with two weakly coupled quantum dots in series, with individual split gates magnetized in parallel or anti-parallel. In tunneling magnetoresistance experiments we find a strongly reduced spin valve conductance for the two anti-parallel configurations, with a single dot polarization of ~27%. This value can be significantly improved by a small external magnetic field and optimized gate voltages, which results in a continuously electrically tunable quantum dot spin polarization of ±80%. Such versatile quantum dot spin filters are compatible with superconducting electronic elements and suitable for single spin projection and correlation experiments, as well as initialization and read-out of spin qubits.
Similar content being viewed by others
Introduction
Spin injection and detection are two of the most fundamental processes in semiconductor spintronics1,2,3,4,5,6, e.g., for quantum spintronic devices and spin-based information processing7,8,9, or to determine and control spin states in quantum physics10,11,12. Significant efforts are dedicated to improve the efficiencies of these processes in a variety of material platforms and physical phenomena13,14,15,16,17. However, a reliable and versatile technique to measure the spin degree of freedom remains elusive, especially for superconductor hybrid devices, where spin phenomena are crucial, e.g., in entanglement generation in solids18,19, or demonstrating topological superconductivity in Majorana-type devices20. Such experiments require highly efficient and gate-tunable spin injectors and detectors in situ of an active device. Most of the present concepts rely on electrical contacts to ferromagnetic reservoirs1, or on magnetic tunnel barriers21, with significant obstacles22 such as a low polarization (20%–40%)23, the magneto-Coulomb effect24,25, the conductivity mismatch at the metallic ferromagnet–semiconductor interface26, or large global external magnetic fields8,27, suppressing the superconductivity and changing significantly the band structure. All these effects are particularly challenging in sub-micrometer-scaled electronic devices.
Here we provide an alternative route for spin injection and detection in semiconductor devices, compatible with superconductors in close proximity, using quantum dots (QDs) spin-polarized by the stray fields of individual nanomagnets. We demonstrate this concept in tunneling magnetoresistance (TMR) experiments in an InAs nanowire (NW) double QD spin valve (DQD-SV). At zero field, we find a suppressed conductance for the antiparallel (ap) magnetization of the nanomagnets, suggesting an individual QD spin polarization of ~27%, which is comparable to metallic ferromagnetic contacts. On applying a small finite magnetic field of B = ±40 mT and optimizing the ferromagnetic split-gate (FSG) voltages, we achieve continuously gate-tunable TMR values (defined below) between +80% and −90%, far beyond conventional spin valves with standard ferromagnetic contacts. Using a simple DQD-SV model allows us to extract a corresponding large, electrically tunable QD spin polarization of up to ±80%, which can, in principle, be further improved to the theoretical limit of 100%.
Results
Device and characterization
As illustrated in Fig. 1a, the spin degeneracy of a QD state can be lifted by a magnetic field, resulting in a spin polarization at the Fermi energy EF of
with Dσ the QD transmission density of states (t-DoS) for spin state σ ∈ {↑, ↓} at EF. This spin-dependent transmission directly results in a spin-polarized current through the QD. In practice, a single QD can be spin-polarized individually by placing it in the narrow gap in a long strip of a ferromagnetic material, which we term FSG. The FSG generates a stray field \({B}_{{\rm{str}}}\) at the QD position in the direction given by its magnetization28,29, either parallel (p) or antiparallel (ap) to its long axis30, and can also be used for electrical gating. The FSG magnetization, and with it \({B}_{{\rm{str}}}\), can be inverted at a characteristic external switching field Bsw, determined by the FSG width in the device design31,32.
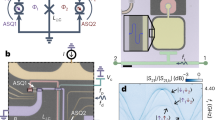
a, b Energy diagram (a) and schematic (b) of a double quantum dot (DQD) spin valve. The split central gate (CG) is used to electrically form the DQD, whereas the ferromagnetic side gates (FSGs) generate a stray magnetic field \({B}_{{\rm{str}}}\) at the individual quantum dot positions and electrically tune them as well. c False color scanning electron microscope image of the investigated InAs nanowire device. d Current I (amperes) as a function of gate voltages VG1 and VG4, at bias voltage VSD = +1 mV, showing bias triangles characteristic for weakly coupled DQDs.
Similar to conventional spin valves with two ferromagnetic contacts with Stoner split bands, we combine two QD-FSG elements with Zeeman split QD states in series to form a DQD-SV. In the first QD-FSG unit (spin injector), a spin-polarized tunnel current is generated, which is then detected at a different position by a second QD-FSG unit (spin detector). This concept is illustrated in Fig. 1a: electrons in state σ from the unpolarized electrical contacts tunnel sequentially through the two QDs with a probability that depends on the FSG states of both QDs, to first order resulting in the respective current \({I}_{\sigma }\propto {D}_{\sigma }^{(1)}{D}_{\sigma }^{(2)}\). Following typical TMR experiments1, we show that in such nano structures both mutually p and both ap magnetization states of the two FSGs can be accessed at zero external magnetic field, B = 0, and reoriented by cycling B. The individual QD polarizations and TMR signals can be continuously electrically tuned up to values close to the theoretical limits. In contrast to previously employed, very large polarizing external magnetic fields27,33,34, the stray and external magnetic fields required for such optimizations are small enough and decay over short enough length scales, to be compatible with various spin injection and detection experiments, e.g., with superconducting components in Cooper pair splitters18,19 for electron spin correlation measurements35, or to demonstrate equal spin Andreev reflection20 at Majorana-type superconducting bound states36,37,38.
A schematic of a DQD-SV and a scanning electron microscopy image of the investigated InAs NW device are shown in Fig. 1b, c, respectively. The FSGs are long Permalloy (Py) strips fabricated by electron beam lithography with a narrow gap at the NW position, forming the split-gate geometry. The strip widths are 120 and 230 nm, respectively, determining the corresponding switching and stray fields, which can be extracted from independent experiments as demonstrated in Supplementary Notes 1 and 2. The electrical contacts at the NW ends are made of titanium/gold with a split central gate (CG) to electrically form the two QDs fabricated in the same step. One part of the narrower FSG and the CG gate are electrically connected accidentally and are tuned in unison, which we refer to as “gate 1” (G1) and “gate 2” (G2), whereas the other FSGs are labeled individually (see Fig. 1c). The DC current I resulting from a bias voltage VSD and the differential conductance G = dI/dVSD, were measured simultaneously using standard DC and lock-in techniques (Vac = 10 μV), at a base temperature of ~50 mK.
In Fig. 1d, we plot I flowing through the DQD-SV at VSD = 1 mV, as a function of VG1 and VG4. This map shows several bias triangles characteristic for a weakly coupled DQD. These triangles originate from one resonance of each QD aligning in energy within the bias transport window39. This allows us to independently extract most of the single QD parameters used for modeling later, e.g., the lever arms of each gate to each QD (see Supplementary Note 3). We now discuss various types of TMR experiments for two resonances, in Figs. 2 and 3, respectively.
a Current I (amperes) for the bias triangles at dc bias VSD = 500 μV. The red arrow specifies the cross-section A investigated in b. b Up (red arrow) and down-sweep (blue arrow) maps of current I as a function of B and gate voltage VG1, measured along cross-section A in a. c Current maximum \({I}_{\max }\) (amperes) vs. B, extracted from figure b, for the up (red) and down (blue) sweep. The magnetization configurations are indicated by i, j ∈ {+, −}. d Differential conductance G as a function of gate voltage VG1 for all four magnetization states at B = 0 and VSD = 0, showing a conductance suppression ΔG for the antiparallel states relative to the parallel magnetization configurations. The arrow indicates the sequence of the experiments.
Tunneling magnetoresistance at zero external magnetic field
We first demonstrate the principle of a TMR experiment and show that all FSG magnetization states can be accessed at B = 0. Figure 2a shows a high-resolution bias triangle of a resonance (not shown in Fig. 1d) at VSD = 500 μV. Our typical TMR experiment consists of first choosing a specific trace for the two gate voltages here by sweeping VG1 and keeping VG4 constant, as indicated by the red arrow, such that no excited states are involved in the transport process. We then measure I as a function of VG1 at a series of external magnetic fields, B, applied in p to the FSG axes, which results in relatively abrupt switchings of the FSG magnetizations. Such a map for the trace in Fig. 2a is shown in Fig. 2b for decreasing and increasing magnetic fields, as indicated by the blue and red arrows, respectively, each starting at fields much higher (+0.5 T), or lower (−0.5 T) than shown, to ensure the formation of only a single magnetic domain along the FSG axes. These maps show a clear hysteresis with a strong dependence on B and the sweep direction. To demonstrate this more explicitly, we extract the position, width (both shown in Supplementary Fig. 4) and the maximum current \({I}_{\max }\) at each B value. \({I}_{\max }\) extracted from Fig. 2b is plotted in Fig. 2c for decreasing (blue) and increasing B (red).
In the up-sweep, \({I}_{\max }\) first increases roughly linearly with increasing B, followed by a maximum at B ≈ −55 mT and a decrease around B = 0. At small positive B, \({I}_{\max }\) becomes flatter, followed by a small maximum at B ≈ 85 mT, and a roughly linear decrease towards more positive B. The down-sweep can be described similarly as the up-sweep, but mirrored at B ≈ 0 leading to a clear hysteresis. This hysteresis can be understood qualitatively by considering a smooth non-monotonous MR of the DQD that changes abruptly with the reorientation of the FSG magnetizations. In the up-sweep, at B > Bsw2 ≈ 5 mT the wider FSG is reoriented p to the now positive B and the two FSG magnetizations become ap. The FSGs become magnetized in p again for B > Bsw1 ≈ 140 mT, when the narrower FSG is also inverted (details are given in Supplementary Note 2). These configurations are shown schematically at the bottom of Fig. 2c for the down (blue) and the up-sweep (red).
As a first quantitative measure for the TMR effect, we use the maximum current values at B = −55 mT, using the maximum value of \({I}_{\max }\) in the p state, and the value in the opposite sweep direction at the same field in the ap state. We define TMR as
which results in TMR ≈ 6% at VSD = 500 μV and B = −55 mT.
To explicitly demonstrate that all four magnetization states (two p and two ap) are accessible at B = 0, we measure the differential conductance G at VSD = 0 as a function of VG1 for each FSG magnetization state. The direction of the stray fields Bstr1 and Bstr2 can be reversed individually by sweeping B beyond the characteristic FSG switching fields. For example, we sweep to B = −500 mT and back to B = 0 to obtain the (−, −) state, followed by sweeping to B = +40 mT and back to B = 0 to obtain the (−, +) state (see Supplementary Note 4 for more details). We note that in the used sequence, p is followed by ap and vice versa. The gate sweeps for the four magnetization states at B = 0 are plotted in Fig. 2d. All curves show a maximum at the same gate voltage, which corresponds to a weakly spin split energy level of each QD (Γ > gμBB) being aligned with the Fermi energy. The conductance is gradually reduced to zero if the QD levels are detuned by VG1. We find very similar maximum conductances for the same relative magnetization orientations and a clear suppression in G for both ap states with respect to the two p states, yielding \({\rm{TMR}}=\frac{\Delta G}{{G}_{{\rm{P}}}+{G}_{{\rm{AP}}}}\approx 7 \%\), similar to the value obtained at a larger bias and a small finite B.
The DQD-SV experiment can be reproduced quantitatively using a very simple model, which also allows us to estimate the QD polarizations: we assume that the current is given by elastic tunneling in two independent spin channels40, which yields for a constant weak inter-dot coupling T12 and the magnetization orientations i, j ∈ {+, −} along the FSG axes,
where Dβσ(E) denotes the spin-dependent t-DoS in dot β ∈ {1, 2} and σ ∈ {↑, ↓} the spin orientation; \(f(E)=1/(1+{e}^{E/({k}_{B}T)})\) is the Fermi-Dirac distribution function and μS,D the electrochemical potential in the source and drain contacts, respectively. To start with, we assume a small bias (linear regime) to obtain the conductance, as in the experiments. Since the Zeeman shift is opposite, but of the same magnitude for opposite spins, the t-DoS of each QD obeys the identity \({D}_{\sigma }^{-}(-B,{E}_{{\rm{F}}})={D}_{-\sigma }^{+}(+B,{E}_{{\rm{F}}})\) due to time-reversal symmetry. At B = 0, this reduces to \({D}_{\sigma }^{-}({E}_{{\rm{F}}})={D}_{-\sigma }^{+}({E}_{{\rm{F}}})\), which yields, using the definition of the QD polarizations in equation (1),
In the last step we assume that both QD polarizations are identical, which results in P ≈ 27% on resonance at B = 0. We stress that this expression for the TMR signal only holds at B = 0 because of the non-constant QD t-DoS, in contrast to devices with ferromagnetic contacts, for which it holds also at finite external fields, limited only by the correlation energy of the band structure.
Optimized tunneling magnetoresistance at finite fields
The non-constant t-DoS of the QDs allows us to go beyond the standard experiments, enabling us to optimize and tune the TMR signals magnetically as well as electrically. To demonstrate this, we investigate cross-section C1 pointed out in Fig. 1d, for which we again plot I as a function of B and VG1 at VSD = 10 μV. Figure 3a shows the up and down sweeps, which again show a clear hysteresis, prominently visible in Fig. 3b, where we plot \({I}_{\max }\) as a function of B for the up and down sweeps (width and position are discussed in Supplementary Fig. 4). These curves show qualitatively similar characteristics as discussed for Fig. 2c. From the current maximum, we find a TMR signal of ~29% at B = 0 and estimate the individual QD spin polarizations as P ≈ 53% using equation (4). These values are larger than for the previously discussed resonance, mostly due to a smaller resonance width.
We now exploit the non-constant t-DOS to optimize the TMR signal. First, we apply a small homogeneous external field of ±40 mT, which is small enough to still access all four FSG magnetization states (B < Bsw1) and compatible with a wide variety of applications, e.g., with many superconducting circuit elements. We measure I along cross-section C2 indicated in Fig. 1d, which is chosen on the resonance maximum along the base of the bias triangle (see Supplementary Note 5) so that a shift in the resonance energies is negligible.
a Maps of current I (amperes) as a function of B and gate voltage VG1 for the up (red arrow) and down-sweep (blue arrow), for the cross-section C1 in Fig. 1d at bias voltage VSD = 10 μV. b Maximum current \({I}_{\max }\) as a function of B for the up (red) and down-sweep (blue) extracted from Fig. 3a. c, I along cross-section C1 parameterized by VG1 for all four magnetization states, with the (−, −) and (+, −) configurations measured at B = −40 mT, and the (+, +) and (−, +) configurations at B = +40 mT. d TMR for magnetization states (+, +) and (−, +) at B = +40 mT for cross sections C2 (red) and Copt (blue). Copt refers to the optimal cross-section along which the TMR for magnetization states (+, +) and (−, +) shows the maximum value. The black dashed line shows the TMR extracted from the model for cross-section Copt, with the parameters obtained from fits to the data in Fig. 3b.
Figure 3c shows the four I(VG1) curves along C2 for the four FSG magnetization states (i, j) (VG4 is the same for each chosen B). The curve for the p (−, −) [blue] and the ap configuration (+, −) [gray] were measured at B = −40 mT, while the ones for (+, +) [purple] and (−, +) [black] were measured at B = +40 mT (see Supplementary Note 4 for sweep sequence). We find that the maximum current and lineshape for both ap configurations are almost identical, while the two p ones slightly differ. Most importantly, the ap curves are reduced in amplitude by ~25% with respect to the p ones. We note that for this cross-section, the maximum occurs at the same VG1 value for both pairs of curves in Fig. 3c.
For any given VG1 and B, we now calculate the TMR signal using equation (2). As an example, this is plotted for the states (+, +) and (−, +) in Fig. 3d (red curve), which shows that the TMR signal is continuously gate-tunable roughly between +50% and −25%. This TMR signal can be improved significantly by exploiting the small, field-induced shifts in the resonance positions. To achieve this, we plot TMR = (I++ − I−+)/(I++ + I−+) at B = 40 mT as a function of VG1 and VG4 in Fig. 4a and find the optimal cross-section labeled Copt. In Fig. 3d, we plot TMR along Copt which shows a continuously gate-tunable TMR with a well separated pronounced maximum and minimum TMR of +80% and −90%, respectively. These values are significantly larger than in most other systems.
a Measured TMR as a function of gate voltages VG1 and VG4 for the magnetization states (+, +) and (−, +) at external magnetic field B = 40 mT. The cross sections C2 and Copt are indicated by dashed lines. Inset: TMR from the model calculations with the parameters extracted from Fig. 3b. b Spin polarization of quantum dot 1 (P1) and quantum dot 2 (P2) as a function of VG1 and constant VG4 from the model at B = 40 mT, showing a large gate tunability of P1 from −0.8 to +0.8.
Discussion
We expect that the QD polarizations are also gate-tunable to large values, but since an external field is applied, the above symmetry argument cannot be used for a simple estimate. We therefore resort to numerically evaluating the model introduced above. To do so, we define the total magnetic fields \({B}_{{\rm{tot}}}^{(\beta )}=B+{B}_{{\rm{str}}}^{(\beta )}\) at the two QD positions β ∈ {1, 2}, and use as the energy-dependent t-DoS of the QDs at energy E the Lorentzian \({\mathcal{L}}(E-{E}_{\beta \sigma })={({\Gamma }_{\beta }/2)}^{2}/[{(E-{E}_{\beta \sigma })}^{2}+{({\Gamma }_{\beta }/2)}^{2}]\), centered at
with \({E}_{\beta }^{(0)}\) an energy offset for states in dot β at zero gate voltages, gβ the corresponding electron g-factors and Γ1 and Γ2 the broadening parameters. The lever arms αβ are extracted independently from the bias triangles (including cross lever arms) and Vgβ are the applied gate voltages. The total current is then calculated using equation (3).
This model reproduces very well the experiments using a single set of parameters for a given resonance, all in the typical range found in literature. For example, we obtain \({I}_{\max }\) as a function of B, as plotted by the black curve in Fig. 3b for the up-sweep, using Bstr1 = 61(±4) mT, Bstr2 = 27(±5) mT (estimated independently, see Supplementary Note 1) and the adjustable parameters g1 = 5.6, g2 = 6.3, Γ1 = 25 μeV and Γ2 = 15 μeV, \({E}_{1}^{(0)}\equiv 0\), \({E}_{2}^{(0)}=8.1(\!\pm\! 0.3)\) μeV, and an inter-dot tunnel coupling T12 = 0.12 adjusted to obtain the correct amplitude. The errors given in brackets indicate the range for a parameter that still gives satisfactory model curves. The same parameters also reproduce the TMR results, shown as an inset in Fig. 4a and the optimized TMR cross-section Copt shown in Fig. 3d (black dashed line). The same parameters also reproduce the width (Supplementary Fig. 4) and Fig. 3c. To reproduce the other investigated resonances, we use slightly different parameters, as summarized in Supplementary Note 6.
In the model it is straight forward to extract the spin polarizations, e.g. P1 for QD1 as a function of VG1 at B = 40 mT, which is plotted in Fig. 4b, with P2 ≈ 27% for QD2, being independent of VG1. P1 can be gate tuned over a large range, with a maximum absolute value of P1 ≈ 80%, and a zero-field value of ≈59%. This analysis demonstrates that the DQD-SV is a highly tunable spin valve with one QD acting as a gate-tunable spin injector and the other as a detector, such that transport through the DQD can be electrically tuned from predominantly spin down electrons to spin up electrons, depending on the orientation of \({B}_{{\rm{str}}}\) and B. The large gate tunability of the QD spin polarizations originates from the resonance widths being of similar magnitude as the Zeeman splitting, Γ1 + Γ2 ~ gμBtot. Increasing the QD life time in the model by only a factor of two, keeping all other parameters the same, we find even stronger polarizations, up to 91%; thus, almost reaching unity. Such sharper line shapes can be obtained with in situ grown InP tunnel barrier41,42,43 or by crystal phase-engineered barriers in InAs NWs44,45. In addition, the QD polarization can be enhanced by stronger \({{\rm{B}}}_{{\rm{str}}}\), either by reducing the FSG gap, e.g., using smaller diameter NWs, or by using other ferromagnetic materials.
In conclusion, we have demonstrated a DQD spin valve in an InAs NW with FSGs that results in a tunneling magnetoresistance electrically tunable between +80% and −90%. Using a simple resonant tunneling model, we extract gate and B field tunable QD spin polarizations up to approximately ±80%, with the possibility of values up to unity. This large benchmark value and the spatially localized stray fields are promising for efficient spin injection, detection, and correlation experiments in a large variety of devices, potentially on the single electron level. We note that our concept is very general and can be applied to any device region with a non-constant transmission T(E) and a finite g-factor. Especially, the small external fields resulting in such large efficiencies are compatible with many superconducting contacts in close proximity (see Supplementary Note 1 for an experimental estimate of \({B}_{{\rm{str}}}\) away from the FSGs) so that the QD-FSG units are ideally suited, e.g., to investigate spin–orbit interactions, to perform spin correlation measurements and electronic Bell tests in a Cooper pair splitter35, or to demonstrate equal spin Andreev reflection at Majorana zero modes20. In addition, a single QD-FSG unit could also prove useful for the initialization and read-out of spin qubits28,29, while arrays of FSG units are expected to result in a variety of novel phenomena, such as magnetic superlattices46, magnetic periodic potentials, and in a synthetic and externally controllable spin–orbit interaction47,48,49.
Methods
The InAs NWs were grown using 30 nm gold (Au) colloid-assisted chemical beam epitaxy50 and have a diameter of 40–45 nm and a length of 2.0–2.3 μm. The NWs were mechanically transferred from the growth substrate to a heavily p-doped silicon substrate serving as a global backgate (BG), with a 400 nm SiO2 insulating top layer. For the electron beam lithography, we employed pre-defined markers and contact pads made of Ti/Au (5 nm/45 nm). The CGs and electrical contacts at the NW ends were first made of Ti/Au (5 nm/45 nm), whereas the FSGs were fabricated in a second step and made of 30 nm-thick Py. Before evaporating the contact material, the native oxide of the NWs is etched with a 1:10 ratio \({({{\rm{NH}}}_{4})}_{2}{S}_{x}\!\!:\!{\mathrm{{{H}}}_{\mathrm{{{2}}}}}{\mathrm{{O}}}\) solution for 3.5 min. The \({({{\rm{NH}}}_{4})}_{2}{S}_{x}\) solution was prepared by mixing 0.96 g of sulfur powder in 10 ml of ammonium sulfide solution (20% in H2O).
Data availability
All data in the publication are available in numerical form at https://doi.org/10.5281/zenodo.3557857.
References
Žutić, I., Fabian, J. & Sarma, S. D. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Dietl, T. & Ohno, H. Dilute ferromagnetic semiconductors: physics and spintronic structures. Rev. Mod. Phys. 86, 187–251 (2014).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
Jansen, R. Silicon spintronics. Nat. Mater. 11, 400–408 (2012).
Hirohata, A. et al. Review on spintronics: principles and device applications. J. Magn. Magn. Mater. 509, 166711 (2020).
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665–667 (1990).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Chuang, P. et al. All-electric all-semiconductor spin field-effect transistors. Nat. Nanotechnol. 10, 35–39 (2014).
Jeon, K.-R. et al. Enhanced spin pumping into superconductors provides evidence for superconducting pure spin currents. Nat. Mater. 17, 499–503 (2018).
Han, W., Maekawa, S. & Xie, X.-C. Spin current as a probe of quantum materials. Nat. Mater. 19, 139–152 (2019).
Nakajima, T. et al. Quantum non-demolition measurement of an electron spin qubit. Nat. Nanotechnol. 14, 555–560 (2019).
Sahoo, S. et al. Electric field control of spin transport. Nat. Phys. 1, 99–102 (2005).
Breton, J.-C. L., Sharma, S., Saito, H., Yuasa, S. & Jansen, R. Thermal spin current from a ferromagnet to silicon by seebeck spin tunnelling. Nature 475, 82–85 (2011).
Varaprasad, B. et al. Spin polarization and gilbert damping of co2fe(GaxGe1-x) heusler alloys. Acta Mater. 60, 6257–6265 (2012).
Spaldin, N. A. & Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212 (2019).
Yang, Z. et al. Spin transport in ferromagnet-InSb nanowire quantum devices. Nano Lett. 20, 3232–3239 (2020).
Hofstetter, L., Csonka, S., Nygård, J. & Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot y-junction. Nature 461, 960–963 (2009).
Schindele, J., Baumgartner, A. & Schönenberger, C. Near-unity cooper pair splitting efficiency. Phys. Rev. Lett. 109, 157002 (2012).
He, J. J., Ng, T., Lee, P. A. & Law, K. Selective equal-spin andreev reflections induced by majorana fermions. Phys. Rev. Lett. 112, 037001 (2014).
Jonker, B. T., Kioseoglou, G., Hanbicki, A. T., Li, C. H. & Thompson, P. E. Electrical spin-injection into silicon from a ferromagnetic metal/tunnel barrier contact. Nat. Phys. 3, 542–546 (2007).
Awschalom, D. D. & Flatté, M. E. Challenges for semiconductor spintronics. Nat. Phys. 3, 153–159 (2007).
Meservey, R. & Tedrow, P. Spin-polarized electron tunneling. Phys. Rep. 238, 173–243 (1994).
van der Molen, S. J., Tombros, N. & van Wees, B. J. Magneto-Coulomb effect in spin-valve devices. Phys. Rev. B 73, 220406 (2006).
Bernand-Mantel, A. et al. Anisotropic magneto-Coulomb effects and magnetic single-electron-transistor action in a single nanoparticle. Nat. Phys. 5, 920–924 (2009).
Rashba, E. I. Theory of electrical spin injection: tunnel contacts as a solution of the conductivity mismatch problem. Phys. Rev. B 62, R16267–R16270 (2000).
Hanson, R. et al. Semiconductor few-electron quantum dot operated as a bipolar spin filter. Phys. Rev. B 70, 241304 (2004).
Pioro-Ladrière, M. et al. Electrically driven single-electron spin resonance in a slanting zeeman field. Nat. Phys. 4, 776–779 (2008).
Obata, T. et al. Coherent manipulation of individual electron spin in a double quantum dot integrated with a micromagnet. Phys. Rev. B 81, 085317 (2010).
Fábián, G. et al. Magnetoresistance engineering and singlet/triplet switching in InAs nanowire quantum dots with ferromagnetic sidegates. Phys. Rev. B 94, 195415 (2016).
Aurich, H. et al. Permalloy-based carbon nanotube spin-valve. Appl. Phys. Lett. 97, 153116 (2010).
Samm, J., Gramich, J., Baumgartner, A., Weiss, M. & Schönenberger, C. Optimized fabrication and characterization of carbon nanotube spin valves. J. Appl. Phys. 115, 174309 (2014).
Folk, J. A., Potok, R., Marcus, C. & Umansky, V. A gate-controlled bidirectional spin filter using quantum coherence. Science 299, 679–682 (2003).
Potok, R. M., Folk, J. A., Marcus, C. M. & Umansky, V. Detecting spin-polarized currents in ballistic nanostructures. Phys. Rev. Lett. 89, 266602 (2002).
Kłobus, W. et al. Entanglement witnessing and quantum cryptography with nonideal ferromagnetic detectors. Phys. Rev. B 89, 125404 (2014).
Mourik, V. et al. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Zhang, H. et al. Quantized majorana conductance. Nature 556, 74–79 (2018).
van der Wiel, W. G. et al. Electron transport through double quantum dots. Rev. Mod. Phys. 75, 1–22 (2002).
Jullière, M. Tunneling between ferromagnetic films. Phys. Lett. A 54, 225–226 (1975).
Fuhrer, A. et al. Few electron double quantum dots in InAs/InP nanowire heterostructures. Nano Lett. 7, 243–246 (2007).
Roddaro, S., Pescaglini, A., Ercolani, D., Sorba, L. & Beltram, F. Manipulation of electron orbitals in hard-wall InAs/InP nanowire quantum dots. Nano Lett. 11, 1695–1699 (2011).
Thomas, F. et al. Highly symmetric and tunable tunnel couplings in InAs/InP nanowire heterostructure quantum dots. Nanotechnology 31, 13 (2019).
Jünger, C. et al. Spectroscopy of the superconducting proximity effect in nanowires using integrated quantum dots. Commun. Phys. 2, 76 (2019).
Nilsson, M. et al. Single-electron transport in InAs nanowire quantum dots formed by crystal phase engineering. Phys. Rev. B 93, 195422 (2016).
Sun, S. Monodisperse FePt nanoparticles and ferromagnetic FePt nanocrystal superlattices. Science 287, 1989–1992 (2000).
Braunecker, B., Japaridze, G. I., Klinovaja, J. & Loss, D. Spin-selective peierls transition in interacting one-dimensional conductors with spin-orbit interaction. Phys. Rev. B 82, 045127 (2010).
Kjaergaard, M., Wölms, K. & Flensberg, K. Majorana fermions in superconducting nanowires without spin-orbit coupling. Phys. Rev. B 85, 020503 (2012).
Desjardins, M. M. et al. Synthetic spin–orbit interaction for majorana devices. Nat. Mater. 18, 1060–1064 (2019).
Gomes, U. P., Ercolani, D., Zannier, V., Beltram, F. & Sorba, L. Controlling the diameter distribution and density of InAs nanowires grown by au-assisted methods. Semiconductor Sci. Technol. 30, 115012 (2015).
Acknowledgements
This work has received funding from the Swiss National Science Foundation, the Swiss Nanoscience Institute, the Swiss NCCR QSIT, the FlagERA project Topograph, the QuantERA SuperTop project network, and the FET Open project AndQC. C.S. has received funding from the European Research Council under the European Union’s Horizons 2020 research and innovation program.
Author information
Authors and Affiliations
Contributions
A. Bordoloi fabricated the devices, performed the measurements, and analyzed the data. V.Z. and L.S. have grown the nanowires. A. Baumgartner provided the model and helped with the measurements and data analysis. A. Bordoloi and A. Baumgartner wrote the paper. C.S. and A. Baumgartner initiated and supervised the project. All authors discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bordoloi, A., Zannier, V., Sorba, L. et al. A double quantum dot spin valve. Commun Phys 3, 135 (2020). https://doi.org/10.1038/s42005-020-00405-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00405-2
This article is cited by
-
Cross-correlations between currents and tunnel magnetoresistance in interacting double quantum dot-Majorana wire system
Scientific Reports (2024)
-
Spin effects on transport and zero-bias anomaly in a hybrid Majorana wire-quantum dot system
Scientific Reports (2023)
-
Spin cross-correlation experiments in an electron entangler
Nature (2022)
-
Spin Seebeck effect of correlated magnetic molecules
Scientific Reports (2021)
-
Anomalous Fano Resonance in Double Quantum Dot System Coupled to Superconductor
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.