Abstract
Describing the ionization of an atom exposed to a strong laser field entails computationally expensive quantum simulations based on the numerical solutions of the time-dependent Shrödinger equation. The well-known Simple Man Model provides a qualitatively accurate description of the ionization process. Here, we propose a quantum generalization of the physical picture given by the Simple Man Model. We describe an approximate solution to the Heisenberg operator equations of motion for an atom in a laser field. We provide justification of this generalization and test its validity by applying it to calculate the coordinate and velocity autocorrelation functions. Both our model and results of the ab initio numerical calculations show distinct types of correlations due to different types of electron’s motion providing insight into the strong field ionization dynamics.
Similar content being viewed by others
Introduction
An atom exposed to a strong laser field can be ionized. The foundation of the quantum theory describing this process in strong fields has been laid out in the seminal paper by Keldysh1 (also known as the strong field approximation or the SFA theory). The Keldysh theory introduces the well-known classification of the ionization phenomena based on the value of the Keldysh parameter \(\gamma =\omega \sqrt{2| {\varepsilon }_{0}| }/E\) (ω, E0, and ∣ε0∣ are the frequency, field strength, and ionization potential of the target system expressed in atomic units). The ionization regime corresponding to the values γ ≫ is known as the multi-photon regime. The opposite limit γ ≲ 1 is known as the tunneling regime2. Depending on the ionization regimes, the ionization process is described in drastically different ways1,2.
The tunneling regime is particularly interesting since many interesting and important phenomena occurring in this regime, such as the high harmonic generation (HHG), the attosecond pulse generation and the above threshold ionization (ATI), can be understood using fairly simple physical picture, the so-called simple man model (SMM)2,3,4,5,6. In the framework of this model, the electron’s motion after the ionization event is described using classical equations of motion for an electron in the presence of the laser field, neglecting the effect of the atomic potential. These equations can be easily solved leading to the testable predictions (such as, e.g., the maximum energy of the direct electrons in the ATI process, or the cutoff photon energy for the HHG process), which often agree remarkably well with results of the ab initio quantum simulations.
The reason for this extraordinary predictive power of the SMM becomes clear if one applies the standard saddle-point technique to evaluate integrals occurring in the expression for the SFA ionization amplitude7. This leads to the reformulation of the theory in terms of the so-called quantum trajectories3,7: the generally complex electron trajectories originating at the (complex) moment of time corresponding to the saddle point, descending further on the real time axis, and propagating in the real time afterwards. The real part of the complex saddle point can be interpreted as the moment when electron enters the under-the-barrier region (hence the complex-valued time and velocity) and the point of the intercept of the quantum trajectory with the real time axis as the moment of time when the electron exits the tunneling barrier8. Basing on the notion of the quantum trajectories, a very useful and powerful method, the so-called imaginary time method (ITM)7,9,10 can be built. The ITM allows to go beyond the SFA and take into account the Coulomb corrections to the SFA ionization amplitude in a systematic way7. The fact that after the ionization event the quantum trajectories resemble closely the classical ones has been exploited with success to model ionization process using methods based on the Monte-Carlo simulations of the trajectories5,11,12. These methods are practically indispensable if the target system is a complicated one, so that the numerical solution of the time-dependent Schrödinger equation (TDSE) is not possible. Accurate quantitative calculations using these approaches have been reported in the literature5,6,13,14,15,16,17.
As we noted above, this link between the SMM and the quantum description emerges when we study the quantum-mechanical ionization amplitudes obtained in the usually employed Schrödinger picture of the quantum mechanics (QM). As it is well-known, there is an equivalent description of the quantum phenomena, provided by the so-called Heisenberg representation of the QM which, to our knowledge, has not been employed to study ionization phenomena. It is known that for the important case of the electron’s motion in the electromagnetic field in the absence of any other forces, not only the classical equations of motion but also their quantum counterpart, the Heisenberg operator equations of motion for the operators of coordinate and momentum, can be solved fairly easily. Indeed, the solutions are practically identical. The question arises can this fact be somehow exploited? In this work, we combine the practical utility of the SMM with the fairly simple expressions for the quantum solutions of the Heisenberg equations of motion in the SMM physical settings, and extend the SMM into the quantum domain. In particular, we represent the time-dependent coordinate operator in the Heisenberg representation as a linear combination of the Heisenberg coordinate operators for the field-free atom and electron moving in presence of only the laser field. We test our quantum version of the SMM by calculating the coordinate and velocity autocorrelation functions, and show that this generalized solution provides new insights in the electron’s motion.
Results
Derivation of the SMM in the Heisenberg picture
We consider a hydrogen atom interacting with the laser pulse. In the Schrödinger picture, the system evolves according to:
where \(\hat{H}(t)={\hat{H}}_{0}+{\hat{H}}_{{\rm{int}}}(t)\), \({\hat{H}}_{0}={\hat{{\bf{p}}}}^{2}/2-1/r\), and we use velocity form \({\hat{H}}_{{\rm{int}}}(t)={\bf{A}}(t)\cdot \hat{{\bf{p}}}+{{\bf{A}}(t)}^{2}/2\) for the interaction operator. Initial state of the system is Ψ(r, 0) = ϕ0(r)−the ground state of the hydrogen atom. Laser pulse is linearly polarized (along the z-axis) and is defined by the vector potential:
with peak field strength E0, carrier frequency ω, and total duration T = 2π∕ω−an optical cycle (o.c.) corresponding to the frequency ω. We use the dipole approximation to describe atom-field interaction, so the expression (2) for the vector potential does not contain the spatial variables. We will consider below the pulses with various peak field strengths E0 and central frequency ω = 0.057 a.u. We use a short pulse of one o.c total duration, so that electric field of the pulse has a well-defined global maximum to facilitate the study of the ionization dynamics.
For the reader’s convenience, we recapitulate first some well-known facts and introduce a few definitions, which we will use below. Eqution (1) describes ionization process in the Schrödinger picture. In the Heisenberg picture, the wave-function does not evolve in time while the operators evolve according to:
where \(\hat{Q}\) stands for either coordinate or momentum operator and \(\hat{U}(t,0)\) is the time-evolution operator, for which we can write a formally closed expression using the Dyson time-ordering operator \(\hat{{\mathscr{T}}}\)18:
In the following we will reserve the subscript H for the operators in the Heisenberg picture, operators without subscripts will correspond to the Schrödinger picture. We will use also the time-dependent operators \({\hat{Q}}_{0}(t)\) and \({\hat{Q}}_{V}(t)\), which we define as:
where \({\hat{U}}_{0}(t,0)=\exp\left\{-i{\hat{H}}_{0}t\right\}\) is the field-free atomic evolution operator, and
is the so-called Volkov time-evolution operator2,7 (hence the subscript “V” in Eq. (5)). This time-evolution operator describes evolution driven by the Volkov Hamiltonian \({\hat{H}}_{V}(t)=\hat{T}+{\hat{H}}_{{\rm{int}}}(t)\) (\(\hat{T}\) is the kinetic energy operator) of a free electron in the field of the pulse (2). We assume that both \({\hat{Q}}_{0}\) and \({\hat{Q}}_{V}\) can be calculated numerically or analytically. Introducing a complete set of the eigenstates ∣n〉 of \({\hat{H}}_{0}\), one can write for \({\hat{Q}}_{0}(t)\):
where summations run over the spectrum (including the continuous spectrum) of \({\hat{H}}_{0}\) with eigenenergies εn. As far as \({\hat{Q}}_{V}(t)\) is concerned, the Heisenberg operator equations of motion can easily be solved for the case of the Volkov Hamiltonian, giving for the physically interesting cases of the coordinate and kinetic momentum operators the simple expressions:
where r and \(\hat{{\bf{p}}}\) are the Schrödinger coordinate and momentum operators. In the atomic units system we use the kinetic momentum coincides with the velocity. We employed, therefore, the notation \({\hat{{\bf{v}}}}_{V}(t)\) in (8). We would like to remind also that we use the velocity gauge to describe atom-field interaction, hence the presence of the vector potential in the second Eq. (8).
Equation (8) look exactly like their classical counterparts used in the SMM. This fact motivated us to try to incorporate them into a quantum version of the SMM, relying on the Heisenberg picture. The exact Heisenberg equations of motion for operators \({\hat{{\bf{r}}}}_{H}(t)\) and \({\hat{{\bf{v}}}}_{H}(t)\) following from the definitions (3):
(here \(\hat{V}({\hat{{\bf{r}}}}_{H}(t))=-1/| {\hat{{\bf{r}}}}_{H}(t)|\) for hydrogen atom, \([\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}\) denotes the commutator of operators \(\hat{A}\) and \(\hat{B}\), and \({\hat{{\bf{v}}}}_{H}(t)={\hat{{\bf{p}}}}_{H}(t)+{\bf{A}}(t)\). The equations are, of course, too complicated to be solved exactly (or even numerically). We can try, however, to find an approximate solution using the time-dependent coordinate and momentum operators we introduced above in Eqs. (7) and (8) and the physical insight we get from the classical SMM.
The predictive power of the SMM shows that the simple expressions for the classical electron’s coordinate and velocity in the laser field which neglect all atomic interactions, can be used with success to explain many an ionization phenomena. It is natural, therefore, to use the quantum counterpart of these classical expressions given by the Eq. (8) in trying to construct an approximate solution to the Heisenberg equations of motion (9). In the limit of the vanishing field the solution should, of course, reduce to the field-free operators \({\hat{{\bf{r}}}}_{0}(t)\) and \({\hat{{\bf{p}}}}_{0}(t)\) obtained by substituting the Schrödinger coordinate and momentum operators, respectively, for the operator \(\hat{Q}\) in Eq. (7). This reasoning suggests the following tentative expression for the approximate solution to the Heisenberg equations of motion for the coordinate operator:
On the right-hand side of this equation, \({\hat{{\bf{r}}}}_{0}(t)\) is the field-free Heisenberg coordinate operator obtained using Eq. (7), r and \(\hat{{\bf{p}}}\) are time-independent Schrödinger operators, and we absorbed the c-number term in the first of the Eq. (8) into the c-number term \(\bar{{\bf{r}}}(t)\) in Eq. (10). That this term coincides with the expectation value of the coordinate can be easily seen from the Eq. (10) by noting that in the Heisenberg picture this expectation value is just the expectation value of the operator \({\hat{{\bf{r}}}}_{H}(t)\) obtained using the wave-function of the ground state of atomic hydrogen. The expectation values of \({\hat{{\bf{r}}}}_{0}(t)\), r, and \(\hat{{\bf{p}}}\) in this state are all zero. The real function α(t) (it must be real to preserve hermicity of the coordinate operator) in Eq. (10) is yet unknown. Basing on the general structure of the Eq. (10) and the simple physical picture of ionization provided by the SMM, we may say that the first term on the r.h.s. of the Eq. (10) describes atomic and the second term describes ionized electrons. The function α(t) then must be related to the ionization probability. This assumption can be justified by the reasoning presented in the Supplementary Note 1.
The expression for the the velocity operator \({\hat{{\bf{v}}}}_{H}(t)\) follows from Eq. (10) by the time differentiation as indicated in the first of the Eq. (9). The canonical momentum can then be found as \({\hat{{\bf{p}}}}_{H}(t)={\hat{{\bf{v}}}}_{H}(t)-{\bf{A}}(t)\). We note that although this procedure gives us the Hermitian Heisenberg coordinate and momentum operators, it does not preserve the correct commutation relations \([\,{\hat{p}}_{H}^{(n)}(t),{\hat{r}}_{H}^{(m)}(t)]=-i{\delta }_{n}^{m}\). This is a consequence of the fact that the transformation of the Schrödinger pair of operators r, \(\hat{{\bf{p}}}\) to the Heisenberg pair \({\hat{{\bf{r}}}}_{H}(t)\), \({\hat{{\bf{p}}}}_{H}(t)\) described by the Eq. (10) is not unitary. The lack of unitarity, however, should not be considered as a serious drawback. Many widely used approaches to the description of the ionization in strong fields, e.g., the SFA approach have a similar problem. The SFA is based on the Schrödinger picture and the non-unitarity of this method manifests itself as a non-unitary evolution of the state vector19. Consequently, the total sum of all the probabilities is not conserved and may not sum up to unity in the SFA. The great success and utility of the SFA show, however, this of unitarity of the method does not constitute a major impediment. We will study below some consequences and testable predictions we may derive from Eq. (10).
Computation of the coordinate and velocity autocorrelation functions
An advantage that the Heisenberg picture offers is the natural way in which the many-time correlation functions, containing detailed information about evolution of the system, can be introduced. Autocorrelation functions have been employed in the literature in the spectroscopic calculations. In particular, various spectra can be obtained as Fourier transforms of appropriate autcocorrelation functions20. Knowledge of the autocorrelation function for the dipole momentum operator, for instance, enables one to calculate the spontaneous emission and the scattered light spectra20,21,22,23.
We will be interested below in the two-time autocorrelation functions with zero expectation values defined as follows:
where ϕ0 is the ground state of the hydrogen atom, \(\hat{Q}(t)\) is an operator in the Heisenberg picture, and \(\bar{Q}(t)\) is the expectation value of \(\hat{Q}(t)\). As we consider only the ground state of hydrogen as the initial state in the present work, we will omit below ϕ0 in the formulas, implicitly understanding that \(\langle \hat{A}\rangle =\langle {\phi }_{0}| \hat{A}| {\phi }_{0}\rangle\) for any operator \(\hat{A}\).
We will consider below as two examples the autocorrelation functions Czz(t2, t1) and \({C}_{{v}_{z},{v}_{z}}({t}_{2},{t}_{1})\) for the components of the coordinate and velocity operators in the direction of the laser field. We will show that studying these autocorrelation functions one can obtain information about the dynamics of the ionization process.
On one hand, we can compute the autocorrelation functions in an ab initio way without any approximations using the well-tested procedure24 we use to solve the TDSE. Considering Czz(t2, t1) as an example, using definition (3), and employing the well-known properties of the time-evolution operators, we may write:
Calculation of this expression requires, thus, first propagating the TDSE starting with Ψ(0) = ϕ0 – the ground state of hydrogen, on the interval (0, t1), thus obtaining the state vector Ψ(t1) at t = t1. Acting with the (Schrödinger) operator z on this vector, we obtain the wave-function Ψ1(t1) = zΨ(t1). Ψ1(t1) is further propagated on the interval (t1, t2) yielding the wave-function Ψ1(t2), from which we obtain Ψ2(t2) = zΨ1(t2). Finally, the autocorrelation function can be found by projecting Ψ2(t2) on the state vector Ψ(t2), obtained by solving the TDSE with the initial condition Ψ(0) = ϕ0 on the interval (0, t2). These calculations were performed using the numerical procedure24 for the solution of the TDSE for hydrogen atom in presence of the laser field given by Eq. (2). Results of the ab initio TDSE calculations of the real and imaginary parts of Czz(t1, t2) for different field strengths are shown in Fig. 1.
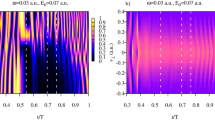
a Real and b imaginary part of Czz(t1, t2) at peak field strength E0 = 0 a.u.; c real and d imaginary part of Czz(t1, t2) at peak field strength E0 = 0.04 a.u.; e real and f imaginary part of Czz(t1, t2) at peak field strength E0 = 0.06 a.u. Times t1 and t2 are rescaled by an optical cycle of the laser field T.
The autocorrelation functions Czz(t1, t2) shown in Fig. 1 show two distinctly different types of correlations. The correlation patterns for small fields—the diagonal stripes in Fig. 1—are reminiscent of those we would obtain for the field-free Heisenberg operators. The origin of the stripes is clear from the expression Eq. (7), from which we can obtain:
where ∣0〉 is the hydrogen ground state. We can also explain the correlations pattern in Fig. 1 qualitatively using a simple classical picture of the atomic periodic motion. Electron’s positions at the moments t and t + kTa, where Ta is the period of the electron’s orbital motion and k is an integer, are clearly correlated; analogously, the electron’s positions at the moments t and t + kTa/2 are anticorrelated; hence, the pattern of the maxima and minima of the autocorrelation function running diagonally. Strictly speaking, this simple classical explanation is applicable to the hydrogen atom with some reservations, as the different terms in the Eq. (7) are not equally spaced in energy. Consequently, the frequencies in Eq. (13) are not integer multiples of some base frequency, as the simple classical picture we alluded to above implies. Had we considered instead of the hydrogen atom the harmonic oscillator with frequency Ω and equally spaced energy levels, Eq. (7) would result in the well-known relation for the coordinate operator in the Heisenberg picture \({\hat{z}}_{H}(t)=z\cos\Omega t+{\hat{p}}_{z}/\Omega \sin\Omega t\)18. For such \({\hat{z}}_{H}(t)\), we would have obtained a pattern of equally spaced maxima and minima of the autocorrelation function running diagonally, for which the classical explanation would be perfectly adequate. Nevertheless, we shall use this line of arguments based on the picture of the electron’s periodic motion for the purposes of the qualitative analysis even for hydrogen, having in mind that for this system this picture may have some limitations. In classical terms, thus, the pattern of correlations in the field-free case just reflects the periodic orbital motion of the electron. For non-zero external fields this field-free pattern of correlations becomes first perturbed (for E0 = 0.04 a.u.) and then is almost completely superseded by a different pattern for E0 = 0.06 a.u., which exhibits horizontal and vertical stripes rather than the diagonal ones, and which shows a good deal of correlated motion for both t1, t2 near the end of the pulse. We shall see below that this new pattern of correlations induced by the field can be explained in considerable detail by our model based on the Eq. (10).
Using Eqs. (10) and (11), we obtain for the autocorrelation function Czz(t2, t1):
where \({C}_{zz}^{0}({t}_{2},{t}_{1})\) is the field-free autocorrelation function, \({\hat{z}}_{0}(t)\) is the z-component of the the field-free Heisenberg coordinate operator obtained using Eq. (7), and z and pz are the usual time-independent Schrödinger operators of the z-components of coordinate and momentum. Calculations of the expectation values appearing in the second line of Eq. (14) can be done as follows. Considering the product \({\hat{z}}_{0}({t}_{2}){\hat{p}}_{z}\) as an example, we may write using the definition of \({\hat{z}}_{0}(t)\): \(\langle {\hat{z}}_{0}({t}_{2}){\hat{p}}_{z}\rangle ={e}^{i\varepsilon {t}_{2}}\langle z{\phi }_{0}| {\hat{U}}_{0}({t}_{2},0)| {\hat{p}}_{z}{\phi }_{0}\rangle\), where \({\hat{U}}_{0}({t}_{2},0)\) is the field-free atomic evolution operator. Calculation of this matrix element requires thus field-free propagation of the initial state \({\hat{p}}_{z}{\phi }_{0}\) on the interval (0, t2), which can be done without difficulties using the numerical procedure we use to solve the TDSE. Calculations of the expectation values in the third line of Eq. (14) does not pose any difficulties. There is one more ingredient that we have to provide to use Eq. (14); it is the function α(t). As we have noted above, the reasoning based on the physical picture of the ionization process suggests that α(t) should be related to the ionization probability P(t). We will use, therefore, the expression α(t) = cP(t) for the function α(t) in Eq. (10) and Eq. (14), where P(t) is the ionization probability and c is a constant factor. We estimate P(t) as:
where WYI(τ) is the well-known Yudin–Ivanov instantaneous ionization rate (YI IIR)25. Our model, thus, has one free parameter c, which we can vary to achieve better agreement between the ab initio \({C}_{zz}^{0}({t}_{2},{t}_{1})\) and the \({C}_{zz}^{0}({t}_{2},{t}_{1})\) we obtain from Eq. (14).
Comparison with numerical solutions of the TDSE
A comparison of the results we obtain in this way, using our model and the ab initio TDSE results, is shown in Fig. 2. To reveal more detail we use a nonlinear scale in the figures, presenting fractional power of Re(Czz(t1, t2)) and Im(Czz(t1, t2)). We can see from Fig. 2 that both TDSE and our model exhibit a new type of correlations—the vertical and horizontal stripes. In the classical picture to which we alluded above, which associated the diagonal stripes in the pattern of correlations dominant for low fields with the correlations due to the periodic motion, this new type of correlations can be accounted for as follows. Correlations between coordinates of the electron at the moments of time t1 and t1 + kTa persist till the moment of time when either t1 or t1 + kTa gets equal to the time of ionization. After the occurrence of the ionization event, different types of correlations are introduced. In the Eq. (14), these types of correlations are described by the second and third lines of the equation. The second line describes the correlations between the electron’s coordinate along the field-free atomic trajectory and the electron’s coordinate along the ionized trajectory. These correlations are responsible for the horizontal and vertical stripes in the correlations pattern in Fig. 2. Employing the simplified classical picture we used above, we might say that this type of correlations arises because the z-coordinate of the ionized electron’s wave-packet is correlated with the electron’s z-coordinate either at the moment of the electron’s birth t = t1, or the electron’s coordinates at the moments of time t = t1 − kTa with a positive integer k, when electron is located at approximately the same spatial point in the course of its orbital motion. Similarly, the minima in the correlations pattern appear because the z-coordinate of the ionized electron’s wave-packet is anticorrelated with the electron’s z-coordinate at the moments of time t = t1 − kTa/2 with a positive integer k, when electron is located at approximately opposite spatial point of its orbit. The area of highly correlated motion seen for the real part of the correlation function in Fig. 2 in the region t1/T > 1∕2, t2/T > 1/2 is due to the term in the third line of the Eq. (14), which describes essentially the propagation of correlations for the free electron motion, which grows with time as t1t2 for large times. We see that all these features are present in both the ab initio TDSE and our model calculation based on the Eq. (14). Our model calculation reproduces these features quite accurately qualitatively and even, as Fig. 2 shows, quantitatively in the case of the real part of the autocorrelation function. Agreement between the imaginary parts Czz(t1, t2) given by the ab initio TDSE and the model calculation based on Eq. (14) is less spectacular but, we believe, can still be considered pretty good given that we use only one adjustable parameter in our model calculations. That our model reproduces the real part of the correlation function better is perhaps not surprising, taking into account that in applying our Eq. (14) we employed only one real positive function α(t) proportional to the ionization probability, discarding thereby all information about phase. Going back to the real part of the autocorrelation function, we would like to draw attention to the fact that the transition between the two types of correlations, which we discussed above: the field-free correlations described by the term in the first line of the Eq. (14) and the correlations between the electron’s coordinate along the field-free atomic trajectory and the electron’s coordinate along the ionized trajectory described by the terms in the second line of the Eq. (14) is quite distinct. Given that correlation function is, in principle, an experimentally measurable quantity26, this offers an intriguing possibility of providing an experimental access to study the somewhat elusive notions such as the moment of the electron’s birth into the continuum and the tunneling time, which have received considerable attention in the literature lately27,28,29,30,31,32,33,34,35,36. The picture we outlined above to explain qualitatively the correlation pattern for the hydrogen atom invokes, thus, two types of correlations: the correlations due to the periodic orbital notion of the electron, which are essentially the same as for the field-free atom, and correlations due to the motion of the ionized electron.
a Real and b imaginary part of Czz(t1, t2) obtained from the TDSE calculation. c Real and d imaginary part of Czz(t1, t2) obtained using the Simple Man Model in the Heisenberg picture approach, with α(t) computed as the ionization probability using Yudin–Ivanov ionization rate (YU IIR). The peak field strength E0 = 0.06 a.u. Times t1 and t2 are rescaled by an optical cycle of the laser field T. The correlation function is exponentiated for improving the visibility of the patterns.
These two types of motion are present for any target. Moreover, any theoretical approach, purporting to describe correctly the essential features of the ionization process, must necessarily include them. We can expect, therefore, that we will obtain qualitatively similar correlation patterns for the targets other than atomic hydrogen as well as in the case of the methods providing an approximate solution to the Schrödinger equation, such as the SFA method. That this is indeed the case can bee seen from Figs. 3 and 4. The autocorrelation function Czz(t1, t2), we obtain if we use the SFA for the laser pulse (2) and the atomic hydrogen as a target is shown in Fig. 3. The autocorrelation function can be computed in this case using the algorithm we applied above for calculating Czz(t1, t2) from the ab initio solution of the TDSE for the atomic hydrogen by noting that time-dependent SFA can be conveniently reformulated as a solution of the inhomogeneous wave equation19, which can be solved numerically using the same procedure we used to solve the TDSE.
One can see that the general features of the autocorrelation function Czz(t1, t2) given by the SFA are qualitatively similar to the pattern shown in Fig. 1, which we obtained by solving the TDSE for the atomic hydrogen. We see the same gradual transition between two types of correlation patterns: the field-free correlation pattern and the correlation pattern induced by the field. There are, of course, some obvious and expected differences. First, in the case of the SFA in Fig. 3a, the diagonal stripes of the field-free pattern are more densely spaced than the stripes in Fig. 1a showing the ab initio TDSE results. The reason for this is the neglect of the excited atomic levels in the SFA. When we apply the Eq. (13) to the atomic hydrogen, the main contribution in the case of the ab initio TDSE calculation comes from the the 1s–2p transition (for which the corresponding dipole matrix element has the largest value). This gives the difference of energies ε1–ε0 = 0.375 a.u. in the exponential in the Eq. (13). If we left only this term in the infinite sum in Eq. (13), the ab initio field-free autocorrelation function Czz(t1, t2) would be a periodic function of t1–t2 with the period ωT∕(ε1–ε0) ≈ 0.15T (to facilitate comparison with the figures we express here the period in units of the optical cycle corresponding to the driving laser frequency ω). This is indeed the interval between the diagonal stripes in Fig. 1a,b showing results of the ab initio TDSE calculation. In the case of the SFA, the transition with the minimum energy difference in Eq. (13), which sets the time scale, is the transition 1s–kp to the low-energy continuum. Corresponding period of the field-free autocorrelation function is then ωT∕∣ε0)∣ ≈ 0.11T, which is close to the interval between the diagonal stripes in Fig. 3a. Another obvious difference between the SFA and the TDSE results, clearly seen from Fig. 1c and Fig. 3b, is a smaller contribution of the correlation pattern due to the ionized electron motion as compared with the TDSE results for the same field strength. This is again an expected feature. The SFA tends to underestimate ionization probability for the systems governed by the Coulomb interaction, and it is only by introducing the Coulomb correction7 that one can make the SFA quantitatively accurate for such systems. It would be more correct, therefore, to compare the SFA and the TDSE results for a system for which we can expect the SFA to provide accurate results.
To do such a comparison we performed another TDSE calculation using as a target a model atom with the short range Yukawa potential V(r) = −1.903e−r∕r. This system has the same ionization potential as the atomic hydrogen. Results (to which we refer as SR results hereafter) for the coordinate autocorrelation function Czz(t1, t2) obtained for the Yukawa potential are shown in Fig. 4. One can see that the SR and the SFA correlation patterns are indeed more similar than the SFA and the TDSE results, especially for higher field strengths, the patterns for the field strength E0 = 0.1 a.u. being practically indistinguishable. We see some difference between Fig. 3a and Fig. 4a, showing real parts of Czz(t1, t2) for the SFA and SR calculations, respectively. The field-free Czz(t1, t2) for the SR calculation has about the same period of ≈0.1T as its SFA counterpart (this can be better seen in Fig. 4b), but the stripes have much poorer visibility in the case of the SR calculation. That the period should be the same as in the SFA case is to be expected. The Yukawa potential we use does not support any excited bound states, the time scale in the Eq. (13) is set, therefore, by the transition from the ground to the low-energy continuum states, just as in the case of the SFA. That the diagonal stripes have poorer visibility for the SR calculation is the consequence of smaller values of the corresponding dipole matrix elements in the Eq. (13) for the Yukawa case.
We see, thus, that particular details of the model we use, such as inclusion or exclusion of the excited levels or Coulomb potential, though certainly altering fine features of the correlation patterns, do not change the qualitative picture we outlined above. The pattern of correlations shown by the autocorrelation function Czz(t1, t2) is, in essence, a combination and interference of the two types of correlations: the correlations due to the orbital notion of the atomic electron and correlations due to the motion of the ionized electron.
In the calculations above we used the expression α(t) = cP(t) for the function α(t) in Eqs. (10) and (14), with P(t) being the ionization probability and c the fitting parameter. We may, in fact, provide an estimate for the parameter c. Reasoning presented in the Supplementary Note 2 shows that c ≈ 1. The most drastic approximation made in obtaining this estimate was replacing the projection operator \({\hat{P}}_{g}\) with the identity operator. Such a replacement is valid, for instance, if \({\hat{P}}_{g}\) acts on a state vector, which differs only slightly from a state vector proportional to ∣ϕ0(t)〉, which would justify this operation for the calculation of the expectation values.
To check that this estimate allows us to obtain reasonable results for autocorrelation functions we consider presently, we performed additional calculations using Eq. (14) with α(t) = P(t). In these calculations, the instantaneous ionization probability P(t) was calculated as:
where ap(t) the instantaneous ionization amplitude obtained by projecting the time-dependent solution of the TDSE on the states of the continuous spectrum of the field-free Hamiltonian of hydrogen atom. This procedure is equivalent to the procedure used in refs. 28,37. We compute in this case the instantaneous ionization probability directly to do an unambiguous check of the estimate α(t) = P(t) we gave above. The results for the autocorrelation function Czz(t1, t2) we obtain in this way for the pulse (2) with the peak field strength E0 = 0.06 a.u. are shown in Fig. 5.
α(t) = P(t) (proportionality constant c = 1) and the total ionization probability P(t) is computed using Yudin–Ivanov ionization rate. The panels show: (a) real and (b) imaginary part of Czz(t1, t2). The peak field strength is E0 = 0.06 a.u. Times t1 and t2 are rescaled by an optical cycle of the laser field T. The correlation function is exponentiated for improving the visibility of the patterns.
These results are to be compared with the results shown in Fig. 2a, b, which show correlation patterns obtained from the TDSE calculation for the same field peak field strength. The comparison shows that we achieve a reasonable agreement with the ab initio TDSE results by using the estimate c = 1 in the relation α(t) = cP(t) in Eq. (14). Had we used a larger value c ≈ 2, we would have obtained yet better visual agreement, the purpose of the comparison was, however, to show that the estimate c = 1 for the proportionality constant allows us to obtain reasonably good results.
Having in our disposal the coordinate autocorrelation function Czz(t1, t2), we can find other correlation functions. An example is shown in Fig. 6, where we present the velocity autocorrelation function \({C}_{{v}_{z}{v}_{z}}({t}_{1},{t}_{2})\) obtained from Czz(t1, t2) as:
The velocity correlation pattern predicted by our model based on the Eq. (17), Eq. (14) agree qualitatively well with the ab initio TDSE results.
a Real and b imaginary part of \({C}_{{v}_{z}{v}_{z}}({t}_{1},{t}_{2})\) obtained from the TDSE calculation. c Real and d imaginary part of \({C}_{{v}_{z}{v}_{z}}({t}_{1},{t}_{2})\) obtained by using the Simple man model in the Heisenberg picture approach, α(t) computed using the Yudin–Ivanov ionization rate (YU IIR). The peak field strength is E0 = 0.06 a.u. Times t1 and t2 are rescaled by an optical cycle of the laser field T.
The utility of our approach allowing to calculate the autocorrelation functions is by no means restricted only to the study of the correlations per se. We may compute other characteristics of the ionization process, e.g., the spectra of the spontaneously emitted and scattered photons. As we noted above, knowing the autocorrelation function for the dipole momentum operator allows one to calculate the spontaneous emission and the scattered light spectra20,21,22,23. Strictly speaking, the calculation of the spectra based on the use of the dipole autocorrelation function is more rigorously justified than the standard recipe based on the use of the expectation value of the dipole momentum operator commonly employed, e.g., for the calculations of the HHG spectra. The quantum-electrodynamical treatment of an atom interacting with the radiation field (assuming that the driving laser pulse is linearly polarized in the z-direction) gives the expression38,39
for the spectral density of a mode k, λ of the radiation field. The quantity 〈μz(t2)μz(t1)〉 in this expression is the two-time autocorrelation function for the dipole momentum operator μz taken in the Heisenberg representation. If one makes the decorrelation assumption 〈μz(t2)μz(t1)〉 = 〈μz(t2)〉〈μz(t1)〉 than this expression reduces to the commonly used formula relating the spectral density and the squared absolute value of the Fourier transform of the expectation value of the dipole momentum operator. It is known38 that in calculating the single-atom response to the laser field, the results of the calculations obtained using the decorrelation assumption may differ considerably form the results of the calculations using the dipole momentum autocorrelation function. The use of the simpler formula, relying only on the expectation value of the dipole momentum operator, is well justified if one is interested in the situation when light is scattered by many atoms with uncorrelated dipole momenta39, which effectively ensures validity of the decorrelation assumption.
The dipole momentum autocorrelation function in the Eq. (18) can be expressed as:
where Czz(t1, t2) is the autocorrelation function we have been studying above, and \(\bar{z}(t)\)- expectation value of the z-coordinate as function of time. We can compute, therefore, the spectra using either the ab initio Czz(t1, t2) provided by the TDSE calculation or the Czz(t1, t2) we obtain using our model. In the latter case we need one more ingredient, the expectation value \(\bar{z}(t)\) of the z-coordinate, which we take from the TDSE calculation. In Fig. 7, we show a comparison of the results given by these two calculations. In the model calculation the autocorrelation function was computed using the same prescription we employed in obtaining the results shown in Fig. 2, i.e., we used Eq. (14) with α(t) computed as α(t) = cP(t), where P(t) is the ionization probability computed using YU IIR and c- the adjustable parameter. For consistency, we used the same value for the parameter c as in the calculations shown above in Fig. 2. One can see that we achieve a reasonably good agreement between the spectra computed using the ab initio TDSE and our model based on the Eq. (14).
Comparison of the photon spectra obtained from the time-dependent Schrödinger equation calculation (TDSE) and the Simple Man Model in the Heisenberg picture with Yudin–Ivanov ionization rate (YI IIR) for the peak field strength E0 = 0.06 a.u. Frequency Ω is rescaled by the laser pulse central frequency ω = 0.057 a.u.
Discussion
To summarize, we presented a simple tentative solution of the Heisenberg operator equations of motion for an atom exposed to electromagnetic field. We might call this solution a SMM in the Heisenberg picture, as our main equation Eq. (10) looks very much like its classical counterpart used in the SMM. We tested the veracity of this tentative expression by applying it to the calculation of the coordinate and velocity autocorrelation functions. As the ab initio TDSE calculations show, these functions are an interesting object of study and, to our knowledge, have not been studied before in the context of the strong field ionization. In particular, their exhibiting the distinct types of correlations due to different types of electron’s motion may offer a useful insight into the physics of strong field ionization.
We may note that our approach is, in a sense, complementary to the traditional approaches relying on the Schrödinger picture. The approach based on the Heisenberg representation is well suited and allows to compute quite naturally the autocorrelation functions of the coordinate and velocity operators, which are more difficult to compute in the Schrödinger picture. As we saw above, which allows us to describe correlations due to the different types of electron’s motion, and to calculate the quantities that can be expressed in terms of the autocorrelation functions for the operator of the dipole momentum, such as the HHG spectra. On the other hand, calculation of the electron energy spectra, for instance the ATI spectra, is more difficult in the framework of the present approach. We could, in principle, employ the recipe of the calculation of the ATI spectra relying on the representation of the projection operator in terms of the energy window operator40,41 to extract the energy spectra. Such a calculation, although feasible, is by no means straightforward. We should note, also, that in the case of the solutions of the Heisenberg operator equations of motion we are dealing with, the link to the quantum and semi-classical trajectories, which is transparent in the case of the SFA relying on the Schrödinger picture, is not so obvious. This fact may seem counter-intuitive (after all, the operator equations of motion (9) look very much like their classical counterparts), but it can be understood by taking into account that in the Heisenberg picture we have no analog of the saddle-point approximation to rely on to reveal the link with the quantum or semi-classical trajectories.
We saw that the autocorrelation functions computed by fairly simple means using the main Eq. (10) agree well with the results of the ab initio TDSE calculations both in reproducing the correlation patterns and the emission photon spectra, thereby confirming the utility of our model.
Data availability
All relevant data are available from the authors upon request.
References
Keldysh, L. V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 20, 1307 (1965).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163 (2009).
Lewenstein, M., Balcou, P., Ivanov, M. Y., L’Huillier, A. & Corkum, P. B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49, 2117 (1994).
Corkum, P. B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994 (1993).
Shvetsov-Shilovski, N. I., Dimitrovski, D. & Madsen, L. B. Ionization in elliptically polarized pulses: multielectron polarization effects and asymmetry of photoelectron momentum distributions. Phys. Rev. A 85, 023428 (2012).
Arbo, D. G. et al. Ionization of argon by two-color laser pulses with coherent phase control. Phys. Rev. A 92, 023402 (2015).
Popruzhenko, S. V. Keldysh theory of strong field ionization: history, applications, difficulties and perspectives. J. Phys. B At. Mol. Opt. Phys. 47, 204001 (2014).
Hofmann, C., Landsman, A. S. & Keller, U. Attoclock revisited on electron tunnelling time. J. Modern Opt. 66, 1052 (2019).
Popov, V. S. Imaginary-time method in quantum mechanics and field theory. Phys. At. Nuclei 68, 686 (2005).
Popruzhenko, S. V. Invariant form of coulomb corrections in the theory of nonlinear ionization of atoms by intense laser radiation. JETP 145, 580 (2014).
Li, M. et al. Classical-quantum correspondence for above-threshold ionization. Phys. Rev. Lett. 112, 113002 (2014).
Shvetsov-Shilovski, N. I. et al. Semiclassical two-step model for strong-field ionization. Phys. Rev. A 94, 013415 (2016).
Hofmann, C., Landsman, A., Cirelli, C., Pfeiffer, A. & Keller, U. Comparison of different approaches to the longitudinal momentum spread after tunnel ionization. J. Phys. B 46, 125601 (2013).
Pfeiffer, A. N. et al. Probing the longitudinal momentum spread of the electron wave packet at the tunnel exit. Phys. Rev. Lett. 109, 083002 (2012).
Dimitrovski, D. & Madsen, L. B. Theory of low-energy photoelectrons in strong-field ionization by laser pulses with large ellipticity. Phys. Rev. A 91, 033409 (2015).
Landsman, A. S. & Keller, U. Attosecond science and the tunnelling time problem. Phys. Rep. 547, 1 (2015).
Hofmann, C., Zimmermann, T., Ziellinski, A. & Landsman, A. Non-adiabatic imprints on the electron wave packet in strong field. New J. Phys. 18, 043011 (2016).
Messiah, A. Quantum Mechanics (John Wiley & Sons, North Holland, 1966).
Ivanov, I. A., Kim, K. T. & Nam, C. H. Strong-field approximation and its modifications as evolution equations. Phys. Rev. A 99, 013417 (2019).
Heller, E. J. The semiclassical way to molecular spectroscopy. Acc. Chem. Res. 14, 168 (1981).
Heller, E. J. Quantum corrections to classical photodissociation models. J. Chem. Phys. 68, 2066 (1978).
Engel, V. The calculation of autocorrelation functions for spectroscopy. Chem. Phys. Lett. 189, 76 (1992).
Praprotnik, M. & Janeži\({\breve{\mathrm{c}}}\), D. Molecular dynamics integration and molecular vibrational theory. iii. the infrared spectrum of water. J. Chem. Phys. 122, 174103 (2005).
Ivanov, I. A. Evolution of the transverse photoelectron-momentum distribution for atomic ionization driven by a laser pulse with varying ellipticity. Phys. Rev. A 90, 013418 (2014).
Yudin, G. L. & Ivanov, M. Y. Nonadiabatic tunnel ionization: Looking inside a laser cycle. Phys. Rev. A 64, 013409 (2001).
Uhrich, P., Castrignano, S., Uys, H. & Kastner, M. Noninvasive measurement of dynamic correlation functions. Phys. Rev. A 96, 022127 (2017).
Torlina, L. et al. Interpreting attoclock measurements of tunnelling times. Nat. Phys. 11, 503 (2015).
Yuan, M., Xin, P., Chu, T. & Liu, H. Exploring tunneling time by instantaneous ionization rate in strong-field ionization. Opt. Express 25, 23493 (2017).
Teeny, N., Yakaboylu, E., Bauke, H. & Keitel, C. H. Ionization time and exit momentum in strong-field tunnel ionization. Phys. Rev. Lett. 116, 063003 (2016).
Ivanov, I. et al. Instantaneous ionization rate as a functional derivative. Commun. Phys. 1, 81 (2018).
Zimmermann, T., Mishra, S., Doran, B. R., Gordon, D. F. & Landsman, A. S. Tunneling time and weak measurement in strong field ionization. Phys. Rev. Lett. 116, 233603 (2016).
Landsman, A. S. et al. Ultrafast resolution of tunneling delay time. Optica 1, 343 (2014).
Douguet, N. & Bartschat, K. Dynamics of tunneling ionization using bohmian mechanics. Phys. Rev. A 97, 013402 (2018).
Camus, N. et al. Experimental evidence for wigner’s tunneling time. Phys. Rev. Lett. 119, 023201 (2017).
Ni, H., Saalmann, U. & Rost, J.-M. Tunneling ionization time resolved by backpropagation. Phys. Rev. Lett. 117, 023002 (2016).
Ni, H., Saalmann, U. & Rost, J.-M. Tunneling exit characteristics from classical backpropagation of an ionized electron wave packet. Phys. Rev. A 97, 013426 (2018).
Ivanov, I. A., Nam, C. H. & Kim, K. T. Endpoint contribution to the instantaneous ionization rate for tunneling ionization. Phys. Rev. A 91, 063404 (2015).
Knight, P. L. & Milonni, P. W. The rabi frequency in optical spectra. Phys. Rep. 66, 21 (1980).
Sundaram, B. & Milonni, P. W. High-order harmonic generation: simplied model and relevance of single-atom theories to experiment. Phys. Rev. A 41, 6571 (1990).
Schafer, K. J. & Kulander, K. C. Energy analysis of time-dependent wave functions: application to above-threshold ionization. Phys. Rev. A 42, 5794 (1990).
Fetić, B. & Milo\({\breve{\mathrm{s}}}\)ević, D. B. High-order above-threshold ionization of the H\({}_{2}^{+}\) ion: the role of internuclear distance. Phys. Rev. A 99, 043426 (2019).
Acknowledgements
This work was supported by IBS (Institute for Basic Science) under IBS-R012-D1.
Author information
Authors and Affiliations
Contributions
I.A.I. and K.T.K. conceived the project. I.A.I. performed the calculations. All authors contributed to discussions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ivanov, I.A., Kim, K.T. Simple man model in the Heisenberg picture. Commun Phys 3, 7 (2020). https://doi.org/10.1038/s42005-019-0279-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0279-5
This article is cited by
-
Models in quantum computing: a systematic review
Quantum Information Processing (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.