Abstract
Quantum simulators allow to explore static and dynamical properties of otherwise intractable quantum many-body systems. In many instances, however, the read-out limits such quantum simulations. In this work, we introduce an innovative experimental read-out exploiting coherent non-interacting dynamics. Specifically, we present a tomographic recovery method allowing to indirectly measure the second moments of the relative density fluctuations between two one-dimensional superfluids, which until now eluded direct measurements. Applying methods from signal processing, we show that we can reconstruct the relative density fluctuations from non-equilibrium data of the relative phase fluctuations. We employ the method to investigate equilibrium states, the dynamics of phonon occupation numbers and even to predict recurrences. The method opens a new window for quantum simulations with one-dimensional superfluids, enabling a deeper analysis of their equilibration and thermalization dynamics.
Similar content being viewed by others
Introduction
Quantum simulators offer entirely new perspectives of assessing the intriguing physics of quantum many-body systems in and out of equilibrium. They are experimental setups allowing to probe properties of complex quantum systems under unprecedented levels of control1,2,3, beyond the possibilities of classical simulations. Among other platforms, experiments with ultra-cold atoms involving large particle numbers or even continuous quantum fields have been particularly insightful4,5,6,7,8,9,10,11,12,13,14.
And yet, key questions remain open for a highly unexpected reason: the read-out of state-of-the-art quantum simulators is limited. In one-dimensional (1D) superfluids, for example, one can probe the dynamics of equilibration4 occurring in the presence of an effective light-cone5 and leading to generalized Gibbs ensembles6. The excellent experimental control over that system allowed to observe coherent recurrences in the dynamics of a system of thousands of atoms8. However, in that particular setup, further quantifying the recent observations is currently obstructed because only phase quadratures but not canonically conjugate density fluctuations can be measured. On the contrary, if both quadratures could be measured, and hence if genuine quantum read-out was possible, then studies of intricate questions on the role of interactions, or entanglement dynamics after a quench, could become possible.
This situation is by no means an exception: In fact, in any quantum simulation platform, read-out prescriptions are always restricted in one way or another, which constitutes a crucial bottleneck towards studying intricate physical questions. For cold atoms in optical lattices, akin to the development which will be laid out in this work, innovations such as the quantum gas microscope15,16,17 directly opened up the path towards studying exciting physical phenomena9,10,11,12,13,14. Sophisticated read-out methods are therefore highly desirable and key to a platform.
In this work, we show that quenching a single global parameter in the system can enable a genuine quantum read-out and even allow for state reconstructions. We hence open a new ‘window’ into a quantum simulator for which so far—as is common in quantum simulation—only incoherent, or ‘classical’, read-out was natively possible.
Tomography of many-body systems is typically limited due to the number of necessary observables and complexity of control. However, often for large systems, the observed dynamics can be described by an effective free field theory capturing the dynamics by means of modes which are long-lived, i.e., not over-damped. We shall demonstrate that observing their dynamics can already suffice to perform reconstructions of the relevant correlation functions for many-body systems. The basic principle is that non-equilibrium evolution can mix ‘quadratures’ (non-commuting operators describing the dynamics of a mode) in such a way that consistency of observed correlations implies constraints regarding the unobserved ones. We will show that they can be quantitatively reconstructed.
Specifically, in this work, we set out to introduce a novel method of tomographic read-out for quantum simulators, by combining known quantum dynamics and available measurements to obtain more information. Related ideas of exploiting known random or deterministic unitary dynamics to get access to otherwise inaccessible types of measurements have been theoretically explored18,19,20,21,22,23. However, closest in spirit are tomographic methods in quantum optics where a harmonic rotation in phase space allows to measure two canonically conjugated quadratures by a detector sensitive to only one of them, and hence perform a ‘quantum measurement’.
Here, we consider this basic idea in a genuine multi-mode setting and demonstrate a practical application of the method to 1D superfluids. We acquire data at different times for many modes at the same time and make use of semi-definite programming techniques for achieving reconstructions insusceptible to noise. After introducing our new recovery method, we explore the physics of 1D superfluids studying the properties of quench dynamics and its initial conditions. We use the quantum read-out information concerning both density and phase fluctuations in momentum space to fit the temperature and the global tunnel coupling parameter of the initial state preparation. Concerning out-of-equilibrium dynamics, we are able to predict recurrences by relying solely on data taken at times away from the recurrence occurrence, demonstrating that the system is coherent throughout the evolution. Finally, we monitor dynamics of phonon occupation numbers constraining their growth over an extensive observation time giving further experimental evidence for the validity of the effective model. The successful functioning of our method demonstrates an excellent agreement of the experiment with the theory of elementary excitations of 1D superfluid24,25. Our approach is based on very general and ubiquitous ingredients, hence the framework that we establish can be expected to be in a natural way applicable to various quantum simulators.
Results
The system considered
In order to apply our read-out method in practice, we will consider the setting of two adjacent 1D Bose gases realized with ultra-cold atoms. Their low-energy relative fluctuations in phase and density, \(\hat{\varphi }\) and \(\delta \hat{\varrho }\), are described by the effective Hamiltonian8,25
with \(m\) being the atomic mass and \({n}_{{\rm{GP}}}\) the average density profile defined by the ground state of a 1D Gross-Pitaevskii (GP) equation. The Hamiltonian describes phonons which are the elementary density-phase excitations, satisfying bosonic commutation relations \([\delta \hat{\varrho }(z),\hat{\varphi }(z^{\prime} )]={\rm{i}}\delta (z-z^{\prime} )\). The corresponding operators are defined within the atomic cloud whose spatial extension \({R}_{1{\rm{D}}}\) is given by the support of \({n}_{{\rm{GP}}}\). Experimentally, one can engineer the density profile \({n}_{{\rm{GP}}}\) through the trapping potential. This determines the density–density interaction strength, which is functionally dependent on the density profile, \(g(z)=g[{n}_{{\rm{GP}}}(z)]\)8,26 (see Supplementary Note 1). For typical experimental parameters, the last term in Eq. (1) has less importance than the first two27, which together make up the Luttinger model. In the Supplementary Note 1, we describe a general numerical scheme for obtaining approximate eigenfunctions of \(\hat{H}\) for any \({n}_{{\rm{GP}}}\) of interest. For a constant density profile, this model gives a linear spectrum and oscillatory eigenfunctions—which is qualitatively also the case for Eq. (1) even with small GP profile inhomogeneities.
As the excitations are confined within the finite atomic cloud, their spectrum \(\{{\omega }_{k},k=1,2,\ldots \!\!\}\) is discrete28. We denote eigenmode operators of phase and density fluctuations by \({\hat{\phi }}_{k}\) and \({\delta \hat{\rho }}_{k}\), respectively, and use their corresponding wave functions \({f}_{k}^{\rho },{f}_{k}^{\phi }\in {C}^{2}([-{R}_{1{\rm{D}}},{R}_{1{\rm{D}}}])\) to decompose the real-space fields as
Note that here we have \([{\delta \hat{\rho }}_{k},{\hat{\phi }}_{k^{\prime} }]={\rm{i}}{\delta }_{k,k^{\prime} }\) where \({\delta }_{k,k^{\prime} }\) is the Kronecker symbol in contrast to the Dirac delta in the commutation relations of the real-space fields above. Written in terms of the eigenmode degrees of freedom \({\hat{\phi }}_{k}\) and \({\delta \hat{\rho }}_{k}\), the Hamiltonian becomes diagonal
Here \({\hat{\rho }}_{0}\) does not contribute to the visible dynamics because it is conjugate to the global phase which carries no energy and is removed from the data. We shall refer to the eigenmode operators as quadratures as they constitute a discrete set of bosonic observables, which harmonically rotate and do not mix between different modes as can be directly seen from their time evolution within the Heisenberg-picture
In the method presented below, we will make use of approximate eigenmodes obtained from the eigenfunctions of a spatial discretization of the considered model which, for simplicity, we will continue to denote by \({\hat{\phi }}_{k},{\delta \hat{\rho }}_{k}\) and \({f}_{k}^{\rho },{f}_{k}^{\phi }\)—see the Supplementary Note 1 for a more detailed discussion. Let us stress that by the time evolution in Eq. (4) density fluctuations, which are not accessible by direct measurements, are dynamically mixed into the observed phase sector which is the foundation to our reconstruction approach.
Quadrature tomography
In this section, we turn to describing the reconstruction procedure, exploiting the known and efficiently tractable Hamiltonian dynamics on the one hand and ideas of reconstruction and signal processing on the other. This gives rise to a practical and versatile method of reconstructing correlation functions of a type inaccessible to direct measurement. The atom chip experiment29 which we are considering here, measures referenced correlation functions of the relative phase through matter-wave interferometry7,8,22,30,31,32
Here we chose to reference the phase with respect to the middle of the system \({z}_{0}=0\ \upmu {\rm{m}}\), which removes from the data the global phase canonically conjugate to \({\hat{\rho }}_{0}\).
We aim to reconstruct the second moments of the initial state of the quadratures \(\hat{r}={({\hat{\phi }}_{1},\ldots,{\hat{\phi }}_{{\mathcal{N}}},{\delta \hat{\rho }}_{1},\ldots ,{\delta \hat{\rho }}_{{\mathcal{N}}})}^{T}\) of the \({\mathcal{N}}\) lowest lying eigenmodes of \(\hat{H}\) satisfying bosonic commutation relations \([{\hat{r}}_{k},{\hat{r}}_{k^{\prime} }]={\rm{i}}{\Omega }_{k,k^{\prime} }\) with \(\Omega = \left({{{0}\atop{-{\mathbb{1}}_{{\mathcal{N}}}}}\; {{{\mathbb{1}}_{{\mathcal{N}}}}\atop{0}}}\right)\). For this, we define the covariance matrix of the initial state as the collection of second moments
It is important to note that a matrix \(V\) constitutes a collection of physically admissible second moments if and only if the matrix \({\mathcal{Q}}(V)=V+\frac{1}{2}{\rm{i}}\Omega \, \succcurlyeq \, 0\) is positive-semidefinite, i.e., has non-negative eigenvalues. This condition reflects the Heisenberg uncertainty principle of canonically conjugated observables33. It will be convenient to use the notation
Note that here we include the interest in both type of correlations, not only those related to phase fluctuations. Altogether, \(V\) allows to provide a Gaussian description of the full unknown state of the system whose validity can be verified by measuring vanishing higher-order connected correlation functions7. In this work, we will consider initial states that are approximately Gaussian and under this assumption determining \(V\) yields a full state reconstruction. For non-Gaussian initial states, the method presented in the following can still reconstruct the second moments \(V\), but will not provide specific information on the higher moments.
Using the decomposition into eigenmodes in Eq. (2), we obtain for the observable second moments defined in Eq. (5)
where \({f}_{z,z^{\prime} }^{j,k}=({f}_{j}^{\phi }(z)-{f}_{j}^{\phi }({z}_{0}))({f}_{k}^{\phi }(z^{\prime} )-{f}_{k}^{\phi }({z}_{0}))\). Note that we have introduced the cut-off \({\mathcal{N}}\) in the summation over the eigenmodes, anticipating that higher energy modes will have a negligible contribution in the measured signal either because they carry too much energy to or due to finite real-space resolution in the experiment.
Next, we exploit that the time evolution of the Hamiltonian in Eq. (3) does not mix quadrature operators of different eigenmodes as stated in Eq. (4) which gives
where \({C}_{t}=\,{\text{diag}}\,(\cos ({\omega }_{k}t),\,k=1,\ldots ,{\mathcal{N}})\) and \({S}_{t}=\,{\text{diag}}(\sin ({\omega }_{k}t), k=1,\ldots ,{\mathcal{N}})\).
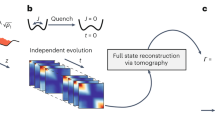
As summarized in Fig. 1, we now have all ingredients needed for quantum read-out. Specifically, based on the relations (8) and (9), we can recover the density correlations through a least-squares recovery problem. For this, we collect all measured values of \(\Phi (z,z^{\prime} ,{t}_{i})\) at different points \(z\) and \(z^{\prime}\) and times \({t}_{i}\) in a vector \(b\). Furthermore, we define a linear map \({\mathcal{A}}(\tilde{V})\) which, given some trial covariance matrix \(\tilde{V}\), outputs the values of \(\Phi (z,z^{\prime} ,{t}_{i})\) sorted as in \(b\) via Eq. (8). The time-evolution is implemented using Eq. (9) such that only the covariance matrix of the initial state is used to fit the observed data. If \(W\) denotes a weighting matrix, then \(W({\mathcal{A}}(\tilde{V})-b)\) is the vector of the weighted least-squares residues. The covariance matrix optimally fitting the data is then given by the solution to the following optimization problem
How can we measure correlation functions of the elementary excitations in superfluids? We first note that the Hamiltonian in the system \(\hat{H}\) (1) is decoupled on the level of momentum space operators \(\{{\hat{\phi }}_{k},\delta {\hat{\rho }}_{k}\}\) involving multiple modes rotating at different frequencies (3). Measurements of real-space continuum fields \(\{\hat{\varphi }(z,t)\}\) yield the referenced two-point correlation functions \(\Phi (z,z^{\prime} ,t)\) defined in Eq. (5). In this work, by means of sophisticated post-processing using tools from signal processing, we are able to recover from real-space data taken at equidistant measurement times the full covariance matrix \(V\) (6) of the non-local eigenmodes of the Hamiltonian. This approach is general and can be applied to any other system in which quenches to non-interacting multi-mode Hamiltonians are available.
The first line implements the minimization of the length \(\parallel \!\! \cdot {\parallel }_{2}\) of the vector of weighted least-squares residues and the condition in the second line ensures that \(V\) is a physical covariance matrix. The optimal solution to this convex quadratic problem with a semi-definite constraint yields the covariance matrix \(V\) of the initial state with a minimal value of \(\Theta\). The optimization can be performed efficiently and reliably numerically with standard methods for semi-definite programming. We use the package cvx34, see the Supplementary Note 2 for more details on the implementation. The most basic idea of an algorithm solving (10) is to repeatedly take a steepest-descent step towards minimizing the least-squares residue and impose \({\mathcal{Q}}(V)\succcurlyeq 0\). Standard convex optimization packages like cvx solve such a problem in a more sophisticated way ensuring numerical accuracy and converge in a matter of seconds. In the implementation, we chose a diagonal weighting matrix \(W\) with entries \(\sigma {[\Phi (z,z^{\prime} ,{t}_{i})]}^{-1}\), where \(\sigma [\Phi (z,z^{\prime} ,{t}_{i})]\) denotes the standard deviation of each measured value. This weighting allows to put more emphasis on more precise values and yields with this a more reliable scheme as we find that \(\Phi (z,z^{\prime} ,t)\) grows typically for increasing spatial separations \(| z-z^{\prime} |\) but \(\Phi (z,z^{\prime} ,t)/\sigma [\Phi (z,z^{\prime} ,t)] \, {\approx}\) const.
Note that the above idea and in fact the whole framework of quantum read-out formulated here is independent of the dimensionality of the Hamiltonian and can be applied, e.g., in two dimensions. There is also no restriction to continuum systems so lattice models can be treated similarly.
Experimental data analysis
Let us consider the state preparation procedure used in the recent experiment8 where recurrent dynamics has been observed. Given an estimate of the average number of atoms per gas \({N}_{{\rm{Avg}}}\simeq 3400\) and the shape of the experimental box-like potential, we can numerically obtain the average density profile \({n}_{{\rm{GP}}}(z)\) from the GP equation. This specifies the Hamiltonian \(\hat{H}\) (1) with \({R}_{1{\rm{D}}}\simeq 25\ \upmu {\rm{m}}\). Hence, we have the full information necessary to compute the eigenmode wave functions needed for the reconstruction procedure in Eq. (8). The number of relevant wave functions \({\mathcal{N}}\approx 10\) can be upper bounded by considering the finite resolution of the interference images. In our case, the phase fluctuations \(\Phi (z,z^{\prime} ,t)\) defined in Eq. (5) can be measured at points \(z,z^{\prime}\) spaced by the pixel size of the camera \(\delta \approx 2\ \upmu {\rm{m}}\)32. In addition, other effects including diffraction limit the resolution. The measured values can be related to theoretical continuum predictions by implementing a real-space cut-off via a Gaussian convolution with standard-deviation \(\sigma \approx 3.5\ \upmu {\rm{m}}\) (see Supplementary Note 2).
Initially the two adjacent gases whose relative phase fluctuations we are studying are strongly coupled. Hence, the state preparation is to a good approximation governed by
where the tunnel coupling term of strength \(J\) is pulling the relative phase field to zero (i.e., \(\langle \cos (\hat{\varphi })\rangle \simeq 1\)). The initial state can be expected to be a low-temperature thermal state of \({\hat{H}}_{\text{Ini}}\). Following that preparation, the system is quenched by suddenly turning off the tunnel coupling. Experimentally, this is realized by separating the two gases over a time of 2 ms until \(J\) drops to zero. The middle of this ramp defines the initial time \(t=\,\text{0}\,\ \,\text{ms}\,\) and the subsequent evolution under the Hamiltonian \(\hat{H}\) (1) is measured in steps \(\Delta t=\,\text{2.5}\,\ \,\text{ms}\,\).
Based on the data from this initial dynamics, we can reconstruct the initial state at \(t=\,\text{0}\,\ \,\text{ms}\,\). In Fig. 2a, we plot the reconstructed phase correlations, showing good agreement with the measured values signifying the consistency of our method. The corresponding covariance matrix of the full initial state is shown in Fig. 2b. Most importantly, note that we are indeed able to infer density fluctuations of the form \(\langle {\delta \hat{\rho }}_{j}{\delta \hat{\rho }}_{k}\rangle\). Using the mode transformation from Eq. (2), this information from the eigenmode-space can be also translated to real-space. However, many physical properties of the initial state can be directly extracted from the eigenmode correlations. We firstly observe that the blocks \({V}^{\phi \phi }\) and \({V}^{\rho \rho }\) are close to being diagonal. Hence, we find that the collective modes of the system are well captured by the numerically obtained wave functions \({f}_{k}^{\phi }\). This supports the expectation that the initial state is thermal with respect to the pre-quench Hamiltonian (11). As the eigenmode wave functions are not strongly affected by the quench for the chosen trap geometry (see Supplementary Note 3), if the system was thermal with respect to the initial Hamiltonian, the reconstructed state should remain diagonal even when expressed in terms of the wave functions of the quench Hamiltonian.
Reconstruction of the full initial state right after decoupling at \(t=\,\text{0}\,\ \,\text{ms}\,\) based on the phase correlations measured during the dephasing dynamics immediately after the quench (t = 1, 3.5, 6, 8.5, 11 and 13.5 ms). a Comparison of the measured phase correlations \({\Phi }_{{\rm{Data}}}(z,z^{\prime} ,t)\) to the reconstructed ones \({\Phi }_{{\rm{Rec}}}\). The time slice presented in the foreground corresponds to \(t=\,\text{1}\,\ \,\text{ms}\,\). We find that the reconstruction yields good agreement with the data, evidenced by the respective weighted difference to the data \(\Delta \Phi =| {\Phi }_{{\rm{Data}}}-{\Phi }_{{\rm{Rec}}}| /\sigma [{\Phi }_{{\rm{Data}}}]\) (right). b Reconstructed covariance matrix \(V\) of the initial state at \(t=0\) for the eigenmodes \(j,k=1,\ldots ,10\). From left to right, the reconstructed phase–phase \({V}^{\phi \phi }\), density–density \({V}^{\rho \rho }\) and phase–density correlations \({V}^{\phi \rho }\) are plotted. The correlations \({V}^{\phi \phi }\) and \({V}^{\rho \rho }\) are close to diagonal in the numerically obtained wave functions \({f}_{k}^{\phi }\), indicating that the eigenmodes of the system are well captured. For an initial thermal state of the Hamiltonian (11), the cross-correlations should vanish \({V}^{\phi \rho }\equiv 0\), here we find a small contribution. Note that the influence of higher-energy modes is suppressed by the limited spatial resolution in the experiment (see Supplementary Note 2). c Comparison of the diagonal elements of \({V}^{\phi \phi }\) (blue bullets) and \({V}^{\rho \rho }\) (red bullets) at \(t=0\) with the predictions for a thermal state of the pre-quench Hamiltonian given in (11) (solid lines). The error bars correspond to the \(80 \%\) confidence intervals obtained from a bootstrap analysis35. The thermal predictions are corrected for the suppression due to the finite imaging resolution, see Supplementary Note 2 and ref. 32. We find the correlations of the first five modes to agree well with a thermal state at \(T=\,\text{52}\,\ \,\text{nK}\,\) and \(J=2\pi \, \times \text{1.1}\,\ \,\text{Hz}\,\) obtained by a combined least-squares fit of \(\langle {\hat{\phi }}_{k}^{2}\rangle\) and \(\langle {\delta \hat{\rho }}_{k}^{2}\rangle\). The strong suppression of the higher mode signals by the imaging renders a meaningful comparison impossible.
On the other hand, we remark that allowing for off-diagonal correlations and cross correlations in \(V\) is necessary for an accurate reconstruction as otherwise the comparison in Fig. 2a is significantly worse. One reason for their presence can be small deviations between the assumed eigenmodes and the true eigenmodes of the system, e.g., due to pre- or post-quench trapping potential imperfections not included in the GP profile. Another reason could be that the initial state is genuinely out of thermal equilibrium, which would be interesting from the quantum information perspective in the context of the resource theory of coherence36,37.
Independent of these subtleties, our read-out method allows us to study how the energy is distributed in the system based on the measured out-of-equilibrium phase fluctuations. We now have access to the phonon occupation numbers given by \({n}_{k}=\frac{1}{2}\langle {\hat{\phi }}_{k}^{2}+{\delta \hat{\rho }}_{k}^{2}\rangle -\frac{1}{2}\) and can study energy expectation values \(\langle \hat{H}\rangle ={\sum }_{k=1}^{{\mathcal{N}}}{\omega }_{k}{n}_{k}\) with \(\hat{H}\) given in Eq. (1). More specifically, we can check from the observed data if the energy is distributed among the modes in a thermal way. The gas is prepared in a double well trap with large tunnel coupling and we expect the prepared state to be thermal with respect to the Hamiltonian (11). Based on Fig. 2b, we find that the reconstructed initial state shows significant suppression of the phase fluctuations which are an order of magnitude smaller than the density fluctuations. This is consistent with the initial energetic penalty on phase fluctuations. In Fig. 2c, we show the quantitative comparison of the reconstructed second moments \(\langle {\hat{\phi }}_{k}^{2}\rangle\) and \(\langle {\delta \hat{\rho }}_{k}^{2}\rangle\) compared to the thermal theory with the Hamiltonian (11). Due to the finite imaging resolution, we are only able to resolve the lowest-lying eigenmodes. We find that their second moments agree with a thermal distribution of the coupled Hamiltonian (11). On the other hand, we also observed that the reconstructed initial state does not agree with the experimental state before the start of the decoupling ramp, as it leads to weaker phase locking than what was measured. This hints at the finite decoupling ramp having a significant influence on the correlations observed in the quench dynamics despite the tunnel coupling decreasing exponentially in the height of the barrier that is being ramped-up. The reconstruction hence extracts an effective initial state of the dynamics. If the physics of the initial Hamiltonian is of particular interest, then this effect might be diminished by performing a faster quench to the free system. On the other hand, let us remark that the physics of quenches of this type is key to the observation of generalized Gibbs ensembles in the considered setup6. In general, it is difficult to model the complete process of state preparation theoretically as it involves a strongly correlated phase of the sine-Gordon model out of equilibrium7 and our method could offer new experimental insights.
Recurrent dynamics
With the reconstruction of the full state of the system, also its evolution beyond the interval of input times can be calculated. Propagating the covariance matrix \(V\) forward or backward in time via (9) allows us to pre- and redict the system’s dynamics. In ref. 8, this dynamics was visualized and quantified through the correlator
The phase-locked initial state corresponds to \(C\approx 1\) independent of the longitudinal separation \(\bar{z}=| z-z^{\prime} |\). In Fig. 3a, we show \(C(\bar{z},t)\) obtained from the experimental data. Due to a linear dispersion relation and an equally spaced spectrum, the involved modes start to rephase after the inital dephasing dynamics leading to partial recurrences of the initial state8. Figure 3b–d shows how this rephasing dynamics can be predicted from the reconstructed states. For the reconstruction based on the initial dephasing dynamics, for example, we obtain a good qualitative prediction of the recurrences (red interval). Quantitative agreement is lost over time due to interaction effects between the modes. These interactions are mediated by higher-order terms beyond the effective model assumed in (1) and can therefore not be captured25. Nevertheless, the reconstruction method is robust enough such that we can obtain an accurate short-time prediction even using data that are seemingly fully dephased, i.e., where \(C(\bar{z},t)\) is nearly indistinguishable from the correlations of a thermal state of the quench Hamiltonian \(\hat{H}\) (blue interval). However, in some cases (green interval), we find that statistical fluctuations can lead to large error bars, an effect reproduced by numerical simulations (see Supplementary Note 3). Note also that the last two intervals were intentionally chosen to be short, including only seemingly dephased data between the recurrences. They cover \(I=5\) input times, during which the slowest eigenmode performs only about a quarter of a rotation. Therefore, the influence of the finite statistical sample size is more severe in these reconstructions.
a Measured phase correlations \(C(\bar{z},t)\) shown together with a cut at \({\bar{z}}_{c}=27.25\ \upmu {\rm{m}}\). Using this experimental dataset, we have performed reconstructions based on input data from a given time window (indicated by red, green and blue intervals) and we calculated the phase correlation functions \(C(\bar{z},t)\) capturing the full spatio-temporal dynamics by evolving the reconstructed states to times beyond the input intervals. b The full spatio-temporal dynamics based on input data indicated by the red interval together with the cut at \({\bar{z}}_{c}\), which shows the quantitative comparison to the measured data. The red-coloured curve corresponds to the propagation of the reconstructed state based on initial times. c Similarly, we show the full spatio-temporal dynamics and a cut at \({\bar{z}}_{c}\) obtained from the reconstructed state based on seemingly dephased data after the quench (green interval). d Likewise, based on the times between the first and second recurrences (blue interval), we are able to obtain a reliable reconstruction. While the dynamical prediction based on the initial dephasing dynamics works well, the reconstructions based on data taken in between the recurrences is limited by the finite sample size (green interval)—an effect reproduced by numerical simulations (see Supplementary Note 3). Note that the quantitative discrepancy at times far away from input intervals is due to terms of higher order not captured by the effective theory of Eq. (1). The shaded area around the curves, as well as the error bars of the data, indicate \(80 \%\) confidence intervals obtained from a bootstrap analysis35.
Phonon occupation dynamics
Besides providing new insights into the state preparation, access to the full covariance matrix can enable entirely new ways of exploring the effects of interactions. The effective model given in (1) is obtained in a perturbative expansion of the Lieb-Liniger Hamiltonian up to second order25. For long evolution times, however, the dynamics can also be affected by the neglected terms that, e.g., can give rise to effects such as Beliaev-Landau damping25. It is challenging to obtain the rates of such processes by numerical calculations as interacting bosonic dynamics are notoriously difficult to treat and various approximations are necessary38,39,40,41. Therefore, it would be interesting to use the atom chip experiments to measure the damping rates and compare with theoretical predictions to validate different methods.
Here we show how the recovery method described above can be used to investigate these higher-order processes. To that end, we perform the recovery procedure for different input intervals of length \(I=8\), with varying starting points. For each interval, we obtain an estimate of the central moments of phase and density fluctuations, \(\langle {\hat{\phi }}_{k}^{2}(t)\rangle\) and \(\langle {\delta \hat{\rho }}_{k}^{2}(t)\rangle\), and calculate the phonon occupation numbers \({n}_{k}(t)=\frac{1}{2}\langle {\hat{\phi }}_{k}^{2}(t)+{\delta \hat{\rho }}_{k}^{2}(t)\rangle -\frac{1}{2}\). Scanning the starting point of the input interval through the measurement times allows us to investigate the dynamics of these observables, as shown in Fig. 4. The interval length is chosen long enough such that the slowest eigenmode picks up enough dynamical phase to ensure a stable reconstruction. At the same time, it is chosen short enough such that interactions between the modes do not influence the reconstruction.
a Phonon occupation numbers \({n}_{k}(t)\) of the first five modes \(k=1,\ldots ,5\) as a function of time \(t\). Each point is based on a reconstruction with an input interval \(\{t,t+\Delta t,\ldots ,t+7\Delta t\}\) of length \(I=8\), illustrated by the black box in the upper left corner. For the ideal mean-field model, \({n}_{k}\) should be a constant of motion. b Time-resolved central moments of the phase and density fluctuations in momentum space \(\langle {\hat{\phi }}_{k}^{2}(t)\rangle\) and \(\langle {\delta \hat{\rho }}_{k}^{2}(t)\rangle\) for the first three modes \(k=1,2,3\). We observe a gradual decay of the oscillation amplitude reflecting the apparent irreversible equilibration present in the system. The error bars indicate the \(80 \%\) confidence intervals obtained from a bootstrap analysis35. The lines connecting the data points are a guide to the eye.
The occupation numbers \({n}_{k}\) are constants of motion of \(\hat{H}\). In Fig. 4a, we show their reconstructed dynamics for the five lowest eigenmodes. We find that overall the occupation numbers do not vary strongly and stay almost constant. This is expected as perturbations to the quench Hamiltonian should be negligible, and in any case they are irrelevant in the sense of the renormalization group. Note, however, that for different measurements with other system sizes, we find indications of a trend of slowly increasing mode occupations (see Supplementary Note 4). While the dynamics of occupation numbers is constant, Fig. 4b shows how at the same time the individual modes rotate between phase and density fluctuations. We find that this dynamics is clearly damped. This hints that the source of the recurrence damping observed in Fig. 3a and ref. 8 is a loss of the initial quadrature ‘squeezing’ \(\langle {\hat{\phi }}_{k}^{2}(0)\rangle /\langle {\delta \hat{\rho }}_{k}^{2}(0)\rangle \ll 1\) within each mode \(k\) rather than changes in their occupations.
Our method makes it possible to extract mode-resolved damping rates of the collective excitations: In the future, using smaller time steps \(\Delta t\) and possibly non-equidistant measurement times should allow to study also higher modes and test theoretical predictions concerning the dynamics under perturbations to the non-interacting effective model.
Discussion
We have formulated and demonstrated the functioning of a new quantum read-out method for quantum simulators where we reconstruct the second moments of pairs of conjugated observables by measuring at different times only one of them. The developed scheme allows us to reliably reconstruct the covariance matrix of non-local low-energy excitations of a 1D superfluid based on experimental data from an atom chip experiment which makes phase measurements but does not directly access density fluctuations.
We found several interesting insights into the physics of the system. Firstly, the strong energetic penalty on phase fluctuations present during the state preparation is reflected in the reconstructed correlations as there are significantly less phase than density fluctuations. The reconstructed state is almost diagonal, which underlines that the eigenmodes before and after the quench are closely related and on a higher level demonstrates that the effective theory captures the relevant degrees of freedom of the system. A fit to a thermal model for the initial state allowed us to estimate the temparature and the effective tunnel coupling in the state preparation. In the considered setting, recurrences of the system have been recently observed8, which are due to an approximately linear spectrum of the phonons. We have demonstrated that our method can take input data from times when the system is seemingly dephased in order to predict recurrences by evolving the reconstructed covariance matrix in time, strongly underlining the predictive power of the obtained recovery scheme. Finally, we have studied the occupation numbers of the eigenmodes over time and obtained strong constraints on the rate of their growth. We have reconstructed the contribution of phase and density fluctuations over time and found that their oscillations are damped. We expect that a quantitative experimental assessment of possible reasons of the deviations from the non-interacting effective model will become possible by following the lines of this work.
Our work paves the way towards new intriguing experiments by giving access to quadrature operators which can be used as the basic ingredients for many quantum information processing protocols42,43,44. The method presented offers a novel window into quantum simulators, allowing to assess initial states, notions of entanglement and various other quantities previous read-out schemes did not allow for. It is our hope that our new quantum read-out method will enable exciting insights into the physics of ultra-cold superfluids, but also due to its generality that it will become a versatile tool used in state-of-the art quantum technologies allowing to fully use the power of the existing quantum simulation platforms45.
Note added
After the completion of the manuscript, we became aware of similar developments in the discrete setting of optical lattices with applications to topological band insulators22,23,46—it would be interesting to also include there our ideas of using semi-definite constraints ensuring that the reconstructed covariance matrix is physical and the recovery stable.
Data availability
Data are available upon reasonable request.
Code availability
Code is available upon reasonable request.
References
Bloch, I., Dalibard, J. & Nascimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267 (2012).
Cirac, J. I. & Zoller, P. Goals and opportunities in quantum simulation. Nat. Phys. 8, 264 (2012).
Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. Nat. Phys. 8, 277 (2012).
Gring, M. et al. Relaxation and pre-thermalization in an isolated quantum system. Science 337, 1318 (2012).
Hofferberth, S., Lesanovsky, I., Fischer, B., Schumm, T. & Schmiedmayer, J. Non-equilibrium coherence dynamics in one-dimensional bose gases. Nature 449, 324–327 (2007).
Langen, T. et al. Experimental observation of a generalised gibbs ensemble. Science 348, 207–211 (2015).
Schweigler, T. et al. Experimental characterization of a quantum many-body system via higher-order correlations. Nature 545, 323 (2017).
Rauer, B. et al. Recurrences in an isolated quantum many-body system. Science 360, 307 (2018).
Endres, M. et al. Observation of correlated particle-hole pairs and string order in low-dimensional mott insulators. Science 334, 200 (2011).
Trotzky, S. et al. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 8, 325 (2012).
Ronzheimer, J. P. et al. Expansion dynamics of interacting bosons in homogeneous lattices in one and two dimensions. Phys. Rev. Lett. 110, 205301 (2013).
Schreiber, M. et al. Observation of many-body localization of interacting fermions in a quasi-random optical lattice. Science 349, 842 (2015).
Cheneau, M. et al. Light-cone-like spreading of correlations in a quantum many-body system. Nature 481, 484–7 (2012).
Kaufman, A. M. et al. Quantum thermalization through entanglement in an isolated many-body system. Science 353, 794 (2016).
Sherson, J. F. et al. Single-atom-resolved fluorescence imaging of an atomic Mott insulator. Nature 467, 68–72 (2010).
Bakr, W. S. et al. Probing the superfluid-to-mott insulator transition at the single-atom level. Science 329, 547–550 (2010).
Weitenberg, C. et al. Single-spin addressing in an atomic Mott insulator. Nature 471, 319–324 (2011).
Merkel, S. T., Riofrio, C. A., Flammia, S. T. & Deutsch, I. H. Random unitary maps for quantum state reconstruction. Phys. Rev. A 81, 032126 (2010).
Ohliger, M., Nesme, V. & Eisert, J. Efficient and feasible state tomography of quantum many-body systems. New J. Phys. 15, 015024 (2013).
Elben, A., Vermersch, B., Dalmonte, M., Cirac, J. I. & Zoller, P. Renyi entropies from random quenches in atomic Hubbard and spin models. Phys. Rev. Lett. 120, 050406 (2018).
Barthel, T. & Lu, J. Fundamental limitations for measurements in quantum many-body systems. Phys. Rev. Lett. 121, 080406 (2018).
Hauke, P., Lewenstein, M. & Eckardt, A. Tomography of band insulators from quench dynamics. Phys. Rev. Lett. 113, 045303 (2014).
Ardila, L. A. P., Heyl, M., & Eckardt, A. Measuring the single-particle density matrix for fermions and hard-core bosons in an optical lattice. Phys. Rev. Lett. 121, 260401 (2018).
Cazalilla, M. A. Bosonizing one-dimensional cold atomic gases. J. Phys. B 37, S1 (2004).
Mora, C. & Castin, Y. Extension of Bogoliubov theory to quasicondensates. Phys. Rev. A 67, 053615 (2003).
Salasnich, L., Parola, A. & Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped bose condensates. Phys. Rev. A 65, 043614 (2002).
Stringari, S. Collective excitations of a trapped bose-condensed gas. Phys. Rev. Lett. 77, 2360 (1996).
Messiah, A. Quantum Mechanics Vol. I (North Holland Publishing, Amsterdam, 1958).
Folman, R. et al. Controlling cold atoms using nanofabricated surfaces: atom chips. Phys. Rev. Lett. 84, 4749–4752 (2000).
Schumm, T. et al. Matter-wave interferometry in a double well on an atom chip. Nat. Phys. 1, 57–62 (2005).
van Nieuwkerk, Y. D., Schmiedmayer, J. & Essler, F. H. L. Projective phase measurements in one-dimensional bose gases. SciPost Phys. 5, 046 (2018).
Schweigler, T. Correlations And Dynamics of Tunnel-coupled One-Dimensional Bose Gases. Ph.D. thesis, TU Wien (2019).
Simon, R., Mukunda, N. & Dutta, B. Quantum-noise matrix for multimode systems: \(u(n)\) invariance, squeezing, and normal forms. Phys. Rev. A 49, 1567 (1994).
Grant, M. & Boyd, S. CVX: Matlab software for disciplined convex programming, version 2.1, http://cvxr.com/cvx (2014).
Efron, B. & Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statist. Sci. 1, 54–75 (1986).
Lami, L. et al. Gaussian quantum resource theories. Phys. Rev. A 98, 022335 (2018).
Streltsov, A., Adesso, G. & Plenio, M. B. Colloquium: quantum coherence as a resource. Rev. Mod. Phys. 89, 041003 (2017).
Mazets, I. E. & Mauser, N. J. Integer partition manifolds and phonon damping in one dimension. Preprint at https://arxiv.org/abs/1804.01374 (2018).
Polkovnikov, A. Phase space representation of quantum dynamics. Ann. Phys. 325, 1790–1852 (2010).
Huber, S., Buchhold, M., Schmiedmayer, J. & Diehl, S. Thermalization dynamics of two correlated bosonic quantum wires after a split. Phys. Rev. A 97, 043611 (2018).
Kukuljan, I., Sotiriadis, S. & Takacs, G. Correlation functions of the quantum sine-Gordon model in and out of equilibrium. Phys. Rev. Lett. 121, 110402 (2018).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621 (2012).
Eisert, J. & Plenio, M. B. Introduction to the basics of entanglement theory in continuous-variable systems. Int. J. Quant. Inf. 1, 479–506 (2003).
Schnabel, R. Squeezed states of light and their applications in laser interferometers. Phys. Rep. 684, 1 (2017).
Acin, A. et al. The European quantum technologies roadmap. New J. Phys. 20, 080201 (2018).
Tarnowski, M. et al. Characterizing topology by dynamics: Chern number from linking number. Nat. Commun. 10, 1728 (2019).
Acknowledgements
We thank C. Riofrio, F. Essler, I. Mazets and A. Steffens for useful discussions and comments. This work has been supported by the ERC (TAQ, QuantumRelax), the European Commission (AQuS), the German DFG (FOR 2724, CRC 183, EI 519/14-1, 519/9-1, EI 519/7-1), the Templeton Foundation, the FQXi, the Austrian Science Fund (FWF) through the doctoral program CoQuS (W1210) (T.S., B.R.) and the SFB 1225 ISOQUANT financed by the DFG and the FWF. This work has also received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 817482 (PASQuanS).
Author information
Authors and Affiliations
Contributions
M.G. formulated and implemented the method following the suggestion of J.S. with contributions of T.S., B.R. and C.K. under the supervision of J.E. B.R., T.S. and J.S. performed the experiment and obtained the data. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gluza, M., Schweigler, T., Rauer, B. et al. Quantum read-out for cold atomic quantum simulators. Commun Phys 3, 12 (2020). https://doi.org/10.1038/s42005-019-0273-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0273-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.