Abstract
Non-linearity and finite signal propagation speeds are omnipresent in nature, technologies, and real-world problems, where efficient ways of describing and predicting the effects of these elements are in high demand. Advances in engineering condensed matter systems, such as lattices of trapped condensates, have enabled studies on non-linear effects in many-body systems where exchange of particles between lattice nodes is effectively instantaneous. Here, we demonstrate a regime of macroscopic matter-wave systems, in which ballistically expanding condensates of microcavity exciton-polaritons act as picosecond, microscale non-linear oscillators subject to time-delayed interaction. The ease of optical control and readout of polariton condensates enables us to explore the phase space of two interacting condensates up to macroscopic distances highlighting its potential in extended configurations. We demonstrate deterministic tuning of the coupled-condensate system between fixed point and limit cycle regimes, which is fully reproduced by time-delayed coupled equations of motion similar to the Lang-Kobayashi equation.
Similar content being viewed by others
Introduction
Time delay is widespread in nature and occurs when the constituents of a given system interact via signals with a finite propagation time1. If the characteristic timescale of the system, such as the period of a simple pendulum, is much longer than the signal propagation time, then one arrives at familiar examples such as Huygens clock synchronisation described by instantaneous interactions2. When propagation times are appreciably long, the role of the system’s history is enhanced and the interactions are said to be time delayed. Such systems dictate the neurological function of our brains, affect traffic flow, influence economic activities, define population dynamics of biological species, regulate physiological systems, determine the stability of lasers, and have application in control engineering3,4. Besides their ubiquity in nature and science, coupled systems with continuous time-delayed interactions exhibit interesting mathematical properties such as an infinite dimensional state space, i.e. for a fixed time-delay \(\tau\) there are infinitely many initial conditions of the system in the time interval \(-\tau \le t\le 0\) needed to predict the dynamics for \(t \, > \, 0\) (ref. 5). Time-delayed interaction or self-feedback is known to greatly increase the dynamical complexity of a system, giving rise to chaotic motion, chimera states6, as well as being able to both stabilise and destabilise fixed point and periodic orbit solutions4.
Technological applications of delay-coupled systems appear in diverse areas such as control engineering7, high speed random-bit generation8, secure chaos communication9, but have also recently emerged in machine learning, where the demand for neuro-inspired computing units has led to various hardware realisations of artificial neural networks10. The intrinsic high-dimensional state space of delay-coupled systems enables an efficient platform for tasks such as pattern recognition, speech recognition, and time series prediction as demonstrated in electronic11, photonic12,13,14, and optoelectronic15,16,17 systems.
In this work, we demonstrate the prospect of an ultrafast microscale platform for engineering time-delayed coupled oscillator networks based on condensates of microcavity exciton–polaritons (from here on polaritons)18,19. Polaritons are bosonic quasi-particles that can undergo a power-driven quantum phase transition to a macroscopically occupied state with long-range phase coherence20. This phase transition is associated with the formation of a polariton condensate, a non-linear matter-wave quantum fluid, which differs from classical cold atom Bose–Einstein condensates, and liquid light droplets21,22 due to its non-equilibrium nature. One of the greatest advantages of polariton condensates for optoelectronic applications is the easy implementation of arbitrary geometries, or graphs, using adaptive optical elements for the excitation laser beam23. We show controllable tuning between steady state (single-colour) and limit-cycle (two-colour) regimes of the two coupled condensate system and explain our observations through time-delayed equations of motion.
Results
Time-delayed coupled matter-wave condensates
Conventionally, networks and lattices of condensates consisting of cold atoms24, Cooper pairs25, photons26, or polaritons27,28 are studied in trap geometries, weakly coupled via tunnelling currents, that allow for the study of solid state physics phenomena such as superfluid-Mott phase transitions29, magnetic frustration30, \(PT\)-symmetric non-linear optics31, and Josephson physics28,32. Here we investigate the inverse case, wherein polariton condensates are freely expanding from small (point-like) sources experiencing dynamics reminiscent to macroscopic systems such as time-delayed coupled semiconductor lasers33. Ballistic expansion extends over two orders of magnitude beyond the pump beam waist, and occurs due to the repulsive potential formed by the uncondensed exciton reservoir injected by the non-resonant pump34. In the case of spatially separated polariton condensates, propagation from one condensate centre to another results in a substantial phase accumulation, interpreted as a retardation of information flow between the condensates. To date, coupled polariton condensates were restricted to distances \(d \, \lesssim \, 40\ \upmu {\rm{m}}\)23,35,36, wherein coupling was assumed to be instantaneous although propagation time was comparable or longer than the characteristic timescale of the systems. To unravel the role of time-delayed interactions, we demonstrate the synchronisation between two tightly pumped condensates separated by up to \(d\approx 114\, \upmu {\rm{m}}\), as shown in Fig. 1a. Figure 1b, c compares schematically the conventional regime of coupled condensates separated by a potential barrier and described by a tunnelling current \(J\), to the macroscopically coupled driven-dissipative matter-wave condensates interacting via radiative particle transfer subject to finite propagation time \(\tau\).
a Schematic showing the cavity plane with two focusing laser beams (red cones) which are spatially displaced by a distance \(d\approx 114\, \upmu {\rm{m}}\) and the experimentally observed photoluminescence of two synchronised, ballistically expanding and interfering condensate centres. Finite particle transfer time \(\tau\) results in time-delayed interaction between condensates \({\Psi }_{1}\) and \({\Psi }_{2}\). Unlike in the case of a conventional bosonic Josephson junction (b) the reported time-delayed coupling mechanism between two tightly pumped polariton condensates (c) is not mediated by a tunnelling current \(J\) (blue dashed line) but by a radiative transfer of particles (blue wavy line).
Dynamics of two interacting condensates
We utilise a strain compensated semiconductor microcavity to enable uninhibited ballistic expansion of polaritons over macroscopic distances37. We inject a polariton dyad with identical Gaussian spatial profiles, with full-width-at-half-maximum (FWHM) of \(\approx \!2\, \upmu {\rm{m}}\), using non-resonant optical excitation at the first Bragg minima of the reflectivity stop-band, and employ spatial light modulation to continuously vary the separation distance from \(6\) to \(94\, \upmu {\rm{m}}\), while keeping constant the excitation density of each pump beam at \({P}_{1,2}\approx 1.5\times {P}_{{\rm{thr}}}^{(1)}\), where \({P}_{{\rm{thr}}}^{(1)}\) is the condensation threshold power of an isolated condensate. For each separation distance \(d\) (more than 400 positions), we record simultaneously the spatial profile of the photoluminescence (real-space), the dispersion (energy vs in-plane momentum in the direction of propagation), and the photoluminescence in reciprocal (Fourier) space (see Supplementary Movie 1). We observe that opposite to the twofold hybridisation of two evanescently coupled condensates28, the macroscopically coupled system is characterised by a multitude of accessible modes of even and odd parity (i.e., 0 and \(\uppi\) phase difference between condensate centres) that alternate continuously between opposite parity states with increasing dyad separation distance. For a range of separation distances only one resonant mode is present in the gain region of the dyad, wherein the polariton dyad is stationary, occupying a single energy level. Between the separation distances, wherein only one mode is present, we observe the coexistence of two resonant modes of opposite parity resulting in non-stationary periodic states.
In Fig. 2 we present an example of the two different regimes, stationary and non-stationary states. Figure 2a, b shows real-space photoluminescence, Fig. 2c, d shows Fourier-space photoluminescence and Fig. 2e, f shows the polariton dispersion along the axis of the dyad with separation distances of (a, c, e) \(d=12.7\, \upmu {\rm{m}}\) and (b, d, f) \(d=37.3\ \upmu {\rm{m}}\). Figure 2g depicts the integrated spectra of Fig. 2e, f using black dots and red squares, respectively. Absolute values of the energy levels are given as a blueshift with respect to the ground-state of the lower polariton branch. Although from the clear fringe pattern in Fig. 2a one could infer that only one mode of odd parity is present, it is through the simultaneous recording of either the Fourier-space or the dispersion that the coexistence of an even parity mode becomes apparent. Each of the two modes has a well defined but opposite parity to the other. We note that as long as we maintain the mirror symmetry of the system by pumping both of the two condensate centres with the same power \({P}_{1}={P}_{2}\), we do not observe formation of non-trivial phase configurations \({\phi }_{1}-{\phi }_{2} \, \ne \, 0,\pi\).
Measured a, b real-space photoluminescence \(| \Psi (x,y){| }^{2}\), c, d momentum-space photoluminescence \(| \Psi ({k}_{x},{k}_{y}){| }^{2}\), and e, f spectrally resolved momentum-space photoluminescence along \({k}_{y}=0\) for two condensates with separation distances (a, c, e) \(d=12.7\, \upmu {\rm{m}}\) and (b, d, f) \(d=37.3\, \upmu {\rm{m}}\), respectively. g Normalised spectra, which are obtained by integrating e and f, are illustrated with black dots and red hollow squares. For better visibility of low-intensity features all images are illustrated in logarithmic grey-scale saturated below 0.001 as shown in f. Scale bars in a, c, e correspond to (\(10\, \upmu {\rm{m}}\), \(1\ \upmu {{\rm{m}}}^{-1}\), \(1\, \upmu {{\rm{m}}}^{-1}\)).
To unravel the dynamics of the coupling on the separation distance between the two condensates, we obtain the spectral position, parity, and spectral weight of both energy levels for pump spot separation distances from \(d=5\, \upmu {\rm{m}}\) to \(d=66\ \upmu {\rm{m}}\). We have recorded configurations with more than two occupied energy levels for several distances \(d\), but with the relative spectral weight of the third peak less than a few percent. In the following, we focus our analysis to the two brightest energy levels for each configuration. The measured normalised spectral weights and spectral positions of the two states versus pump spot separation distance \(d\) are illustrated in Fig. 3a, b using black dots for even parity states and red hollow squares for odd parity states, respectively. Figure 3a shows that the system follows an oscillatory behaviour in the spectral weights of the two parity states giving rise to continuous transitions between even and odd parity states interleaved by configurations exhibiting both parity states. Interestingly, each period of these oscillations in relative intensity (starting and ending with a vanishing spectral weight) displays an ‘energy branch’ featuring a notable reduction in energy with increasing pump spot separation distance \(d\) as is shown in Fig. 3b. The energy of an isolated condensate is measured in the same sample space and its value \(\approx {\!}2.22\ {\rm{meV}}\), above the ground state energy of the lower polariton dispersion, is illustrated with a blue dashed horizontal line. We observe that the phase-coupling of two spatially separated condensate centres is dominated by a spectral redshift with respect to the energy of an isolated condensate. The spectral size of each ‘energy branch’, i.e., the measurable redshift, is decaying from branch-to-branch with increasing pump spot separation distance \(d\). The two dyad configurations exhibiting single-colour and two-colour states shown in Fig. 2 are indicated with grey vertical dashed lines in Fig. 3. Interestingly, it has been shown that the observation of phase-flip transitions, accompanied with changes in oscillation frequency to another mode is a universal characteristic of time-delayed coupled non-linear systems5,38. Such dynamics can be associated with neuronal systems39,40,41, and coupled semiconductor lasers33,42, but have also been demonstrated experimentally for other types of time-delayed coupled systems such as non-linear electronic circuits38,43, living organisms44, chemical oscillators45, and candle-flame oscillators46.
a Spectral weight and b measured blueshift of even (black dots) and odd (red hollow squares) parity states formed by the coupling of two spatially separated polariton condensates with distance \(d\). The energy level of a single condensate pumped with the same non-resonant excitation power density, i.e. 1.5 times the condensation threshold of a single condensate, is illustrated with a horizontal blue dashed line. The vertical dashed lines at \(d=12.7\) and \(37.3\, \upmu {\rm{m}}\) indicate a two-colour and single-colour state, respectively.
Time averaged measurements over \(\sim \!1000\) realisations of the system as presented in Fig. 2a, c, e cannot reveal whether the system of two coupled polariton condensates exhibits periodic dynamics in the form of two-colour states or whether it stochastically picks one of the two parity states. However, it is well known that the power spectrum of a time-dependent signal is related to its auto-correlation function by means of Fourier-transform (Wiener–Khinchin theorem). A two-colour solution, as shown in Fig. 2g, results in the periodic disappearance and revival of the first-order temporal coherence function \({g}^{(1)}(\bar{\tau })\). To characterise the temporal evolution of \({g}^{(1)}(\bar{\tau })\), we perform interferometric measurements of the two coupled condensates and extract the fringe visibility \({\mathcal{V}}\) which—up to a normalisation factor—is proportional to the magnitude of the coherence function \(\left|{g}^{(1)}\right|\). Assuming two coexisting states of opposite parity but equal spectral weight, one may simplify the complex amplitudes of the two coupled condensates \({\Psi }_{1}\) and \({\Psi }_{2}\) as
with time-independent complex amplitude \({\psi }_{0}\) and relative phase \(\phi\) between the two modes of opposite parity and energy \({\mu}_{{\rm{e}}},\, {\mu }_{{\rm{o}}}\) for the even and odd mode respectively. The mixture of two modes, with energy splitting \(\hslash \Delta =\left|{\mu }_{{\rm{e}}}-{\mu }_{{\rm{o}}}\right|\), causes an antiphase temporal beating in the intensities \({\left|{\Psi }_{1,2}\right|}^{2}\) similar to oscillatory population transfer in coupled bosonic Josephson junctions. Therefore, while the occupation amplitude of both condensate centres oscillates with a period \(T=2\pi/\Delta\), they feature a relative phase shift of \(\pi\) due to mixture of even and odd parity states. We use a Michelson interferometer, comprising a retroreflector mounted on a translational stage, and measure both the time averaged interference of the photoluminescence of the same condensate \({I}_{11}(\bar{\tau })=\langle{\left|{\Psi }_{1}(t)+{\Psi }_{1}(t+\bar{\tau })\right|}^{2}\rangle\) as well as the time averaged interference of the photoluminescence of opposite condensates \({I}_{12}(\bar{\tau })=\langle{\left|{\Psi }_{1}(t)+{\Psi }_{2}(t+\bar{\tau })\right|}^{2}\rangle\), where \(\bar{\tau }\) is the relative time delay controlled by the adjustable position of the retroreflector. Examples of the interferometric images are illustrated in Fig. 4a for two condensates with a separation distance of \(d=10.3\, \upmu{\rm{m}}\), which demonstrates condensation in both an even and an odd parity state as shown in Fig. 4b. Assuming the spectral composition as noted in Eqs. (1) and (2) the corresponding interferometric visibilities \({\mathcal{V}}\) can be written as
The experimentally extracted visibilities \({\mathcal{V}}_{11}(\bar{\tau })\) and \({\mathcal{V}}_{12}(\bar{\tau })\) versus relative time delay \(\bar{\tau }\) are illustrated in Fig. 4c with blue circles and red squares, respectively. In agreement with the predicted correlations [Eqs. (3) and (4)] we observe high fringe visibility \({\mathcal{V}}_{11}(0) \, > \, 0.8\) for the interference of one condensate with itself and almost vanishing fringe visibility \({\mathcal{V}}_{12}(0) \, < \, 0.1\) for the interference of opposite condensates at zero time delay. Furthermore, we find periodic disappearance and revival of fringe visibility with period \(T\approx 15.3\ {\rm{ps}}\), which is consistent with the observed energy splitting of the two modes \(\hslash \Delta =270\, \upmu {\rm{eV}}\) (see Fig. 4b). The relative phase shift between the two visibilities \({\mathcal{V}}_{11}(\bar{\tau })\) and \({\mathcal{V}}_{12}(\bar{\tau })\) is a direct result of the periodic population transfer between the two condensates. For comparison the inset in Fig. 4c shows the expected visibilities (Eqs. (3) and (4)) multiplied with an exponential decay accounting for the finite coherence time of the system.
The emission of a polariton dyad with condensation centres \({\Psi }_{1,2}\) pumped with \({P}_{1,2}=1.5{P}_{{\rm{thr}}}^{(1)}\) at locations \((x=\pm \!d/2,\;y=0)\) with \(d\approx 10.3\, \upmu {\rm{m}}\) is interferometrically and spectrally investigated in a–c. a Time integrated real space photoluminescence of both condensates and the interference patterns of one condensate centre \({\Psi }_{1}(t)\) interfering with a delayed version of itself \({\Psi }_{1}(t+\bar{\tau })\) or with a delayed version of the spatially displaced condensate \({\Psi }_{2}(t+\bar{\tau })\). b Corresponding spectrally resolved real-space photoluminescence along the axis of the dyad \(y=0\). The colour-scale of the normalised counts is saturated above 0.5 for better visibility. c Extracted fringe visibilities for the interference of same condensate centres (blue hollow circles) and opposite condensate centres (red hollow squares) versus relative time delay \(\bar{\tau }\) of the two interferometer arms. The inset in c illustrates the expected visibilities (Eqs. (3) and (4)) multiplied with an exponentially decaying envelope. d Comparison of the temporal decay of coherence extracted from the interference of the same condensate \(\langle {\left|{\Psi }_{1}(t)+{\Psi }_{1}(t+\bar{\tau })\right|}^{2}\rangle\) for two coupled condensates with separation distances \(d=20\) and \(20.5\, \upmu {\rm{m}}\), as well as a single isolated condensate. In all three cases each condensate is pumped equally with \(P\approx 1.7{P}_{{\rm{thr}}}^{(1)}\). The error bars are calculated as the standard deviation of the extracted visibility within the full-width at half-maximum (\(\approx \!2\, \upmu {\rm{m}}\)) of each condensate. Lines represent exponential fits for the decay of coherence for the single-mode polariton dyad and the single condensate, respectively.
In Fig. 4d we show the decay of temporal coherence for two coupled condensates in a single-colour state (\(d=20\, \upmu {\rm{m}}\)), a two-colour state (\(d=20.5\, \upmu {\rm{m}}\)), and for an isolated condensate excited with the same pump power density. We note that the coherent exchange of particles in both regimes of the coupled condensate system results in an enhanced coherence time. For the single-colour state (\(d=20\, \upmu {\rm{m}}\)) and the isolated condensate the coherence time \({\bar{\tau }}_{{\rm{c}}}\) can be extracted from exponential fits yielding \(25.5\) and \(10.2\ {\rm{ps}}\), respectively.
Numerical analysis
The dynamics of polariton condensates can be modelled via the mean field theory approach where the condensate order parameter \(\Psi ({\bf{r}},t)\) is described by a two-dimensional (2D) semiclassical wave equation often referred as the generalised Gross–Pitaevskii equation coupled with an excitonic reservoir which feeds non-condensed particles to the condensate47. In Supplementary Note 1 we give numerical results of the spatiotemporal dynamics of the dyad reproducing semi-quantitatively the experimentally observed results. We also provide a supplemental animation showing the calculated evolution of the two-colour condensate (Supplementary Movie 2).
In the following, we show that our experimental observations are described as a system of time-delayed coupled non-linear oscillators. For simplicity we consider the one-dimensional (1D) Schrödinger equation corresponding to the problem of \(\mathrm s\)-wave scattering of the condensate wavefunctions with \({\rm{\delta }}\)-shaped complex-valued, pump induced, potentials. We start by characterising the energies of the time-independent non-hermitian single particle problem:
where \(V(x)\) describes complex-valued \(\delta\)-shaped potentials separated by a distance \(d\), \(V(x)={V}_{0}\left(\delta (x+d/2)+\delta (x-d/2)\right)\), and \({V}_{0}\) lies in the first quadrant of the complex plane, i.e. repulsive interactions and gain. The eigenfunctions of Eq. (5) describing normalisable solutions of outwards propagating waves from the potential (non-resonant pump) centres are written as
where \(k\) also belongs to the first quadrant of the complex plane. This problem is well known for the case of lossless attractors (\(\Re ({V}_{0}) \, < \, 0\), \(\Im ({V}_{0})=0\)) describing electron states in a 1D diatomic Hydrogen molecule ion. The resonance condition of the system is written as
The solutions of Eq. (7) can explicitly be written as
with \(\tilde{V}=m{V}_{0}/{\hslash }^{2}\). Equation (8) describes infinitely many solutions of the system of even \((+)\) and odd \((-)\) parity, where \({W}_{n}\) are the branches of the Lambert \(W\) function. The corresponding complex-valued eigenvalues,
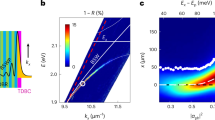
are illustrated in Fig. 5 and qualitatively reproduce the experimental findings of the multiple energy branches shown in Fig. 3. We interpret the experimental occurrence of predominantly two lasing modes with the behaviour of the imaginary values of \({E}_{n}\) for the simplistic 1D-toy model. While there are periodically alternating regions of even and odd-parity solutions dominating the gain, we expect distances at which two modes (of opposite parity) have equal gain and thus can operate with equal intensity. It is worth noting that the Lambert \(W\) function naturally arises for problems involving delay differential equations48.
Calculated a imaginary part and b real part of the eigenvalues \(E\) in Eq. (9) for \(\Re ({V}_{0})=1\ {\rm{meV}}\ \upmu {\rm{m}}\), \(\Im ({V}_{0})=2{\rm{meV}}\ \upmu {\rm{m}}\), \(m=0.28\ {\rm{meV}}\ {{\rm{ps}}}^{2}\ \upmu {{\rm{m}}}^{-2}\), \({\gamma }_{{\rm{c}}}=1/5.5\ {{\rm{ps}}}^{-1}\). The two solutions with largest gain (imaginary part of \(E\)) are illustrated as lines; other solutions are shown as dotted branches.
The time-dependent problem can be formulated as a superposition of two displaced, normalisable, and ballistically propagating waves \({\psi }_{1,2}(x)\), each emerging from one of the condensate centres,
Here, in analogy with Eq. (6), the normalised ansatz is written as \({\psi }_{1,2}(x)=\sqrt{\kappa }{\mathrm{e}}^{ik| {x}\!\pm\!{d/2}|}\), with a complex-valued wavevector \(k={k}_{{\rm{c}}}+i\kappa\). When the coupling between condensates is weak, i.e. small \(\xi =\exp(-\kappa{d})\), one can omit all terms of order \({\mathcal{O}}({\xi }^{2})\) and higher. Then plugging Eq. (10) into the time-dependent form of Eq. (5) and integrating out the spatial degrees of freedom, assuming that Eq. (7) is satisfied, one gets (see Supplementary Note 2),
where \(j=3-i\) and \(i=1,2\) are the condensate indices. When setting \({c}_{i}=\pm \!{c}_{j}\), and solving for stationary states, the above equation recovers the exact resonant solutions dictated by Eq. (8). Equation (11) then shows that inter-condensate interaction is in the form of a coherent influx of particles from condensate \(j\) onto the condensate centre of condensate \(i\) (and vice versa), with a phase retardation of \({k}_{{\rm{c}}}d\). When \({c}_{i}\) and \({c}_{j}\) oscillate at a fixed frequency \(\omega\) we can transform the phase-shifting term \(\exp (i{k}_{{\rm{c}}}d)\) into an effective time delay,
The time delay \(\tau\) corresponds to an interaction lag between condensate centres \(i\) and \(j\) caused by their spatial separation and is given by \(\tau ={k}_{{\rm{c}}}d/\omega\). In the case of weak coupling, i.e. small changes in oscillation frequency \(\omega\) compared to the frequency \({\omega }_{0}\) of a single unperturbed condensate, the time-delay is approximately proportional to the dyad separation distance \(d\), i.e. \(\tau \approx {k}_{{\rm{c}},0}d/{\omega }_{0}\) where we also use the notation \({k}_{0}={k}_{{\rm{c}},0}+i{\kappa }_{0}\) for the wavevector of the single unperturbed condensate. The exponentially decaying term on the right-hand side of Eq. (12) accounts for the 1D spatial decay of particles propagating in between the two condensate centres. Introducing local non-linear interactions, reservoir gain, and blueshift one can write the full non-linear equation of motion for the two coupled condensates as47
Here, \({n}_{i}\) correspond to the pump induced exciton reservoirs providing blushift and gain into their respective condensates, \(g\) is the polariton-reservoir interaction strength, \(R\) is the rate of stimulated scattering of polaritons into the condensate from the active reservoir, \(\alpha\) is the interaction strength of two polaritons in the condensate, \(v={\omega }_{0}/{k}_{{\rm{c}},0}\) is the phase velocity of the polariton wavefunction, and \({\Gamma }_{{\rm{A}}}\) is the radiative decay rate of the bottleneck reservoir excitons. The parameter \(\Omega ={\Omega }_{0}-i\Gamma\) captures the self-energy of each condensate which will, in general, have a contribution from a background of optically inactive dark excitons generated at the pump spot, and \(\Gamma\) denotes the effective linewidth of the polaritons expanding away from the pump spot. The complex valued coupling is written \(J\exp (i\beta )={V}_{0}\kappa \exp (-\kappa d)\) for brevity. Equation (13) is then in the form of a discretised complex Gross–Pitaevskii equation but with time-delayed interaction between the bosonic particle ensembles: which greatly increases the dimensionality of phase-space and complexity of the coupled system. Our system then has strong similarity with the famous Lang–Kobayashi equation49,50 where in our case each condensate acts as a radiating antenna of symmetrically expanding waves. The two spatially separated antennas interfere and maximise their gain by adjusting both their common frequency and their relative phase difference \(\phi =\arg ({c}_{i}^{* }{c}_{j})\). Similarities of the dynamics of coupled polariton condensates to equations of motion in the form of the Lang–Kobayashi equation was discussed in theoretical works recently for instantaneously coupled condensates with complex-valued couplings51. Unlike trapped ground state bosonic systems, such as cold atoms, the ballistically expanding polariton matter-wave condensates necessarily experience time-delayed coupling since \({k}_{{\rm{c}},0}d\gg 1\) similar to inter-cavity coupling of semiconductor lasers33.
In order to accurately reproduce experimentally observed spectra using Eqs. (13) and (14) we fit the distance dependence of the coupling amplitude \(J(d)\) to the spatial envelope of a single condensate. It is known that in a 2D system the 0-order Hankel function of the first kind describes the cylindrically symmetric radial outflow of particles in the linear regime34, therefore we choose
where \({J}_{0}\) is a parameter describing the coupling strength (see Supplementary Note 3). Numerical integration of Eqs. (13) and (14) is computed for separation distances \(d \, > \, 10\, \upmu {\rm{m}}\) using Gaussian white noise as initial conditions which, in close analogy to the experimental findings, reproduces periodic parity-flip transitions accompanied by cyclic solutions in the transition region. Figure 6a depicts the experimentally measured and normalised emission spectra of the polariton dyad versus pump spot separation distance \(d\) on a grey-scale colour-map, for which the extracted two most dominant spectral peaks are depicted in Fig. 3. The red dots represent the numerically calculated spectral peak from Eq. (13) when in single mode operation, or the two most dominant spectral peaks when multiple spectral components exist, showing excellent agreement with experiment. As an example, we illustrate a continuous transition of the system from an anti-phase to in-phase state described by the time-delayed coupled model in Fig. 6b and c showing the corresponding spectral decomposition and phase-space diagrams of the system for an increasing set of distances \(d\) from \(20\) to \(21\, \upmu {\rm{m}}\). Similar stationary and oscillatory behaviour, for separation distances \(d=20\) and \(20.5\, \upmu {\rm{m}}\) respectively, is shown in Fig. 4d. The numerically simulated phase-space diagrams depict periodic orbits in the transition region, involving periodic oscillations of the phase difference \(\phi =\arg ({c}_{1}^{* }{c}_{2})\) and population imbalance \(z=(| {c}_{1}{| }^{2}-| {c}_{2}{| }^{2})/(| {c}_{1}{| }^{2}+| {c}_{2}{| }^{2})\), which is also confirmed by 2D-simulations of the generalised Gross–Pitaevskii equation (see Supplementary Note 1). We have verified through numerics that time-delay physics are indeed an accurate representation of the coupled condensate dynamics (see Supplementary Note 2).
a Comparison of experimentally measured spectra of two coupled polariton condensates coupled with separation distance \(d\) and numerically simulated spectral peaks using Eqs. (13)–(15). Experimentally measured spectra are normalised for each distance \(d\) and the grey-scale colour-map is saturated above 0.5 for better visibility. b and c illustrate the spectral decomposition and phase-diagram for the anti-phase to in-phase transition of the system by increasing the distance \(d\) from \(20\) to \(21\ \upmu {\rm{m}}\). Simulation parameters: \(\hslash \Omega =(1.22-i0.5)\ {\rm{meV}}\), \(\hslash \alpha =0.1\ \upmu {\rm{eV}}\), \(\hslash R=0.5\ \upmu {\rm{eV}}\), \(\hslash g=0.5\ \upmu {\rm{eV}}\), \(v=1.9\ \upmu {\rm{m}}\ {{\rm{ps}}}^{-1}\), \(P=100\ {{\rm{ps}}}^{-1}\), \({\Gamma }_{{\rm{A}}}=0.05\ {{\rm{ps}}}^{-1}\), \(\hslash {J}_{0}=1.1\ {\rm{meV}}\), \({k}_{0}=(1.7+i0.014)\, \upmu {{\rm{m}}}^{-1}\) and \(\beta =-1\).
We note that in the limit of fast active reservoir relaxation, \({\Gamma }_{{\rm{A}}}^{-1}\ll {\Gamma }^{-1}\), one can adiabatically eliminate Eq. (14) and introduce an effective non-linear term to Eq. (13), \(({\alpha }_{\text{eff}}-i\sigma )| {c}_{i}{| }^{2}\), accounting for polariton–polariton and polariton–reservoir interactions, as well as condensate gain saturation. The dynamical equations of two coupled condensates are then described by time-delayed coupled Stuart–Landau oscillators,
Numerical analysis of Eq. (16) is given in Supplementary Note 4 showing qualitative agreement with experiment.
Discussion
We present an extensive experimental and theoretical study of a system of two ballistically expanding (untrapped) interacting polariton condensates, the fundamental building block of polariton graphs with higher connectivity. We demonstrate a regime for coupled matter-wave condensates, wherein the coupling is not instantaneous but mediated by a particle flow inherently connected with time retardation effects. We observe deterministic selection of steady state (single-colour) or dynamical (two-colour) modes of the system by controlling the separation distance between the condensates. Time-delay polaritonics potentially offers an ultrafast platform for simulating the dynamics of real-world systems of time-delayed coupled non-linear oscillators that appear in photonics, electronics, and neural circuits. Given the high non-linearities of polaritons and the ease of optically imprinting multiple condensates of arbitrary geometries on planar microcavities, the system offers promising applications for neuromorphic devices based on lattices of history dependent, non-trapped, strongly interacting, polariton condensates with a wide range of coupling strengths, fast optical operations (input), dynamics (processing), and readout.
Methods
Microcavity sample and experimental methods
The microcavity sample used is a strain compensated \(2\lambda\) GaAs microcavity with three pairs of 6 nm InGaAs quantum wells embedded at the anti-nodes of the electric field37. The intracavity layer contains a wedge and the position on the sample is chosen such that the cavity photonic mode is redshifted from the excitonic mode at zero inplane wavevector (\(| {\bf{k}}| =0\)) by \(\approx -5.5\) meV. For all experiments the microcavity is held in a cold finger cryostat (temperature \(T\approx 6\, {\mathrm{K}}\)) and is optically pumped with a circularly polarised continuous wave monomode laser blue-detuned above the cavity stopband (\(\lambda \approx 785\ {\rm{nm}}\)). To prevent heating of the sample, an acousto-optic modulator is used to generate square wave packets at a frequency of 10 kHz and duty cycle of \(5 \%\). A liquid crystal spatial light modulator (SLM) imprints a phase pattern such that when the beam is focused through the 0.4 numerical aperture microscope objective lens it excites the sample with the desired spatial geometry. The phase patterns are carefully designed so that when changing the pump separation distance \(d\) of the two-spot excitation pattern, the diffraction efficiency of the SLM remains constant and both pump spots retain equal excitation power and width. The photoluminescence is collected in reflection geometry and spectrally resolved using an 1800 grooves/mm grating in a \(750\ {\rm{mm}}\) spectrometer, which is equipped with a charge-coupled device (CCD). Real-space, Fourier-space and dispersion images are acquired using exposure times in the order of milliseconds.
Interferometry
A modified Michelson interferometer, where one mirror is replaced with a retroreflector mounted on a translational stage, is used for measuring the interference and temporal coherence of the emission. By tilting the angle of the emission entering the interferometer, we select to spatially overlap the emission of either opposing condensates or the same condensates onto a CCD camera. Interference fringe visibilities are extracted from the normalised \({{\rm{first}}}\) diffraction order of the computed discrete Fourier transform of each interference image.
Image processing
Image displayed in Fig. 1a has been digitally processed with a low-pass filter to increase the visibility of interference fringes.
Data availability
The data that support the findings of this study are openly available from the University of Southampton repository (https://doi.org/10.5258/SOTON/D1149)52.
References
Mackey, M. C. & Glass, L. Oscillation and chaos in physiological control systems. Science 197, 287–289 (1977).
Oliveira, H. M. & Melo, L. V. Huygens synchronization of two clocks. Sci. Rep. 5, 11548 (2015).
Erneux, T. Applied Delay Differential Equations, Vol. 3 (Springer-Verlag, New York, 2009).
Atay, F. M. Complex Time-Delay Systems: Theory and Applications (Springer-Verlag, Berlin Heidelberg, 2010).
Schuster, H. G. & Wagner, P. Mutual entrainment of two limit cycle oscillators with time delayed coupling. Prog. Theor. Phys. 81, 939–945 (1989).
Larger, L., Penkovsky, B. & Maistrenko, Y. Virtual chimera states for delayed-feedback systems. Phys. Rev. Lett. 111, 054103 (2013).
Schöll, E. & Schuster, H. G. Handbook of Chaos Control, Vol. 2 (Wiley-VCH, Weinheim, 2008).
Uchida, A. et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photonics 2, 728 (2008).
Argyris, A. et al. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 438, 343 (2005).
Van der Sande, G., Brunner, D. & Soriano, M. C. Advances in photonic reservoir computing. Nanophotonics 6, 561–576 (2017).
Appeltant, L. et al. Information processing using a single dynamical node as complex system. Nat. Commun. 2, 468 (2011).
Larger, L. et al. Photonic information processing beyond turing: an optoelectronic implementation of reservoir computing. Opt. Express 20, 3241–3249 (2012).
Brunner, D., Soriano, M. C., Mirasso, C. R. & Fischer, I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 4, 1364 (2013).
Vandoorne, K. et al. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 5, 3541 (2014).
Paquot, Y. et al. Optoelectronic reservoir computing. Sci. Rep. 2, 287 (2012).
Martinenghi, R., Rybalko, S., Jacquot, M., Chembo, Y. K. & Larger, L. Photonic nonlinear transient computing with multiple-delay wavelength dynamics. Phys. Rev. Lett. 108, 244101 (2012).
Larger, L. et al. High-speed photonic reservoir computing using a time-delay-based architecture: million words per second classification. Phys. Rev. X 7, 011015 (2017).
Kavokin, A., Baumberg, J. J., Malpuech, G. & Laussy, F. P. Microcavities (Oxford University Press, Oxford, 2007).
Li, F. et al. Tunable open-access microcavities for solid-state quantum photonics and polaritonics. Adv. Quantum Technol. 2, 1900060 (2019).
Kasprzak, J. et al. Bose-Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006).
Wu, Z. et al. Cubic-quintic condensate solitons in four-wave mixing. Phys. Rev. A 88, 063828 (2013).
Zhang, Z. et al. Particlelike behavior of topological defects in linear wave packets in photonic graphene. Phys. Rev. Lett. 122, 233905 (2019).
Berloff, N. G. et al. Realizing the classical xy Hamiltonian in polariton simulators. Nat. Mater. 16, 1120–1126 (2017).
Bloch, I. Ultracold quantum gases in optical lattices. Nat. Phys. 1, 23 (2005).
Cataliotti, F. et al. Josephson junction arrays with Bose-Einstein condensates. Science 293, 843–846 (2001).
Dung, D. et al. Variable potentials for thermalized light and coupled condensates. Nat. Photonics 11, 565 (2017).
Kim, N. Y. et al. Dynamical d-wave condensation of exciton-polaritons in a two-dimensional square-lattice potential. Nat. Phys. 7, 681 (2011).
Abbarchi, M. et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 9, 275–279 (2013).
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a mott insulator in a gas of ultracold atoms. Nature 415, 39 (2002).
Struck, J. et al. Quantum simulation of frustrated classical magnetism in triangular optical lattices. Science 333, 996–999 (2011).
Zhang, Z. et al. Observation of parity-time symmetry in optically induced atomic lattices. Phys. Rev. Lett. 117, 123601 (2016).
Albiez, M. et al. Direct observation of tunneling and nonlinear self-trapping in a single bosonic josephson junction. Phys. Rev. Lett. 95, 010402 (2005).
Soriano, M. C., García-Ojalvo, J., Mirasso, C. R. & Fischer, I. Complex photonics: dynamics and applications of delay-coupled semiconductors lasers. Rev. Mod. Phys. 85, 421–470 (2013).
Wouters, M., Carusotto, I. & Ciuti, C. Spatial and spectral shape of inhomogeneous nonequilibrium exciton-polariton condensates. Phys. Rev. B 77, 115340 (2008).
Christmann, G. et al. Oscillatory solitons and time-resolved phase locking of two polariton condensates. N. J. Phys. 16, 103039 (2014).
Ohadi, H. et al. Nontrivial phase coupling in polariton multiplets. Phys. Rev. X 6, 031032 (2016).
Cilibrizzi, P. et al. Polariton condensation in a strain-compensated planar microcavity with ingaas quantum wells. Appl. Phys. Lett. 105, 191118 (2014).
Prasad, A. et al. Universal occurrence of the phase-flip bifurcation in time-delay coupled systems. Chaos: an interdisciplinary. J. Nonlinear Sci. 18, 023111 (2008).
Adhikari, B. M., Prasad, A. & Dhamala, M. Time-delay-induced phase-transition to synchrony in coupled bursting neurons. Chaos: an interdisciplinary. J. Nonlinear Sci. 21, 023116 (2011).
Barardi, A., Sancristóbal, B. & Garcia-Ojalvo, J. Phase-coherence transitions and communication in the gamma range between delay-coupled neuronal populations. PLoS Comput. Biol. 10, e1003723 (2014).
Dotson, N. M. & Gray, C. M. Experimental observation of phase-flip transitions in the brain. Phys. Rev. E 94, 042420 (2016).
Clerkin, E., O’Brien, S. & Amann, A. Multistabilities and symmetry-broken one-color and two-color states in closely coupled single-mode lasers. Phys. Rev. E 89, 032919 (2014).
RamanaReddy, D. V., Sen, A. & Johnston, G. L. Experimental evidence of time-delay-induced death in coupled limit-cycle oscillators. Phys. Rev. Lett. 85, 3381–3384 (2000).
Takamatsu, A., Fujii, T. & Endo, I. Time delay effect in a living coupled oscillator system with the plasmodium of physarum polycephalum. Phys. Rev. Lett. 85, 2026–2029 (2000).
Cruz, J. M. et al. Phase-flip transition in coupled electrochemical cells. Phys. Rev. E 81, 046213 (2010).
Manoj, K., Pawar, S. A. & Sujith, R. I. Experimental evidence of amplitude death and phase-flip bifurcation between in-phase and anti-phase synchronization. Sci. Rep. 8, 11626 (2018).
Wouters, M. & Carusotto, I. Excitations in a nonequilibrium Bose-Einstein condensate of exciton polaritons. Phys. Rev. Lett. 99, 140402 (2007).
Asl, F. M. & Ulsoy, A. G. Analysis of a system of linear delay differential equations. J. Dyn. Syst. Meas. Control 125, 215–223 (2003).
Lang, R. & Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quant. Electronics 16, 347–355 (1980).
Kozyreff, G., Vladimirov, A. & Mandel, P. Global coupling with time delay in an array of semiconductor lasers. Phys. Rev. Lett. 85, 3809 (2000).
Kalinin, K. P. & Berloff, N. G. Polaritonic network as a paradigm for dynamics of coupled oscillators. Preprint at https://arxiv.org/abs/1902.09142 (2019).
Töpfer, J. D., Sigurdsson, H., Pickup, L. & Lagoudakis, P. G. Data for Time-Delay Polaritonics (University of Southampton Repository, 2019).
Acknowledgements
The authors are grateful to N. G. Berloff for fruitful discussions and acknowledge the support of the UK’s Engineering and Physical Sciences Research Council (grant EP/M025330/1 on Hybrid Polaritonics).
Author information
Authors and Affiliations
Contributions
P.G.L. led the research project. P.G.L., J.D.T., and L.P. designed the experiment. J.D.T. and L.P. carried out the experiments and analysed the data. J.D.T. and H.S. developed the theoretical modelling. H.S. performed numerical simulations. All authors contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Töpfer, J.D., Sigurdsson, H., Pickup, L. et al. Time-delay polaritonics. Commun Phys 3, 2 (2020). https://doi.org/10.1038/s42005-019-0271-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0271-0
This article is cited by
-
Magneto-optical induced supermode switching in quantum fluids of light
Communications Physics (2023)
-
Modified Bose-Einstein condensation in an optical quantum gas
Nature Communications (2021)
-
Geometric frustration in polygons of polariton condensates creating vortices of varying topological charge
Nature Communications (2021)
-
Quantum fluids of light in all-optical scatterer lattices
Nature Communications (2021)
-
Time-delay polaritonics
Communications Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.