Abstract
The optical fibre is an essential tool for our communication infrastructure since it is the main transmission channel for optical communications. The latest major advance in optical fibre technology is space-division multiplexing, where new fibre designs and components establish multiple co-existing data channels based on light propagation over distinct transverse optical modes. Simultaneously, there have been many recent developments in the field of quantum information processing, with novel protocols and devices in areas such as computing and communication. Here, we review recent results in quantum information based on space-division multiplexing optical fibres, and discuss new possibilities based on this technology.
Similar content being viewed by others
Introduction
Quantum information processing is a field that has seen tremendous growth over the many years since Richard Feynman’s seminal talk on the use of quantum computers to simulate physical systems1. When information bits are encoded on individual or entangled quantum states, a gain over traditional systems can be seen for some information processing tasks. A famous example is the well-known Shor’s algorithm for prime number factorisation running on a quantum computer, where an impressive reduction in resources is obtained when compared to classical algorithms2. Another major application of quantum information processing is in communication security, where the fact that unknown quantum states cannot be faithfully cloned3 is exploited to detect the presence of an eavesdropper. This concept was used as the core foundation behind quantum key distribution (QKD), a communication protocol designed to distribute random private keys among remote parties4,5. As the first application to showcase in practice the benefits of quantum information processing, QKD has experienced huge developments ever since6,7,8,9. QKD is part of a more general family of protocols called quantum communications, which include other schemes such as quantum teleportation and entanglement swapping10,11, aiming to be the communication backbone supporting future networks of quantum computers12,13.
During the last decades a number of technological features were developed by the telecommunication community in order to support the continuous increase in demand for more transmission bandwidth over a communication channel. These developments have been motivated by several applications that have cropped up along the years, from the internet to social networking and high-quality on-demand video streaming. Arguably the optical fibre has played a major role in the success of the telecommunication infrastructure, mainly due to its high transparency and high-bandwidth support14. Technologies such as wavelength division multiplexing15, and the erbium doped fibre amplifier16 have been major catalysts to the extremely high capacities and ultra-long transmission distances available today. The latest technological drive towards maintaining the bandwidth growth is called space-division multiplexing (SDM), and it consists of employing the transverse spatial properties of a light beam to multiplex information and increase the data capacity17. SDM nowadays routinely allows hundreds of Tbit s−1 of transmission capacity18, ensuring that the bandwidth demand can keep growing.
In photonic quantum information processing, different degrees-of-freedom of a single-photon such as polarisation, frequency and its transverse momentum, are used for encoding quantum systems of arbitrary dimension19,20,21. Of particular interest, for instance, is the strategy that relies on encoding a quantum system in terms of the transverse optical modes available, which provides versatility to define high-dimensional Hilbert spaces22,23,24,25,26. It has already been proven to be useful for quantum information processing with photonic integrated circuits19,27,28,29, aimed at improving the robustness and compactness of experimental setups. However, remarkably, propagation over optical fibres for such quantum states has been a major challenge due to the fact that many optical fibres are designed to support only the fundamental gaussian propagation mode. Although multi-mode fibres exist, they support hundreds of modes, requiring complex auxiliary optoelectronic systems to reconstruct the original wavefront30. Fortunately, SDM optical fibres and components can be used to cover this gap. In this topical review we go through the different SDM technologies, and cover a number of key experiments that have recently shown the advantages and new possibilities that this technology offers for quantum information processing. We also tackle the complex problem of successful integration of quantum communication systems with classical telecommunication networks31,32,33, by discussing the more recent SDM optical fibre-based network infrastructure.
Space-division multiplexing technology for optical communications
Space-division multiplexing optical fibres
A typical telecommunication optical fibre is a cylindrical dielectric silica waveguide composed of a core and the surrounding cladding, possessing extremely low losses (<0.2 dB km−1 at 1550 nm)14. A major advance for increasing transmission capacity was achieved when multiple data channels were multiplexed using different wavelengths over a single fibre, a technique called wavelength division multiplexing (WDM)15. Although WDM, together with other technologies, has been incredibly successful in sustaining the internet growth, optical fibres are nevertheless reaching their maximum capacities17. A promising avenue to continue expanding data rates over the fibre-optical infrastructure is to explore different transverse optical modes of a light beam to multiplex data channels, thus increasing the spatial data density. This technique is the spatial analogue of WDM, and aptly named space-division multiplexing17.
Any fibre that can support more than one transverse optical mode of propagation is, in principle, suitable for SDM. Different types of SDM optical fibre can be seen in Box 1a. The most direct approach is to embed several single-mode cores in a single fibre cladding, thus producing a multi-core fibre (MCF)34,35. If the transverse core separation is larger than ~40 μm, the attenuation of cross-coupled optical power between the cores exceeds several tens of dBs, and thus they can be approximated as independent fibres in most applications. These fibres are referred to as weakly-coupled MCFs35, and the main advantage is that multiple-input multiple-output receivers36 are not needed for detection of the spatial channels. The price to be paid is a lower spatial channel density, since the cladding diameter cannot be much larger than approximately 200 μm to avoid rupture due to bending37. Nevertheless successful results have recently been obtained for 19-core weakly-coupled MCFs38. In order to minimise inter-core coupling, lower refractive-index “trenches” or holes are often used around the cores (Box 1b), at the once again expense of lower spatial density.
Another alternative is to use a fibre with a single core, but which is capable of supporting more than one transverse mode for light propagation39. Standard telecommunication multi-mode optical fibres are actually not very useful in this regard since they support many propagation modes requiring multiple-input multiple-output detection systems with extremely high complexities35. Recently, significant progress has been achieved using fibres that only support a few linearly polarised (LP) transverse modes of propagation (typically 3 or 6), the so-called few-mode fibres40,41. The main difference with a single-mode fibre is a larger core area, and borrowing from multi-mode fibre technology, parabolic refractive index profiles can be used to minimise mode group velocity dispersion (Box 1b). With only a few modes present intermodal crosstalk is limited and thus multiple-input multiple-output decoding is feasible. Significant progress has been made recently, combining MCFs with few-mode fibre technology, yielding fibres with multiple cores where each core can support a few modes (few-mode-MCFs, see Box 1a)42. Due to an increased spatial channel density, these fibres can greatly increase the transmission capacity43. Finally, owing to their multi-core nature, and due to the fact that the higher-order modes have a larger mode field diameter than the fundamental linearly polarised (LP01) mode, lower refractive index trenches are also employed to minimise cross-talk from adjacent cores42,43.
The last strategy for space-division multiplexing of data channels has been the use of transverse optical modes carrying orbital angular momentum (OAM)44. A Laguerre-Gaussian beam carries discrete orbital orthogonal angular momentum modes characterised by an integer l, called the topological charge. Each associated photon carries an OAM of lħ, where ħ is Planck’s constant divided by 2π45. Recently, OAM-encoded beams have been used for space-division multiplexing and to demonstrate the possibility of Tbit s−1 data rates over free-space links46. Following that, demonstrations of the transmission of these beams over optical fibres with high-index ring refractive index profiles were reported47, thus expanding the toolbox of such optical modes towards fibre communications. These fibres are usually referred to as ring- or air-core fibres48,49, due to their characteristic high refractive-index ring profile (Box 1b).
Table 1 lists relevant properties of SDM fibres that were reported in some recent experiments. Modal crosstalk refers to the possibility that a single-photon leaks from one spatial mode to another during propagation. The modal delay is relevant since spatially encoded single-photon quantum states are typically encoded in terms of a modal superposition and, therefore, may suffer decoherence effects depending on this delay. Chromatic dispersion is more of a concern when short pulses are used.
Multiplexers and demultiplexers
Multiplexers and demultiplexers (also commonly called fan-in and fan-out devices respectively) are employed to combine and split different data streams into corresponding spatial channels in an SDM fibre. Here we try to focus on passive components that can already be implemented directly integrated within the fibres or through photonic chips (i.e. without resorting to bulk optical elements). All passive SDM components take N independent single-mode input fibres, and map them onto a particular mode on the SDM fibre. For MCFs, mux/demuxes can be directly constructed using integrated waveguides written three-dimensionally onto silica chips using ultrafast laser writing50. The appropriate fibres are then connected to the chip. Alternatively, discrete components (based on fibre bundles or compact lenses for example) may be used51,52. For few-mode fibres, devices called photonic lanterns are normally used53, where the input single-mode fibres are tapered together (in parallel) ending in a multi-mode fibre at the other end. If the single-mode fibres have slightly different sized cores, then a mode-selective lantern can be built54, yielding considerably better mode excitation/separation than using identical single-mode inputs/outputs. Lanterns built onto integrated photonic chips have also been developed, allowing better integration possibilities55. For OAM-carrying optical modes, there are demultiplexers, typically called mode sorters, and they have been done mostly using bulk optic components/active elements56,57. Recently, significant progress has been made towards all-fibre OAM sorters, thus making possible the use of compact and passive multiplexing elements for OAM carrying optical modes as well58. Finally, fan-in/fan-out units for few-mode-MCF fibres can also be constructed in integrated photonics chips resorting to the 3D-femtosecond laser writing technique and integrated lanterns59. In Table 1 some examples of recently reported multiplexers and demultiplexers for the main SDM fibre types are reported, with some physical parameters. Of particular interest for system designers is the insertion loss and the expected crosstalk between the different spatial modes.
Quantum information with SDM fibres
High-dimensional quantum key distribution over SDM fibres
Many fundamental and applied tasks in quantum information benefit when d-dimensional (d > 2) quantum systems (qudits) are employed, such as larger violations of Bell inequalities, improvement of communication complexity problems, QKD without signal monitoring and entanglement certification in the presence of higher noise60,61,62,63,64. The drawback is that more detection outputs are needed. One popular realisation for high-dimensional photonic quantum information processing is path encoding22,23,25,28,62,65. A d-dimensional path-encoded qudit has the general form \(|\psi \rangle = \frac{1}{{\sqrt C }}\sum_{d = 0}^d e^{\phi _{\mathrm{d}}}|d\rangle\), where |d〉 represents the dth path, ϕd is the relative phase in path d and C the normalisation constant. A direct advantage gained in quantum communication when using qudits is increasing the transmission rate of QKD systems66, due to the fact that we can encode log2d bits onto a d-dimensional quantum state. This is a similar approach to what has always been done to increase the number of bits sent per symbol in classical communication systems67. This technique is particularly useful, when it becomes too resource-intensive to simply increase the transmission rate by employing faster modulation and demodulation/detection through opto-electronic devices. For instance, in the scenario of high repetition rates and low losses (i.e. tens of kilometres propagation distance), that is, when the detectors are limited by their dead times, then employing higher-dimensional systems is the only way to improve the detection rate68.
QKD’s goal is to generate a shared secret string of bits (a key) between spatially separated parties (usually referred to as Alice and Bob) through the transmission of properly encoded single-photons5. Current experiments in optical fibres can reach distances over 400 kms69, and generate a few Mbit/s of final sifted key rate over metropolitan distances70. The security of QKD relies on the simple fact that an unknown quantum system cannot be faithfully cloned3, and this is explored in the well known BB84 protocol4. Alice randomly chooses a quantum state to be transmitted and Bob does a random measurement on it, while recording the result. After many such rounds, Alice and Bob perform classical reconciliation and post-processing procedures to distill a shared secret key. Many factors affect the key generation rate, from the channel losses, the optical quality of the setup to the physical specifications of the detectors.
BB84-based proof-of-principle high-dimensional quantum key distribution (HD-QKD) experiments were already performed many years ago relying on the linear transverse momentum of single-photons71. The two employed bases consisted of imaging and Fourier optical systems (by changing the appropriate lenses). The main limitation of this scheme is that the states had to be manually prepared and measured by changing the lenses and moving pinholes. An important next step occurred when spatial light modulators were used, capable of dynamically generating sets of parallel slits, which allowed the encoding of a high-dimensional qudit onto a single-photon propagating through these slits72,73. This was then combined with synchronised Field Programmable Gate Array electronics to perform the first automated BB84 session in higher-dimensions using attenuated optical pulses74. Here a QKD session using path-encoded 16-dimensional quantum states was realised by dynamically using the spatial light modulators to prepare and measure the states, allowing 4 bits to be sent in each round. On the other hand, there has been considerable effort to implement HD-QKD using OAM encoding strategies through free-space75, which was also later done with a fully automated setup76 and even over free-space intra-city channels77.
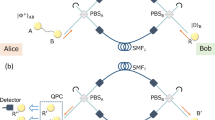
One major challenge remained in order to implement spatial HD-QKD over optical fibres: the difficulty of preserving the phase wavefront of the single-photons during propagation through fibres. Some efforts had been done a few years ago using a 30-cm-long photonic crystal fibre78, which is unfortunately not practical for long-distance propagation. The parallel development of SDM fibres came to change this paradigm, since spatial-mode-supporting fibres became widely available at a reasonable cost. Two experiments performed simultaneously kick-started this trend. In the first (Fig. 1a79) a 300-m-long four-core fibre was used to perform a HD-QKD session using deformable mirrors as the phase modulators, yielding improvements over the previous efforts with spatial light modulators74. This result is the longest distance ever reported for the transmission of path-qudit states, showing that MCFs can be used for high-fidelity propagation over distances of practical interest. The other experiment also showed a successful HD-QKD session using a 4-core fibre, but with Alice and Bob’s hardware fully implemented on integrated silicon photonics circuits80 (Fig. 1b). Thermal elements on the chip were employed to perform active modulation. Both experiments also carried out rigorous security analyses showing that much longer distances could be achieved while still being capable of positive secret key rates. It was also shown that MCFs can be used to deliver keys in parallel choosing separate sets of cores81. More recently, ring-core-type fibres have also been employed for remote QKD sessions using OAM encoded qudits. The first one (Fig. 1c) was actually done in a 2-dimensional space over a 60 m vortex fibre with no active state preparation82, while the second one (Fig. 1d) employed hybrid polarisation/OAM states to perform an HD-QKD session using ququarts over 1.2-km-long air-core fibre83.
a 300-m-long high-dimensional (HD) QKD session using path-encoding with a 4-core fibre. Reprinted with permission from79. b HD-QKD session with path-encoded states based on integrated silicon photonic circuits using 4-cores in a 3-m-long fibre. Reprinted with permission from80. c Proof-of-principle QKD demonstration using 2-dimensional orbital angular momentum (OAM) states through a 60-m vortex (ring-core) fibre. Reprinted with permission from82. d HD-QKD demonstration using hybrid OAM/polarisation states through 1.2 km air-core fibre. Reprinted with permission from83.
Entanglement distribution
The successful distribution of photonic entanglement over long optical fibres is an important operational toolbox in quantum information. Many experiments have been performed using different degrees of freedom of a single-photon over optical fibres, mainly using polarisation84,85,86,87 and energy-time/time-bin88,89,90,91. For many years the distribution of spatial entanglement (i.e., entanglement between quantum systems encoded in terms of the transverse optical modes of light) over optical fibres has been out of reach. This has been mainly due to the fact that (i) single-mode fibres, by their very nature, do not support more than one spatial mode; and (ii) mode coupling scrambles the multi-mode spatial state during propagation. Nevertheless, significant progress has been made recently using both custom-made and standard commercially available optical fibres. In common, all experiments employ fibres that support only a few spatial modes, in order to minimise significant mode coupling.
The first experiment to be able to propagate spatially entangled photons employed a 30-cm long hollow-core photonic crystal fibre to transmit one of the photons of the pair, while successfully measuring a Bell inequality violation over the pair of qubits78. This was an important first step demonstrating the feasibility of distributing spatially entangled states, but the use of specialty fibres hampers practical use. This was improved upon with standard polarisation maintaining fibres that were used as few-mode fibres (by working with single-photons at 810 nm), and then two of the three possible linearly polarised modes in the fibre were used for each single-photon of the pair (LP01 and the even LP11 mode)92.
Nevertheless, one immediate advantage of resorting to spatial entanglement is the possibility of reaching higher-dimensional Hilbert spaces. When combined with fibre propagation, this allows the execution of more interesting high-dimensional quantum information tasks, where physical separation between parties who do not share line-of-sight is no longer a restriction. Going in this direction more recent experiments have taken direct advantage of the possibilities allowed by newly developed SDM hardware. As shown by H. J. Lee et al.93, 4-dimensional spatial entanglement has been distributed over short-distances (30 cm) 4-core fibres. Entanglement was verified through quantum state tomography, and this was later expanded to a Bell inequality test94 (Fig. 2a). Another experiment taking direct advantage of SDM fibres was95, where a 1-km-long FMF was used to test if polarisation and time-bin entanglement can be propagated through the different modes.
a High-dimensional Bell inequality test over multi-core fibres. The spatially entangled single-photons propagate each through 4-core fibres that are 30 cms in length. Reprinted with permission from94. b Distribution of three-dimensional orbital angular momentum entanglement over a 1-km-long few-mode fibre. This experiment employed modal dispersion pre-compensation, which is critical when photonic states are encoded across multiple modes of the same core over large distances. Reprinted with permission from96.
Very recent progress has also shown the propagation of OAM entangled quantum states over optical fibres. One of the photons of a 3-dimensional OAM entangled state was successfully propagated over a 1-km step-index fibre96, supporting up to six linearly polarised modes (Fig. 2b). The employed fibre required careful alignment of the input axis in order to properly excite and later decode the OAM modes. This experiment also featured compensation of modal dispersion, which is necessary as the fibre length increases, even more so for entangled states produced by down-conversion processes, due to the typical low temporal coherence involved. Another experiment started with a polarisation-entangled photon pair, where one of the photons gets further encoded with a superposition of OAM modes (vector vortex mode) to generate hybrid three-qubit entanglement97. The hybrid-encoded photon is transmitted through a 5-m-long air-core fibre, showing that hybrid high-dimensional entanglement can be propagated over SDM fibres. Then, another experiment demonstrated hybrid OAM/polarisation entanglement with one of the photons propagated through 250 m of single-mode telecom fibre, which works as a few-mode fibre at the working wavelength in the experiment of 810 nm98. The main drawback here is the much greater attenuation (>2 dB/km) when compared to working with standard SDM few-mode fibres at telecom wavelengths.
Integration with classical telecommunication optical networks
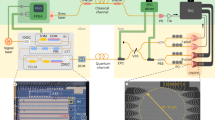
Compatibility with optical networks is a major driving force for the widespread deployment of quantum communication31,32,33. The next logical step is to ensure compatibility of quantum communication systems with the next-generation SDM optical networks. A first proof-of-principle experiment (over a short distance of 2 m) has shown that space-division multiplexing of a classical and a quantum channel is possible on a few-mode fibre99. Then a compatibility experiment between QKD and classical data co-existing in the same fibre using separate cores over a MCF was carried out (Fig. 3a)100. The centre core was reserved for the QKD channel, while the side cores were pairwise-filled with 10 Gbit s−1 data streams from opposite directions. A 7-core fibre was employed with a relatively high core-to-core distance (47 μm), such that inter-core crosstalk was rather low at approximately −60 and −80 dB at the forward and backwards propagation directly. Nevertheless this crosstalk was still high enough to ensure that the quantum and classical channels could not share the same wavelengths on separate cores (Fig. 3b). If these limitations are taken into account, co-existence between quantum and classical signals in the same fibre is possible, as with single-mode fibres. A follow-up study characterised the difference in impact between trench-assisted and non-trench-assisted MCFs101, while having the same core-to-core distance in both fibres (41.1 μm). All cores were simultaneously loaded with high speed traffic (112 Gbit s−1), at different wavelengths. Non-trench-assisted-MCFs are interesting to be studied for compatibility, since they allow a higher core density due to the absence of lower refractive index trenches surrounding the cores. The results showed that compatibility is also possible, with a larger penalty imposed by the classical channels on the non-trench-assisted-MCF, as expected due to the higher cross-talk.
a Experiment demonstrating co-existence of QKD and classical data over a multi-core fibre (MCF). Reprinted with permission from Dynes et al.100. b Wavelength channel allocation in a multi-core fibre. A wavelength is assigned to the QKD channel (in the centre core for example, shown in orange), and has to be kept free in the adjacent cores (shaded blue) to prevent in-band inter-core crosstalk100,101,102,103. The other wavelengths in each core may be assigned to data channels. c Co-existence experiment of continuous-variable-QKD and classical channels over an MCF. Reprinted with permission from104. d Spontaneous Raman scattering generated when a classical channel is present in the same core can contaminate a QKD channel. Following propagation through the core of an MCF, spontaneous Raman scattered photons are produced from a classical channel (pump) over a broad wavelength range, eventually becoming strong noise to the QKD channel band. After the receiver’s filtering stage, these scattered photons are detected as an increase in the dark counts of the QKD system, lowering the generated secret key rate. e Experimental demonstration of spontaneous Raman scattering over all cores of non-trench-assisted and trench-assisted-MCFs. Reprinted with permission from107. I stands for optical intensity, while λ for the wavelength.
Recently, improved classical channel data rates have been achieved over a 7-core fibre while simultaneously allocating the centre core to a QKD channel102. Other works have also studied the use of a dedicated side-core for QKD while having neighbouring cores filled with classical data103, the inter-core crosstalk produced from classical channels on MCFs affecting continuous-variable QKD systems (Fig. 3c)104 and performed detailed modelling on SDM based QKD integration105. Finally, a major increase in key generation rate has been achieved by sending out parallel keys over 37 cores of a MCF, while also propagating a 10 Gbit s−1 data stream within each core, wavelength-multiplexed with the QKD channel106. One important limitation for co-existence is spontaneous Raman scattering, where photons from classical channels are inelastically scattered over a broad wavelength range31. Even if the cross-talk produced from in-band photons can be fully removed (with high-quality filtering for instance), these scattered photons will fall back to the QKD channel band over the fibre link (Fig. 3d). Therefore, the overall system design needs to take this issue into account32. Recently, spontaneous Raman scattering has been demonstrated for the first time in each core of an MCF (Fig. 3e)107, indicating as expected the same limitations when simultaneously propagating quantum and classical signals in the same core of an MCF. Table 2 lists relevant quantum information experiments using SDM fibres.
Outlook and open challenges
There has been a rapid acceptance of SDM fibres and devices by the quantum information community with promising results reported so far. On the one hand the ability of these fibres to successfully manipulate and propagate high-dimensional quantum states over long distances has proven very fruitful for quantum information processing. On the other hand, their use for a number of quantum information protocols will ease the integration of both quantum and classical network systems based on the SDM optical fibre infrastructure. In addition to aiming compatibility with the future SDM optical networks, the results discussed here show that good control over the spatial domain has been achieved over optical fibres. This validates the use of spatial qudits as an alternative to other high-dimensional degrees-of-freedom, such as time or frequency.
The SDM technologies discussed can already be used to support a “hybrid internet”, where quantum and classical communication systems co-exist over the telecommunication SDM fibre-optical infrastructure (Box 2). Here, as an example, one party (Alice) wishes to send information encoded on the path of single-photons (represented by two red arrows) to a remote party (Bob). Other degrees-of-freedom may be used. Alice and Bob both have quantum nodes, which could be QKD terminals for instance. The classical traffic is processed in internet exchange points, where several local data streams are aggregated for transmission over a high-capacity optical link to another exchange point for delivery. Two geographically separate routes exist in this example for Alice’s single-photons to reach Bob, and which one will be used depends on network availability. The blue clockwise direction propagates over MCFs and goes through intermediate Node 1. There a reconfigurable add-drop multiplexer is employed to drop one of the classical channels (green) to be processed by the local internet exchange point, and a new one (yellow) is added towards another exchange point located at Bob. The rest of the traffic originated at Alice (both quantum and classical) is forwarded to Bob.
The counter-clockwise route (pink) is composed of a few-mode fibre link going through intermediate Node 2, before arriving at Bob. In a slightly different configuration only single-photons are sent from Alice through this route, since there is no classical traffic to be dropped at Node 2. At this node, another internet exchange point adds a classical data stream (blue) to be delivered at the other exchange point located at Bob. This classical channel will be coupled into one of the spatial modes (represented as the dual colour LP11a mode in the fibre cross-section) that are used by the single-photons, with wavelength separation. At each station either integrated spatial multiplexers59 or hybrid wavelength/spatial reconfigurable optical add-drop multiplexers108 are employed to correctly map each input/output to the corresponding mode in the fibre. This example illustrates a possible case in network channel allocation, where routes are dynamically assigned depending on availability. Although the example only discussed single-photons, sources of entangled photons could be placed at either the end or intermediate nodes, and entanglement shared using the same SDM structure as appropriate. For this to be feasible, the network must be transparent in terms of the employed SDM technology.
Nevertheless, many challenges await that the community needs to handle to ensure that experiments based on SDM technology yield better results. Multi-core fibres have shown good promise for long-distance propagation and ease of integration with photonic circuits. Furthermore, high-quality devices can be built directly in the fibre itself109. Next it is important to see if they can support propagation distances for high-dimensional states that is comparable to single-mode fibres (i.e. hundreds of kms). They also need to be validated for states of even higher dimensionality, by employing fibres with a higher core number, such as 7 or 19. Regarding telecom compatibility, it is important to verify more stringent limits such as noise produced from non-linear effects such as Raman scattering and four-wave mixing produced from classical channels in different wavelengths from different cores.
Although ring-core and even step-index fibres have also proved fruitful for OAM propagation, further experiments need to be carried out to verify their support for high-dimensions (only one experiment managed to go further than OAM qubits, and even then only OAM qutrits were employed96). This is worth pursuing since experiments in classical communications show that several modes can be simultaneously supported110,111, although multiple-input multiple-output detection was still required, so better mode isolation will be needed for quantum communication experiments. By far most OAM-based experiments have resorted to bulk-optics-based mode sorters, although recent results open up a new path towards integration for OAM29,58. Few-mode fibres also need to be studied in this regard, to verify their ability to coherently propagate superpositions of linearly polarised (LP) modes over long distances. The successful use of few-mode fibres would open a direct path towards the transmission of much higher dimensional states, since they can be directly combined with MCFs. For instance, a fibre with 36 cores where each core supports the three lowest order LP modes, yielding a possible 108-dimensional space, has been demonstrated112.
An important challenge to be tackled comes from the modal dispersion. This problem is even more critical for entangled states due to their short coherence time. This has been done so far by pre-compensating the mode delay before transmission in the optical fibre83,96. Further efforts need to be carried out to demonstrate feasibility over much longer distances, as well as ability to cover compensation for a wide range of modes, aiming at high-dimensionality.
It is quite fortunate that the technological developments that are sustaining the growth of communication networks can be directly applied for quantum information technologies. This has been the case since the dawn of photonic quantum information, and will continue to be so. We have highlighted here the key developments in the nascent intersection of SDM and quantum information, with already many experiments having been able to directly benefit from SDM. We envisage that (i) integration between SDM networks and quantum information systems will be inevitable, and (ii) SDM offers the hardware to support efficient, high-fidelity, high-dimensional quantum information processing, which will be a major cornerstone of future developments in quantum technologies.
Data availability
No datasets were generated or analysed during the current study.
References
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467 (1982).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Sci. Stat. Comput. 26, 1484 (1997).
Wootters, W. K. & Zurek, W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).
Bennett, C. H. & Brassard., G. Quantum cryptography: public key distribution and coin tossing. Proc. IEEE Int. Conf. Comput. Syst. Signal Process. 175, 8 (1984).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution Nat. Photon 8, 595 (2014).
Diamanti, E., Lo, H.-K., Qi, B. & Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2, 16025 (2016).
Xu, F., Ma, X., Zhang, Q., Lo, H.-K. & Pan, J.-W. Quantum cryptography with realistic devices. Preprint at http://arxiv.org/abs/1903.09051 (2019).
Pirandola, S. et al. Advances in Quantum Cryptography. Preprint at http://arxiv.org/abs/1906.01645 (2019).
Gisin, N. & Thew, R. Quantum communication. Nat. Photon. 1, 165–171 (2007).
Pirandola, S., Eisert, J., Weedbrook, C., Furusawa, A. & Braunstein, S. L. Advances in quantum teleportation. Nat. Photon. 9, 641–652 (2015).
Pirandola, S. & Braunstein, S. L. Unite to build a quantum Internet. Nature 532, 169 (2016).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, 303 (2018).
Agrawal, G. P. Fiber-optic communication systems. 3rd edn (Wiley, New York, 2002).
Brackett, C. A. Dense wavelength division multiplexing networks: principles and applications. IEEE J. Sel. Areas Commun. 8, 948–964 (1990).
Mears, R. J., Reekie, L., Jauncey, I. M. & Payne, D. N. Low-noise Erbium-doped fiber amplifier at 1.54 μm. Electron. Lett. 23, 1026–1028 (1987).
Richardson, D. J., Fini, J. M. & Nelson, L. E. Space-division multiplexing in optical fibres. Nat. Photon. 7, 354–362 (2013). Review introducing space-division multiplexing, including optical fibres and components.
Wakayama, Y. et al. 266.1-Tbit/s transmission over 90.4-km 6-mode fiber with inline dual C + L-band 6-mode EDFA. IEEE J. Lightwave Technol. 37, 404–410 (2019).
Flamini, F., Spagnolo, N. & Sciarrino, F. Photonic quantum information processing: a review. Rep. Prog. Phys. 82, 016001 (2018).
Erhard, M., Fickler, R., Krenn, M. & Zeilinger, A. Twisted photons: new quantum perspectives in high dimensions. Light Sci. Appl. 7, 17146 (2018).
Erhard, M., Krenn, M. & Zeilinger, A. Advances in High Dimensional Quantum Entanglement. Preprint at http://arxiv.org/abs/1911.10006 (2019).
Neves, L. et al. Generation of entangled states of qudits using twin photons. Phys. Rev. Lett. 94, 100501 (2005).
O’Sullivan-Hale, M. N., Ali Khan, I., Boyd, R. W. & Howell, J. C. Pixel entanglement: experimental realization of optically entangled d = 3 and d = 6 qudits. Phys. Rev. Lett. 94, 220501 (2005).
Gröblacher, S., Jennewein, T., Vaziri, A., Weihs, G. & Zeilinger, A. Experimental quantum cryptography with qutrits. New J. Phys. 8, 75 (2006).
Rossi, A., Vallone, G., Chiuri, A., De Martini, F. & Mataloni, P. Multipath entanglement of two photons. Phys. Rev. Lett. 102, 153902 (2009).
Aguilar, E. A. et al. Certifying an irreducible 1024-dimensional photonic state using refined dimension witnesses. Phys. Rev. Lett. 120, 230503 (2018).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S. & O’Brien, J. L. Silica-on-Silicon Waveguide Quantum Circuits. Science 320, 646–649 (2008).
Wang, J. et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 360, 285–291 (2018).
Chen, Y. et al. Mapping twisted light into and out of a photonic chip. Phys. Rev. Lett. 121, 233602 (2018).
Choi, Y. et al. Scanner-free and wide-field endoscopic imaging by using a single multimode optical fiber. Phys. Rev. Lett. 109, 203901 (2012).
Chapuran, T. E. et al. Optical networking for quantum key distribution and quantum communications. N. J. Phys. 11, 105001 (2009).
Patel, K. A. et al. Coexistence of high-bit-rate quantum key distribution and data on optical fiber. Phys. Rev. X 2, 041010 (2012).
Eriksson, T. A. et al. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2, 1 (2019).
Iano, S., Sato, T., Sentsui, S., Kuroha T. & Nishimura, Y. Multicore optical fiber. In Optical Fiber Communication Conference (OFC) 1979, OSA Technical Digest (Optical Society of America, 1979) paper WB1 (OSA, 1979).
Saitoh, K. & Matsuo, S. Multicore fiber technology. IEEE J. Lightwave Technol. 34, 55 (2016).
Foschini, G. J. Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Tech. J. 1, 41–59 (1996).
Saitoh, K. & Matsuo, S. Multicore fibers for large capacity transmission. Nanophotonics 2, 441–454 (2013).
Sakaguchi, J. et al. 19-core MCF transmission system using EDFA with shared core pumping coupled via free-space optics. Opt. Express 22, 90–95 (2014).
Berdagué, S. & Facq, P. Mode division multiplexing in optical fibers. Appl. Opt. 21, 1950–1955 (1982).
Sillard, P., Bigot-Astruc, M. & Molin, D. Few-mode fibers for mode-division-multiplexed systems. IEEE J. Lightwave Technol. 32, 2824–2829 (2014).
Rademacher, G. et al. High capacity transmission with few-mode fibers. IEEE J. Lightwave Technol. 37, 425–432 (2019).
Xia, C. et al. Hole-assisted few-mode multicore fiber for high-density space-division multiplexing. IEEE Photon. Technol. Lett. 24, 1914–1917 (2012).
van Uden, R. G. H. et al. Ultra-high-density spatial division multiplexing with a few-mode multicore fibre. Nat. Photon. 8, 865–870 (2014).
Gibson, G. et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 12, 5448–5456 (2004).
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185 (1992).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 6, 488–496 (2012).
Bozinovic, N. et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 340, 1545–1548 (2013).
Brunet, C. et al. Design of a family of ring-core fibers for OAM transmission studies. Opt. Express 23, 10553–10563 (2015).
Gregg, P., Kristensen, P. & Ramachandran, S. Conservation of orbital angular momentum in air-core optical fibers. Optica 2, 267–270 (2015).
Thomson, R. R. et al. Ultrafast laser inscription of a 121-waveguide fan-out for astrophotonics. Opt. Lett. 37, 2331–2333 (2012).
Watanabe, K., Saito, T., Imamura, K. & Shiino, M. Development of fiber bundle type fan-out for multicore fiber. In IEEE 17th Opto-Electronics and Communications Conference (2012).
Tottori, Y., Kobayashi, T. & Watanabe, M. Low loss optical connection module for seven-core multicore fiber and seven single-mode fibers. IEEE Photon. Technol. Lett. 24, 1926–1928 (2012).
Birks, T. A., Gris-Sánchez, I., Yerolatsitis, S., Leon-Saval, S. G. & Thomson, R. R. The photonic lantern. Adv. Opt. Photon. 7, 107–167 (2015).
Yerolatsitis, S., Gris-Sánchez, I. & Birks, T. A. Adiabatically-tapered fiber mode multiplexers. Opt. Express 22, 608–617 (2014).
Riesen, R. R., Gross, S., Love, J. D. & Withford, M. J. Femtosecond direct-written integrated mode couplers. Opt. Express 22, 29855–29861 (2014).
Berkhout, G. C. G., Lavery, M. P. J., Courtial, J., Beijersbergen, M. W. & Padgett, M. J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 105, 153601 (2010).
Lavery, M. P. J. et al. Refractive elements for the measurement of the orbital angular momentum of a single photon. Opt. Express 20, 2110–2115 (2012).
Zeng, X. et al. All-fiber orbital angular momentum mode multiplexer based on a mode-selective photonic lantern and a mode polarization controller. Opt. Lett. 43, 4779–4782 (2018).
Riesen, N., Gross, S., Love, J. D., Sasaki, Y. & Withford, M. J. Monolithic mode-selective few-mode multicore fiber multiplexers. Sci. Rep. 7, 6971 (2017).
Kaszlikowski, D., Gnaciński, P., Żukowski, M., Miklaszewski, W. & Zeilinger, A. Violations of local realism by two entangled N-dimensional systems are stronger than for two qubits. Phys. Rev. Lett. 85, 4418–4421 (2000).
Araújo, M., Costa, F. & Brukner, C. Computational advantage from quantum-controlled ordering of gates. Phys. Rev. Lett. 113, 250402 (2014).
Martinez, D. et al. High-dimensional quantum communication complexity beyond strategies based on Bell’s theorem. Phys. Rev. Lett. 121, 150504 (2018).
Sasaki, T., Yamamoto, Y. & Koashi, M. Practical quantum key distribution protocol without monitoring signal disturbance. Nature 509, 475–478 (2014).
Ecker, S. et al. Overcoming Noise in Entanglement Distribution. Phys. Rev. X. 9, 041042 (2019).
Cañas, G. et al. Applying the simplest Kochen-Specker set for quantum information processing. Phys. Rev. Lett. 113, 090404 (2014).
Cerf, N. J., Bourennane, M., Karlsson, A. & Gisin, N. Security of quantum key distribution using d-level systems. Phys. Rev. Lett. 88, 127902 (2002). Security bounds of high-dimensional quantum key distribution, which shows the advantages over the standard bi-dimensional case.
Proakis, J. G. & Salehi, M. Digital Communications 5th edn. (McGraw-Hill, New York USA, 2008).
Lee, C. et al. Large-alphabet encoding for higher-rate quantum key distribution. Opt. Express 27, 17539–17549 (2019).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
Patel, K. A. et al. Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks. Appl. Phys. Lett. 104, 051123 (2014).
Walborn, S. P., Lemelle, D. S., Almeida, M. P. & Souto Ribeiro, P. H. Quantum key distribution with higher-order alphabets using spatially encoded qudits. Phys. Rev. Lett. 96, 090501 (2006).
Lima, G., Vargas, A., Neves, L., Guzmán, R. & Saavedra, C. Manipulating spatial qudit states with programmable optical devices. Opt. Express 17, 10688–10696 (2009).
Lima, G. et al. Experimental quantum tomography of photonic qudits via mutually unbiased basis. Opt. Express 19, 3542 (2011).
Etcheverry, S. et al. Quantum key distribution session with 16-dimensional photonic states. Sci. Rep. 3, 2316 (2013). High-dimensional quantum key distribution session based on the original BB84 protocol.
Mafu, M. et al. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys. Rev. A 88, 032305 (2013).
Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. New J. Phys. 17, 033033 (2015).
Sit, A. et al. High-dimensional intracity quantum cryptography with structured photons. Optica 4, 1006–1010 (2017).
Löffler, W. et al. Fiber transport of spatially entangled photons. Phys. Rev. Lett. 106, 240505 (2011).
Canãs, G. et al. High-dimensional decoy-state quantum key distribution over multicore telecommunication fibers. Phys. Rev. A 96, 022317 (2017). High-dimensional quantum key distribution session based on spatial qudits over multi-core fibres, covering 300 m of distance.
Ding, Y. et al. High-dimensional quantum key distribution based on multicore fiber using silicon photonic integrated circuits. npj Quantum Inf. 3, 25 (2017). High-dimensional quantum key distribution session using multi-core fibers and integrated photonic circuits for the transmitting/receiving modules.
Bacco, D., Ding, Y., Dalgaard, K., Rottwitt, K. & Oxenløwe Space division multiplexing chip-to-chip quantum key distribution. Sci. Rep. 7, 12459 (2017).
Sit, A. et al. Quantum cryptography with structured photons through a vortex fiber. Opt. Lett. 43, 4108–4111 (2018).
Cozzolino, D. et al. Orbital angular momentum states enabling fiber-based high-dimensional quantum communication. Phys. Rev. Appl. 11, 064058 (2019). Long-distance transmission of orbital angular momentum encoded single-photons over long-distance through optical fibres.
Poppe, A. et al. Practical quantum key distribution with polarization entangled photons. Opt. Express 12, 3865–3871 (2004).
Hübel, H. et al. High-fidelity transmission of polarization encoded qubits from an entangled source over 100 km of fiber. Opt. Express 15, 7853–7862 (2007).
Zhong, T. et al. High-quality fiber-optic polarization entanglement distribution at 1.3 μm telecom wavelength. Opt. Lett. 35, 1392–1394 (2010).
Wangerowski, S. et al. Entanglement distribution over a 96-km-long submarine optical fiber. Proc. Natl Acad. Sci. USA 116, 6684–6688 (2019).
Tittel, W., Brendel, J., Zbinden, H. & Gisin, N. Violation of Bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 81, 3563–3566 (1998).
Marcikic, I. et al. Distribution of time-bin entangled qubits over 50 km of optical fiber. Phys. Rev. Lett. 93, 180502 (2004).
Cuevas, A. et al. Long-distance distribution of genuine energy-time entanglement. Nat. Commun. 4, 2871 (2013).
Inagaki, T., Matsuda, N., Tadanaga, O., Asobe, M. & Takesue, H. Entanglement distribution over 300 km of fiber. Opt. Express 21, 23241–23249 (2013).
Kang, Y. et al. Measurement of the entanglement between photonic spatial modes in optical fibres. Phys. Rev. Lett. 109, 020502 (2012).
Lee, H. J., Choi, S.-K. & Park, H. S. Experimental demonstration of four-dimensional photonic spatial entanglement between multi-core optical fibres. Sci. Rep. 7, 4302 (2017). Demonstration of entanglement distribution over multi-core fibres.
Lee, H. J. & Park, H. S. Generation and measurement of arbitrary four-dimensional spatial entanglement between photons in multicore fibers. Photon. Res. 7, 19–27 (2019).
Cui, L., Su, J., Li, X. & Ou, Z. Y. Distribution of entangled photon pairs over few-mode fibers. Sci. Rep. 7, 14954 (2017).
Cao, H. et al. Distribution of high-dimensional orbital angular momentum entanglement at telecom wavelength over 1 km OAM fiber. Preprint at http://arxiv.org/abs/1811.12195v1 (2018).
Cozzolino, D. et al. Air-core fiber distribution of hybrid vector vortex-polarization entangled states. Adv. Photon. 1, 046005 (2019).
Liu, J. et al. Multi-dimensional entanglement transport through single-mode fibre. Preprint at http://arxiv.org/abs/1904.03114v1 (2019).
Carpenter, J. et al. Mode multiplexed single-photon and classical channels in a few-mode fiber. Opt. Express 21, 28794–28800 (2013).
Dynes, J. F. et al. Quantum key distribution over multicore fiber. Opt. Express 24, 8081 (2016). Compatibility study between classical and quantum data streams over a multi-core fibre.
Lin, R. et al. Telecom compatibility validation of quantum key distribution co-existing with 112 gbps/λ/core data transmission in non-trench and trench-assistant multicore fibers. 2018 European Conference on Optical Communications (ECOC), paper We1A.3.
Hugues-Salas, E., Wang, R., Kanellos, G. T., Nejabati, R. & Simeonidou, D. Co-existence of 9.6 Tb/s classical channels and a quantum key distribution (QKD) channel over a 7-core multicore optical fibre. In 2018 IEEE British and Irish Conference on Optics and Photonics (BICOP). (IEEE, 2019).
Cai, C. et al. Experimental wavelength-space division multiplexing of quantum key distribution with classical optical communication over multicore fiber. Opt. Express 27, 5125–5135 (2019).
Eriksson, T. A. et al. Inter-Core Crosstalk Impact of Classical Channels on CV-QKD in Multicore Fiber Transmission. In Optical Fiber Communication Conference (OFC) 2019, OSA Technical Digest (Optical Society of America, 2019) paper Th1J.1 (OSA, 2019).
Ureña, M., Gasulla, I., Fraile, F. J. & Capmany, J. Modeling optical fiber space division multiplexed quantum key distribution systems. Opt. Express 27, 7047–7063 (2019).
Bacco, D. et al. Boosting the secret key rate in a shared quantum and classical fibre communication system. Commun. Phys. 2, 140 (2019).
Lin, R. et al. Spontaneous Raman Scattering Effects in Multicore Fibers: Impact on Coexistence of Quantum and Classical Channels. In Optical Fiber Communication Conference (OFC) 2019, OSA Technical Digest (Optical Society of America, 2019) paper M4C.2 (OSA, 2019).
Wang, S. et al. On-chip reconfigurable optical add-drop multiplexer for hybrid wavelength/mode-division-multiplexing systems. Opt. Lett. 42, 2802–2805 (2017).
Cariñe, J. et al. Multi-port beamsplitters based on multi-core optical fibers for high-dimensional quantum information. Submitted (2019).
Wang, A. et al. Directly using 8.8-km conventional multi-mode fiber for 6-mode orbital angular momentum multiplexing transmission. Opt. Express 26, 10038–10047 (2018).
Zhu, G. et al. Scalable mode division multiplexed transmission over a 10-km ring-core fiber using high-order orbital angular momentum modes. Opt. Express 26, 594–604 (2018).
Sakaguchi, J. et al. Large spatial channel (36 − core × 3 mode) heterogeneous few-mode multicore fiber. IEEE J. Lightwave Technol. 34, 93–103 (2016).
Acknowledgements
G.X. acknowledges Ceniit Linköping University, the Swedish Research Council (VR 2017-04470) and the Knut and Alice Wallenberg Foundation for financial support. G.L. acknowledges the support of Fondecyt 1160400, and Millennium Institute for Research in Optics, MIRO.
Author information
Authors and Affiliations
Contributions
G.X. and G.L. have both contributed equally to this manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xavier, G.B., Lima, G. Quantum information processing with space-division multiplexing optical fibres. Commun Phys 3, 9 (2020). https://doi.org/10.1038/s42005-019-0269-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0269-7
This article is cited by
-
A QTCP/IP reference model for partially trusted-node-based quantum-key-distribution-secured optical networks
Quantum Information Processing (2024)
-
Quantum random number generation based on a perovskite light emitting diode
Communications Physics (2023)
-
Analysis of wavelength sensitivity of coupling coefficients and inter-core crosstalk in a 9 core fiber
Journal of Optics (2023)
-
Integrated photonics in quantum technologies
La Rivista del Nuovo Cimento (2023)
-
Polarization and orbital angular momentum coupling for high-dimensional measurement-device-independent quantum key distribution protocol
Quantum Information Processing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.