Abstract
By connecting light to magnetism, cavity magnon-polaritons (CMPs) can link quantum computation to spintronics. Consequently, CMP-based information processing devices have emerged over the last years, but have almost exclusively been investigated with single-tone spectroscopy. However, universal computing applications will require a dynamic and on-demand control of the CMP within nanoseconds. Here, we perform fast manipulations of the different CMP modes with independent but coherent pulses to the cavity and magnon system. We change the state of the CMP from the energy exchanging beat mode to its normal modes and further demonstrate two fundamental examples of coherent manipulation. We first evidence dynamic control over the appearance of magnon-Rabi oscillations, i.e., energy exchange, and second, energy extraction by applying an anti-phase drive to the magnon. Our results show a promising approach to control building blocks valuable for a quantum internet and pave the way for future magnon-based quantum computing research.
Similar content being viewed by others
Introduction
The cavity magnon-polariton (CMP)1,2,3,4 is a hybrid quasiparticle arising from strong coupling between photons and magnon excitations. It interconnects light with magnetism presenting itself as an excellent candidate to combine quantum information with spintronics5,6. The first CMP-based devices, such as a gradient memory7 and radio-frequency-to-optical transducers8 have already been developed. The latter ones, in particular, are crucial devices for a quantum internet, for instance, because they bridge microwave-frequency based quantum processors to long range optical quantum networks. Since the recent emergence of this hybrid quasiparticle, three different models, in particular, have helped to unravel the physics of CMPs over the last years: first, the picture of two coupled oscillators, which is the most intuitive one; the underlying physics, however, is only revealed from an electromagnetic viewpoint, which is the second model and shows a phase correlation between cavity and magnon excitation9; and finally, the quantum description of the CMP, which has, for instance, given the theoretical framework for a coupling of magnons to a superconducting qubit10,11. Many spectroscopic experiments have led to new insights about loss channels3,12,13, their temperature dependence14,15,16, and to the observation of level attraction17,18,19. These spectroscopic measurements, however, are performed under continuous driving, and while they have yielded great physical insight into these hybrid systems, flexible and universal information processing requires the manipulation of such physical states on demand and on nanosecond timescales. Despite this necessity for fast manipulation, the literature about time resolved experiments with either an yttrium iron garnet (YIG) waveguide20 or CMPs2,7,21,22 is scarce and confined to cavity-pulsing. A simultaneous and coherent control over both subsystems has yet to be demonstrated, which is the subject of this work.
Here, we establish the control over the cavity and magnon system by using coherent manipulation pulses on the timescale of nanoseconds. We observe the transition from maximum energy exchange to no energy exchange between cavity photons and magnons depending on the applied pulses. We employ these results for a dynamic control of the different modes and for the extraction of the total energy from the system by destructive interference within the sample. Moreover, all results are validated by numerical simulations.
Results
Theoretical background
In our experiments the electromagnetic resonance of a copper cavity interacts with the Kittel mode - the uniform ferromagnetic resonance (FMR)23 - of a YIGsphere mounted inside the cavity. The Landau-Lifshitz-Gilbert (LLG) equation24 describes the Kittel-mode as a macrospin with dynamic magnetization \(m(t)=m{e}^{-i\omega t}\) in an external magnetic field H. The cavity resonance can be modeled as an RLC circuit, with resistor \(R\), inductance \(L\) and capacitance \(C\). Following the model proposed by Bai et al.9, a linear coupling between both systems arises from their mutual back actions, leading to a phase correlation. The changing magnetization of the FMR induces an electric field in the cavity according to Faraday’s law. Following Ampère’s law, the cavity field gives rise to a cavity current, which produces a magnetic rf-field (radio frequency) \(h(t)=h{e}^{-i\omega t}\) driving the FMR. Combining the LLG, the RLC equation and Maxwell’s laws, we obtain a system of coupled equations for \(h\) and \(m\) (Supplementary Note 1). If both subsystems are close to resonance, these equations can be simplified to the eigenvalue equations of two coupled harmonic oscillators with constant coupling strength \(g\):
Here, \({\tilde{\omega }}_{{\rm{c}}}\) and \({\tilde{\omega }}_{{\rm{r}}}\) denote the complex eigenfrequencies of the cavity and magnon system, respectively. They are defined as \({\tilde{\omega }}_{{\rm{c}}}={\omega }_{{\rm{c}}}-i\beta {\omega }_{{\rm{c}}}\) and \({\tilde{\omega }}_{{\rm{r}}}={\omega }_{{\rm{r}}}-i\alpha {\omega }_{{\rm{c}}}\) with bare cavity frequency \({\omega }_{{\rm{c}}}=1/\sqrt{LC}\), bare magnon frequency \({\omega }_{{\rm{r}}}=\gamma \sqrt{| H| (| H| +{M}_{0})}\), where \(\alpha\), \(\beta\) are damping factors, \(\gamma\) the gyromagnetic ratio of the Kittel-mode and \({M}_{0}\) its saturation magnetization. Since the right hand side of Eq. (1) is zero, the equation describes the system during free evolution. The driven case can be modeled by inserting two harmonic drive tones \({F}_{{\rm{c,m}}}={A}_{{\rm{c,m}}}\cos ({\omega }_{0}t-{\varphi }_{{\rm{c}},{\rm{m}}})\), one to each line and differing in phase \(\varphi\) and amplitude \(A\). Combining driven case and free evolution, Eq. (1) can be numerically integrated for various pulse combinations yielding simulated data of our experiments (Supplementary Note 2).
If both subsystems are exactly on resonance, i.e, at their crossing point, \({\omega }_{{\rm{c}}}={\omega }_{{\rm{r}}}={\omega }_{0}\), the eigenfrequencies of Eq. (1) are given by \({\omega }_{\pm }={\omega }_{0}\pm g\) with the eigenvectors \({\xi }_{\pm }=(1,\ \pm 1)\), the so-called normal modes. A single, short pulse to the cavity prepares the system in the non-eigenstate \({\xi }_{0,{\rm{c}}}={\xi }_{+}+{\xi }_{-}=(1,\ 0)\), known as beat mode. The excitation, and therefore the energy, periodically oscillates between cavity and magnon. Hence, the system displays classical magnon-Rabi oscillations2,22. Figures 1a–c illustrate these different modes in the intuitive picture of two coupled pendula. To observe the normal modes \({\xi }_{\pm }\), where no energy is exchanged, one has to coherently and simultaneously excite the cavity and magnon system while recording the cavity response.
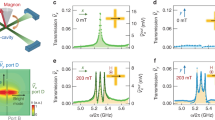
a–c Pendula representation of the different cavity magnon-polariton modes: in-phase mode \({\xi }_{+}\), anti-phase mode \({\xi }_{-}\), and beat-mode \({\xi }_{0}\). d The time domain setup comprises the following three parts: the magnon manipulation line, the cavity manipulation line, and the recording line for the cavity response. A continuous signal of the microwave source is up-converted with pulses from the digital-to-analog-converter (DAC), which then excite cavity and magnon system. The reflected and down-converted signal from the cavity is recorded by an analog-to-digital-converter (ADC). e Typical pulse sequence used in the experiments to prepare the system in its normal mode. The recording line describes the time span in which experimental data is shown, and hence omitting the ring-up behavior for clarity.
Experimental setup
Our sample consists of a copper reentrant cavity4 resonating at \({{\omega }_{r}}/2\pi =\,{6.58}\,{\mathrm{GHz}}\). An additional stripline with a second microwave port is fixed to the bottom of the cavity. This port allows for the direct manipulation of the magnon mode, similar to the work of Wang et al.25 and Boventer et al.19, in a YIG sphere with a diameter of 0.5 mm. The sphere is placed close to the magnetic antinode of the cavity. The cavity’s magnetic rf-field, the stripline rf-field and the external bias field stand all perpendicular to each other (Supplementary Note 3), which minimizes unwanted crosstalk between the two rf-fields. Measurements are performed with a time-domain setup (Fig. 1d) comprising three parts: magnon manipulation, cavity manipulation, and recording. It enables us to independently but coherently pulse the two subsystems and record the reflected signal, i.e., the outgoing photons, of the cavity. Figure 1e depicts the pulse scheme that we employ to prepare the system in its normal modes by varying the following two parameters: An arbitrary phase offset \(\varphi\) between the pulses, and the applied power ratio \({\Delta }^{2}={A}_{{\rm{m}}}^{2}/{A}_{{\rm{c}}}^{2}\), allowing for an amplitude matching and thus equal excitation of cavity and magnon system. Unless otherwise stated, the manipulation pulses are 10 ns short. This results in a bandwidth of the pulses much larger than the linewidths of cavity and magnon. However, only the ratio of stored energy is of importance and we chose such short drive tones to only set the initial state of the system and to not drive the CMP into its steady state response.
System characterization
As a first step, we characterize the system spectroscopically. The avoided level crossing data (Fig. 2a) show a coupling strength of \(g/2\pi ={24.6}\,{\mathrm{MHz}}\), as theoretically expected for this cavity magnon-system14, and identical decay rates (Supplementary Note 4) at the crossing point of \({\kappa }_{{\rm{crp}}}/2\pi ={2.1}\,{\mathrm{MHz}}\) due to equal hybridization. We hence conclude that our system is strongly coupled. This result is also validated in the time domain (Fig. 2b). The external field, and therefore \({\omega }_{{\rm{r}}}\), is swept and only the cavity is excited with a single short pulse in between the sweep steps. The reflected signal shows clear Rabi-oscillations confirming the coupling strength of \(g/2\pi =\text{24.6}\,\text{MHz}\) and thus exhibiting an oscillation period of \({t}_{{\rm{R}}}=2\pi /g=\text{40.6}\,\text{ns}\,\) for \({\omega }_{{\rm{c}}}={\omega }_{{\rm{r}}}\). The measured decay time of \(\tau =\text{77.6}\,\text{ns}\,\) is also in good agreement with \(1/{\kappa }_{{\rm{crp}}}=\text{75.8}\,\text{ns}\). Both, time resolved and spectroscopic data exhibit another weakly coupled magnon-mode at around 234 mT, which slightly distorts the signal of the pure Kittel mode but is not of interest for our experiments.
a Avoided level crossing of the CMP, probed spectroscopically. b Time evolution of the reflected cavity signal revealing magnon-Rabi oscillations after a single pulse to the cavity. Between each recorded time trace the external field is swept. Close to 234 mT another spurious mode is visible, particularly between 100 ns and 200 ns. c Cavity time evolution after phase and amplitude-matched pulses to both cavity and magnon. Rabi oscillations on resonance (green dashed line) are suppressed since the system is prepared in one normal mode. d Comparison of the cavity’s time evolution in one normal mode \({\xi }_{\pm }\) (green line) and beat mode \({\xi }_{0}\) (gray line) at the crossing point. Time traces are line cuts along the dashed lines in b and c.
After the characterization of our system, we apply a simultaneous pulse directly to the magnon system, as displayed in Fig. 1e. The cavity response of such a two-pulse experiment is shown in Fig. 2c. The two pulses are phase and amplitude-matched for the on-resonance case in order to prepare the system in its normal mode. Since no energy is exchanged in the normal modes, a pure exponential decay is expected and observed at the crossing point. However, if \({\omega }_{{\rm{c}}} \, \ne \, {\omega }_{{\rm{r}}}\), the amplitude and phase-matching does not hold and Rabi oscillations are visible. But when the system approaches its crossing point (green dashed line in Fig. 2c), the dips of the oscillations become more shallow than in Fig. 2b, until they are almost completely suppressed. The slight remaining oscillations left are due to experimental imperfections. Figure 2d shows a line cut at the crossing point of the single and two-pulse experiment emphasizing the different responses of the normal mode and beat mode. The two-pulse response reveals the expected exponential decay of either one of the normal modes \({\xi }_{\pm }\). Following the external drive pulses, the cavity and magnon field have the same amplitude and oscillate in-phase (anti-phase) for \({\xi }_{+}\) (\({\xi }_{-}\)), which is characteristic for the normal modes9. These results are in excellent agreement with numerical simulation of Eq. (1), which can be found in Supplementary Note 5.
Transition to normal modes
We also monitor the transition from \({\xi }_{0}\) to \({\xi }_{\pm }\) directly at the crossing point with the same pulse sequence (Fig. 1e) by sweeping the phase offset and power ratio of the two pulses. The cavity response during free evolution is recorded for every combination of these two parameters, and fitted to the following formula (See Supplementary Note 6 for details on the derivation):
which describes the cavity response during free evolution. The parameter \(\lambda\) has inherent bounds of \(-1\) to 1 and determines the behavior of the system. \(\lambda =1\) gives a damped sine function and thus represents the beat mode \({\xi }_{0}\), whereas \(\lambda =-1\) yields the pure exponential decay of the normal modes \({\xi }_{\pm }\). A proportionality constant \({p}_{0}\) normalizes the different input powers, \({\phi }_{0}\) describes the initial phase of the beating and \(\tau\) the decay time. Figure 3a displays the extracted values for \(\lambda\) corresponding to the different modes for the measured data and can be compared to the analytic solution (Fig. 3b). As expected from the oscillator and the electromagnetic model9, where the phase between magnon field and cavity field at the crossing point is locked to either in phase or complete anti-phase for the two eigenmodes, the system is prepared in the normal modes (red regions) for matching powers and phase offsets of \(18{0}^{\circ }\) and \(36{0}^{\circ }\). In the experiment, the red regions are shifted to lower phase offset values by roughly \(3{0}^{\circ }\) and occur at different power ratios (attenuations). Investigating these deviations with numerical simulation, we find that this phase shift translates to a timing mismatch between the two applied pulses below 0.1 ns, which is beyond the precision of our setup. The difference in attenuation between the normal mode regions is either due to direct crosstalk \(\zeta\) describing the amount of cavity pulse amplitude acting on the magnon system and vice versa (Supplementary Eqs. (S2) and (S3)), as displayed in Fig. 3c, or due to small drifts of the external magnetic field resulting in a detuning of the two oscillating systems \(\Delta f=({\omega }_{{\rm{r}}}-{\omega }_{{\rm{c}}})/2\pi\), which can be seen in Fig. 3d. Apart from these little discrepancies, which are purely limitations of the experimental setup, our collected data agrees well with theory (Further information in Supplementary Note 7). We can continuously change the parameter \(\lambda\) and therefore the CMP mode composition. Thus, with a second pulse, the phase relation between cavity current and magnon magnetization can be set to an arbitrary value. These results extend the work of Bai et. al, where the phase relation between the two systems is fixed by the external field9. This pulsed mode control of the CMP may hence benefit future spin rectification26 experiments and applications.
The mode composition depends on applied power ratio \({{\Delta }^{2}}\) and phase offset \(\varphi\) between the two pulses. Experimental data of the cavity response (a) are fitted to Eq. (2) and can then be compared to analytic data (b) and simulations considering experimental imperfections (c and d). The chosen attenuation in the magnon line (y-axis of a) corresponds to the power ratio of the drive pulses used in b–d with an experimentally inaccessible offset. The parameter \(\lambda\) translates to the mode composition of the CMP. Within the red ellipses, the CMP is predominantly excited in its normal modes. Experimentally found normal mode ellipses are slightly shifted to lower phase values and differ in power ratio compared to the analytic solution. Simulations reveal small timing mismatches \(\delta t\) of the applied pulses, direct crosstalk \(\zeta\) or small frequency drifts \(\Delta f\) in the system as possible reasons for the discrepancy.
Coherent and dynamic control
The external control of the CMP mode composition, which we showed and described, is directly linked to the amplitude control of Rabi oscillation and thus to the amount of energy transferred between the two subsystems. Seizing this opportunity, we now demonstrate a coherent and also dynamic control over the CMP during one single decay by choosing an arbitrary period in which the magnon-Rabi oscillations are allowed to occur (Fig. 4a). Having prepared the system on resonance, we excite both magnon and cavity with phase and amplitude-matched pulses, to bring the CMP into its normal mode \({\xi }_{\pm }\) and observe a pure exponential decay. We then increase the energy of the magnon subsystem by pulsing it again with a short pulse. The whole system is now in a superposition of \({\xi }_{+}\) and \({\xi }_{-}\), i.e., in its beat mode. Rabi oscillations are visible and energy is exchanged. After a few oscillations, a third pulse in anti-phase to the incoming photons from the cavity and with lower amplitude, due to energy loss in the system, extracts the additional energy, previously introduced to the magnon subsystem, by destructive interference and brings the whole system back to its normal mode. The Rabi oscillations stop and a simple exponential decay is visible, again. In the picture of two coupled pendula, the three different segments of the decay correspond to (I) both pendula oscillating in phase, (II) a strong drive of one pendulum introduces energy leading to the beat mode, and (III) a careful short deacceleration brings the system back to the normal mode. Simulating this experiment with the same pulse sequences, we find a good agreement of experimental results and simulated data (dashed line in Fig. 4a).
a Time trace of the cavity response showing dynamic control over the time span of energy exchange. The time trace is divided into three parts: (I) The system is in its normal mode with almost no energy exchange; (II) An additional pulse to the magnon system introduces an energy difference leading to Rabi oscillations; (III) A third pulse to the magnon extracts energy out of the system by destructive interference, bringing it back to the normal mode. b Cavity time trace showing energy extraction by an anti-phase drive of the magnon, which counters the energy coming from the cavity. Photons interfere destructively and the CMP is deexcited by destructive interference after the magnon pulse. Solid brown and blue lines represent the applied pulse sequences for the cavity and magnon system, respectively (pulse-height not scaled). The ring up of cavity and magnon system, \(t \, < \, \text{0}\,\text{ns}\,\), is omitted for clarity. Insets show the corresponding coupled pendula visualizations.
In a second experiment (Fig. 4b), we apply the technique used for active noise control27,28 in acoustics to the CMP: the cavity is excited by a short pulse and the energy is transferred to the magnon system and back to the cavity. Here, we found a good result applying a longer pulse of 40 ns to the cavity. However, we note that the experiment is independent of the pulse length. During the second energy transfer to the magnon, we drive the magnon in an anti-phase manner to the oscillation of the incoming photons. A destructive interference extracts the stored energy from the system and thus the reflected power of the cavity drops within a few nanoseconds by roughly 20 dB, before the signal reaches the baseline of the measurement setup. This behavior can also be understood intuitively in the picture of the coupled pendula: A first pulse tilts only one pendulum, the energy is transferred with time and the second pendulum starts oscillating. Exactly in the moment when all energy is transferred, i.e., the first pendulum is at rest, the other pendulum is stopped abruptly by the external second pulse and the whole system is deexcited. Again, the simulated data agrees well with the experiment, showing a drop of 20 dB after the magnon pulse. In the simulation the Rabi oscillations continue whereas in the experiment the signal is limited by the dynamic range of the analog-to-digital-converter (ADC) and also affected by unwanted pulse reflections in the setup. These two experiments presented here demonstrate the fundamentals of dynamic and coherent control over the CMP.
Discussion
We presented coherent time-domain control of both cavity and magnon while recording the cavity response, as well as real-time manipulation of the CMP. We also showed the transition from the beat mode to the normal modes of the CMP and explained it with the theory models provided by Bai et al.9. The CMP can be set in an arbitrary superposition of its eigenmodes depending on the phase offset and amplitude of the applied pulses. This pulse influence agrees well with theory considering the finite time resolution of our setup. Furthermore, we demonstrated a coherent control over the CMP, with which the amount of transferred energy as well as the total amount of energy in the system can be manipulated at any given time.
Spectroscopic two-tone experiments predicted and observed the regime of level attraction17,19,29. Following the proposal of Yuan et al.30, this regime has also been linked to an entanglement of photon and magnon with predictions for the time evolution of the system. Using the presented technique here and also slightly modifying our sample according to the geometry of Boventer et al.19 would allow for a preparation of the CMP in the level attraction regime. Its state can then be recorded in time. Although our demonstration was purely classical, the presented control can readily be applied at cold temperatures, i.e., in the single magnon regime, and the predicted entanglement in the level attraction regime may be verified.
Moreover, our demonstration of dynamic and coherent control can be extended by adding a non-linearity to the system, e.g., a superconducting qubit,10,11. This would allow for an encoding of qubit states in magnons31 with gate schemes similar to the works on superconducting resonators32,33 and subsequently the implementation of universal gates34,35 for magnon systems. The CMP’s significant potential as an interface from radio frequency to optics8,36,37,38 balances the short lifetime of magnons compared to superconducting resonators. Thus, our results are a promising step towards a link between the different building blocks for a quantum network39 and open new ways for magnon-based quantum computation research.
Finally, our work demonstrates the fundamental principle of time-control of the individual components in hybrid systems. Applied to other compound devices featuring polaritons from the strong coupling of electromagnetic waves with electric or magnet excitations, such as optomechanics40 or electromechanics41, it provides a flexible platform that intrigues fundamental coherent control of the strong light-matter interaction dynamics.
Methods
Experimental setup
The experimental setup is adapted from quantum simulation experiments with superconducting qubits42. Its core components are a microwave source, an arbitrary waveform generator (AWG) with two sets of digital-to-analog-converters (DAC), and a two-channel ADC-card. For our experiments it is vital that the phase between magnon and cavity control pulses is independently controllable but also stable over the entire experiment. We ensure this by using a single microwave source and two DAC sets in combination with the internal clock of the AWG for both DAC sets. The continuous signal generated by the microwave source is up-converted to \({\omega }_{0}\) via separate but identical IQ-mixers (in-phase/quadrature) and 10 ns short IQ-pulses with a carrier frequency of 250 MHz from the AWG. The up-conversion preserves the phase offset and the envelope of the IQ-pulses emitted by the AWG. A voltage controllable attenuator in combination with a 26 dB amplifier inserted in the magnon line enables us to adjust the excitation amplitude and hence vary the power ratio between magnon and cavity excitation pulses.
Data acquisition
The cavity response is recorded by measuring the IQ components of the down converted, filtered and amplified signal with the ADC-card. A subsequent digital down conversion removes the 250 MHz carrier frequency and yields amplitude and phase data.
Experimental technique
The initial two pulses for the cavity and magnon system have to reach the sample simultaneously in order to ensure a good phase and amplitude matching. We therefore calibrate the cable delay between the two input lines by emitting two Gaussian shaped pulses simultaneously at the AWG, which are sent to both subsystems. Due to undeterrable crosstalk, a part of the pulse applied to magnon system is transferred to the recording line of the cavity. Recording the reflected cavity pulse and the transmitted magnon pulse, we find a cable delay of \(\,\text{7}\,\text{ns}\) by fitting the pulses and extracting their mean values. However due to simplicity, square pulses are used for most experiments. Because of inaccessible and fluctuating parameters, such as uncorrectable cable delays below 1 ns, drifts in the external fields and unknown reflected parts of the emitted pulses, the correct phase offsets and power ratio for the specific experiments are found experimentally by a sweep of these two parameters. Although the eigenfrequencies are shifted by \(g\) compared to the bare resonator frequency, the system is always pulsed at \({\omega }_{0}\). This gives the best experimental compromise for equally exciting the different modes of the system. All experiments are performed in the linear regime (Supplementary Note 8).
Sample details
The employed YIG sphere is commercially available from Ferrisphere Inc. The stripline is \(50\,\Omega\) matched and open-ended. It is made from a Rogers TMM10i copper cladded (35 µm) substrate with a thickness of 0.64 mm.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
All data acquisition and analysis are performed with the open source measurement suite qkit https://github.com/qkitgroup/qkit. The implementation of the numerical simulations and the fitting procedure are available from the corresponding author upon reasonable request.
References
Huebl, H. et al. High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids. Phys. Rev. Lett. 111, 127003 (2013).
Zhang, X., Zou, C.-L., Jiang, L. & Tang, H. X. Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113, 156401 (2014).
Tabuchi, Y. et al. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 113, 083603 (2014).
Goryachev, M. et al. High-cooperativity cavity QED with magnons at microwave frequencies. Phys. Rev. Appl. 2, 054002 (2014).
Lachance-Quirion, D., Tabuchi, Y., Gloppe, A., Usami, K. & Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Express 12, 070101 (2019).
Karenowska, A. D., Chumak, A. V., Serga, A. A. & Hillebrands, B. in Handbook of Spintronics. (eds. Xu, Y., Awschalom, D.D., Nitta, J.) 1505–1549 (Springer Netherlands, Dordrecht, 2016).
Zhang, X. et al. Magnon dark modes and gradient memory. Nat. Commun. 6, 8914 (2015).
Hisatomi, R. et al. Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93, 174427 (2016).
Bai, L. et al. Spin pumping in electrodynamically coupled magnon-photon systems. Phys. Rev. Lett. 114, 227201 (2015).
Tabuchi, Y. et al. Coherent coupling between a ferromagnetic magnon and a superconducting qubit. Science 349, 405–408 (2015).
Lachance-Quirion, D. et al. Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet. Sci. Adv. 3, e1603150 (2017).
Kosen, S., van Loo, A. F., Bozhko, D. A., Mihalceanu, L. & Karenowska, A. D. Microwave magnon damping in YIG films at millikelvin temperatures. APL Mater. 7, 101120 (2019).
Pfirrmann, M. et al. Magnons at low excitations: Observation of incoherent coupling to a bath of two-level systems. Phys. Rev. Res. 1, 032023 (2019).
Boventer, I. et al. Complex temperature dependence of coupling and dissipation of cavity magnon polaritons from millikelvin to room temperature. Phys. Rev. B 97, 184420 (2018).
Zhang, D. et al. Cavity quantum electrodynamics with ferromagnetic magnons in a small yttrium-iron-garnet sphere. npj Quant. Inf. 1, 15014 (2015).
Golovchanskiy, I. et al. Interplay of magnetization dynamics with a microwave waveguide at cryogenic temperatures. Phys. Rev. Appl. 11, 044076 (2019).
Grigoryan, V. L., Shen, K. & Xia, K. Synchronized spin-photon coupling in a microwave cavity. Phys. Rev. B 98, 024406 (2018).
Harder, M. et al. Level attraction due to dissipative magnon-photon coupling. Phys. Rev. Lett. 121, 137203 (2018).
Boventer, I. et al. Control of the coupling strength and the linewidth of a cavity-magnon polariton. Preprint at http://arxiv.org/abs/1904.00393 (2019).
van Loo, A. F., Morris, R. G. E. & Karenowska, A. D. Time-resolved measurements of surface spin-wave pulses at millikelvin temperatures. Phys. Rev. Appl. 10, 044070 (2018).
Morris, R. G. E., Loo, A. Fv, Kosen, S. & Karenowska, A. D. Strong coupling of magnons in a YIG sphere to photons in a planar superconducting resonator in the quantum limit. Sci. Rep. 7, 11511 (2017).
Match, C., Harder, M., Bai, L., Hyde, P. & Hu, C.-M. Transient response of the cavity magnon-polariton. Phys. Rev. B 99, 134445 (2019).
Kittel, C. On the theory of ferromagnetic resonance absorption. Phys. Rev. 73, 155–161 (1948).
Landau, L. D. & Lifshitz, E. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjet. 8, 153–169 (1935).
Wang, Y.-P. et al. Bistability of cavity magnon polaritons. Phys. Rev. Lett. 120, 057202 (2018).
Harder, M., Gui, Y. & Hu, C.-M. Electrical detection of magnetization dynamics via spin rectification effects. Phys. Rep. 661, 1–59 (2016).
Elliott, S. & Nelson, P. The active control of sound. Electron. Commun. Eng. J. 2, 127 (1990).
Kuo, S. M. & Morgan, D. R. Active noise control: a tutorial review. Proc. IEEE 87, 943–973 (1999).
Zhang, D., Luo, X.-Q., Wang, Y.-P., Li, T.-F. & You, J. Q. Observation of the exceptional point in cavity magnon-polaritons. Nat. Commun. 8, 1368 (2017).
Yuan, H. Y. et al. Steady Bell state generation via magnon-photon coupling. Preprint at http://arxiv.org/abs/1905.11117 (2019).
Rezende, S. M. & Zagury, N. Coherent magnon states. Phys. Lett. A 29, 47–48 (1969).
Hofheinz, M. et al. Generation of Fock states in a superconducting quantum circuit. Nature 454, 310–314 (2008).
Leghtas, Z. et al. Deterministic protocol for mapping a qubit to coherent state superpositions in a cavity. Phys. Rev. A 87, 042315 (2013).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon schrödinger cat states. Science 342, 607–610 (2013).
Heeres, R. W. et al. Implementing a universal gate set on a logical qubit encoded in an oscillator. Nat. Commun. 8, 94 (2017).
Zhang, X., Zhu, N., Zou, C.-L. & Tang, H. X. Optomagnonic whispering gallery microresonators. Phys. Rev. Lett. 117, 123605 (2016).
Osada, A. et al. Cavity optomagnonics with spin-orbit coupled photons. Phys. Rev. Lett. 116, 223601 (2016).
Haigh, J., Nunnenkamp, A., Ramsay, A. & Ferguson, A. Triple-resonant brillouin light scattering in magneto-optical cavities. Phys. Rev. Lett. 117, 133602 (2016).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Regal, C.A. and Lehnert, K.W. From cavity electromechanics to cavity optomechanics. J. Phys. Conf. Ser. 264, 012025 (2011).
Braumüller, J. et al. Analog quantum simulation of the Rabi model in the ultra-strong coupling regime. Nat. Commun. 8, 779 (2017).
Acknowledgements
We acknowledge valuable discussions with Konrad Dapper, Bimu Yao and Can-Ming Hu. This work was supported by the European Research Council (ERC) under the Grant Agreement 648011, Deutsche Forschungsgemeinschaft (DFG) within Project No. WE4359/7-1 and INST 121384/138-1 FUGG, through SFB TRR 173/Spin+X, and the Initiative and Networking Fund of the Helmholtz Association. T.W. acknowledges financial support by Helmholtz International Research School for Teratronics (HIRST), A.St. by the Landesgraduiertenförderung (LGF) of the federal state Baden-Württemberg, A.Sch. by the Carl-Zeiss-Foundation and R.M. by the Leverhulme Trust. A.V.U. acknowledges partial support from the Ministry of Education and Science of the Russian Federation in the framework of the contract No. K2-2017-081.
Author information
Authors and Affiliations
Contributions
T.W. and M.W. conceived the experiment. T.W. performed the measurements with support by Al.S., An.S., and I.B. T.W. carried out data analysis with contributions from A.St. and R.M. T.W. wrote the manuscript with input from and discussions with all co-authors. A.V.U., M.K., and M.W. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wolz, T., Stehli, A., Schneider, A. et al. Introducing coherent time control to cavity magnon-polariton modes. Commun Phys 3, 3 (2020). https://doi.org/10.1038/s42005-019-0266-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0266-x
This article is cited by
-
Imaging and phase-locking of non-linear spin waves
Nature Communications (2022)
-
Advances in coherent magnonics
Nature Reviews Materials (2021)
-
Magnon-driven dynamics of a hybrid system excited with ultrafast optical pulses
Communications Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.