Abstract
High-precision low-temperature thermometry is a challenge for experimental quantum physics and quantum sensing. Here we consider a thermometer modeled by a dynamically-controlled multilevel quantum probe in contact with a bath. Dynamical control in the form of periodic modulation of the energy-level spacings of the quantum probe can dramatically increase the maximum accuracy bound of low-temperatures estimation, by maximizing the relevant quantum Fisher information. As opposed to the diverging relative error bound at low temperatures in conventional quantum thermometry, periodic modulation of the probe allows for low-temperature thermometry with temperature-independent relative error bound. The proposed approach may find diverse applications related to precise probing of the temperature of many-body quantum systems in condensed matter and ultracold gases, as well as in different branches of quantum metrology beyond thermometry, for example in precise probing of different Hamiltonian parameters in many-body quantum critical systems.
Similar content being viewed by others
Introduction
Precise probing of quantum systems is one of the keys to progress in diverse quantum technologies, including quantum metrology1,2,3, quantum information processing (QIP)4, and quantum many-body manipulations5. The maximum amount of information obtained on a parameter of a quantum system is quantified by the quantum Fisher information (QFI), which depends on the extent to which the state of the system changes for an infinitesimal change in the estimated parameter6,7,8,9,10. Ways to increase the QFI, thereby increasing the precision bound of parameter estimation, are therefore recognized to be of immense importance11,12. Recent works have studied QFI for demonstrating the criticality of environmental (bath) information13, QFI enhancement in the presence of strong coupling14 or by dynamically controlled quantum probes9, and the application of quantum thermal machines to quantum thermometry15.
Here, we propose the synthesis of two concepts: quantum thermometry8,12,14,15,16,17,18,19,20,21,22 and temporally periodic dynamical control that has been originally developed for decoherence suppression in QIP23,24,25,26,27. We show that such control can strongly increase the QFI that determines the precision bound of temperature measurement, particularly at temperatures approaching absolute zero. Accordingly, such control may boost the ultralow-temperature precision bound of diverse thermometers, e.g., those based on Coulomb blockade28, metal–insulator–superconductor junctions29, kinetic inductance30, and novel hybrid superconductors31. Alternatively, dynamical control may allow theese thermometers to accurately estimate a broad range of temperatures.
Results
Model
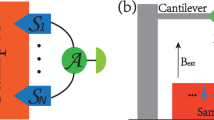
An example of our dynamically controlled quantum thermometer (DCQT) is a quantum wavepacket trapped in a potential and subjected to periodic modulation, while it is immersed in a thermal bath (Fig. 1a). Measurements of the wavepacket after it has reached a steady-state provide information about the bath temperature. Another example of a DCQT is the internal state of either a two-level or a multilevel system coupled to a spin-chain bath32,33. The level separation is periodically modulated by a control field (e.g., a field-induced alternating current Stark shift) and its level populations are finally read out by laser-induced fluorescence in the optical range (Fig. 1b). Many of the advanced thermometers14,15,16,28,29,30,31 may be adapted to such dynamically controlled operation.
a Schematic realization of a dynamically controlled quantum thermometer by a motional wavepacket of a state of a cavity, or an ion/atom trapped in an optical lattice potential. The frequency of the trap is periodically varied (black arrow) by modulating the length of the cavity, or the amplitudes of the lasers forming the trap. The wavepacket is in contact with a phonon bath, and relaxes to the corresponding thermal steady-state at long times. b Same, for a spin-chain bath coupled to a two-level system whose resonant frequency is periodically modulated.
The proposed DCQT is described by a Hamiltonian \(H(t)\), subjected to a modulation with time period \(\tau =2\pi /\Delta\):
The DCQT is coupled to a bath through the interaction Hamiltonian of the form \({\hat{H}}_{I}={\sum }_{k}{\hat{H}}_{Ik}={\sum }_{k}{\hat{S}}_{k}\otimes {\hat{B}}_{k}\). Here, \({\hat{S}}_{k}\) and \({\hat{B}}_{k}\) are, respectively, the \(k\)-th mode DCQT and bath operators. In cases where the \(k\)-th bath mode acts as a Markovian environment characterized by a mode-dependent unknown temperature \({T}_{k}\), the corresponding DCQT mode thermalizes to the temperature \({T}_{k}\) at long times, thus enabling us to perform mode-dependent thermometry. Alternatively, if the bath is thermal with an unknown temperature \(T\), a single-mode DCQT suffices for bath-temperature estimation.
Analysis
For simplicity, we restrict our analysis below to a thermal bath with temperature \(T\), probed by an \({\mathcal{N}}\)-level DCQT that is described by the Hamiltonian \(\hat{H}(t)\) = \(\hslash {\sum }_{n=0}^{{\mathcal{N}}}{\omega }_{n}(t)\left|n\right\rangle \left\langle n\right|\) with energy spectrum \({\omega }_{n}(t)\) = \(n\omega (t)\) for real positive \(\omega (t)\), and an interaction Hamiltonian \({\hat{H}}_{I}=\hat{S}\otimes \hat{B}\). Here, \(n\) denotes the level index, and we assume \(\hat{S}\) to be a system operator belonging to a Lie algebra. For a two-level system, \(\hat{S}\equiv {\hat{\sigma }}_{x}\), the \(x\) Pauli operator, while for a harmonic oscillator, \(\hat{S}\equiv \left(\hat{a}+{\hat{a}}^{\dagger }\right)\), where \(\hat{a}\), \({\hat{a}}^{\dagger }\) denote the annihilation and creation operators, respectively. For a single-mode DCQT, we consider a generic, periodic, diagonal (frequency) modulation:
where \(s({m}^{\prime}),c({m}^{\prime})\) are adjustable real constants, corresponding to the \({m}^{\prime}\)-th frequency harmonic. One can extend this analysis to a multi-mode DCQT probing a multi-mode bath (see Methods).
Here, we focus on controls with \(\tau\) much smaller than the thermalization time of the system, such that one can adopt the secular approximation, thereby averaging out all rapidly oscillating terms and arriving at a time \(t\gg \tau\) at the steady-state \(\hat{\rho }(t\to \infty )={\sum }_{n=0}^{{\mathcal{N}}}{\varrho }_{n}\left|n\right\rangle \left\langle n\right|\)34,35,36. The level populations \({\varrho }_{n}\) are functions of the bath temperature \(T\), the bath response (correlation) functions \(G({\omega }_{m})\) (see Methods)37,38 at the \(m\)-th sideband frequency \({\omega }_{m}={\omega }_{0}+m\Delta\), and the modulation-dependent \(m\)-th sideband weight \({P}_{m}\ge 0\) (see Methods and Supplementary Notes 2–5). Here, the sidebands \(m=0,\pm1\pm2,\ldots\) arise due to the periodic modulation, the mean frequency \({\omega }_{0}=\left({\int }_{0}^{\tau }\omega (t)dt\right)/\tau\), and \({P}_{m}\)’s satisfy the constraint \({\sum }_{m}{P}_{m}=1\)34,35,36. As can be expected in experiments, we impose an upper bound on the available resources for dynamical control, by considering only frequency modulations such that \(\max \left[{m}^{\prime}\right]\Delta \, < \, {\omega }_{0}\). Unless otherwise stated, we take \(\hslash\) and \({k}_{B}\) to be unity, and assume the bath response obeys the standard Kubo–Martin–Schwinger condition \(G(-\omega )/G(\omega )=\exp \left(-\omega /T\right)\)37.
We may infer the bath temperature \(T\) from measurements of \({\varrho}_{n}\) of the thermometer: e.g., through measurement of the average phonon occupation number of a trapped-wavepacket probe (Fig. 1a)39, or the fluorescence of a two-level system probe (Fig. 1b). We can assess the effectiveness of our measuring scheme from the QFI as a function of the system and bath parameters. The relative error \(\delta T/T\) is bounded by the minimal achievable error \(\xi\), dictated by the Cramer-Rao bound for optimal positive-operator valued measure, which in this case are the level-population measurements. It obeys the relation6,9,40
Here, \({\mathcal{M}}\) denotes the number of measurements, and \({\mathcal{H}}=-2\mathop{\mathrm{lim}}\nolimits_{\epsilon \to 0}{\partial }^{2}F(\hat{\rho }(T,t),\hat{\rho }(T+\epsilon ,t))/\partial {\epsilon }^{2}={\sum }_{n=0}^{{\mathcal{N}}}| \partial {\varrho }_{n}/\partial T{| }^{2}/{\varrho }_{n}\) is the QFI at temperature \(T\)7,8,41,42, \(F({\hat{\rho }}_{1},{\hat{\rho }}_{2})={\rm{Tr}}\left[\sqrt{\sqrt{{\hat{\rho }}_{1}}{\hat{\rho }}_{2}\sqrt{{\hat{\rho }}_{1}}}\right]\) being the fidelity between \({\hat{\rho }}_{1}\) and \({\hat{\rho }}_{2}\).
The dynamics of the DCQT, and consequently also the resultant steady-state, depends crucially on the factors \({P}_{m}G({\omega }_{m})\); in general, a large \({P}_{m}G({\omega }_{m})\) is beneficial for estimating temperatures \(T \sim {\omega }_{m}\) (see below, Methods and Supplementary Notes 1–5)36. Although we cannot control the bath correlation functions (spectral-response) \(G({\omega }_{m})\), nevertheless for a given \(G({\omega }_{m})\), we can tailor the thermometry QFI to our advantage by judicious choices of the periodic control fields, and hence of the corresponding \({P}_{m}\)’s and \({\omega }_{m}\)’s. For example, a versatile thermometer, which can measure a wide range of temperatures with high-accuracy bound would require a modulation that corresponds to large QFI over a broad range of temperatures, in order to yield \(\xi \ll 1\) for finite \({\mathcal{M}}\). The above scenario can be realized using modulations, which give rise to multiple non-negligible \({P}_{m}\)’s, or equivalently, large \({P}_{m}G({\omega }_{m})\) over a broad range of frequencies. In particular, it is exemplified below using a sinusoidal modulation characterized by a single, or few frequencies. On the other hand, a different modulation would enable the same thermometer to measure temperatures with higher accuracy bound (or, equivalently, larger QFI), but at the expense of the changing of the temperature range over which the DCQT can measure accurately. This can for example be realized using periodic \(\pi\)-pulses, which give rise to only two sidebands, viz., non-negligible \({P}_{\pm 1}\)34.
Therefore, in contrast to thermometry in the absence of any control, DCQT gives us the possibility of tuning the range and accuracy bound of measurable temperatures. This necessitates an appropriate choice of control parameters (\(\Delta ,{m}^{^{\prime} },s({m}^{^{\prime} }),c({m}^{^{\prime} })\)) in Eq. (2) depending on the temperatures of interest.
Harmonic-oscillator DCQT for sub-Ohmic baths
As a generic example of DCQT, we consider the probe to be a periodically modulated harmonic oscillator. The interaction Hamiltonian is \({\hat{H}}_{I}=\left(\hat{a}+{\hat{a}}^{\dagger }\right)\otimes \hat{B}\), where \(\hat{a}\) (\({\hat{a}}^{\dagger }\)) denotes the annihilation (creation) operator of the DCQT, and \(\hat{B}\) is a bath operator.
We first consider the thermometry of a broad class of bath spectral-response functions18,43
under the Kubo–Martin–Schwinger condition. Here, \(\gamma\) is a positive constant determining the system-bath coupling strength. Since we focus on the weak-coupling limit, such that the thermalization time \(\sim {\gamma }^{-1}\gg \tau ,{\omega }_{m}^{-1}\), the secular approximation is valid37. Expression (4) yields sub-Ohmic, Ohmic and super-Ohmic bath spectra for \(s \, < \, 1\), \(s=1\) and \(s \, > \, 1\), respectively.
To show the full advantage of our control scheme, we start by focusing on a sub-Ohmic bath spectrum, since it has a non-zero \(G(\omega )\) infinitesimally close to \(\omega =0\), even though \(G(\omega )\) vanishes at \(\omega =0\) (cf. Eq. (4)), which is ideal for low-temperature thermometry17. To simplify the treatment, we take the limit of small \(\gamma\) in Eq. (4) to ensure weak-coupling, \(s\to 0\) to generate small \({\omega }_{\min }\), and \({\omega }_{c}\to \infty\) to realize high-cutoff frequency, and arrive at the nearly flat bath spectrum (NFBS)
for \({\omega }_{\min } \, \lesssim \, \omega \ll {\omega }_{c}\), with \({\omega }_{\min }\approx s{\omega }_{c}\) (see Supplementary Notes 4 and 5). Hence, \({\omega }_{\min }\) can be as small as \(s{\omega }_{c}\), thus enabling us to probe the bath very close to the absolute zero (see below). The comparison of our results with those obtained for a sub-Ohmic bath spectrum with finite \(s\) and \({\omega }_{c}\) is shown in Figs. 2 and 3. The extension of our results to the case of a generic bath spectrum is presented below.
Relative error bound \(\xi\) for estimation of bath temperature \(T\) (in units of \({\omega }_{0}\)) by a harmonic-oscillator dynamically controlled quantum thermometer (DCQT) under sinusoidal modulation for the following bath spectra: nearly flat bath spectrum (magenta solid curve), sub-Ohmic bath spectrum with \(s=0.1,{\omega }_{c}=100\) (black dashed curve) and the same spectra in the absence of control (turquoise dotted curve). For low temperatures in the absence of control, \(\xi \to \infty\), thus making it impossible to measure low temperatures as shown. In contrast, our dynamical control scheme reduces \(\xi\) to finite values at low temperatures, for nearly flat, as well as sub-Ohmic bath spectra, thus showing the advantage of DCQT. Inset: Quantum Fisher Information (\({\mathcal{H}}\)) as a function of temperature \(T\) (in units of \({\omega }_{0}\)) for DCQT under sinusoidal modulation and in the absence of control, for the bath spectra in the main figure (same curve colors). DCQT increases the quantum Fisher information significantly at lower temperatures, giving rise to a peak at \(T\approx {T}_{-1}\) (magenta dot), in addition to the peak at \(T\approx {T}_{0}\) (turquoise dot). Here, the modulation amplitude \(\mu =0.2,{\omega }_{0}=1,\Delta =0.9\) (see Eq. (6)), \(m=0,\pm 1,\pm 2,\pm 3\) and the number of measurements \({\mathcal{M}}=1\). The thermalization time \(\sim {\gamma }^{-1}\) is assumed to be long enough such that the secular approximation is valid.
Relative error bound \(\xi\) for the estimation of bath temperature at \(T={T}_{-1}=({\omega }_{0}-\Delta )/4\), by a harmonic-oscillator dynamically controlled quantum thermometer under sinusoidal modulation (cf. Eq. (6)), for the following bath spectra: nearly flat bath spectrum (magenta solid curve), sub-Ohmic bath spectrum with \(s=0.1,{\omega }_{c}=100\) (black dashed curve) and the same spectra in the absence of control (turquoise dotted curve). Dynamical control reduces the relative error bound significantly, with \(\xi\) remaining constant over a broad range of low temperatures \(T\ll {\omega }_{0}\). The sidebands \(m=0,\pm 1,\pm 2,\pm 3\) are included in the calculation. Here, the modulation amplitude \(\mu =0.2\), and \({\omega }_{0}=1\). Inset: Corresponding spectral-response functions scaled by \(\gamma\).
Below we choose the control scheme Eq. (2) to have \(c({m}^{\prime})={\omega }_{0}{\delta }_{{m}^{\prime},0}\) and \(s({m}^{\prime})=\mu \Delta {\delta }_{{m}^{\prime},1}\), so that \(\omega (t)\) is varied sinusoidally:
In the limit of weak-modulation (\(0\le \mu \ll 1\)), only the sidebands \(m=0\) and \(m=\pm 1\) have significant weights \({P}_{m}\) in the harmonic (Floquet) expansion of the system response34: the \(m\)th sideband weight \({P}_{m}\), corresponding to the Floquet (harmonic) frequency \({\omega }_{m}={\omega }_{0}+m\Delta\), falls off rapidly with increasing \(| m|\). The QFI can then be written as (see Supplementary Note 4)
Here, \({{\mathcal{H}}}_{\pm 1}\) are the contributions to the QFI arising from to the \(m=\pm 1\) sidebands with \({P}_{\pm 1}\simeq {\mu }^{2}/4\), and \({{\mathcal{H}}}_{0}\) includes the \(m=0\) contribution.
The advantages of DCQT are then revealed for a control scheme with \(\Delta\) chosen such that
so that
with the average occupation number given by
The QFI is then predominantly associated with the \({{\mathcal{H}}}_{-1}\) term, with the maximum located at the temperature
If higher sidebands (\(| m| \ge 2\)) are taken into account, the results remain valid, except for a marginal increase of the relative error bound \(\xi\) at low temperatures (see Supplementary Notes 2–5).
By contrast, in the absence of any control (\(\mu =0\)), \({\varrho }_{n}\) is still given by Eq. (8), with the average phonon occupation number
which vanishes in the limit \(T\ll {\omega }_{0}\). The corresponding QFI is given by
which has a single peak at \(T={T}_{0}\), where \({T}_{0}\) satisfies the equation \({T}_{0}={\omega }_{0}\coth \left({\omega }_{0}/2{T}_{0}\right)/4\) (cf. inset of Fig. 2).
One can infer from the above results that a weak sinusoidal modulation (small \(\mu\)) with appropriately large \(\Delta\) results in a double-peaked QFI, attaining maxima at \(T\approx {T}_{-1}\) and \(T\approx {T}_{0}\), owing to contributions from \({{\mathcal{H}}}_{-1}\) and \({{\mathcal{H}}}_{0}\), respectively (Fig. 2). This double-peaked QFI signifies the applicability of DCQT for estimating a much broader range of temperatures, viz., in the vicinity of \(T={T}_{-1}\), which can be tuned according to our temperature of interest by tuning \({\omega }_{-1}\), and \(T={T}_{0}\). In comparison, an uncontrolled quantum thermometer can accurately measure temperatures only in the vicinity of \(T={T}_{0}\) for probes characterized by a single energy gap, or at multiple fixed (untunable) temperatures, for probes characterized by highly degenerate multiple energy-levels with arbitrary spacings12.
For a sub-Ohmic bath spectrum with a low-frequency edge \({\omega }_{\min }\), the minimum error bound \(\xi (T={T}_{-1})\) per measurement (\({\mathcal{M}}=1\)) remains finite and approximately constant at (see Supplementary Note 4)
where \(\Delta \uparrow {\omega }_{0}\) signifies \(\Delta\) approaching \({\omega }_{0}\) from below. Condition (14) yields the maximum possible advantage offered by our control scheme close to the absolute zero (i.e., for \(T\approx {T}_{-1}\ll {\omega }_{0}\)), and is valid in the regime
An error bound \(\xi\), which does not diverge at low temperatures \(T\ll {\omega }_{0}\) (as in standard quantum thermometry), but instead stays constant as the temperature decreases in that range, is deemed to be highly advantageous, since it allows us to measure such low temperatures. We have thus obtained a remarkable result: the advantage offered by our control scheme, expressed by the bound Eq. (14) close to the absolute zero (i.e., for \(T\ll {\omega }_{0}\)), is maximal for a sub-Ohmic, nearly flat bath spectrum (NFBS) with small, but non-zero, lower edge, such that the bath interacts weakly with the DCQT at all non-zero frequencies. Regime (15) ensures that the dynamics is Markovian (see Methods).
Conditions (14), (15) allow us to achieve thermometry with a high-precision bound for very low temperatures; viz., only a finite number of measurements \({\mathcal{M}}\gg {e}^{4}/(4{\mu }^{2})\) ensures a relative error bound, which is constant, i.e., temperature-independent, and has the finite value \(\exp \left(2\right)/2\mu \sqrt{{\mathcal{M}}}\). For given small values of \({G}_{0}\) and \({\omega }_{\min }\), we then arrive at a minimum (limiting) temperature bound that is measurable with the error bound (14) per measurement:
In particular, for a sub-Ohmic NFBS (Eq. (5)) coupled very weakly with the thermometer at all frequencies such that \({G}_{0}\ll {\omega }_{\min }\to 0\), one has \({T}_{\mathrm{lim}}\to 0\), thus enabling us (at least under ideal circumstances, i.e., in absence of any other source of error) to accurately measure temperatures very close to the absolute zero.
The only penalty for a small \({G}_{0}\ll {\omega }_{\min }\) is long thermalization time. Yet, even if \({G}_{0}\) corresponds to divergent thermalization times (e.g., for \({G}_{0},{\omega }_{\min }\to 0\)), one can use optimal control to reach the steady-state at the minimal (quantum speed limit) time44: one can initially apply a strong brief pulse to take the thermometer to an optimal state, from which it takes the least time to thermalize, as detailed in ref. 45. Following this initial pulse, one can periodically modulate the system, as presented here. This behavior is in sharp contrast to that of an unmodulated thermometer, where \(\xi (T)\) diverges for \(T\to 0\), thus precluding any possibility of precise temperature estimation at very low temperatures17.
This novel effect of keeping \(\xi\) finite even in close proximity to the absolute zero is a direct consequence of our control scheme, and is unachievable without modulation for any non-zero \({\omega }_{0}\). Extension of the analysis to multipeak QFI is given in the Supplementary Note 6 (also see Fig. 4).
Relative error bound \(\xi\) and Quantum Fisher Information \({\mathcal{H}}\) (in inset) as a function of temperature \(T\) (in units of \({\omega }_{0}\)) in the absence of any modulation (turquoise dotted curve) and under multi-harmonic modulation \(\omega (t)={\omega }_{0}+\Delta \left({\mu }_{l}\sin \left(lt\Delta \right)+{\mu }_{{l}^{\prime}\ne l}\sin \left({l}^{\prime}t\Delta \right)\right)\) (magenta solid curve), for harmonic-oscillator dynamically controlled quantum thermometer probing a bath with nearly flat bath spectrum. Our control scheme reduces the lowest temperatures measurable with finite \(\xi\) by almost two orders of magnitude (arrow). Here, \(l=80,\,{l}^{\prime}=99,\,{\mu }_{80}=0.394,\,{\mu }_{99}=0.115,\,\,\Delta =0.01\), \({\omega }_{0}=1\), \({\omega }_{\min }\ll 0.01\) and \({\mathcal{M}}=1\).
As discussed above, optimal thermometry demands choosing a \(\Delta\) such that the QFI has a maximum at the temperature regime of interest, which is always possible for small enough \({\omega }_{\min }\) (cf. Eq. (16)). However, even for a bath spectrum with small but finite \({\omega }_{\min }\), one can perform low-temperature thermometry with a low-relative error bound in the regime \({G}_{0}\ll T \, < \, {\omega }_{\min }\) via suboptimal DCQT whose response is peaked at a temperature close to, but larger than \({\omega }_{\min }\). In this case the QFI, albeit not maximal, would be still significantly higher than that of the same thermometer in the absence of dynamical control. For example, in order to measure temperatures of the order \(T \sim 1{0}^{-3}{\omega }_{0}\), ideally one would need \({\omega }_{m} \sim 1{0}^{-3}{\omega }_{0}\). However, even a suboptimal modulation with \({\omega }_{m} \sim 1{0}^{-2}{\omega }_{0}\), which leads to QFI with a maximum at \(T \sim {\omega }_{m} \sim 1{0}^{-2}{\omega }_{0}\), results in \({\mathcal{H}}\approx 14.3\) at \(T=1{0}^{-3}{\omega }_{0}\) (see inset of Fig. 4). In contrast, \({\mathcal{H}}\) is vanishingly small (i.e., \({\mathcal{H}}\ll 1/{T}^{2}\) such that \(\xi \gg 1/\sqrt{{\mathcal{M}}}\); cf. Eq. (3)) for the same temperature regime in the absence of control, thus exhibiting the advantage of our DCQT even for suboptimal thermometry at \(T \,< \, {\omega }_{\min }\).
Thermometry of arbitrary bath spectra
The advantage offered by DCQT is not restricted to the specific bath spectra considered above. In fact, the key result of significant improvement in low-temperature thermometry by dynamical control holds for arbitrary bath spectra satisfying the Kubo–Martin–Schwinger condition (see Eq. (30) of Methods), as long as \(G(\omega \, > \, 0)\) is independent of temperature. Choosing a control scheme satisfying (see Eq. (11))
for a positive constant \(\kappa\) of the order of unity, leads to a QFI, which diverges quadratically with temperature:
The above result Eq. (18), which is valid for any bath spectra, arises due to \({\omega }_{-1}\) being vanishingly small (see Eq. (17)). The lowest temperature for which Eq. (18) is valid is given by the condition
As in the case of sub-Ohmic NFBS, condition (19) ensures that the thermalization time is long enough for the secular approximation to remain valid. This in turn results in a relative error bound
which is not explicitly dependent on the temperature, even for low temperatures \(T\ll {\omega }_{0}\) (see Fig. (3)). Although the relative error bound \(\xi\) is not explicitly dependent on temperature, the QFI and consequently \(\xi\) still depend on the details of the bath spectral function \(G(\omega )\) at \(\omega ={\omega }_{-1}\), which in turn is determined by the temperature through Eq. (17). The maximum QFI in this case is obtained by modulations satisfying the optimal condition
The above condition ensures that the sidebands \(m\ne -1\) are insignificant, so as to yield a small relative error bound at \(T \sim {\omega }_{-1}\) (see Supplementary Note 3).
Condition (21) shows that one needs to tailor the control scheme to the bath spectrum at hand. For example, in the case of a bath spectrum characterized by \(G({\omega }_{0})\gg G({\omega }_{-1})\), one needs to design a modulation with \({P}_{-1}\gg {P}_{0}\), in order for our control scheme to be beneficial for estimating temperatures \(T \sim {T}_{-1}\ll {\omega }_{0}\). This can be realized using a periodic \(\pi\)-pulse modulation, in which case \({P}_{\pm 1}\approx 4/{\pi }^{2}\) and \({P}_{m\ne \pm 1}\approx 0\)34.
Discussion
We have shown that by subjecting a generic quantum thermometer to an appropriate dynamical control, we may increase its maximum accuracy bound of measuring a chosen range of temperatures. The class of quantum thermometers considered here relies on the measurement of the energy-level populations \({\varrho }_{n}\) at the steady-state, as well as knowledge of the resonant frequency \({\omega }_{0}\) of the thermometer, the modulation parameters \(\mu\) and \(\Delta\) (cf. (6)) and (at least crudely) the bath spectral density \(G(\omega )\) (see Supplementary Note 1). It falls in the category of secondary thermometers. The advantage of the proposed DCQT becomes especially apparent at low temperatures, where, for generic bath spectra \(G(\omega )\), its accuracy bound of measuring the bath temperature, quantified by the QFI, is dramatically higher than that of its unmodulated counterpart. Namely, dynamical control allows us to perform low-temperature thermometry with temperature-independent relative error bound, at temperatures above the bound set by Eq. (16). Our proposed control scheme can be tailored according to the bath spectra at hand, in order to maximize the QFI, and determine the number of its peaks and sensitivity ranges, thus making it highly versatile.
In addition to our diagonal Hamiltonian \(\hat{H}(t)={\sum }_{n=0}^{{\mathcal{N}}}{\omega }_{n}(t)\left|n\right\rangle \left\langle n\right|\), off-diagonal interaction terms of the form \({\sum }_{n,m=0}^{{\mathcal{N}}}({h}_{n,m}\left|n\right\rangle \left\langle m\right|+h.c.)\) may incur non-adiabatic effects, which may cause spurious transitions between the energy levels, even in the absence of any external bath. In order to avoid such excitations one should require \(\omega (t)\gg {h}_{n,m}\) for all \(t,n,m\), thereby ensuring adiabaticity.
The dynamical control studied here has already been realized experimentally, in the context of probing the system-environment coupling spectrum46. One can utilize similar dynamical control to realize DCQT in different multilevel systems (see Supplementary Note 1): (i) a harmonic-oscillator DCQT can be implemented by the mode of a cavity of length \(l(t)\), whose frequency \(\omega (t)\propto 1/l(t)\) is modulated with the inverse of the cavity length47. (ii) A two-level DCQT can be implemented by a qubit whose level spacing is modulated by a time-dependent magnetic field, for example in nuclear magnetic resonance48 and nitrogen-vacancy (NV)-center49 experiments. Experimentally, one can probe the thermal steady-state \(\hat{\rho }(t\to \infty )\) of the DCQT at large times, after decoupling it from the bath, followed by ceasing the dynamical control (i.e., first setting \(\gamma =0\), and then \(\mu =0\)). In a harmonic-oscillator thermometer one can then estimate the temperature \(T\) through measurement of the mean number of quanta of the thermometer \({N}_{{\rm{avg}}}\), for example through motional sideband spectroscopy, which relies on the asymmetry between phonon absorption (proportional to \({N}_{{\rm{avg}}}\)) and phonon emission (proportional to \({N}_{{\rm{avg}}}+1\))50. In a two-level NV-center thermometer51,52, spin readout using photoluminescence may enable us to measure the N–V temperature.
The thermal energy-level population measurements \({\varrho }_{n}\) (see Eq. (9)), which constitute the optimal positive-operator valued measure for estimating temperature40, are characterized solely by the average number of quanta \({N}_{{\rm{avg}}}\). Consequently, measurement of \({N}_{{\rm{avg}}}\) gives us the complete knowledge of \(\hat{\rho }(t\to \infty )\), which in turn enables us to approach the minimum error bound \(\xi\) of bath-temperature estimation. However, while DCQT can dramatically reduce the error bound of temperature estimation (see Eqs. (19) and (20)), additional experimental errors may arise from the finite accuracy of measuring \(\Delta\), or the energy-level populations. These errors, which depend on the experimental apparatus, may prevent us from reaching the fundamental theoretical bound of Eq. (20) (see Supplementary Note 2).
DCQT can be highly advantageous for thermometry of diverse baths realized by many-body quantum systems in condensed matter and ultracold atomic gases, with spectra and modulations satisfying the optimal condition Eq. (21).
The temperatures measurable with low-relative error bound using our control scheme are presented in Table 1.
In a microwave cavity subjected to sinusoidal modulation with \({\omega }_{0}-\Delta \sim 1{0}^{x}\) Hz, DCQT results in QFI attaining a peak at temperatures of the order of \(1{0}^{x-12}\) K, \(x\) being real. We thereby open new avenues for the study of cavity quantum electrodynamics and quantum information processing4 at extremely low temperatures. The caveat noted above is that although the dynamical control can be expected to significantly reduce the error in low-temperature thermometry, however, experimental errors may preclude the attainment of theoretical bound of temperature resolution.
DCQT can be expected to be highly beneficial in baths exhibiting the widely studied \(1/{f}^{\alpha }\) (\(\alpha \ge 0\)) noise spectra43 in vacuum tubes53 or in thick film resistors54. This kind of spectra ensures that for a sinusoidal modulation with small \({\omega }_{-1}\), the most dominant contribution arises from the \(m=-1\) sideband, thus enabling us to probe low frequencies with high-precision bound.
An intriguing application of the proposed DCQT concerns experimentally studying the third law of thermodynamics for low-temperature many-body quantum systems, in the sense of understanding the scaling of the cooling rate with temperature55,56,57. In view of predictions that the cooling rate does not vanish as the absolute zero is approached for baths with anomalous dispersion, such as magnon (ferromagnetic) spin chains58, high-precision low-temperature thermometry is imperative.
In many-body quantum systems59,60,61,62,63, interactions may keep a system non-equilibrated for a long time after a quench37, during which time its different collective modes \(k\) may have their own temperatures \({T}_{k}\). High-precision multi-mode thermometry over a wide range of temperatures using our DCQT can verify whether different modes have different temperatures, and thus avoid thermalization.
The versatility of our DCQT can be well-suited for simultaneous multi-mode probing of a bath with high-accuracy bound, which can be especially useful for nanometer-scale thermometry in biological systems64,65.
The recently discussed need for thermometers with vanishing energy gaps for measuring low-temperatures in many-body quantum systems17 and in strongly coupled quantum systems18, suggests the importance of control schemes capable of tuning the gap of a quantum thermometer to our advantage. Application of our control scheme to thermometers modeled by many-body quantum systems, or to thermometers coupled strongly to the bath, in order to achieve high-precision low-temperature thermometry, is an interesting question, which we aim to address in the future.
The control scheme presented above may have diverse applications in quantum metrology beyond thermometry. For example, periodic modulation of energy levels in many-body quantum critical systems may be applicable to precise probing of inter-particle coupling strengths in these systems66.
Methods
Thermalization under periodic modulation
We consider a multi-mode DCQT system with its state \(\rho (t)\) given as a direct product of single-mode states \({\rho }_{k}\): \(\rho (t)={\otimes }_{k}{\rho }_{k}(t)\), interacting with a multi-mode bath, again described by the direct product state \({\rho }_{B}={\otimes }_{k}{\rho }_{{B}_{k}}\). Here, \({\rho }_{{B}_{k}}\) denotes the state of the \(k\)-th mode of the bath. For each \(k\), \({\rho }_{k}(t)\) evolves under the action of a periodic Hamiltonian, satisfying Eq. (1). The system is coupled to the bath mode through the interaction Hamiltonian
where each of the independent \(k\)-th mode baths has a spectrum wide enough to give rise to Markovian dynamics; for example, a finite-Q cavity mode, or a finite-lifetime phonon mode. In case the above assumption is violated, leading to non-Markovian dynamics26,37, the DCQT may be useful for revealing the absence of thermalization. Here, we allow for baths with mode-dependent temperatures \({T}_{k}\), which we aim to measure accurately using our DCQT.
We sketch below the derivation of the master equation describing the thermalization of a system under periodic control. We refer to refs. 34,35,36,37 for details of the derivation, and ref. 46 for experimental studies of open quantum system in presence of dynamical control. (For reviews on periodically driven open quantum systems, see refs. 36,67.)
The time evolution operator for the periodic Hamiltonian Eq. (1) is given by
\(\hat{{\mathcal{T}}}\) being the time ordering operator. According to the Floquet theorem, one can decompose the time evolution operator as \({\hat{U}}_{k}(t,0)={\hat{P}}_{k}(t){e}^{{\hat{R}}_{k}t}\), where \({\hat{P}}_{k}(t+\tau )={\hat{P}}_{k}(t)\) and \({\hat{R}}_{k}\) is a constant operator. Taking into account \({\hat{U}}_{k}(0,0)={\mathbb{1}}\), and the periodicity of \({\hat{P}}_{k}(t)\), one obtains \({\hat{P}}_{k}(0)={\mathbb{1}}\) and hence \({\hat{U}}_{k}(\tau ,0)={\hat{P}}_{k}(\tau ){e}^{{\hat{R}}_{k}\tau }=\hat{P}(0){e}^{{\hat{R}}_{k}\tau }={e}^{{\hat{R}}_{k}\tau }\). One can now identify the operator \({\hat{R}}_{k}\) with an effective Hamiltonian \({\hat{H}}_{k,{\rm{eff}}}\) averaged over a period of \({\hat{H}}_{k}(t)\), as
with eigen energies \({\Omega }_{k,r}\) and eigen states \(\left|{r}_{k}\right\rangle\), through the relation
The Fourier components \({\hat{S}}_{{\omega }_{k},m}\) of the system operator \({\hat{S}}_{k}(t)\) (cf. Eq. (22)) in the interaction picture with respect to the evolution (23), are given as
where \(\Delta =2\pi /\tau\), \(m\) are integers, and \(\{{\omega }_{k}\}\) is defined as the set of all transition frequencies \({\Omega }_{k,{r}^{^{\prime} }}-{\Omega }_{k,r}\) between the levels of \({\hat{H}}_{k,{\rm{eff}}}\) and the operators \({\hat{S}}_{{\omega }_{k},m}\) are the \(m\)th-harmonic transition operators associated with these levels36.
Next, we focus only on the dynamics of the \(k\)-th mode of the thermometer and the bath. Under the standard Born–Markov approximation in the weak thermometer-bath coupling limit, we arrive at the master equation37
where \({{\rm{Tr}}}_{{B}_{k}}\) denotes trace over the bath mode \(k\), and \({\hat{H}}_{Ik}(t)\) is the \(k\)-th mode interaction Hamiltonian in the interaction picture.
We now assume that the thermalization time of the thermometer induced by the bath is much longer than \(\tau\) or \({\omega }_{k,m}^{-1}\equiv {\left({\omega }_{k}+m\Delta \right)}^{-1}\). Consistently, we adopt the secular approximation (SA) to average out the rapidly oscillating terms of the form \(\exp [\pm i({\omega }_{k,m}-{\omega }_{{k}^{\prime},{m}^{\prime}})t]\) at times \(t\gg \tau ,{\omega }_{k,m}^{-1}\), such that only the terms with \(k={k}^{\prime}, \, m={m}^{\prime}\) survive68. We then finally arrive at the master equation34,35,36,37, which is a weighted sum of Lindbladian superoperators, each valid for system-bath coupling centered at \({\omega }_{k,m}:={\omega }_{k}+m\Delta\):
Here,
and
where \({\hat{B}}_{k}(t)={e}^{i{\hat{H}}_{B}t}{\hat{B}}_{k}{e}^{-i{\hat{H}}_{B}t}\), \({\hat{H}}_{B}\) being the bath Hamiltonian, represents the bath spectral-response or auto-correlation function sampled at the frequency harmonics \(\pm \left({\omega }_{k}+m\Delta \right)\). The Kubo–Martin–Schwinger condition must be imposed, i.e.,
Eqs. (29), (30) imply that, within the approximations assumed above, \({\rho }_{k}\) equilibrates to a thermal (Gibbs) state at temperature \({T}_{k}\). The level populations are determined by the weighted bath response at the resonance frequencies \({\omega }_{k}\) shifted by Floquet harmonics of modulation, \({\omega }_{k,m}={\omega }_{k}+m\Delta\).
Data availability
All relevant data are available to any reader upon reasonable request.
Code availability
All relevant codes are available to any reader upon reasonable request.
References
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222 (2011).
Braun, D. et al. Quantum-enhanced measurements without entanglement. Rev. Mod. Phys. 90, 035006 (2018).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proc. Natl Acad. Sci. 112, 3866–3873 (2015).
Hauke, P., Heyl, M., Tagliacozzo, L. & Zoller, P. Measuring multipartite entanglement through dynamic susceptibilities. Nat. Phys. 12, 778 (2016).
Strobel, H. et al. Fisher information and entanglement of non-gaussian spin states. Science 345, 424 (2014).
Paris, M. G. A. et al. Quantum estimation for quantum technology. Int. J. Quant. Inf. 07, 125–137 (2009).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).
Correa, L. A., Mehboudi, M., Adesso, G. & Sanpera, A. Individual quantum probes for optimal thermometry. Phys. Rev. Lett. 114, 220405 (2015).
Zwick, A., Álvarez, G. A. & Kurizki, G. Maximizing information on the environment by dynamically controlled qubit probes. Phys. Rev. Appl. 5, 014007 (2016).
Pasquale, A. D., Rossini, D., Fazio, R. & Giovannetti, V. Local quantum thermal susceptibility. Nat. Comm. 7, 12782 (2016).
Gefen, T., Jelezko, F. & Retzker, A. Control methods for improved fisher information with quantum sensing. Phys. Rev. A 96, 032310 (2017).
Campbell, S., Genoni, M. G. & Deffner, S. Precision thermometry and the quantum speed limit. Quant. Sci. Technol. 3, 025002 (2018).
Zwick, A., Álvarez, G. A. & Kurizki, G. Criticality of environmental information obtainable by dynamically controlled quantum probes. Phys. Rev. A 94, 042122 (2016).
Correa, L. A. et al. Enhancement of low-temperature thermometry by strong coupling. Phys. Rev. A 96, 062103 (2017).
Hofer, P. P., Brask, J. B., Perarnau-Llobet, M. & Brunner, N. Quantum thermal machine as a thermometer. Phys. Rev. Lett. 119, 090603 (2017).
Brunelli, M., Olivares, S., Paternostro, M. & Paris, M. G. A. Qubit-assisted thermometry of a quantum harmonic oscillator. Phys. Rev. A 86, 012125 (2012).
Potts, P. P., Brask, J. B. & Brunner, N. Fundamental limits on low-temperature quantum thermometry with finite resolution. Quantum 3, 161 (2019).
Hovhannisyan, K. V. & Correa, L. A. Measuring the temperature of cold many-body quantum systems. Phys. Rev. B 98, 045101 (2018).
Kiilerich, A. H., De Pasquale, A. & Giovannetti, V. Dynamical approach to ancilla-assisted quantum thermometry. Phys. Rev. A 98, 042124 (2018).
Tuoriniemi, J. Physics at its coolest. Nat. Phys. 12, 11 (2016).
Mehboudi, M., Sanpera, A. & Correa, L. A. Thermometry in the quantum regime: recent theoretical progress. J Phys. A 52, 303001 (2019).
Pasquale De, A. & Stace, T. M. “Quantum Thermometry”, in Thermodynamics in the Quantum Regime: Fundamental As-pects and New Directions, edited by F. Binder, L. A. Correa, C. Gogolin, J. Anders, and G. Adesso (Springer International Publishing, Cham, 2018) pp. 503–527.
Agarwal, G. S. Control of decoherence and relaxation by frequency modulation of a heat bath. Phys. Rev. A 61, 013809 (1999).
Agarwal, G. S., Scully, M. & Walther, H. Accelerating decay by multiple 2\(\pi\) pulses. Phys. Rev. A 63, 044101 (2001).
Shiokawa, K. & Lidar, D. A. Dynamical decoupling using slow pulses: efficient suppression of \(1/f\) noise. Phys. Rev. A 69, 030302 (2004).
Zwick, A., Álvarez, G. A., Bensky, G. & Kurizki, G. Optimized dynamical control of state transfer through noisy spin chains. New J. Phys. 16, 065021 (2014).
Suter, D. & Álvarez, G. A. Colloquium. Rev. Mod. Phys. 88, 041001 (2016).
Meschke, M., Engert, J., Heyer, D. & Pekola, J. P. Comparison of coulomb blockade thermometers with the international temperature scale plts-2000. Int. J. Thermophys. 32, 1378 (2011).
Räisänen, I. M. W., Geng, Z., Kinnunen, K. M. & Maasilta, I. J. Normal metal-insulator-superconductor thermometers and coolers with titanium-gold bilayer as the normal metal. J. Phys.: Conf. Ser. 969, 012090 (2018).
Giazotto, F. et al. Ultrasensitive proximity josephson sensor with kinetic inductance readout. Appl. Phys. Lett. 92, 162507 (2008).
Giazotto, F., Solinas, P., Braggio, A. & Bergeret, F. S. Ferromagnetic-insulator-based superconducting junctions as sensitive electron thermometers. Phys. Rev. Appl. 4, 044016 (2015).
Ghosh, A., Sinha, S. S. & Ray, D. S. Langevin-bloch equations for a spin bath. J. Chem. Phys. 134, 094114 (2011).
Ghosh, A., Sinha, S. S. & Ray, D. S. Canonical formulation of quantum dissipation and noise in a generalized spin bath. Phys. Rev. E 86, 011122 (2012).
Gelbwaser-Klimovsky, D., Alicki, R. & Kurizki, G. Minimal universal quantum heat machine. Phys. Rev. E 87, 012140 (2013).
Alicki, R. Quantum thermodynamics. an example of two-level quantum machine. Open Syst. Inf. Dyn. 21, 1440002 (2014).
Gelbwaser-Klimovsky, D., Niedenzu, W. & Kurizki, G. in Advances In Atomic, Molecular, and Optical Physics. Science Direct. Vol. 64, 329–407 (2015).
Breuer, H.P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford Universi Press, 2002).
Yan, F. et al. Distinguishing coherent and thermal photon noise in a circuit quantum electrodynamical system. Phys. Rev. Lett. 120, 260504 (2018).
Raymer, M. G. & Beck, M. in Quantum State Estimation. 235–295 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2004). .
Brunelli, M., Olivares, S. & Paris, M. G. A. Qubit thermometry for micromechanical resonators. Phys. Rev. A 84, 032105 (2011).
Pezzé, L. & Smerzi, A. Entanglement, nonlinear dynamics, and the heisenberg limit. Phys. Rev. Lett. 102, 100401 (2009).
Kacprowicz, M., Demkowicz-Dobrzanski, R., Wasilewski, W., Banaszek, K. & Walmsley, I. A. Experimental quantum-enhanced estimation of a lossy phase shift. Nat. Photonics 4, 357 (2010).
Milotti, E. \(1/f\) noise: a pedagogical review. arXiv:physics/0204033 (2002).
Lapert, M., Zhang, Y., Braun, M., Glaser, S. J. & Sugny, D. Singular extremals for the time-optimal control of dissipative spin \(\frac{1}{2}\) particles. Phys. Rev. Lett. 104, 083001 (2010).
Mukherjee, V. et al. Speeding up and slowing down the relaxation of a qubit by optimal control. Phys. Rev. A 88, 062326 (2013).
Almog, I. et al. Direct measurement of the system-environment coupling as a tool for understanding decoherence and dynamical decoupling. J. Phys. B 44, 154006 (2011).
Macrì, V. Nonperturbative dynamical casimir effect in optomechanical systems: vacuum casimir-rabi splittings. Phys. Rev. X 8, 011031 (2018).
Prigl, R., Haeberlen, U., Jungmann, K., zu Putlitz, G. & von Walter, P. A high precision magnetometer based on pulsed NMR. Nucl. Instrum. Methods Phys. Res. Sec. A 374, 118–126 (1996).
Casola, F., van der Sar, T. & Yakoby, A. Probing condensed matter physics with magnetometry based on nitrogen-vacancy centres in diamond. Nat. Rev. Mater. 3, 17088 (2018).
Safavi-Naeini, A. H. et al. Observation of quantum motion of a nanomechanical resonator. Phys. Rev. Lett. 108, 033602 (2012).
Hopper, D. A., Shulevitz, H. J. & Bassett, L. C. Spin readout techniques of the nitrogen-vacancy center in diamond. Micromachines 9, 437 (2018).
Tran, T.T. et al. Anti-stokes excitation of solid-state quantum emitters for nanoscale thermometry. arXiv:1810.05265 (2018).
Johnson, J. B. The schottky effect in low frequency circuits. Phys. Rev. 26, 71–85 (1925).
Pellegrini, B., Saletti, R., Terreni, P. & Prudenziati, M. \(\frac{1}{{f}^{\gamma }}\) noise in thick-film resistors as an effect of tunnel and thermally activated emissions, from measures versus frequency and temperature. Phys. Rev. B 27, 1233–1243 (1983).
Masanes, L. & Oppenheim, J. A general derivation and quantification of the third law of thermodynamics. Nat. Commun. 8, 14538 (2017).
Freitas, N. & Paz, J. P. Fundamental limits for cooling of linear quantum refrigerators. Phys. Rev. E 95, 012146 (2017).
Cleuren, B., Rutten, B. & Van den Broeck, C. Cooling by heating: refrigeration powered by photons. Phys. Rev. Lett. 108, 120603 (2012).
Kolář, M., Gelbwaser-Klimovsky, D., Alicki, R. & Kurizki, G. Quantum bath refrigeration towards absolute zero: challenging the unattainability principle. Phys. Rev. Lett. 109, 090601 (2012).
Rigol, M., Dunjko, V. & Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 452, 854 (2008).
Eisert, J., Friesdorf, M. & Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phy. 11, 124 (2015).
Calabrese, P., Essler, F. H. L. & Fagotti, M. Quantum quench in the transverse-field ising chain. Phys. Rev. Lett. 106, 227203 (2011).
Álvarez, G. A., Suter, D. & Kaiser, R. Localization-delocalization transition in the dynamics of dipolar-coupled nuclear spins. Science 349, 846–848 (2015).
Kaufman, A. M. et al. Quantum thermalization through entanglement in an isolated many-body system. Science 353, 794–800 (2016).
Kucsko, G. et al. Nanometre-scale thermometry in a living cell. Nature 500, 54 (2013).
Baffou, G., Rigneault, H., Marguet, D. & Jullien, L. A critique of methods for temperature imaging in single cells. Nat. Methods 9, 899 (2014).
Zanardi, P., Paris, M. G. A. & Campos Venuti, L. Quantum criticality as a resource for quantum estimation. Phys. Rev. A 78, 042105 (2008).
Kosloff, R. Quantum thermodynamics: a dynamical viewpoint. Entropy 15, 2100–2128 (2013).
Mukherjee, V., Niedenzu, W., Kofman, A. G. & Kurizki, G. Speed and efficiency limits of multilevel incoherent heat engines. Phys. Rev. E 94, 062109 (2016).
Acknowledgements
We acknowledge Wolfgang Niedenzu for helpful discussions. The support of DFG (FOR 7024), EU-FET Open (PATHOS) project, ISF, VATAT, NSFC (11474193), CONICET, CNEA, Shuguang (14SG35), STCSM (18010500400 and 18ZR1415500), the Program for Eastern Scholar and the Ramóny Cajal program (RYC-2017-22482) of the Spanish MINECO, Initiation Grant (2018513) and SRG/2019000289 are acknowledged.
Author information
Authors and Affiliations
Contributions
V.M. and G.K. conceived the idea. V.M. and A.Z. performed the analytical calculations and numerical simulations. V.M., A.Z., A.G., X.C., and G.K. were involved in the interpretation of the results and in the discussions during the writing of the manuscript. V.M. and G.K. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mukherjee, V., Zwick, A., Ghosh, A. et al. Enhanced precision bound of low-temperature quantum thermometry via dynamical control. Commun Phys 2, 162 (2019). https://doi.org/10.1038/s42005-019-0265-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0265-y
This article is cited by
-
Introduction to quantum thermodynamic cycles
Journal of Chemical Sciences (2023)
-
Optimal probes for global quantum thermometry
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.