Abstract
Unconventional superconductivity in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) has been intensively studied for decades. However, the nature of pairing continues to be widely debated. Here we develop a detailed ab initio theory, coupling quasiparticle self-consistent GW approximation with dynamical mean field theory (DMFT), including both local and non-local correlations to address the subtle interplay among spin, charge and orbital degrees of freedom. We report that the superconducting instability has multiple triplet and singlet components. In the unstrained case the triplet eigenvalues are larger than the singlets. Under uniaxial strain, the triplet eigenvalues drop and the singlet components increase. This is concomitant with our observation of spin and charge fluctuations shifting closer to wave-vectors favoring singlet pairing. We identify a complex mechanism where charge fluctuations and spin fluctuations co-operate in the even-parity channel under strain leading to increment in critical temperature (Tc), thus proposing a novel mechanism for pushing the frontier of critical temperature (Tc) in unconventional ‘triplet’ superconductors.
Similar content being viewed by others
Introduction
The origin of superconducting pairing in unconventional superconductor \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) (SRO) has been one of the most debated topics1 in materials research over past two decades. The superconductivity in SRO has signatures supporting a spin-triplet origin, which raises the possibility that it can sustain Majorana states conducive for topological quantum computing2, making it an active field of research and a case to study with advanced theoretical and experimental methods. A series of recent experimental findings, including strain-dependent enhancement in \({{{T}}}_{\mathrm{c}}\)3 and the pronounced drop in \({{\rm{O}}}^{17}\) NMR4 measurements, have challenged the existing beliefs and demands a fresh look into the enigmatic problem of superconductivity in SRO.
SRO single crystals were first shown to exhibit superconductivity below 1.5 K in 19945. Within few years of its discovery, it was established that the superconductivity is highly sensitive to disorder6. Ever since efforts have been made to understand the mechanism of pairing and drive the \({{{T}}}_{\mathrm{c}}\) higher. The superconducting transition temperature, \({{{T}}}_{\mathrm{c}}\), has been observed to increase to 3 K in eutectic crystals of SRO, in the vicinity of Ru inclusions7,8,9. While enhancement of \({T}_{\mathrm{c}}\) was traditionally associated with a reduced volume fraction, a recent series of experiments3,10 on bulk single crystals of SRO subject to uniaxial strain show an increase to 3.4 K for compressive strain in the [1 0 0] direction, which we denote as \({\epsilon }_{x}\). These apparently dissimilar studies hint towards a more common underlying mechanism for enhancement of \({T}_{\mathrm{c}}\), since Ru inclusions induce local stresses, which include uniaxial strain. In the tensile experiments, \({T}_{\mathrm{c}}\) can be controlled by varying \({\epsilon }_{x}\). It reaches a maximum value at \({\epsilon }_{x}\) = 0.6%3, beyond which it falls rapidly. In what follows we will denote \({\epsilon }_{x}\) = 0.6% as \({\epsilon }_{x}^{* }\).
These observations challenge the established belief that SRO is a spin-triplet (odd-parity) superconductor. Under strain, the tetragonal symmetry of the compound is lost, and it is no longer possible to find a triplet order parameter from two degenerate components, such as the usual \({p}_{x}+i{p}_{y}\) or \({d}_{xz}+i{d}_{yz}\). This raises the possibility for alternative mechanisms that could be responsible for pairing under strain.
The effect of strain on the Fermi surface has been studied with density functional theory (DFT)3, and complementary minimal model Hamiltonian approaches11,12, which identified a change in Fermi surface topology. In particular, a Van Hove singularity3 approaches the Fermi level, with a concomitant increase in charge carriers, which has been suggested as a possible mechanism for the increment in \({T}_{\mathrm{c}}\)13 under strain. Such a picture identifies an important property resulting from strain, but it is not sufficient to explain the enhancement of \({T}_{\mathrm{c}}\). In particular, the multi-orbital nature of the spin and charge fluctuations and many-body correlations are shown to be important in SRO14,15,16,17. Novel electron correlations originating from competition between non-local Coulomb repulsion and the large Hund’s coupling14,18,19 are also significant.
It is a formidable challenge to adequately describe the single- and two-particle responses needed for insights into the origin and nature of superconductivity in SRO. As we show here, an accurate theoretical formulation, which includes both local and non-local correlation effects in space, momentum, and time, and for all relevant degrees of freedom, is essential. Recently, a significant advance has been achieved by combining the quasi-particle self-consistent GW (QSGW) approximation, with dynamical mean field theory (DMFT)20,21. Merging these two state-of-the-art methods captures the effect of both strong local dynamic spin fluctuations (captured well in DMFT), and non-local dynamic correlation22 effects (captured by QSGW), relying on neither model hamiltonians nor on DFT, and avoiding the concomitant limitations they each carry. Also, non-local spin, charge, and pairing susceptibilities can also be obtained from vertices computed from the local two-particle Green’s sampled by DMFT and bubble diagrams, via the solutions of Bethe–Salpeter equations (BSEs) in respective channels. The full numerical implementation is discussed in Pashov et al.23 and codes are available on the open source electron structure suite Questaal24. Our GW implementation is adapted from the original ecalj package25.
Here we apply this methodology to SRO, studying the pristine compound and also the effect of strain. Through the vertices and susceptibilities, we can identify what drives superconductivity, and also what causes the non-monotonic dependence of \({T}_{\mathrm{c}}\) on strain. The pairing instability has multiple singlet and triplet components; nodal structure in the singlet channel and nodeless odd-frequency structure in the triplet channel. We find that the pairing is favored by even-parity couplings in both spin and charge channels as \({\epsilon }_{x}\) approaches \({\epsilon }_{x}^{* }\) from below, while for \({\epsilon }_{x}\ > \ {\epsilon }_{x}^{* }\) incoherent spin fluctuations suppress the superconducting order. Our observations are in remarkable agreement with recent neutron scattering experiments26.
Results
Evolution of Fermi surface topology under strain
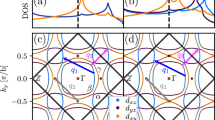
Fermi surfaces in the basal plane are shown in Fig. 1. The critical change in topology on the line connecting (0, 0) and (0, \(\pi\)) (points \(\Gamma\) and M) occurs at \({\epsilon }_{x}\) = 0.6%, in excellent agreement with \({\epsilon }_{x}^{* }\). This is the strain where one Van Hove singularity crosses \({E}_{\mathrm{F}}\) (see Supplementary Fig. 1 and Note 1), as was noted in a prior DFT study, although in DFT it does so at a much larger \({\epsilon }_{x}\) (see Fig. 1). The Fermi surface generated by QSGW closely matches recent high-resolution bulk Fermi surface observed in quantum oscillation studies28, angle-resolved photoemission spectroscopy (ARPES)27,29; indeed, they can only be easily distinguished at higher resolution (as shown in Supplementary Fig. 1). That QSGW simultaneously yields the topology change close to the observed \({\epsilon }_{x}^{* }\), and can reproduce fine details of the ARPES Fermi surface, is a reflection of its superior ability to generate good effective noninteracting Hamiltonians. We also note that the relative orientation (center of mass) of different Ru-d and O-p orbitals changes beyond the critical strain (see Supplementary Fig. 2 and Note 2). By analyzing the real part of the QSGW self-energy, we observe that the momentum-resolved quasi-particle weights evolve differently for bands with primarily \({{{d}}}_{xy}\) and \({{{d}}}_{xz,yz}\) orbital characters under strain (see Supplementary Fig. 3 and Note 3).
The quasi-particle self-consistent (QSGW) Fermi surfaces in the basal plane are shown in a–d, for a [1 0 0] compressive strain with \({\epsilon }_{x}\) = (0%, 0.3%, 0.6%, and 0.9%) respectively. Spin–orbit coupling is included (its omission makes a modest change to the Fermi surfaces). In a high-resolution angle-resolved photoemission spectroscopy (APRES) data27 (figure is replotted using the raw angle-resolved photoemission spectroscopy (APRES) data) for the Fermi surfaces are shown (figure reproduced with due permission) in the background of our QSGW theoretical data. For a higher-resolution comparison please see the Supplementary Fig. 1. States derive almost exclusively of Ru \({t}_{2g}\) orbitals \(xy\), \(xz\), and \(yz\); the orbital character of each pocket changes moving around the contour. \(xy\) character is present on the entire Fermi surface: it resides on the blue pocket on the \(\Gamma\)-X line, and on the green on the \(\Gamma\)-M line. Under strain, the four M points lose the 4-fold rotational symmetry, and at \({\epsilon }_{x}={\epsilon }_{x}^{* }\) the topology of the green band changes. e–h show corresponding results for density functional theory. In density functional theory, the transition also occurs, but near \({\epsilon }_{x}\) = 1.8% as shown in h, instead of \({\epsilon }_{x}^{* }\).
Spin fluctuations: incommensurability and coherence
Spin (\({\chi }^{\mathrm{m}}\)) and charge (\({\chi }^{\mathrm{d}}\)) susceptibilities are computed from momentum-dependent BSEs (eq. 1) in magnetic (spin) and density (charge) channels.
\({\chi }^{0}\) is the non-local (\(k\)-dependent) polarization bubble computed from single-particle QSGW Green’s functions dressed by DMFT and \(\Gamma\) is the local irreducible two-particle vertex functions computed in magnetic and density channels. \(\Gamma\) is a function of two fermionic frequencies \(\nu\) and \(\nu ^{\prime}\) and the bosonic frequency \(\omega\). The susceptibilities \({\chi }^{m(d)}({\bf{q}},i\omega )\) are computed by closing \({\chi }_{{{{\alpha }_{1},{\alpha }_{2}}\atop{{\alpha }_{1},{\alpha }_{2}}}}^{m(d)}{(i\nu ,i{\nu }^{\prime})}_{{\bf{q}},i\omega }\) with spin or charge bare vertex \(\gamma\) (\(\gamma\) = 1/2 for spin and \(\gamma\) = 1 for charge) and summing over frequencies (\(i\nu\), \(i{\nu }^{\prime}\)) and orbitals (\({\alpha }_{1,2}\)) (see Supplementary Fig. 4 and Note 4 for Feynman diagram representation and derivations).
We focus first on the \(\Gamma\)-X line of the Brillouin zone, where peaks appear in inelastic neutron scattering measurements30,31,32 at the incommensurate vector \({q}^{{\rm{IC}}}=(0.3,0.3,0)\) (in units \(2\pi /a\)), which a maximum in frequency near \(\omega\) = 10 meV. Using DMFT, we compute \({\chi }^{m}({\bf{q}},\omega )\) by obtaining the local two-particle vertex in the spin channel and solving the BSE33, for varying amounts of strain. Consider first the unstrained case, where measurements are available. Figure 2 shows \({\chi }^{m}(q,\omega )\) on the \(\Gamma\)-X line and in planes \({q}_{z}\) = 0, 1/4, and 1/2 (in units of \(2\pi /c\)). The peak noted above \([{q}^{{\rm{IC}}}=(0.3,0.3,0),\,\omega =10\ {\rm{meV}}]\) is nearly independent of \({q}_{z}\), and moreover it disperses all the way up to 80 meV. All of these findings are in excellent agreement with experimental observations34. We also found significant spin fluctuations at the ferromagnetic (FM) vector \(q=(0,0,0)\) (also seen in very recent neutron measurements26) and almost no intensity at the anti-FM nesting vector (1/2,1/2,0). The FM signal is important, because of its implications for superconductivity26 and whether the pairing is of triplet or singlet character. We find that the intensity of \({\chi }^{m}(q=0)\) is ~1/5 of the dominant IC peak when spin–orbit coupling (SOC) is suppressed. SOC lifts band degeneracies at high symmetry points and reduces this ratio slightly, to ~1/7. Thus, \({\chi }^{m}\) seems to be dominated by fluctuations at \({q}^{{\rm{IC}}}\). Such spin fluctuations should favor pairing mainly in the spin singlet channel, which is absent in other channels to provide extra glue for a triplet pairing. However, the continuum of spin excitations elsewhere in the Brillouin zone also contribute to the glue.
Imaginary part of the dynamic spin susceptibility \({\chi }^{m}(q,\omega )\) are shown in the Cartesian xy plane at different values \({q}_{z}\), and for different strains \({\epsilon }_{x}\). The unstrained compound shows a spin fluctuation spectrum strongly peaked at \((0.3,0.3,{q}_{z})\) (units \(2\pi /a\)). At \({\epsilon }_{x}\) = 0, \({\chi }^{m}\) is nearly independent of \({q}_{z}\), a, d, g, but it begins to depend on \({q}_{z}\) for \({\epsilon }_{x}> 0\). With increasing strain, fluctuations become more coherent and strongly peaked, reaching a zenith at \({\epsilon }_{x}={\epsilon }_{x}^{* }\) (0.6%), where critical temperature (Tc) is maximum. b, e, h For \({\epsilon }_{x} \, \, > \, \, {\epsilon }_{x}^{* }\), this peak becomes more diffuse; c, f, i show a secondary incoherent peak emerges at \((0.15,0.15,{q}_{z})\), and the quasi-anti-ferromagnetic vector \((1/2,1/2,a/2c)\) acquires spectral weight around \(\omega =40\) meV (c). Note also the spectral weight near the ferromagnetic (FM) vector (0,0,0), and its evolution with \({\epsilon }_{x}\).
As strain is applied \({\rm{Im}}{\chi }^{m}(q,\omega )\) becomes sharper and more coherent, reaching a maximum coherence at \({\epsilon }_{x}={\epsilon }_{x}^{* }\): the peak intensity remains at \({q}^{{\rm{IC}}}\), but nearly doubles in strength and shifts to slightly smaller \(\omega\). Also, \({\rm{Im}}{\chi }^{m}\) loses its two-dimensional character: the \({q}_{z}\) dependence is significant and the dominant peak is most intense at 1/4. For still larger \({\epsilon }_{x}\), coherence begins to be lost. At \({\epsilon }_{x}=1.2\)%, the IC peak \((0.3,0.3,{q}_{z})\) survives, but \({\chi }^{m}\) becomes incoherent and diffused over a range of \(q\) both in the plane and out of it, with another peak appearing near \((0.15,0.15,0)\). In short, for \({\epsilon }_{x} \, > \, {\epsilon }_{x}^{* }\), two prominent changes are observed: incommensurate but nearly FM excitations at \((0.15,0.15,0)\) and commensurate gapped anti-FM spin excitations at \((1/2,1/2,a/2c)\).
Charge susceptibilities and commensurability
The evolution of the spin and charge susceptibilities are instructive to understand the changes in the gap symmetries under strain and their underlying even- or odd-parity characters. We found that the real part of the charge susceptibilities in the static limit, \({\chi }^{d}(q,\omega \to 0)\), has strong peaks at ~(0.2,0.2,0), in the vicinity of the FM vector, and also near the anti-FM vector (1/2,1/2,0) (Fig. 3). Raghu et al.35 discuss a possible route to superconductivity through charge fluctuations originating from the quasi one-dimensional bands \({d}_{xz}\) and \({d}_{yz}\). Their analysis relies on the quasi one-dimensional character of these states. Our ab initio calculation partially supports this picture. However, we also observe nearly comparable multi-orbital charge fluctuations, both intra- and inter-orbital in nature, in all active bands (Fig. 3). Inter-orbital charge fluctuations originating from \({d}_{xz}\) and \({d}_{yz}\) and the two-dimensional \({d}_{xy}\) are comparable to, or even larger than the intra-orbital contributions.
Real part of the static charge susceptibility \({\chi }^{d}(q,\omega =0)\), shown along the Cartesian (000) to (110) direction, and for different strains \({\epsilon }_{x}\). The unstrained compound shows three-peaked charge fluctuation, with sharp peaks at incommensurate (IC) vector (0.2, 0.2, 0) (and by symmetry at (0.8, 0.8, 0)) and a broad peak at (0.5, 0.5, 0). With strain, the structure becomes sharply single peaked at commensurate (0.5, 0.5, 0). The peak at the commensurate vector develops at the cost of the charge fluctuation weights from the incommensurate (IC) vectors. The systematic evolution from large wavelength triplet to shorter wavelength singlet fluctuations, under strain, is common to all inter- (a, d) and intra-orbital (b, c) charge fluctuations. b, c show that strong, often the most dominant, inter-orbital charge fluctuations can be observed in Ru-\({{d}}_{xy-xz}\) and Ru-\({{d}}_{xy,yz}\) channels.
In the unstrained case, nearly uniform long-wavelength coherent charge fluctuations support a triplet pairing channel mainly through multi-orbital charge fluctuations. There is a significant peak in \({\chi }^{d}\) at small \(q\), near (0.2,0.2,0). However, there is another broad peak near (1/2,1/2,0). Under strain, the latter peak becomes more coherent and larger, while the former decays, and at the critical strain, \({\epsilon }_{x}^{* }\), only the latter peak remains. Also, \({\chi }^{m}\) and \({\chi }^{d}\) become increasingly coherent close to a vector that favors singlet pairing. This is strikingly different from the unstrained scenario where both spin and charge fluctuations have favorable triplet components as well. For \({\epsilon }_{x} \, \, > \, \, {\epsilon }_{x}^{* }\), \({\chi }^{d}\) at (1/2,1/2,0) becomes large. Simultaneous shifts in spin fluctuation weight towards more commensurate lower \(q\) (larger wavelength) leaves \({\chi }^{m}({q}^{{\rm{IC}}})\) incoherent, which in turn weakens the ability to form Cooper pairs.
Superconducting pairing: nodal character and dimensionality
The superconducting pairing susceptibility \({\chi }^{{p-p}}\) is computed by dressing the non-local pairing polarization bubble \({\chi }^{0,{{p-p}}}({\bf{k}},i\nu )\) with the pairing vertex \({\Gamma }^{{irr,p-p}}\) using the BSE in the particle–particle channel (see Supplementary Fig. 5 for Feynman diagram representation).
\({\Gamma }^{{irr,p-p}}\) in the singlet (s) and triplet (t) channels are obtained from the magnetic (spin) and density (charge) particle–hole reducible vertices by
Finally, \({\chi }^{{p-p}}\) can be represented in terms of eigenvalues \(\lambda\) and eigenfunctions \({\phi }^{\lambda }\) of the Hermitian particle–particle pairing matrix (see the SM for detailed derivation).
The pairing susceptibility diverges when the leading eigenvalue approaches unity. The corresponding eigenfunction represents the momentum structure of \({\chi }^{{p-p}}\). However, unlike hole-doped cuprates or doped single-band Hubbard model36, the unconventional superconductivity in SRO is multi-orbital in nature with a close-packed eigenvalue spectrum, which warrants more detailed investigation of the different eigenfunctions.
As is apparent from Eqs. 4, 5, at what wave vector spin and charge fluctuations are strong is of central importance to the kind of superconducting pairing symmetry they can form. If superconductivity is driven by fluctuations near the FM point (0,0,0), the spin part of the Cooper pair is symmetric and the superconductivity should have triplet symmetry. If, on the other hand, the fluctuations (spin or charge) are more proximate to \((1/2,1/2,{q}_{z})\), the symmetry is more likely to be singlet.
Before presenting QSGW + DMFT + BSE results for the pairing susceptibility, we summarize a few key findings in the past year which have dramatically altered (and obfuscated) the consensus for origins of superconductivity in SRO. New experiments have sown considerable doubt that the gap function \(\Delta\) is a chiral \(p\) wave. Much of the basis for the long held consensus that SRO is a spin-triplet superconductor, with chiral order parameter \({p}_{x}\pm i{p}_{y}\), was derived from observation that the Knight shift did not change through the superconducting transition37. Kerr effect38 and muon spin rotation39 measurements also provide evidence for broken TRS. Recently, however4, it was found that the Knight shift does change through \({T}_{\mathrm{c}}\) (the original measurement was an artifact of sample heating). Also, recent measurements of thermal conductivity present evidence for vertical line nodes in \(\Delta\)40, making a case for the \({H}_{c2}\) anomaly in SRO. Such nodes preclude the possibility of a \(p\) wave order parameter, at least one driven by symmetry. In a recent specific heat study, under angular variation of magnetic field at very low temperatures, Kittaka et al.41 found horizontal line nodes in the gap structure.
Singlet channel
QSGW+DMFT+BSE calculations yield three dominant eigenvalues in the superconducting gap instabilities. For \({\epsilon }_{x}=0\) we find that all eigenvalues are degenerate within numerical precision. The corresponding eigenfunctions are shown in Fig. 4. They all change sign; thus, the gap instabilities have nodes. In the \({d}_{xy,xy}\) channel, the gap function is a \(d\)-wave, approximately \(\cos {k}_{x}-\cos {k}_{y}\), with a \({{\rm{D}}}_{4h}\)-\({{\rm{B}}}_{1g}\) irreducible representation. The other two eigenfunctions are, respectively, \(\cos {k}_{x}\) and \(\cos {k}_{y}\) in the \({d}_{xz,xz}\) and \({d}_{yz,yz}\) channels. In particular, when a Cooper pair forms with the two quasi-particles belonging to different orbitals, it is possible to get an in-phase extended s-wave symmetry with a \({d}_{xz,yz}\) gap function \(\cos {k}_{x}+\cos {k}_{y}\) with irreducible representation \({{\rm{A}}}_{1g}\). Cooper pairs may also form with the quasi-particles out of phase, leading to a \({d}_{xz,yz}\) gap function with d-wave \(\cos {k}_{x}-\cos {k}_{y}\) symmetry.
The superconducting pairing gap symmetries for \({\epsilon }_{x}\) = 0 are shown in the conventional basal plane; eigenfunctions corresponding to first three eigenvalues in singlet (s) symmetries are shown in a–c and triplets (t) are in the shown in d–f. g shows evolution of triplet and singlet eigenvalues (at 380 K) under strain. Under strain singlet eigenvalues increase and surpass the triplet eigenvalues.
Triplet channel
A very different story emerges. We find three nodeless odd-frequency gap instabilities as shown in Fig. 4. In the \({d}_{xz,xz}\) and \({d}_{yz,yz}\) channels, we observe instabilities of the form \({\delta }_{0}+\cos {k}_{x}\) and \({\delta }_{0}+\cos {k}_{y}\), leading to the possibility of an extended nodeless s-wave 2\({\delta }_{0}+\cos {k}_{x}+\cos {k}_{y}\) gap structure with \({{\rm{A}}}_{1g}\) irreducible representation in the \({d}_{xz,yz}\) basis. The out-of-phase coupling between these two quasi-particles will lead to \({{\rm{B}}}_{1g}\) nodeless d-wave gap structure. We also observe an extended s-wave gap function in the \({d}_{xy,xy}\) channel. However, additionally we find a doubly degenerate set of eigenvalues in an off-diagonal \({d}_{xz,xy}\) and \({d}_{yz,xy}\) channel.
Discussion
On the nature of Δ in the unstrained case
Our calculations for \(\Delta\) are performed in the normal phase of SRO, probing all possible particle–particle instabilities that could precipitate in the formation of a superconducting gap. They do not describe the superconducting state itself, and do not include the possibility of spontaneously breaking time reversal symmetry (TRS). To properly resolve the character of the gap function, a full description of the ordered state is needed. Eigenfunctions displayed here are in the orbital basis of d states, and they are useful to distinguish intra- and inter-orbital character of the pairing. But to project the superconducting gap on the Fermi surfaces, these functions must be recast in the basis of eigenfunctions. The momentum-dependent superconducting gap at the Fermi surface can be obtained by diagonalizing a Bogoliubov Hamiltonian constructed in the band basis42. These capabilities we have not yet developed. Nevertheless, the eigenvalues calculated in the normal phase are robust: what is dominant in the orbital basis should remain so in the basis of eigenstates. Thus, these instabilities show what states are available to form order parameters prescribed in earlier theoretical works, notably by Raghu et al.35, Scaffidi et al.43, and Mackenzie et al.1 Such an order parameter can result in a nodeless gap structure, which can also lead to TRS breaking and chiral superconductivity. Also, two-component odd-frequency gap functions can lead to observed Kerr rotation in SRO44. Also, our observation of nodal gap instabilities is consistent with nodal gap structures reported from several measurements and previous theoretical studies based on model Hamiltonians and first principles45,46,47,48,49,50,51,52.
Table 1 shows how different gap structures transform under spin exchange \(\hat{S}\), orbital exchange \(\hat{O}\), time exchange \(\hat{T}\), and parity \(\hat{P}\) operators. This allows us to characterize their irreducible representations in terms of \(D_{4h}\) lattice symmetry, while noting that under uniaxial strain considered below, this symmetry reduces to \(D_{2h}\) and properties relying on 4-fold rotational symmetry no longer apply. Comparing singlet and triplet channels at fixed temperature, the triplet eigenvalues are nearly two times larger than singlet eigenvalues (see Fig. 4), suggesting that even while the triplet is dominant, the singlet can contribute significantly to Cooper pair formation (in the absence of strain).
Spin–charge co-operation in singlet channel under strain
The relative strengths of singlet and triplet channels reverse under strain. We find that the eigenvalues in the triplet channel decrease rapidly, while the singlet eigenvalues increase (see Fig. 4). Additionally, we find that the triplet eigenvalues are weakly dependent on temperature at this critical \({\epsilon }_{x}^{* }\), while the singlet eigenvalues strongly increase with lowering \(T\) (see Supplementary Fig. 4). The singlet eigenvalues begin to overtake the triplet eigenvalues, suggesting a suppression of the triplet superconducting instability for \({\epsilon }_{x} \, > \, 0\). This is fully consistent with the susceptibility calculations, which suggest that under strain both spin and charge fluctuations becomes more intense close to singlet vectors, and far from triplet \(q=0\). This transition was already conjectured in the original work of Steppke et al.3, based on an interpretation of \({H}_{c2}\).
To address the issue conclusively, we compute the eigenvalues with and without the charge vertex functions. In the full calculation, we observe that triplet eigenvalues are larger than the singlet eigenvalues at \({\epsilon }_{x}=0\). Redoing the calculation suppressing the charge vertex, we find that at \({\epsilon }_{x}=0\) triplet eigenvalues remain larger than the singlet eigenvalues. However, \({\epsilon }_{x}\ > \ 0\), suppressing the charge vertex causes triplet eigenvalues to become larger than the singlet eigenvalues, reversing the relative importance of the two. This is a strong indication that both spin and charge vertex functions co-operate under strain in the singlet channel. In Table 2 we show the eigenvalues with and without the charge vertex to quantify this argument.
Multiple singlet and triplet superconducting instabilities are observed in SRO. A purely spin-triplet superconductivity needs sufficient coherent and low energy spin fluctuation glue near FM vector \(q=0\). However, our results show that the dominant spin fluctuations are at \((0.3,0.3,{q}_{z})\), which is closer to the singlet-pairing vector, combined with the smaller peak at the quasi-FM “triplet” vector. Multi-orbital charge correlations also play a central role in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\): they provide additional glue both at low-\(q\) and \((0.5,0.5,{q}_{z})\) through strong intra- and inter-orbital fluctuations. Together, they lead to multiple triplet and singlet Cooper pair instabilities, with triplet eigenvalues exceeding singlet in the absence of strain.
When strain is applied the dominant character of Cooper pair instability changes. \({\chi }^{m}(q=0.3,0.3,{q}_{z})\) becomes more coherent up to a critical strain \({\epsilon }_{x}^{* }\). Simultaneously the spectral weight under the low-\(q\) charge peak gets fully transferred to a more coherent quasi-anti-FM vector \((0.5,0.5,{q}_{z})\). Together, they suggest spin and charge co-operate to sustain an even-parity pairing channel, which maximize \({T}_{\mathrm{c}}\) at \({\epsilon }_{x}^{* }\). For \({\epsilon }_{x} \, > \, {\epsilon }_{x}^{* }\), the spin fluctuation weight drifts toward larger wavelength, more uniform quasi-FM vectors and charge fluctuates more strongly at the quasi-anti-FM vector. This emergent spin incoherence and spin–charge separation, split by quasi-FM spin fluctuation peak and quasi-anti-FM charge fluctuation peak, is not conducive for sustaining the even-parity superconductivity and hence lowers and suppresses \({T}_{\mathrm{c}}\). Our observations suggest that the pathway to maximize superconductivity in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) would be to cause spin and charge fluctuations to act in symphony in an even-parity channel.
Methods
We use a recently developed quasi-particle self-consistent GW + DMFT (QSGW+DMFT)20,21, as implemented in the all-electron Questaal package24. Paramagnetic DMFT is combined with nonmagnetic QSGW via local projectors of the Ru 4\(d\) states on the Ru augmentation spheres to form the correlated subspace. We carried out the QSGW calculations in the tetragonal and strained phases of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) with space group 139/I4mmm. DMFT provides a non-perturbative treatment of the local spin and charge fluctuations. We use an exact hybridization expansion solver, namely, the continuous time Monte Carlo (CTQMC)53, to solve the Anderson impurity problem.
The one-body part of QSGW is performed on a \(16\times 16\times 16\) k-mesh and charge has been converged up to \(1{0}^{-6}\) accuracy, while the (relatively smooth) many-body static self-energy \({\Sigma }^{0}({\bf{k}})\) is constructed on a \(8\times 8\times 8\) k-mesh from the dynamical GW \(\Sigma ({\bf{k}},\omega )\). \({\Sigma }^{0}({\bf{k}})\) is iterated until convergence (RMS change in \({\Sigma }^{0}\ <1{0}^{-5}\) Ry). \(U\) = 4.5 eV and \(J\) = 1.0 eV54 were used as correlation parameters for DMFT. The DMFT for the dynamical self-energy is iterated, and converges in \(\approx \!20\) iterations. Calculations for the single-particle response functions are performed with \(1{0}^{9}\) QMC steps per core and the statistics is averaged over 64 cores. The two particle Green’s functions are sampled over a larger number of cores (40,000–50,000) to improve the statistical error bars. We sample the local two-particle Green’s functions with CTQMC for all the correlated orbitals and compute the local polarization bubble to solve the inverse BSE for the local irreducible vertex. Finally, we compute the non-local polarization bubble \(G({\bf{k}},\omega )G({\bf{k}}-{\bf{Q}},\omega -\Omega )\), and by combining with the local irreducible vertex33, we obtain the full non-local spin and charge susceptibilities \({\chi }^{m,d}({\bf{Q}},\Omega )\). The susceptibilities are computed on a \(16\times 16\times 16\) Q-mesh. BSE equations in the particle–particle pairing channels are solved on the same k-mesh to extract the susceptibilities and the Eliashberg eigenvalue equations are solved to extract the eigenvalue spectrum and corresponding pairing symmetries36.
Data availability
All input data are provided in the Source Data file. Using them, QSGW and QSGW+DMFT calculations can be launched. The commandlines for launching them are also provided in the same file.
Code availability
The source code for QSGW is available from Questaal website under the terms of the AGPLv3 license. The DMFT code can be downloaded from Kristjan Haule’s website: http://hauleweb.rutgers.edu/tutorials/.
References
Mackenzie, A. P., Scaffidi, T., Hicks, C. W. & Maeno, Y. Even odder after twenty-three years: the superconducting order parameter puzzle of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). npj Quant. Mater. 2, 40 (2017).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Sarma, S. D. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083 (2008).
Steppke, A. et al. Strong peak in \({T}_{c}\) of \({T}_{c}\) under uniaxial pressure. Science 355, eaaf9398 (2017).
Pustogow, A. et al. Pronounced drop of \({\rm{O}}\) \({\rm{O}}\) knight shift in superconducting state of \({\rm{O}}\). Nature 574, 72–75 (2019).
Maeno, Y. et al. Superconductivity in a layered perovskite without copper. Nature 372, 532 (1994).
Mackenzie, A. et al. Extremely strong dependence of superconductivity on disorder in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. Lett. 80, 161 (1998).
Maeno, Y. et al. Enhancement of superconductivity of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) to 3 k by embedded metallic microdomains. Phys. Rev. Lett. 81, 3765 (1998).
Kittaka, S., Nakamura, T., Yaguchi, H., Yonezawa, S. & Maeno, Y. Spatial development of superconductivity in the \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\)-Ru eutectic system. J. Phys. Soc. Jpn. 78, 064703 (2009).
Ying, Y. et al. Suppression of proximity effect and the enhancement of p-wave superconductivity in the \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\)-Ru system. Phys. Rev. Lett 103, 247004 (2009).
Hicks, C. W. et al. Strong increase of tc of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) under both tensile and compressive strain. Science 344, 283–285 (2014).
Imai, Y. & Sigrist, M. Topological aspect and the pairing symmetries on spin-triplet chiral p-wave superconductor under strain. Phys. B 536, 72–74 (2018).
Liu, Y.-C., Zhang, F.-C., Rice, T. M. & Wang, Q.-H. Theory of the evolution of superconductivity in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) under anisotropic strain. npj Quantum Mater. 2, 12 (2017).
Barber, M. E., Gibbs, A. S., Maeno, Y., Mackenzie, A. P. & Hicks, C. W. Resistivity in the vicinity of a van hove singularity: \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) under uniaxial pressure. Phys. Rev. Lett. 120, 076602 (2018).
Mravlje, J. et al. Coherence-incoherence crossover and the mass-renormalization puzzles in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. Lett. 106, 096401 (2011).
Veenstra, C. et al. Spin–orbital entanglement and the breakdown of singlets and triplets in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) revealed by spin- and angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 112, 127002 (2014).
Acharya, S., Laad, M. S., Dey, D., Maitra, T. & Taraphder, A. First-principles correlated approach to the normal state of strontium ruthenate. Scientific Rep. 7, 43033 (2017).
Boehnke, L., Werner, P. & Lechermann, F. Letter Multi-orbital nature of the spin fluctuations in Sr2RuO4. Europhys. Lett. 122, 57001 (2018).
Baskaran, G. Why is \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) not a high tc superconductor? electron correlation, hund’s coupling and p-wave instability. Phys. B 223, 490–495 (1996).
Acharya, S., Dey, D., Maitra, T. & Taraphder, A. Quantum criticality associated with dimensional crossover in the iso-electronic series \({{\rm{Ca}}}_{2-x}{{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). J. Phys. Commun. 2, 075004 (2018).
Acharya, S. et al. Metal-insulator transition in copper oxides induced by apex displacements. Phys. Rev. X 8, 021038 (2018).
Sponza, L. et al. Self-energies in itinerant magnets: a focus on fe and ni. Phys. Rev. B 95, 041112 (2017).
Tomczak, J. M., van Schilfgaarde, M. & Kotliar, G. Many-body effects in iron pnictides and chalcogenides: nonlocal versus dynamic origin of effective masses. Phys. Rev. Lett. 109, 237010 (2012).
Pashov, D. et al. Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique. Comput. Phys. Commun. 107065 (2019). https://doi.org/10.1016/j.cpc.2019.107065.
Questaal website. https://www.questaal.org.
ecalj package. https://github.com/tkotani/ecalj/.
Steffens, P. et al. Spin fluctuations in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) from polarized neutron scattering: Implications for superconductivity. Phys. Rev. Lett. 122, 047004 (2019).
Tamai, A. et al. High-resolution photoemission on \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) reveals correlation-enhanced effective spin-orbit coupling and dominantly local self-energies. Phys. Rev. X 9, 021048 (2019).
Bergemann, C., Mackenzie, A., Julian, S., Forsythe, D. & Ohmichi, E. Quasi-two-dimensional fermi liquid properties of the unconventional superconductor \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Adv. Phys. 52, 639–725 (2003).
Liu, S. et al. Fermi surface sheet-dependent band splitting in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) revealed by high-resolution angle-resolved photoemission spectroscopy. Phys. Rev. B 86, 165112 (2012).
Braden, M. et al. Inelastic neutron scattering study of magnetic excitations in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. B 66, 064522 (2002).
Braden, M. et al. Incommensurate magnetic ordering in \({\mathrm{Sr}}_{2}{\mathrm{Ru}}_{1-x}{\mathrm{Ti}}_{x}{O}_{4}\). Phys. Rev. Lett. 88, 197002 (2002).
Ishida, K. et al. Ru nmr probe of spin susceptibility in the superconducting state of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. B 63, 060507 (2001).
Park, H. Haule, K. Kotliar, G. Magnetic excitation spectra in BaFe2As2: a two-particle approach within a combination of the density functional theory and the dynamical mean-field theory method. Phys Rev Lett. 107, 137007 (2011).
Iida, K. et al. Inelastic neutron scattering study of the magnetic fluctuations in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. B 84, 060402 (2011).
Raghu, S., Kapitulnik, A. & Kivelson, S. Hidden quasi-one-dimensional superconductivity in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. Lett. 105, 136401 (2010).
Park, H. The Study of Two-particle Response Functions in Strongly Correlated Electron Systems within the Dynamical Mean Field Theory. Ph.D. thesis, Rutgers University-Graduate School-New Brunswick (2011).
Ishida, K. et al. Spin-triplet superconductivity in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) identified by 17 O knight shift. Nature 396, 658 (1998).
Xia, J., Maeno, Y., Beyersdorf, P. T., Fejer, M. & Kapitulnik, A. High resolution polar kerr effect measurements of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\): evidence for broken time-reversal symmetry in the superconducting state. Phys. Rev. Lett. 97, 167002 (2006).
Luke, G. M. et al. Time-reversal symmetry-breaking superconductivity in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Nature 394, 558 (1998).
Hassinger, E. et al. Vertical line nodes in the superconducting gap structure of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. X 7, 011032 (2017).
Kittaka, S. et al. Searching for gap zeros in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) via field-angle-dependent specific-heat measurement. J. Phys. Soc. Jpn. 87, 093703 (2018).
Yin, Z., Haule, K. & Kotliar, G. Spin dynamics and orbital-antiphase pairing symmetry in iron-based superconductors. Nat. Phys. 10, 845 (2014).
Scaffidi, T., Romers, J. C. & Simon, S. H. Pairing symmetry and dominant band in \({{\rm{sr}}}_{2}{{\rm{ruo}}}_{4}\). Phys. Rev. B 89, 220510 (2014).
Komendová, L. & Black-Schaffer, A. M. Odd-frequency superconductivity in \({{\rm{sr}}}_{2}{{\rm{ruo}}}_{4}\) measured by kerr rotation. Phys. Rev. Lett. 119, 087001 (2017).
Zhang, L.-D., Huang, W., Yang, F. & Yao, H. Superconducting pairing in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) from weak to intermediate coupling. Phys. Rev. B 97, 060510 (2018).
Eremin, I., Manske, D., Ovchinnikov, S. & Annett, J. Unconventional superconductivity and magnetism in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) and related materials. Ann. Phys. 13, 149–174 (2004).
Litak, G., Annett, J., Györffy, B. & Wysokiński, K. Horizontal line nodes in superconducting \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Stat. Sol. B 241, 983–989 (2004).
Contreras, P., Walker, M. & Samokhin, K. Determining the superconducting gap structure in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) from sound attenuation studies below \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. B 70, 184528 (2004).
Ishida, K. et al. Anisotropic superconducting gap in the spin-triplet superconductor \({{\rm{sr}}}_{2}{{\rm{ruo}}}_{4}\) : evidence from a ru-nqr study. Phys. Rev. Lett. 84, 5387–5390 (2000).
Zhitomirsky, M. & Rice, T. Interband proximity effect and nodes of superconducting gap in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. Lett. 87, 057001 (2001).
Contreras, P., Walker, M. & Samokhin, K. Determining the superconducting gap structure in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) from sound attenuation studies below \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Phys. Rev. B 70, 184528 (2004).
Gingras, O., Nourafkan, R., Tremblay, A.-M.S. & Côté, M. Superconducting symmetries of \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\) from first-principles electronic structure. Phys. Rev. Lett. 123, 217005 (2019).
Haule, K. & Kotliar, G. Strongly correlated superconductivity: a plaquette dynamical mean field theory study. Phys. Rev. B 76, 104509 (2007).
Deng, X., Haule, K. & Kotliar, G. Transport properties of metallic ruthenates: A DFT+DMFT investigation. Phys. Rev. Lett. 116, 256401 (2016).
Acknowledgements
We acknowledge Anna Tamai and F. Baumberger for sharing with us the raw ARPES data for Fermi surfaces. S.A. acknowledges discussions with James Annett, Martin Gradhand. and Astrid Romer. This work was supported by the Simons Many-Electron Collaboration, and EPSRC (Grants EP/M011631/1 and EP/M011038/1). H.P. is supported by the United States Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. For computational resources, we were supported by the ARCHER UK National Supercomputing Service, UK Materials and Molecular Modeling Hub for computational resources, (EPSRC Grant EP/P020194/1) and computing resources provided STFC Scientific Computing Department’s SCARF cluster. We acknowledge PRACE for awarding us access to SuperMUC at GCS@LRZ, Germany.
Author information
Authors and Affiliations
Contributions
S.A. has conceived and designed the research. S.A., D.P., and M.V.S. have carried out the calculations. S.A., D.P., H.P., M.V.S., and L.S. have contributed codes. D.P., M.V.S., and C.W. have prepared the figures. All authors have contributed to the writing of the paper and the analysis of the data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Acharya, S., Pashov, D., Weber, C. et al. Evening out the spin and charge parity to increase \({T}_{c}\) in \({{\rm{Sr}}}_{2}{{\rm{RuO}}}_{4}\). Commun Phys 2, 163 (2019). https://doi.org/10.1038/s42005-019-0254-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0254-1
This article is cited by
-
Competition between d-wave superconductivity and magnetism in uniaxially strained Sr2RuO4
npj Quantum Materials (2024)
-
Magnon interactions in a moderately correlated Mott insulator
Nature Communications (2024)
-
Distinct spin and orbital dynamics in Sr2RuO4
Nature Communications (2023)
-
A theory for colors of strongly correlated electronic systems
Nature Communications (2023)
-
Vertex dominated superconductivity in intercalated FeSe
npj Quantum Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.