Abstract
Unravelling superradiance, also known as superfluorescence, relies on an ensemble of phase-matched dipole oscillators and the suppression of inhomogeneous broadening. Here we report a superradiance platform that combines an optical lattice free from the ac Stark shift and a hollow-core photonic crystal fibre, enabling an extended atom-light interaction over 2 mm free from the Doppler effect. This system allows control of the atom spatial distribution and spectral homogeneity whilst efficiently coupling the radiation field to an optical fibre. The experimentally-observed and theoretically-corroborated temporal, spectral and spatial dynamic behaviours of the superradiance, e.g., superradiance ringing and density-dependent frequency shift, demonstrate a unique interplay between the trapped atoms and the fibre-guided field with multiple transverse modes. Our theory indicates that the resulting temporal evolution of the guided light shows a minimal beam radius of 3.1 µm which is three times smaller than that of the lowest-loss fibre mode.
Similar content being viewed by others
Introduction
Superradiance (SR) has been the subject of active research since the pioneering work of Dicke in 19541. Such a collective effect arises from an ensemble of two-level emitters spontaneously locking their dipole oscillations in phase2, giving rise to an enhanced decay rate γSR many times faster than the spontaneous emission rate γ0 of individual emitters and a strong peak intensity of radiation in quadratic proportion to the excited-state population. The other SR signature manifests as a collective frequency shift and broadening, which are underpinned by fascinating physical phenomena such as the energy-level shift due to virtual photon exchange (collective Lamb shift)3 or van der Waals dephasing2. In addition to its undisputed importance in fundamental science, SR also has substantial applications in various fields. For example, lasing based on SR has been proved to be a potentially outstanding frequency reference because of its strong immunity to environmental perturbations4,5. In quantum information, SR is utilized in realizing quantum memories6,7 and single photon sources8. Also, SR has been recently used for cooling mechanisms by means of cooperative emission9,10.
Despite the observations of SR in various gaseous and solid-state samples11,12,13,14,15,16,17,18,19, capturing the full picture of SR properties within a single experimental platform still remains an ongoing target. The chief challenge in unravelling the SR dynamics is to find the best trade-off between maximising the number of phase-locked emitters coupled to the common radiation field and preserving the inter-emitter phase correlation. The enhancement of SR emission rate scales as the former while the latter is a prerequisite for the SR generation. The conventional SR schemes adopt an ensemble of emitters densely packed within a sub-radiation-wavelength volume, i.e., Dicke regime11,12,13,14, to achieve the SR. Recently, a large number of atoms confined inside optical cavities4,5,6,7,8,9,10 or coupled to waveguides19 have been a successful alternative for SR generation. This is based on the fact that the fraction of photon energy emitted into the SR mode Nη/(1 + Nη) approaches unity for the atomic number N ≫ 1 even when the single-atom cooperativity parameter η = γSR/γ0, which is a geometric parameter characterizing the emissive coupling of an atom to the cavity mode, is much less than unity8.
Research at the interdisciplinary frontier between the fields of cold atoms and photonic materials reports promising results in controlling ultracold atoms with photonic waveguides20, which holds the potential of offering a strong cooperative enhancement while keeping the low atomic density. Indeed, ultracold atoms are especially attractive materials since they possess the distinct feature of being precisely controllable by optical lattice21. In particular, when ultracold atoms are confined in an optical lattice tuned to the magic wavelength, the optical excitation of atomic transition is not only free from the Doppler shift but also free from the lattice-field-induced ac Stark shift22, offering an ideal platform for investigating SR based on well-isolated atomic systems. In addition, low-loss photonic waveguides allow a strongly enhanced one-dimensional (1D) atom-light interaction, as they allow an interaction length much longer than the Rayleigh range \(z_{\mathrm{R}} = \pi w_0^2/\lambda _0\) at the wavelength λ0 while still keeping a small light-beam waist of radius w0. Successful combination of ultracold atoms and photonic waveguide has been exemplified by the works with nanofibers23,24, photonic waveguides19, and hollow-core fibers25. The long-range atom-atom interaction is accomplished via guided photons of the so-called alligator photonic crystal waveguide19, and the resulting single-atom cooperativity reaches η = 0.34. Ultracold atoms are successfully loaded inside a hollow-core photonic crystal fibre (HCPCF) and trapped in a 1D magic-wavelength optical lattice25, revealing 10-kHz-wide linewidth of the transition without being affected by wall-atom collisions.
In the present work, we report on the observation of SR from ultracold atoms confined in the magic optical lattice inside the HCPCF26. We couple an HCPCF-transmitted SR to a single-mode fibre to measure the signal by employing a highly sensitive heterodyne technique, which allows investigating temporal, spectral and spatial dynamic behaviours of SR with a single-shot measurement. We observe a ringing and accelerated decay that is up to 55 times faster than the spontaneous emission of single atoms. By analysing the inphase/quadrature components of the signal, we measure a density-dependent frequency shift. Finally, we discuss the multimode dynamics of SR in the HCPCF, where a superposition of specific guided modes contributes to the photon-mediated SR, complemented with theoretical predictions. The dense cigar-shaped atomic cloud restricts the guided SR field mainly within a diameter three times smaller than that of the fundamental fibre mode. For an in-fibre atom number of N = 2.5 × 105 with the single-atom cooperativity η = 4.1 × 10−5 available for the HCPCF, the N-atom cooperativity parameter8 Nη can be as high as 10, leading to a near-unity coupling efficiency to the guided mode of the hollow-core fibre.
Results
Experimental scheme
Figure 1a shows the schematic of our experiment. A 32-mm-long hypocycloid-core-shaped Kagome-lattice HCPCF26 is horizontally placed in a vacuum chamber. The inner diameter of the hollow-core fibre reaches 40 μm. The optical fibre guides light via the inhibited-coupling mechanism27 and supports multiple transverse modes whose transverse profiles are very close to those of a dielectric capillary28. The Gaussian-like fundamental LP01 core mode has a 1/e2 waist radius w0 = 11.8 μm (1/e radius is 8.34 μm). 88Sr atoms are laser cooled and trapped in a two-stage magneto-optical trap (MOT)29 at z ≈ −1 mm (the origin of z-coordinates is set at the entrance end of the HCPCF) and loaded into an optical lattice which passes through the HCPCF (see Methods). The counter-propagating linearly-polarized lattice lasers match the LP01 mode and operate at the wavelength λL = 813 nm. A bias magnetic field \({\mathbf{B}}_0 = \left( {0.14\,{\mathrm{mT}}} \right){\hat{\mathbf{e}}}_x\) is applied to define the quantization axis. We focus on the 1S0 − 3P1(m = 0) intercombination transition of 88Sr at the frequency ω0 = 2π × 435 THz with the natural linewidth γ0 = 2π × 7.5 kHz and the dipole moment D = 0.087 ea0 (elementary charge e and Bohr radius a0). The lattice laser polarization is tuned to cancel out the ac Stark shift difference between 1S0 and 3P1(m = 0) states caused by the optical lattice21,25.
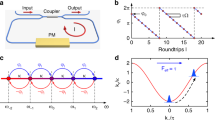
Experimental setup. a Schematic of experimental setup. Ultracold 88Sr atoms are loaded from a two-stage magneto-optical trap (MOT) into an optical lattice and then transported inside the hollow-core photonic crystal fibre (HCPCF) at z = 2 mm by the moving lattice. The magnetic field B0 = (0.14mT) \({\hat{\mathbf{e}}}_x\) is applied to define the quantization axis of the system. The superradiance (SR) emission strongly couples to the guided modes of the fibre while the spontaneously emitted photons hardly match the fibre modes. The HCPCF guided SR is coupled to a single-mode fibre (SMF) that is mainly mode matched to the LP01-mode component in SR. A part of the SR output is detected by a photomultiplier tube (PMT) to measure the total intensity of SR including the higher order modes. b Fluorescence images of atoms inside the HCPCF by exciting the 1S0 − 1P1 transition at 461 nm, which are taken by an electron multiplying charge-coupled device (EMCCD) camera through the fibre wall. The FWHM of the atomic distribution is lz = 0.87 mm for the unexpanded cloud and lz = 2.1 mm for the expanded one. c A pump laser at 689 nm with a linewidth less than 1 kHz is split into two paths. One is coupled to a SMF and used as a local-oscillator ELO cos ωLOt, while the other is used as the pump light with the amplitude Ep at the frequency ωp = ω0 + Δp shifted by an acousto-optic modulator (AOM). The SR field from the HCPCF is coupled to the SMF and balanced-heterodyned with the local field. The resultant signal \(V_{{\mathrm{RF}}}\left( t \right) \propto {\mathrm{Re}}\left\{ {\left[ {\int} {{\int} {E_{{\mathrm{LO}}}\left( {\mathbf{r}} \right)} } {E_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right)d^2{\mathbf{r}}} \right]e^{ - i{\mathrm{\Omega }}_0t}} \right\}\) at around Ω0 = 2π × 50 MHz is band-pass-filtered (BPF) and recorded by a digital storage oscilloscope (DSO). d Frequency relations. In respect to the 1S0 − 3P1(m = 0) transition frequency ω0, the SR, pump-light, and local-oscillator frequencies are given by ωSR = ω0 + ΔSR, ωp = ω0 + Δp, and ωLO = ω0 − Ω0, respectively
The loaded atoms are further transported to the position z ≈ 2 mm inside the hollow-core fibre by a moving lattice with its depth of 300 μK25. By turning off one of the two lattice lasers, the atomic gas, which is radially guided by a travelling-wave lattice laser, spreads axially to a full width at half maximum (FWHM) lz. Then, the lattice laser is switched on again to recapture the atoms. We consider two cloud widths, i.e. unexpanded (lz = 0.87 mm) and expanded (lz = 2.1 mm) clouds (see Fig. 1b), corresponding to the number of lattice sites NL = lz/(λL/2) = 2.1 × 103 and 5.2 × 103, respectively (see Methods). Each lattice site forms a pancake-shaped harmonic potential, where the atoms are distributed within a transverse 1/e radius of ra = 1.7 μm in the x–y plane and a longitudinal 1/e width of la = 54 nm along the fibre axis. Varying the number of loaded atoms N tunes the on-site density of atoms \(\rho = N_{\mathrm{a}}/\left( {\pi r_{\mathrm{a}}^2l_{\mathrm{a}}} \right)\) with the average number of atoms in each lattice site Na = N/NL. We note that the multiple photon scattering caused by the periodic spatial distribution of atoms30 hardly affects the atom-light interaction as the lattice period λL/2 does not fulfil the Bragg condition for the transition wavelength λ0.
Superradiance ringing
All atoms are initialized in the 1S0 ground state. We apply an \({\hat{\mathbf{e}}}_x\) - polarized light pulse Ep with a duration τp = 500 ns to pump the atoms. The pump-laser beam is matched to the LP01 fibre core mode, and the in-fibre amplitude Ep is set to Ep = ħπ/Dτp with ħ being the reduced Planck constant. The pump-laser frequency ωp is stabilized to an optical cavity made of an ultralow-expansion (ULE) glass with a drift rate ~1 kHzh−1 and detuned Δp = ωp − ω0 from the atomic resonance ω0. The observed SR field at the fibre output end can be written as \({\mathbf{E}}_{{\mathrm{SR}}}\left( {{\mathbf{r}},t} \right) = \left( {{\hat{\mathbf{e}}}_x/2} \right)E_{{\mathrm{SR}}}\left( {{\mathbf{r}},t} \right)e^{ - i\omega _0t} + {\mathrm{c}}.{\mathrm{c}}\). with the radial coordinate \({\mathbf{r}} = x{\hat{\mathbf{e}}}_x + y{\hat{\mathbf{e}}}_y\). We observe that the SR field propagates in the same direction as the pump light, which is consistent with the directed spontaneous emission of the timed Dicke state3,31. The radiation power \(P_{{\mathrm{SR}}}\left( t \right) \propto {\int} {{\int} {|{\mathbf{E}}_{{\mathrm{SR}}}({\mathbf{r}},t)|^2} } d^2{\mathbf{r}}\) is typically on the order of nW, requiring the low noise detection. To address this issue, we utilize the balanced-heterodyne technique32 (see Fig. 1c). The SR output is coupled to a single-mode fibre (SMF) and mixed with a local oscillator \({\mathbf{E}}_{{\mathrm{LO}}}\left( {{\mathbf{r}},t} \right) = {\hat{\mathbf{e}}}_xE_{{\mathrm{LO}}}\left( {\mathbf{r}} \right){\mathrm{cos}}\omega _{{\mathrm{LO}}}t\) by a 50:50 fibre coupler (see Methods). The power and the frequency of local oscillator are on the order of 1 mW and ωLO = ω0 − Ω0 with Ω0 = 2π × 50 MHz respectively. The relation among ω0, ωp, and ωLO is summarized in Fig. 1d. Furthermore, the SMF acts as a spatial mode filter to mainly extract the LP01 component from the SR output (see Methods) as given by \({\mathbf{E}}_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right) = \left( {{\hat{\mathbf{e}}}_x/2} \right)E_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right)e^{ - i\omega _0t} + {\mathrm{c}}.{\mathrm{c}}.\), where a prime, such as E', denotes the LP01 component.
The heterodyne signal VRF(t) is band-pass filtered with a bandwidth of 4 MHz to improve the signal-to-noise ratio (SNR) of the measurement (see Methods), and then is recorded by a digital storage oscilloscope (DSO). Upper panel of Fig. 2a shows a typical trace of the single-shot heterodyne signal VRF(t), where a yellow-shaded region corresponds to a 500-ns-long pump pulse. The envelope exhibits a ringing behaviour, where the first pulse-shaped envelope with a 0.7-μs width corresponds to the pumping process while the following bursts are caused by the reabsorption and reemission of radiation between different parts of atomic cloud33,34. The temporal widths of the bursts after the pump pulse are much shorter than the spontaneous emission lifetime 1/γ0 = 21 μs of single atom, manifesting the occurrence of SR. In particular, the first-SR burst with a temporal \(1/\sqrt e\) width of \(\gamma _{{\mathrm{bw}}}^{ - 1} = 0.38\) μs gives a photon-emission enhancement factor of γbw/γ0 = 55. Lower panel of Fig. 2a shows a temporal variation of SR power ∝|VRF(t)|2 in the logarithmic scale. Thanks to the heterodyne detection, we achieve the measurement dynamic range over five orders of magnitude. Such sensitive detection scheme will allow accessing orders of magnitude weaker subradiant process, which usually falls behind the SR process35,36, by extending the measurement time sufficiently longer than \(\gamma _0^{ - 1}\). Figure 2b shows the normalized burst width γbw/γ0 as a function of the number of atoms N, indicating the characteristic feature of the SR or cooperative emission that is proportional to N. A linear fit to the data determines the single-atom cooperativity \(\eta _{{\mathrm{bw}}} = \frac{{\gamma _{{\mathrm{bw}}}}}{{N\gamma _0}} = 4.9 \times 10^{ - 4}.\)
Superradiant ringing. a Ringing behaviour of the filtered heterodyne signal VRF(t) (black) after applying the resonant (Δp = 0) pump pulse with the duration τp = 0.5 µs (indicated by a yellow-shaded region) and the amplitude Ep = ℏπ/(Dτp). N ≈ 9.4 × 104 atoms are distributed over lz = 0.85 mm along the fibre axis. The first 0.7-μs-long peak corresponds to the pumping process, which is followed by four superradiance (SR) bursts within 10 μs. The inset shows the zoom up to reveal the carrier oscillation at about Ω0. The time-dependent SR power proportional to \(V_{{\mathrm{RF}}}^2\left( t \right)\) is given by the red curve. The SR decay rate γbw of the first-SR burst is evaluated by the reciprocal of the temporal width at \(1/\sqrt e\) of the peak amplitude. For N ≈ 9.4 × 104, γbw reaches 55γ0. b Experimentally measured burst width γbw as a function of the number of atoms N. The curve fitting gives the linear relation γbw/γ0 = (4.9 × 10−4) × N, manifesting the SR feature. The error bars, which are given for three representative data, show the standard deviations
Frequency shift
The signal VRF(t) carries also frequency information. Indeed, the amplitude of SR light output from the SMF may be rewritten as \(E_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right) = A_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right)e^{ - i\Delta _{{\mathrm{SR}}}t}\), where the complex function \(A_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right)\) is related to the envelope of VRF(t) and \(\Delta _{{\mathrm{SR}}} = \omega _{{\mathrm{SR}}} - \omega _0\) corresponds to the shift of the centre frequency ωSR of the SR light from the atomic-transition frequency ω0 (Fig. 1d). The frequency shift ΔSR can be extracted by I/Q demodulating the carrier signal of VRF(t) recorded by DSO (see Fig. 3a) into the in-phase VI(t) and quadrature-phase VQ(t) components, i.e. VRF(t) = VI(t) cos Ω0t + VQ(t) sin Ω0t. Figure 3b shows an example of an amplitude \(V\left( t \right) = \sqrt {V_{\mathrm{I}}\left( t \right)^2 + V_{\mathrm{Q}}\left( t \right)^2}\) and a phase θ(t) = ArcTan[VQ(t)/VI(t)] obtained from the I/Q signals, where we repeat the measurement of VRF(t) ten times and average the data. The linearly varying phase θ(t) in time indicates the frequency shift of the emitted light ΔSR = dθ/dt, which is nearly constant over 15 μs except the discontinuities at the nodes of the amplitudes that cause π-phase jump. The same I/Q signals are parametrically mapped onto the I/Q plane as shown in Fig. 3c, where the purple line corresponds to the trajectory from t = 1.48–8.38 μs. By taking a certain rotating frame ΔSR = dθ/dt, the trajectory can be projected to a line as indicated by the blue colour (see Methods). We thus determine ΔSR ≈ −2π × 93(10) kHz for the unexpanded atomic cloud with N = 9.4 × 104(ρ = 8.8 × 1013 cm−3). A slight departure of the phase θ(t) from dashed lines in Fig. 3b, which corresponds to finite width of the blue trajectory in Fig. 3c, may indicate a frequency chirp in the emitted signal. Further investigation on the chirping effect will be given elsewhere. In the following, we analyse ΔSR in the latter method as illustrated in Fig. 3c, assuming ΔSR to be constant.
Frequency shift of superradiant emission. a In-phase VI(t) and quadrature-phase VQ(t) components are obtained by demodulating the VRF(t) signal stored in digital storage oscilloscope. b Example of an amplitude \(V\left( t \right) = \sqrt {V_{\mathrm{I}}\left( t \right)^2 \, + \, V_{\mathrm{Q}}\left( t \right)^2}\) (black line) and a phase θ(t) = ArcTan[VQ(t)/VI(t)] (red line) measured for N ≈ 9.4 × 104. A linear phase shift in time indicates the constant frequency shift of the emitted light. Dashed lines with dθ/dt = 2π × 93kHz are shown for guides to eyes. c Mapping VI(t) and VQ(t) into an I/Q plane. In order to get rid of the influence of the pump field and to ensure enough signal-to-noise ratio, VI(t) and VQ(t) within 1.48 μs ≤ t ≤ 8.38 μs are adopted to derive the frequency shift to be 93(10)kHz. d Dependence of the frequency shift ΔSR = ωSR − ω0 on the average on-site atomic density ρ under the resonant-pump (Δp = 0) condition. Black (red) symbols correspond to unexpanded (expanded) atomic clouds. The error bars are given by the frequency where the value of the evaluation function is doubled. e. ΔSR as a function of the pump-pulse detuning Δp measured for different numbers of atoms N. We apply unexpanded atomic clouds with lz = 0.85 mm
We investigate the conditions that may affect the frequency shift ΔSR of the SR field. Figure 3d shows the dependence of ΔSR on the atomic density ρ for the resonant pumping Δp = 0. It is seen that ΔSR is negative and |ΔSR| grows up linearly with ρ. A linear fit finds the coefficient for the frequency shift to be ΔSR/ρ ~ −1 × 10−9 Hz cm3, which is consistent with the values measured in the absorption spectrum25,37, suggesting the emission and absorption spectra are subject to the same density shift. We also measure ΔSR as a function of the pump-field detuning Δp with the same amplitude and duration of the pump pulse as that of the π-pulse with Δp = 0. As shown in Fig. 3e, for a given density ρ, ΔSR stays nearly constant over a wide range of Δp, which indicates that the shift ΔSR arises entirely from the density shift and is independent of the pumping frequency ωp. For N = 2 × 105 atoms confined in the unexpanded lattice, the mean site-occupancy is about 102 and the interatomic separation is 300 nm, leading to a collective Lamb shift plus a Lorentz-Lorenz shift38 of about γ0. The frequency shift observed in experiment well exceeds any of them. Indeed, the resonant dipole-dipole interactions (RDDIs) between the atoms in the same lattice site primarily contribute to the observed density-dependent frequency shift. The linear dependence between ΔSR and ρ is well reproduced by our numerical simulation (see below and Supplementary Note 5).
Efficiency of superradiance
We further consider the efficiency of SR that weighs the energy transfer from the pump field to the SR light. In the spontaneous emission, the emitted photons are randomly oriented in free space and thereby hardly coupled to the fibre modes. In contrast, the SR shows a well-defined direction depending upon the sample’s geometry. The multi-transverse-mode propagation in the HCPCF may support an in-fibre beam which matches the atomic cloud aligned along the fibre axis. As a result, the light power output from the fibre provides the attenuated pumping pulse by the absorption of atoms and the SR field emitted from the atoms. We investigate the efficiency of SR by measuring the total radiation power PSR(t) for the applied pump power Pp(t).
The measurement procedure is illustrated in Fig. 1a. The light output from the HCPCF is split into two paths by a beam splitter. In one arm, a photomultiplier tube (PMT) measures the total light intensity to determine the coupling efficiency κ of the SR to multi-spatial modes while in the other arm, the beam enters the SMF. The light output from the SMF is in a superposition state of the fibre LP01, LP02, and LP03 modes, where the LP01 component dominates the weight. This light beam is detected by an avalanche photodiode (APD) so as to measure the coupling efficiency κ0, which is mostly determined by the LP01 mode, i.e. the efficiency of transferring the pumping power to a specific mode (see Methods). The photon-counting mode is applied for both measurements, where the neutral-density (ND) filters are inserted in front of the detectors to attenuate the signal down to the photon-counting level.
Figure 4a shows a typical data obtained by the PMT after averaging 25,000 measurements with N = 9.4 × 104. The green curve displays the result in the absence of the atoms, i.e. the power of the pump-light Pp(t), while the red line denotes the measurement with the presence of lattice-confined atoms, i.e. the power of the light passing through the atoms and superradiantly emitted by the atoms PSR(t). The blue line corresponds to the difference ΔP(t) = PSR(t) − Pp(t), where the positive (negative) area is proportional to the total emitted Pem (absorbed Pab) power. The efficiency κ is then given by the ratio κ = |Pem/Pab|. Figure 4b shows the dependence of κ on the atomic number N for the unexpended (black solid squares) and expanded (red solid circles) atomic clouds. It is seen that in both cases κ goes up monotonically and approaches unity asymptotically as N is increased. The absorbed energy in the pumping process can be converted into either the SR radiation or the spontaneously emitted radiation. The former, whose power scales as N2γSR with the average SR emission rate γSR of single atom, is collectively coupled to the HCPCF with an efficiency χ. In contrast, the latter is proportional to Nγ0 and hardly matches the HCPCF modes. Thus, the efficiency κ can be formulated as \(\kappa = \chi \frac{{\eta N}}{{1 + \eta N}}\), where η = γSR/γ0 denotes the single-atom cooperativity. The curve fitting to filled symbols in Fig. 4b gives χ ≈ 1 and η ≈ 4.1 × 10−5, which reasonably agrees with the geometrically estimated value ηΩ = NA2/4 ≈ 10−4 with the numerical aperture NA = λ0/πw0 ≈ 0.02 for coupling to the guided fibre mode.
Efficiency of superradiance. a Time evolution of radiation measured by a photomultiplier tube (PMT), where the pump pulse resonantly (Δp = 0) excites the unexpanded atomic cloud with N ≈ 9.4 × 104 and lz = 0.85 mm. The red (green) curve corresponds to the PMT signal with (without) atoms inside the fibre. The non-overlapping areas within the pumping regimes t ≤ τp and \(t \, > \, \tau _{\mathrm{p}}\) denote the energies absorbed and emitted by the atoms, respectively. The difference between two curves is given by the blue line. b Total efficiency κ of the superradiance (SR) coupling to multiple transverse modes (shown by filled symbols) and efficiency κ0 of the SR coupling to the fundamental LP01 mode (empty symbols) as a function of the atomic number N for unexpanded (lz = 0.85 mm, shown by black) and expanded (lz = 2.1 mm, shown by red) atomic clouds. Two solid lines give the single-atom cooperativity η = 4.1 × 10−5 (filled black), η = 3.2 × 10−5 (filled red) with χ ≈ 1. The error bars representing the standard deviation are given for four data points
Similarly, we obtain the coupling efficiency κ0 of the superposition state of the fibre LP01, LP02, and LP03 modes, as shown in Fig. 4b by open square symbols. It is found that κ0 is maximized around Nm ≈ 105 and then decreases as N is further increased, suggesting that fibre higher-order modes take up more SR energy for N > Nm. The SR rate γSR may be separated into two parts, which respectively contribute to the fundamental LP01- and high-order-mode SR fields, i.e. \(\gamma _{{\mathrm{SR}}} = \gamma _{{\mathrm{SR}}}^{\left( \mathrm{f} \right)} + \gamma _{{\mathrm{SR}}}^{(\mathrm{h})}\), and \(\kappa _0 = \left( {\gamma _{{\mathrm{SR}}}^{\left( {\mathrm{f}} \right)}/\gamma _{{\mathrm{SR}}}} \right)\kappa\). Since the atoms emit the guided light within the cross-sectional area of the atomic cloud, whose radius ra is much smaller than the LP01-mode beam radius w0, the higher-order fibre modes (such as LP02 and LP03) with their central-peak radii smaller than w0 get enhanced prior to LP01 and hence \(\gamma _{{\mathrm{SR}}}^{\left( {\mathrm{f}} \right)}\, < \, \gamma _{{\mathrm{SR}}}\). For a larger N, less power is transferred to LP01 and \(\gamma _{{\mathrm{SR}}}^{\left( {\mathrm{f}} \right)}\) becomes smaller, resulting in a reduced efficiency κ0. Our numerical simulation qualitatively confirms the similar dependence of κ and κ0 on N (see below and Supplementary Note 5). We find that η is about ten times smaller than η(bw) that is derived based on the first-SR burst. This may be attributed to the fact that the first-SR burst does not behave exponentially.
Discussion
To understand the subtle mechanism behind the above experimental observations, we need to simulate the collective atom-light interplay under the experimental detection conditions. A similar in-fibre SR model has been studied in a recent theoretical work39, where the physical system is simplified and only the collective decay of excited atoms, rather than the photon emission, is focused on. Here, we model the practical physical system by employing Maxwell-Bloch equations (MBEs)2 and derive the in-fibre light field directly. The theoretical model takes into account the effects of the inhomogeneous atomic distribution, the multi-transverse-fibre-mode propagation, and the resonant dipole-dipole interactions40,41 among atoms in the same lattice site (see Supplementary Note 1–4). The fibre modes are calculated via the full-vector finite element method42 and the 4th order Runge-Kutta technique is applied to solve MBEs. Choosing fibre modes is crucial for the numerical simulation. Since the SR light is emitted within the cross section of the atomic cloud, the higher-order fibre modes, whose intensity distributions have a central peak with a radius larger than or similar to the radial radius ra of the atomic cloud, should be considered. We consider up to nine transverse fibre modes, among which the intensity patterns of the modes in Group I (i.e. LP01, LP02, and LP03) are maximized at the central point of the fibre core while the others in Group II (i.e. \({\mathrm{LP}}_{{\mathrm{11}}}^{{\mathrm{a}},{\mathrm{b}}}\), \({\mathrm{LP}}_{{\mathrm{21}}}^{{\mathrm{a}},{\mathrm{b}}}\), and \({\mathrm{LP}}_{{\mathrm{31}}}^{{\mathrm{a}},{\mathrm{b}}}\)) do not have central peaks (see Supplementary Note 4), in the simulation. The Gaussian-like fundamental mode LP01 has a waist radius w0 = 11.8 μm, at which the intensity drops to 1/e2 of the maximum value. The maximum loss (caused by the limited light confinement strength of the cladding design) experienced by the selected modes over the atom-light interaction region is estimated to be lower than 10−2 dB and is thus negligible. Besides these selected modes, other transverse modes may also propagate inside the actual fibre. However, including more fibre modes requires large amount of computer memory and computational time and may also mismatch the numerical-simulation and experimental results (see below).
Figure 5a displays the simulated SR temporal trace in the same conditions as Fig. 2a. The heterodyne signal Vcal(t) is presented in the black colour while the red line shows the envelope of the signal \(\tilde V_{{\mathrm{cal}}}\left( t \right) \propto A_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right)\) without the band-pass filtering. It is seen that the ringing behaviour is well replicated. The intervals between two adjacent nodes are consistent with the experimental measurement, proving the validity of simulation. As illustrated by \(\tilde V_{{\mathrm{cal}}}\left( t \right)\), the first node occurs within the pumping process, meaning the SR starts before the pump pulse end. It is also found that the band-pass filter affects the measurement in two aspects: the rapid rising edges of the first two pulses in \(\tilde V_{{\mathrm{cal}}}\left( t \right)\) are stretched, which explains the fact that the envelope peak corresponding to the pumping pulse in Vcal(t) is lower than that of the first-SR burst in Vcal(t); and the variation of Vcal(t) falls behind \(\tilde V_{{\mathrm{cal}}}\left( t \right)\) by a retarded time of about 0.2 μs. It is worth noting that the multimode propagation is crucial to this ringing phenomenon. The superposition of multiple transverse modes can sustain an in-fibre beam radius similar to the transverse 1/e radius ra of the atomic cloud, magnifying the collective atom-light interplay (see below and Supplementary Movie 1). We should also note that when extra transverse modes (for example, LP04) with a central-peak radius smaller than that of LP03 are involved in Group I in the numerical simulation, the separations between inter-adjacent envelop nodes of Vcal(t) are strongly shortened, which is inconsistent with the experimental measurement and manifests the negligible effect of these high-order modes in the atom-light interface.
Numerical simulation of the ringing behaviour. a Numerical result of heterodyne signal Vcal(t) (black) for N ≈ 9.4 × 104 assuming the resonant (Δp = 0) pump pulse with the duration τp = 0.5 µs and the amplitude Ep = ℏπ/(Dτp), which is corresponding to the experimental measurement. In comparison, the envelope of the raw signal \(\tilde V_{{\mathrm{cal}}}\left( t \right)\) (red) before entering the band-pass filter is also presented. Here, we have used the coupling efficiencies of the fibre LP01, LP02, and LP03 modes to SMF cLP01 = 0.60, cLP02 = 0.33, and cLP03 = 0.05. b Time evolution of fibre-mode weights. The weights of components LP01, LP02, and LP03 in the output SR field ESR(r, t) vary in time. Examples of SR pattern at several selected times are presented. The pattern deviates from the Gaussian-like distribution at each node of the SR ringing shown in Fig. 5a. Away from ringing nodes, the transverse beam radius of the output SR is about three times smaller than that of the fundamental LP01 fibre mode. c. Numerical first-SR-burst width γbw vs. the number of atoms N. The solid line shows the curve fitting. All system parameters are same to Fig. 5a
As we have pointed out above, the multi-transverse-fibre-mode propagation plays an important role in the atom-light coupling. Figure 5b depicts the time-dependent weights of several fibre modes and SR patterns at selected times. The more detailed time evolution of SR pattern can be found in Supplementary Movie 1. The results reveal a unique feature whereby the sequence of the pump absorption and the SR bursts is imprinted in the time evolution of the intensity profile of the fibre-guided modes. The initial state of the pump coupling into the fibre is illustrated by the LP01-like mode intensity profile at t = 0 μs. The doughnut-shaped pattern during the pumping pulse denotes the strong absorption within the cross section of atomic cloud. The SR events are represented by a Gaussian-like pattern with a beam radius smaller than w0. This profile results from a linear combination of the LP01, LP02, and LP03 modes. Hence, the SR in multimode HCPCF can sustain a strong atom-light interplay, which differs from the situation of the atoms coupled to a single-mode fibre or a cavity4,5. In addition, around each node ESR(r, t) ≈ 0 of SR, the transverse profile becomes different from the Gaussian-like distribution, indicating the strong influence from the non-central-peak fibre modes in Group II. Only when away from the nodes, the modes in Group I get enhanced prior to the modes in Group II. Moreover, from the numerical simulation one may derive the SR decay rate γbw corresponding to the first-SR burst. Our theoretical result predicts a linear dependence of γbw on the number of atoms N (see Fig. 5c), γbw/γ0 ≈ 5.4 × 10−4N, consistent with the experimental measurement in Fig. 2b.
Our numerical model also reproduces other experimental results as illustrated in Fig. 6. Performing the Fourier transform on the numerically-simulated amplitude ESR(r, t), one obtains the SR spectrum \(S\left( \omega \right) \propto \left| {\int_{\tau _{\mathrm{p}}}^\infty {\left[ {{\int} {{\int} {E_{{\mathrm{SR}}}\left( {{\mathbf{r}},t} \right)d^2{\mathbf{r}}} } } \right]} e^{i\left( {\omega - \omega _0} \right)t}dt} \right|^2\) (see Fig. 6a), from which the frequency shift ΔSR is read out by deducting the envelope-oscillation frequency introduced by the ringing behaviour. The dependence of ΔSR on the average on-site atomic density ρ is plotted in Fig. 6b, which agrees with the experimental results. We also theoretically reproduce the counterparts of Fig. 4a, b in Fig. 6c, d. In comparison, the numerical results of the efficiencies of SR coupling to all fibre modes (κ) and to the fundamental mode (κ0) are both lower than the experimental results. This is mainly because the calculated transverse modes are not exactly the same as those existing in the actual fibre. A slight mismatch can lead to an apparent difference. Furthermore, the insufficient number of the fibre transverse modes in Group II joining in the atom-light interaction may give rise to an erroneous increment of the power absorption within the pumping process, resulting in the reduced κ and κ0. Nevertheless, the numerical and experimental results still exhibit similar behaviours.
Numerical simulation for the resonantly-pumped unexpanded atomic cloud. a Superradiance (SR) spectrum S(ω) with the atom number N = 9.4 × 104. The spectrum peak is shifted to the red side of ω0 by 2π × 152 kHz. Deducting the envelope-oscillation frequency of the SR field, which is 2π × 54 kHz, gives ΔSR = −2π × 98 kHz. b Frequency shift ΔSR vs. the average on-site atomic density ρ. The filled black symbols correspond to the numerical results whose curve fitting, i.e. ΔSR/ρ = 2π × 1.07 × 10−12 kHz cm3, is given by the solid line. c Numerically-derived time-dependent powers of pump beam Pp(t) (green), SR field PSR(t) (red) and their difference ΔP(t) (blue). The blue line denotes the energies emitted (absorbed) by the atoms when the ΔP(t) is positive (negative). d Total efficiency κ of the SR coupling to multiple transverse modes (filled symbols) and efficiency κ0 of the SR coupling to the fundamental LP01 mode (empty symbols) as a function of the atomic number N. The curve fitting of κ leads to η = 3.6 × 10−5 and the efficiency χ = 0.87
In summary, we have demonstrated the multimode dynamics of collective spontaneous emission based on an engineered in-fibre atom-light-interface architecture. This platform may be applicable to explore more exotic quantum phenomena such as photonic band gaps in 1D ordered atomic structure, quantum jumps of many-body systems with long-range interaction, the open-system Dicke-model phase transition43, and the competing process between virtual and real photon exchanges for the atom-atom interaction44. Confining two atomic clouds at two ends of a long fibre allows the fibre-based remote macro-entanglement and quantum information transmission45. Especially, substituting the long-lived 1S0−3P0 clock transition for the intercombination transition enables the miniaturization of the physics package of optical lattice clocks25. This compact and transportable setup may facilitate the high-level comparison of optical clocks and time keeping46.
Methods
Loading ultracold atoms into HCPCF
Ultracold 88Sr atoms are prepared via the two-stage MOT29 and then captured at the antinodes of the optical lattice that is formed by a pair of linearly-polarized counter-propagating λL = 813 nm lasers. Both lattice beams match the fundamental LP01 fibre mode with a power of 200 mW. The lattice antinodes are moved along the axial direction (i.e. the z-axis) at a velocity of v(t) = δL(t)λL/2 by introducing time-dependent detuning |δL(t)| ≤ 90 kHz between two lattice lasers. The atomic cloud is transported by a distance of 3.25 mm within a moving time of about 160 ms at a maximum velocity of 32.5 mms−1 The temperature of atoms is measured to be ~4.0 μK by the Doppler width of the spectrum, which suggests the averaged vibrational occupations of na ~ 0.5 and nr ~ 33, for the axial and radial motions, respectively.
The atom-light interaction length can be extended via expanding the atomic cloud inside the fibre by shutting off either of lattice lasers to remove the periodic lattice potential. Then, the atomic cloud experiences a Gaussian-like optical potential in the x − y plane and an axial expansion with the velocity satisfying the Maxwell-Boltzmann distribution. After a short duration, the lattice laser, which has been turned off, is switched on again. The atomic cloud with an expanded axial width lz is recaptured by the lattice potential. During the expanding process, the atom loss is negligible. Figure 1b shows the distribution of the atomic cloud with and without 80-ms-long expansion. We then adiabatically reduced the lattice power to 20 mW, which is one tenth of the initial power, to moderate the density shift and residual light shift for observing SR.
Mode coupling between HCPCF and SMF
A portion of SR light output from the HCPCF enters the SMF (see Fig. 1a). The optical path between HCPCF and SMF is aligned to maximize the coupling efficiency to the fundamental LP01 mode of the HCPCF, which is about 50%. The Gaussian-like ground mode ϕ0(r) of the SMF approximates as \(\phi _0\left( {\mathbf{r}} \right) = \sqrt {2/\left( {\pi \tilde w_0^2} \right)} e^{ - \left| {\mathbf{r}} \right|^2/\tilde w_0^2}\) with the beam radius of \(\tilde w_0 = 0.4w_0\). The coupling efficiency between LP01 and ϕ0(r) is calculated to be \(c_{{\mathrm{LP}}_{{\mathrm{01}}}} = \left| {{\int} {{\int} {\psi _0^ \ast \left( {\mathbf{r}} \right)\phi _0\left( {\mathbf{r}} \right)d^2{\mathbf{r}}} } } \right|^2 = 0.60\), consistent with the experimental measurement (~50%). Here ψ0(r) corresponds to the transverse distribution of LP01. Similarly, the coupling efficiencies of selected high-order modes of HCPCF to SMF are given by \(c_{{\mathrm{LP}}_{{\mathrm{02}}}} = 0.33\), \(c_{{\mathrm{LP}}_{{\mathrm{03}}}} = 0.05\), and \(c_{{\mathrm{LP}}_{{\mathrm{11}}}^{{\mathrm{a}},{\mathrm{b}}}} = c_{{\mathrm{LP}}_{{\mathrm{21}}}^{{\mathrm{a}},{\mathrm{b}}}} = c_{{\mathrm{LP}}_{{\mathrm{31}}}^{{\mathrm{a}},{\mathrm{b}}}} = 0.00\). Thus, the fundamental mode LP01 contributes dominantly in energy at the output end of SMF.
Balanced-heterodyne detection
As depicted in Fig. 1c, two Si PIN photodiodes are used to convert the optical-frequency interference down to a radio-frequency (RF) signal \(V_{{\mathrm{RF}}}\left( t \right) \propto {\mathrm{Re}}\left\{ {\left[{\int} {{\int} {E_{{\mathrm{LO}}}\left( {\mathbf{r}} \right)} } {E_{{\mathrm{SR}}}^\prime \left( {{\mathbf{r}},t} \right)d^2{\mathbf{r}}} \right]e^{ - i{\mathrm{\Omega }}_0t}} \right\}\), where Re{…} gives the real part. Setting the power of the local optical oscillator ELO at PLO ≈ 1 mW, whose shot noise well exceeds the circuit noise, the measurement SNR is approximately given by \(\sqrt {2KP_{{\mathrm{SR}}}/\left( {\pi e{\mathrm{\Delta }}f} \right)}\) where K = 0.42 AW−1 is the photodiodes’ responsivity. We further adopt a band-pass filter (see Fig. 1c) with a FWHM bandwidth of Δf = 4 MHz and a centre frequency of Ω0/2π = 50 MHz to improve the SNR for observing the time-varying radiation amplitude ESR(r, t).
Deriving radiation frequency shift ΔSR
The 10-times-averaged VRF(t) is demodulated into the in-phase VI(t) and quadrature-phase VQ(t) components. We then map the point VI(t) + iVQ(t) within the period from 1.48 μs to 8.38 μs into a complex coordinate system (see the purple line in Fig. 3c). Assuming the frequency shift ΔSR is time independent, the plot can be formulated as \(V\left( t \right)e^{i\Delta _{{\mathrm{SR}}}t + \theta _0}\), where \(V\left( t \right) = \sqrt {V_{\mathrm{I}}^2\left( t \right) + V_{\mathrm{Q}}^2\left( t \right)}\) denotes the distance from the point VI(t) + iVQ(t) to the origin of the coordinate and θ0 is the initial phase, because the phase components are demodulated with the frequency of ω0 (see Figs. 1d and 3a). If we rotate the frame around the origin of the coordinate at a frequency of ω′ and with a phase offset of θ', the plot may be re-expressed as \(V\left( t \right)e^{i\left( {{\mathrm{\Delta }}_{{\mathrm{SR}}} - \omega^\prime } \right)t + \left( {\theta _0 - \theta^\prime } \right)}\). By assigning \(\omega^\prime = \Delta _{{\mathrm{SR}}}\) and θ′ = θ0, the point moves only on the real axis. To find ΔSR from two phase components, we prepare an evaluation function that integrates the square of the imaginary part with respect to time and adopt ω′ that minimizes the evaluation function related to ΔSR. The blue line in Fig. 3c shows the plot in the rotating frame that suppresses the imaginary part and ΔSR is determined to be \(\Delta _{{\mathrm{SR}}} \approx - 2\pi \times 93(10)\,{\mathrm{kHz}}\). Here the uncertainty is estimated by the frequency where the value of the evaluation function is doubled.
Data availability
All data and computer code supporting the findings of this study are available from the corresponding author on reasonable request.
References
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Gross, M. & Haroche, S. Superradiance: an essay on the theory of collective spontaneous emission. Phys. Rep. 93, 301–396 (1982).
Scully, M. O. Collective Lamb shift in single photon Dicke superradiance. Phys. Rev. Lett. 102, 143601 (2009).
Norcia, M. A., Winchester, M. N., Cline, J. R. K. & Thompson, J. K. Superradiance on the millihertz linewidth strontium clock transition. Sci. Adv. 2, e1601231 (2016).
Norcia, M. A. et al. Frequency measurements of superradiance from the strontium clock transition. Phys. Rev. X 8, 021036 (2018).
Chou, C. W., Polyakov, S. V., Kuzmich, A. & Kimble, H. J. Single-photon generation from stored excitation in an atomic ensemble. Phys. Rev. Lett. 92, 213601 (2004).
Reimann, R. et al. Cavity-modified collective Rayleigh scattering of two atoms. Phys. Rev. Lett. 114, 023601 (2015).
Black, A. T., Thompson, J. K. & Vuletić, V. On-demand superradiant conversion of atomic spin gratings into single photons with high efficiency. Phys. Rev. Lett. 95, 133601 (2005).
Chan, H. W., Black, A. T. & Vuletić, V. Observation of collective-emission-induced cooling of atoms in an optical cavity. Phys. Rev. Lett. 90, 063003 (2003).
Wolke, M., Klinner, J., Keßler, H. & Hemmerich, A. Cavity cooling below the recoil limit. Science 337, 75–78 (2012).
DeVoe, R. G. & Brewer, R. G. Observation of superradiant and subradiant spontaneous emission of two trapped ions. Phys. Rev. Lett. 76, 2049–2252 (1996).
Scheibner, M. et al. Superradiance of quantum dots. Nat. Phys. 3, 106–110 (2007).
Laurent, T. et al. Superradiant emission from a collective excitation in a semiconductor. Phys. Rev. Lett. 115, 187402 (2015).
Peyrot, T. et al. Collective Lamb shift of a nanoscale atomic vapor layer within a sapphire cavity. Phys. Rev. Lett. 120, 243401 (2018).
Mlynek, J. A., Abdumalikov, A. A., Eichler, C. & Wallraff, A. Observation of Dicke superradiance for two artificial atoms in a cavity with high decay rate. Nat. Commun. 5, 5186 (2014).
Skribanowitz, N., Herman, I. P., MacGillivray, J. C. & Feld, M. S. Observation of Dicke superradiance in optically pumped HF gas. Phys. Rev. Lett. 30, 309–312 (1973).
Inouye, S. et al. Superradiant Rayleigh scattering from a Bose-Einstein condensate. Science 285, 571–574 (1999).
Araújo, M. O., Krešić, I., Kaiser, R. & Guerin, W. Superradiance in a large and dilute cloud of cold atoms in the linear-optics regime. Phys. Rev. Lett. 117, 073002 (2016).
Goban, A. et al. Superradiance for atoms trapped along a photonic crystal waveguide. Phys. Rev. Lett. 115, 063601 (2015).
Bajcsy, M. et al. Efficient all-optical switching using slow light within a hollow fiber. Phys. Rev. Lett. 102, 203902 (2009).
Bloch, I. Ultracold quantum gases in optical lattices. Nat. phys. 1, 23–30 (2005).
Ido, T. & Katori, H. Recoil-free spectroscopy of neutral Sr atoms in the Lamb-Dicke regime. Phys. Rev. Lett. 91, 053001 (2003).
Kien, F. L., Gupta, S. D., Nayak, K. P. & Hakuta, K. Nanofiber-mediated radiative transfer between two distant atoms. Phys. Rev. A 72, 063815 (2005).
Corzo, N. V. et al. Waveguide-coupled single collective excitation of atomic arrays. Nature 566, 359–362 (2019).
Okaba, S. et al. Lamb-Dicke spectroscopy of atoms in a hollow-core photonic crystal fibre. Nat. Commun. 5, 4096 (2014).
Wang, Y. Y., Wheeler, N. V., Couny, F., Roberts, P. J. & Benabid, F. Low loss broadband transmission in hypocycloid-core Kagome hollow-core photonic crystal fiber. Opt. Lett. 36, 669–671 (2011).
Couny, F., Benabid, F., Roberts, P. J., Light, P. S. & Raymer, M. G. Generation and photonic guidance of multi-octave optical-frequency combs. Science 318, 1118–1121 (2007).
Marcatili, E. A. J. & Schmetzer, R. A. Hollow metallic and dielectric waveguides for long distance optical transmission and lasers. Bell Syst. Tech. J. 43, 1783–1809 (1964).
Katori, H., Ido, T., Isoya, Y. & Kuwata-Gonokami, M. Magneto-optical trapping and cooling of strontium atoms down to the photon recoil temperature. Phys. Rev. Lett. 82, 1116–1119 (1999).
Schilke, A., Zimmermann, C., Courteille, P. W. & Guerin, W. Photonic band gaps in one-dimensionally ordered cold atomic vapors. Phys. Rev. Lett. 106, 223903 (2011).
Scully, M. O. & Svidzinsky, A. A. The super of superradiance. Science 325, 1510–1511 (2009).
Yuen, H. P. & Chan, V. W. S. Noise in homodyne and heterodyne detection. Opt. Lett. 3, 177–179 (1983).
Heinzen, D. J., Thomas, J. E. & Feld, M. S. Coherent ringing in superfluorescence. Phys. Rev. Lett. 54, 677–680 (1985).
Greiner, C., Boggs, B. & Mossberg, T. W. Superradiant emission dynamics of an optically thin material sample in a short-decay-time optical cavity. Phys. Rev. Lett. 85, 3793–3796 (2000).
Bienaime, T., Piovella, N. & Kaiser, R. Controlled Dicke subradiance from a large cloud of two-level systems. Phys. Rev. Lett. 108, 123602 (2012).
Guerin, W., Araújo, M. O. & Kaiser, R. Subradiance in a large cloud of cold atoms. Phys. Rev. Lett. 116, 083601 (2016).
Ido, T. et al. Precision spectroscopy and density-dependent frequency shifts in ultracold Sr. Phys. Rev. Lett. 94, 153001 (2005).
Friedberg, R., Hartmann, S. R. & Manassahab, J. T. Frequency shifts in emission and absorption by resonant systems of two-level atoms. Phys. Rep. 7, 101–179 (1973).
Ostermann, L., Meignant, C., Genes, C. & Ritsch, H. Super- and subradiance of clock atoms in multimode optical waveguides. New J. Phys. 21, 025004 (2019).
Lehmberg, R. H. Radiation from an N-Atom System. I. General Formalism. Phys. Rev. A 2, 883–888 (1970).
Olmos, B. et al. Long-range interacting many-body systems with alkaline-earth-metal atoms. Phys. Rev. Lett. 110, 143602 (2013).
Alharbi, M. et al. Hypocycloid-shaped hollow-core photonic crystal fiber Part II: cladding effect on confinement and bend loss. Opt. Express 21, 28609–28616 (2013).
Dimer, F., Estienne, B., Parkins, A. S. & Carmichael, H. J. Proposed realization of the Dicke-model quantum phase transition in an optical cavity QED system. Phys. Rev. A 75, 013804 (2007).
Welsch, D.-G., Dung, H. T. & Knöll, L. Dipole-dipole coupling in the presence of dispersing and absorbing bodies. Fortschr. Phys. 51, 255–261 (2003).
Northup, T. E. & Blatt, R. Quantum information transfer using photons. Nat. Photon. 8, 356–363 (2014).
Koller, S. B. et al. Transportable optical lattice clock with 7 × 10−17 uncertainty. Phys. Rev. Lett. 118, 073601 (2017).
Acknowledgements
This work is supported by JST ERATO Grant No. JPMJER1002 10102832 (Japan), by JSPS Grant-in-Aid for Specially Promoted Research Grant No. JP16H06284, and by the Photon Frontier Network Program of the Ministry of Education, Culture, Sports, Science and Technology, Japan (MEXT). F.B. acknowledges financial supports from Agence Nationale de la Recherche (ANR).
Author information
Authors and Affiliations
Contributions
H.K. envisaged and initiated the experiments. H.K. and S.O. designed the apparatus and experiments. S.O. carried out the experiments and analysed the data. S.O. and H.K. discussed experimental results and equally contributed to the experiments. D.Y. developed theoretical models for the experiments. F.B. designed and fabricated the fibre for the experimental requirements and assessed the in-fibre dipole spontaneous emission, and L.V. calculated the fibre modal fields. All authors participated in discussions and the writing of the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Okaba, S., Yu, D., Vincetti, L. et al. Superradiance from lattice-confined atoms inside hollow core fibre. Commun Phys 2, 136 (2019). https://doi.org/10.1038/s42005-019-0237-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0237-2
This article is cited by
-
Theoretical study of superradiant masing with solid-state spins at room temperature
Science China Physics, Mechanics & Astronomy (2024)
-
Full characterization of superradiant pulses generated from a free-electron laser oscillator
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.