Abstract
Quantum imaging has a potential of enhancing the precision of objects reconstruction by exploiting quantum correlations of the imaging field, in particular for imaging with low-intensity fields up to the level of a few photons. However, it generally leads to nonlinear estimation problems. The complexity of these problems rapidly increases with the number of parameters describing the object and the correlation order. Here we propose a way to drastically reduce the complexity for a wide class of problems. The key point of our approach is to connect the features of the Fisher information with the parametric locality of the problem, and to reconstruct the whole set of parameters stepwise by an efficient iterative inference scheme that is linear on the total number of parameters. This general inference procedure is experimentally applied to quantum near-field imaging with higher-order correlated light sources, resulting in super-resolving reconstruction of grey compound transmission objects.
Similar content being viewed by others
Introduction
Quantum metrology exploits the quantum features of measurement schemes to infer the parameters of interest with enhanced precision, compared with classical schemes1. In some cases, such as interferometry2,3, the number of parameters to be determined is small, and inferring them from measurement results is straightforward. However, for a large number of parameters, the problem of inferring them from measurement results can be quite demanding, even when it is linear. It might require a prohibitive amount of measurement and computational effort to be solved. For example, to reconstruct the state of a moderate number (say, a few dozen) of the simplest quantum objects, qubits, one already needs some simplifying assumptions, such as a low rank of the state4,5,6,7, the possibility to approximate the state by a matrix product8, or by a permutationally invariant state9,10,11. For nonlinear problems, the task is even more difficult12,13. A typical case of multiparameter determination is quantum imaging14. Images with improved optical resolution can be obtained from higher-order correlation functions of the light field, thanks to correlation in the illumination sources15,16,17. For this problem, the number of parameters can be related to the number of pixels in the image to be reconstructed.
Here, we present an efficient method for nonlinear estimation problems that applies for the important class of parametrically localized measurements. For this class, the result of a particular measurement is dependent on a limited subset of parameters only. Such measurements are common for objects consisting of components well separated in physical or phase space. For example, measurements on individual systems in ion traps18 or optical lattices19, direct20 and near-field imaging14, or data-pattern tomography21 fall into this category. For such measurements, we develop an iterative sliding-window method (SWM) by reconstructing on each step only a subset of parameters that can be much smaller than the total number of parameters. The complexity for such an approach depends linearly on the number of times one needs to shift the window to cover the whole parameter set. To establish the use of the SWM, we develop an informational approach for the analysis of the measurement scheme. We apply here the Fisher information matrix (FIM) for the analysis of the problem and for designing the SWM. Nowadays, Fisher information analysis is firmly establishing itself as an operational tool in quantum tomography and imaging schemes22,23,24,25,26. We show how the structure of the FIM can be exploited for estimating the size and structure of the parameter subset of the SWM iterations. We demonstrate the efficiency of our method with the practically important problem of imaging with correlated photons by measuring a second- or higher-order correlation function for position–momentum-entangled photons generated by spontaneous parametric downconversion (SPDC) and pseudo-thermal light. We predict the existence of an optimal degree of photon correlations in the imaging field to achieve the best resolution for a given object. The FIM analysis allows us also to uncover the possibility to increase the resolution by using biased estimation with a bias stemming from physical limitations on the set of the problem parameters.
Results
Theoretical background
To elucidate our approach, let us start with the simplest linear measurement model described with the probabilities \(p_k = \mathop {\sum}\nolimits_{j = 1}^M {C_{kj}} \theta _j\), where θj are the parameters in question and Ckj is the square Hermitian measurement matrix. We call the measurement strictly parametrically l-local, if l < M and Ckj = 0 for |k − j| > l, i.e., the matrix C is l-banded, and the (l + 1)th and other side diagonals are equal to zero. It means that each probability pj depends on no more than 2l neighboring parameters. The key observation here is the possibility to approximate the inverses of banded matrices with approximately banded matrices27,28. It would mean that the estimator of the parameter θj depends only on probabilities in the vicinity of pj. Such a locality provides the possibility of getting an accurate estimate for some θh, for example, by minimization of the distance between a set of experimentally measured frequencies, fk, k ∈ [h − J, h + J], where J ≥ l is an interval around h, and the probabilities estimated as \(p_k \approx \mathop {\sum}\nolimits_{j = h \,-\, J}^{h \,+\, J} {C_{kj}} \theta _j\)8. Estimation can be performed for a sequence of h, thus, shifting the estimation window along the whole set of parameters. The complexity of the SWM is linear on the number of shifts required to cover the whole set of parameters. Below we elaborate on this possibility. Notice that the consideration given above holds also for non-strictly parametrically local measurements (Supplementary Note 1).
Now let us consider the general nonlinear parametric measurement model pk = Ck(θ1, …θM). Strict parametric l-locality for the case would mean \(\frac{{\partial p_j}}{{\partial \theta _m}} = 0\) for |m − j| > l. Our suggestion is to estimate the influence of a given change of a particular parameter on the other parameters with help of the FIM and the Cramer–Rao bound (CRB). By assuming the completeness of the measurement set, \(\mathop {\sum}\nolimits_k {p_k} = 1\), the FIM for this case reads
For the unbiased estimate, the CRB connects the elements of the inverse FIM with the variance of the estimators, Δ2(θj) ≥ [F−1]jj/N, where N gives the total number of events. A banded structure of the FIM would mean that an error estimate for a particular parameter, θh, can be influenced by variations of the parameters only in some vicinity [h − J, h + J]. Our suggestion is to use this clue for designing the SWM as it was described above for the linear case. Also, FIM and CRB can be used for optimization of the measurement scheme aiming at lowering the error bounds per given number of measured events, N. One can minimize the bound for the total measurement error described by the trace of the inverse FIM. A banded structure of the FIM gives a clue to the connection between the width of the FIM and the total error: generally, for given diagonal elements of the FIM, increasing the width (i.e., a number and value of bands) leads to an increase in the inverse trace and the total error (Supplementary Note 2). One can also define an empirical Rayleigh criterion for the parameter resolution from the banded structure: when the FIM is strongly diagonally dominant, \(F_{jj} \gg \mathop {\sum}\nolimits_{k \ne j} | F_{jk}|\), then statistical errors for estimation of the parameter θj are defined mainly by the measured fj, and the parameters can be well estimated by individual measurements. Notice that the diagonal dominance is a quite strong property imposing locality (Supplementary Note 1). For example, for a strictly one-banded diagonally dominant FIM, a lower bound on the variance of θj is defined by elements Fjk with |j − k| ≤ 229.
Imaging with higher-order correlation functions
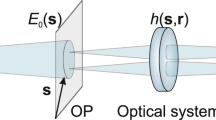
We illustrate the previous discussion by applying the SWM to practically relevant examples of quantum near-field imaging by means of higher-order correlation functions. Measuring higher-order correlation functions14,30,31,32 is one of the ways to increase the resolution of imaging33,34,35,36,37 and to go beyond the empirical Rayleigh limit38. The scheme of the measurement setup is depicted in Fig. 1. The source produces the linearly polarized field with the density matrix ρ. This field passes through the object described by the transmission function \(A(\overrightarrow {\mathbf{s}} )\) and then through the imaging system characterized by the point-spread function \(h(\overrightarrow {\mathbf{s}} ,\overrightarrow {\mathbf{r}} )\). Afterward, the field goes to the detectors. The field amplitude operator at the object plane, \(E_{\mathrm{o}}(\overrightarrow {\mathbf{s}} )\), relates to the field amplitude operator at the image plane, \(E(\overrightarrow {\mathbf{r}} )\), in the following way:
where \(h(\overrightarrow {\mathbf{s}} ,\overrightarrow {\mathbf{r}} )\) is a PSF describing the field propagation between the object and the image plane14. Integration in Eq. (2) is over the object plane O. We represent the object as a superposition of M pixels \(A(\overrightarrow {\mathbf{s}} ) = \mathop {\sum}\nolimits_{j = 1}^M {d_j} (\overrightarrow {\mathbf{s}} )x_j\), where the function \(d_j(\overrightarrow {\mathbf{s}} )\) describes the unit transmission through the jth pixel, and xj is the value of the transmission assigned to the jth pixel. We measure the nth-order intensity correlation function, \(G_k^{(n)} = {\mathrm{Tr}}\left\{ \left[ {\mathop {\prod}\nolimits_{l = 1}^n E (\overrightarrow {\mathbf{r}} _l^{(k)})} \right]^\dagger \left[ {\mathop {\prod}\nolimits_{l = 1}^n E (\overrightarrow {\mathbf{r}} _l^{(k)})} \right]\rho \right\}\), where the index k numbers some set of n points, \(\overrightarrow {\mathbf{r}} _1^{(k)},\overrightarrow {\mathbf{r}} _2^{(k)} \ldots \overrightarrow {\mathbf{r}} _n^{(k)}\), in the image plane. The detection probabilities are
The coefficients D(k)(l1…ln; m1…mn) are defined by the imaging system and the state of the source. In Supplementary Note 3, D(k) are derived for SPDC-entangled photons, and pseudo-thermal states used for experimental implementations.
Scheme of the imaging setup. The source produces the field with the density matrix ρ; this field passes through the object described by the transmission function \(A(\overrightarrow {\mathbf{s}} )\) and then through the imaging system characterized by the point-spread function \(h(\overrightarrow {\mathbf{s}} ,\overrightarrow {\mathbf{r}} )\). Afterward, the field is detected at the image plane
Sliding-window method for imaging
The problem of the object inference is to find a set of transmission values {xj} fitting the measured data described by the set of frequencies fk in the best way. For the realization of the SWM, we implement the following iterative scheme: in the first step, we define the pixels (the functions \(d_j(\overrightarrow {\mathbf{s}} )\)) in such a way that the FIM, i.e., Eq. (1), is strongly diagonally dominant and infers the initial approximation. Then, we divide each initial pixel in a subgroup of smaller pixels, assign to each of them the transmittance of the parent pixel, and calculate the FIM. Next, we define the window to be shifted as some set of adjacent “core” pixels and some “border” pixels around the “core”. Thereby, we use the number and relative value of major bands of the FIM for defining the size of the “border” and perform the fitting. Notice that for building the procedure, one does not need to know the object beforehand or to perform some preliminary estimation. The pixel size and the window structure can be defined for the model object and the used imaging setup. The details of the SWM method and the pseudocode are provided in the “Methods” section.
Object inference
Let us illustrate the mechanics of the SWM with transmitting 1D and 2D objects. We take for our examples common “workhorses” of the quantum imaging field: a pseudo-thermal state39 and a position–momentum-entangled state produced by SPDC40. In Fig. 2, one can see an illustration of the SWM for a 1D object for the simulated G(2) (Supplementary Note 3). Figure 2a, b shows an example of the typical strongly diagonally dominant FIM for a pixel larger than the Rayleigh limit (Fig. 2a), and the FIM with a pixel smaller than the Rayleigh limit (Fig. 2b). However, the FIM of Fig. 2b is still narrowly banded, and thus the inference problem is treatable by the SWM. The rule of thumb here is to choose the size of the border region larger than the number of the major bands of the FIM. Figure 2c shows the object. Figure 2d shows the simulated G(2) for the object of Fig. 2c for the thermal source. The image of the object (Fig. 2c) is shown in Fig. 2d, e. The process of reconstruction by moving the “window” is depicted in Fig. 2f (see the Methods section). The result of the reconstruction is shown in Fig. 2g, h. Notice that for this case, we have come beyond the Rayleigh limit Δl, shown with the red bar in Fig. 2h: the reconstruction result 2g is close to the original object shown in Fig. 2c, while the diagonal part of the image 2e looks differently. The object inference for the higher-order correlation functions can be realized similarly to the procedure described above.
The sliding-window method. Examples of the Fisher information matrix for large pixels (a) and for super-resolution regime (b) for reconstruction of a one-dimensional image with the second-order correlation function. Horizontal axes number the pixels. The object (c) is used for simulation of G(2) (panels d and e present the correlation map and its normalized diagonal part; axes in panel d number the pixels), for 106 joint detection events. The sliding-window method is schematically shown in panel f, the reconstruction result is shown in panel g. The result of the reconstruction (solid line) is compared with the original model object (dashed line) and diagonal part of G(2) (gray line) in plot (h); the horizontal axis in panel h numbers pixels. Simulations are performed for a thermal source
Experiment
The experimental verification of the SWM was done with the particular realizations of a generic measurement scheme depicted in Fig. 1 for both, a pseudo-thermal and a spontaneous downconversion (SPDC) source (see the Methods section). To produce pseudo-thermal light, a rotating ground glass disk was illuminated by a monochromatic laser39,41 operating at 405 nm. Type-0 position–momentum-entangled two-photon states were generated by a SPDC source40. Thereby, we use a 12-mm-long periodically poled potassium titanyl phosphate (PPKTP) nonlinear crystal pumped by a continuous-wave laser centered at 405 nm. The entangled photons are then emitted at 810 nm. Detection at the image plane was done for the pseudo-thermal light by using SuperEllen, a single-photon- sensitive 32 × 32-pixel single-photon avalanche diode (SPAD) array detector manufactured in complementary metal–oxide–semiconductor (CMOS) technology17,42; and by scanning single photon counters for the entangled photons40. Figure 3 shows the results of the SWM for experimental data. Figure 3b shows the reconstructed 2D object inferred from the measurement of G(3) for the pseudo-thermal source shown in Fig. 3a (only the diagonal part is shown). Figure 3c, d presents reconstruction of the 1D object from G(2) for the SPDC imaging state. Resolution beyond the Rayleigh limit (shown by red bars) is demonstrated for both sources.
Experimental data and reconstructed pixel transmissions. Pseudo-thermal light source and a digit “5” object (190 × 311 μm) from group 2 of a negative 1951 U.S. Air Force (USAF) resolution test chart: a diagonal part of a measured G(3) function, b reconstruction result. Spontaneous downconversion source and a one-dimensional object being the positive 1951 U.S. Air Force resolution test slits with 31.25-μm width: c measured G(2)(x1, x2), d reconstruction result. The red segments correspond to the Rayleigh limit Δl for the used optical system
Optimization of the imaging state
The informational approach allows us to predict the optimal correlation width of the used illumination source for the object resolution in the super-resolution regime. Intuitively, it seems that the smaller the correlation width is, the better the resolution should be. However, the analysis of the collected information shows that for the object inference, perfectly correlated photons might not be the best choice. It follows from an optimization of the lower bound on the total reconstruction error. This prediction is valid for an arbitrary reconstruction method for the measurement of the second-order correlation function with both twin-photon and quasi-thermal imaging source. In Fig. 4a, an example of the optimization is shown for the image reconstruction from a G(2) function for a pseudo-thermal state. The trace of the inverse FIM and the infidelity of the reconstruction are shown for different correlation widths wc. There is an optimal wc allowing to increase the reconstruction quality for the same number of detector counts in the super-resolution regime. One can describe the most optimal state with the following rule of thumb: the correlation width should be close to the smallest object details to be resolved, i.e., to the pixel size. In the super-resolution regime, the measurement of the second-order intensity correlation gives the most information per detected photon coincidence event about the object when the photons going through the neighboring pixels are correlated. This prediction is confirmed by the experimental results shown in Fig. 4b by using the pseudo-thermal source with various correlation widths of the generated speckles (Supplementary Note 3). A similar relation between the optimal photon correlation width and the size of the object features also holds for a SPDC source (Supplementary Note 4). For pixel size exceeding the Rayleigh limit, this effect disappears; decreasing the correlation width brings about enhancement of the resolution (Fig. 4c).
Inverse Fisher information matrix trace and reconstruction infidelity for 1D pseudo-thermal light images. a Calculated dependence of the total measurement error on wc for the object in the inset. The solid and dashed lines correspond to d/Δl = 0.41, 0.5. The object pixel size d is normalized by the Rayleigh limit Δl. Vertical dotted lines correspond to wc = 1.5 pix (the value of the minimum). b Measured infidelity for the same object and super-resolution regime as in a. Red bars show the standard deviations of the reconstruction results for the analysis of 12 independent 1D datasets taken from a single 2D experiment. c Calculated dependence of the total measurement error on d/Δl for the top object in the insets in d. Dotted, dot-dashed, solid, and dashed lines correspond to wc = ∞, 2, 1, and 0 pixels. Vertical dashed lines correspond to d/Δl = 0.5. d Calculated infidelity for the objects in the inset. Thick lines correspond to black-and-white objects and thin lines to gray objects
Inference bias
The informational approach and the SWM can capture the possibility of a considerable improvement of resolution stemming from constraints imposed on the parameters. For the special case of parameters being on the borders of the allowed regions, the estimation is generally biased. The bias can significantly modify the error bounds43,44 (see Supplementary Note 5 and Fig. 4d). For the imaging of binary black-and-white objects (i.e., for xj being either 0 or 1; see bottom inset and thick lines in Fig. 4d), one can go far beyond the resolution limit found for gray images (top inset and thin lines in Fig. 4d) even without any prior assumption of the binary object structure. The reason for it is the dependence of the error bounds on the bias derivative with respect to the parameters43. Generally, the SWM shifts the estimators near borders. The closer the estimated value is to the border, the larger is the respective shift and the error-bound deviation. Notice that for the object inference demonstrated in Fig. 3, this bias effect was actually seen.
Discussion
We developed an inference method for nonlinear parametrically local problems and showed how the analysis of the information allows one to develop an estimation scheme making the complexity of the problem linear on the total number of parameters. Then, the scheme was applied to the experimental data for super-resolution imaging based on higher-order correlation measurements with nonclassical two-photon and pseudo-thermal states. It was shown how the FIM can be applied to optimize the imaging state for better resolution, in particular, for the correlation width of the twin-photon or pseudo-thermal imaging fields. Generally, the correlation width should be close to the smallest details to be resolved. This prediction is experimentally confirmed for measurements with pseudo-thermal light. It was also demonstrated that bias due to marginal values of estimated parameters can improve the resolution. We believe that the suggested SWM and an information approach for nonlinear inference problems will find applications for the design and optimization of inference schemes in imaging, quantum diagnostics, and tomography.
Methods
The sliding-window method
The practical application of the SWM to the quantum imaging problem consists of the following steps.
First, an initial rough estimate of the object transmission amplitude is found. The pixel size is chosen in such a way that the inverse of the FIM for the reconstruction of the object, expressed in terms of pixels of this size, \(d_0^{\left( 0 \right)}\), is diagonally dominant. The problem is strongly local, and a single run of the SWM is sufficient for getting the initial estimate.
Then, the estimate is refined by representing the object in terms of smaller pixels (size d) and applying the reconstruction algorithm again. The pixel size d limits the size of the object features that can be successfully reconstructed, and therefore, determines the achievable resolution.
Here, the pseudocode for the iterative reconstruction is presented. Both algorithms (the one for the first approximation inference and the one for refinement) are mathematically very similar, the only difference is the role of the window border: the first algorithm implies that pixels inside the border are unknown and not reliable (at each step): they need to be reconstructed but then discarded; the second algorithm implies that pixels inside the border are known (at each step) and thus can be included in the optimization problem as known constants (Fig. 5).
An example of two adjacent reconstruction steps for a general two-dimensional case. Panels a, b correspond to obtaining the first approximation, and c, d correspond to iterative refinement. Although pixels are divided after the first approximation is obtained, here the pixel size is chosen to be the same for both cases in order to show mathematical similarity of the first approximation inference and refinement. Letter “X” denotes pixels for which the optimization problem will be stated (“unknown” pixels), digit “0” denotes pixels that will be completely ignored at the iteration (“irrelevant” pixels), and letter “V” denotes pixels whose values will be included in the optimization problem as known constants (“known” pixels). Dashed frame shows the core of the window, solid frame shows the whole window, the core, and the border
The pseudocode for the first approximation inference algorithm reads as follows:
For given core window dimensions, compute all core window positions that lead to the object being fully covered by non overlapping core windows. For each position of the core window:
-
1.
For a given border size, build a complete window: core + border.
-
2.
Map the resulting full window to the image plane.
-
3.
Find all detectors inside the obtained window in the image plane.
-
4.
Combine the obtained detectors according to the order of correlations and other constraints if present.
-
5.
For the obtained detector combinations, load the corresponding experimental joint detection frequencies.
-
6.
Build a function that maps pixels inside the full window to residuals between theoretical joint detection probabilities and experimental frequencies. The theoretical probabilities are computed by assuming all pixels but those inside the window to be zero.
-
7.
Perform numerical minimization of the function thus obtained. Pixels inside the full window are subjected to physical constraints.
-
8.
Update object pixels inside the core window with the corresponding values obtained from the minimization procedure. Discard other pixel values.
Because the algorithm first computes all core window positions and then applies one iteration per core window position, it is easily paralleled.
The pseudocode for the iterative refinement algorithm reads as follows:
-
1.
For a given core window position and a given border size, build a complete window: core + border.
-
2.
Map the resulting window to the image plane.
-
3.
Find all detectors inside the obtained window in the image plane.
-
4.
Combine the obtained detectors according to the order of correlations and other constraints if present.
-
5.
For the obtained detector combinations, load the corresponding experimental joint detection frequencies.
-
6.
Build a function that maps pixels inside the core window to the residuals between theoretical joint detection probabilities and experimental frequencies. The theoretical probabilities are computed by assuming pixels outside the core window but inside the full window to be known, they are set to constant values. Pixels outside the full window are set to zero.
-
7.
Perform numerical minimization of the function thus obtained. Pixels inside the core window are subject to physical constraints.
-
8.
Update pixels inside the core window with the values obtained. Move the core window one step further.
Experiments
In the first experiment, we illuminate a rotating ground glass disk (RGGD) with an attenuated, monochromatic laser operating at λ = 405 nm (Fig. 6). An additional lens (L1) in front of the disk allows to vary the beam waist radius at the position of the RGGD. Subsequently, we insert a far-field lens (L2) in a 2f setting (f = 75 mm) in order to collimate the light and remove the spherical wave front given by the point-like source. (The latter has shown to induce distortions in the subsequent imaging setup.) The object plane (OP) is then located in the far field of the source. An object is then imaged onto the image plane (IP) by means of L3 (f = 150 mm), which is additionally endowed with a variable-size pinhole (PH) to control the resolution, i.e., the Rayleigh limit of the setup. The diameter of the PH was fixed to 1.7 mm. The magnification factor m = si/so of the imaging system is m = 1.94, whereas the object distance is so = 234 mm, and the imaging distance is given by si = 454 mm. At the image plane, photons are detected by SuperEllen, a single-photon-sensitive 32 × 32-pixel SPAD array detector manufactured in CMOS technology with a pixel pitch of 44.64 μm and a fill factor of 19.7%17,42. SuperEllen is able to provide frames with a data acquisition window of 30 ns, and a readout time of 10 μs at a frame rate of 800 kHz. The spatial correlations between pixels were evaluated between consecutive frames with a resolution of 10 μs given by the frame separation. This procedure allows for the resolution of the coherence time of the speckles of the order of microseconds. Second- and third-order correlation functions are measured with SuperEllen.
Pseudo-thermal light imaging setup. A monochromatic laser is focused onto a rotating ground glass disk (RGGD) by means of lens L1. The subsequent lens L2 provides the far-field speckle pattern at the object plane (OP). The resolution of the single-lens (L3) imaging system can be modified by a variable-size pinhole (PH). Single photons are detected at the image plane (IP) by SuperEllen
The here-presented pseudo-thermal light setup was used to obtain the following two results: first, the digit “5” (Group 2) from a negative U.S. Air Force (USAF) test chart was imaged and then reconstructed from the data of a G(3) function measurement. This is shown in Fig. 3a, b of the main text. Second, a negative USAF chart three-slit pattern (Group 3, Element 2) was imaged from the object plane to the image plane for various correlation widths wc. The latter was modified by changing the distance between the focusing lens L1 and the RGGD, and therefore the beam waist radius. Based on a G(2) measurement, this allowed to demonstrate the dependence of the image reconstruction quality on the correlation width of the source shown in Fig. 4b of the main text.
The setup for imaging with entangled photons is shown in Fig. 7. Our source generates type-0 position–momentum-entangled photon states by pumping a 12-mm-long PPKTP nonlinear crystal (NLC) with a continuous-wave (CW) laser centered at 405 nm40. The entangled photons are then emitted at 810 nm. The residual pump beam is subsequently blocked by a long-pass filter (LF), and the subsequent band-pass filter (BF) transmits photons at 810 nm with a spectral full width at half maximum (FWHM) of 10 nm to the detectors. The experimental setup contains two imaging systems: the first system consists of a 4-f image by using lenses L1 and L2 both with focal length f = 50 mm. This configuration maps the entangled photon states transverse momentum distribution from the OP1 at the center of the NLC to the OP with a magnification factor of m = 1. The OP is then imaged with a single-lens system onto the fiber tips of two multimode fibers (MMFs). Thereby, we have a magnification factor of m = 12 for so = 65 mm and si = 780 mm. Both detection stages can be scanned in horizontal direction. This setup was used to record the image of a three-slit pattern of a positive USAF resolution chart (Group 4, Element 1) by measuring a second-order correlation function of the photons. The experimental correlation map and the reconstructed object can be seen in Fig. 3c, d of the main text.
SPDC setup. A monochromatic laser is weakly focused into a PPKTP nonlinear crystal (NLC) to generate type-0 SPDC. The two-photon state is imaged via a 4-f arrangement from the center of the NLC to the object plane (OP) by using lenses L1 and L2. A long-pass filter (LF) blocks the pump and a band-pass filter (BF) transmits photons at 810 nm. A single-lens imaging system with lens L2 maps the OP onto the image plane (IP), which coincides with the fiber tip of two multimode fibers (MMFs) connecting the detection stages D1 and D2 in a coincidence circuit. The resolution of the imaging system is modified by a variable-size pinhole (PH)
Data availability
The datasets generated and analyzed during the current study are available from the depository of the Center for Quantum Optics and Quantum Information of B. I. Stepanov Institute of Physics, National Academy of Sciences of Belarus http://master.basnet.by/Informational-approach-for.data.rar.
Code availability
The source codes used for the sliding-window method are available from the corresponding author upon reasonable request.
References
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Phot. 5, 222–229 (2011).
Sanders, B. C. & Milburn, G. J. Optimal quantum measurements for phase estimation. Phys. Rev. Lett. 75, 2944 (1995).
Berry, D. W. & Wiseman, H. M. Optimal states and almost optimal adaptive measurements for quantum interferometry. Phys. Rev. Lett. 85, 5098–5101 (2000).
Candes, E. J., Romberg, J. K. & Tao, T. Stable signal recovery from incomplete and inaccurate measurements. IEEE Trans. Inform. Theory 52, 489–509 (2006).
Donoho, D. L. Compressed sensing. Information theory. IEEE Trans. Inform. Theory 52, 1289–1306 (2006).
Gross, D., Liu, Y.-K., Flammia, S. T., Becker, S. & Eisert, J. Quantum state tomography via compressed sensing. Phys. Rev. Lett. 105, 150401 (2010).
Riofrio, C. A. et al. Experimental quantum compressed sensing for a seven-qubit system. Nat. Comm. 8, 15305 (2017).
Cramer, M. et al. Efficient quantum state tomography. Nat. Comm. 1, 1–149 (2010).
Tóth, G. et al. Permutationally invariant quantum tomography. Phys. Rev. Lett. 105, 250403 (2010).
Moroder, T. et al. Permutationally invariant state reconstruction. New J. Phys. 14, 105001 (2012).
Schwemmer, C. et al. Efficient tomographic analysis of a six photon state. Phys. Rev. Lett. 113, 040503 (2014).
Thiebaut, E. & Young, J. Principles of image reconstruction in optical interferometry: tutorial. JOSA A 34, 904–923 (2017).
Ortega, J. M. & Rheinboldt, W. C. Iterative Solution of Nonlinear Equations in Several Variables (Academic Press Inc, San Diego, 1970).
Shih, Y. H. Quantum imaging. IEEE J. Sel. Top. Quantum Electron. 13, 1016–1030 (2007).
Giovannetti, V., Lloyd, S., Maccone, L. & Shapiro, J. H. Sub-Rayleigh diffraction-bound quantum imaging. Phys. Rev. A 79, 013827 (2009).
Tsang, M. Quantum imaging beyond the diffraction limit by optical centroid measurements. Phys. Rev. Lett. 102, 253601 (2009).
Unternährer, M., Bessire, B., Gasparini, L., Perenzoni, M. & Stefanov, A. Super-resolution quantum imaging at the Heisenberg limit. Optica 5, 1150–1154 (2018).
Haffner, H. R. et al. Scalable multiparticle entanglement of trapped ions. Nature 438, 643–646 (2005).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885 (2008).
Tetienne, J.-Ph et al. Quantum imaging of current flow in graphene. Sci. Adv. 3, e1602429 (2017).
Rehacek, J., Mogilevtsev, D. & Hradil, Z. Operational tomography: fitting of data patterns. Phys. Rev. Lett. 105, 010402 (2010).
Tsang, M., Nair, R. & Lu, X.-M. Quantum theory of superresolution for two incoherent optical point sources. Phys. Rev. X 6, 031033 (2016).
Nair, R. & Tsang, M. Far-field superresolution of thermal electromagnetic sources at the quantum limit. Phys. Rev. Lett. 117, 190801 (2016).
Motka, L. et al. Optical resolution from Fisher information. Eur. Phys. J. 131, 130 (2016).
Rehacek, J. et al. Multiparameter quantum metrology of incoherent point sources: towards realistic superresolution. Phys. Rev. A 96, 062107 (2017).
Seveso, L., Rossi, M. A. C. & Paris, M. G. A. Quantum metrology beyond the quantum Cramér-Rao theorem. Phys. Rev. A 95, 012111 (2017).
Bickel, P. & Lindner, M. Approximating the inverse of banded matrices by banded matrices with applications to probability and statistics. Theory Probab. Appl. 56, 1–20 (2012).
Demko, S., Moss, W. F. & Smith, P. W. Decay rates for inverses of band matrices. Math. Comp. 43, 491–499 (1984).
Politi, T. & Popolizio, M. A note on estimates of diagonal elements of the inverse of diagonally dominant tridiagonal matrices. JIPAM 9, 31 (2008).
Zhang, P., Gong, W., Shen, X., Huang, D. & Han, S. Improving resolution by the second-order correlation of light fields. Opt. Lett. 34, 1222–1224 (2009).
Chen, X.-H. et al. High-visibility, high-order lensless ghost imaging with thermal light. Opt. Lett. 53, 1166–1668 (2010).
Zhou, Y., Simon, J., Liu, J. & Shih, Y. Third-order correlation function and ghost imaging of chaotic thermal light in the photon counting regime. Phys. Rev. A 81, 043831 (2010).
Monticone, D. G. et al. Beating the Abbe diffraction limit in confocal microscopy via nonclassical photon statistics. Phys. Rev. Lett. 113, 143602 (2014).
Israel, Y., Tenne, R., Oron, D. & Silberberg, Y. Quantum correlation enhanced super-resolution localization microscopy enabled by a fibre bundle camera. Nat. Comm. 8, 14786 (2017).
Tenne, R. et al. Super-resolution enhancement by quantum image scanning microscopy. Nat. Phot. 13, 116 (2019).
Classen, A. et al. Superresolving imaging of arbitrary one-dimensional arrays of thermal light sources using multiphoton interference. Phys. Rev. Lett. 117, 253601 (2016).
Classen, A., von Zanthier, J., Scully, M. O. & Agarwal, G. S. Superresolution via structured illumination quantum correlation microscopy. Optica 4, 580–587 (2017).
Born, M. & Wolf, E. Principles of Optics (Cambridge University Press, Cambridge, UK, 1999).
Martienssen, W. & Spiller, E. Coherence and fluctuations in light beams. Am. J. Phys. 32, 919 (1964).
Walborn, S. P., Monken, C. H., Padua, S. & Ribeiro, P. H. Spatial correlations in parametric down-conversion. Phys. Rep. 495, 87 (2010).
Goodman, J. W. Statistical properties of laser speckle patterns. In Laser Speckle and Related Phenomena, Vol. 9 of Toppics in Applied Physics (ed. Dainty, J. C.) 9–75 (Springer, Berlin, 1975).
Gasparini, L. et al. A 32 × 32-pixels time-resolved singlephoton image sensor with 44.64-μm pitch and 19.48% fill-factor with on-chip row/frame skipping features reaching 800 khz observation rate for quantum physics applications. Proceedings of the 2018 IEEE International Solid-State Circuits Conference, 2018 98–100, 11–15 (2018).
Eldar, Y. C. Rethinking biased estimation: improving maximum likelihood and the Cramer–Rao bound. Found. Trends Signal Process. 1, 305–449 (2008).
Eldar, Y. C. Minimum variance in biased estimation: bounds and asymptotically optimal estimators. IEEE Trans. Signal Process. 52, 1915–1930 (2004).
Acknowledgements
A.M., B.B., I.K., A.A.S., A.S., and D.M. acknowledge support from the EU project Horizon-2020 SUPERTWIN id.686731. The authors are thankful to Leonardo Gasparini, Majid Zarghami, and Matteo Perenzoni from the Fondazione Bruno Kessler FBK in Trento, Italy, for the provision of SuperEllen. A.M., I.K., A.A.S., and D.M. acknowledge support from the National Academy of Sciences of Belarus program “Convergence”. A.M., I.K., and A.A.S. acknowledge support from BRFFR project F18U-006.
Author information
Authors and Affiliations
Contributions
The theory was conceived by D.M., A.M., B.B., I.K., A.A.S., and A.S. Numerical calculations were performed by A.M., I.K., and A.A.S. The experiment was conceived and carried out by B.B., M.U., and A.S. D.M., A.M., B.B., D.A.L., D.L.M., and I.K. have written the paper. D.M. and A.S. supervised the project. All the authors participated in discussions and checking the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mikhalychev, A.B., Bessire, B., Karuseichyk, I.L. et al. Efficiently reconstructing compound objects by quantum imaging with higher-order correlation functions. Commun Phys 2, 134 (2019). https://doi.org/10.1038/s42005-019-0234-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0234-5
This article is cited by
-
Lost photon enhances superresolution
npj Quantum Information (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.