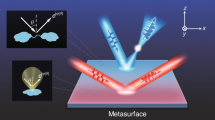
Abstract
Conventional multicolor metaholograms suffer from the fundamental limitations of low resolution and irreducible noise because the unit structure functionality is still confined to a single wavelength. Here, we propose wavelength-decoupled metasurfaces that enables to control chromatic phase responses independently in a full range from 0 to 2π for each wavelength. The propagation phase associated with the geometric phase of rectangular dielectric nanostructures plays a critical role to embed a dual phase response into a single nanostructure. A multicolor metahologram is also demonstrated to verify the feasibility of our method that breaks through the fundamental constraints of conventional multicolor metaholograms. Our approach can be extended to achieve complete control of chromatic phase responses in the visible for general dual-wavelength diffractive optical elements.
Similar content being viewed by others
Introduction
Metasurfaces that consist of subwavelength antenna arrays have applications as lenses1,2,3, holograms4,5,6,7,8,9, perfect absorbers10,11,12, optical isolators13, beam splitters14,15, color filters16,17, optical cloaks18, and orbital angular momentum generation19,20,21. These applications can be also realized by conventional optical components, but the final devices are bulky and usually contain many components that are connected to each other in complex ways. In contrast, metasurfaces show the same or even better performance despite small thicknesses that are comparable to the working wavelengths. This characteristic is a result of strong interaction between the subwavelength structures and incident light. Early metasurface research has achieved fundamental design principles for full-phase manipulation22,23,24, spectrum control25,26, and increased efficiency27,28. Much current metasurface research has aimed to exploit the established principles to embed multi-functionality29,30,31 and active tunability32,33,34.
Wavelength decoupling is a key element for versatile applications, especially of metalenses and metaholograms which require different functions by wavelengths. For the purpose, a unit structure of a metasurface should control chromatic phase responses independently. Achromatic metalenses have already demonstrated by compensation of group delay and its dispersion35. However, design principles of achromatic metalenses are invalid for general applications such as multicolor metaholograms because they require independent full-phase control by wavelengths. Although many multicolor metaholograms have been demonstrated based on interleaved subarrays36,37,38,39,40 and multiple positions41,42,43, their unit structure functionality is still confined to a single wavelength resulting fundamental limitations of low resolution and irreducible noise.
Here, we present a design principle for wavelength-decoupled metasurfaces that enable independent full-phase control of different wavelengths. Then we experimentally demonstrate a multicolor metahologram to verify our design principle. The wavelength-decoupled metasurface features a dual phase response embedded in a single nanostructure. The principle is based on the propagation phase of rectangular dielectric nanostructures associated with their geometric phase. Rotation of the structure induces equal geometric phases for different wavelengths whereas disparate structures cause different propagation phase gradients by wavelengths. One structure generates continuous phase variation by rotation, and thereby a finite structure set enables full-phase manipulation for different wavelengths. Similar works on combined propagation phase and geometric phase have been demonstrated, but they aimed independent phase control by polarization directions at a single wavelength20,21,44,45,46,47,48. The experimentally demonstrated multicolor metahologram verifies our design principle overcoming fundamental limitations of conventional multicolor metaholograms, so our approach to designing wavelength-decoupled metasurfaces is capable of realizing general dual-wavelength optical devices.
Results
Principle of independent phase manipulation
Using the propagation phase alone, we need m2 structure configurations with appropriate dispersion to realize full-phase control for two wavelengths divided by m phase steps for each wavelength49,50. For example, if m = 6, then coverage of the whole phase range with a corresponding phase step of π/3 requires 36 structures. The number of necessary structures equals to the total number of permutations of 6 phase values for each wavelength. This is straightforward, but impractical because the existence of those 36 structures with the desired dispersion is not guaranteed under limited pitch sizes and structure configurations such as rectangles or ellipses. Simulation of all the configurations may identify such structures, but the computation cost is high. As m increases, the situation becomes increasingly difficult and complex. To avoid these complications, an alternative design approach is necessary.
The geometric phase provides the intuitive way to realize multicolor metaholograms by reducing the design complexity of the m2 structures (Fig. 1a), because the geometric phase is applied to both wavelengths in the same manner and amount51,52,53. When left-handed circularly-polarized light (LCP) is incident to the rectangular dielectric nanorod, the Jones vector of the transmitted wave can be expressed as54
where TL and TS represent complex transmission coefficients of the nanorod along the long and short axis, respectively, α is the rotation angle of the nanorod, and the argument of (TL−TS)/2 represents the propagation phase of the transmitted right-handed circularly-polarized light (RCP). For example, if we express a phase pair of a certain nanorod as (φ1, φ2) which means that this nanorod generates a propagation phase of φ1 for one wavelength and φ2 for the other wavelength, then other arbitrary phase pairs of (φ1 + 2α, φ2 + 2α) can also be represented by rotating the nanorod by angle α (Fig. 1b). The sign of α changes depending on the rotation direction and on the incident polarization. By carefully choosing three values of φ1, φ2 and α, one structure with appropriate rotation angles can cover m phase pairs. Hence, the total number of structural configurations is reduced from m2 to m. Here, we use the phase step of π/3 which is the case of m = 6, and two wavelengths of 532 nm and 635 nm.
Operation schematic of the wavelength-decoupled metasurface. a By illumination of green (λ = 532 nm) and red (λ = 635 nm) light, multicolor holographic images can be generated from the metasurface. It features a dual phase response embedded in a single nanostructure that enables independent phase control for two wavelengths. b Illustration of the design principle. The lower white line represents an arbitrary cross-polarization propagation phase curve of a certain dielectric nanorod while φ1 and φ2 indicate specific values at wavelengths of λ1 and λ2, respectively. A phase pair of this state can be represented as (φ1, φ2). If this nanorod rotates by the angle α, the phase curve moves parallel by 2α. Therefore, the phase pair becomes (φ1 + 2α, φ2 + 2α); hence, any phase pairs in which phase difference equals to (φ1 − φ2) can be represented by one nanorod with appropriate rotation angles. Dashed lines are to guide the eye
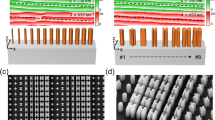
To cover the whole phase range from 0 to 2π for both wavelengths, we need six-kind structures in which propagation phase difference (PPD) of two different wavelengths varies linearly at intervals of π/3. Hydrogenated amorphous silicon (a-Si:H) based rectangular nanostructures are used as unit structures (Fig. 2a), and the a-Si:H benefits from lower optical loss than typical amorphous silicon in the visible (Fig. 2b). Rigorously-coupled wave analysis is used to calculate the PPD for the two wavelengths (Fig. 2c), and we have six-kind rectangular structures with PPDs that are linearly spaced from −π to 2π/3 (Fig. 2d). Cross-polarization transmission amplitudes are also calculated for both wavelengths (Fig. 2e, f). Although the conversion efficiency is not high enough for practical applications due to the optical loss of a-Si:H, it is sufficient to demonstrate our principle. Other structure sets can also be used if they satisfy the linear relationship of PPDs because absolute values of PPDs do not affect to the operation.
Rigorously-coupled wave analysis for rectangular nanostructures. a The unit cell configuration of the wavelength-decoupled metasurface. The hydrogenated amorphous silicon (a-Si:H) is used as structuring material on the glass substrate; height is 300 nm and pitch is 450 nm; length and width are adjusted to achieved a desired dispersion. The rotation angle is represented by α. b Measured refractive index of a-Si:H thin film using ellipsometry. The red line indicates a real part (n), and the blue line represents an imaginary part (k) of the refractive index. c Calculated propagation phase differences depending on the length and width of the structure. Length varies from 100 nm to 420 nm; width varies from 40 nm to each length L. Six circles represent unit structure parameters used in this work. (length (nm), width (nm)) = S1(182, 113), S2(223, 101), S3(272, 201), S4(297, 172), S5(231, 162), S6(198, 72). d Propagation phase differences of the six unit structures. The linear relation at intervals of π/3 should be satisfied to cover a full-phase range for both wavelengths. The dotted line is to guide the eye. e, f Calculated cross-polarization transmission amplitude for λ = 532 nm and λ = 635 nm on a log scale, respectively. Length varies from 100 nm to 420 nm; width varies from 40 nm to each length L. Six circles also represent our choices
Propagation phase plots of the six structures demonstrate the phase pairs generated by each structure with its rotation. When two wavelengths have the same incident polarization state, structure rotation moves two phase values in the same direction. Therefore, phase pairs that differ by PPDs of a certain nanorod can be represented using this nanorod with an appropriate angle α. For example, S1 nanorod produces propagation phases of −π/3 at λ = 532 nm, and of 2π/3 at λ = 635 nm without rotation (Fig. 3a). Its phase pair can be represented as (−π/3, 2π/3). When this nanorod rotates by π/6, the phase pair changes to (0, π) because each phase value increases by π/3 (Eq. 1). Other phase pairs of (π/3, 4π/3), (2π/3, 5π/3), (π, 2π) and (4π/3, 7π/3) can be also represented as the S1 nanorod rotates, so it produces 6 of the total 36 phase pairs. In the same manner, the other five structures from S2 to S6 generate the remaining 30 phase pairs (Fig. 3b–f); hence, total 36 phase pairs can be achieved using six structures with their rotation (Table 1).
Propagation phase curves of six unit structures. a–f Black solid lines show calculated propagation phases for each structure with no rotation. Two black dots on each plot indicate phase values at λ = 532 nm and λ = 635 nm, respectively. Propagation phase differences of ∆φ linearly vary from −π to 2π/3 at interval of π/3 from S1 to S6, and φ532 represent specific phase values at λ = 532 nm. For design convenience, phase values at λ = 532 nm are set to 0 by additional rotation angles of −φ532/2 for each structure. Dashed lines and arrows are to guide the eye
Demonstration of multicolor metahologram
A multicolor metahologram is demonstrated to verify the calculation result. The typical Gerchberg–Saxton algorithm with a phase step of π/3 is used to derive two individual phase profiles for Fourier holograms corresponding two different wavelengths55. Original images and their phase profiles all have pixel numbers of 1200 by 1200. By comparing two phase profiles, necessary phase pairs for each pixel can be derived, and all the pairs belong to the 36 phase pairs that we have already calculated. The final unit cell design for the multicolor metahologram can be obtained by locating the structures with appropriate rotation on each pixel.
A fabricated metahologram produces the multicolor holographic images. Conventional electron beam lithography is used to fabricate our metahologram (Fig. 4a). Two laser beams, in which wavelengths are 532 nm and 635 nm, respectively, are incident on our metahologram (Fig. 4b). Both beams have the same circular polarization state before incidence. Two different images are encoded in our metahologram (Fig. 4c, d), and a multicolor image can be represented by superposition of two monochromatic images (Fig. 4e). We choose two images that occupy both sides of the zeroth order beam in the image plane in order to show that our multicolor metahologram can generate holographic images throughout the whole image plane without the space loss. Experimentally demonstrated holographic images agree well with both monochromatic simulation images (Fig. 4f, g), and the multicolor image can be constructed by simultaneous illumination of two laser beams (Fig. 4h). The intermediate colors such as yellow and orange are represented by the intensity ratio between two monochromatic images. Our approach can be a promising metasurface design platform overcoming fundamental constraints of conventional multicolor metaholograms that are based on interleaved subarrays36,37,38,39,40 and multiple positions41,42,43. The interleaved metasurfaces are comprised of spatial integration of a few metasurfaces. Since each structure of the interleaved metahologram has only one monochromatic phase response, the number of structures that produce one holographic image is always less than the total number of structures. This causes pixel loss reducing image fidelity. The fundamental efficiency is also limited by structures that have zero conversion efficiency. Since incident light on these structures cannot contribute to form holographic images, these structures are no more than an optical screen except for each target wavelength. In metaholograms based on multiple positions, undesired images must appear at the same image plane in Fourier holography, or different image planes in Fresnel holography. These images cannot be removed or darkened in principle because this type of metaholograms can have only a single phase profile; hence, the available space and fundamental efficiency are limited. In contrast, our metahologram possesses a dual phase profile corresponding to two different wavelengths, so every structure of our metahologram contributes to form all holographic images without pixel loss and image degradation. Moreover, our metahologram has no fundamental limitations on space and efficiency because holographic images appear at desired positions only.
Experimental demonstration of the multicolor metahologram. a A scanning electron micrograph of the fabricated metasurface. (scale bar: 1 μm) b An optical setup to generate holograms. LP represents a linear polarizer; λ/2 denotes half-wave plates; λ/4 indicates an achromatic quarter-wave plate. Two incident beams have an identical circular-polarization direction, and beam diameters are large enough to cover the whole metasurface. c, d Simulated holographic images encoded by the Gerchberg-Saxton algorithm for green (λ = 532 nm) and red (λ = 635 nm) light, respectively. e A result of superposition of simulated green and red images. f–h Experimentally demonstrated holographic images by illumination of laser λ = 532 nm, 635 nm and both wavelengths, respectively. Images on the screen are captured by a camera, and intermediate colors such as yellow and orange are represented by controlling the intensity of two monochromatic images
Discussion
Despite these advantages, the demonstrated metahologram has the background noise and crosstalk. A non-uniform phase profile determined by the argument of (TL + TS)/2 of transmitted co-polarization components contributes to the background noise (Supplementary Note 1). Since TL and TS are already regulated by designing a cross-polarization phase profile, the co-polarization phase is not controllable; however, the intensity of the background noise can be decreased by reducing co-polarization transmittance or increasing the conversion efficiency. The crosstalk between two wavelengths is caused by disturbance of cross-polarization phase profiles (Supplementary Note 2). In this work, the propagation phase is calculated in periodic boundary conditions, and we assume that the propagation phase is invariable to the structure rotation. However, the actual propagation phase deviates depending on the structure rotation because of destruction of periodic boundary conditions. This deviation disturbs the designed phase profile resulting the crosstalk. Fabrication error also contributes the crosstalk because the propagation phase is sensitive to the structure shape.
The experimental demonstration validates our design principle, and further development is possible. Our current metasurface suffers from low efficiency. Hologram efficiency is defined by a ratio of optical power of holographic images to the total incident optical power. The measured efficiency of our metahologram is 2.5% at λ = 532 nm, and 7.6% at λ = 635 nm. In this work, simple rectangular nanostructures based on a-Si:H is used to verify the feasibility of our method, so the efficiency is not enough for practical applications due to intrinsic optical loss by silicon and insufficient unit cell designs limited in the rectangular shape. In other words, there are still rooms for further improvement of efficiency in terms of structuring materials and unit cell configurations. We can replace a-Si:H with low-loss dielectrics such as titanium dioxide2, gallium nitride3 or nanoparticle composite56 to improve the efficiency by minimizing material absorption, and these low-loss dielectrics can provide PPD distributions which are broad enough to achieve necessary PPD values as we do using a-Si:H as well as higher conversion efficiency than that of a-Si:H (Supplementary Fig. 6).
Using sophisticated structures can also be beneficial to improve the efficiency because the single rectangular structures significantly limit our choices of the unit cell configuration to obtain desired propagation phase gradients with high conversion efficiency. Various kinds of sophisticated structures have been investigated to satisfy one’s requirements not only in metaholograms, but also other metasurfaces such as metalenses. For example, Chen et al. used multiple nanorods to realize achromatic metalenses35, and Wang et al. demonstrated the achromatic metalens using inverse nanostructures for the desired dispersion3. We can also use optimization algorithms to figure out structure designs to meet our requirements such as phase dispersion or efficiency57,58. Any of these approaches are not exploited in this work because single rectangular nanorods are enough to satisfy our phase requirements. Our metahologram suffers from the low efficiency because we did not fully explore the design space yet, not because of any fundamental limitations; hence, the efficiency of our metasurface can be further improved using these approaches.
In conclusion, we present the wavelength-decoupled metasurface design principle based on the propagation phase associated with the geometric phase to embed independent dual-wavelength functions into a single nanostructure. The experimental demonstration of the multicolor metahologram based on this principle verifies the feasibility of our method that can be a significant breakthrough overcoming fundamental limitations in multicolor metaholograms.
Methods
Metasurfaces fabrication
The metasurface was fabricated using electron beam lithography59. A 300-nm-thick layer of a-Si:H was deposited on a glass substrate at 300 °C by plasma-enhanced chemical vapor deposition. The flow rates were 10 sccm for silane gas and 75 sccm for hydrogen gas; the deposition rate was 1.3 nm s−1. A positive resist (495 PMMA A2, MICROCHEM) was spin-coated by 2000 rpm on the a-Si:H resulting the resist thickness of 50 nm. Then the sample was baked on a hot plate at 180 °C for 5 min. Conductive polymer was also spin-coated by 2000 rpm on the resist to prevent charge accumulation during electron beam exposure. Then electron beam lithography was used to draw patterns on the resist. After the exposure, the sample was immersed into deionized water for 1 min to remove the conductive polymer, and development solution (MIBK:IPA=1:3, MICROCHEM) at 0 °C for 12 min. The low temperature of the solution lowers the reaction speed enabling precise control of final pattern shapes. A 30-nm-thick chromium (Cr) was deposited on the sample by electron beam evaporation. Then, the sample was immersed into acetone for lift-off to define a Cr mask on the a-Si:H thin film, which was then etched along the Cr mask using inductively coupled plasma reactive ion etching. The mask residue was removed using Cr etchant. Full scanning electron micrographs of the final metasurface can be found in Supplementary Fig. 7.
Materials characterization
The optical property of the a-Si:H thin film was measured using ellipsometry. A silicon substrate with 100-nm-thick silicon dioxide layer on the top was used to increase measurement accuracy. The incident beam angle was 65°. We used the Tauc-Lorentz model which is suitable for absorptive amorphous material. The imaginary part of the dielectric function of the Tauc-Lorentz model is given by
where A is the strength of the absorption peak, B is the broadening term, E0 is the energy position of the absorption peak, and EG is the optical band gap energy. We used fitting parameters of A = 101.2592 eV, B = 1.247 eV, E0 = 4.137 eV, and EG = 1.628 eV.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Arbabi, A. et al. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations. Nat. Commun. 7, 13682 (2016).
Khorasaninejad, M. et al. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016).
Wang, S. et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 13, 227–232 (2018).
Huang, L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 4, 2808 (2013).
Lee, G.-Y. et al. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 10, 4237–4245 (2018).
Yoon, G., Lee, D., Nam, K. T. & Rho, J. Pragmatic metasurface hologram at visible wavelength: the balance between diffraction efficiency and fabrication compatibility. ACS Photonics 5, 1643–1647 (2018).
Kim, I. et al. Outfitting next generation displays with optical metasurfaces. ACS Photonics 5, 3876–3895 (2018).
Ansari, M. A. et al. A spin-encoded all-dielectric metahologram for visible light. Laser Photonics Rev. 13, 1900065 (2019).
Ansari, M. A. et al. Engineering spin and antiferromagnetic resonances to realize an efficient direction-multiplexed visible meta-hologram. Nanoscale Horiz. (2019).
Liu, N., Mesch, M., Weiss, T., Hentschel, M. & Giessen, H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 10, 2342–2348 (2010).
Li, W. et al. Refractory plasmonics with titanium nitride: broadband metamaterial absorber. Adv. Mater. 26, 7959–7965 (2014).
Yoon, G. et al. Electrically tunable metasurface perfect absorber for infrared frequencies. Nano Convergence 4, 36 (2017).
Kim, M. et al. A broadband optical diode for linearly polarized light using symmetry‐breaking metamaterials. Adv. Opt. Mater. 5, 1700600 (2017).
Khorasaninejad, M. & Crozier, K. B. Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat. Commun. 5, 5386 (2014).
Yoon, G., Lee, D., Nam, K. T. & Rho, J. Geometric metasurface enabling polarization independent beam splitting. Sci. Rep. 8, 9468 (2018).
Kumar, K. et al. Printing colour at the optical diffraction limit. Nat. Nanotechnol. 7, 557–561 (2012).
Jang, J. et al. Kerker-conditioned dynamic cryptographic nanoprints. Adv. Opt. Mater. 7, 1801070 (2018).
Ni, X., Wong, Z. J., Mrejen, M., Wang, Y. & Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 349, 1310–1314 (2015).
Pu, M. et al. Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv. 1, e1500396 (2015).
Devlin, R. C., Ambrosio, A., Rubin, N. A., Mueller, J. P. B. & Capasso, F. Arbitrary spin-to–orbital angular momentum conversion of light. Science 358, 896–901 (2017).
Zhang, F. et al. All-dielectric metasurfaces for simultaneous giant circular asymmetric transmission and wavefront shaping based on asymmetric photonic spin–orbit interactions. Adv. Funct. Mater. 27, 1704295 (2017).
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Staude, I. et al. Tailoring directional scattering through magnetic and electric resonances in subwavelength silicon nanodisks. ACS Nano 7, 7824–7832 (2013).
Arbabi, A., Horie, Y., Bagheri, M. & Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 10, 937–943 (2015).
Flauraud, V., Reyes, M., Paniagua-Domínguez, R., Kuznetsov, A. I. & Brugger, J. Silicon nanostructures for bright field full color prints. ACS Photonics 4, 1913–1919 (2017).
Sun, S. et al. All-dielectric full-color printing with TiO2 metasurfaces. ACS Nano 11, 4445–4452 (2017).
Zheng, G. et al. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 10, 308–312 (2015).
Devlin, R. C., Khorasaninejad, M., Chen, W. T., Oh, J. & Capasso, F. Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc. Natl Acad. Sci. USA 113, 10473–10478 (2016).
Kamali, S. M. et al. Angle-multiplexed metasurfaces: encoding independent wavefronts in a single metasurface under different illumination angles. Phys. Rev. X 7, 041056 (2017).
Maguid, E. et al. Multifunctional interleaved geometric-phase dielectric metasurfaces. Light. Sci. Appl. 6, e17027 (2017).
Yoon, G., Lee, D., Nam, K. T. & Rho, J. “Crypto-display” in dual-mode metasurfaces by simultaneous control of phase and spectral responses. ACS Nano 12, 6421–6428 (2018).
Yao, Y. et al. Electrically tunable metasurface perfect absorbers for ultrathin mid-infrared optical modulators. Nano Lett. 14, 6526–6532 (2014).
Huang, Y.-W. et al. Gate-tunable conducting oxide metasurfaces. Nano Lett. 16, 5319–5325 (2016).
Zhu, Z., Evans, P. G., Haglund, R. F. & Valentine, J. G. Dynamically reconfigurable metadevice employing nanostructured phase-change materials. Nano Lett. 17, 4881–4885 (2017).
Chen, W. T. et al. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 13, 220–226 (2018).
Montelongo, Y. et al. Plasmonic nanoparticle scattering for color holograms. Proc. Natl Acad. Sci. USA 111, 12679–12683 (2014).
Huang, Y.-W. et al. Aluminum plasmonic multicolor meta-hologram. Nano Lett. 15, 3122–3127 (2015).
Wang, B. et al. Visible-frequency dielectric metasurfaces for multiwavelength achromatic and highly dispersive holograms. Nano Lett. 16, 5235–5240 (2016).
Wang, B. et al. Polarization-controlled color-tunable holograms with dielectric metasurfaces. Optica 4, 1368–1371 (2017).
Dong, F. et al. Information encoding with optical dielectric metasurface via independent multichannels. ACS Photonics 6, 230–237 (2019).
Li, X. et al. Multicolor 3D meta-holography by broadband plasmonic modulation. Sci. Adv. 2, e1601102 (2016).
Wan, W., Gao, J. & Yang, X. Full-color plasmonic metasurface holograms. ACS Nano 10, 10671–10680 (2016).
Jin, L. et al. Noninterleaved metasurface for (26-1) spin- and wavelength-encoded holograms. Nano Lett. 18, 8016–8024 (2018).
Balthasar Mueller, J. P., Rubin, N. A., Devlin, R. C., Groever, B. & Capasso, F. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 118, 113901 (2017).
Wang, B. et al. Rochon-prism-like planar circularly polarized beam splitters based on dielectric metasurfaces. ACS Photonics 5, 1660–1664 (2018).
Wu, L., Tao, J. & Zheng, G. Controlling phase of arbitrary polarizations using both the geometric phase and the propagation phase. Phys. Rev. B 97, 245426 (2018).
Zhao, R. et al. Multichannel vectorial holographic display and encryption. Light. Sci. Appl. 7, 95 (2018).
Xu, H.-X. et al. Completely spin-decoupled dual-phase hybrid metasurfaces for arbitrary wavefront control. ACS Photonics 6, 211–220 (2019).
Arbabi, E., Arbabi, A., Kamali, S. M., Horie, Y. & Faraon, A. High efficiency double-wavelength dielectric metasurface lenses with dichroic birefringent meta-atoms. Opt. Express 24, 18468–18477 (2016).
Shi, Z. et al. Single-layer metasurface with controllable multiwavelength functions. Nano Lett. 18, 2420–2427 (2018).
Bomzon, Z., Kleiner, V. & Hasman, E. Pancharatnam–Berry phase in space-variant polarization-state manipulations with subwavelength gratings. Opt. Express 26, 1424–1426 (2001).
Huang, L. et al. Dispersionless phase discontinuities for controlling light propagation. Nano Lett. 12, 5750–5755 (2012).
Kang, M., Feng, T., Wang, H.-T. & Li, J. Wave front engineering from an array of thin aperture antennas. Opt. Express 20, 15882–15890 (2012).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Gerchberg, R. W. & Saxton, W. O. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik 35, 237–246 (1972).
Kim, K., Yoon, G., Baek, S., Rho, J. & Lee, H. Facile nanocasting of dielectric metasurfaces with sub-100 nm resolution. ACS Appl. Mater. Interfaces 11, 26109–26115 (2019).
Sell, D., Yang, J., Doshay, S. & Fan, J. A. Periodic dielectric metasurfaces with high-efficiency, multiwavelength functionalities. Adv. Opt. Mater. 5, 1700645 (2017).
Shrestha, S., Overvig, A. C., Lu, M., Stein, A. & Yu, N. Broadband achromatic dielectric metalenses. Light. Sci. Appl. 7, 85 (2018).
Yoon, G., Lee, D. & Rho, J. Demonstration of equal-intensity beam generation by dielectric metasurfaces. J. Vis. Exp. 148, e59066 (2019).
Acknowledgements
This work is financially supported from the LGD-SNU Incubation program funded by LG Display and the National Research Foundation grants (NRF-2019R1A2C3003129, CAMM-2019M3A6B3030637, NRF-2019R1A5A8080290, NRF-2018M3D1A1058998, NRF-2015R1A5A1037668) funded by the Ministry of Science and ICT (MSIT), Republic of Korea.
Author information
Authors and Affiliations
Contributions
G.Y. and J.K. contributed equally to this work. J.R. and G.Y. conceived the idea and initiated the project. G.Y. and J.M. conducted optical simulation. G.Y. and J.K. fabricated the devices. G.Y. and D.L. did optical experiments. K.T.N. provided materials characterization. G.Y. wrote the manuscript. All authors confirmed the final manuscript. J.R. guided the entire project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yoon, G., Kim, J., Mun, J. et al. Wavelength-decoupled geometric metasurfaces by arbitrary dispersion control. Commun Phys 2, 129 (2019). https://doi.org/10.1038/s42005-019-0232-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0232-7
This article is cited by
-
Thermally-curable nanocomposite printing for the scalable manufacturing of dielectric metasurfaces
Microsystems & Nanoengineering (2022)
-
A hybrid broadband metalens operating at ultraviolet frequencies
Scientific Reports (2021)
-
Optical spin-symmetry breaking for high-efficiency directional helicity-multiplexed metaholograms
Microsystems & Nanoengineering (2021)
-
Nanoimprint lithography for high-throughput fabrication of metasurfaces
Frontiers of Optoelectronics (2021)
-
Top-down nanofabrication approaches toward single-digit-nanometer scale structures
Journal of Mechanical Science and Technology (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.