Abstract
Since the introduction of bolometers more than a century ago, they have been used in various applications ranging from chemical sensors, consumer electronics, and security to particle physics and astronomy. However, faster bolometers with lower noise are of great interest from the fundamental point of view and to find new use-cases for this versatile concept. We demonstrate a nanobolometer that exhibits roughly an order of magnitude lower noise equivalent power, \(20\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\), than previously reported for any bolometer. Importantly, it is more than an order of magnitude faster than other low-noise bolometers, with a time constant of 30 μs at \(60\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\). These results suggest a calorimetric energy resolution of 0.3 zJ = h × 0.4 THz with a time constant of 30 μs. Further development of this nanobolometer may render it a promising candidate for future applications requiring extremely low noise and high speed such as those in quantum technology and terahertz photon counting.
Similar content being viewed by others
Introduction
Bolometry is one of the oldest radiation-sensing techniques1 dating back to 1880. Yet, it remains competitive and widespread2,3,4,5, mainly owing to the flexibility bolometers offer in terms of the center frequency, bandwidth, and dynamic range, as well as the possibility of energy-resolving calorimetric operation6. These properties render bolometers, devices that detect radiation-generated heat in an absorber, interesting for the emerging quantum technological systems such as superconducting quantum computers7,8. Bolometers could, for example, be used as broadband measurement devices9 for solid-state or flying qubits10 and for characterization of cryogenic environments, cabling, and microwave components11,12,13,14,15,16 at powers in the single-photon regime. The quantum technological devices operate at such ultralow powers, and consequently call for characterization and calibration in the single-photon regime.
Very recently, Opremcak et al.17 demonstrated a readout scheme for superconducting qubits where a microwave bolometer may appear useful in bringing flexibility for the frequency band of the readout signal. Although future development of the method and qubits may bring a relief on the speed (≲1 μs time constant) and energy resolution (≲100 yJ) requirements realized by Opremcak et al.17, this potential application calls for improvements on the state-of-the-art fast ultralow-noise bolometers.
Outside quantum technology, bolometers are widely utilized by astronomers in both ground18 and space-based observatories19,20, and in other types of detectors21,22. Although this is a mature field requiring relatively high technology readiness levels and scalability for the detectors, some of the future applications call for improvements in the intrinsic noise of the existing bolometers. Interestingly, microwave bolometers have recently emerged as a potential candidate for the detection element in the dark matter experiments23,24,25, where the bolometer could either be used to directly measure the extremely low powers arising from photons generated in axion haloscopes26 or they could be applied to detect dark matter-generated quasiparticles that diffuse into the bolometer. In the former case, the advantage of bolometers over microwave amplifiers is that they are resilient to quantum fluctuations, but further development in the bolometer noise level is needed to achieve reasonable integration times in the experiments.
The noise equivalent power (NEP) quantifies the input power resolution of the bolometer in a unit bandwidth. Relatively recently, thermal conductances below 1 fW/K between bolometers and their environment have been measured27,28, implying that the lower bound for NEP set by thermal energy fluctuations can be reduced down to at least \(10\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\). To date, however, the lowest measured NEPs for bolometers are around \(300\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\)29,30, achieved using transition edge sensors31 (TESs) in far-infrared regime. For example, the expected power level to be detected in the Axion Dark Matter Experiment32 is of the order of 10−22 W. With the current state-of-the-art bolometers, the integration time to reach unit signal-to-noise ratio is of an order of a thousand hours. Thus, lowering noise of bolometers to \(10\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\) would bring the integration time to the reasonable single-hour time scale.
Promising NEPs have also been reported in the terahertz range for alternative device concepts, such as kinetic inductance detectors (KIDs) \((400\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}} )\)33 and proof-of-principle quantum-capacitance detectors (of order \(10\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\))34,35. Both of these detect radiation-generated non-equilibrium quasiparticles in a superconductor. In addition, the background rate of the random telegraph noise in semiconducting charge sensors shows potential for extremely low NEP \((1\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}} )\)36,37 in the terahertz regime. However, the coupling efficiency to a radiation source is expected to be low and full experimental characterization of the efficiency has not been reported.
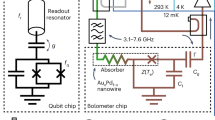
We recently introduced a threshold microwave detector based on superconductor–normal-metal–superconductor (SNS) junctions38 and showed that it can detect weak microwave pulses down to the zeptojoule level in a time-gated detection mode28. In this work, in contrast, we implement a continuously operating SNS bolometer. We measure an \({\mathrm{NEP}} \approx 50\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\) with a time constant of 0.6 ms. We can tune the time constant, in situ, below 100 μs at the expense of increasing the NEP to \(80\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\), which is nevertheless still lower than the lowest previously reported bolometer NEPs29,30. By introducing a Josephson parametric amplifier39 (JPA) to the bolometer readout circuit, we further reduce the NEP to a record low value of \(20\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\). For an NEP of \(60\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\), we achieve response times down to about 30 μs using the JPA, which is one to two orders of magnitude faster than those reported for the most sensitive TESs30. Although the experiments described here focus on the measurement of the input power, the achieved NEP and time constant suggest that, in a calorimetric mode of operation, the energy resolution may be well below the current 1.1-zJ record for thermal detectors28. Furthermore, we study the feasibility of the SNS bolometer in the terahertz regime by simulating a silicon lens with double-slot terahertz antenna coupled to the bolometer. Our results suggest a single-photon detection rate of 100 photons per second at 1.3 THz from a 3-K thermal source.
Results
Device and measurement setup
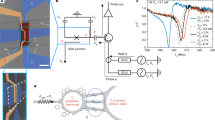
Figure 1a, b shows the detector and its measurement scheme. We couple the detector to an 8.4-GHz microwave source through a 50-Ω transmission line, which allows us to calibrate the heater power Ph incident at the detector input with a decibel level of uncertainty. Essentially all incident heater power is absorbed by the long SNS junction between the leads H and G since the junction is long enough for its impedance to be almost entirely real, 36 Ω, and well matched to the transmission line impedance of Z0 = 50 Ω. The imaginary part of the impedance, arising from the capacitor C1, is roughly −i0.2 Ω and an order of an ohm from parasitic series inductance at 8.4 GHz, and can be therefore neglected. Thus, an increase in Ph leads to an increase in the electron temperature Te in the AuxPd1−x (x ≈ 0.6) nanowire used as the normal-metal part in the SNS junctions. This in turn results in an increased inductance of the short SNS junctions40,41 between leads P and G, which implies a lower resonance frequency of the effective LC oscillator formed by the short SNS junctions, the on-chip meander inductor Ls, and the on-chip parallel plate capacitors C1 and C2. We detect this change by measuring the reflection coefficient at the detector gate capacitor Γ(Te, ωp) at a fixed probe frequency fp = ωp/2π. See Methods for the extraction of Γ from the detector output voltage at the digitizer V. Furthermore, we have the option to amplify the readout signal with a JPA42 (Fig. 1c, see Methods).
Measurement setup and device characterization. a–c Simplified detector measurement setup (a) together with micrographs of the superconductor–normal-metal–superconductor (SNS) junctions between leads H, G, and P taken from a similar device (b) and of a similar Josephson parametric amplifier (JPA) (c). The impedance Z(Te) of the series of short SNS junctions forms a temperature-sensitive resonant circuit together with a meander inductor Ls ≈ 1.2 nH and the capacitors C1 ≈ 87 pF and C2 ≈ 33 pF. The gate capacitance is Cg ≈ 0.87 pF. There is an 8.4-GHz bandpass filter connected to lead H. The scale bar in b indicates 1 μm and in c 15 μm (top) and 400 μm (bottom). d Phase of the reflection coefficient at the gate capacitor Γ as a function of probe frequency fp and power Pp, without heating and with the JPA off. e Example of the ensemble-averaged detector output voltage at the digitizer V (top curve) and voltage in the other quadrature (bottom curve), with the JPA on. The blue curves show exponential fits to the rising and falling edges of the signal. f, g Change in the detector output voltage at the digitizer after the heater is turned on (markers, see e) as a function of the finite heater power Ph with the JPA off (f) and on (g). The typical error of voltage measurement is of the order of size of the symbols. The (fp, Pp) operation points are indicated in d. The JPA shifts the resonance frequency slightly, thus the highest output is found at slightly different operating point. The bath temperature is Tb = 25 mK for all data in this paper
Characterization experiments
Figure 1d shows the phase of the reflection coefficient at the gate capacitor (see Methods for details) as a function of probe frequency and probe power, at zero heater power. The most striking feature in Fig. 1d is the decreasing resonance frequency as the probe tone begins to significantly heat the electrons in the SNS junctions above Pp = −135 dBm. This electrothermal feedback43 can be used to optimize the sensitivity and the time constant of the detector or even induce temperature bistability28 (not visible in Fig. 1d).
The NEP is determined by how noisy the readout signal is relative to the responsivity of the signal to changes in Ph (see Methods). Thus in Fig. 1e, we show an example of the detector output voltage V, which is defined as the voltage in the quadrature providing the greatest response to the heater power after amplification (≈103 dB), demodulation, and an optimally chosen phase rotation. In Fig. 1e, we first set Ph to a small value (3 aW) for a period of several tens of milliseconds, then turn Ph off for a similar period, and finally average over repetitions of this modulation pattern. From such data we extract the quasistatic voltage response at the digitizer and the time constant using exponential fitting functions. Figure 1f, g shows the quasistatic response of the detector output voltage to the heater power up to 3 aW. We define the detector responsivity as the ratio of the voltage response and the corresponding heater power. We also employ this information to choose an appropriate power level for the heater in our experiments discussed below.
Dimensionless susceptibility
To understand the detector response at high probe power, we develop a model for the electrothermal feedback28,44 (see Methods for details). We define a dimensionless susceptibility as
where ΔP equals the amount of additional heat flowing from the nanowire electrons to their thermal bath. Therefore, χ is the factor by which the probe-induced electrothermal feedback enhances the heating of the bolometer relative to the externally applied power Ph.
Detector responsivity and noise
In Fig. 2a, b, we show the responsivity of the detector output voltage. Note that the NEP is unaffected by the calibration of the gain of the readout circuitry since the measured responsivity and noise are both amplified equally. The responsivity is maximized for probe frequencies close to the resonance. As the probe power is increased, the width of the resonance decreases, leading to a sharp increase in the responsivity. Note that the color scales are different in Fig. 2a, b, since the JPA adds gain in excess of 20 dB.
Noise equivalent power (NEP) and thermal time constant. a–d Quasistatic responsivity of the probe voltage to the heater power (a, b) and probe voltage spectral density (c, d) as functions of probe frequency and power with the Josephson parametric amplifier (JPA) off (a, c) and on (b, d) averaged over noise frequencies between 20 and 100 Hz. e, f Noise equivalent power as a function of probe frequency and power with the JPA off (e) and on (f) averaged over noise frequencies between 20 and 100 Hz. g, h NEP (black) and thermal time constant (red) with the JPA off at fixed Pp = −126 dBm (g) and with the JPA on at Pp = −126.5 dBm (h). The error bars indicate the standard error of the mean for the time constant and error arising from heater power calibration for NEP
Interleaved with the measurements of the responsivity, we also record separate noise spectra for the detector output voltage and for the out-of-phase quadrature at each probe power and frequency. In Fig. 2c, d, we show the voltage noise spectral density across the same range of fp and Pp as for the responsivity. Let us first discuss the low-probe-power limit (Pp ≲ −132 dBm) with the JPA off in Fig. 2c. In this case, the electrothermal feedback is negligible (χ ≈ 1), ΔP vanishes, and the spectrum is dominated by noise added by the amplifiers in the readout circuitry. Furthermore, the noise power assumes a similar value on and off resonance. However, with the JPA on in Fig. 2d, we consistently observe a peak in the noise near the resonant probe frequency, indicating that amplifier noise is not dominating the signal even at the lowest probe powers shown (−132.5 dB). With the JPA off, the thermal fluctuations of the detector surpass the amplifier noise only at high Pp.
NEP and time constant
Figure 2e, f presents the main results of this paper, that is, the measured NEP for an 8.4-GHz input over a range of probe powers and frequencies. We compute the NEP by dividing the voltage spectral density by the quasistatic responsivity and multiplying the result by a factor \(\sqrt {1 + (2\pi \tau f_{\mathrm{n}})^2}\), where fn is the noise frequency. This factor takes into account the fact that the thermal time constant τ decreases the responsivity of the detector with respect to the quasistatic case (see Methods). Figure 2e, f shows the NEP with the JPA on and off, respectively, averaged over noise frequencies from 20 to 100 Hz.
In Fig. 2g we show the NEP and the time constant as functions of the probe frequency at fixed Pp = −126 dBm with the JPA off. Figure 2h is measured in identical conditions except that the JPA is on and the probe power is set to −126.5 dBm. The electrothermal feedback is strong and positive (χ ≫ 1) at probe frequencies just below the resonance frequency. In contrast, the electrothermal feedback is strongly negative (χ ≪ 1) at probe frequencies just above the resonance. This is clearly visible in the time constant τ = χτb, which increases by nearly an order of magnitude as the probe approaches the resonance despite the fact that the bare thermal time constant τb simultaneously decreases owing to increased electron temperature. Here, τb denotes the time constant in the absence of electrothermal feedback (see Methods). The lowest NEP of \(20\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\) in Fig. 2h coincides with the peak of the time constant (1 ms), suggesting that at Pp = −126.5 dBm the NEP is optimized at the frequency that maximizes χ.
As the probe frequency exceeds the resonance, the time constant quickly decreases by more than an order of magnitude below 100 μs. In this regime, the positive effect of the JPA is particularly clear: the NEP degrades quickly with increasing probe frequency if the JPA is disabled, but stays roughly constant when it is enabled. The fact that the NEP remains relatively flat at \(60\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\) with the JPA on (Fig. 2h) is an indication that the internal fluctuations of the detector are limiting the performance instead of amplifier noise. This is an example of the convenient in situ tunability of the SNS detector, that is, we can choose a different trade off between the NEP and the time constant by a small change of the probe frequency or power. We can also tune the time constant and the dynamic range by changing the bath temperature or by applying an additional constant heating power through the heater port. However, such an optimization is left for future work.
Noise analysis
In Fig. 3a, b, we present the full noise spectrum of the output signal at Pp = −126 dBm and Pp = −126.5 dBm with the JPA off and on, respectively. Above 1 Hz and below 1 kHz, the noise increases up to 14.5 dB above the broadband background set by the amplifier noise for probe frequencies near resonance. Far off-resonance we find only the broadband amplifier noise floor in addition to 1/fn noise. We also observe in Fig. 3b noise peaks at multiples of 1.4 Hz, matching the frequency of vibrations caused by the pulse tube cryocooler. Note that these peaks are clearly visible only when the JPA is on and the probe is far from the resonance, suggesting that the pulse tube noise does not couple directly to the detector, but rather to the amplifiers. At operation points with low NEP, the pulse tube noise is masked by the noise generated by the detector itself.
Frequency spectra of voltage noise and noise equivalent power (NEP). a, b Spectral density of the noise in the signal quadrature of the down-converted probe tone with the Josephson parametric amplifier (JPA) off (a) and on (b) as functions of the noise frequency fn. The bottommost curve shows the spectral density far off resonance at fp = 539.275 MHz and Pp = −132.5 dBm, whereas the green, blue, orange, and yellow curves are measured at Pp = −126 dBm (JPA off) and Pp = −126.5 dBm (JPA on), and span a narrow frequency range near the resonance. Specifically, the probe frequencies are fp = 540.6125 MHz − δ, where the values of δ are indicated in a. For clarity, the curves have been offset vertically in increments of 10 dBm/Hz. The two peaks above 1 kHz in b are due to the aliased JPA idler. The excess noise at multiples of 1.4 Hz is attributed to the pulse tube (PT) cryocooler. The dashed line indicates a first-order RC filter response with a time constant identical to that in the δ = 0 trace in b. c NEP with the JPA on as a function of the noise frequency at Pp = −126.5 dBm and fp = 541.9625 MHz. These data yield 0.3 zJ for the energy resolution estimate of the detector (see text). Discontinuity in the data on all panels near 2 kHz is caused by the fact that we measure the high- and low-frequency noise separately with different time steps
Predicted energy resolution
In Fig. 3c, we present the NEP measured with the JPA on as a function of the noise frequency at a (fp, Pp) point selected for short time constant and low NEP. From the NEP, we can obtain an estimate for an upper bound on the energy resolution45
By restricting the above frequency integration below the thermal cutoff frequency 1/(2πτ) = 5.8 kHz, the data in Fig. 3c yields ε = 0.32 zJ = h × 480 GHz, surpassing, for example, the anticipated resolution of the TES-based Fourier transform spectrometer19 specified to have about an octave of resolution in the band of 1.4–9 THz. Increasing the cutoff frequency to 10 kHz yields ε = 0.26 zJ = h × 390 GHz. Here, h denotes the Planck’s constant.
Feasibility for terahertz detection
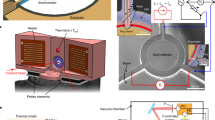
Inspired by the above-suggested energy resolution, we theoretically study the future feasibility of the SNS bolometer as a THz detector. We simulate a complete experiment, including a possible THz antenna design, aimed at detecting individual photons from a thermal source. The THz coupling scheme is based on a substrate-lens-coupled planar antenna. An extended hemispherical silicon lens (diameter 1 mm) integrated with a double-slot antenna as a feed46 was designed for the center frequency of 1.3 THz (see Fig. 4a). We employ electromagnetic simulations to study the performance in THz detection. Note that at the considered signal frequency range, well exceeding the Bardeen–Cooper–Schrieffer gap frequency, even a fully superconducting bolometer acts as a resistive load, and therefore no separate load resistor is needed. Thus, for simplicity, the bolometer is modeled as a 50-Ω port in the simulations. We have designed band-stop filters at 1.3 THz to prevent the bolometer readout circuitry from interfering with the antenna47. The radiation patterns at 1.3 THz (Fig. 4b) show −3-dB beam widths of about 8°. The detector efficiency is quantified by the effective area Ae, peaking to 0.35 mm2 at 1.3 THz (Fig. 4c).
Terahertz antenna and detection simulations. a Electromagnetic simulation model of an extended hemispherical silicon lens with a double-slot antenna as a feed. b Antenna gain at 1.3 THz as a function of the incident angle in the two principal planes, H-plane (dashed line) and E-plane (solid line). The H-plane (E-plane) is the plane containing the magnetic (electric)-field vector and the direction of maximum radiation49. c Effective detection area as a function of frequency. d Planck spectral irradiance at T = 3.0 K (solid line), and projected frequency-selective surface (FSS) filter transmission (dashed line) for blackbody measurements. e Computed photon rate power spectral density (PSD) corresponding to d. f Computed total detected photon rate (dashed line) and the corresponding detected power (solid line) as a function of the temperature of the blackbody emitter
To analyze the detected power and photon count rates, we assume a blackbody thermal source represented by the Planck spectral irradiance for a single polarity expressed as Br(f) = (hf3/c2)/{exp[hf/(kBT)] − 1}, where kB is the Boltzmann constant, T is the temperature of the source, and c is the speed of the light. We aim at a detection band above the peak frequency at hf ~ kBT. Thus, we must filter the low-frequency tail very efficiently, as it represents orders of magnitude higher power density in comparison to the band of interest.
Such filtering between the blackbody source and the detector can be achieved, for example, by metal mesh structures acting as frequency-selective surfaces (FSSs)48. Filter systems based on FSS structures have been demonstrated previously in the context of low-power detector experiments: de Visser et al.33 employ a bandpass-filter system with a low-frequency roll-off above 60 dB per octave, and a stop-band rejection of more than 60 dB. For our purposes, we aim to capture the essential features of such filters by defining a high-pass filter with a comparable roll-off, stop-band transmission of −60 dB, and a 3-dB cutoff at 1.3 THz.
The obtained frequency response η(f) is shown in Fig. 4d, along with the Planck spectral irradiance for T = 3.0 K. From these data, the detected power spectral density is obtained as S(f) = ∫ηBrAeΩdf, where Ω is the solid angle corresponding to the antenna beam width. Taking the optical throughput AeΩ from the antenna simulations of Fig. 4b, we show the spectral density of the detected photon count per unit bandwidth S(f)/(hf) in Fig. 4e. The total detected power and photon count are shown in Fig. 4f as functions of the blackbody temperature. In the vicinity of the blackbody temperature of T ≈ 3 K, the power level is well within the sensitivity range of the detector, and the photon rates are compatible with the speed of the detector. Thus, this seems a possible scenario to demonstrate terahertz photon counting in the future using the SNS detector.
Discussion
Our demonstration of an NEP of \(20\,{\mathrm{zW}}/\sqrt {{\mathrm{Hz}}}\) for an SNS junction-based bolometer is an order of magnitude improvement over results reported for TESs and KIDs. In this sensitivity range, we also report response times down to 30 μs, that is, detector bandwidth of about 5 kHz. For comparison, the most sensitive TESs and KIDs operate at bandwidths of order 100 Hz19,33. The observed detector speed and NEP predict an energy resolution compatible with single-photon detection extending down to the low terahertz range, ~400 GHz.
Recently, superconducting qubits have shown great progress in detecting single microwave photons50,51,52,53,54, but this technology is currently limited to frequencies below 10 GHz. Thus, the SNS detector provides a valuable complementary approach for future research.
Accommodating the SNS detector with a terahertz antenna in the future is supported by our simulations of an experimental detection scheme in the terahertz regime. Note, that the impedance of the SNS detector may be varied by the choice of the normal-metal size and aspect ratios thus providing flexibility in impedance matching. Furthermore, the radio frequency (rf) readout of SNS detectors is naturally suited for frequency multiplexing19,55,56. Thus, future development of the SNS detector may render it a potential candidate for various applications.
The design of the SNS detector is naturally compatible with the integration of superconductor–insulator–normal-metal junctions to the absorber57. This may allow direct cooling of the normal-metal electrons, and thus a possibility to increase the dynamic range of the detector using feedback. We estimate the achievable cooling power, and hence the dynamic range, to be well in the pW range57.
Methods
Sample fabrication and measurement setup
For details of the sample fabrication methods and of the measurement setup, see Govenius et al.28.
Reflection coefficient
Before feeding the probe signal into the cryostat, we split a fraction of it into a reference tone. We digitize both signals, the reference and the eventual probe signal, which is reflected from the detector gate and subsequently amplified and guided out of the cryostat. We define \({\tilde{\mathrm{\Gamma }}}\left( {T_{\mathrm{e}},\omega _{\mathrm{p}}} \right)\) as the ratio of the reflected signal and the reference signal. We obtain the reflection coefficient at the gate capacitor Γ(Te, ωp) by first measuring \({\tilde{\mathrm{\Gamma }}}\left( {T_{\mathrm{e}},\omega _{\mathrm{p}}} \right)\) with high probe and heating power (~−120 dBm) and dividing the subsequent measurements by this high-power reference, that is, \({\mathrm{\Gamma }}\left( {T_{\mathrm{e}},\omega _{\mathrm{p}}} \right) = {\tilde{\mathrm{\Gamma }}}\left( {T_{\mathrm{e}},\omega _{\mathrm{p}}} \right)/{\tilde{\mathrm{\Gamma }}}\left( {T \gg T_{\mathrm{e}},\omega _{\mathrm{p}}} \right)\). The high power shifts the resonance far from its low-power position, thus providing an accurate calibration for the low-power experiments.
Josephson parametric amplifier
The utilized JPA is that referred to as Device A by Simbierowicz et al.42. It is a lumped-element rf resonator where an array of 200 superconducting quantum interference devices (SQUIDs) forms a non-linear inductor. The SQUIDs are direct current biased and rf pumped with magnetic flux, generating a three-wave mixing process in the JPA. We use the JPA in the non-degenerate mode where the flux pump is at 2(fp + 21.875 kHz). Since the pump is at approximately twice the bolometer resonance frequency, we avoid residual heating of the bolometer by the JPA.
Thermal time constant and electrothermal feedback
In the low-Pp limit, Γ is independent of the probe power. If the probe power is increased, however, the power (1 − |Γ(Te, ωp)|2)Pp absorbed from the probe starts to significantly heat the bolometer and shifts the resonance to a lower frequency, as shown in Fig. 1c. More precisely, the nanowire electron temperature Te is determined by
if we model the electrons in the nanowire using a single heat capacity Ce and assume that the electrical degrees of freedom relax to a quasistationary state quickly compared to the thermal relaxation time28. Here, Pe − b(Te, Tb) is the heat flow from the electrons to their thermal environment at temperature Tb and Px is a constant parasitic heating term arising from uncontrolled noise sources.
Let us analyze the increase in the power flow from the nanowire electrons to their thermal environment, as compared to the case Ph = Pp = 0. We define this increase as
It is convenient to discuss ΔP rather than Te because ΔP can be directly measured28 and it allows us to simplify Eq. (2) to
where τb(ΔP) = C(ΔP)∂TePe−b[Te(ΔP), Tb] is the bare thermal time constant28, not including the effects of the electrothermal feedback, and \({\mathrm{\Delta }}\dot P\) denotes ∂tΔP.
We concentrate on the non-bistable regime where Eq. (4) has a unique stationary solution. In this regime, we can define the single-valued dimensionless susceptibility given by Eq. (1). The susceptibility also allows us to further simplify Eq. (4) into
for small deviations around ΔP = ΔP0 that solves Eq. (4) in steady state44. From Eq. (5) we observe that the effective thermal time constant is given by
Noise equivalent power
We define NEP2(fn) of a noisy bolometer as the one-sided power spectral density of input power fluctuations (units: W2/Hz) that yields for an ideal bolometer a noise spectral density in the output signal identical to that of the noisy bolometer. Here, the ideal bolometer refers to a noiseless conversion of input power into output signal with a responsivity equal to that of the noisy bolometer. Equivalently, \(2\sqrt {2{\mathrm{B}}} \times {\mathrm{NEP}}(f_{\mathrm{n}})\) describes, in a narrow bandwidth B centered at fn, the peak-to-peak amplitude by which the input power needs to be modulated at fn for unit signal-to-noise ratio in the output.
Specifically in this work, the NEP (shown in Fig. 2e–h) is given by
where RP→V(fn) is the frequency-dependent responsivity (shown in Fig. 2a, b) and SV(fn) is the single-sided power spectral density of the output signal V (Fig. 2c, d shows \(\sqrt {S_V}\)). Note that B × SV(fn) equals the ensemble variance if the signal is filtered to a narrow bandwidth B centered at fn.
In practice, we measure SV(fn) by averaging periodograms according to Bartlett’s method and determine the frequency-dependent responsivity from
where \(|\partial _{P_{\mathrm{h}}}V|\) is the measured quasistatic responsivity and τ is the measured time constant. Based on the adequate quality of the fits used to extract τ (see Fig. 1e), this single-time-constant approximation is justified at least up to frequencies of the order of 1/(2πτ). We note that Eqs. (7) and (6) are identical to those used for NEP in the previous literature33,58.
Terahertz simulations
The simulation tool in analyzing the THz coupling was Ansys Electromagnetic Suite v. 19. The received power of an antenna can be calculated as P = AeS, where Ae is the effective area and S is the power density of an incoming wave. The effective area is Ae = Gλ2/4π, where G is the maximum realized gain as a function of frequency, and λ is the corresponding wavelength59. The realized antenna gain can be written as G = ηpD, where ηp is the power efficiency, that is, the ratio between the radiated power and the input power, and D is directivity59. Here, G includes the loss due to impedance mismatch. The directivity is defined as follows: In a given direction, the part of the radiation intensity corresponding to a given polarization divided by the total radiation intensity averaged over all directions49.
Data availability
The data that support the findings of this study are available at https://doi.org/10.5281/zenodo.3384598.
References
Langley, S. P. The bolometer and radiant energy. In Proc. American Academy of Arts and Sciences Vol. 16, 342–358 (JSTOR 1880).
Armengaud, E. et al. LUMINEU: a search for neutrinoless double beta decay based on ZnMoO4 scintillating bolometers. J. Phys. 718, 062008 (2016).
Karasik, B. S., McGrath, W. R., Gershenson, M. E. & Sergeev, A. V. Photon-noise-limited direct detector based on disorder-controlled electron heating. J. Appl. Phys. 87, 7586–7588 (2000).
Golubev, D. & Kuzmin, L. Nonequilibrium theory of a hot-electron bolometer with normal metal-insulator-superconductor tunnel junction. J. Appl. Phys. 89, 6464–6472 (2001).
Nahum, M. & Martinis, J. M. Ultrasensitive-hot-electron microbolometer. Appl. Phys. Lett. 63, 3075–3077 (1993).
Gray, D. et al. The first tests of a large-area light detector equipped with metallic magnetic calorimeters for scintillating bolometers for the LUMINEU neutrinoless double beta decay search. J. Low Temp. Phys. 184, 904–909 (2016).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Macklin, C. et al. A near-quantum-limited Josephson traveling-wave parametric amplifier. Science 350, 307–310 (2015).
Govia, L. C. G. et al. High-fidelity qubit measurement with a microwave-photon counter. Phys. Rev. A 90, 062307 (2014).
Yeh, J.-H., LeFebvre, J., Premaratne, S., Wellstood, F. & Palmer, B. Microwave attenuators for use with quantum devices below 100 mk. J. Appl. Phys. 121, 224501 (2017).
Naaman, O. et al. Josephson junction microwave modulators for qubit control. J. Appl. Phys. 121, 073904 (2017).
Pechal, M. et al. Superconducting switch for fast on-chip routing of quantum microwave fields. Phys. Rev. Appl. 6, 024009 (2016).
Abdo, B., Brink, M. & Chow, J. M. Gyrator operation using josephson mixers. Phys. Rev. Appl. 8, 034009 (2017).
Sliwa, K. et al. Reconfigurable josephson circulator/directional amplifier. Phys. Rev. X 5, 041020 (2015).
Kokkoniemi, R. et al. Flux-tunable phase shifter for microwaves. Sci. Rep. 7, 14713 (2017).
Opremcak, A. et al. Measurement of a superconducting qubit with a microwave photon counter. Science 361, 1239–1242 (2018).
Revéret, V. et al. HERSCHEL—PACS bolometer arrays for submillimeter ground-based telescopes. J. Low Temp. Phys. 151, 32–39 (2008).
Jackson, B. D. et al. The SPICA-SAFARI detector system: TES detector arrays with frequency-division multiplexed SQUID readout. IEEE Trans. THz Sci. Technol. 2, 12–21 (2011).
Karasik, B. S., Sergeev, A. V. & Prober, D. E. Nanobolometers for THz photon detection. IEEE Trans. THz Sci. Technol. 1, 97–111 (2011).
Monfardini, A. et al. NIKA: A millimeter-wave kinetic inductance camera. Astron. Astrophys. 521, A29 (2010).
Baselmans, J. et al. A kilo-pixel imaging system for future space based far-infrared observatories using microwave kinetic inductance detectors. Astron. Astrophys. 601, A89 (2017).
Hochberg, Y., Lin, T. & Zurek, K. M. Detecting ultralight bosonic dark matter via absorption in superconductors. Phys. Rev. D. 94, 015019 (2016).
Krauss, L., Moody, J., Wilczek, F. & Morris, D. E. Calculations for cosmic axion detection. Phys. Rev. Lett. 55, 1797–1800 (1985).
Anastassopoulos, V. et al. New CAST limit on the axion–photon interaction. Nat. Phys. 13, 584–590 (2017).
McAllister, B. T. et al. The ORGAN experiment: an axion haloscope above 15 GHz. Physics of the Dark Universe 18, (67–72 (2017).
Wei, J. et al. Ultrasensitive hot-electron nanobolometers for terahertz astrophysics. Nat. Nanotechnol. 3, 496–500 (2008).
Govenius, J., Lake, R. E., Tan, K. Y. & Möttönen, M. Detection of zeptojoule microwave pulses using electrothermal feedback in proximity-induced Josephson junctions. Phys. Rev. Lett. 117, 030802 (2016).
Karasik, B. S. & Cantor, R. Demonstration of high optical sensitivity in far-infrared hot-electron bolometer. Appl. Phys. Lett. 98, 193503 (2011).
Suzuki, T. et al. Performance of SAFARI short-wavelength-band transition edge sensors (TES) fabricated by deep reactive ion etching. IEEE Trans. THz Sci. Technol. 4, 171–178 (2014).
Ullom, J. N. & Bennett, D. A. Review of superconducting transition-edge sensors for x-ray and gamma-ray spectroscopy. Supercond. Sci. Technol. 28, 084003 (2015).
ADMX Collaboration et al. Search for invisible axion dark matter with the axion dark matter experiment. Phys. Rev. Lett. 120, 151301 (2018).
de Visser, P. J., Baselmans, J. J. A., Bueno, J., Llombart, N. & Klapwijk, T. M. Fluctuations in the electron system of a superconductor exposed to a photon flux. Nat. Commun. 5, 3130 (2014).
Echternach, P., Pepper, B., Reck, T. & Bradford, C. Single photon detection of 1.5 THz radiation with the quantum capacitance detector. Nat. Astron. 2, 90–97 (2018).
Echternach, P. M. et al. Photon shot noise limited detection of terahertz radiation using a quantum capacitance detector. Appl. Phys. Lett. 103, 053510 (2013).
Komiyama, S., Astafiev, O., Antonov, V., Kutsuwa, T. & Hirai, H. A single-photon detector in the far-infrared range. Nature 403, 405–407 (2000).
Komiyama, S. Single-photon detectors in the terahertz range. IEEE J. Sel. Top. Quantum Electron. 17, 54–66 (2011).
Govenius, J. et al. Microwave nanobolometer based on proximity Josephson junctions. Phys. Rev. B 90, 064505 (2014).
Vesterinen, V. et al. Lumped-element Josephson parametric amplifier at 650 MHz for nano-calorimeter readout. Superconductor Sci. Technol. 30, 085001 (2017).
Lake, R. E. et al. Microwave admittance of gold-palladium nanowires with proximity-induced superconductivity. Adv. Electron. Mater. 3, 1600227 (2017).
Giazotto, F. et al. Ultrasensitive proximity Josephson sensor with kinetic inductance readout. Appl. Phys. Lett. 92, 162507 (2008).
Simbierowicz, S. et al. A flux-driven Josephson parametric amplifier for sub-GHz frequencies fabricated with side-wall passivated spacer junction technology. Superconductor Sci. Technol. 31, 105001 (2018).
de Visser, P. J., Withington, S. & Goldie, D. J. Readout-power heating and hysteretic switching between thermal quasiparticle states in kinetic inductance detectors. J. Appl. Phys. 108, 114504 (2010).
Govenius, J. Towards Calorimetric Detection of Individual Itinerant Microwave Photons. Doctoral thesis, Aalto Univ., Helsinki (2016).
Moseley, S. H., Mather, J. C. & McCammon, D. Thermal detectors as x-ray spectrometers. J. Appl. Phys. 56, 1257–1262 (1984).
Filipovic, D. F., Gearhart, S. S. & Rebeiz, G. M. Double-slot antennas on extended hemispherical and elliptical silicon dielectric lenses. IEEE Trans. Microw. Theory Technol. 41, 1738–1749 (1993).
Luukanen, A., Kiuru, T., Leivo, M. M., Rautiainen, A. & Varis, J. Passive three-colour submillimetre-wave video camera. In Passive and Active Millimeter-Wave Imaging XVI, Vol. 8715, 87150F (International Society for Optics and Photonics, 2013).
Ade, P. A., Pisano, G., Tucker, C. & Weaver, S. A review of metal mesh filters. In Millimeter and Submillimeter Detectors and Instrumentation for Astronomy III, Vol. 6275, 62750U (International Society for Optics and Photonics, 2006).
IEEE Standard for Definitions of Terms for Antennas. IEEE Std 145-2013 (Revision of IEEE Std 145-1993) 1–50 (2014).
Inomata, K. et al. Single microwave-photon detector using an artificial λ-type three-level system. Nat. Commun. 7, 12303 (2016).
Narla, A. et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. X 6, 031036 (2016).
Besse, J.-C. et al. Single-shot quantum nondemolition detection of individual itinerant microwave photons. Phys. Rev. X 8, 021003 (2018).
Kono, S., Koshino, K., Tabuchi, Y., Noguchi, A. & Nakamura, Y. Quantum non-demolition detection of an itinerant microwave photon. Nat. Phys. 14, 546–549 (2018).
Lescanne, R. et al. Detecting itinerant microwave photons with engineered non-linear dissipation. Preprint at http://arxiv.org/abs/1902.05102 (2019).
Day, P. K., LeDuc, H. G., Mazin, B. A., Vayonakis, A. & Zmuidzinas, J. A broadband superconducting detector suitable for use in large arrays. Nature 425, 817–821 (2003).
Dobbs, M. A. et al. Frequency multiplexed superconducting quantum interference device readout of large bolometer arrays for cosmic microwave background measurements. Rev. Sci. Instrum. 83, 073113 (2012).
Giazotto, F., Heikkilä, T. T., Luukanen, A., Savin, A. M. & Pekola, J. P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 78, 217–274 (2006).
de Visser, P. J. Quasiparticle Dynamics in Aluminium Superconducting Microwave Resonators., Doctoral thesis, Delft Univ. Technology, Delft (2014).
Lindell, I. & K., N. Antenniteoria 4th edn (Otatieto, Helsinki, 1995).
Acknowledgements
We acknowledge the provision of facilities and technical support by Aalto University at OtaNano – Micronova Nanofabrication Center. We have received funding from the European Research Council under Consolidator Grant No. 681311 (QUESS) and under Proof-of-Concept Grant No. 727305 (SNABO), European Commission through H2020 program projects EFINED (grant agreement 766853) and QMiCS (grant agreement 820505, Quantum Flagship), the Academy of Finland through its Centers of Excellence Program (project nos 312300, 312059, and 312294) and grants (Nos. 314447, 314449, 276528, 305237, 308161, and 314302), the Vilho, Yrjö, and Kalle Väisälä Foundation, the Technology Industries of Finland Centennial Foundation, the Jane and Aatos Erkko Foundation, and the Finnish Cultural Foundation.
Author information
Authors and Affiliations
Contributions
R.K. participated in the measurements and data analysis. V.V. integrated the JPA to the measurement setup, and participated to the measurements and data analysis. J.G., K.Y.T. and R.E.L. developed the fabrication process for the detector sample. J.G. and R.E.L. designed and fabricated the detector sample. J.G. designed the measurement setup. A.M.G. carried out preliminary measurements with J.G. The lens antenna simulations and terahertz detection rate computations were carried out by A.L. and J.H. All authors have contributed to preparing the manuscript, although most of the work was carried out by R.K., J.G., V.V. and M.M. In addition, V.V., S.S., L.G., J.L., M.P., J.H. and O.-P.S. provided the JPA and M.M. supervised the work in general.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kokkoniemi, R., Govenius, J., Vesterinen, V. et al. Nanobolometer with ultralow noise equivalent power. Commun Phys 2, 124 (2019). https://doi.org/10.1038/s42005-019-0225-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0225-6
This article is cited by
-
Single-shot readout of a superconducting qubit using a thermal detector
Nature Electronics (2024)
-
A SQUID cools down after a slip
Nature Physics (2023)
-
Bolometer operating at the threshold for circuit quantum electrodynamics
Nature (2020)
-
Record electron self-cooling in cold-electron bolometers with a hybrid superconductor-ferromagnetic nanoabsorber and traps
Scientific Reports (2020)
-
Electric field control of radiative heat transfer in a superconducting circuit
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.