Photoacoustics of core–shell nanospheres using comprehensive modeling and analytical solution approach

Abstract

Photoacoustic visualization of nanoparticles is capable of high contrast imaging at depth greater than that of traditional optical imaging techniques. Identifying the impact of various parameters on the photoacoustic signal is crucial in the design of effective medical imaging and diagnostics. Here, we develop a complete model of Fourier heat conduction incorporating the interfacial thermal resistance and photoacoustic equation for core-shell nanospheres in a fluid under nanosecond pulsed laser illumination. An analytical solution is obtained, elucidating the contribution of each region (core, shell, or the fluid) in the generation of the photoacoustic signal. The model reveals that the sharper the laser pulse temporal waveform is, the higher the sensitivity of the generated photoacoustic signal will be to the interfacial thermal resistance, and, thus, the higher the possibility of photoacoustic signal amplification will be using silica-coating. The comprehensive model and adopted analytical solution reveal the underlying physics of the photoacoustic signal generation  form core-shell nanosphere systems.

Introduction

Photoacoustics of colloidal nanosystems, in which thermal transport and surface processes are of high importance, are still not well characterized. Despite the long history of the photoacoustic (PA) effect and its very successful use as a spectroscopic technique^1,2, typical length scales in these colloids are so small that common approximations of negligible heat transfer out of the heated volume (thermal confinement) and little stress propagation from the heated region (stress confinement) are normally violated. Since the heat spreads from the nanoparticle photoabsorber to the environment, it is also unclear what the relative magnitudes of the contributions are from the different materials. These questions have become important in the design of nanoparticles for nanoparticle-augmented PA imaging, a new modality of non-invasive biomedical imaging in which the nanoparticles act as high-efficiency absorbers, molecularly specific imaging contrast agents, and highly localized in situ sensors^3,4.

We have recently shown experimentally that despite the exogenous nature of metal nanoparticle acting as PA contrast agents, the signal itself is generated mostly by the solvent that the nanoparticles are suspended in, and, therefore, carries the signature of the thermomechanical properties of the solvent⁵. Consequently, the process of heat transfer from the nanoparticle to the environment can play a significant role particularly with core–shell nanoparticles.

Several experimental and computational efforts have been undertaken to quantify and elucidate some of the physics of the pulsed laser irradiation of nanospheres^{5,6,7,8,9,10,11}. However, the impact of many physical parameters on the PA signal has not been fully investigated, and the full description of the underlying physics is currently lacking. Using an experimental approach, we have investigated the PA of nanoparticles (both nanospheres and nanorods) and the potential benefit of silica-coating nanoparticles in amplifying PA signals^5,8. These experimental results reveal that the majority of the signal originates from the immediate fluid layer surrounding the nanoparticle; however, the size or extent of the signal generating region, which have relevance in cellular and molecular imaging, have not been obtained and, more importantly, cannot be easily obtained experimentally.

On the computational and theoretical side, Prost et al. adopted a numerical approach and solved the heat equation and the PA equations for gold nanospheres in water. They particularly focused on the temperature dependency of water thermal expansion coefficients and resulting PA deviations from the point-absorber model of Calasso et al. ¹². Hatef et al. analyzed the PA signal of gold–silver alloy nanospheres using the commercial multiphysics package (COMSOL)⁹. Both groups, however, did not consider the silica-coating of the nanospheres, or model the interfacial thermal resistance¹⁰ at the gold–water interface, which can have a significant impact on the PA signal, as our model demonstrates. Kumer et al. also adopted an approach using the commercial computational package, COMSOL¹¹. They considered silica-coated nanoparticles and computed the PA signal of core–shell nanospheres. However, their model is based on the assumption of the thermal confinement of the core (i.e., the temperature profile of the core is identical to the pulsed laser profile), which, as shown in the next section (and also shown by Prost et al.¹⁰), is not a fateful approximations of the physics, and the core temperature can significantly deviate from the pulsed laser profile. Moreover, all previous studies lack the consideration of the pulsed laser temporal waveform and its impact on the resultant PA signal, which one may conceive important considering the PA signal is directly related to the second-order temporal derivative of temperature.

We herein introduce a comprehensive modeling of heat transfer and PA signal generation from core–shell gold nanosphere irradiated with a nanosecond pulsed laser. Central to the model introduced here is the incorporation of interfacial thermal resistance (or conversely, interfacial thermal conductance) at the two interfaces (nanosphere/shell and shell/fluid), as well as considering the role of laser pulse temporal waveform. The model is based on the following assumptions: (1) continuum mechanics and the validity of local equilibrium thermodynamics, (2) the absence of any phase transitions, (3) the constancy of all material parameters, (4) the independence of the optical and thermal processes, and (5) the spatial constancy of the temperature in the core. We also restrict the analysis to long heating pulses so that electronic processes can be neglected. Here we use an approximation that neglects the reflections of the stress at the outer boundaries. We consider core temperature rise of a few tens of Kelvin and thus the assumption of the constant material properties (e.g., the constancy of thermal expansion coefficient of water) is justified. The Fourier heat conduction is used to describe the heat transfer from the core to the shell and the fluid environment.

For solving the resulting heat and photoacoustics equations, we adopt an analytical approach based on the Laplace transformation. This approach is particularly effective in revealing some of the underlying PA physics with relevance in medical imaging applications and in facilitating the nanoparticle design process for an optimized PA imaging contrast agent.

By comprehensively modeling of a core–shell gold nanosphere, we quantify the contribution of the core and the fluid to the total PA signal; based on the maximum absolute value of pressure, the core contribution can be as high as 7% of the total signal. Moreover, our model reveals the extent of the fluid-generating region; it is a spherical shell approximately twice as thick as the radius of the nanosphere. Finally, we demonstrate the impact of the interfacial thermal resistance and the pulsed laser waveform on the relative performance of silica-coated nanospheres and uncoated nanospheres.

Results

Temperature profile

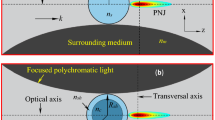
We consider the situation of an isolated spherical nanoparticle with a shell in a fluid (Fig. 1), in which only the core is optically absorbing and heat generating; the shell and the fluid are assumed to be fully transparent.

Fig. 1

Schematics of the core–shell nanosphere. The expected general temperature profile represents the typical features: a spatially constant temperature in the core; discontinuities at the interfaces dependent on the interfacial heat resistances at each interface; and ambient temperature at a larger distance from the sphere

We neglect the angular dependency of heat sources and, thus, consider heating in spherical symmetry with spatial dependency only in the radial direction. The reason for this is that the angular inhomogeneity is weak for small spheres due to diffractive distortions of the incident light, resulting in even smaller temperature inhomogeneities due to a high heat transfer rate in metals¹³. We further suppose that the temperature of the metal core is uniform in the radial direction, and it only depends on time ${T}_{1}={T}_{1}(t)$. Using dimensional analysis, one may show that this assumption can be applied to cases in which the optical skin layer, $\delta$, is significantly smaller than the radius of the particle¹³. For gold nanospheres with refractive index of ${n}_{{\mathrm{{p}}}}=n^{\prime}_{\mathrm{{p}}} +n^{\prime\prime}_{\mathrm{{p}}} =0.45+2.4i$ and $\delta =\frac{c}{2\omega n^{\prime\prime}_{\mathrm{{p}}} }=17\,{\mathrm{{nm}}}$, $n^{\prime}_{\mathrm{{p}}}$ and $n^{\prime\prime}_{\mathrm{{p}}}$ are real and imaginary parts of the refractive index, and $\omega$ is the angular frequency of the laser¹³. Under this condition, the heat source can be well approximated by the isotropic energy release at the surface of the particle. Thus, the temperature field inside the particle satisfies the homogeneous Laplace equation whose only non-singular solution is constant solution in radial position (i.e., $T(r,t)=T(t)$ for the inside the particle¹³). Therefore, this model of a spatially constant core temperature profile is acceptable for the range of particle radii of $r\ge 30\,{\mathrm{{nm}}}$.

The following notations are used. The core and shell carry indices $1$ and ${\mathrm{{s}}}$ and radii $a$ and $b$, respectively. The fluid carries the index $2$, and ${r}_{{\mathrm{{d}}}}$ is the radial position at which the temperature rise from an initial temperature, $T({r}_{{\mathrm{{d}}}},t)$, at time $t$, is determined. At each of the interfaces, the temperature profile may experience a discontinuity due to an interfacial thermal resistance or, conversely, due to a finite interfacial thermal conductance. The interfacial thermal conductance for the core–shell interface is ${G}_{1{\mathrm{{s}}}}$ and for the shell–solution interface is ${G}_{{\mathrm{{s}}}2}$. Each material is characterized by a thermal heat conductance $k$, a specific heat capacity at constant volume ${c}_{{\mathrm{{v}}}}$, and a density $\rho$. We suppose the maximum temperature rise is limited by a few tens of Kelvins and, thus, the thermophysical properties are considered constant.

Due to the spatially constant temperature profile, the homogeneous heat equation can be solved for the shell and the surrounding fluid; both do not absorb light and, therefore, contain no heat sources.

$$\frac{1}{{r}_{{\mathrm{{d}}}}^{2}}\frac{\partial }{\partial {r}_{{\mathrm{{d}}}}}\left({r}_{{\mathrm{{d}}}}^{2}\frac{\partial {T}_{2,{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}},t)}{\partial {r}_{{\mathrm{{d}}}}}\right)=\frac{1}{{\alpha }_{2,{\mathrm{{s}}}}}\frac{\partial {T}_{2,{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}},t)}{\partial t},$$

(1)

where $\alpha =\frac{k}{\rho {c}_{{\mathrm{{v}}}}}$ is the thermal diffusivity. The initial conditions are a zero temperature rise at time $t=0$. The boundary conditions based on temperature and heat flux balances are:

$${T}_{2}(r=\infty ,t)=0,$$

(2)

$${T}_{1}({r}_{{\mathrm{{d}}}}\le a,t)={T}_{{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}}=a,t)-{\frac{{k}_{{\mathrm{{s}}}}}{{G}_{1{\mathrm{{s}}}}}\frac{\partial {T}_{{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}},t)}{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}={a}^{+}},$$

(3)

$${T}_{{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}}=b,t)={T}_{2}({r}_{{\mathrm{{d}}}}=b,t)-\frac{{k}_{2}}{{G}_{{\mathrm{{s}}}2}}{\frac{\partial {T}_{2}({r}_{{\mathrm{{d}}}},t)}{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}={b}^{+}},$$

(4)

$$\frac{4\pi {a}^{3}}{3}Q(t)={\rho }_{1}{c}_{{\mathrm{{v}}}1}\frac{4\pi {a}^{3}}{3}\frac{\partial {T}_{1}(t)}{\partial t}-{k}_{{\mathrm{{s}}}}(4\pi {a}^{2}){\frac{\partial {T}_{{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}},t)}{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}={a}^{+}},$$

(5)

$${k}_{{\mathrm{{s}}}}{\frac{\partial {T}_{{\mathrm{{s}}}}({r}_{{\mathrm{{d}}}},t)}{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}={b}^{-}}={k}_{2}{\frac{\partial {T}_{2}({r}_{{\mathrm{{d}}}},t)}{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}={b}^{+}},$$

(6)

where $Q(t)$ is the volumetric heat rate applied to the core.

To facilitate the solution of the above system, the following dimensionless variables are introduced:

$$r =\frac{{r}_{{\mathrm{{d}}}}}{a};\quad \tau =\frac{{\alpha }_{2}t}{{a}^{2}};\quad {\Theta }_{2,{\mathrm{{s}}}}=r\frac{{k}_{2}}{{a}^{2}{Q}_{0}}{T}_{2,{\mathrm{{s}}}};\quad {K}_{r}=\frac{{k}_{2}}{{k}_{{\mathrm{{s}}}}}; \!\!\\ {D}_{r} =\frac{{\alpha }_{2}}{{\alpha }_{{\mathrm{{s}}}}};\quad {I}_{1}=\frac{{k}_{s}}{a{G}_{1s}};\quad {I}_{2}=\frac{{k}_{2}}{a{G}_{s2}};\quad {C}_{r}=\frac{{c}_{{\mathrm{{v}}}1}{\rho }_{1}}{{c}_{{\mathrm{{v}}}2}{\rho }_{2}},$$

(7)

with the understanding that if no shell is present, ${K}_{r}={D}_{r}=1$, ${I}_{1}={k}_{2}/(a{G}_{12})$, and ${I}_{2}=0$. ${Q}_{0}$ is the amplitude of the heat generated in the nanoparticle so that $Q(t)={Q}_{0}H(t)$, and $H(t)$ is a normalized and dimensionless heating function. Additionally, $\Theta$ is chosen to not only be dimensionless, but also to simplify the heat equation Eq. (1) for the shell. The dimensionless heat equations for the shell and the fluid are

$$\frac{{\partial }^{2}{\Theta }_{{\mathrm{{s}}}}}{\partial {r}^{2}}={D}_{r}\frac{\partial {\Theta }_{{\mathrm{{s}}}}}{\partial \tau },$$

(8a)

$$\frac{{\partial }^{2}{\Theta }_{2}}{\partial {r}^{2}}=\frac{\partial {\Theta }_{2}}{\partial \tau }.$$

(8b)

After eliminating the core temperature from Eq. (5) using Eq. (3), the three boundary conditions can be written in the dimensionless form as

$${{\Theta }_{{\mathrm{{s}}}}\Bigg|}_{r=1/A}=(1+{I}_{2}A){{\Theta }_{2}\Bigg|}_{r=1/A}-{I}_{2}{\frac{\partial {\Theta }_{2}}{\partial r}\Bigg|}_{r=1/A},$$

(9a)

$$H(\tau)={C}_{r}(1+{I}_{1}){\frac{\partial {\Theta }_{{\mathrm{{s}}}}}{\partial \tau }\Bigg|}_{r=1}-{C}_{r}{I}_{1}{\frac{{\partial }^{2}{\Theta }_{{\mathrm{{s}}}}}{\partial r\partial \tau }}\Bigg|_{r=1}-\frac{3}{{K}_{r}}{\frac{\partial {\Theta }_{{\mathrm{{s}}}}}{\partial r}\Bigg|}_{r=1}+{\frac{3}{{K}_{r}}{\Theta }_{{\mathrm{{s}}}}}\Bigg|_{r=1},$$

(9b)

$${\frac{\partial {\Theta }_{{\mathrm{{s}}}}}{\partial r}\Bigg|}_{r=1/A}-{A{\Theta }_{{\mathrm{{s}}}}}\Bigg|_{r=1/A}={K}_{r}{\frac{\partial {\Theta }_{2}}{\partial r}\Bigg|}_{r=1/A}{\,-\,{K}_{r}A{\Theta }_{2}}\Bigg|_{r=1/A},$$

(9c)

where $A=\frac{a}{b}$. Transformation to Laplace space, with $F(r,s)={\mathcal{L}}(\Theta (r,\tau))$ and with the use of initial conditions, yields the two general solutions to Eqs. (8a) and (8b):

$${F}_{{\mathrm{{s}}}}(r,s)={g}_{{\mathrm{{s}}}}(s){{\mathrm{{e}}}}^{-r\sqrt{{D}_{r}s}}+{h}_{{\mathrm{{s}}}}(s){{\mathrm{{e}}}}^{r\sqrt{{D}_{r}s}},$$

(10)

$${F}_{2}(r,s)={g}_{2}(s){{\mathrm{{e}}}}^{-r\sqrt{s}}+{h}_{2}(s){{\mathrm{{e}}}}^{r\sqrt{s}}.$$

(11)

The auxiliary condition that the temperature must be zero for $r=\infty$, Eq. (2), requires that ${h}_{2}(s)=0$. Thus,

$${F}_{2}(r,s)={g}_{2}(s){{\mathrm{{e}}}}^{-r\sqrt{s}}.$$

(12)

The characteristic functions ${g}_{{\mathrm{{s}}}},{h}_{{\mathrm{{s}}}}$ and ${g}_{2}$ in Eqs. (10) and (12) are determined by the Laplace transformation of the boundary conditions:

$${g}_{2}=\frac{{g}_{s}{{\mathrm{{e}}}}^{\frac{\sqrt{s}-\sqrt{{D}_{r}s}}{A}}+{h}_{s}{{\mathrm{{e}}}}^{\frac{\sqrt{{D}_{r}s}+\sqrt{s}}{A}}}{A{I}_{2}+{I}_{2}\sqrt{s}+1},$$

(13)

$${h}_{{\mathrm{{s}}}}=\frac{G{e}^{-\sqrt{{D}_{r}s}}-{g}_{{\mathrm{{s}}}}{{\mathrm{{e}}}}^{-2\sqrt{{D}_{r}s}}\left({C}_{r}{I}_{1}s\sqrt{{D}_{r}s}+{C}_{r}({I}_{1}+1)s+\frac{3\sqrt{{D}_{r}s}}{{K}_{r}}+\frac{3}{{K}_{r}}\right)}{-{C}_{r}{I}_{1}s\sqrt{{D}_{r}s}+{C}_{r}({I}_{1}+1)s-\frac{3\sqrt{{D}_{r}s}}{{K}_{r}}+\frac{3}{{K}_{r}}},$$

(14)

$${g}_{2}=\frac{{g}_{{\mathrm{{s}}}}{{\mathrm{{e}}}}^{\frac{\sqrt{s}-\sqrt{{D}_{r}s}}{A}}\left(A+\sqrt{{D}_{r}s}\right)-{h}_{s}{{\mathrm{{e}}}}^{\frac{\sqrt{Drs}+\sqrt{s}}{A}}\left(\sqrt{{D}_{r}s}-A\right)}{{K}_{r}\left(A+\sqrt{s}\right)},$$

(15)

where $G$ is the Laplace transform of the heating function, $G=G(s)={\mathcal{L}}[H(t)]$. The above system of equations (Eqs. (13)–(15)) consists of three equations and three unknowns–${g}_{{\mathrm{{s}}}}(s),{h}_{{\mathrm{{s}}}}(s),$ and ${g}_{2}(s)$– where one of the unknowns is

$${g}_{s}(s)= \left\{G(s){K}_{r}{{\mathrm{{e}}}}^{\frac{(2-A)\sqrt{{D}_{r}s}}{A}}\left[\left(\sqrt{{D}_{r}s}-A\right)\left({I}_{2}\left(A+\sqrt{s}\right)+1\right)+{K}_{r}\left(A+\sqrt{s}\right)\right]\!\right\}\!/\hfill\\ \left\{\left[{{\mathrm{{e}}}}^{\frac{2(1-A)\sqrt{{D}_{r}s}}{A}}\Big({A}^{2}\left(-{I}_{2}\right)+A\left({I}_{2}\sqrt{{D}_{r}s}+{I}_{2}\left(-\sqrt{s}\right)+{K}_{r}-1\right)\right.\right.\hfill\\ +\sqrt{{D}_{r}s}\left({I}_{2}\sqrt{s}+1\right)+{K}_{r}\sqrt{s}\Big)\hfill\\ \left({C}_{r}{K}_{r}s\left({I}_{1}\sqrt{{D}_{r}s}+{I}_{1}+1\right)+3\left(\sqrt{{D}_{r}s}+1\right)\Big)\right]\hfill\\ +\Big[\left({K}_{r}\left(A+\sqrt{s}\right)-(A+\sqrt{{D}_{r}s})\left({I}_{2}\left(A+\sqrt{s}\right)+1\right)\right)\hfill\\ \left({\hskip -3pt}-{C}_{r}{K}_{r}s\left(-{I}_{1}\sqrt{{D}_{r}s}+{I}_{1}+1\right)+3\sqrt{{D}_{r}s}-3\right)\Big]\Big\} .$$

(16)

Using this expression for ${g}_{{\mathrm{{s}}}}(s)$, and Eq. (14) yields an expression for ${h}_{{\mathrm{{s}}}}(s)$. Similarly, using ${g}_{{\mathrm{{s}}}}(s)$, ${h}_{{\mathrm{{s}}}}(s)$ and Eq. (15), an expression for ${g}_{2}(s)$ is obtained.

Using the boundary condition at the core surface, Eq. (3), the temperature profile in the core can be calculated as

$$r{F}_{1}(s)=(1+{I}_{1}+{I}_{1}\sqrt{{D}_{r}s}){{\mathrm{{e}}}}^{-\sqrt{{D}_{r}s}}{g}_{{\mathrm{{s}}}}(s)+(1+{I}_{1}-{I}_{1}\sqrt{{D}_{r}s}){{\mathrm{{e}}}}^{\sqrt{{D}_{r}s}}{h}_{{\mathrm{{s}}}}(s).$$

(17)

Here, $r$ is carried explicitly to avoid introducing an r-dependence and ${F}_{1}(s)={\mathcal{L}}[\frac{{k}_{2}}{{a}^{2}{Q}_{0}}{T}_{1}(t)]$. Eqs. (10) and (12) cannot be transformed back to physical space using an analytical inverse Laplace transform, and a numerical inverse Laplace transformation is required.

Supplementary Note 1 gives the verification of these temperature expressions with analytical expressions in the case of no shell and no interfacial resistance. The details of implementation including the numerical inverse Laplace transform, used to obtain the temperature and pressure expressions in the physical space, are given in Supplementary Note 2.

Pressure profile

The equation of motion written for radial displacement ${u}_{{\mathrm{{r}}}}$ in spherical symmetry for a medium with bulk and shear elastic modulus $K$ and $\mu$, density $\rho$, and volumetric thermal expansion $\beta$^5,14 is

$$\frac{{\partial }^{2}{u}_{r}}{\partial {t}^{2}}=-\frac{K\beta }{\rho }\frac{\partial T}{\partial {r}_{d}}+\left(\frac{K}{\rho }+\frac{4\mu }{3\rho }\right)\left(\frac{{\partial }^{2}{u}_{r}}{\partial {r}_{d}^{2}}+2\frac{\partial }{\partial {r}_{d}}\left(\frac{{u}_{r}}{{r}_{d}}\right)\right)$$

(18)

We denote $p$ as the pressure and introduce the characteristic speed ${c}_{{\mathrm{{L}}}}$ and the scalar potential $\varphi$ as

$${c}_{{\mathrm{{L}}}}^{2}=\left(\frac{K}{\rho }+\frac{4\mu }{3\rho }\right),$$

(19)

$$\frac{\partial {u}_{r}}{\partial t}=\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}},\quad p=-\rho \frac{\partial \varphi }{\partial t}.$$

(20)

Then, taking the partial derivative of Eq. (18) in $t$ yields

$$\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}=-\frac{K\beta }{\rho }\frac{\partial T}{\partial t}+{c}_{{\mathrm{{L}}}}^{2}\left(\frac{{\partial }^{2}\varphi }{\partial {r}_{{\mathrm{{d}}}}^{2}}+\frac{2}{{r}_{{\mathrm{{d}}}}}\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\right)=-\frac{K\beta }{\rho }\frac{\partial T}{\partial t}+{c}_{{\mathrm{{L}}}}^{2}\Delta \varphi ,$$

(21)

or

$$\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}-{c}_{{\mathrm{{L}}}}^{2}\Delta \varphi =-\frac{K\beta }{\rho }\frac{\partial T}{\partial t}.$$

(22)

Thus, the PA equation is

$$\frac{{\partial }^{2}p}{\partial {t}^{2}}-{c}_{{\mathrm{{L}}}}^{2}\Delta p=K\beta \frac{{\partial }^{2}T}{\partial {t}^{2}}.$$

(23)

In this equation, the right-hand side features the second time derivative of temperature, signifying the role of temporal temperature variation, which, in turn, is related to the temporal laser waveform (how fast the laser pulse changes in time). This will be investigated in the next section. The velocity potential equation, (22), is solved for each medium with appropriate initial and boundary conditions. Zero velocity and acceleration are used for initial conditions, yielding zero velocity potential and its derivative at time $t=0$, i. e.,

$${\varphi ({r}_{d},t)\Bigg|}_{t=0}=0,\quad \frac{\partial \varphi }{\partial t}{\Bigg|}_{t=0}=0.$$

(24)

Zero velocity at the sphere center and infinity and the continuity of velocity and the time rate of stress across interfaces are imposed as boundary conditions. Denoting the properties on either side of an interface with “+” or “−”, the boundary conditions are

$${\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}=0}=0,$$

(25a)

$${\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}_{{r}_{{\mathrm{{d}}}}\to \infty }=0,$$

(25b)

$${\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}^{-}={\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\Bigg|}^{+},$$

(25c)

$${\left[-K\beta \frac{\partial T}{\partial t}+\rho {c}_{{\mathrm{{L}}}}^{2}\left(\frac{{\partial }^{2}\varphi }{\partial {r}_{{\mathrm{{d}}}}^{2}}+\frac{2}{{r}_{{\mathrm{{d}}}}}\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\right)-4\rho {c}_{{\mathrm{{T}}}}^{2}\frac{\partial \varphi }{{r}_{{\mathrm{{d}}}}\partial {r}_{{\mathrm{{d}}}}}\right]}^{-} \,\,\,\,\,\,\,\,\,\\ ={\left[-K\beta \frac{\partial T}{\partial t}+\rho {c}_{{\mathrm{{L}}}}^{2}\left(\frac{{\partial }^{2}\varphi }{\partial {r}_{{\mathrm{{d}}}}^{2}}+\frac{2}{{r}_{{\mathrm{{d}}}}}\frac{\partial \varphi }{\partial {r}_{{\mathrm{{d}}}}}\right)-4\rho {c}_{{\mathrm{{T}}}}^{2}\frac{\partial \varphi }{{r}_{{\mathrm{{d}}}}\partial {r}_{{\mathrm{{d}}}}}\right]}^{+},$$

(25d)

with

$${c}_{{\mathrm{{T}}}}^{2}=\frac{\mu }{\rho }.$$

(26)

Analogous to the temperature solution, the solution of the velocity potential equation with the initial and boundary conditions, Eqs. (22) and (25d), is sought by first writing the equations in a dimensionless form using a change of variable to a dimensionless velocity potential as

$$\psi (r,\tau)=\frac{r\varphi ({r}_{{\mathrm{{d}}}},t)}{{\alpha }_{2}}$$

(27)

and other dimensionless variables defined in Eq. (7). Now, denoting

$${c}_{{\mathrm{{S}}}}^{2}=\frac{K}{\rho },\quad {c}_{{\mathrm{{t}}}}=\frac{{\alpha }_{2}}{a},\quad {C}_{{\mathrm{{L}}}}=\frac{{c}_{{\mathrm{{L}}}}}{{c}_{{\mathrm{{t}}}}},\quad {C}_{{\mathrm{{S}}}}=\frac{{c}_{{\mathrm{{S}}}}}{{c}_{{\mathrm{{t}}}}},\quad {B}_{r}=\frac{{Q}_{0}\beta {a}^{2}}{{k}_{2}},$$

(28)

the dimensionless velocity potential equation becomes

$$\frac{{\partial }^{2}\psi }{\partial {\tau }^{2}}-{C}_{{\mathrm{{L}}}}^{2}\frac{{\partial }^{2}\psi }{\partial {r}^{2}}=-{C}_{{\mathrm{{S}}}}^{2}{B}_{r}\frac{\partial \Theta }{\partial \tau }.$$

(29)

The dimensionless pressure $P$ is

$$P=\frac{p}{\rho {c}_{{\mathrm{{t}}}}^{2}}=-\frac{1}{r}\frac{\partial \psi }{\partial \tau }.$$

(30)

The dimensionless boundary conditions are

$$\mathop{\mathrm{lim}}\limits_{r\to 0}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}-\frac{\psi }{{r}^{2}}\right)=0,$$

(31a)

$$\mathop{\mathrm{lim}}\limits_{r\to \infty }\left(\frac{1}{r}\frac{\partial \psi }{\partial r}-\frac{\psi }{{r}^{2}}\right)=0,$$

(31b)

$${\left(\frac{\partial \psi }{\partial r}-\frac{\psi }{r}\right)}^{-}={\left(\frac{\partial \psi }{\partial r}-\frac{\psi }{r}\right)}^{+}$$

(31c)

$${\left[{\rho }_{r}\left(-{C}_{{\mathrm{{S}}}}^{2}{B}_{r}\frac{\partial \Theta }{\partial \tau }+{C}_{{\mathrm{{L}}}}^{2}\frac{{\partial }^{2}\psi }{\partial {r}^{2}}-4{C}_{{\mathrm{{T}}}}^{2}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}-\frac{\psi }{{r}^{2}}\right)\right)\right]}^{-} \,\,\,\,\,\,\,\,\,\\ ={\left[{\rho }_{r}\left(-{C}_{{\mathrm{{S}}}}^{2}{B}_{r}\frac{\partial \Theta }{\partial \tau }+{C}_{{\mathrm{{L}}}}^{2}\frac{{\partial }^{2}\psi }{\partial {r}^{2}}-4{C}_{{\mathrm{{T}}}}^{2}\left(\frac{1}{r}\frac{\partial \psi }{\partial r}-\frac{\psi }{{r}^{2}}\right)\right)\right]}^{+},$$

(31d)

where

$${\rho }_{r}=\frac{\rho }{{\rho }_{2}},{C}_{{\mathrm{{T}}}}=\frac{{c}_{{\mathrm{{T}}}}}{{c}_{{\mathrm{{t}}}}}.$$

(32)

Transformations of Eqs. (29) and (31a) to the Laplace space and the use of initial conditions of zero temperature, zero velocity potential, and its time derivative, Eq. (24), yields

$${s}^{2}H(r,s)-{C}_{{\mathrm{{L}}}}^{2}\frac{{\partial }^{2}H(r,s)}{\partial {r}^{2}}=-{C}_{{\mathrm{{S}}}}^{2}{B}_{r}sF(r,s),$$

(33)

and

$$\mathop{\mathrm{lim}}\limits_{r\to 0}\left(\frac{1}{r}\frac{\partial H}{\partial r}-\frac{H}{{r}^{2}}\right)=0,$$

(34a)

$$\mathop{\mathrm{lim}}\limits_{r\to \infty }\left(\frac{1}{r}\frac{\partial H}{\partial r}-\frac{H}{{r}^{2}}\right)=0,$$

(34b)

$${\left(\frac{\partial H}{\partial r}-\frac{H}{r}\right)}^{-}={\left(\frac{\partial H}{\partial r}-\frac{H}{r}\right)}^{+}$$

(34c)

$${\left[{\rho }_{r}\left(-s{C}_{{\mathrm{{S}}}}^{2}{B}_{r}F+{C}_{{\mathrm{{L}}}}^{2}\frac{{\partial }^{2}H}{\partial {r}^{2}}-4{C}_{{\mathrm{{T}}}}^{2}\left(\frac{1}{r}\frac{\partial H}{\partial r}-\frac{H}{{r}^{2}}\right)\right)\right]}^{-} \,\,\,\,\,\,\,\,\,\\ ={\left[{\rho }_{r}\left(-s{C}_{{\mathrm{{S}}}}^{2}{B}_{r}F+{C}_{{\mathrm{{L}}}}^{2}\frac{{\partial }^{2}H}{\partial {r}^{2}}-4{C}_{{\mathrm{{T}}}}^{2}\left(\frac{1}{r}\frac{\partial H}{\partial r}-\frac{H}{{r}^{2}}\right)\right)\right]}^{+},$$

(34d)

where $H=H(r,s)={\mathcal{L}}[\psi (r,\tau)]$ and $F=F(r,s)={\mathcal{L}}[\Theta (r,\tau)]$. Using the solution of dimensionless temperature in the Laplace space, Eqs. (10), (17), and (12), the general solution of Eq. (33) for the core, the shell, and the fluid are

$${H}_{1}(r,s)={A}_{11}{e}^{\frac{rs}{{C}_{{\mathrm{{L}}}}}}+{A}_{12}{e}^{-\frac{rs}{{C}_{{\mathrm{{L}}}}}}-\frac{{C}_{{\mathrm{{S}}}}^{2}{B}_{r}}{s}{F}_{1},$$

(35)

$${H}_{{\mathrm{{s}}}}(r,s)={A}_{{\mathrm{{s}}}1}{e}^{\frac{rs}{{C}_{{\mathrm{{L}}}}}}+{A}_{{\mathrm{{s}}}2}{e}^{-\frac{rs}{{C}_{{\mathrm{{L}}}}}}+\frac{{C}_{{\mathrm{{S}}}}^{2}{B}_{r}}{D{C}_{{\mathrm{{L}}}}^{2}-s}({g}_{{\mathrm{{s}}}}{e}^{-r\sqrt{Ds}}+{h}_{{\mathrm{{s}}}}{e}^{r\sqrt{Ds}}),$$

(36)

$${H}_{2}(r,s)={A}_{21}{e}^{\frac{rs}{{C}_{{\mathrm{{L}}}}}}+{A}_{22}{e}^{-\frac{rs}{{C}_{{\mathrm{{L}}}}}}+\frac{{C}_{{\mathrm{{S}}}}^{2}{B}_{r}}{{C}_{{\mathrm{{L}}}}^{2}-s}{g}_{2}{e}^{-r\sqrt{s}}.$$

(37)

Imposing the first boundary condition yields

$${H}_{1}(r,s)=2{A}_{11}\sinh \left(\frac{rs}{{C}_{{\mathrm{{L}}}}}\right)-\frac{{C}_{{\mathrm{{S}}}}^{2}{B}_{r}}{s}{F}_{1},$$

(38)

and the second to the last condition yields

$${H}_{2}(r,s)={A}_{22}{e}^{-\frac{rs}{{C}_{{\mathrm{{L}}}}}}+\frac{{C}_{{\mathrm{{S}}}}^{2}{B}_{r}}{{C}_{{\mathrm{{L}}}}^{2}-s}{g}_{2}{e}^{-r\sqrt{s}}.$$

(39)

Imposing the remaining boundary conditions, namely the continuity of the velocity and the stress across interfaces, gives four equations, which can be solved to determine the four unknown characteristics, ${A}_{11}$, ${A}_{{\mathrm{{s}}}1},{A}_{{\mathrm{{s}}}2}$, and ${A}_{22}$. Since the pressure signal can only be measured in the fluid, we herein present discussions and expressions for ${A}_{22}$ and ${H}_{2}(r,s)$ and determine the contribution of each medium to the total measurable signal. Linearity dictates

$${H}_{2}(r,s)={H}_{22}(r,s)+{H}_{2s}(r,s)+{H}_{21}(r,s),$$

(40)

where ${H}_{22},{H}_{2s}$, and ${H}_{21}$ are the fluid, shell, and core contributions to the total pressure signal in the fluid, respectively. The total dimensionless pressure in the fluid is obtained by the numerical inverse Laplace transform of $-s{H}_{2}/r$. Specifically,

$$P=-{{\mathcal{L}}}^{-1}\left[\frac{s{H}_{2}(r,s)}{r}\right],$$

(41a)

$$p=-{\rho }_{2}{c}_{{\mathrm{{t}}}}^{2}{{\mathcal{L}}}^{-1}\left[\frac{s{H}_{2}(r,s)}{r}\right].$$

(41b)

Detailed expressions of the fluid, shell, and the core contributions in the Laplace space are given in Supplementary Note 3.

Physics of PA signal

Using the derived analytical expressions above, we now reveal some of the physics of the PA signal. First, the temperature profiles are presented, followed by the PA signal composition and the generating volume. Then, the impact of interfacial thermal conductance coefficients and the laser pulse temporal wave form for both uncoated and silica-coated gold nanospheres are quantified. Finally, the impact of the core and the shell size on the PA signal are demonstrated and discussed. All thermophysical and mechanical properties used are given in Supplementary Note 4.

For core sizes of $30-100$ nm, and for the gold spheres and laser wavelength of $532$ nm, the optical skin depth is smaller than the core size and thus rate of volumetric heating ${Q}_{0}$ due to laser heating can be computed as

$${Q}_{0}=\frac{3{Q}_{{\mathrm{{abs}}}}F}{4a},$$

(42)

where $a$ is the radius of the core, $F$ is the laser intensity in $\text{W}\,{\text{m}}^{-2}$, and ${Q}_{{\mathrm{{abs}}}}$ is the dimensionless absorption efficiency, computed using exact Mie theory and experimental data on optical properties of gold¹³. The values of dimensionless absorption efficiency, ${Q}_{{\mathrm{{abs}}}}$, falls in the range of $4-1.5$ and approximately decreases sublinearly with the core radius. We use, for each core size, ${Q}_{\text{abs}}$ reported in ref. ¹³ and the laser intensity of $F=2.7\times 1{0}^{9}\,{{\mathrm{{W}}}}{{\mathrm{{m}}}}^{-2}$. We present samples of temperature profiles obtained using the derived expressions for the case of a pulsed laser with a Gaussian profile of $10$ ns width at $532$ nm and a $a=30$ nm gold sphere placed in water. Results for two cases of uncoated and silica-coated (with a shell radius of $b=45$ nm) are given. The interfacial thermal conductance coefficients are chosen as ${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, interfacial conductance of ${G}_{1{\mathrm{{s}}}}=20$, and ${G}_{{\mathrm{{s}}}2}=1000\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, falling in the range of reported values in the literature^{15,16,17,18,19,20}. The results are depicted in Fig. 2, showing the top and bottom panels for uncoated and coated nanospheres. The right panels in the figure compare the temperature temporal profile to the input laser waveform, clearly showing the deviation of the temperature profile from the laser profile and, thus, confirming the violation of the thermal confinement assumption used in a previous work¹¹. A spatial variation of the temperature and a three-dimensional representation of temperature are also given in the middle and left-side panels of the figure. Significant temperature drops at the interfaces of core–water and core–shell are observed, which are the consequences of the interfacial thermal resistance.

Fig. 2

Temperature profile due to a Gaussian laser pulse. a–c $a=30$ nm uncoated gold sphere placed in water with interfacial conductance of ${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$. d–f $a=30$ nm gold sphere with $15$ nm silica shell in water with interfacial conductance coefficients of ${G}_{1s}=20$ and ${G}_{s2}=1000\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$. c and f The Gaussian laser pulse form (in red) and the temporal temperature profile for a point inside water at the gold–water interface (in blue, in c) or inside the silica shell at the gold–silica interface (in blue, in f). b and e The spatial temperature profile at the time of maximum laser power. Laser pulse with a Gaussian profile of $10$ ns width at $532$ nm wavelength is used

The developed core–shell model facilitates the determination of the fluid region surrounding the core responsible for the bulk of the generated PA signal, referred to as the generating region or volume. The size of the generating region (or its thickness) is obtained by first dividing the whole fluid into two separate regions, one spanning from the core surface to a certain distance (i.e., a spherical water shell with a certain thickness), and the other consisting of the remaining fluid. Then, the contribution of each region is computed using the expression for ${H}_{22}$ and ${H}_{2s}$, respectively, but the properties of the “shell” region is assigned as that of water for a varying thicknesses of the water shell. The contribution of the core is computed using ${H}_{21}$ and the total PA signal is the sum of all three. In the sequence of graphs in Fig. 3, a water shell is increased stepwise in a water environment with a gold sphere of $a=30$ nm and ${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$. As the water shell thickness increases, the contribution of the shell region (that is adjacent to the core) increases, and the remaining region diminishes, while the total PA signal remains constant. Surprisingly, the contribution from the fluid directly surrounding the gold shell is small despite the fact that the temperature is highest here. Shell and core signals (with no significant amplitude) have higher frequencies, and the signal contribution from the outer layers interferes to reduce the frequency. Significant contributions come from regions with a thickness >$2a=60$ nm.

Fig. 3

Composition of the photoacoustic signal for uncoated gold sphere. a No fluid shell. b$15$ nm fluid shell. c 45 nm fluid shell. d$60$ nm fluid shell. e $90$ nm fluid shell. f $180$ nm fluid shell. The core radius is $a=30$ and it is placed in water with ${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, computed at ${r}_{{\mathrm{{d}}}}=10a=300$ nm, with the differentiating feature in each panel being the thickness of the surrounding fluid region (“fluid shell”); revealing a signal generating volume (“fluid shell”) with a thickness >$2a=60$ nm

We had previously shown experimentally that the PA signal is mostly generated by the non-absorbing environment surrounding the light-absorbing nanoparticle^5,8, and that the nanoparticle itself only contributed a few percent at the frequencies used for biomedical imaging. A theoretical estimate that accompanied the original experimental results is confirmed here in the complete model. Based on the maximum absolute value of the pressure amplitude, the core contributes only $7 \%$ of the total signal. A PA signal is directly proportional to the speed of heat diffused from the core to the surrounding medium. This speed, in turn, is controlled by thermal diffusivity of the surroundings (in Fourier’s model of heat conduction) and the interfacial thermal conductance coefficients. For the case of coating, the silica shell stores some of the thermal energy it receives from the core, and, thus, conducts less energy to the surrounding fluid. A lower thermal energy arriving in the fluid, in turn, results in a lower PA signal. Thus, since silica has a much smaller volumetric thermal expansion coefficient compared to water, all parameters (interfacial conductance coefficients, laser pulses, etc.) being equal, the silica-coated nanospheres have a lower PA efficiency than the uncoated ones. However, the silica shell can potentially enhance the overall heat diffusion from the core to the fluid by enhancing the interfacial thermal conductance coefficients. The literature provides some estimates of interfacial conductance coefficients. For a silica–gold interface, values in the range of ${G}_{1s}=20-200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ are expected^19,20, while, for a silica–water interface, values in excess of ${G}_{2s}=1000\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ are reasonable^15,16. For a gold–water interface, values in the range of ${G}_{12}=100-200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ have been reported^17,18. The latter is, however, for a low initial temperature or for a low laser power heating where the temperature rise in the water at the interface is small¹⁸. As the initial temperature or the power heating increases, the water is increasingly warmer at the interface, and, thus, has lower density, or it can even evaporate resulting in a lower interfacial conductance or higher thermal resistance¹⁸. This dependency of the gold–water interfacial conductance coefficient is expected to be much weaker in the silica–water interface, since the temperature rise at the silica–water interface is smaller due to partial heat absorption by the silica shell. Experiments revealed that with a rise of water temperature, an increasingly higher signal amplification for silica-coated nanospheres is obtained⁵, suggesting the inverse relationship between the temperature and the gold–water interfacial conductance. Therefore, a scenario of high power heating or water temperature giving rise to a very high gold–water interface resistance might be feasible. In the next subsection, we quantify the effect of low and high values of interfacial conductance on the PA signal generation efficiency.

In addition to the interfacial conductance, the shape of the laser pulse or the frequency content of the laser pulse (e.g., for the Gaussian pulse controlled by its full width) has significant impact on the PA signal, not only because the second time derivative of temperature $(\frac{{\partial}^{2}T}{\partial{t}^{2}})$ enters the photoacoustic equation (23), but also because it has a competing role with the interfacial thermal conductance; for maximum PA generation efficiency, the sharper the pulse, the higher the interfacial thermal conductance needs to be. Hence, any consideration of the interfacial thermal conductance impact should include the temporal waveform of the laser pulse. A qualitative analysis explaining the effects of interfacial thermal conductance and a laser pulse temporal waveform can be obtained using dimensional analysis. Let us consider the dimensionless form of Eqs. (3) and (5) for the uncoated nanosphere and eliminate the spatial derivative to obtain

$${{\Theta}_{2}}\Big|_{(r=1,{\tau})}={{\Theta}_{1}}\Big|_{(r=1,{\tau})}-{I}_{1}\Big(H({\tau})-\frac{{C}_{r}}{3}{\frac{\partial {\Theta}_{1}}{\partial {\tau}}}\Big|_{(r=1,{\tau})}\Big).$$

(43)

As is evident, the dimensionless temperature drop in the solvent is related to the dimensionless interfacial thermal resistance multiplied by the laser pulse temporal waveform $H({\tau})$ and its derivative (since the temporal temperature derivative is directly related to the temporal derivative of the pulse waveform, Eq. (16)). Hence, for the case of finite interfacial resistance, the interfacial conductance $(\frac{1}{{I}_{1}})$ and the sharpness of the pulse (signified by the temporal derivative of temperature in Eq. (43)) play an opposite role in the magnitude of the temperature drop across the interface, and, thus, the resultant PA signal (the bulk [more than $90 \%$] comes from the solvent). A quantitative assessment revealing the precise physical mechanism now follows for both uncoated and silica-coated spheres.

The PA pressure amplitude from a gold sphere with $30$ nm radius core surrounded with water under a Gaussian laser pulse irradiation with intensity $1{0}^{9}\,{\mathrm{{W}}}\,{{\mathrm{{m}}}}^{-2}$ and pulse width of $10$ ns is of order of a few tens of Pascals. The PA signal increases linearly with the laser intensity to a limit where the nonlinear effects become significant. We investigate the effect of the gold–water interfacial thermal resistance on a PA signal for two different Gaussian pulses: ten-nanosecond-wide and two-nanosecond-wide pulses corresponding to $\Delta t=10$ and $\Delta t=2$ ns, respectively, in the expression for the Gaussian pulse $H(t)=\exp \left(-{(t-{t}_{0})}^{2}/(2{\Delta}{t}^{2})\right.$. Both cases involve an identical laser intensity and absorption cross section. A sphere of size $a=30$ nm is used. A two-fold to three-fold larger sphere yields similar results. For each laser pulse, three interfacial thermal conductances of ${G}_{12}=2\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, ${G}_{12}=20\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, and ${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ are considered. The results are shown in Fig. 4. As seen from the figure, while in the blunt pulse ($10$ ns) illumination, only the lowest value of interfacial conductance displays a significant reduction in the signal amplitude, compared to the highest level of conductance (${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$); in the sharper pulse ($2$ ns) case, a significant reduction takes place at the intermediate value of conductance (${G}_{12}=20\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$). Consistent with the essence of the above dimensional analysis, this reveals that sharper pulses are more sensitive to an interfacial thermal resistance, and lower thermal resistances (higher conductances) are required to avoid efficiency loss in the PA generation.

Fig. 4

Photoacoustic signal comparison for an uncoated nanosphere ($a=30$ nm). a Ten-nanosecond-wide Gaussian laser pulse. b Two-nanosecond-wide Gaussian laser pulse. The nanosphere is placed in water and three different values of ${G}_{12}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, ${G}_{12}=20\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, ${G}_{12}=2\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$. Higher sensitivity of the generated photoacoustic signal with the interfacial resistance for the sharper laser pulse is evident

The effect of silica coating a nanosphere on a PA signal modulation is considered for the same two Gaussian laser pulses of $10$ and $2$ ns wide. A sphere with a $30$ nm radius and shell of $5$ nm is chosen. Two levels of silica–gold interfacial conductances of ${G}_{1s}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ and ${G}_{1s}=20\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ are used, as these values are close to the expected low and high ${G}_{1s}$ values that are reported in the literature^19,20. The silica–water conductance is chosen as ${G}_{1{\mathrm{{s}}}}=1000\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ again consistent with reported values^17,18. A comparison is carried out with the corresponding uncoated nanosphere, with the gold–water interfacial conductance being ${G}_{12}=20$$\text{MW}{\text{m}}^{-2}{\text{K}}^{-1}$, as discussed above, representing cases corresponding to higher heating powers. The results are shown in Fig. 5. In the blunt laser pulse case ($10$ nm width), the coated spheres result in an insignificant PA amplification for ${G}_{1s}=200$$\text{MW}{\text{m}}^{-2}{\text{K}}^{-1}$, while for ${G}_{1s}=20$$\text{MW}{\text{m}}^{-2}{\text{K}}^{-1}$, not only there is no gain, but a significant loss in the PA amplitude is obtained by coating the nanosphere. However, in the sharp laser pulse, while coating the sphere with the low value of ${G}_{1s}$ results in a loss of the PA amplitude, the higher conductance, ${G}_{1s}=200$$\text{MW}{\text{m}}^{-2}{\text{K}}^{-1}$, displays a significant PA amplification. This PA efficiency gain occurs because at this rate of laser irradiation, the chosen value of gold–water interfacial conductance is already slowing down heat transfer from the core to the water, as discussed in the previous subsection. Therefore, the lower values of ${G}_{12}$ and sharper pulses would result in an even higher gain relative to the uncoated case. Although, the application of sharper pulses can certainly be envisioned, the manifestation of lower values of ${G}_{12}$ in the practical cases are not clear. One possibility is in the higher heating powers, which causes a higher interfacial temperature, in turn reducing the density on the layer next to the sphere surface. This interfacial conductance is further reduced as the initial temperature of the medium increases.

Fig. 5

Photoacoustic signal comparison for silica-coated nanospheres. a Ten-nanosecond-wide laser pulse. b Two-nanosecond-wide laser pulse. Silica shell of size $5$ nm shell size are used for nanosphere in water at two levels of interfacial thermal conductance, ${G}_{1s}=200\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ and ${G}_{1s}=20\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$ against an uncoated nanosphere ($a=30$ nm) in water with ${G}_{12}=20\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$. Significant signal enhancement due to coating only with the sharper pulse and only at the higher silica–gold interfacial thermal conductance coefficient is seen

In short, for a coated nanosphere to outperform uncoated sphere, in addition to having a small shell thickness, the following desirable conditions should be satisfied simultaneously: (1) a high value of ${G}_{1s}$; (2) a low or intermediate value of ${G}_{12}$; and (3) a sharp laser pulse waveform.

Using our developed analytical model, we next investigate the impact of the core size and the shell thickness on the magnitude of the PA pressure signal from core–shell gold–silica nanospheres. In addition to a single nanosphere, we also present estimates of the PA pressure signals arising from an aggregation of nanospheres in a suspension. For an aggregates of nanospheres, the PA signal can be estimated as superposition of the PAs from individual nanospheres, provided the optical and heating behaviors of nanospheres remain unchanged as they are brought together^21,22.

Regarding the effect of shell thickness, for three different core sizes of $a=30, 60$, and $90$ nm with the corresponding dimensionless absorption coefficients of ${Q}_{\mathrm{abs}}=3.68,1.75$, and $1.71$, respectively, the PA pressure amplitudes, at a fixed distance from the nanosphere centers, ${r}_{{\mathrm{{d}}}}=1{\mathrm{{\mu m}}}$, are computed as a function of the silica thickness. The pressure amplitudes are normalized with that of the uncoated nanosphere with a radius of $a=30$ nm. A 10-ns-wide Gaussian laser pulse is used and interfacial conductance coefficients are chosen as ${G}_{1s}=110\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, ${G}_{s2}=1000\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, and ${G}_{12}=150\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$. The results are shown in Fig. 6a. As it is evident from the figure, increasing the shell size yields a reduced PA signal. Since the thermal expansion coefficient of the silica is much smaller than that of water, increasing the silica thickness increases thermal energy absorption within the silica without producing proportional pressure signal, and reduces the thermal energy transport to the water, the major PA signal producer, and, thus, the reduction in the overall PA signal. The estimation of the PA pressure amplitude for a fixed concentration of aggregates of nanospheres in a suspension are given in Fig. 6b, where the data for the single nanosphere are scaled by the volume of the nanospheres. In addition to the effect of shell thickness, these figures demonstrate the effect of the core size on the PA signal. While for the single sphere, the PA signal increases with increasing the core size, for aggregates of spheres, the PA signal drops with increasing the core size.

Fig. 6

Normalized photoacoustic signal amplitude $(p/p({r}_{{\mathrm{{d}}}}=30\,{\mathrm{{nm}}}))$ versus the shell thickness. a Single silica–gold core–shell nanosphere. b Suspension of nanospheres. For each case, data for three difference core radii are given. A 10-ns-wide Gaussian laser pulse is used and interfacial conductance coefficients are chosen as ${G}_{1s}=110\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, ${G}_{s2}=1000\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$, and ${G}_{12}=150\,{\mathrm{{{MW}}}}\,{\mathrm{{{m}}}}^{-2}\,{\mathrm{{{K}}}}^{-1}$

Before explaining these trends and for more comprehensive investigation, let us first compute and present the PA pressure amplitude for two other configurations of the core–shell nanospheres: (1) one in which the ratio of the total radius to the core radius remains fixed, $\frac{b}{a}=1.5$, as the core radius increases; and (2) the other in which the silica shell thickness is kept fixed, $b-a=15$ nm. The maximum pressure amplitudes are computed and normalized by dividing with the pressure obtained for the smallest core size of $30$ and $15$ nm silica shell thickness. The results for 10-ns Gaussian laser pulse irradiation of a single nanosphere are depicted in Fig. 7a. For both configurations of the core–shell structure, the PA signal displays an overall increasing function w.r.t. radius. A higher increase is seen for the case of the fixed shell thickness. This is expected since the higher thickness of silica absorbs higher thermal energy without giving rise to a proportionate thermoelastic expansion. The results for a suspension of nanospheres are shown in Fig. 7b.

Fig. 7

Normalized photoacoustic signal $(p/p({r}_{{\mathrm{d}}}=30{\,}{\mathrm{nm}}))$ as functions of radius. a Single nanosphere. b Suspension of nanospheres. For each cases, $(p/p({r}_{{\mathrm{d}}}=30{\,}{\mathrm{nm}}))$ is given for two configurations of of $\frac{b}{a}=1.5$ and $b-a=15$ nm. A 10-ns-wide Gaussian laser pulse is chosen for gold–silica nanosphere irradiation

For a single core–shell nanosphere, the overall increasing trend of the PA signal with an increasing core size can be explained using dimensional analysis. From the photoacoustic equation (23) and the Duhammel formula in theory of wave propagation²³, we have

$$p\propto K\beta \frac{{\partial }^{2}T}{\partial {t}^{2}}\propto \frac{K\beta }{\Delta {t}^{2}}T=\frac{K\beta }{\Delta {t}^{2}}\frac{a{Q}_{{\mathrm{{abs}}}}F}{r{k}_{2}}\Theta ({C}_{r},{D}_{r},{K}_{r},{I}_{1},{I}_{2},A),$$

(44)

where $\Delta t$ is the width of the laser pulse, $\Theta$ is the dimensionless temperature, and ${I}_{1}$ and ${I}_{2}$ are dimensionless interfacial resistance coefficients. Eq. (44) reveals that the pressure is linearly proportional to both the core radius and the absorption efficiency. The absorption efficiency, itself, is a function of radius, and the reduction of ${Q}_{{\mathrm{{abs}}}}$ with core radius is sublinear¹³. Thus, with increasing the core size, an increasing PA signal is expected. Furthermore, the more subtle effect comes from reduction in dimensionless interfacial resistance, $I$. As the core radius increases, the interfacial resistance ${I}_{1}=\frac{{k}_{s}}{a{G}_{1s}}$ drops, and, thus, contributing in enhanced heat transport to the surrounding medium, in turn, yielding further enhancement of the PA signal.

As seen from Fig. 7b, contrary to the PA signal from the single core–shell sphere, for suspension of nanospheres, the PA signal drops as the sphere core size increases, which is consistent with the experimental data^24,25. This is because for a fixed concentration, a solution with smaller spheres consist of higher number of spheres, since the number of spheres is inversely proportional to the volume of the spheres. Therefore, the PA signal from an aggregate of spheres in a suspension drops superlinearly as the core size increases, overcoming an almost linear increase in the PA signal from individual spheres, yielding an overall drop of the PA signal from suspension of nanospheres.

Discussion

Our comprehensive model of the Fourier heat condition and the photoacoustics of the core–shell nanospheres incorporating the interfacial thermal resistance and the adopted analytical solution strategy prove to be highly effective in revealing some of the underlying physics of the photoacoustics of core–shell nanosphere systems not known to date. The contribution of the core and the fluid to the overall PA signal is quantified, as well as the extent of the region surrounding the core responsible for the bulk of the generated signal. We also discovered and quantified through our modeling the impact of the laser pulse temporal waveform on the sensitivity of the PA signal intensity to the interfacial thermal resistance coefficients.

The present model based on Fourier’s heat conduction does not consider the finite speed of heat transfer (the heat flux relaxation time), and the efficiency of the heat transfer from the core to outside is controlled solely by the introduction of an interfacial thermal resistance. It may be useful to consider a more comprehensive model based on hyperbolic heat conduction taking into account heat flux relaxation times. Considering the short laser pulses on the order of nanoseconds and small core sizes of a few tens of nanometers, incorporation of other heat conduction models, such as Cattaneo’s law^26,27 representing heat conduction with the finite speed of propagation might also be useful. Such models, besides thermal conductivity coefficient, require the value of heat flux relaxation time whose value for even most common substances are either not known or the reported values include a very large variances.

Validation of these two models, Fourier and hyperbolic heat conduction, requires appropriate experimental data, which is currently not available. Thus, careful experiments with varying levels of laser fluences and wave sharpness are also required to finely control the heating power, its rate, and the interfacial temperature and interfacial conductance. The combination of the modeling and the experiment would reveal more details of the underlying physics and estimates of macroscopic properties.

The modeling can be easily extended to consider photoacoustics of biological media by introducing a shear modulus for the core-surrounding medium. The extension of the model to gold nanorods is also valuable in view of their more favorable optical properties compared to nanospheres, including a higher refractive index sensitivity and a tunable longitudinal plasmon band, which is achieved by adjusting their aspect ratio^28,29.

The physical insights revealed using our modeling provide guidance in the application of gold nanoparticles in medical PA imaging. As demonstrated, the magnitude of thermal interfacial resistance and the laser pulse temporal waveform have a dramatic impact on the magnitude of a generated PA signal. Thus, strategies should be adopted to reduce interfacial resistance, such as avoiding excessive heating, which can yields vapor generation at the core–solvent interface and with high interfacial resistance. The details of the laser pulse temporal waveform are also required, as the realization of the full benefit of sharper pulses is dependent on ensuring low interfacial resistance. Also, it is important to note that the strategy of silica-coating nanospheres may not automatically yield high PA signals, and conditions of a sharp laser pulse waveform and low thermal interfacial resistance at the gold–silica interface must be satisfied.

In addition to providing guidance in the design of nanoparticle-augmented PA imaging, the developed model can be used in combination with an in vivo PA signal measurement to map and identify the local cellular environment (e.g., revealing the macroscopic properties of thermal expansions and, in turn, yielding the type of biological environment).