Abstract
The dynamical Casimir effect is the generation of pairs of real particles or photons from the vacuum as a result of a non-adiabatic change of a system parameter or boundary condition. As opposed to standard parametric amplification where the modulation occurs both in space and in time, this fundamental process requires a pure modulation in time, which makes its detection particularly challenging at optical frequencies. In this paper we experimentally demonstrate a realization of the analogue dynamical Casimir effect in the near-infrared optical regime in a dispersion-oscillating photonic crystal fibre. The experiments are based on the equivalence of the spatial modulation of the fibre core diameter to a pure temporal modulation when this is considered in the co-moving frame of the travelling pump pulse. We provide evidence of optical dynamical Casimir effect by measuring quantum correlations between the spectrally resolved photon pairs and prove their non-classical nature with photon anti-bunching.
Similar content being viewed by others
Introduction
One of the most outstanding predictions of quantum field theory is that pairs of real particles can be generated from the vacuum as a result of a strong non-adiabatic change of a system parameter or boundary condition1,2. This is referred to as the Dynamical Casimir Effect (DCE)1,3,4,5,6 and is usually described as a process in which a cavity with periodically oscillating mirrors produces pairs of photons from the vacuum. For a sinusoidal modulation at frequency Ω, the pair will be generated at frequency Ω/2. Although the original DCE proposal was based on the mechanical movement of mirrors, an analogue effect can be achieved by simply imposing a time dependence on one of the system parameters. Indeed a recent work7 divides all DCE theoretical proposals into two groups: experiments where the pair generation is due to a mechanical movement of mirrors, named “mechanical” DCE, and setups where the boundary conditions are changed without moving mirrors, but simply by modulating a system parameter, hence the label “parametric” DCE. We prefer to refer to this second class of proposals as “analogue” DCE, due to historical reasons, but the two terms are interchangeable. An alternative to oscillating mirrors is an optical cavity either filled with or constituted by a medium of refractive index n: a periodic change of n in time (and that is uniform in all spatial coordinates) is equivalent to a periodic change of the boundary conditions, as pointed out by Lambrecht8 and Mendonça9,10. Of particular relevance to this work, Lambrecht’s proposal relies on the use of an optical nonlinearity to achieve the periodic modulation of \(n = \sqrt \varepsilon\) where the dielectric permittivity is modulated by an oscillating electric field, E, through the second-order susceptibility χ(2): \(\varepsilon = \varepsilon _0 + \chi ^{(2)}E\) 8. The same physics can be realised also in a medium with a third order nonlinear susceptibility χ(3)11. The key observation is that for the case in which the χ(2)− or χ(2)-medium is shorter than the driving E-field wavelength, the medium will oscillate uniformly and the parametric amplification of photons from the vacuum state takes on a formal analogy with the mechanical DCE.
Yablonovitch3 noted the fundamental connection between DCE and parametric amplification, a connection which has been deeply analysed more recently by Nation et al.6. It is thus worth to point out that the physics of DCE and parametric amplification, for instance spontaneous four wave mixing in a χ(3) medium, carries more than a formal resemblance. The distinguishing physical feature between standard parametric amplification and DCE is that the former relies on a polarisation wave propagating in a long medium so the modulation occurs both in (longitudinal propagation) space and in time whereas the latter refers to a temporal variation of the medium that is uniform along the longitudinal propagation direction. This last condition can be obtained for example, as mentioned above, by ensuring that the medium is significantly thinner than the wavelength of the input E-field driving the polarisation wave8,11. This subtle difference renders the experimental realisation of a DCE experiment particularly challenging as it would require large (to overcome the low amplification gain from sub-wavelength films) and fast (non-adiabatic) modulations of the refractive index. Recent experiments demonstrated analogue DCE photon pair emission at low frequency (5 GHz) in superconducting circuits12 and in a Josephson metamaterial13, and DCE-like emission (albeit with no quantum signature in the emission) was reported for acoustic waves in a Bose–Einstein condensate14. However, the generation of photon pairs by DCE in the optical region, e.g. by nonlinear optical process, has not been demonstrated to date.
In this paper we experimentally demonstrate a realisation of the DCE in the near-infrared optical regime mediated by the χ(3) nonlinearity in a dispersion-oscillating photonic crystal fibre. Photonic crystal fibres with a periodic modulation of the group-velocity dispersion (GVD) are also called dispersion-oscillating fibres (DOFs) and they are obtained by periodically modulating the core diameter during fabrication15,16,17,18. We first describe the longitudinal spatial modulation of the fibre core diameter as a temporal modulation when this is considered in the comoving frame of the travelling pump pulse. We then provide experimental evidence of optical DCE by measuring quantum correlations between the spectrally resolved photon pairs, expressed by the conventional coincidence-to-accidental ratio. Finally, in order to demonstrate the non-classical nature of the measured light, we provide evidence of anti-bunching photon statistics.
Results
Theory
Photon-pair generation in fibres has a long history and is usually interpreted in terms of spontaneous four-wave mixing (SFWM). Parametric amplification of the vacuum fluctuations in a fibre was first realised by optically pumping with laser pulses whose carrier wavelength was chosen to be close to the zero dispersion wavelength of the fibre19. Phase matching and high efficiency photon pair generation was thus achieved by the balance between nonlinear phase contributions and the linear anomalous dispersion. Successively, the possibility to achieve phase matching was also shown in the normal dispersion regime20 as a result of a negative fourth order dispersion term.
Parametric amplification (in the classical regime) in fibres with periodic spatial perturbations21 and DOFs18,22 has also been observed and interpreted in terms of quasi-phase matching, in analogy to quasi-phase matched spontaneous parametric down-conversion in χ(2) nonlinear crystals23.
A schematic layout of the fibre geometry use in this work is shown in Fig. 1a, where we consider the specific case in which the optical pump pulse is significantly shorter than the periodicity Λ of the DOF oscillation. We then consider the evolution of the boundary conditions as perceived by such a short pulse in the reference frame of the pulse itself. The pulse will experience a uniform oscillation in time of the surrounding medium parameters at a frequency Ω′ that is proportional to the fibre longitudinal periodicity \(K = 2\pi /{\mathrm{\Lambda }}\) (primed quantities refer to the frame comoving at the group velocity vg of the laser pulse). In this reference frame, the DCE predicts that two photons will be generated at frequencies \(\omega \prime = m{\mathrm{\Omega }}\prime /2\), where the integer m accounts for the possibility to have resonances also at frequencies that are multiples of the boundary modulation. If the medium has no optical dispersion, the phase velocity is equal to the group velocity \(v = v_g\) and thus in the comoving frame the electric field does not oscillate in time. In this case, the only contribution to any time-variation in the comoving frame originates from the periodic fibre oscillation acting on the nonlinear refractive index \({\mathrm{\Delta }}n \propto \chi ^{(3)}|E|^2\). The presence of dispersion \(v \ne v_g\) will lead to a slip of the pulse electric field E underneath the pulse envelope, generating an additional temporal oscillation due to the oscillating electric field. This in turn creates an additional nonlinear polarisation term that is proportional to χ(3)E(2) and thus oscillates at twice the pulse comoving frequency \(2\omega _{0\prime }\). In the case of our dispersive fibre therefore we have a modified DCE condition that must account for both temporally oscillating terms, i.e. \(\omega \prime = m{\mathrm{\Omega }}\prime /2 + \omega _{0\prime }\). In order to determine the emitted frequencies that will be observed in the laboratory frame, we take the energy conservation relation for signal and idler photons:
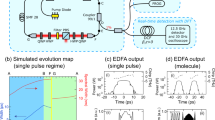
Dynamical Casimir effect in a dispersion-oscillating fibre. a Concept of the Dynamical Casimir effect (DCE) in a dispersion-oscillating fibre (DOF): a short pulse propagating though the fibre experiences a fast modulation of the group velocity dispersion (GVD). b Schematics of the experimental setup for quantum correlation measurements. Signal and idler beams generated inside the DOF are separated and filtered from the pump by a 4-f grating system. A half wave plate (HWP) is used to rotate the polarization and gratings are labelled G1, G2 and G3. Photons are detected by single photon avalanche detectors (SPAD) named s1, s2 and i
Applying a relativistic boost into the lab frame to all frequencies ω′ = γ(ω − vgk), where k = k(ω), and imposing that the temporal modulation is zero in the lab frame (Ω = 0), we finally obtain (see details of the derivation in Supplementary Note 2):
This expression predicts that the DCE photons will be observed in the laboratory frame in symmetric sidebands around the pump frequency and provides a quantitative estimate of the exact spectral location of these photons. Interestingly, this formula, derived in the comoving frame as a DCE, is in perfect agreement with the result from a calculation based on the quasi-phase-matching condition for standard parametric amplification in the lab frame18,22, and therefore, underlines once again the connection between the DCE and parametric oscillation.
Quantum emission measurements
Figure 1b shows a schematic view of the experimental setup used for quantum emission and correlation measurements. For classical characterization the output of the DOF can be sent to an optical spectrum analyzer. The GVD modulation of the photonic crystal fibre used in the experiments is illustrated in Fig. 2a, with an average value <β2> = 0.45 ps2 km−1 at the pump wavelength λp = 1052.44 nm used in the experiment. The pump pulse duration is 600 ps, equivalent to a length of 0.12 m, which is much shorter than the 5 m periodicity of the fibre. Figure 2b shows a spectrum taken at high pump peak power (Pp = 12 W, together with the prediction of the spectral sidebands from Eq. (2) for m = 3 (dashed black lines at 954 nm and 1173 nm, conventionally named signal and idler). Only these solutions of Eq. (2) will be considered from now on, since they display the largest parametric gain, as confirmed by classical simulations (see Supplementary Fig. 1). More details about the fibre fabrication and characterization are provided in the Methods section.
Classical characterization of the fibre. a Zoom of the longitudinal evolution of the measured group velocity dispersion (GVD) with average value <β2> = 0.45 ps2 km−1 at the pump wavelength λp = 1052.44 nm. The total length of the fibre is 80 m. b Optical spectrum measured at the output of the dispersion-oscillating fibre (solid blue line) for high pump power Pp = 12 W and theoretical prediction from Eq. (2) (dashed black lines) for the third harmonic of the modulation frequency (m = 3)
For the quantum correlation measurements diffraction gratings are used to filter out the pump power and to spectrally separate signal and idler beams, as illustrated in Fig. 1b. A spectral bandwidth of 1 nm on both channels is selected in order to maximise the collection of DCE pairs and to minimise the residual contribution due to Raman scattering. The electronic signals generated by single photon detectors (SPADs) are time-stamped and correlations between signal and idler are measured by a time-to-digital converter (TDC) module. A histogram of coincidences as a function of the delay between the arrival time of the photons on the signal channel (s1 or s2) and those on the idler (i) channel is shown in Fig. 3a. The observed peak of coincidence counts between signal and idler at zero delay Ns,i(0) (i.e. within the same pump laser pulse) is several times larger than the coincidence rates at different delays (i.e. between different laser pulses). This unambiguously implies non-classical correlations between the signal and the idler beams24. The coincidence-to-accidental ratio (CAR) is defined as the ratio between the coincidences due to correlated photon pairs and those due to accidental counts. It can be estimated as:
where Ns,i(0) is the area, within a coincidence time window Δt, of the peak at zero delay and Ns,i(τ) is the average of the areas of non-zero-delay peaks.
Photon pairs and coincidence-to-accidental ratio (CAR). a Histogram of coincidence counts between signal photons at λs = 954 nm and idler photons at λi = 1173 nm (bandwidth 1 nm) for pump λp = 1052.44 nm and Pp = 0.03 W. In inset a zoom around the zero delay peak. b 2D map of the CAR as a function of the signal and idler wavelengths for Pp = 0.03 W and a coincidence time window Δt = 1.7 ns
In Fig. 3b we show the measured CAR as a function of the signal and idler wavelengths, obtained by scanning the signal and idler slits after the grating G1 with a step resolution of 1 nm. It is evident that the CAR remains large for wavelength-pairs that satisfy Eq. (2) but otherwise quickly drops to zero. The best CAR (around 5) and the highest photon count rates are found for λs = 954 nm and λi = 1173 nm, and this choice of wavelengths position will be used in the following analysis. The double-peak structure observed in Fig. 3b and similarly in Fig. 2b is ascribed to hopping of the pump laser between two modes of the laser cavity.
In Fig. 4a the CAR is measured for different pump peak powers between 0.03 W and 0.15 W and is seen to decrease with increasing power. This is due to the fact that accidental counts grow quadratically with the number of single-photon counts (originating from both DCE and Raman amplification), whereas the true coincidence counts grow only linearly. The estimated value of the CAR is dependent also on the time window, Δt, within which coincidences are counted and increases as we decrease Δt [compare the green and red curves in Fig. 4a]. A very narrow time window of 240 ps allows us to collect most of the coincidences, while filtering out most of the background Raman and dark counts.
Evidence of quantum correlations and photon anti-bunching. a Coincidence-to-accidental ratio (CAR) as a function of power for two different choices of the coincidence time window, Δt = 240 ps (red) and Δt = 1.7 ns (green). The dashed lines are simulated for different ratios between Raman and Casimir (DCE) photons on the idler channel. b Intensity auto-correlation function g(2)(0) at zero delay. The blue dashed line is a simulation assuming only single photon states |1〉 from DCE and Raman photons. All error bars assume a Poisson distribution of the number of coincidence counts, i.e. going as \(\sqrt N\), where N is the measured average number
At very low powers on the idler channel most of the counts come from Raman scattering (Raman scattering emission occurs mostly at red-shifted wavelengths), whereas on the signal channel most of the single counts are due only to the detector dark counts (see Supplementary Note 3 for more details). Therefore we use a model, described in details in Supplementary Note 4 and Supplementary Fig. 3, in order to isolate the contribution of DCE pairs. We assume a quadratic dependence for the DCE photon-pair production process (two photons from the pump are annihilated for each pair produced) and a linear dependence for the Raman process. The dashed lines in Fig. 4a correspond to the resulting calculations based on the detected single photon rates, the estimated collection and detection efficiency and by using the ratio between Raman and DCE photons as a free parameter. From these calculations we estimate that about 2 × 10−3 DCE pairs per pump pulse are generated in the fibre versus 0.18 Raman photons for Pp = 0.03 W, or 0.05 DCE pairs versus 0.9 Raman photons at Pp = 0.15 W.
We use these numbers to verify that the measured CAR is due to vacuum seeded photons and cannot be ascribed to seeding by the spontaneous Raman emission. This can be demonstrated by estimating the number of temporal modes contained in 1 nm of detected spectrum. From the Fourier transform of the 600 ps pump pulse we estimate a pump bandwidth of 3 GHz, to be compared with a detection bandwidth of about 300 GHz. Therefore we estimate roughly 100 temporal modes detected in 1 nm of spectrum. With 0.18–0.9 Raman photons per pulse, we therefore have between 1.8 × 10−3 and 9 × 10−3 Raman photons per temporal mode at the fibre output that are negligible when compared to the 1/2-photon/mode from the vacuum, thus supporting the quantum vacuum-origin of the observed DCE photon coincidence counts.
Finally, we perform a heralded Hanbury–Brown Twiss experiment by using a beam splitter on the signal path and measuring the coincidences at the two output ports, heralded by the idler photons. The second-order coherence at zero delay g(2)(0) is then evaluated as:25
where Ni indicates the measured single count rate at the idler channel, Nx,y the measured coincidence rates between the two beam splitter ports x = s1 or x = s2 on the signal channel and the idler y = i, Ns1,s2,i the triple coincidences between the three channels. g(2)(0) < 1 is taken to be evidence of non-classicality25.
The results are shown in Fig. 4b for different values of CAR, corresponding to different pump powers. The case of CAR = 0 is obtained by moving the idler slit in order to collect only Raman radiation on the idler and the corresponding g(2)(0) is found to be nearly equal to 1, as expected. The dashed blue line represents the calculated g(2)(0) in the case of only pure single photon states due to DCE pairs (the derivation is given in Supplementary Note 5). All experimental points lie slightly above the calculated curve, indicating a small contribution in the measurements from higher photon number states. The main result of Fig. 4b is that g(2)(0) clearly drops below 1 for CAR > 1, thus providing a clear indication of non-classical emission.
Discussion
We have proposed a dispersion-oscillating photonic crystal fibre system for observing an optical realisation of the DCE. Our proposal represents an optical analogue of the mechanical DCE in the sense that the mechanical motion of mirrors is replaced by a time modulation of a system parameter, the refractive index. A pump laser pulse creates a refractive index variation through the nonlinear Kerr effect, which in the comoving frame experiences a temporal oscillation and, under the condition that the pulse is shorter than the fibre oscillation period, produces photon pairs according to the DCE condition. The time oscillation of the fibre in the comoving frame provides the mechanism to transfer energy from the pump beam to the vacuum states, in the same way as the modulation of the position of mirrors in a cavity allows the transfer of mechanical energy into photon pairs. Experiments confirm the presence of correlated photon pairs emitted at the predicted wavelengths with non-classical statistics, supporting the origin from vacuum-seeded DCE. Therefore we propose that dispersion-oscillating fibres could provide a suitable test-bed for studying the DCE physics, for instance by changing the shape of the fibre modulation. Moreover, we showed that correlated pairs are produced with a narrow spectral bandwidth at frequencies, which can be easily tuned by acting on the shape and period of the fibre modulation, thus providing a new source of light for quantum applications.
Methods
Optical fibre characterization
The fused silica photonic crystal fibre used in the experiments is fabricated by using the stack-and-draw technique26. The outer diameter of the fibre, whose length is 80 m, is modified during the drawing process to obtain a Gaussian-shaped modulation of the GVD with a full width at half maximum of 0.5 m, repeated with a periodicity of 5 m as shown in Fig. 2a. The average GVD value is <β2> = 0.45 ps2 km−1 (red dotted line in Fig. 2a) and the maximum excursion of GVD at the top of each spike is estimated to be about \(\beta _2^{{\mathrm{Max}}} = 1.7\,{\mathrm{ps}}^2\,{\mathrm{km}}^{ - 1}\). We pump the DOF with a fibre-amplified laser with a carrier wavelength λp = 1052.44 nm and 2 MHz repetition rate. The pulse duration is 600 ps, equivalent to a length of 0.12 m (accounting for the refractive index n = 1.45 of the fibre core) and is thus much shorter than the 5 m modulation periodicity. Note that we can assume that the pulse duration remains constant over all the fibre length. The pulse duration was measured at the output of the fibre and found the same as at the input. This is also supported by a calculation based on the the dispersion length27 that is orders of magnitude larger than the actual fibre length, even by considering the peak dispersion value (1.7 ps2 km−1). Therefore dispersive effects on the pulse shape are negligible in our experiments. The specific shape of the modulation is chosen in order to maximise the parametric gain at frequencies that lie far from the Raman gain spectrum. Experiments have also been carried out with a sinusoidal modulated fibre (corresponding to the simplest kind of modulation in DCE), and similar results to those described in this paper were found, although with slightly worse evidence of non-classical behaviour (lower CAR values). Figure 2b provides an example of the fibre output spectrum for a pump peak power Pp = 12 W acquired with an optical spectrum analyser, showing parametric gain narrow peaks around 954 nm (signal) and 1173 nm (idler) and the broader contribution of Raman scattering mainly around 1100 nm. The dashed line corresponds to the prediction for DCE emission from Eq.2 for m = 3, by using the experimental parameters measured for λp = 1052.44 nm, <β2> = 0.45ps2km−1 and <β4> = −1.2 × 10−55 s4 m−1 (see Supplementary Note 1 for more details).
Experimental setup for quantum correlation measurements
Figure 1b shows the experimental setup used for quantum correlation measurements. We use a diffraction grating (G1) to filter out the pump spectrum and to also spectrally separate the photon pairs. Two additional gratings (G2 and G3) in a 4-f configuration are used as tunable passband filters in order to reduce the contribution of broadband residual Raman scattering. Slits are arranged in order to select 1 nm of spectrum in both the low (idler) and high frequency (signal) photon paths, which roughly corresponds to the DCE bandwidth, as illustrated in Figs. 2b, 3b. The slit size (400 μm) was indeed chosen in order to optimise the observed coincidence-to-accidental ratio (CAR). On the signal photon path we add a 50:50 beam splitter to perform anti-bunching measurements. Finally, photons are coupled into multi-mode fibres and sent to single-photon avalanche detectors (SPADs). We use two InGaAs gated SPADs (Aurea Technology) and one visible silicon SPAD (Excelitas). The outputs from the single photon detectors are sent to a time-to-digital converter (from IDQuantique), which registers the arrival times of the photons, which are used to perform correlations. We operate the pump laser at low powers between Pp = 0.03 W and Pp = 0.15 W in order to ensure low gain and thus single photon-pair emission.
Data availability
All data are available at DOI 10.17861/9b7e182a-e985-4912-862a-ff6cd8fe54f4. All relevant data are available from the authors.
References
Moore, G. T. Quantum theory of the electromagnetic field in a variable length one dimensional cavity. J. Math. Phys. 11, 2679 (1970).
Fulling, S. A. & Davies, P. C. W. Radiation from a moving mirror in two dimensional space-time: conformal anomaly. P. Roy. Soc. A-Math. Phy. 348, 393 (1976).
Yablonovitch, E. Accelerating reference frame for electromagnetic waves in a rapidly growing plasma: Unruh-Davies-Fulling-Dewitt radiation and the nonadiabatic casimir effect. Phys. Rev. Lett. 62, 1742–1745 (1989).
Schwinger, J. Casimir energy for dielectrics. Proc. Natl Acad. Sci. USA 89, 4091–4093 (1992).
Dodonov, V. V. Current status of the dynamical casimir effect. Phys. Scr. 82, 038105 (2010).
Nation, P. D., Johansson, J. R., Blencowe, M. P. & Nori, F. Colloquium. Rev. Mod. Phys. 84, 1–24 (2012).
Macr, V. et al. Nonperturbative dynamical casimir effect in optomechanical systems: vacuum casimir-rabi splittings. Phys. Rev. X 8, 011031 (2018).
Dezael, F. X. & Lambrecht, A. Analogue casimir radiation using an optical parametric oscillator. EPL (Europhys. Lett.) 89, 14001 (2010).
Mendonça, J. T. Theory of photon acceleration (CRC Press, Bristol, UK, 2000).
Mendonça, J. & Guerreiro, A. Time refraction and the quantum properties of vacuum. Phys. Rev. A 72, 063805 (2005).
Faccio, D. & Carusotto, I. Dynamical Casimir Effect in optically modulated cavities. Eur. Phy. Lett. 96, 24006 (2011).
Wilson, C. M. et al. Observation of the dynamical casimir effect in a superconducting circuit. Nature 479, 376–379 (2011).
Lähteenmäki, P., Paraoanu, G. S., Hassel, J. & Hakonen, P. J. Dynamical casimir effect in a josephson metamaterial. Proc. Natl Acad. Sci. USA 110, 4234–4238 (2013).
Jaskula, J.-C. et al. Acoustic analog to the dynamical casimir effect in a bose-einstein condensate. Phys. Rev. Lett. 109, 220401 (2012).
Droques, M., Kudlinski, A., Bouwmans, G., Martinelli, G. & Mussot, A. Experimental demonstration of modulation instability in an optical fibre with a periodic dispersion landscape. Opt. Lett. 37, 4832–4834 (2012).
Armaroli, A. & Biancalana, F. Tunable modulational instability sidebands via parametric resonance in periodically tapered optical fibres. Opt. Express 20, 25096–25110 (2012).
Armaroli, A. & Biancalana, F. Suppression and splitting of modulational instability sidebands in periodically tapered optical fibres because of fourth-order dispersion. Opt. Lett. 39, 4804–4807 (2014).
Mussot, A., Conforti, M., Trillo, S., Copie, F. & Kudlinski, A. Modulation instability in dispersion oscillating fibres. Adv. Opt. Photon. 10, 1–42 (2018).
Li, X., Chen, J., Voss, P., Sharping, J. & Kumar, P. All-fibre photon-pair source for quantum communications: improved generation of correlated photons. Opt. Express 12, 3737–3744 (2004).
Rarity, J. G., Fulconis, J., Duligall, J., Wadsworth, W. J. & Russell, P. S. J. Photonic crystal fibre source of correlated photon pairs. Opt. Express 13, 534–544 (2005).
Matera, F., Mecozzi, A., Romagnoli, M. & Settembre, M. Sideband instability induced by periodic power variation in long-distance fibre links. Opt. Lett. 18, 1499–1501 (1993).
Droques, M. et al. Fourth-order dispersion mediated modulation instability in dispersion oscillating fibres. Opt. Lett. 38, 3464–3467 (2013).
Boyd, R. Nonlinear Optics (Academic Press, Orlando, FL, USA, 2008).
Loudon, R. The Quantum Theory of Light. (Clarendon Press, Oxford, 1973).
Bocquillon, E., Couteau, C., Razavi, M., Laflamme, R. & Weihs, G. Coherence measures for heralded single-photon sources. Phys. Rev. A 79, 035801 (2009).
Russell, P. Photonic Crystal fibres. Science 299, 358–362 (2003).
Agrawal, G. Nonlinear fibre Optics, 5th edon (Academic Press, Amsterdam, 2012).
Acknowledgements
This work was partly supported by the Agence Nationale de la Recherche through the High Energy All fibre Systems (HEAFISY), the Labex Centre Europeen pour les Mathematiques, la Physique et leurs Interactions (CEMPI) and Equipex Fibres optiques pour les hauts flux (FLUX) through the Programme Investissements d’Avenir, by the Ministry of Higher Education and Research, Hauts de France council and European Regional Development Fund (ERDF) through the Contrat de Projets Etat-Region (CPER Photonics for Society, P4S) and FEDER through the HEAFISY project. D.F. acknowledges financial support from the European Research Council under the European Union Seventh Framework Programme (FP/2007-2013)/ERC GA 306559 and EPSRC (UK, Grant No. EP/P006078/2). N.W. acknowledges support from EPSRC CM-CDT Grant No. EP/L015110/1.
Author information
Authors and Affiliations
Contributions
A.M., F.B. and D.F. conceived the idea. S.V., H.D.S. and A.M. developed the experimental setup and collected the data. A.K. designed and fabricated the fibre. N.W., A.P., F.B. and D.F. developed the theoretical framework. S.V., E.L. and A.M. analyzed the data. All authors discussed the results, provided critical feedback and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vezzoli, S., Mussot, A., Westerberg, N. et al. Optical analogue of the dynamical Casimir effect in a dispersion-oscillating fibre. Commun Phys 2, 84 (2019). https://doi.org/10.1038/s42005-019-0183-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0183-z
This article is cited by
-
Transport in electron-photon systems
Frontiers of Physics (2023)
-
Analogue cosmological particle creation in an ultracold quantum fluid of light
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.