Abstract
Generally, the lack of long-range order in materials prevents from experimentally addressing their electronic band dispersion by angle-resolved photoelectron spectroscopy (ARPES), limiting such assessment to single crystalline samples. Here we demonstrate that the ARPES spectra of azimuthally disordered transition metal dichalcogenide (TMDC) monolayers with 2 H phase are dominated by their band dispersion along the two high symmetry directions Γ-K and Γ-M. We exemplify this by analyzing the ARPES spectra of four prototypical TMDCs within a mathematical framework, which allows to consistently explain the reported observations. A robust base for investigating TMDC monolayers significantly beyond single crystal samples is thus established.
Similar content being viewed by others
Introduction
Transition-metal dichalcogenide (TMDC) monolayers have gained attention as semiconductors for next-generation nanoscale electronic devices owing to their unique electronic properties that originate from their low-dimensionality and high-symmetry structure1,2,3. Recently, heterostructures of monolayer TMDC combinations have been employed in novel devices with superior optoelectronic performance4,5,6,7,8,9,10. Furthermore, they can be used to explore physical phenomena like topological edge states11 or the spin Hall effect12,13,14. The key for their fundamental understanding, and notably also for rational device design, is understanding the electronic structure of TMDC monolayers and their heterostructures. To obtain detailed information on semiconductor band structures, angle-resolved photoemission spectroscopy (ARPES) is a very effective method and it has been widely applied to single crystalline materials for decades15. However, sufficiently large single crystalline samples are required for conventional ARPES measurements (ca. mm2 range), which is still challenging for TMDC monolayers and thus limits obtaining the desired information on the electronic band structure for many interesting systems. Specifically, TMDC monolayers fabricated by various methods generally comprise flakes (typical lengths ranging from a few 10 nm to several 10 µm) with azimuthal (φ) disorder, i.e., samples are two-dimensional (2D) powders16,17,18,19,20. Accordingly, the electronic band dispersion of each azimuthally rotated flakes contributes to the ARPES spectra, generally prohibiting band dispersion observation due to the angular averaging. Notably, Zhou et al. reported the observation of dispersing bands in ARPES of highly oriented pyrolytic graphite (HOPG; in terms of surface structure also a 2D powder) and they suggested Van Hove singularities as reason for the defined electronic band dispersion in the “angle dependent” density of states (quasi 1D-DOS)21. Using the same proposition, others have observed and explained ARPES spectra exhibiting energy dispersion for azimuthally disordered MoS2 and WSe2 samples22,22.
These reported ARPES spectra are the result of a summation over a large number of single crystal flakes with random azimuthal orientation. However, the existence of Van Hove singularities along certain directions over extended energy and momentum values, as invoked earlier to explain 2D powder spectra using the concept of an angle-dependent DOS21, should be challenged. According to the quasi 1D-DOS approach proposed by Zhou et al.21, Van Hove singularities should occur along the high-symmetry directions in disordered samples. Since Van Hove singularities do only occur at specific points of the Brillouin zone of a single crystal (see Supplementary Note 1), this approach might not be appropriate to explain the ARPES features of disordered TMDC samples, calling for a revision of the quasi 1D-DOS concept. Here, we propose an alternative explanation for the observed dispersing bands in ARPES of 2D powders, without the need of using the concept of quasi 1D-DOS and Van Hove singularities.
In this contribution, we evidence high-symmetry induced sharp dispersion for TMDC monolayer samples with azimuthally disordered flakes by ARPES measurements and we consolidate our observations with the help of density functional theory (DFT) calculations and angular averaging considerations. With high-resolution ARPES spectra of single crystalline and azimuthally disordered WSe2 monolayers we reveal the impact of the azimuthal disorder and rationalize that the two high-symmetry directions [Γ-K and Γ-M of the Brillouin zone (BZ)] dominate the ARPES spectra of azimuthally disordered samples. This is a consequence of the angular integration of the single crystal TMDC monolayer band structure. The same is evidenced for three further prototypical semiconducting TMDCs (MoS2, MoSe2, and WS2), allowing the experimental determination of band dispersion in the two most important BZ directions for azimuthally disordered TMDC monolayers.
Results
Sharp band dispersion in azimuthally disordered TMDCs
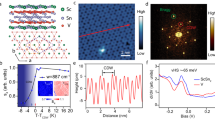
Figure 1a shows the BZ of a single crystalline TMDC with D3h symmetry, with its high-symmetry directions and high-symmetry points. In typical ARPES measurements the detection area is on the order of 1 mm2, while a TMDC monolayer sample typically comprises many single crystalline flakes with typical lengths of several 100 nm up to a few 100 μm with random azimuthal orientation (see Supplementary Note 2). This leads to a spectral summation over the individual flakes’ contributions along φ, as schematically shown in Fig. 1b. As a consequence, the angularly superimposed BZs of individual flakes lead to a spherical symmetry around Γ. As shown in Fig. 1c, remarkably, sharp electronic band dispersion is observed in an ARPES spectrum as a function of radial momentum (kr), corresponding to “path 1 + path 2” of Fig. 1b. Notably, the measured band dispersion compares well with the calculated band structure along the high-symmetry directions Γ-K-M (path 1) and Γ-M-Γ (path 2) shown in Fig. 1d, strongly suggesting that these directions dominantly contribute to the ARPES spectrum. As explained in the following, the measured dispersion is due to the fact that the angular summation returns an effective spectrum that contains only kr as parameter and is dominated by contributions from the high-symmetry directions.
Azimuthally disordered 2D transition-metal dichalcogenide. a Brillouin zone (BZ) scheme of a single crystalline monolayer transition-metal dichalcogenide (TMDC) with high-symmetry points (cyan = M, red = K, black = Γ). Dashed lines indicate two selected high-symmetry paths (green: path 1 = Γ-K-M, violet: path 2 = Γ-M-Γ). b Schematic illustration of angular superposition of BZs of many single crystal TMDC flakes rotated azimuthally (φ), with circles centered around the Γ point (cyan circle = M, red circle = K, and black circle = Γ). Dashed line indicates combination of two high-symmetry paths. c Experimental angle-resolved photoemission spectroscopy spectrum (hν = 21 eV) of an azimuthally disordered WSe2 monolayer/highly oriented pyrolytic graphite sample as a function of binding energy and radial momentum along the path indicated in b. d Band structure of a single crystal WSe2 monolayer calculated along the high-symmetry directions Γ-K-M (path 1) and Γ-M-Γ (path 2). The energy of the calculated electronic bands is rigidly shifted to match the measured spectra (valence band maximum at Γ)
Calculation of photoelectron intensity
The measured photoelectron intensity I\(\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) as a function of energy E and radial momentum kr, shown in Fig. 1c, is proportional to the number of flakes N that emit photoelectrons with this E and kr. For an azimuthally disordered sample, it is necessary to obtain the number of flakes that contribute at a certain E to \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\). Given a sufficiently large N with random orientation, we can assume that an angular (φ) interval of \(\Delta \varphi = 2\pi /N\) represents one flake. For each interval Δφ, the corresponding absolute energy change \(\left| {\Delta E} \right|\) due to dispersion along φ can be calculated based on its derivative and is given by:
\(|\nabla _{\mathrm{\varphi }}E\left( {{\mathbf{k}}_{\mathbf{r}},\varphi } \right)|\) is the partial derivative of the energy with respect to φ direction. Using the above relation, we can count the N \(\left( {E,{\mathbf{k}}_{\mathbf{r}},\varphi } \right)\) that contribute to a certain energy interval δE (e.g., the experimental energy resolution):
Due to the azimuthal disorder, \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) is obtained by summing over all \(\varphi\) directions, leading to:
From Eq. (3) it becomes clear that \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\)is inversely proportional to \(\left| {\nabla _\varphi E({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\). This implies that the intensity measured in ARPES at a certain (E, kr) is high for \(\left| {\nabla _\varphi E({\mathbf{k}}_{\mathbf{r}},\varphi )} \right| \to 0\), because this corresponds to a large number of flakes contributing to the same E (within the range of \(E \pm \delta E/2\)) at the corresponding (kr, φ). Note that the derivation of Eq. (3) is exact only if the number of flakes approaches infinity and the energy and angular resolution approach zero. Since in any experiment δE, Δφ, and N are finite, (lower) intensity between the high-symmetry directions may still be observed in ARPES spectra. Importantly, even though our formula reflects the one used by Zhou et al.21, we do not rely on a discussion of the DOS, which remains two-dimensional for the 2D powders.
Symmetry of TMDC band structure and photoelectron intensity
To better understand why measured spectra of 2D powders are dominated by the high-symmetry directions for TMDCs, energy maps of the valence band (VB) and 1/\(\left| {\nabla _{\mathrm{\varphi }}E_{{\mathrm{VB}}}({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) - maps are calculated for the four different TMDCs. Figure 2a–d show the calculated valence band (VB) energy maps for single crystal BZs of monolayer TMDCs as a function of momentum (kr, φ), and they agree well with previous calculations23. The energy maps of all four TMDCs are very similar, since they have the same 2H-phase classified by its 3-fold dihedral symmetry group (D3h).
Valence band (VB) and 1/\(\left| {\nabla _{\mathbf{\varphi }}{{E}}_{{\mathbf{VB}}}({\mathbf{k}}_{\mathbf{r}},{\boldsymbol{\varphi }})} \right|\) – maps. Calculated energy maps of the valence band in a free-standing single crystal monolayer of a WSe2, b WS2, c MoSe2, and d MoS2 as a function of momentum. The hexagonal Brillouin zone and high-symmetry points (Γ, M, K) are denoted by dashed black lines and black dots, respectively. The lower row plots show corresponding 1/\(\left| {\nabla _{\mathbf{\varphi }}{{E}}_{{\mathbf{VB}}}({\mathbf{k}}_{\mathbf{r}},{\boldsymbol{\varphi }})} \right|\) - maps for e WSe2, f WS2, g MoSe2, and h MoS2, which are helpful to discuss angle-resolved photoemission spectroscopy on 2D powders of these materials (see text)
Figure 2e–h show the corresponding \(1/\left| {\nabla _{\mathrm{\varphi }}E_{{\mathrm{VB}}}({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) maps of the four monolayer TMDCs. Looking along the φ direction, the VB energy map in a single crystalline BZ with D3h symmetry must be symmetric with respect to the two high-symmetry directions (Γ-K and Γ-M). Thus, the band structure along these inevitably has local maxima and minima, where \(\left| {\nabla _{\mathrm{\varphi }}E({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) tends towards zero, returning high values of \(1/\left| {\nabla _{\mathrm{\varphi }}E_{{\mathrm{VB}}}({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) as clearly seen in Fig. 2e–h. High values of \(1/\left| {\nabla _{\mathrm{\varphi }}E_{{\mathrm{VB}}}({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) are mostly found in the colored areas that form “lines” along Γ-K and Γ-M. Therefore, only these two directions contribute notably to \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) where N\(\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) is counted along the φ direction using Eq. (3). Consequently, while information on non-high-symmetry directions is missing (or appears with small intensity in ARPES), the high values of \(1/\left| {\nabla _{\mathrm{\varphi }}E_{{\mathrm{VB}}}({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) allow measuring the electronic band dispersion in the two high-symmetry directions of azimuthally disordered TMDC monolayer flake samples, which is a key information to understand the behavior of electrons in a solid.
Interpretation of photoelectron intensity
To directly compare the calculated \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) with our measured spectra, we first calculate \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) for selected kr values (see Fig. 3a with color-coded kr radii), using Eq. (3) based on the valence energy map of a single crystal WSe2 monolayer (see Fig. 3b). In Fig. 3c, which depicts the calculated \(I\left( {E,{\mathbf{k}}_{\mathbf{r}}} \right)\) as a function of energy for the (φ-integrated) circles with corresponding kr, high intensity points are observed. In Fig. 3d, the experimentally measured electronic band dispersion of WSe2 is shown. The calculated high intensity points at the corresponding kr values are superimposed on the spectrum. The comparison yields very good agreement between calculated and experimental results, evidencing the relation between \(1/\left| {\nabla _{\mathrm{\varphi }}E_{VB}({\mathbf{k}}_{\mathbf{r}},\varphi )} \right|\) and the ARPES signal for dominating band dispersion directions for 2D powders of WSe2. It should be mentioned at this point that matrix element effects can modify the spectral intensity distribution. Notably, the matrix element effects in photoemission can be influenced by several experimental factors such as the excitation energy, light incidence angle, orbital distribution, and their binding energy. However, this does not affect the above-mentioned arguments about azimuthal integration and the observation of the band structure along the (single-crystal) high-symmetry directions in disordered samples.
A comparison between calculated and measured photoelectron intensity. a Schematic of φ direction integration for different kr (from Γ up to R4). b Calculated valence energy map of a single crystal WSe2 monolayer as a function of momentum. c Measured energy distribution curves with calculated number of photoelectrons \(I\left({E,{\boldsymbol{k}}_{\mathrm{r}}} \right)\), based on Eq. (3) \(\left[ {\delta E = 25\;{\mathrm{meV}},\;{\mathrm{\Delta }}\varphi = 0.3^\circ } \right]\) as a function of energy for the selected kr values shown in a and d (from Γ to R4). d Experimental angle-resolved photoemission spectroscopy (ARPES) spectrum (hν = 21 eV) of azimuthally disordered WSe2 on highly oriented pyrolytic graphite as a function of kr together with high intensity points from c. The calculated electronic bands are rigidly shifted in energy to match the measured spectra at Γ
Comparison of single crystal and azimuthally disordered WSe2
To consolidate the single crystal versus 2D powder picture developed above, Fig. 4 shows measured ARPES spectra of (a) single crystalline and (b) azimuthally disordered WSe2 monolayer samples as a function of momentum and sliced at different constant binding energies (EB). The EB values were chosen such that the spectra correspond to clearly different, but matching regions of the single crystal and φ-angular averaged spectra. Note that the EB values differ for the two samples since different substrates were used (WSe2 is physisorbed on both substrates and the band structure is virtually the same except for a rigid shift), i.e., the electronic levels are differently aligned with respect to Fermi energy22. Next to the experimental data, simulated spectra of a single crystalline and an azimuthally disordered WSe2 monolayer are plotted in Fig. 4c, d, respectively. In 2D powders, since almost all of the photoemission signal stems from the two high-symmetry lines, Fig. 4d is constructed by performing rotational symmetry of the two line-cuts along the two high-symmetry directions (Γ-K and Γ-M).
Constant binding energy (EB) map of single crystal and azimuthally disordered WSe2 monolayer. a Angle-resolved photoemission spectroscopy (ARPES) EB maps measured (hν = 100 eV) for a single crystalline WSe2 monolayer/sapphire sample. b ARPES EB maps measured (hν = 21.22 eV, He I) for an azimuthally disordered WSe2 monolayer/highly oriented pyrolytic graphite (HOPG) sample. c EB map simulated spectra for a single crystalline and d an azimuthally disordered WSe2 monolayer. The energy of simulated electronic bands is rigidly shifted to match the measured spectra (valence band maximum at K), respectively
Excellent agreement between theory and experiment is observed for the single crystal case, as seen from Fig. 4a, c. For the azimuthally disordered monolayer (Fig. 4b), the ARPES spectra sliced at different EB exhibit no appreciable dependence on the azimuthal parameter φ. Overall, the simulated energy maps in Fig. 4d have the same circular shape as the ARPES spectra sliced at the corresponding EB values in Fig. 4b. Illustrative is a comparison of the two bottommost plots in Fig. 4a, b, where a clear difference in the intensity distribution is observed, which underscores the impact of an integration along the φ direction. Likewise, the comparison of Fig. 4b, d clearly demonstrates that the measured ARPES spectra dominantly consist of the two high-symmetry electronic band dispersion lines, which is in excellent agreement with the predictions above.
Electronic band dispersion of different TMDCs
Finally, we demonstrate that the symmetry induced sharp electronic band dispersion can as well be observed experimentally for other TMDC monolayer 2D powders, as shown in Fig. 5 for (a) WSe2, (b) WS2, (c) MoSe2, and (d) MoS2 on HOPG. The measured spectra are overlaid with the calculated electronic band structure of the two high-symmetry directions (Γ-K-M and Γ-M- Γ); the agreement is very satisfactory. In addition, also the electronic structure of the HOPG substrate can be discerned in the spectra of Fig. 5, which is known to be nearly linear around the Fermi energy at the K point (green circles, 1.70 Å−1)21. To facilitate a clear discrimination between spectral contributions from the HOPG substrate and the TMDC monolayers, the spectra of bare HOPG, MoS2 on sapphire (without HOPG contributions), and MoS2 on HOPG are displayed in the Supplementary Note 3. Consequently, it should be possible to determine the electronic band structure of various TMDCs independently of the substrate.
Angle-resolved photoemission spectroscopy (ARPES) spectra of TMDCs family on highly oriented pyrolytic graphite (HOPG). ARPES spectra (hν = 21.22 eV, He I) of an azimuthally disordered monolayer of a WSe2, b WS2, c MoSe2, and d MoS2 on HOPG together with calculated bands along the two high-symmetry directions (dashed lines: Γ-K-M and solid lines: Γ-M-Γ). The energy of calculated bands is rigidly shifted to match the measured spectra
Discussion
We evidence that well-resolved electronic band dispersion along two high-symmetry directions of the BZ can be determined in ARPES for azimuthally disordered TMDC monolayer samples. By comparing data of single crystalline and 2D powder monolayers, we derive, with the help of calculated band structures, that two high-symmetry directions (Γ-K and Γ-M) dominate the intensity in ARPES spectra. In addition, we demonstrate that the materials’ dihedral group symmetry enables ARPES measurements in azimuthally disordered monolayer TMDCs. The insight provided here constitutes a solid base for investigating the electronic band dispersion of 2D powders featuring appropriate φ direction energy dispersion and lifts the restrictions of finding a sufficiently large single crystal.
Methods
Angle-resolved photoemission
The spectra of single crystalline and azimuthally disordered WSe2 monolayers were measured at the beamline PM4 (BESSY II, Germany), the beamline BL7U (UVSOR, Japan) and the Humboldt Universität zu Berlin using Scienta DA30 analyzer, employing 100 eV, 21 eV, and 21.22 eV (He I) photon energy, respectively24. The resolution determination and energy calibration of the instruments were done by measuring the Fermi edge of a clean Au sample. The total energy resolution was 110 meV, 100 meV, and 105 meV for the beamline PM4, beamline BL7U, and Scienta DA30, respectively.
Density functional theory calculations
Density functional theory (DFT) calculations were performed for a free-standing TMDC monolayer using the Vienna ab initio simulation package (VASP) with the Perdew-Burke-Ernzerhof (PBE) functional including spin-orbit coupling implemented in the model25,26,27,28. The electronic iteration convergence condition was 1 × 10−6 eV, and a 11 × 11 × 3 Γ centered K-point mesh was used with an energy cutoff of 500 eV. The lattice constants of MoS2, MoSe2, WS2, and WSe2 monolayers were 3.18 Å, 3.32 Å, 3.19 Å, and 3.32 Å, respectively, corresponding to the relaxed lattices after structure optimization. The use of a free-standing TMDC and PBE functional might lead to small discrepancies when comparing calculations and experiments.
Sample preparation
Monolayer TMDCs were fabricated by chemical vapor deposition on sapphire substrates and were transferred to the HOPG substrate using poly (methyl methacrylate) (PMMA)29,30. The samples were annealed overnight at 350 °C in an ultra-high vacuum chamber (10−9 mbar) to remove contaminants and PMMA residue before ARPES measurements.
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Ye, M., Winslow, D., Zhang, D., Pandey, R. & Yap, Y. Recent advancement on the optical properties of two-dimensional molybdenum disulfide (MoS2). Thin Films Photon. 2, 288–307 (2015).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Britnell, L. et al. Field-effect tunneling transistor based on vertical graphene heterostructures. Science 335, 947–950 (2012).
Gannett, W. et al. Boron nitride substrates for high mobility chemical vapor deposited graphene. Appl. Phys. Lett. 98, 242105 (2011).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Georgiou, T. et al. Vertical field-effect transistor based on graphene–WS2 heterostructures for flexible and transparent electronics. Nat. Nanotechnol. 8, 100–103 (2013).
Yu, W. J. et al. Highly efficient gate-tunable photocurrent generation in vertical heterostructures of layered materials. Nat. Nanotechnol. 8, 952–958 (2013).
Pospischil, A., Furchi, M. M. & Mueller, T. Solar-energy conversion and light emission in an atomic monolayer p–n diode. Nat. Nanotechnol. 9, 257–261 (2014).
Gong, Y. et al. Vertical and in-plane heterostructures from WS2 /MoS2 monolayers. Nat. Mater. 13, 1135–1142 (2014).
Gmitra, M., Kochan, D., Högl, P. & Fabian, J. Trivial and inverted Dirac bands and the emergence of quantum spin Hall states in graphene on transition-metal dichalcogenides. Phys. Rev. B 93, 155104 (2016).
Garcia, J. H., Cummings, A. W. & Roche, S. Spin hall effect and weak antilocalization in graphene/transition metal dichalcogenide heterostructures. Nano Lett. 17, 5078–5083 (2017).
Savero Torres, W. et al. Spin precession and spin Hall effect in monolayer graphene/Pt nanostructures. 2D Materials 4, 041008 (2017).
Avsar, A. et al. Spin–orbit proximity effect in graphene. Nat. Commun. 5, 4875 (2014).
Stefan Hüfner. Photoelectron Spectroscopy: Principles and Applications. (Springer, Springer-Verlang, Berlin - Heidelberg 1995).
Ly, T. H. et al. Observing grain boundaries in CVD-grown monolayer transition metal dichalcogenides. ACS Nano 8, 11401–11408 (2014).
Zhou, J. et al. A library of atomically thin metal chalcogenides. Nature 556, 355–359 (2018).
van der Zande, A. M. et al. Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat. Mater. 12, 554–561 (2013).
Li, B. et al. Solid-vapor reaction growth of transition-metal dichalcogenide monolayers. Angew. Chem. Int. Ed. 55, 10656–10661 (2016).
Bussolotti, F. et al. Electronic properties of atomically thin MoS2 layers grown by physical vapour deposition: band structure and energy level alignment at layer/substrate interfaces. RSC Adv. 8, 7744–7752 (2018).
Zhou, S. Y. et al. Coexistence of sharp quasiparticle dispersions and disorder features in graphite. Phys. Rev. B 71, 161403 (2005).
Park, S. et al. Direct determination of monolayer MoS2 and WSe2 exciton binding energies on insulating and metallic substrates. 2D Materials 5, 025003 (2018).
Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 84, 153402 (2011).
Vollmer, A. et al. Two dimensional band structure mapping of organic single crystals using the new generation electron energy analyzer ARTOF. J. Electron Spectrosc. Relat. Phenom. 185, 55–60 (2012).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Li, M.-Y. et al. Epitaxial growth of a monolayer WSe2-MoS2 lateral p-n junction with an atomically sharp interface. Science 349, 524–528 (2015).
Ma, D. et al. A universal etching-free transfer of MoS2 films for applications in photodetectors. Nano Res. 8, 3662–3672 (2015).
Acknowledgements
This work was supported by the DFG (SFB951 and AM 419/1-1) and the Alexander von Humboldt-Stiftung. We thank the HZB and the IMS for allocating synchrotron radiation beam time (Bessy ΙΙ, PM4 and UVSOR, BL7U). We are grateful to Prof. Torsten Fritz for insightful discussions.
Author information
Authors and Affiliations
Contributions
S.P., T.S., and P.A. wrote the manuscript and derived equations with the help of M.M. and S.K. under the supervision of N.K.; S.P., T.S., P.A., X.X., R.O., P.B., T.Y. and A.O. measured and analyzed ARPES spectra of the TMDCs. A.A., A.H. and L.-J.L. prepared 2D TMDCs samples. All authors commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Park, S., Schultz, T., Han, A. et al. Electronic band dispersion determination in azimuthally disordered transition-metal dichalcogenide monolayers. Commun Phys 2, 68 (2019). https://doi.org/10.1038/s42005-019-0166-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0166-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.