Abstract
Searching for effective pathways for the production of proton-rich and neutron-rich isotopes is one of the main driving forces behind experimental and theoretical nuclear reaction studies as well as for practical applications in nuclear transmutation of radioactive waste. To produce nuclei effectively, an optimal combination of reaction mechanism and energy is required. We report a study on incomplete fusion induced by deuteron, which contains one proton and one neutron with a weak binding energy and is easily broken up. This reaction study was achieved by measuring directly the cross sections for both proton and deuteron for 107Pd at 50 MeV/u via inverse kinematics technique. The results provide direct experimental evidence for the onset of a cross-section enhancement at high energy, indicating the potential for incomplete fusion induced by loosely-bound nuclei for creating proton-rich isotopes and nuclear transmutation of radioactive waste.
Similar content being viewed by others
Introduction
For hundreds of years, efforts have been made to discover laboratory reactions to induce chemical changes, since the first alchemy trial, which aim to transmute base metal to gold. The new age of “modern alchemy” started with the rise of nuclear physics at the beginning of the 20th century1. Thanks to progress in nuclear reaction studies, making elements in a laboratory has become possible and great success has been achieved since then in creating elements in a laboratory by synthesizing atomic nuclei via various nuclear reactions, such as fission, fragmentation, and low-energy fusion2. However, these conventional reactions3 have difficulties in accessing proton-rich and neutron-rich isotopes because their production is very suppressed. The cross section for fission and fragmentation drops drastically for both proton-rich and neutron-rich nuclei. The target thickness is very limited in fusion due to its low reaction energy, although fusion has a large cross section to produce proton-rich nuclei. The question of how to effectively make nuclei becomes one of the main motivations of recent nuclear reaction studies, as well as of nuclear transmutation studies of radioactive waste4. Multi-nucleon transfer reaction has been recently proposed5 for the production of neutron-rich nuclei due to its large cross sections. In contrast, no good candidate with optimized energy has been found to overcome the limitation in the production of proton-rich nuclei.
An alternative reaction for producing proton-rich nuclei via incomplete fusion (ICF) induced by loosely bound nuclei has been proposed, and this possibility has been recently demonstrated for deuteron by theoretical studies6,7,8. To produce isotopes with increased charge (ΔZ = +1), the breakup of deuteron allows ICF; namely, absorption of the proton released during the breakup in addition to complete fusion (CF) of deuterons, as displayed in Fig. 1a–c. The compound process of ICF will lead to a large enhancement in the cross section at an energy higher than that of CF and thus may increase the target thickness and maintain a large cross section, resulting in high production of proton-rich nuclei. This scenario, however, has not yet been truly addressed experimentally. We note that ICF at energies near Coulomb barrier was intensively studied experimentally and theoretically9,10,11.
Schematic illustration of the different components in deuteron-induced reaction. a Complete fusion, where deuteron interacts with a colliding nucleus as a whole set. b Incomplete fusion (of breakup proton as an example), where deuteron is broken up, and proton is absorbed and neutron is emitted. c Elastic breakup, where deuteron disintegrates into proton and neutron while the breakup nucleons have no interactions or elastically interact with the colliding nucleus. In both (a) and (b), an excited compound nucleus is formed after absorption, and thus, other nuclei can be produced from the statistical decay of compound states by emission of γ rays, neutron (n), proton (p), alpha (α), and/or other light particles. In (c), the colliding nucleus remains unexcited and thus has no contribution to the production of other nuclei
The experimental challenge in the observation of such an ICF effect arises from the cross-section measurement requiring direct isotopic identification of the reaction products. To date, ICF has mainly been investigated by bombarding target materials with beams of loosely bound nuclei6,7,9,12,13,14,15. This method requires the accumulation of γ rays or α particles, and data are therefore limited to only a few isotopes. In addition, the cross sections on deuteron were measured up to only 60 MeV6,7, which is much lower than the predicted energy of the enhancement. To clarify the effect of ICF, we report direct measurements of the absolute production cross sections of the reaction products were performed for 107Pd on proton and deuteron at 50 MeV per nucleon (MeV/u) at the Radioactive Isotope Beam Factory (RIBF) operated by RIKEN Nishina Center and the Center for Nuclear Study, University of Tokyo.
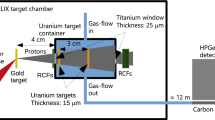
The measurements were performed using the inverse kinematics technique, in which a radioactive beam of 107Pd, produced at the in-flight separator BigRIPS16, bombarded a proton/deuteron target, and the reaction products were identified directly and unambiguously via the ZeroDegree spectrometer16. To overcome the technical difficulties in the production of 50-MeV/u beams and identification of the reaction products involving a charge-state distribution and large energy loss, several modifications were used: an energy-control method in BigRIPS17, gas hydrogen and deuterium targets at high pressure, dispersive mode of ZeroDegree spectrometer16 and a large-area plastic18 and segmented ion chamber (IC)19. Details are provided in the section “Methods”.
Results
Particle identification for reaction products
An example of a particle identification plot indicating the reaction products obtained with the ZeroDegree spectrometer is presented in Fig. 2. The high resolving power for particle identification enables clear identification of ions in different charge states, namely, fully stripped (Q = Z), hydrogen-like (Q = Z − 1), and helium-like (Q = Z − 2).
Particle identification plots for the reaction residues produced by the 107Pd beam on the deuterium target and detected by the ZeroDegree spectrometer. a Two-dimensional plot of atomic number Z versus mass-to-charge ratio A/Q. The horizontal dashed lines show the Z gate that was adopted for selecting the Pd isotopes. b The A/Q spectrum for the Pd isotopes by selecting 45.5 ≤ Z ≤ 46.5, as indicated by the horizontal dashed lines in a. The fully stripped ions could be separated from other ones in different charge states. The red solid line represents the total fit resulting from two Gaussian shapes
Isotopic distribution cross section
The isotopic distribution of cross sections on proton (σp) and deuteron (σd) measured in the present work for 107Pd at 50 MeV/u are displayed together in Fig. 3. Each panel displays the results for one element, namely Fig. 3a for Ag (Z = 47), Fig. 3b for Pd (Z = 46), Fig. 3c for Rh (Z = 45), Fig. 3d for Ru (Z = 44), Fig. 3e for Tc (Z = 43), and Fig. 3f for Mo (Z = 42). The measurement for cross section was limited down to 1 mb due to statistics. The errors shown in Fig. 3 are from statistical contributions. The systematic error includes the target thickness (2%) and the charge-state distribution (3%). For the ΔZ = +1 reaction, both newly measured σp and σd are found to be much larger than their values at 100 MeV/u, in particular for 103,104Ag, and such cross-section increases are more significant than those observed from 200 to 100 MeV/u for both proton and deuteron20, as presented in Fig. 3a. Moreover, σd at 50 MeV/u becomes much larger than σp at 100 MeV/u for 103,104Ag, indicating a different behavior from heavier Ag isotopes, where these two values are similar to each other. The large σp value is probably because the total incident energy (E) of 50 MeV is close to that of the compound process of proton fusion21. For deuteron, the cross-section increase appears at E of 100 MeV, which is much higher than the typical value of the compound process for CF of deuteron, indicating a different mechanism.
Isotopic distribution of the measured cross sections for proton (circles) and deuteron (squares) at 50 MeV/u. (a) Ag, (b) Pd, (c) Rh, (d) Ru, (e) Tc, and (f) Mo. The errors shown in the figure are from statistical contributions. The cross sections on proton (crosses) at 100 MeV/u20 are displayed for comparison. The deuteron-induced cross sections (diagonal crosses) at 100 MeV/u20 for the Ag isotopes are also displayed
Effect of ICF on cross section
To investigate the nature of the cross-section increase, both σd and σp are plotted as a function of E in Fig. 4 for 103,104,105Ag. Typically, in the ΔZ = + 1 reaction, the cross section presents a maximum in a compound process after the absorption of nucleon(s) and a smooth decrease with E due to the emission of light particles during the pre-equilibrium decay22,23. Indeed, in the case of protons, the large σp(E) values at 50 MeV for 103,104Ag reflect a compound process after fusion21. For deuterons, a significant enhancement in σd(E) at 100 MeV is highlighted by our 104Ag data compared to the linear extrapolation at high energy, revealing the characteristic of absorption of nucleon(s). As discussed before, the absorption of breakup protons can produce ΔZ = +1 isotopes and lead to a second compound process in addition to CF6,7,8. Thus, the enhancement of σd(E) in the 104Ag results of the present work provides direct experimental evidence for ICF of breakup proton.
Proton-induced and deuteron-induced cross sections for the Ag isotopes produced by 107Pd as a function of total incident energy. (a) 105Ag, (b) 104Ag, and (c) 103Ag. Cross sections on proton and deuteron are displayed by circles and squares, respectively. Filled symbols indicate the results of the present work and open symbols indicate the high-energy data at 100 and 185 MeV/u20. It is noted that the error bars are smaller than the symbol sizes. Dashed, dot-dashed, and solid lines are DEURACS calculations of incomplete fusion (ICF), complete fusion (CF), and their sum (ICF+CF), respectively
Theoretical calculations of cross sections for 103,104,105Ag using a newly developed deuteron-induced reaction analysis code system (DEURACS)8,24 are presented in Fig. 4. In DEURACS, deuteron-induced cross section is defined as the incoherent summation of contributions from the CF of deuteron and ICF of proton and/or neutron released during the breakup. The formation of compound nuclei in CF and ICF are calculated independently by the Glauber model25. The pre-equilibrium and equilibrium decays of compound nuclei made in both CF and ICF are calculated by the exciton model and Hauser–Feshbach statistical model26, respectively. Nucleon optical potentials (OPs) of Koning and Delaroche27 are applied for breakup proton and neutron in ICF; OPs of An and Cai28 are used for deuteron in CF. As described by Nakayama et al.8, in order to obtain a reliable value with a wide energy range up to 200 MeV/u, the calculated isotopic-distribution cross sections are renormalized using the deuteron-induced total reaction cross sections given by the Minomo–Washiyama–Ogata formula29, which is based on a microscopic three-body reaction model. Details on the definition of CF and ICF in DEURACS are provided in the section “Methods”.
The calculations clearly show that the σd(E) enhancement in 103,104Ag corresponds to the compound ICF process. In addition, the calculations reveal that the energy of ICF increases with the number of evaporation neutrons in a similar manner to CF. This explains that the newly measured σd(E) for 105Ag corresponds to the pre-equilibrium process, resulting in a smooth increase from high energy to 100 MeV. For all Ag isotopes, the calculations indicate that ICF plays a primary role in σd(E) towards high energy because of its moderate decrease. The overall agreement between the DEURACS results and data provides further evidence that the σd(E) enhancement is a consequence of ICF of breakup proton.
It is very instructive to compare σd(E) with σp(E) for the different processes of ICF. In the pre-equilibrium process, σd(E) is found to follow a similar tendency as σp(E). Their common tendency is consistent with the two experimental findings for the ΔZ = +1 reaction at high energy: (1) σd is approximately half of σp at the same beam energy per nucleon, as displayed in Fig. 3a and reported in the measurements for 107Pd20, 93Zr30, 90Sr31, 137Cs31, and 136Xe32. (2) σp(E) is known to be inversely proportional to the total incident energy21,33. Considering that a deuteron has two nucleons, these two findings result in the relation σd(E) ≈ 1/2 × σp(E/2) ≈ σp(E) by using the total incident energy, supporting the observation of ~200 MeV in Fig. 4. Around the compound process, σd(E) is enhanced and becomes 4–5 times larger than σp(E), which remains in the pre-equilibrium process. This observation demonstrates the potential of loosely bound nuclei for nuclei production when the reaction energy is chosen for the compound ICF process.
Discussion
The isotopic measurement on σd provides further insight on the role of CF and ICF in the Ag production. As mentioned above, CF and ICF components are predominant at respective low and high energy regions for each Ag isotope, and both excitation functions move to the higher energy side when more neutrons are evaporated. Considering the incident energy is fixed to be 100 MeV in the present study, the σd data therefore correspond to ICF for the heavy-mass isotopes and access to CF for the light-mass ones as demonstrated in Fig. 4a–c. In another word, the σd data for different Ag isotopes indicate the heavy Ag ions are mainly produced by ICF and the role of CF increases towards the light ones.
Moreover, contributions from CF and ICF components change in different elements. For the products close to the projectile in mass, σd and σp are close to each other as presented in Fig. 3b, c for heavy Pd and Rh isotopes, respectively. For these isotopes, DEURACS indicates that contributions from CF and ICF are comparable to each other as discussed in ref. 8. When more nucleons are removed from the projectile, it is found that σd becomes larger than σp and the difference increases towards the neutron-deficient side within one isotopic chain as displayed in Fig. 3b–d. These light-mass ions are mainly produced via central collision, where the production cross section depends on the energy deposited. As discussed by Wang et al. 20,31 and Kawase et al. 30, the larger σd value is due to a higher energy deposit relative to proton because both two nucleons in deuteron contribute to the reaction indicating that CF is dominant to produce these light-mass ions. Indeed, the CF contributions are found to be more than one order magnitude larger than the ICF ones for Ru, Tc, and Mo as discussed by the DEURACS calculations by Nakayama et al. 8. Such picture is further supported by the fact that σd at 50 MeV/u and σp at 100 MeV/u are similar to each other for the light-mass ions as displayed in Fig. 3c–f. In the CF, deuteron interacts with nucleus as a whole set, and thus deuteron-induced reaction at 50 MeV/u and proton-induced one at 100 MeV/u dissipate similar energy, resulting in a similar production.
Our experimental observation of ICF provides an alternative path to produce ΔZ = +1 isotopes. Taking 104Ag as an example, the total incident energy of the ICF maximum is 100 MeV, while that for CF is predicted to be 50 MeV8. This energy difference enables an increase in the range of deuteron in the Pd material by more than a factor of 334. Considering a 50% reduction in cross section, the ICF component will lead to an increase of at least 50% in production compared to the CF component. Moreover, the ICF of deuterons may result in similar production as that obtained for a proton at 100 MeV even though the range of a deuteron is shortened by 40% compared to that of a proton because σd is almost four times larger than σp. The relative mass difference between a proton and deuteron is 2, which is much larger than the difference between heavy isotopes with Z > 1. Thus, a higher production yield may be expected for ICF of a loosely bound nucleus than from CF of other isotopes. This is crucial for fusion reactions involving unstable isotopes, which are normally loosely bound, and thus, is an important step in the search for a powerful tool in “modern alchemy”.
ICF has a strong impact on the optimization of deuteron beam energy for nuclear transmutation of long-lived fission products (LLFPs) in high-level radioactive waste. It has been discussed that the deuteron-induced spallation reaction could be a candidate for the transmutation of the LLFP nucleus 107Pd20. The transmutation of 107Pd may be beneficial for the energy of ICF because it maintains both a large cross section and a certain depth in the LLFP material. Moreover, the free neutrons produced during breakup may continuously interact with the LLFP material, leading to further transmutation, together with those emitted from the evaporation of compound nuclei. A detailed simulation including the effect of ICF is desired for nuclear engineering to evaluate LLFP transmutation by deuteron.
In conclusion, our results provide direct experimental evidence for ICF, which causes a σd(E) enhancement at the energy much higher than that for CF, and further emphasizes its potential in both the production of proton-rich nuclei and nuclear transmutation of LLFP nuclei. In addition, we have shown that the cross-section measurement via inverse kinematics is essential for verifying the ICF. Extending our knowledge of reaction mechanisms induced by loosely bound nuclei plays a key role in understanding element synthesis and the application of nuclear reactions. We expect that ICF induced by heavy loosely bound nuclei, such as the production of ΔZ = +2 isotopes via ICF induced by 9Be15 and 6He12,13, can be measured in the future.
Methods
Details on the experimental setup
The radioactive beams around 107Pd were produced from in-flight fission of U at 345 MeV/u. The average primary beam intensity was ~12 particle nanoamperes (pnA). The momentum acceptance of BigRIPS was set to 0.1% by using the slits at the dispersive focal plane F1. A special configuration of degraders and detectors in BigRIPS was used based on an energy-control method, and a detailed description can be found in ref. 17. The method enabled the beam energy to be 64 MeV/u in front of the secondary targets and to select only the N = 61 isotones around 107Pd. Particles in the secondary beams were identified event-by-event by time-of-flight (TOF) and magnetic rigidities (Bρ), as described in ref. 35. The intensity and purity of the 107Pd beam was 6.0 × 102 particles per second (pps) and 16%, respectively.
The 107Pd beam impinged on the gaseous hydrogen and deuterium targets, which were in a cylindrical cell with a diameter of 36 mm36. The temperatures of the hydrogen and deuterium gases were 32.7 and 36.0 K, respectively, and the pressure was 4 atmosphere (atm) for both. The average thicknesses of the proton and deuteron targets were 23.2 and 34.5 mg/cm2, respectively. The beam energy was 50 MeV/u in the middle of the secondary targets. Data collection was also performed using a cell without any target material (empty cell) to deduce the contributions from the beam-line materials.
The reaction residues were analyzed by the ZeroDegree spectrometer in dispersive mode, where the final focus F11 was momentum dispersive. In such mode, the momentum acceptance was 4%, and the horizontal and vertical angular acceptances were 40 and 60 mrad, respectively16. To cover a broad range of fragments and study the charge-state distribution, several different magnetic rigidity settings were applied: −6%, −4%, −2%, 0%, +2%, +4%, and +6% relative to the Bρ value of the beam. At F11, a new plastic scintillation detector18 with a large effective area of 240 × 150 mm2 was developed to cover a wide momentum acceptance, and a new segmented IC19, which had a length of 750 mm along the beam direction and consisted of 15 units for the readout pad, was developed. The reaction products were stopped in the IC.
The reaction products were identified by measuring TOF, Bρ, ΔE, and total energy E. The TOF information was obtained using two plastic scintillators at the entrance of ZeroDegree spectrometer (F8) and F11, and a trajectory reconstruction was applied to determine the Bρ value using position and angle measurements at F11. Both ΔE and E were deduced from the IC19. Atomic number Z was determined using the TOF, ΔE, and E information, and the mass-to-charge ratio A/Q was obtained from the TOF–Bρ correlation. The detection efficiencies of the detectors for particle identification were higher than 95%. The resolution in Z and A/Q for the Pd isotopes was 0.60 [given here as full width at half maximum (FWHM)] and 3.7 × 10−3 (FWHM), respectively. Due to the high A/Q resolution of the ZeroDegree spectrometer, ions in the fully stripped, hydrogen-like, and helium-like charge states were clearly identified (Fig. 2b), and their respective fractions were 12%, 41%, and 43%, respectively, for Z = 46 isotopes in the deuterium-target case.
The σp and σd values were obtained by using the data for the hydrogen and deuterium targets after subtraction of the contributions of the beam-line materials using the empty-cell run.
Details on the DEURACS calculations
The CF cross section is defined as
where \(\sigma _{{\mathrm{d - ABS}}}\) represents the cross section for the absorption of deuteron. \(\sigma _{{\mathrm{A(d,x)B}}}\) is the production cross sections of nucleus B from deuteron-induced reaction on nucleus A, and \(\sigma _{{\mathrm{A(d,rea)}}}\) accounts for the deuteron total reaction cross section on A.
The ICF cross section for the breakup proton is defined as
where \(\sigma _{{\mathrm{{p}}} - {\mathrm{ABS}}}\left( {E_{\mathrm{{d}}}} \right)\) represents the cross section for the breakup process, where proton is absorbed, and neutron is emitted. \(f\left( {E_{\mathrm{{p}}}} \right)\) is the normalized energy distribution of the absorbed proton and it is obtained kinematically from the angular-integrate spectra of the neutron emitted during the breakup, which is calculated with the Glauber model. \(\sigma _{{\mathrm{A(p,x)B}}}\) is the production cross sections of nucleus B from proton-induced reaction on nucleus A, and \(\sigma _{{\mathrm{A(p,rea)}}}\) is the proton total reaction cross section on A. The complete description on DEURACS is provided in ref. 8.
Data availability
Raw data were obtained at the RI Beam Factory at the RIKEN Nishina Center, Japan. All the data used to support the findings of this study are available from the authors upon reasonable request.
References
Rutherford, E. F. R. S. The scattering of α and β particles by matter and the structure of the atom. Lond. Edinb. Dublin Philos. Mag. J. Sci. 21, 669–688 (1911).
Thoennessen, M. Current status and future potential of nuclide discoveries. Rep. Prog. Phys. 76, 056301 (2013).
Thoennessen, M. & Sherrill, B. From isotopes to the stars. Nature 473, 25–26 (2011).
IAEA Technical Reports. Implications of Partitioning and Transmutation in Radioactive Waste Management. Series No. 435 (2004).
Watanabe, Y. X. et al. Pathway for the production of neutron-rich isotopes around the N = 126 shell closure. Phys. Rev. Lett. 115, 172503 (2015).
Avrigeanu, M. et al. Low energy deuteron-induced reactions on Fe isotopes. Phys. Rev. C 89, 044603 (2014).
Avrigeanu, M. et al. Deuteron-induced reactions on Ni isotopes up to 60 MeV Phys. Rev. C 94, 014606 (2016).
Nakayama, S., Furutachi, N., Iwamoto, O. & Watanabe, Y. Role of breakup processes in deuteron-induced spallation reactions at 100-200 MeV/nucleon. Phys. Rev. C 98, 044606 (2018).
Shrivastava, A. et al. Role of the cluster structure of 7Li in the dynamics of fragment capture. Phys. Lett. B 718, 931–936 (2013).
Boselli, M. & Diaz-Torres, A. Quantifying low-energy fusion dynamics of weakly bound nuclei from a time-dependent quantum perspective. Phys. Rev. C 92, 044610 (2015).
Diaz-Torres, A. & Quraishi, D. Effects of unconventional breakup modes on incomplete fusion of weakly bound nuclei. Phys. Rev. C 97, 024611 (2018).
Raabe, R. et al. No enhancement of fusion probability by the neutron halo of 6He. Nature 431, 823–826 (2004).
Kolata, J. J. et al. Sub-barrier fusion of 6He with 209Bi. Phys. Rev. Lett. 81, 4580 (1998).
Dasgupta, M. et al. Effect of breakup on the fusion of 6Li, 7Li, and 9Be with heavy nuclei. Phys. Rev. C 70, 024606 (2004).
Dasgupta, M. et al. Fusion versus breakup: observation of large fusion suppression for 9Be + 208Pb. Phys. Rev. Lett. 82, 1395 (1999).
Kubo, T. et al. BigRIPS separator and Zerodegree spectrometer at RIKEN RI Beam Factory. Prog. Theor. Exp. Phys. 2012, 03C003 (2012).
Sumikama, T. et al. Slowed-down RI beams of 93Zr and 107Pd at 50 Mev/u produced for spallation reaction. RIKEN Accel. Prog. Rep. 50, 166 (2017).
Chiga, N. et al. Development of beam trigger detector with compact geometry. RIKEN Accel. Prog. Rep. 50, 163 (2017).
Chiga, N. et al. Development of new ionization chamber for low energy heavy ions. RIKEN Accel. Prog. Rep. 50, 164 (2017).
Wang, H. et al. Spallation reaction study for the long-lived fission product 107Pd. Prog. Theor. Exp. Phys. 2017, 021D01 (2017).
Nieckarz, W. J. & Caretto, A. A. Production of 111In and 114 mIn from the separated isotopes of cadmium using 70- to 400-MeV protons. Phys. Rev. 178, 1887 (1969).
Hodgson, P. E. Pre-equilibrium processes in nuclear reactions. Nature 292, 671–672 (1981).
Gadioli, E. & Hodgson, P. E. Pre-equilibrium Nuclear Reaction. (Oxford University Press, New York, 1992).
Nakayama, S. et al. Theoretical model analysis of (d, xn) reactions on 9Be and 12C at incident energies up to 50 MeV. Phys. Rev. C 94, 014618 (2016).
Ye, T. et al. Analysis of inclusive (d, xp) reactions on nuclei from 9Be to 238U at 100 MeV. Phys. Rev. C 84, 054606 (2011).
Iwamoto, O. The CCONE code system and its application to nuclear data evaluation for fission and other reactions. Nucl. Data Sheets 131, 259–288 (2016).
Koning, A. J. & Delaroche, J. P. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl. Phys. A 713, 231–310 (2003).
An, H. & Cai, C. Global deuteron optical model potential for the energy range up to 183 MeV. Phys. Rev. C 73, 054605 (2006).
Minomo, K., Washiyama, K. & Ogata, K. Deuteron-nucleus total reaction cross sections up to 1 GeV. J. Nucl. Sci. Technol. 54, 127–130 (2017).
Kawase, S. et al. Study of proton- and deuteron-induced spallation reactions on the long-lived fission product 93Zr at 105 MeV/nucleon in inverse kinematics. Prog. Theor. Exp. Phys. 2017, 093D03 (2017).
Wang, H. et al. Spallation reaction study for fission products in nuclear waste: Cross section measurements for 137Cs and 90Sr on proton and deuteron. Phys. Lett. B 754, 104–108 (2016).
Alcántara-Núñez, J. et al. Isotopic yields of spallation residues produced in 136Xe-induced reactions on deuterium at 500AMeV. Phys. Rev. C 92, 024607 (2015).
D’Auria, J. M. et al. Inclusive measurement of quasifree (p,xn) charge exchange reactions on bismuth from 62 to 800 MeV. Phys. Rev. C 30, 236 (1984).
Tarasov, O. & Bazin, D. Lise++: Radioactive beam production with in-flight separators. Nucl. Instru. Methods B 266, 4657–4664 (2008).
Fukuda, N. et al. Identification of new neutron-rich isotopes in the rare-earth region produced by 345 MeV/nucleon 238U J. Phys. Soc. Jpn. 87, 014202 (2018).
Ryuto, H. et al. Liquid hydrogen and helium targets for radioisotope beams at RIKEN. Nucl. Instrum. Methods A 555, 1–5 (2005).
Acknowledgements
The authors are grateful to the accelerator staff of RIKEN Nishina Center for providing the 238U beam. This work was funded by ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan). The authors acknowledge the support from MEXT KAKENHI grants no. 18H05404.
Author information
Authors and Affiliations
Contributions
H.W. performed offline data analyses. H.W., H.O. and H.Sak. mainly wrote the manuscript. H.W., H.O., S.Kawas. and S.T. designed the experiment. N.C., K.C., A.H. and D.S. prepared the new ion chamber and plastics. T.Su., D.S.A., N.F., Y.S., H.Sat., H.Su., H.T. and K.Y. tuned the BigRIPS fragment separator. H.B. was responsible for the data-acquisition system. H.W., S.Kawas., S.T., K.C., S.D.C., M.L.C., R.H., T.I., S.Kawak., Y.K., S.Ku., Y.M., S.Ma., S.Mi., I.M., T.N., K.N., T.O., A.S., T.Sa., S.S., P.A.S., Y.S., X.H.S., J.S., M.T., Y.T., T.T., H.Y., M.Y. and Y.W. checked data accumulation online and accomplished the experiment. S.K., R.N. and M.N. prepared the targets. S.N. performed the DEURACS calculations. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, H., Otsu, H., Chiga, N. et al. Enhancement of element production by incomplete fusion reaction with weakly bound deuteron. Commun Phys 2, 78 (2019). https://doi.org/10.1038/s42005-019-0165-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0165-1
This article is cited by
-
Modeling of Deuteron-Induced Reactions on Molybdenum at Low Energies
Journal of Fusion Energy (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.