Abstract
The superconducting proximity effect has recently attracted a renewed interest as the basis of topologically nontrivial states in materials with a large spin–orbit interaction, with protected boundary states useful for quantum information technologies. However, spectroscopy of these states is challenging because of the limited control of conventional tunnel barriers. Here we report electronic spectroscopy measurements of the proximity gap in a semiconducting indium arsenide nanowire segment coupled to a superconductor, using quantum dots formed deterministically during the crystal growth. We extract characteristic parameters describing the proximity gap, which is suppressed for lower electron densities and fully developed for larger ones. This gate-tunable transition of the proximity effect can be understood as a transition from the long to the short junction regime of subgap bound states in the NW segment. Our device architecture opens up the way to systematic, quantitative spectroscopy studies of subgap states, such as Majorana-bound states.
Similar content being viewed by others
Introduction
Coupling a superconductor (SC) to a metal or a semiconductor results in the so-called superconducting proximity effect in the normal material1. If the proximitized material is a low-dimensional semiconductor, this phenomenon can, for example, be used as a source of spin-entangled electrons2,3 or superconducting magnetometers4. By combining an s-wave SC with a one-dimensional semiconducting nanowire (NW) with large spin–orbit interaction, one can artificially create a proximity region with superconductivity of p-wave character. This can give rise to exotic quantum states at the ends of the SC, such as Majorana-bound states5,6,7,8, potentially useful as building blocks for topological quantum information processing9,10. However, a systematic characterization of superconducting subgap states and the proximity region in NWs remains challenging. Several theoretical proposals suggest to use a quantum dot (QD) as a spectrometer to investigate Majorana-bound state lifetimes11,12, spin texture13, or parity14. A first experiment was reported recently in which the QD was defined by electrical gating7. However, systematic and deterministic spectroscopy requires a spatially well defined, weakly coupled QD with sharp tunnel barriers across the complete NW, which does not hybridize with the bound states or the SC under investigation. In contrast to earlier spectroscopy experiments in NWs15,16, we use integrated QDs for the tunnel spectroscopy, which separates the spectrometer from the investigated region in a predictable way. To probe the evolution of the proximity effect in a NW segment close to the superconducting contact, we use an in-situ grown axial QD in an InAs NW, which homogeneously covers the complete diameter of the NW, in contrast to the standard gate-defined QDs. Compared with previous experiments investigating the spatial distribution and length scales of the superconducting proximity effect in metals17,18, the semiconducting NWs also allow us to control the carrier density and all related parameters, such as the Fermi velocity, in the system. We demonstrate two types of tunnel spectroscopy distinguished by the transport mechanism through the integrated QD, both probing the NW density of states (DOS): the cotunneling regime, where the QD can be seen as a single tunnel barrier, and the sequential tunneling regime, where the QD acts as an energy filter with Coulomb blockade (CB) resonances. The complementary measurements allow us to draw a clear picture of how the proximity gap forms in a NW segment, for which we present an intuitive explanation supported by numerical simulations.
Results
Device and characterization
The QD is defined by two potential barriers that form when the NW crystal structure is changed from zincblende (ZB) to wurtzite (WZ), which can be achieved with atomic precision by controlling the growth parameters19,20. These QDs are electrically and spatially well defined, which allows us to probe the induced gap in the NW segment at a precise distance from the QD and with predictable coupling parameters. Similar in-situ grown barriers have been used previously to investigate double QD physics21,22.
We use an InAs NW with an in-situ-grown axial QD formed by controlling its crystal phase structure in the growth direction20: two thin segments (30 nm) of WZ phase are grown in the otherwise ZB NW. These segments act as atomically precise hard-wall tunnel barriers for electrons, because the ZB and WZ band structure align with a conduction band offset of ~100 meV23,24. Consequently, a QD is formed in the ZB section (20 nm) between the two barriers23. A false color scanning electron micrograph of the device discussed here is shown in Fig. 1a, together with a transmission electron micrograph of the atomically precise interface in a representative NW, shown in the inset. The superconducting electrode consists of titanium/aluminum (Ti/Al) and the normal contact of titanium/gold (Ti/Au), fabricated by electron beam lithography. The differential conductance G = dI/dVSD as a function of the backgate voltage VBG in the normal state (in an external magnetic field of B = 50 mT) shows regularly spaced CB resonances (see Supplementary Fig. 1a in Supplementary Note 1) for which we find a systematic increase in the total tunnel coupling Γ with increasing VBG (see Supplementary Fig. 1b in Supplementary Note 1), consistent with the lowering of the tunnel barrier when the band structure is shifted to lower energies with respect to the Fermi energy (see schematic in Supplementary Fig. 2 in Supplementary Note 1)23.
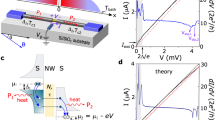
Crystal phase engineered quantum dot in a superconductor - quantum dot - normal device. a False color scanning electron micrograph of the investigated device, consisting of a superconductor S (blue)–indium arsenide (InAs) nanowire (NW)–normal metal N (yellow) junction (scale bar: 100 nm). A quantum dot (QD, red) forms between two in-situ grown tunnel barriers (green) in the wurtzite phase. The distance between the QD and S is L ≈ 350 nm. The measurement scheme is shown schematically. The inset shows a high-resolution transmission electron micrograph of the atomically sharp zincblende/wurtzite interface of a comparable NW. b Schematic energy diagram of such a system with an illustration of the proximity gap Δ* in the lead segment (LS), with a conductance GN in the normal and GS in the superconducting state. c Differential conductance G (e2/h) as a function of the backgate voltage VBG and the source-drain bias VSD in the superconducting state. The inset shows a single Coulomb blockade (CB) resonance in more detail. d CB diamonds at VBG exhibiting a gap in the transport characteristics
In the device discussed here, the QD is located about L ≈ 350 nm from the Al electrode, leaving a bare NW segment of this length between the QD and the SC, which we refer to as the “lead segment” (LS). This provides a new experimental situation, as the QD is not directly coupled to the SC (as it might be the case in other experiments25,26,27) and can be used to probe the LS. VBG here directly tunes the chemical potential in both the LS and the QD. We record G as a function of the bias voltage VSD applied between the SC and the normal metal contact. If the electrons would tunnel directly from the QD to the superconducting electrode, we would expect to see a gap similar to the one of the bulk value Δ ≈ 210 μeV28 of the SC, independent of VBG. As most of the bias drops over the QD, G is proportional to the DOS in the LS. This is the case for positive VBG where carriers accumulate in the NW. Therefore, we can perform spectroscopy on the LS by tunneling from the QD (see Fig. 1b).
An interesting transition in the conductance can already be found in the overview data in Fig. 1c, d presenting regular CB diamonds in the superconducting state (charging energy Ec ≈ 6 meV, level spacing ε ≈ 1.5 meV to 2 meV) for two different regimes of VBG. While for positive gate voltages, VBG > 3 V, we observe a superconducting gap around zero bias (c.f. Fig. 1d), for low gate voltages (Fig. 1c) we do not find any features related to superconductivity, but rather the sequence of diamonds expected for the normal state.
The QD can be used as a spectrometer in two different regimes. In the first regime, the QD is kept deep in the CB regime where the charge is fixed for bias voltages in the range of the proximity induced gap Δ*, as Δ* ≪ Ec. In this regime, transport is mediated by cotunneling, which is a second-order process involving the virtual occupation of a QD state29. Here, the QD can be thought of as a single tunnel barrier. In the second regime, the QD electrochemical potential is tuned to a CB resonance, with transport occurring as first order sequential tunneling. In the following, we discuss the experiments in the two regimes one after the other.
Cotunneling spectroscopy
First, we investigate the cotunneling regime, where we can understand the SC–LS as an S-N junction, which is weakly coupled to the QD. An example of a measured spectrum is shown in Supplementary Fig. 3a in Supplementary Note 1. It can be characterized by four quantities: the magnitude of the observed gap Δ*, the full width at half the maximum (FWHM) of the peaks at the gap edge, the normal state conductance GN measured at a bias |VSD| > Δ*/e and GS the conductance at VSD = 0. As the conductance is not fully suppressed at zero bias, we characterize this softness by defining the suppression factor S = GS/GN.
Figure 2a–c show G as a function of VBG and VSD for three different backgate regimes. Cross-sections (Fig. 2c: averaged over 20 cross-sections in the CB diamond centers) at different VBG in the CB regime are plotted as blue lines. At large gate voltages (VBG ≈ 7 V, Fig. 2a) we find a clear gap around zero bias, which can be detected down to VBG ≈ 2.6 V (Fig. 2b). The same cross-sections normalized to GN are shown in Supplementary Fig. 3a in Supplementary Note 1. All cross-sections exhibit a suppression of G at VSD = 0 and Δ* ≈ 150 μeV (position of the peak maxima). The FWHM and S are shown to be roughly constant over the investigated gate range, see Supplementary Fig. 3b in Supplementary Note 1, with FWHM ≈ 65 μeV ± 10 μeV and S ≈ 0.5 ± 0.1, respectively. In an ideal SC and weak coupling, S should be close to zero for a strong tunnel barrier. Larger values are often observed for proximity-induced gaps, and referred to as soft gap30,31,32. For lower gate voltages VBG < 2.6 V (Fig. 2b) it is difficult to perform this analysis, because the cotunneling signal is very low compared with the noise floor of the experiment (G ≈ 10−5 e2/h). However, we can still observe broad peaks down to VBG ≈ 1.8 V. For VBG < 1.8 V, the differential conductance is too low to observe any signatures of superconductivity with the resolution of our measurement. For even lower gate voltages VBG ≈ 0.2 V (Fig. 2c), no features inside the CB diamonds can be resolved anymore. In summary, in the regime accessible by the cotunneling experiments, the proximity gap characteristics are roughly independent of the gate voltage.
Proximity gap probed by cotunneling spectroscopy. The color bar is the differential conductance G (e2/h) as a function of backgate voltage VBG and source-drain voltage bias VSD for a high, b middle, and c low backgate voltages VBG. Blue lines are averaged over 20 cross-sections taken in the center of the Coulomb blockade diamonds. The cross-sections shown in c are averaged over the Coulomb blockade region between the Coulomb resonances
Sequential tunneling spectroscopy
To extract characteristics of the LS for a larger gate range than in the cotunneling regime, we now use the QD resonances (first-order process through the QD). Panels (i) (“Exp.”) of Fig. 3a–d show detailed measurements of a CB resonance in different backgate regimes, whereas panels (ii) show a simulated map (“model”) discussed below, and panels (iii) show cross-sections at VBG, as indicated in panels (i, ii). We will first discuss the experimental results presented in panels (i) of Fig. 3a–d. Afterwards we will compare our findings with the calculated results of a resonant tunneling model, which are presented in panels (ii) of each Fig. 3a–d. In an S–QD–N system, the Coulomb diamond pattern is expected to be affected by superconductivity as presented in Fig. 3e. The tips of the Coulomb diamonds are expected to be shifted by ΔVSD = 2Δ*/e in bias and by ΔVBG = 2Δ*/βe in gate voltage (with β the lever arm of the QD)26,33.
Proximity gap in the resonant tunneling regime. a–d Experiment (i), resonant tunneling model (ii), and cross-sections of both (iii) for different Coulomb blockade (CB) resonances. The color bar is the differential conductance G (e2/h) as a function of the backgate voltage VBG and the source-drain bias voltage VSD. Light green and orange lines indicate the VBG of the cross-sections in (iii). e Relative positions of the electrochemical potentials of the normal contact (μN), the superconductor (μS = μN − eVSD) and the quantum dot (μQD) for selected points (I, II, III) in the charge stability diagram. The tips of the diamonds are shifted in gate voltage by ΔVBG = 2Δ*/(βe) with β the lever arm of VBG. In a, the tunnel coupling is almost a factor of 3 larger than in b–d. From the model, the tunnel coupling Γ is essentially constant for b–d, whereas the value for the induced superconducting energy gap varies from Δ* = 165 μeV in a, Δ* = 145 μeV in b, Δ* = 85 μeV in c, to Δ* < 10 μeV in d
From the QD characteristics in the normal state (see Supplementary Fig. 1a in Supplementary Note 1), we find that the tunnel coupling Γ increases significantly for VBG > 2.5 V. For large Γ, e.g., at VBG ≈ 6.6 V, a CB pattern is shown in Fig. 3a. The CB resonances are broad, but clearly show a suppressed conductance around zero bias. We find a gap of Δ* ≈ 150 μeV, confirming the value obtained in the cotunneling regime (Fig. 2).
A CB resonance with a smaller Γ value at VBG ≈ 2.1 V is shown in Fig. 3b, which is similar to the one in Fig. 3a, but with an additional resolved resonance. As expected (see Fig. 3e), the “CB diamond tips” are shifted in energy by ±Δ*/e and ΔVBG in gate voltage, yielding a consistent value of Δ* ≈ 150 μeV. We observe an additional resonance that crosses through the gap (white arrows). This line corresponds to the alignment of the Fermi levels of the two reservoirs with the QD state. We attribute this resonance to tunneling through the non-zero DOS remaining at zero bias (see position I in Fig. 3e).
At VBG ≈ 0.2 V, the conductance suppression is significantly reduced, as shown in Fig. 3c. The CB diamond tips appear to be only slightly separated and shifted. We note that in this gate range we cannot resolve any signal in the cotunneling spectrum, as discussed in Fig. 2.
At even lower gate voltages, e.g., VBG ≈ 80 mV (Fig. 3d), we do not observe any influence of the superconducting contact, but a regular CB resonance, as found in the normal state.
To extract the characteristic numbers from these data, we use a resonant tunneling model for a S–QD–N junctions. The current is then given by26,34 \(I = {\int}_{ - \infty }^\infty d ED_{\mathrm{N}}(E) \cdot D_{\mathrm{S}}(E + eV_{{\mathrm{SD}}}) \cdot T_{{\mathrm{QD}}}(E,V_{{\mathrm{BG}}},V_{{\mathrm{SD}}}) \cdot [f_{\mathrm{N}}(E) - f_{\mathrm{S}}(E + eV_{{\mathrm{SD}}})]\), with DN(E) the constant DOS of the normal metal, TQD(E, VBG, VSD) a Lorentzian transmission function, accounting for the resonant tunneling through the QD, and including a broadening due to the finite coupling to the electrodes. fS/N are the Fermi distribution functions for the respective contacts. To account for the softness of the gap, the DOS in the LS can be expressed using the phenomenological Dynes parameter δ by \(D_{\mathrm{S}} = |{\mathrm{Re}}(E - i\delta /\sqrt {(E - i\delta )^2 - {\mathrm{\Delta }}^{ \ast 2}} )|\)35. By adjusting the magnitude of the gap Δ*, the QD resonance broadening Γ and the Dynes parameter δ, we get the conductance maps presented in panel (ii) of each Fig. 3a–d (“model”).
We can reproduce the characteristics of the CB resonance in Fig. 3a using Γ = 150 μeV, which is slightly smaller than what we obtained in the normal state. For the size of the gap we find Δ* = 165 μeV and δ = 0.4 ⋅ Δ* (δ = 65 μeV), resulting in a suppression of S ≈ 0.5, similar to what is found in the cotunneling regime. To reproduce the data in Fig. 3b, we use Γ = 40 μeV (similar to the numbers in the normal state), Δ* ≈ 145 μeV and δ = 0.4 ⋅ Δ*(δ ≈ 60 μeV), i.e., the parameters are almost identical to the ones we obtained in the cotunneling regime at higher gate voltages. The corresponding cross-sections agree well with the experiment. We note that the conductance enhancement at the gap edge, as well as the negative differential conductance are well reproduced by the model. We point out that in the sequential tunneling regime, we can extract gap characteristics down to backgate voltages of 0.2 V, which is not possible in the cotunneling regime.
To reproduce the characteristics of the CB resonance in Fig. 3c (VBG ≈ 200 mV), we find that the tunnel coupling is similar to the one in Fig. 3b (Γ = 60 μeV) and δ = 0.5 ⋅ Δ*(δ ≈ 40 μeV). However, the size of the superconducting energy gap is Δ* ≈ 85 μeV, significantly smaller than that found at larger gate voltages. Also here, the model reproduces the data well, illustrated in the corresponding cross-sections.
Using the resonant tunneling model to simulate the resonance around VBG ≈ 80 mV (Fig. 3d) we extract Γ = 50 μeV and an upper limit for Δ* of 10 μeV. The model reproduces very well the characteristics of the CB resonance, which essentially corresponds to an N–QD–N device. The resonances in the experiment at higher bias outside the CB are due to excited states, which are not included in the model.
To summarize the measurements in the CB resonance regime (Fig. 3), we observe a transition from a region where the LS acts as a superconducting lead (large gate voltages) with Δ* ≈ 165 μeV to 150 μeV to an intermediate regime with a reduced Δ* ≈ 85 μeV, to a regime without effects of superconductivity. The parameters extracted from the resonant tunneling model demonstrate a clear evolution of Δ* in the LS.
Discussion
The evolution of the induced gap Δ* as a function of VBG is summarized in Fig. 4a. The curve shows a sharp transition from a clearly resolved energy gap for VBG > 0 to a fully suppressed gap at VBG < 0.
Proximity induced gap as a function of gate voltage. a Proximity gap Δ* as a function of the backgate voltage VBG. The inset shows a schematic of the device with the relevant parameters: superconducting gap Δ in the bulk superconductor S, induced gap \(\widetilde \Delta\) below the superconductor inside the nanowire (gray), and the induced gap Δ* in the nanowire lead segment (LS). The quantum dot (QD) is located L = 350 nm from S. Background colors indicate the short junction limit (green) and the long junction limit (blue), depending on the relation of the the critical length Lc compared with the length of the junction L. Bars indicate the uncertainty of the extracted values of Δ*. b Calculated local density of states (LDOS) as a function of energy for different gate voltages VBG at a fixed distance from the interface, L = 350 nm
Although the observed proximity feature can be well fitted by a broadened BCS DOS, this approach is not an adequate description, as there are only few states in the quasi one-dimensional NW lead. Qualitatively, one can understand the transition by considering only a few modes in the LS. All electrons at energies within the gap of the SC are Andreev reflected (AR) at the SC, giving rise to Andreev-bound states (ABSs).
We interpret the observed transition in Δ* qualitatively as a gate-tunable transition of ABSs forming in the LS from the long to the short junction limit. Both limits are defined by comparing the physical length of the junction, L, with the characteristic length scale \(L_{\mathrm{c}} = \hbar v_{\mathrm{F}}/\widetilde \Delta\), which is often called coherence length in the ballistic limit36. Assuming a rather low Fermi velocity (vF = 2 × 105 m/s), we find Lc ≈ 850 nm. Here vF is the Fermi velocity in the LS, ℏ the Planck constant, and \(\widetilde \Delta\) the proximity gap induced by the aluminum contact in the NW directly below the SC (see inset of Fig. 4a).
In the short junction limit (L ≪ Lc) the energy of the ABSs (EABS) in the LS is dominated by the phase change due to AR at the SC/LS interface (dashed line in schematic), where \(\widetilde \Delta\) is assumed to change abruptly. In this limit, the energies of the ABSs are “pushed” to \(E_{{\mathrm{ABS}}} \cong \widetilde \Delta\), resulting in a superconducting proximity gap in the LS similar to \(\widetilde \Delta\), i.e., \(\Delta ^ \ast \sim \widetilde {\mathrm{\Delta }}\)37. In the long junction limit (L ≫ Lc), EABS is determined by the phase acquired in the LS, which scales with kF = m* ⋅ vF/ℏ ∝ vF, with m* the effective electron mass. In this limit, EABS can take on smaller values, thus filling the proximity gap36. We therefore can tune EABS by tuning vF and the electron density in the LS using VBG. For very positive gate voltages, EF is relatively far up in the conduction band with a correspondingly large vF, resulting in a large Lc, bringing the LS to the short junction limit, L < Lc. In contrast, when we align the bottom of the conduction band to EF by lowering VBG, vF and Lc are strongly reduced, bringing the LS into the long junction limit, L > Lc, and \(E_{{\mathrm{ABS}}} < \widetilde {\mathrm{\Delta }}\). As a result, the apparent gap Δ* is reduced by the ABSs moving into the gap. We note that \(\widetilde \Delta\) in the NW segment below the SC is screened by the SC and is therefore not gate tunable.
To support this qualitative picture, we employ a numerical model, in which we combine the Green’s function method with a tight binding model. The properties of the SC are taken into account as a self-energy dressing the bare Green’s function in a NW section below S, where a superconducting gap \(\widetilde \Delta\) is induced depending only on the coupling to S (details can be found in the Supplementary Note 2). This region is coupled to a bare NW segment (of length L = 350 nm) modeling the LS (see inset of Fig. 4a). We then investigate the local DOS at a distance L = 350 nm as a function of the gate voltage in the NW (Fig. 4b). Like for the experimental data, we extract Δ* as the distance between the maxima in the DOS. Here the number of ABSs as well as the ABS energy is determined by the length of the LS. The resulting Δ* of this calculation is plotted as a function of VBG as a red line in Fig. 4a. In excellent agreement with the experiment, we observe a sharp transition in the detected gap, corresponding to the transition from the short to the long junction limit. In the model, Δ* tends to zero when EF is aligned to the bottom of the conduction band (VBG ≈ −0.2 V), just before the LS is fully depleted and vF → 0. For a better understanding we study the dependence of an individual ABS as a function of VBG in Supplementary Fig. 4 in the Supplementary Note 3. Evolving from the long to the short junction limit, the states with energy E < Δ* move toward the gap, resulting in a fully formed smooth proximity gap Δ*. We note that in this model the width of the ABS is a free parameter, which we set to 25 μeV. In seeming contradiction to the depleted LS, the experiment still shows several CB resonances below this gate voltage, which we attribute to evanescent modes from the NW segment below S (which is not depleted) that couples weakly to the QD wavefunctions, rendering the QD couplings highly asymmetric with very low transmission amplitudes, as observed in the experiment.
The gap in our devices is soft, i.e., the conductance suppression at zero bias is significantly lower than in NWs with an epitaxial Al shell38,39. The reason for this remains unclear and is a priori not expected from the model. The evaporated bulk Al shows a hard gap (S ≈ 0.01) when used in standard, large-area metallic S–I–S tunnel junctions measured in a similar experimental setup (see Supplementary Fig. 5 in Supplementary Note 4). Introducing random spatial potential fluctuations at the NW–S interface40,41 in the presented numerical model does not account for the observed small suppression either (see Supplementary Fig. 6 in Supplementary Note 5). However, we cannot exclude other types of disorder or non-ideal material interfaces as the origin of the “soft gap”. In the ABS picture, the softness of the gap is determined by the life time of the ABSs in the LS. This broadening can have different physical origins, namely (1) tunneling to the QD, which should exhibit a similar tunability as the QD life time, (2) single particle tunneling to the NW segment below S, e.g., by an inverse proximity effect due to the gold nanoparticle used for the NW growth, and (3) quasiparticle excitation by microwave radiation absorption that might be different in NW devices compared to metallic ones.
In conclusion, we present a systematic study of the apparent transport gap in a NW segment induced by a proximity coupled SC. For this purpose we introduce QD tunnel spectroscopy enabled by in-situ-grown axial tunnel barriers. We observe a gate-tunable transition of the gap amplitude from a fully developed, constant proximity gap at large electron densities to smaller values and ultimately a complete suppression of the gap at low densities. The data are consistent with a transition from the short junction limit of an S-N device to the long junction limit with ABSs forming at energies also below the gap energy. This transition occurs when the Fermi energy is close to the bottom of the conduction band and the respective Fermi velocity tends toward zero. Our experiments demonstrate that NWs with in-situ-grown barriers, in our example with crystal phase engineered barriers, are very useful to perform transport spectroscopy in SC–semiconductor hybrid systems. We have thus introduced a novel spectroscopy tool, which is well suited to study superconducting bound states in semiconducting NWs, and might be useful to tackle fundamental limitations found in recent studies of Majorana-bound states42,43. The next steps toward investigating Majorana devices on this platform include technological progress, e.g., the possibility to contact the NW epitaxially with a SC as well as precise alignment of this contact close to the in-situ-grown QD.
Methods
Fabrication and measurement techniques
The InAs NWs were grown by metal-organic-vapor-phase epitaxy and have an average diameter of 70 nm. The two segments of WZ crystal phase forming the tunnel barriers have a thickness of 30 nm. The zinc-blende segment in between, which defines the QD, has a width of 25 nm.
The NWs were transferred mechanically from the growth substrate to a degenerately p-doped silicon substrate with a SiO2 capping layer (400 nm). The substrate is used as a global back gate. For the electron beam lithography we employ pre-defined markers and contact pads made of Ti/Au (5 nm /45 nm). The normal metal contact to the NW is made of Ti/Au (5 nm/70 nm) and the superconducting contact of Ti/Al (5 nm/80 nm). Before each evaporation step, the native oxide of the NW is removed by an Argon ion sputtering.
All measurements were carried out in a dilution refrigerator at a base temperature of 20 mK. Differential conductance has been measured using standard lock-in techniques (Vac = 10 μV, fac = 278 Hz).
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Beenakker, C. W. J. Quantum transport in semiconductor-superconductor microjunctions. Phys. Rev. B 46, 12841–12844 (1992).
Hofstetter, L., Csonka, S., Nygård, J. & Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot y-junction. Nature 461, 960–963 (2009).
Schindele, J., Baumgartner, A. & Schönenberger, C. Near-unity cooper pair splitting efficiency. Phys. Rev. Lett. 109, 157002 (2012).
Cleuziou, J.-P., Wernsdorfer, W., Bouchiat, V., Ondarçuhu, T. & Monthioux, M. Carbon nanotube superconducting quantum interference device. Nat. Nanotechnol. 1, 53–59 (2006).
Mourik, V. et al. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Albrecht, S. M. et al. Exponential protection of zero modes in majorana islands. Nature 531, 206–209 (2016).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Zhang, H. et al. Quantized majorana conductance. Nature 556, 74–79 (2018).
Alicea, J., Oreg, Y., Refael, G., von Oppen, F. & Fisher, M. P. A. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 7, 412–417 (2011).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Sarma, S. D. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Leijnse, M. & Flensberg, K. Scheme to measure majorana fermion lifetimes using a quantum dot. Phys. Rev. B 84, 140501 (2011).
Hoffman, S., Chevallier, D., Loss, D. & Klinovaja, J. Spin-dependent coupling between quantum dots and topological quantum wires. Phys. Rev. B 96, 045440 (2017).
Chevallier, D., Szumniak, P., Hoffman, S., Loss, D. & Klinovaja, J. Topological phase detection in rashba nanowires with a quantum dot. Phys. Rev. B 97, 045404 (2018).
Gharavi, K., Hoving, D. & Baugh, J. Readout of majorana parity states using a quantum dot. Phys. Rev. B 94, 155417 (2016).
van Dam, J. A., Nazarov, Y. V., Bakkers, E. P. A. M., Franceschi, S. D. & Kouwenhoven, L. P. Supercurrent reversal in quantum dots. Nature 442, 667–670 (2006).
Lee, E. J. H. et al. Spin-resolved andreev levels and parity crossings in hybrid superconductor–semiconductor nanostructures. Nat. Nanotechnol. 9, 79–84 (2013).
Guéron, S., Pothier, H., Birge, N. O., Esteve, D. & Devoret, M. H. Superconducting proximity effect probed on a mesoscopic length scale. Phys. Rev. Lett. 77, 3025–3028 (1996).
Cherkez, V. et al. Proximity effect between two superconductors spatially resolved by scanning tunneling spectroscopy. Phys. Rev. X 4, 011033 (2014).
Dick, K. A., Thelander, C., Samuelson, L. & Caroff, P. Crystal phase engineering in single InAs nanowires. Nano Lett. 10, 3494–3499 (2010).
Lehmann, S., Wallentin, J., Jacobsson, D., Deppert, K. & Dick, K. A. A general approach for sharp crystal phase switching in InAs, GaAs, InP, and GaP nanowires using only group v flow. Nano Lett. 13, 4099–4105 (2013).
Rossella, F. et al. Nanoscale spin rectifiers controlled by the stark effect. Nat. Nanotechnol. 9, 997–1001 (2014).
Nilsson, M. et al. Tuning the two-electron hybridization and spin states in parallel-coupled InAs quantum dots. Phys. Rev. Lett. 121, 156802 (2018).
Nilsson, M. et al. Single-electron transport in InAs nanowire quantum dots formed by crystal phase engineering. Phys. Rev. B 93, 195422 (2016).
Chen, I.-J. et al. Conduction band offset and polarization effects in InAs nanowire polytype junctions. Nano Lett. 17, 902–908 (2017).
Doh, Y.-J., Franceschi, S. D., Bakkers, E. P. A. M. & Kouwenhoven, L. P. Andreev reflection versus coulomb blockade in hybrid semiconductor nanowire devices. Nano Lett. 8, 4098–4102 (2008).
Gramich, J., Baumgartner, A. & Schönenberger, C. Resonant and inelastic andreev tunneling observed on a carbon nanotube quantum dot. Phys. Rev. Lett. 115, 216801 (2015).
Gramich, J., Baumgartner, A. & Schönenberger, C. Andreev bound states probed in three-terminal quantum dots. Phys. Rev. B 96, 195418 (2017).
Court, N. A., Ferguson, A. J. & Clark, R. G. Energy gap measurement of nanostructured aluminium thin films for single cooper-pair devices. Supercond. Sci. Technol. 21, 015013 (2007).
Franceschi, S. D. et al. Electron cotunneling in a semiconductor quantum dot. Phys. Rev. Lett. 86, 878–881 (2001).
Doh, Y.-J. Tunable supercurrent through semiconductor nanowires. Science 309, 272–275 (2005).
Sand-Jespersen, T. et al. Kondo-enhanced andreev tunneling in InAs nanowire quantum dots. Phys. Rev. Lett. 99, 126603 (2007).
Jellinggaard, A., Grove-Rasmussen, K., Madsen, M. H. & Nygård, J. Tuning Yu-Shiba-Rusinov states in a quantum dot. Phys. Rev. B 94, 064520 (2016).
Gramich, J., Baumgartner, A. & Schönenberger, C. Subgap resonant quasiparticle transport in normal-superconductor quantum dot devices. Appl. Phys. Lett. 108, 172604 (2016).
Yeyati, A. L., Cuevas, J. C., López-Dávalos, A. & Martn-Rodero, A. Resonant tunneling through a small quantum dot coupled to superconducting leads. Phys. Rev. B 55, R6137–R6140 (1997).
Dynes, R. C., Narayanamurti, V. & Garno, J. P. Direct measurement of quasiparticle-lifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509–1512 (1978).
Bagwell, P. F. Suppression of the josephson current through a narrow, mesoscopic, semiconductor channel by a single impurity. Phys. Rev. B 46, 12573–12586 (1992).
Bena, C. Metamorphosis and taxonomy of andreev bound states. Eur. Phys. J. B 85, 196 (2012).
Krogstrup, P. et al. Epitaxy of semiconductor–superconductor nanowires. Nat. Mater. 14, 400–406 (2015).
Chang, W. et al. Hard gap in epitaxial semiconductor–superconductor nanowires. Nat. Nanotechnol. 10, 232–236 (2015).
Takei, S., Fregoso, B. M., Hui, H.-Y., Lobos, A. M. & Sarma, S. D. Soft superconducting gap in semiconductor majorana nanowires. Phys. Rev. Lett. 110, 186803 (2013).
Liu, C.-X., Setiawan, F., Sau, J. D. & Sarma, S. D. Phenomenology of the soft gap, zero-bias peak, and zero-mode splitting in ideal majorana nanowires. Phys. Rev. B 96, 054520 (2017).
Liu, C.-X., Sau, J. D., Stanescu, T. D. & Sarma, S. D. Andreev bound states versus majorana bound states in quantum dot-nanowire-superconductor hybrid structures: Trivial versus topological zero-bias conductance peaks. Phys. Rev. B 96, 075161 (2017).
Reeg, C., Dmytruk, O., Chevallier, D., Loss, D. & Klinovaja, J. Zero-energy andreev bound states from quantum dots in proximitized rashba nanowires. Phys. Rev. B 98, 245407 (2018).
Acknowledgements
This work has received funding from the Swiss National Science Foundation, the Swiss Nanoscience Institute, and the Swiss NCCR QSIT. C.S. has received funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program: grant agreement 787414, ERC-Adv TopSupra. D.C. received funding from the European Unions Horizon 2020 research and innovation program (ERC Starting Grant, agreement number 757725). S.L., M.N., K.A.D. and C.T. acknowledge financial support by the Knut and Alice Wallenberg Foundation (KAW) and the Swedish Research Council (VR). We thank C. Reeg and S. Hoffman for fruitful discussions.
Author information
Authors and Affiliations
Contributions
C.J. fabricated the devices and performed the measurements together with R.D. C.J., R.D. and A.B. analyzed the data. A.B. provided the resonant tunneling model. D.C. provided the numerical calculations. S.L., M.N., K.A.D. and C.T. developed the nanowire structure. C.S. and A.B. planned and designed the experiments, and participated in all discussions. All authors contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jünger, C., Baumgartner, A., Delagrange, R. et al. Spectroscopy of the superconducting proximity effect in nanowires using integrated quantum dots. Commun Phys 2, 76 (2019). https://doi.org/10.1038/s42005-019-0162-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0162-4
This article is cited by
-
Spin-filtered measurements of Andreev bound states in semiconductor-superconductor nanowire devices
Nature Communications (2023)
-
Quench dynamics of Fano-like resonances in the presence of the on-dot superconducting pairing
Scientific Reports (2023)
-
Intermediate states in Andreev bound state fusion
Communications Physics (2023)
-
From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires
Nature Reviews Physics (2020)
-
Quantum-dot assisted spectroscopy of degeneracy-lifted Landau levels in graphene
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.