Abstract
Hexagonal boron nitride (h-BN) has been predicted to exhibit an in-plane thermal conductivity as high as ~ 550 W m−1 K−1 at room temperature, making it a promising thermal management material. However, current experimental results (220–420 W m−1 K−1) have been well below the prediction. Here, we report on the modulation of h-BN thermal conductivity by controlling the B isotope concentration. For monoisotopic 10B h-BN, an in-plane thermal conductivity as high as 585 W m−1 K−1 is measured at room temperature, ~ 80% higher than that of h-BN with a disordered isotope concentration (52%:48% mixture of 10B and 11B). The temperature-dependent thermal conductivities of monoisotopic h-BN agree well with first principles calculations including only intrinsic phonon-phonon scattering. Our results illustrate the potential to achieve high thermal conductivity in h-BN and control its thermal conductivity, opening avenues for the wide application of h-BN as a next-generation thin-film material for thermal management, metamaterials and metadevices.
Similar content being viewed by others
Introduction
Hexagonal boron nitride (h-BN) is a technologically important layered material used as a dielectric spacer, encapsulant, ultraviolet laser emitter, and hyperbolic material in electronic and photonic applications1,2,3. More recently, h-BN has attracted attention for thermal management of electronics as theoretical calculations4 predicted an in-plane thermal conductivity as high as kr~ 550 W m−1 K−1 at room temperature, though, highly anisotropic with a two orders of magnitude smaller out-of-plane thermal conductivity (kz~ 5 W m−1 K−1). The high in-plane thermal conductivity, as well as atomic flatness, makes h-BN an ideal substrate material for next-generation thin-film devices since waste heat can be spread quickly laterally through a large area, avoiding formation of localized hot spots5,6. In addition, h-BN could be a good reinforcing filler for thermal interface and encapsulation composite materials due to its high thermal conductivity and electrical resistivity7,8. Despite its predicted favorable thermal properties, experimental results are few and varied. Reported kr values range from 220 to 420 W m−1 K−1 4,9,10, well below the predicted maximum value. Developing insight into this discrepancy and driving h-BN thermal conductivity to higher values is of great interest both fundamentally and for enabling enhanced thermal engineering.
Quantized lattice vibrations (phonons) in crystals synthesized from elements with natural isotopic concentration scatter due to mass variations of the isotopes in the lattice, thus reducing thermal conductivity11. Enhanced thermal conductivity has been demonstrated in monoisotopic materials (isotopically purified to >99% one isotope), such as in silicon12, germanium13, gallium arsenide14, diamond15, and graphene16. Naturally occurring BN materials are made with two stable B isotopes (19.9% 10B and 80.1% 11B), which present a large mass modulation, and an opportunity to control its thermal conductivity by manipulating the B isotope concentration. Large B isotope effect has been observed in BN nanotubes17, whereas experimental evidence of isotope effects in h-BN has not been possible to date because suitable samples have not been available. In terms of theoretical predictions, the conventional Callaway approach13,18,19 based on the Boltzmann transport equation (BTE) and formulated within a single-mode relaxation time approximation (RTA) has been widely used to study the isotope effect in numerous material systems, but has challenges in anisotropic layered systems such as h-BN. Often, phonon scattering processes in layered systems cannot be treated as independent resistive processes, an assumption of the RTA20. Ab initio approaches based on full solution of the BTE in combination with first principles density functional theory (DFT) have demonstrated accuracy in describing the thermal conductivity of anisotropic layered materials with natural isotopic concentrations21,22, however, experimental data for monoisotopic layered materials are not available for model validations.
Only recently have isotopically engineered h-BN crystals become available23,24,25. To date, investigations have focused on fundamental isotope effects related to Raman phonon lifetimes and the electronic bandgap23,24. In this work, we experimentally demonstrate the effect of boron isotope concentration on the thermal conductivity of bulk h-BN crystals using a transient thermoreflectance (TTR) technique. The monoisotopic 10B h-BN crystals have in-plane thermal conductivity as high as 585 W m−1 K−1 at room temperature, ~ 80% larger than that of h-BN with disordered isotope concentrations (52%:48% mixture of 10B and 11B). Our measurements are compared with state-of-the-art ab initio thermal conductivity calculations.
Results
h-BN crystals and microstructural characterization
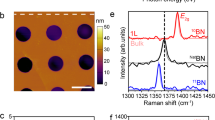
h-BN crystals were prepared from monoisotopic boron powders (10B and 11B), with the process described in Liu et al.25. This allowed the control of the boron isotope composition from 50%:50% (the most disordered composition) to monoisotopic 10B or 11B. Four h-BN crystals were grown, with input isotope compositions of 99% 10B (monoisotopic 10B), 48% 11B (isotopically disordered), 78% 11B (near-natural), and 99% 11B (monoisotopic 11B), respectively (see Methods). Supplementary Fig. 1 shows an optical micrograph of typical flake-like samples with size around 1 mm. Flake thicknesses were determined by optical microscopy to be 15 ± 2 µm by measuring the height difference between the sample surface and the underlying substrate. Figure 1a shows Raman spectra of the high-energy E2g mode from the different isotopically engineered h-BN crystals (see Methods). The energy of this E2g phonon is 1393 cm−1, 1379 cm−1, 1367 cm−1, and 1357 cm−1 for monoisotopic 10B, isotopically disordered, near-natural and monoisotopic 11B h-BN, respectively. The Raman shifts of the samples were benchmarked against the established relationship between Raman shifts and the isotope ratios24, verifying that the resulting h-BN crystals have the same isotope ratios as the input material (see details in Supplementary Note 1). As expected, the Raman linewidths are much narrower for the monoisotopic 10B h-BN (2.9 cm−1) and monoisotopic 11B h-BN (3.1 cm−1) than for the isotopically disordered h-BN (7.6 cm−1) and near-natural h-BN (7.9 cm−1). The linewidths are in part determined by phonon–isotope interactions in the disordered materials, a feature that was correlated with low-loss phonon-polariton modes in monoisotopic h-BN previously24.
Hexagonal boron nitride (h-BN) crystals Raman and microstructural characterizations. a Raman spectra of the E2g mode, obtained using 532 nm excitation, of the 99% 10B (monoisotopic 10B), 48% 11B (isotopically disordered), 78% 11B (near-natural), and 99% 11B (monoisotopic 11B) h-BN samples at room temperature. b Selected area electron diffraction (SAED) image, showing a hexagonal diffraction pattern consistent with diffraction into (hki0) reflections and a [0001] surface normal of the specimen. c Scanning electron microscopy (SEM) micrograph, steps are marked with yellow arrows; scale bar, 100 μm. d, e Electron back-scattered diffraction (EBSD) color map obtained by scanning a selected (60 µm × 90 µm) area with 1 µm step size: d inverse pole figure, illustrating the top surface of the sample being the (0001) plane of the hexagonal structure of h-BN. e Orientation deviation mapping, showing misorientation (tilt) up to ~ 2° between grains; scale bar is 30 μm. f Bright-field and g dark-field transmission electron microscopy (TEM) images under two beam diffracting conditions with \(g = 11\bar 20\), in-plane (near-screw) dislocations were observed (indicated by purple arrows) in (f), which dissociated into closely spaced partial dislocations (indicated by yellow arrows) in (g); scale bar is 1 μm. h Bright-field TEM image, sub-grain boundary, visible as fringes indicated by purple arrows; scale bar is 1 μm. Note that using TEM, the crystal was found to have areas a few tens of microns across which were free of defects. Images (f–h) were taken at selected area of h-BN where defects were observed
The crystal microstructure of the h-BN samples was characterized with selected area electron diffraction (SAED), transmission electron microscopy (TEM), scanning electron microscopy (SEM), and electron back-scattered diffraction (EBSD) (see Methods), with results shown in Fig. 1b–h from a representative h-BN specimen (monoisotopic 10B h-BN; for results of all samples see Supplementary Fig. 2). The SAED pattern (Fig. 1b) showed a single-oriented hexagonal crystal structure consistent with a [0001] surface. The SEM image (Fig. 1c) and EBSD inverse pole figure (Fig. 1d) confirmed the size of single crystal domains are larger than >150 μm. There were steps between these large domains, which are natural features in hexagonal crystals grown from solutions26. Using TEM, the single crystal domain was found to have areas a few tens of microns across which are free of defects. In some locations, in-plane (near-screw) dislocations with Burgers vectors \({\mathrm{a}}/3\langle 11\bar 20\rangle\) were observed, as seen in the bright-field TEM image in Fig. 1f. Such dislocations describe a rotation about [0001] between successive layers, estimated to be up to ~0.02° in Fig. 1f. In the dark-field TEM in Fig. 1g, taken in weak-beam diffracting conditions, the in-plane perfect dislocations are seen to be dissociated into closely spaced partial \({\mathrm{a}}/3\langle 10\bar 10\rangle\) dislocations on a fine scale. In some areas, sub-grain boundaries were observed, visible as fringes in the bright-field TEM image in Fig. 1h. The boundary indicates the misorientation (tilt) between the two grains with the misorientation angle estimated to be up to ~ 1°. This conclusion is consistent with that from EBSD (Fig. 1e). The misorientations (tilt) between the grains across the sample were small, about 2° or less. In short, the fabricated h-BN samples had high-quality large single-crystalline domains with a very low density of dislocations and tilt.
Anisotropic thermal conductivity characterization
The thermal conductivity of h-BN, kr—in-plane and kz—out-of-plane, were measured using a nano-second laser-based TTR technique27,28,29 (see Methods). Figure 2a shows the schematics of the TTR technique. The h-BN crystal was coated with a 50 nm Au thin film, which serves as a transducer. A 10 ns, 355 nm pulsed pump laser heats the surface of the Au transducer, creating a temperature response. A continuous 532 nm laser was used to monitor the surface temperature response via the induced change in Au reflectivity. Figure 2b shows an example of the monitored normalized thermoreflectance transient. An analytical photothermal pulses-induced thermal transport model was built based on the geometric and temporal characteristics of the pump pulse, experimental structure and boundary conditions shown in Fig. 2c to analyze the measured transients. We use \(S_{x_0} = \frac{{\partial \left( {{\mathrm{ln}}T} \right)}}{{\partial \left( {{\mathrm{ln}}x_0} \right)}}\) to quantify the sensitivity of the temperature response (T) to the parameter, x0, which is either of the thermal conductivities of h-BN (kr, kz) or the thermal boundary resistance between the Au transducer and h-BN (TBReff) (see Methods). Figure 2d shows the calculated sensitivity results. The sensitivity to kz (Sz) and TBReff (STBR) increases rapidly from 10 to 100 ns, whereas sensitivity to kr (Sr) remains mostly constant. With further increasing time, Sz remains relatively constant and STBR increases slowly, whereas Sr gradually increases and exceeds STBR and Sz at ~ 500 ns. Taking advantage of the distinct sensitivity time scales of the thermoreflectance transients, the parameters, kz, kr, and TBReff, were determined simultaneously via fitting the monitored TTR transients with the analytical thermal transport model (see Methods). The best fit of our model results to an example measured transient for the monoisotopic 10B h-BN sample at 300 K is given in Fig. 2b. The ±25% bound curves shown in Fig. 2b illustrate that TTR signals are mainly sensitive to kz at short time scales (10–500 ns) and more sensitive to kr at longer time scales (>500 ns).
Thermal conductivity measurements of hexagonal boron nitride (h-BN) crystals. a Schematic of the nano-second transient thermoreflectance (TTR) technique. b Monitored thermoreflectance transients for the monoisotopic 10B h-BN sample (black solid line), normalized to the peak reflectivity modulation. Out-of-plane thermal conductivity (kz), in-plane thermal conductivity (kz) and the thermal boundary resistance between the Au transducer and h-BN (TBReff), were determined simultaneously via fitting the monitored TTR transients with the analytical thermal transport model. The error bars after the determined values correspond to the uncertainty of results (see Methods for the details of fitting and uncertainty analysis). Best fitting curve (red solid line) is overlaid with the measured TTR transients. The dashed curves are ±25% bounds on the best fitted kz and kr values. c Sample zoom-up; the carbon tape supporting the h-BN sample is considered thermally insulating due to its low thermal conductivity. d Sensitivity analysis with respect to kr (Sr), kz (Sz), and TBReff (STBR) for h-BN (material parameters taken here are kr = 400 W m−1 K−1, kz = 4 W m−1 K−1, heat capacity Cp = 740 J kg−1 K−1, TBReff = 50 m2 K GW−1, which are the typical values of h-BN4,42)
Figures 3a, b give the measured values of kr and kz for the four crystals, as a function of temperature. Also shown are the results of (BTE)/(DFT) calculations using three-phonon and phonon–isotope scattering from quantum perturbation methods as inputs4 (see Methods). The predicted curves for monoisotopic 10B h-BN and 11B h-BN give the h-BN intrinsic thermal conductivities determined solely by three-phonon scattering processes. Theory and experiment for kr are in good quantitative agreement for the monoisotopic h-BN for temperatures >150 K. Discrepancies for <150 K are likely due to the extrinsic scattering of phonons from crystal imperfections not included in the theoretical calculations. Such extrinsic defects may include sub-grain boundaries, dislocations (apparent in TEM micrographs Fig. 1f–h), and point defects such as vacancies and carbon impurities (carbon impurity concentrations of 7.5–27 × 1019 cm−3 have been measured in h-BN crystals grown from identical synthesis methods24). The phonon mean free paths in h-BN at 100–150 K range from a few hundred nanometers to 10 μm, and the lower the temperature the longer the phonon mean free paths4. This suggests that sub-grain boundaries are a possible contributor to reducing the thermal conductivity of h-BN at low temperature considering the long phonon mean free path is comparable to the grain size, as evident in TEM and EBSD micrographs (Figs 1e, h). Point defects, such as carbon impurities, may also scatter phonons as strongly as isotope variations due to the mass and force fluctuations around the defect sites30,31. Such defects, like isotope variations, become more important at lower temperature where the intrinsic phonon–phonon scattering is weak. Figure 3a also shows the theoretical kr of natural and isotopically disordered h-BN. The measured results compare well with theoretical calculations >225 K; differences at lower temperatures again may arise from the presence of defects. As shown in Fig. 3b, the out-of-plane thermal conductivities (kz) for all samples compare favorably with the calculations, over the temperature range measured. Weak van der Waals bonding between h-BN planes gives smaller acoustic velocities perpendicular to the planes, whereas strong in-plane covalent bonding of the light B and N atoms gives fast phonons along the planes4. Thus, kz is much smaller than kr. There is a relatively small but apparent increase in thermal conductivity for the monoisotopic samples compared with the disordered ones. Extrinsic phonon scattering from grain boundaries and point defects is expected to have a smaller effect on kz due to the much shorter phonon mean free paths (about a few tens of nanometers4) in the out-of-plane direction, and therefore agreement between simulations and measurements over a broader temperature range is found.
Temperature-dependent thermal conductivities and anisotropic ratio of hexagonal boron nitride (h-BN) crystals, and comparison with model predictions: a in-plane thermal conductivity kr, b out-of-plane thermal conductivity kz, and c anisotropic ratio (kr/kz) for h-BN samples with differently tuned isotope ratios. Lines for the experimental data are guides for the eye. The error bars in (a, b) correspond to the uncertainty of measured thermal conductivity results (see Methods for the details of uncertainty analysis)
The in-plane thermal conductivities kr of 585 ± 80 W m−1 K−1 and 550 ± 75 W m−1 K−1 measured at 300 K for the monoisotopic 10B and 11B h-BN, respectively, are the highest room temperature values reported to date in the literature for h-BN. The measured kr value for near-natural h-BN (78% 11B) is 408 ± 60 W m−1 K−1 is consistent with previously reported values for natural h-BN (80% 11B) by Sichel et al.10 and Jiang et al.4, and about twice larger than that measured by Simpson et al.9. Isotopically disordered h-BN has the lowest measured kr, 330 ± 42 W m−1 K−1. At 300 K, the measured out-of-plane thermal conductivities, kz, are 3.5 ± 0.8 W m−1 K−1, 4.5 ± 1.4 W m−1 K−1, 3.3 ± 0.8 W m−1 K−1 and 2.3 ± 0.5 W m−1 K−1 for the monoisotopic 10B, monoisotopic 11B, near-natural and isotopically disordered h-BN crystals, respectively. All these values are comparable to those reported for natural h-BN in Jiang et al.4 and Simpson et al.9. Note that the isotope effect on kz is not clearly distinguishable experimentally due to relatively large error bars of experimental data.
The calculations of kr and kz for monoisotopic 10B h-BN predict it to be somewhat larger than those of monoisotopic 11B h-BN, despite both systems being free of phonon–isotope scattering. Phonon frequencies roughly scale with mass−1/2. This results in slightly faster acoustic phonons and less scattering from higher frequency optic phonons in monoisotopic 10B h-BN compared with monoisotopic 11B h-BN. These both lead to larger thermal conductivities (kr and kz) in monoisotopic 10B h-BN. This variance is within the error bars of the measured data and therefore not clearly distinguishable experimentally. The enhancement of the thermal conductivity, kr, in monoisotopic 10B h-BN and 11B h-BN, with respect to the natural BN is 43 and 35%, respectively, at room temperature. This is smaller than monoisotopic enhancements reported in graphene (~ 58%16) and diamond (~ 50%15), although the natural isotopic disorder and resulting mass variance is larger in naturally occurring h-BN (19.9% 10B and 80.1% 11B) than in naturally occurring carbon materials (98.9% 12C and 1.1% 13C). One important factor to consider when comparing the carbon-based materials and bulk h-BN is the discrepancy between the frequency scales of their phonon dispersions. Covalent C-C bonds are stronger than that of B-N bonds, which results in “harder” phonons in graphene and diamond. Besides reducing acoustic phonon velocities, the softer phonons in h-BN exhibit two important effects, which reduce the kr enhancement: (1) h-BN has weaker phonon–isotope scattering as this scales as frequency to the power four32, and (2) h-BN has stronger intrinsic phonon–phonon scattering as the phase space for interactions increases as the dispersion frequency scale decreases33. The stronger intrinsic phonon scattering in h-BN compared with diamond and graphene is indirectly observed when comparing the isotopically purified thermal conductivities: 585 ± 80 W m−1 K−1, ~ 4000 W m−1 K−1 16, and ~ 3300 W m−1 K−1 15 for monoisotopic 10B h-BN, graphene and diamond, respectively.
The predicted anisotropic ratio (kr/kz) is as high as 125 at 300 K, displayed in Fig. 3c, in reasonable agreement with measurements. We note that the difference in measured kr/kz between monoisotopic and isotopically disordered samples is large (>40 for T < 200 K) despite the presence of point defects reducing kr at low temperatures. This demonstrates that isotope engineering makes tuning of the thermal conductivity anisotropy possible in h-BN over a large range. Recently, tuning thermal anisotropy in materials has been demonstrated to allow precise manipulation of heat flux including for heat shielding, heat concentrators, macroscopic diodes, chip heat management, and energy harvesting34,35,36,37,38. Traditional thermal metamaterials used for these applications are designed from two or more constituent materials with large thermal conductivity contrast, to realize the required anisotropic and inhomogenous conductivity profiles by spatially adjusting their volume filling ratios. Coefficient of thermal expansion contrast can then result in challenges including mechanical instability and complicated fabrication processes35. Clearly, engineering materials via isotope concentration alone is more straightforward, and the resulting product is a single phase material with negligible differences of heat capacity (see Supplementary Fig. 7), density23, and temperature-dependent lattice constant23 (leading to similar thermal expansion), providing a promising route to enhanced thermal metamaterials and metadevices.
Discussion
Through isotope engineering, we have experimentally demonstrated the manipulation of the thermal conductivity of h-BN. The measured temperature-dependent thermal conductivity of monoisotopic h-BN provides a means for the verification of DFT calculations of thermal conductivity as solely impacted by intrinsic phonon–phonon scattering processes. At room temperature, the in-plane thermal conductivity (kr) of monoisotopic 10B h-BN was measured as high as 585 W m−1 K−1, the highest room temperature values for h-BN reported in the literature, and in good agreement with theoretical predictions. The enhanced kr in monoisotopic h-BN makes it a promising candidate for managing heat in higher power dissipation compact thin-film devices. A highly tuneable conductivity anisotropy ratio of h-BN by isotope engineering, may extend the application of h-BN to thermal metamaterial and metadevice applications.
Methods
h-BN crystal growth
h-BN single crystals were synthesized using the Ni-Cr flux method. High-purity 10B (99.22 at%) and 11B (99.41 at%) powders were mixed with Ni and Cr powders to give overall concentrations of 4 wt% B, 48 wt% Ni, and 48 wt% Cr. Manipulating the mass ratio of 10B to 11B in the source material renders different isotope compositions of resulting h-BN crystals. After loading the crucible, the furnace was evacuated, then filled with N2 and forming gas (5% hydrogen in balance argon) to ~850 torr. The N2 and forming gases continuously flowed through the system during crystal growth with flow rates of 125 sccm and 25 sccm, respectively. The system was heated to 1550 °C for a dwell time of 24 h. The h-BN crystals were formed by cooling at a rate of 0.5 °C h−1 to 1525 °C, then quenched to room temperature. Four different mass ratios of 10B to 11B (100%:0, 50%:50%, 20%:80%, and 0:100%) were input as source material, resulting in four different isotope compositions (1, 48, 78, and 99% 11B) in the resulting h-BN crystals. Crystals ranged up to a few mm in size.
Raman measurements
Raman measurements were performed using a 532 nm laser line with a Renishaw Raman microscope. In all, <10 mW laser power was directed at the sample through a 50 × 0.75 N.A. objective, with the Raman scattered light collected back through the same objective. The scattered light was dispersed using a 2400 groove mm−1 grating onto a silicon charge-coupled device. The spectral positions of the Raman lines were calibrated against a silicon reference sample. For each h-BN crystal studied, four measurements were performed, reporting the average spectral position and linewidth.
Microscopic analysis
SAED and TEM plan-view images were acquired at 200 kV in a Philips EM430 TEM. The dark-field and bright-field TEM was operated in the two beam diffracting conditions with \(g = 11\bar 20\). SEM and EBSD measurements were performed on Zeiss Evo MA10 LaB6 with an instrument probe equipped with EBSD. The EBSD mapping image was constructed by scanning a ~ 600 µm2 rectangular area with a 1 µm step size. Lattice constants of h-BN were taken from literature reported data23 for the EBSD analysis.
For the SAED and TEM analysis, small pieces of h-BN were crushed from the as-grown crystals and then adhered onto a holey silicon nitride support membrane for imaging. For the SEM and EBSD analysis, the as-grown crystals were mounted on the carbon tape and the first few layers were exfoliated using Scotch tape to expose the clean surface for imaging.
TTR measurements
The TTR measurement configuration is shown in Fig. 2a. To prepare the samples for the TTR measurements, the h-BN flakes were first cleaned with acetone, and then attached to a large glass slide using carbon tape. The first few layers were exfoliated using Scotch tape, to create a clean surface, before depositing a 50 nm (±5%) Au transducer film, with a 10 nm Ti interlayer for good adhesion. The Au film serves as a transducer in the TTR measurements. The schematic of TTR sample is shown in Fig. 2b mounted on a copper disk in the Linkam THMS600 cryostat, which was used to control the sample temperature from 100 K to 300 K during the measurements. The pump beam is a 10 ns, 355 nm frequency tripled Nd:YAG laser with a 30 kHz repetition rate. After passing through a beam expander and dichroic beam splitter, it is directed through a 15 × 0.3 N.A. quartz objective to a de-focused spot on the sample with a Gaussian profile (1/e2 radius of 41 μm). The pump laser power incident at the sample surface is less than 5 mW (time averaged, peak of 15 W). The transient surface reflectivity change is monitored using a CW 532 nm laser probe beam focused at the sample surface to 2 μm, in the central location of the pump spot. The reflected beam intensity is sampled by a beam splitter and detected by a silicon photodiode transimpedence amplifier (2.3 ns rise time) and a digital oscilloscope (300 MHz bandwidth). To ensure no residual light from the pump beam is detected, a long-pass filter is placed before the detector. We note alternative to TTR often time domain thermoreflectance (TDTR)39,40 is employed to measure thermal conductivity. However, TTR is more sensitive to anisotropy of thermal conductivities. TDTR, typically uses ultrashort (fs/ps) high-frequency pulse lasers. As the thermal penetration depth of a short laser pulse is much smaller than that of the laser spot size, one-dimensional heat transfer is generally assumed making the conventional TDTR insensitive to radial heat conduction. Although, e.g., pump and probe offset TDTR41 and variable pump spot size TDTR42 has been employed to enable an increased sensitivity to radial heat conduction and hence allow measurement of anisotropic thermal conductivities, the TTR technique is easier to use.
Analytical photothermal pulses-induced thermal transport model for the analysis of the TTR data
The thermal conductivity of h-BN was determined by comparing the measured TTR transients with an analytical photothermal pulses-induced thermal transport model. The model considers heat conduction in N-layer films (in this study: N = 3 (Au, Ti and h-BN layers)). The i-th layer of the film with thickness di, is taken having an in-plane thermal conductivities (ki-r), out-of-plane thermal conductivities (ki-z), density (ρi), and specific heat capacity Ci, with i = 1, 2, …N. The material (carbon tape) used for mounting the h-BN sample, indexed as N + 1, is considered a thermal insulator due to its low thermal conductivity. At time t = 0 when the system is in thermal equilibrium with ambient temperature T0, an energy pulse is absorbed on the top surface of the film, resulting in heat diffusion in the out-of-plane (z) direction as well as in the in-plane (r) directions. Considering the anisotropic thermal properties, the heat conduction equation for temperature rise εi = T − T0 in layer i is given by
For the heat absorption on the top surface,
where Q(r, t) is the input energy flux, which is spatially and temporally dependent. Here, we adopted the approach described by Hui et al.43,44 to solve Eqs. (1) and (2) by using Laplace and Hankel transforms:
The problem defined by (1) and (2) can be recast to obtain the transformed temperature in the spatial and temporal frequency domain (β, s) as
Repeating the solution procedure described in43,44 yields identical analytical results for εi, except \(\gamma _i\) in Eq. (5) is defined by
This analytical model was validated against the solutions obtained by a finite elements method in ANSYS for the same problem, yielding identical results for both cases (see Supplementary Note 2).
Based on the analytical model, the measured transients are a function of the h-BN out-of-plane (kz) and in-plane (kr) thermal conductivities, density, specific heat capacity, thickness of each layer/material, and geometrical and temporal characteristics of the pump pulse. Except for the anisotropic thermal conductivity (kz and kr) of h-BN, and the thermal boundary resistance between the Au transducer and h-BN (TBReff), all other parameters are input as fixed values (see Supplementary Note 3). Therefore, TBReff, kz, and kr are treated as free variables, adjusted to fit the analytical model results to the measured traces. A least squares algorithm was built for multi-parameter fitting. The uncertainty (error bar) was determined by individually varying each variable about the solution minima and finding the change in the variable that causes a 5% change in the least squares value, i.e., the error bar represents a 95% confidence level. Note that TBReff is determined by the ratio of Ti thickness to its fitted thermal conductivity. All fitted results of TBReff are shown in Supplementary Fig. 3. Supplementary Fig. 4 shows the simulated temperature rise (∆T) at the surface of h-BN. The maximum ∆T is ~ 45 K. At 100 ns, ∆T drops to 10 K and after 1000 ns, ∆T reduces to ~ 1 K. Thus, the fitted h-BN thermal property values approximate the values at ambient temperature. To ensure that the measured thermal conductivity results are reliable and repeatable, at the beginning of each h-BN sample measurement, we tested an in-house-made reference sample (Au/Ti coated undoped high-purity single crystal silicon) to make sure the measured silicon thermal conductivity result at room temperature is always equal to the standard value, 150 W/mK45,46.
Sensitivity analysis
The sensitivity of the temperature decay curve (T) to a parameter, x0, which is either thermal conductivity or thermal boundary resistance, is defined as:28
When x0 changes by ±10% within the timescale of interest:
Figure 2d shows an example of the sensitivity to kr, kz and TBReff for a h-BN sample (the properties are taken as kr = 400 W m−1 K−1, kz = 4 W m−1 K−1, Cp = 740 J kg−1 K−1 and TBReff = 50 m2 K GW−1, which are typical values for h-BN4,42).
First principles thermal conductivity calculations
Calculations of the thermal conductivity of h-BN are derived from Peierls–Boltzmann phonon transport32,47,48 with interatomic force constants (harmonic and third-order anharmonic) from DFT49,50,51 as implemented by the plane-wave Quantum Espresso package51 within the local density approximation using norm-conserving pseudopotentials. Electronic structure and relaxation (12 × 12 × 8 integration grid and 110 Ryd plane-wave energy cutoff) gave lattice parameters, a = 2.478 Å and c = 6.425 Å4, somewhat smaller than measurements52. Density functional perturbation theory50 (8 × 8 × 6 integration grid) was used to calculate harmonic force constants and long range Coulomb corrections. Γ-point-only electronic structure calculations (200 atom supercells, interactions restricted to 2.8 Å within the plane and 4.2 Å for neighboring layers) were used to determine third-order anharmonic force constants for constructing three-phonon matrix elements4. Thermal resistance from three-phonon interactions32,47 and phonon–isotope scattering11,53,54 is determined from quantum perturbation theory. More details specific to the DFT calculations and phonon properties (e.g., dispersions and scattering rates) are given in4.
Data availability
The data that support the plots and findings of this paper are available at https://doi.org/10.5523/bris.16v9rfpzb3pl221yzel7x5u5ce.
References
Watanabe, K., Taniguchi, T., Niiyama, T., Miya, K. & Taniguchi, M. Far-ultraviolet plane-emission handheld device based on hexagonal boron nitride. Nat. Photonics 3, 591–594 (2009).
Li, P. N. et al. Hyperbolic phonon-polaritons in boron nitride for near-field optical imaging and focusing. Nat. Commun. 6, 7507 (2015).
Izyumskaya, N. et al. Recent development of boron nitride towards electronic applications. Adv. Electron. Mater. 3, 1600485 (2017).
Jiang, P. Q., Qian, X., Yang, R. G. & Lindsay, L. Anisotropic thermal transport in bulk hexagonal boron nitride. Phys. Rev. Mater. 2, 064005 (2018).
Akinwande, D., Petrone, N. & Hone, J. Two-dimensional flexible nanoelectronics. Nat. Commun. 5, 5678 (2014).
Zhang, Z. W., Hu, S. Q., Chen, J. & Li, B. W. Hexagonal boron nitride: a promising substrate for graphene with high heat dissipation. Nanotechnology 28, 225704 (2017).
Yuan, C. et al. Thermal conductivity of polymer-based composites with magnetic aligned hexagonal boron nitride platelets. Acs Appl. Mater. Inter. 7, 13000–13006 (2015).
Xie, B. et al. Targeting cooling for quantum dots in white QDs-LEDs by hexagonal boron nitride platelets with electrostatic bonding. Adv. Funct. Mater. 28, 1801407 (2018).
Simpson, A. & Stuckes, A. D. Thermal conductivity of highly orientated pyrolytic boron nitride. J. Phys. Part C. Solid 4, 1710–1718 (1971).
Sichel, E. K., Miller, R. E., Abrahams, M. S. & Buiocchi, C. J. Heat-capacity and thermal-conductivity of hexagonal pyrolytic boron-nitride. Phys. Rev. B 13, 4607–4611 (1976).
Lindsay, L., Broido, D. A. & Reinecke, T. L. Phonon-isotope scattering and thermal conductivity in materials with a large isotope effect: a first-principles study. Phys. Rev. B 88, 144306 (2013).
Inyushkin, A. V., Taldenkov, A. N., Gibin, A. M., Gusev, A. V. & Pohl, H. J. On the isotope effect in thermal conductivity of silicon. Phys. Status Solidi C. 1, 2995–2998 (2004).
Ozhogin, V. I. et al. Isotope effect in the thermal conductivity of germanium single crystals. J. Exp. Theor. Phys. 63, 490–494 (1996).
Inyushkin, V. et al. Thermal conductivity of isotopically enriched. (GaAs)-Ga-71 crystal. Semicond. Sci. Tech. 18, 685–688 (2003).
Anthony, T. R. et al. Thermal-diffusivity of isotopically enriched C-12 diamond. Phys. Rev. B 42, 1104–1111 (1990).
Chen, S. S. et al. Thermal conductivity of isotopically modified graphene. Nat. Mater. 11, 203–207 (2012).
Chang, C. W. et al. Isotope effect on the thermal conductivity of boron nitride nanotubes. Phys. Rev. Lett. 97, 085901 (2006).
Wei, L. H., Kuo, P. K., Thomas, R. L., Anthony, T. R. & Banholzer, W. F. Thermal-conductivity of isotopically modified single-crystal diamond. Phys. Rev. Lett. 70, 3764–3767 (1993).
Morelli, D. T., Heremans, J. P. & Slack, G. A. Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III-V semiconductors. Phys. Rev. B 66, 195304 (2002).
Lindsay, L., Broido, D. A. & Mingo, N. Flexural phonons and thermal transport in multilayer graphene and graphite. Phys. Rev. B 83, 235428 (2011).
Fugallo, G. et al. Thermal conductivity of graphene and graphite: collective excitations and mean free paths. Nano Lett. 14, 6109–6114 (2014).
Lindroth, D. O. & Erhart, P. Thermal transport in van der Waals solids from first-principles calculations. Phys. Rev. B 94, 115205 (2016).
Vuong, T. Q. P. et al. Isotope engineering of van der Waals interactions in hexagonal boron nitride. Nat. Mater. 17, 152–158 (2018).
Giles, A. J. et al. Ultralow-loss polaritons in isotopically pure boron nitride. Nat. Mater. 17, 134–139 (2018).
Liu, S. et al. Single crystal growth of millimeter-sized monoisotopic hexagonal boron nitride. Chem. Mater. 30, 6222–6225 (2018).
Shtukenberg, A. G. et al. Illusory spirals and loops in crystal growth. Proc. Natl Acad. Sci. USA 110, 17195–17198 (2013).
Goodson, K. E., Kading, O. W., Rosler, M. & Zachai, R. Experimental investigation of thermal conduction normal to diamond-silicon boundaries. J. Appl. Phys. 77, 1385–1392 (1995).
Garrelts, R., Marconnet, A. & Xu, X. F. Assessment of thermal properties via nanosecond thermoreflectance method. Nanosc. Microsc. Therm. 19, 245–257 (2015).
Anufriev, R., Ramiere, A., Maire, J. & Nomura, M. Heat guiding and focusing using ballistic phonon transport in phononic nanostructures. Nat. Commun. 8, 15505 (2017).
Katre, A., Carrete, J., Dongre, B., Madsen, G. K. H. & Mingo, N. Exceptionally strong phonon scattering by B substitution in cubic SiC. Phys. Rev. Lett. 119, 075902 (2017).
Polanco, C. A. & Lindsay, L. Thermal conductivity of InN with point defects from first principles. Phys. Rev. B 98, 014306 (2018).
Ziman, J. M. Electrons and Phonons; The Theory of Transport Phenomena in Solids (Clarendon Press, Oxford, 1960).
Lindsay, L. & Broido, D. A. Three-phonon phase space and lattice thermal conductivity in semiconductors. J. Phys.-Condens. Mat. 20, 165209 (2008).
Ma, Y. G., Liu, Y. C., Raza, M., Wang, Y. D. & He, S. L. Experimental demonstration of a multiphysics cloak: manipulating heat flux and electric current simultaneously. Phys. Rev. Lett. 113, 205501 (2014).
Ma, Y. G., Lan, L., Jiang, W., Sun, F. & He, S. L. A transient thermal cloak experimentally realized through a rescaled diffusion equation with anisotropic thermal diffusivity. Npg Asia Mater. 5, e73 (2013).
Li, J. Y., Gao, Y. & Huang, J. P. A bifunctional cloak using transformation media. J. Appl. Phys. 108, 074504 (2010).
Narayana, S. & Sato, Y. Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett. 108, 214303 (2012).
Mateti, S. et al. Bulk hexagonal boron nitride with a quasi-isotropic thermal conductivity. Adv. Funct. Mater. 28, 1707556 (2018).
Cahill, D. G. et al. Nanoscale thermal transport. J. Appl. Phys. 93, 793–818 (2003).
Koh, Y. K., Cao, Y., Cahill, D. G. & Jena, D. Heat-transport mechanisms in superlattices. Adv. Funct. Mater. 19, 610–615 (2009).
Feser, J. P. & Cahill, D. G. Probing anisotropic heat transport using time-domain thermoreflectance with offset laser spots. Rev. Sci. Instrum. 83, 104901 (2012).
Jiang, P. Q., Qian, X. & Yang, R. G. Time-domain thermoreflectance (TDTR) measurements of anisotropic thermal conductivity using a variable spot size approach. Rev. Sci. Instrum. 88, 074901 (2017).
Hui, P. & Tan, H. S. A transmission-line theory for heat-conduction in multilayer thin-films. IEEE T. Compon. Pack. B 17, 426–434 (1994).
Chen, G. & Hui, P. Pulsed photothermal modeling of composite samples based on transmission-line theory of heat conduction. Thin Solid Films 339, 58–67 (1999).
Glassbrenner, C. J. & Slack, G. A. Thermal conductivity of silicon and germanium from 3 degrees K to melting point. Phys. Rev. 134, A1058 (1964).
Schmidt, A. J., Chen, X. Y. & Chen, G. Pulse accumulation, radial heat conduction, and anisotropic thermal conductivity in pump-probe transient thermoreflectance. Rev. Sci. Instrum. 79, 114902 (2008).
Srivastava, G. P. The Physics of Phonons (A. Hilger, Bristol, Philadelphia, 1990).
Lindsay, L. First principles peierls-boltzmann phonon thermal transport: a topical review. Nanosc. Microsc. Therm. 20, 67–84 (2016).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 136, B864 (1964).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001).
Giannozzi, P. et al. Quantum Espresso: a modular and open-source software project for quantum simulations of materials. J. Phys.-Condens. Mat. 21, 395502 (2009).
Paszkowicz, W., Pelka, J. B., Knapp, M., Szyszko, T. & Podsiadlo, S. Lattice parameters and anisotropic thermal expansion of hexagonal boron nitride in the 10–297.5 K temperature range. Appl. Phys. A 75, 431–435 (2002).
Tamura, S. Isotope scattering of large-wave-vector phonons in GaAs and InSb - deformation-dipole and overlap-shell models. Phys. Rev. B 30, 849–854 (1984).
Lindsay, L. & Broido, D. A. Enhanced thermal conductivity and isotope effect in single-layer hexagonal boron nitride. Phys. Rev. B 84, 155421 (2011).
Acknowledgements
C.Y., J.W.P., and M.K. acknowledge support from the Engineering and Physics Science Research Council Grant EP/P00945X/1, J.L., S.L., and J.H.E. from the Materials Engineering and Processing program of the National Science Foundation, award number CMMI 1538127. First principles calculations were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. We gratefully acknowledge M. Singh for the help of samples preparation for TTR and TEM analysis, C. Jones for support with EBSD, and W. Waller for multi-parameter fitting programming and H. Chandrasekar and R. Baranyai for fruitful discussions.
Author information
Authors and Affiliations
Contributions
J.L. and S.L. synthesized the h-BN samples under the direction of J.H.E.; C.Y. performed the Raman, SEM, EBSD, and TTR measurements under direction of M.K.; C.Y. and J.W.P. performed the TTR data analysis. D.C. performed the TEM measurements and analysis. L.L. performed the first principles thermal conductivity calculations. All authors discussed results at all stages and participated in the development of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yuan, C., Li, J., Lindsay, L. et al. Modulating the thermal conductivity in hexagonal boron nitride via controlled boron isotope concentration. Commun Phys 2, 43 (2019). https://doi.org/10.1038/s42005-019-0145-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0145-5
This article is cited by
-
Anomalous isotope effect on mechanical properties of single atomic layer Boron Nitride
Nature Communications (2023)
-
Thermal Conductivity of Polymer Composite Material Based on Phenol-Formaldehyde Resin and Boron Nitride
Russian Physics Journal (2022)
-
Emerging Flexible Thermally Conductive Films: Mechanism, Fabrication, Application
Nano-Micro Letters (2022)
-
Matryoshka phonon twinning in α-GaN
Communications Physics (2021)
-
The reduction of the thermal quenching effect in laser-excited phosphor converters using highly thermally conductive hBN particles
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.