Abstract
One of the major strategies to control magnetism in spintronics is to utilize the coupling between electron spin and its orbital motion. The Rashba and Dresselhaus spin–orbit couplings induce magnetic textures of band electrons called spin momentum locking, which produces a spin torque by the injection of electric current. However, joule heating had been a bottleneck for device applications. Here, we propose a theory to generate further rich spin textures in insulating antiferromagnets with broken spatial inversion symmetry (SIS), which is easily controlled by a small magnetic field. In antiferromagnets, the ordered moments host two species of magnons that serve as internal degrees of freedom in analogy with electron spins. The Dzyaloshinskii–Moriya interaction introduced by the SIS breaking couples the two-magnon-degrees of freedom with the magnon momentum. We present a systematic way to design such texture and to detect it via magnonic spin current for the realization of antiferromagnetic memory.
Similar content being viewed by others
Introduction
Development of tunable magnetic structure has long been a key issue for detecting and controlling magnetic domains electrically toward application to memory devices1. Besides the conventional domain walls that appear in real space, particular focus is given on emergent spin textures in reciprocal space, called “spin momentum locking”. The spin textures are classified into Rashba-types2,3,4 and Dresselhaus-types5 that exhibit vortex and anti-vortex geometries along the closed Fermi surfaces. Since the wave number k distinguishes the electronic state of matter, such spin texture allows for the selection of magnetic moment the state/current carries. This has brought about fundamentally important and technologically promising phenomena including spin Hall effect6,7,8,9, spin–orbit (SO) torque10,11, and Rashba-Edelstein effect12,13,14.
In insulating magnets, an excitation is carried by the quasiparticle called magnon, which represents a quantum mechanical spin precession propagating in space. Such propagation is predominantly mediated by the standard magnetic exchange interaction JSi · Sj, between spins, Si and Sj. In a uniform ferromagnet, a simple exchange interaction, J(<0), generates non-degenerate quadratic magnon bands. When the spatial inversion symmetry (SIS) is broken, an antisymmetric spin exchange called Dzyaloshinskii–Moriya (DM) interaction15,16, D · (Si × Sj), appears, depending on the crystal symmetry. This term bends the propagation of magnons in space in a similar manner to the cyclotron motion of electrons in the presence of magnetic flux17. Thus, when D is parallel to the magnetization, magnon bands in a ferromagnet become asymmetric, reflecting the “nonreciprocal” propagation18,19,20,21,22,23,24,25. Nevertheless, the phenomena related to magnons in non-centrosymmetric ferro or ferrimagnets lack abundance compared to the rich counterparts of the conducting Rashba electrons. This is because the ferromagnetic magnons carry spins that are pointing in a unique direction, and cannot afford up and down spin degrees of freedom like electrons.
In antiferromagnets (J > 0) with a doubled magnetic unit cell, the magnon bands are folded and a doubly-degenerate linear dispersion appears at Γ-point. What if we regard two different species of magnons each belonging to the degenerate band as an analog of the electronic spin degrees of freedom? If this degrees of freedom couples to the magnon momentum via a DM interaction, such that the SO coupling does in electron systems, one may expect as rich phenomena as those of the Rashba-electronic systems in insulators. So far, however, non-descript bipartite antiferromagnets did not show any magnon-based phenomena such as a thermal Hall effect already found in the kagome and pyrochlore magnets26,27,28,29,30,31,32,33, indicating that the situation is not as simple. In this article, we demonstrate that a typical two-dimensional (2D) antiferromagnet can afford a variety of spin textures not even found in electronic systems. We introduce a pseudo-spin degrees of freedom based on the two species of magnons belonging to antiferromagnetic sublattices, and show that the reduction of SU(2) symmetry of these pseudo-spins is required to have spin textures in momentum space. We classify the way how the symmetry is reduced step-by-step by the interplay of DM interaction, spin anisotropy, and magnetic field in a series of one-dimensional (1D) antiferromagnets, which determines the degree of variety of the spin textures. A systematic way to design 2D spin textures is thus given based on the building blocks of these 1D antiferromagnets.
Results
Model systems
We consider a quantum spin system with nearest neighbor exchange interaction, J(>0), spin anisotropy, Λ, the DM interaction, Dij, and a uniform external magnetic field, h. The general form of the Hamiltonian is given as
where \(S_i^{\mathrm{\Lambda }}\) is the spin moment in the Λ-direction. In our 2D antiferromagnet, we consider an easy plane anisotropy normal to Λ-axis (||z), namely Λ > 0. If we take Λ < 0, an easy axis anisotropy is realized, which we apply shortly to a series of 1D magnets. We take the x-axis and y-axis in the direction rotated by π/4 from the bond direction. We place the in-plane magnetic field h perpendicular to the z-axis. The DM interaction emerges when the midpoint of two magnetic sites lacks the inversion symmetry. There are two different ways of aligning the D-vector; In defining the spin indices that couples to Dij in an order, i → j, the D-vectors can take either a uniform or a staggered configuration along that direction. The former breaks the global SIS of the crystal, whereas the latter keeps the site-centered SIS. Since the staggered DM interaction does not play any role in the physics presented here, we focus on the uniform DM in the following.
We consider the physics realized for small Di,j and Λ compared to J = 1, where we always find a canted antiferromagnetic order in the ground state. The spin moments, MA and MB, on the magnetic two-sublattices are confined within the easy plane, and their directions are described by the in-plane magnetic field angle, ϕ against the x-axis, and the canting angle, θM (see Fig. 1a). The degree of spin canting is as small as θM = arcsin(h/8JS) ~ 1.5° and 8° for h = 0.5J and 3J, respectively. The magnetic excitations are described by two species of Holstein–Primakoff bosons (magnons)34; The z-component of spin operators belonging to sublattices A an B is given as \(S_i^z = S - a_i^\dagger a_i\) and \(S_i^z = - S + b_i^\dagger b_i\), where \(a_i^\dagger {\mathrm{/}}a_i\) and \(b_i^\dagger {\mathrm{/}}b_i\), are the magnon creation/annihilation operators. The resultant spin wave Hamiltonian of magnons spanned on a particle-hole space is given as
where HBdG(k) takes the form of the bosonic Bogoliubov-de Gennes (BdG) Hamiltonian (see Methods), and \({\mathrm{\Phi }}_{\bf{k}} = (a_{\bf{k}},b_{\bf{k}},a_{ - {\bf{k}}}^\dagger ,b_{ - {\bf{k}}}^\dagger )^T\) represents the particle and hole pairs of A and B magnons in reciprocal space (see Methods). The eigenvalues of HBdG(k) give the magnon bands, ω±(k). The spin moment carried by magnons on these bands at each k is evaluated as35,
using the local spectral weight at k of ω±-band, dA/B(ω±(k)), on sublattice A/B (see Methods).
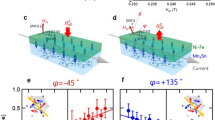
2D spatial inversion symmetry broken antiferromagnet and its spin texture in momentum space. a Schematic illustration of our lattice model with easy-xy-plane anisotropy (Λ > 0). Open/filled circles represent the A/B magnetic sublattice, and the red arrows are the schematic classical spin configurations MA and MB of the ground state characterized by the field angle ϕ and the canting angle θM. The Dzyaloshinskii–Moriya vector, Dij, has in-plane elements, depicted by defining i → j direction as unit vectors eij = +δ1 and +δ2, for two bond directions. We show Rashba/Dresselhaus-type configuration of D, characterized by the polarization vector Pij = eij × D. b, c Textures of Sk,− of the lower magnon band ω−(k) over the first Brillouin zone with S = 5/2, J = 1.0, D = |D| = 0.1, Λ = 0.05, and h = |h| = 3J. We plot (b) Rashba-type and the (c) Dresselhaus-type ones for field angles, ϕ = 0, π/4, π/2, and 3π/4. The amplitude, |Sk,−|, is given by the density plot, and the arrow indicates its direction. d How the direction with (long black arrow: δII) and without(short gray arrow: δIII) spin textures is elucidated by the relative relationships between the summation of D of the two different bond directions and h. e Sketch of how the typical Rashba-type and Dresselhaus-type spin textures are modified according to the magnetic field and to the symmetries kept at ϕ = 0
Rashba and Dresselhaus magnons
We first demonstrate that the 2D SIS broken antiferromagnets can exhibit as rich spin textures as those of Rashba and Dresselhaus electronic systems. For a 2D square lattice, there are two different ways of constructing a model Hamiltonian Eq. (1) in terms of uniform DM interaction; We call the ones shown in the upper and lower panels of Fig. 1a Rashba and Dresselhaus antiferromagnets, respectively. Here, Dij vectors are depicted in the directions defined by taking the indices i → j pointing in the +δ1 and +δ2 directions along the two bonds. We do not consider explicitly the component of Dij normal to the 2D plane. This is because the out-of-plane component generally takes the form of the staggered DM interaction as can be elucidated for the case of Ba2MnGe2O7 with space group \(P\bar 42_1m\)36, which contributes neither to the spin textures nor to the nonreciprocity of magnon bands. (see Supplementary Note 1 and Supplementary Fig. 1 for details).
It is convenient to classify the two types of antiferromagnets by a polarization vector, Pij = eij × D, where the unit vector eij points to either +δ1 or +δ2 along the bonds. The Rashba-type antiferromagnet in the upper panel of Fig. 1a has the C4 symmetry where bulk polarization is induced by the broken SIS. This kind of polarization is symmetrically equivalent to the ones induced by the field perpendicular to the plane, whose gradient generates a Rashba SO coupling. For the one in the lower panel of Fig. 1a, the DM vector keeps the \(\bar C_4\) symmetry, where bulk polarization is absent even though the global SIS is broken. It is realized in crystals with D2d or Td point group symmetry, and is related to the Dresselhaus-type of SO interaction. Another way to look at is to perform a C4-rotation to δ1 and δ2 in the clockwise direction, and we find that D rotates in the anti-clockwise direction in the Dresselhaus-case, and clockwise in the Rashba-case.
Figure 1b, c show the direction and the amplitude of the spin carried by magnons, Sk,±, of the lower magnon band, ω−(k) over the Brillouin zone for the Rashba and Dresselhaus magnons. We take D/J = 0.1, Λ/J = 0.05, and h/J = 3.0. The upper band not shown here hosts similar texture, while the component perpendicular to h points in the opposite direction (see Supplementary Fig. 1). The total net moment is opposite to h. This is because the magnons represent the shrinking of classical magnetization by definition, and the magnetic moments cant toward h. A series of panels show how the spin textures evolve by the rotation of the magnetic field. The magnitude of h controls the amplitude of Sk,±, while the same order of |Sk,±| and as rich texture sustain down to h \(\rightarrow\) 0 (see Supplementary Fig. 2).
One can understand overall spin textures in analogy with the well-known electronic counterparts. Figure 1d shows the typical Rashba-type and Dresselhaus-type spin textures observed in electronic systems; the former has C4 symmetry about the kz-axis and four mirror planes (kx, ky) = (0, 1)(1, 0), (1, ±1), and the latter has \(\bar C_4\) about the kz-axis, (1, ±1)-mirror planes, and C2 symmetries about the kx-axes and ky-axes. Note that the Hamiltonian of the Rashba-type and Dresselhaus-type antiferromagnets shown in Fig. 1a have the same crystal point group symmetry with their electronic counterparts. After modifying them to have a net moment opposite to the magnetic field, h, we see a rough orientation of Sk,± over the k-space; the examples are given in Fig. 1d for h || ex (ϕ = 0). The magnetic ordering and the magnetic field break the point group symmetry, but some of the space group symmetries are preserved, e.g., the Rashba-type antiferromagnet keeps a glide symmetry along the y-axis, so that the spin textures are invariant under mirror operation along the ky-axis. The Dresselhaus-type one keeps two-fold screw axis along the x-axis, and thus the textures remain unchanged after the C2 operation about the kx-axis.
Types of spin textures
Even though the spin momentum locking itself refer to the fixing of the angle between particle momentum k and spin moment Sk,±, it does not necessarily mean the emergent texture of spins. To be more precise, there are three classes of spin textures, (i) spin moment is quantized in each band, namely |Sk,±| = 1 and the direction is unique throughout each band, (ii) amplitude of the spin moment depends on k, but the direction is unique for each band, and (iii) both the direction and amplitude of the spin moment vary with k. Among them, only (iii) affords rich spin texture as in Fig. 1. Reference35 showed the sufficient condition to have (i) (see Supplementary Note 2).
One can afford (i) and (ii) even when D = 0. To have case (iii) the uniform DM interaction is thus important. For example, if we take D = 0 in Eq. (1), we find case (ii), with dA(ω±(k)) = dB(ω±(k)) ≡ d(ω±(k)) and
As we see shortly, the uniform DM interaction and the noncollinear spin texture together serve as a necessary condition for (iii) in antiferromagnets described by Eq. (1). The components of the magnetic field and the staggered DM interactions perpendicular to the plane do not contribute.
Analogy of two-sublattice magnons with electrons
We see how one can qualify the antiferromagnets a property analogous to the electronic systems with SO coupling. (Details of the formulation are given in Supplementary Discussion). To this end, we consider a noninteracting 1D electronic system with a SO coupling, α, and a magnetic field, h, shown in Fig. 2a. The Hamiltonian is given as \({\cal H}\) = (−2tcosk)σ0 + (2αsink)σz − hσx, where σμ (μ = x, y, z) is the Pauli matrix whose z-component classifies the up and down spin-1/2 of electrons, and σ0 is a unit matrix. When α = h = 0, the energy bands are doubly degenerate as shown in Fig. 2a, which implies an SU(2) symmetry represented by the operator σμ. By the introduction of α ≠ 0, the two bands split, and the symmetry reduces from SU(2) to U(1). Because of this U(1) symmetry, the spin moments the two bands carry are allowed to point only along the z-direction up and down. Finally, the magnetic field h ≠ 0 breaks the U(1) symmetry down to {e}, and the magnetic moments the energy bands carry start to depend on k. The extension of the above discussion to 2D is straightforward: to realize Rashba or Dresselhaus types of spin textures, the symmetry reduction of SU(2) to {e} is required.
Comparison of 1D electronic and magnonic systems. a Dispersion of 1D electronic system with the spin–orbit coupling and the magnetic field. b The 1D antiferromagnet with the uniform Dzyaloshinskii–Moriya (DM) interaction and the magnetic field. Red arrows indicate the classical spin configuration in the ground state, and blue arrows indicate the uniform DM vector. c Dispersion of the 1D antiferromagnet with the uniform DM interaction and the magnetic field. The DM interaction in the antiferromagnet corresponds to the spin–orbit coupling in the electronic system
A similar argument applies to antiferromagnets. Let us consider a 1D system with a DM interaction and a magnetic field shown in Fig. 2b, whose Hamiltonian is given as Eq. (1) with Dj,j+1 = Dez, Λ = Λez (Λ < 0), and h = hex. For the simplest antiferromagnet with Λ = D = h = 0, the corresponding BdG Hamiltonian takes the form, \(H_{{\mathrm{BdG}}}^{SU(2)}\) = \((\tau ^0 \otimes \sigma ^0)2JS\) +\((\tau ^x \otimes \sigma ^x)2JS\,{\mathrm{cos}}(k)\), where τμ and σμ (μ = x, y, z) are Pauli matrices acting on a particle-hole space and a sublattice space, respectively. It has an SU(2) symmetry, to which we intend not in terms of the spin operator, but of the product space of sublattice and particle-hole degrees of freedom. The SU(2) operator to classify this symmetry is given by
which all commute with \(H_{{\mathrm{BdG}}}^{SU(2)}({\bf{k}})\). The reduction of SU(2) to Uz(1) symmetry is done by introducing D ≠ 0 supported by Λ > 0, \(H_{{\mathrm{BdG}}}^{U^z(1)}\) = \((\tau ^0 \otimes \sigma ^0)2(J + \Lambda )S\) + \((\tau ^x \otimes \sigma ^x)2JS\,{\mathrm{cos}}(k)-(\tau ^y \otimes \sigma ^y)2DS\,{\mathrm{sin}}(k)\). Among Jμ’s, only the z-component fulfills \(\left[ {H_{{\mathrm{BdG}}}^{U^z(1)}({\bf{k}}),J^z} \right] = 0\). Here, we specify Uz(1) as the U(1) symmetry about the z-axis in order to discriminate from the one about the x-axis we see shortly. The classification of U(1) about the spatial axis is required, since the definition of Pauli matrices τμ are sticked to the real space axis, which is not the case for the usual electronic spins.
To obtain a k-dependent spin texture, one further needs to break the Uz(1) symmetry of magnons, which is done by applying the magnetic field in the x-direction. Here, the magnetic field parallel to z only adds to the Hamiltonian a (τ0 ⊗ σz) term which does not break the Uz(1) symmetry.
Notice that the magnon spin textures near k = 0 differ from those of the electronic systems (see Fig. 2c). Also, the energy dispersions differ in that the electrons have Fermi level, whereas the magnons do not, and instead have a particle-hole gap. Although the particle-hole symmetric form of the BdG Hamiltonian makes the formulation rather complicated, the A and B sublattice degrees of freedom thus plays a role similar to the electronic spins, and so as D ≠ 0 to the SO coupling of electrons. The full breaking of SU(2) symmetry down to {e} gives a necessary and sufficient condition to afford k-dependent spin texture in 2D, as well as in 1D antiferromagnets.
1D antiferromagnets as building blocks
Besides the one we showed in Fig. 2b, there are several ways to construct the 1D antiferromagnet with uniform DM interaction in a magnetic field. For completeness, we now provide a classification that applies to all of them. Let us start by reminding of a simple 1D antiferromagnet with only a Heisenberg exchange J. In contrast to the ferromagnets, it hosts two-fold degenerate magnon branches that cross at k = 0 (see Fig. 3), and by the easy axis anisotropy, Λ < 0, the gap opens, but the energy bands remain degenerate. The DM interaction perpendicular to the magnetic moments does not change the band structure, which is shown in Fig. 3a. The SU(2) symmetry is preserved for all these cases. By the introduction of D parallel to the magnetic moments, the symmetry reduces to Uz(1). The two branches of bands shift in opposite directions35,37,38 as shown in Fig. 3b. These two cases are already studied in experiments38.
Classification of representative one-dimensional (1D) antiferromagnets with magnetic anisotropy and uniform Dzyaloshinskii–Moriya interaction. a–c Schematic illustrations of the models and magnon bands calculated for h = 0 and D ≠ 0. d Relative relationships between MA, MB, D, and h, classified into four cases I–IV. All possible types of 1D antiferromagnets including (a–c) fit one of these cases when h ≠ 0. Among three different classes of spin textures given in the main text, symbol multiplication sign (×) denotes (i) having quantized spin moment with U(1) symmetry about the z-axis, open triangle (Δ) denotes (ii) k-dependent |Sk,±| with U(1) symmetry about the x-axis, and open circle (○) a fully k dependent spin texture (iii) with broken symmetry, {e}. The nonreciprocity is present for (i) and (ii) with open circle (○) and absent for the other two
We now examine the easy plane antiferromagnet in Fig. 3c. When Λ > 0, one of the modes becomes gapped, which is responsible for the in-plane stretching mode. The gap of the remaining mode opens when the in-plane rotational symmetry is broken by h. Again, when we set D ⊥ MA, MB (upper panel), the magnon band structures remain unchanged. The direction of the spin carried by magnon does not vary with k since the system has U(1) symmetry about the x-axis, which we denote Ux(1). If we rotate MA and MB within the easy plane off the direction parallel to D, the energy band is slightly modified by D. These cases become important when we apply a field.
By the application of h, MA and MB are canted off the collinear alignment and gain a net moment in the field direction. The excitation against this weak ferromagnetic element couples to D depending on the relative angle between h and D, which falls onto either of II–IV in Fig. 3d. Case I is realized by applying a magnetic field parallel to the collinear magnetic moments with easy axis anisotropy. Its dispersion is actually observed experimentally in the noncentrosymmetric antiferromagnet, α-Cu2V2O738. In a finite magnetic field and for a noncollinear spin configuration, magnons start to carry spin moment Sk,± that has a net value opposite to h ∝ MA + MB; Since Sk,± is a linear combination of vectors MA and MB (Eq. (3)35), having a noncollinear MA and MB is the necessary condition to vary both the direction and the amplitude of Sk,±. Although this condition is fulfilled for Cases II–IV in Fig. 3d, only Case II breaks the SU(2) symmetry down to {e} and exhibits directional variation of Sk,± on k.
In the other three cases, the spin texture is restricted by the symmetry of the BdG Hamiltonian; In Case I, the Uz(1) symmetry leads to the quantization of Sk,±. In Case II, the Ux(1) symmetry allows |Sk,±| to vary, while they all point in the same direction following Eq. (4). Case IV does not have a Ux(1) symmetry, but Sk,± again follows Eq. (4). This is because the bosonic BdG Hamiltonian satisfies a similar condition, [HBdG(k), JxK] = 0, assisted by a complex conjugate operator, K. We denote this as \(\bar U^x(1)\) symmetry for convenience.
Similar discussion can be developed for the ferromagnets with uniform DM interaction and for the antiferromagnets with staggered DM interaction, that completes the classification of the role of DM interactions on ferro and antiferromagnets and adds to Fig. 3a–c the relationships with other cases (see Supplementary Note 3). For example, the antiferromagnet shown in Fig. 3b is then regarded as the combination of two ferromagnets with uniform DM interaction, each showing nonreciprocity in opposite directions which is explicitly shown in Supplementary Fig. 3. However, the magnetic moments are quantized on each of the magnon branches.
Designing 2D spin textures
Based on the above mentioned classification I–IV, one can design a spin texture of a 2D antiferromagnet by hand. Our Rashba and Dresselhaus type magnon spin textures offer a good example; Let us configure the direction, δII, that reproduces case II in Fig. 3d along which the spin textures emerge in a most significant manner. This is done by taking the linear combination of δ1 and δ2, so as to have the combination of the two D’s attached to them become perpendicular to h (see the black arrow in Fig. 1e). As h rotates clockwise, the direction of δII rotates anti-clockwise/clockwise for Rashba/Dresselhaus-type antiferromagnets. The other direction, δIII, that the locking does not occur is defined perpendicular to δII, in a way that the combination of their two D's points toward h. We also put a constraint that the net moment points in the direction opposite to h. These considerations allow us to figure out the overall textures without detailed calculation.
As one can anticipate from the evolution of spin texture, the band profile rotates following the field-angle ϕ = 0 → 2π, clockwise and anti-clockwise for Dresselhaus and Rashba-types, respectively. Accordingly, the nonreciprocity appears in the (kx, ky) = (cosϕ, −sinϕ)-direction for the Dresselhaus-type, and in the direction perpendicular to the field for the Rashba-type (see Supplementary Fig. 1).
Discussion
Based on the symmetry arguments and the idea of constructing the 2D antiferromagnets using the building blocks of 1D antiferromagnetic chains, a strategy to design a variety of spin textures is thus provided. Previously, active discussions on the physics of magnons were given in ferro or ferrimagnets with its magnetic moments parallel to the DM interactions; for the staggered DM interaction that does not break SIS, a topological magnon contributing to the thermal Hall effect is observed, and for uniform DM interaction, a nonreciprocity of ferromagnetic magnons were reported. Here, we clarified another aspect of magnons that the uniform DM interactions breaking global SIS in the antiferromagnet can generate as rich spin-textures as the Rashba and Dresselhaus electronic semiconductors. The two degenerate energy branches of the uniform antiferromagnet carry the magnetization pointing in the nearly opposite directions, which are regarded as the internal pseudo-spin degrees of freedom relevant to magnetic sublattices. The uniform DM interaction serves as a pseudo-spin orbit coupling of magnons and generate a spin texture over the whole reciprocal space. To activate such fictitious pseudo-SO coupling of magnons, an interplay with a magnetic field and a spin anisotropy plays a crucial role, that fully breaks the pseudo-spin-SU(2) symmetry. The resultant textures are easily controlled by the magnetic field angle.
The 2D Dresselhaus antiferromagnet is actually realized in a noncentrosymmetric spin-5/2 antiferromagnet Ba2MnGe2O7, with space group \(P\bar 42_1m\). It undergoes a Néel transition at TN = 4 K into an easy plane type antiferromagnetic phase36,39, where the microwave non-reciprocity is indeed observed40. A spin-3/2 multiferroic Ba2CoGe2O741,42, possibly of space group \(P\bar 42_1m\), is considered to have a similar property. The exchange interactions in Ba2MnGe2O7 is J ~ 27 μeV39, which is much smaller than the other materials of the same family, possibly allowing for the examination of the present phenomena by several experimental probes, and with a very small magnetic field of less than few tesla. Our theory shows that even for the materials with much larger J, one can obtain a similar spin texture by setting h < 0.1J (see Supplementary Fig. 2). Besides such noncentrosymmetric antiferromagnets, the interface of typical centrosymmetric antiferromagnets is expected to show magnonic spin momentum locking. Thus, the scheme we proposed may give a strong command of designing spin textures toward the application for antiferromagnetic spintronics43.
Although spin textures and nonreciprocity were difficult to realize within previous considerations on antiferromagnets, there is one rare example on a honeycomb lattice44,45 exhibiting nonreciprocity46 with toroidal ordering, and thermal Hall effect47,48. The crystal structure of the material keeps the SIS, and the DM interaction acts on next nearest neighboring sites belonging to the same sublattice, and align in the staggered manner. In our scheme, it can be regarded as a staggered assembly of 1D ferromagnets with uniform DM interactions, that may provide a generalized interpretation on its properties (see Supplementary Fig. 3g).
The advantage of having spin texture in insulators is to store information directly by controlling the texture itself, and how to characterize and read the information is the important and challenging part of device applications. On the top of that, it is starting to be recognized that antiferromagnets have several advantages for a memory storage device over ferromagnets43. Since the antiferromagnetic state does not generate stray fringing fields, it is robust against any perturbation. Writing speed of memory is generally limited by the resonance frequency, which can be much higher in the antiferromagnets than in ferromagnets. Nevertheless, the potential abilities of antiferromagnets remained unexplored.
Our results in Fig. 1b, c indicate that the magnonic spin current can be a good probe for spin textures: the magnetic moment Sk,± at relatively large k depends on the sign of k. Therefore, by the experimental setup shown in Fig. 4a, one can selectively excite magnons that generate a nearly pure spin current. The electromagnetic waves of frequency f ~ 101–103 GHz emitted from a micro antenna on the antiferromagnetic sample generates antiferromagnetic magnons with wave vectors +k and −k, which have an amplitude typically of an inverse of antenna width d. The group velocity of the excited magnons, dω-(k)/dk, together with the amount of excited spin density |Sk,− − S−k,−| is shown as functions of k in Fig. 4b, c. The gradual increase of spin current with |k| and D is common to noncentrosymmetric ferromagnets25. The group velocity shows a sharp and linear increase from k = 0 and saturates at small k, which is the feature of the antiferromagnetic magnon with nearly linear dispersion at small k, and it works as an advantage for the experimental observation. By probing the direction of spin current through an inverse spin Hall voltage of Pt electrode, one can figure out the structure of the texture in a rotating field. Unlike the diffusive spin current carried by conduction electrons in the presence of SO coupling, the magnon spin current in insulators are stable regardless of the D and Λ-terms49, as far as the direct couplings with lattices or impurities are not included. For the dissipation due to such an extrinsic effect, the phenomenological theories will give the evaluation of the propagation length, which is sensitive to circumstances50. The present study provides a roadmap to electrically detect and control spin textures in ubiquitous antiferromagnets, opening up a pathway for antiferromagnetic spintronics.
Device applications. a Illustration of the experiment to probe the structure of a noncentrosymmetric antiferromagnet by generating a nearly pure spin current of wave numbers, k and −k. The width of the antenna is designed to selectively excite magnons of |k| ~ 1/d. The inverse spin Hall voltage of Pt electrode is used to detect the spin current. b Group velocity dω−(k)/dk and (c) |Sk,− − S−k,−|, for k = kx (ky = 0 line for Rashba-type ϕ = 0) with D/J = 0.1, 0.05, and 0.01, where we set h = 0.5J. The right panel is the h-dependence for k/π = 0.1, 0.05 and 0.01. At h ~ 2J, the two magnon bands touch at Γ-point, which enhances the mixing of spins and gives a sharp peak in |Sk,− − S−k,−|
Methods
We perform a spin wave analysis on two sublattice antiferromagnets. The starting point is a collinear or a canted antiferromagnetic classical order. We apply a local unitary transformation, \(U^\dagger {\cal H}U\), and set the z-axis of the spin operator space to the direction of the magnetic moments. For example, the unitary operator for 2D easy plane antiferromagnets on a square lattice shown in Fig. 1a is given as
which sets the spin operators in fictitious local space antiparallel. Here, rj, is the spatial coordinate of site-j, and the ordering wave vector Q satisfies \({\mathrm{e}}^{i{\bf{Q}} \cdot {\bf{r}}_j} = \pm 1\) for sublattices A and B, respectively. The linearized Holstein-Primakoff transformation is given as
for sublattice-A, and
for sublattice-B. After the Holstein-Primakoff and Fourier transformations, \(U^\dagger {\cal H}U \simeq {\mathrm{const}} + {\cal H}_{{\mathrm{SW}}}\), the spin wave Hamiltonian is written finally in the quadratic form as Eq. (2). The bosonic BdG Hamiltonian is written as
Here Ξk and Δk are 2 × 2 matrices satisfying \({\mathrm{\Xi }}_{\bf{k}}^\dagger = {\mathrm{\Xi }}_{\bf{k}}\) and \({\mathrm{\Delta }}_{ - {\bf{k}}}^\dagger = {\mathrm{\Delta }}_{\bf{k}}^ \ast\). HBdG(k) is diagonalized analytically using the paraunitary matrix51. The actual diagonalization is done by solving the following eigenvalue equation,
with Σz = τz ⊗ σ0. The eigenvectors of magnons, t±(k) = (u±,A(k), u±,B(k), v±,A(k), v±,B(k))T, satisfy the normalization condition, \({\bf{t}}_\eta ^\dagger ({\bf{k}}){\mathrm{\Sigma }}^z{\bf{t}}_{\eta \prime }({\bf{k}}) = \delta _{\eta ,\eta \prime }\) with η, η′ = ±. We obtain the analytical form of the magnon dispersions ω±(k) and corresponding eigenvectors t±(k) consisting of two branches. The local spectral weight used in Eq. (3) is given as
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for Rashba spin-orbit coupling. Nat. Mat. 14, 871 (2015).
Rashba, E. I. Properties of semiconductors with an extremum loop. I. Cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop. Sov. Phys. Solid State 2, 1109 (1960).
Casella, R. C. Toroidal energy surfaces in crystals with wurtzite symmetry. Phys. Rev. Lett. 5, 371–373 (1960).
Bychkov, Y. A. & Rashba, E. I. Oscillatory effects and the magnetic susceptibility of carriers in inversion layers. J. Phys. C. 17, 6039 (1984).
Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 100, 580–586 (1955).
Murakami, S., Nagaosa, N. & Zhang, S. C. Dissipationless quantum spin current at room temperature. Science 301, 1348 (2003).
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin hall effect in semiconductors. Science 306, 1910 (2004).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Wunderlich, J., Kaestner, B., Sinova, J. & Jungwirth, T. Experimental observation of the spin-Hall effect in a two-dimensional spin-orbit coupled semiconductor system. Phys. Rev. Lett. 94, 047204 (2005).
Miron, I. M. et al. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nautre Mat. 9, 230–234 (2010).
Kurebayashi, H. et al. An antidamping spin-orbit torque originating from the Berry curvature. Nat. Nanotech. 9, 211–217 (2014).
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commum. 73, 233–235 (1990).
Kato, K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Current-induced spin polarization in strained semiconductors. Phys. Rev. Lett. 93, 176601 (2004).
Silov, A. Yu et al. Current-induced spin polarization at a single heterojunction. Appl. Phys. Lett. 85, 5929 (2004).
Dzyaloshinsky, I. Thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 214–255 (1958).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91 (1960).
Matsumoto, R. & Murakami, S. Theoretical prediction of a rotating magnon wave packet in ferromagnets. Phys. Rev. Lett. 106, 197202 (2011).
Melcher, R. L. Linear contribution to spatial dispersion in the spin-wave spectrum of ferromagnets. Phys. Rev. Lett. 30, 125 (1973).
Kataoka, M. Spin waves in systems with long period helical spin density waves due to the antisymmetric and symmetric exchange interactions. J. Phys. Soc. Jpn. 56, 3635 (1987).
Zakeri, Kh et al. Asymmetric spin-wave dispersion on Fe(110): direct evidence of the Dzyaloshinskii-Moriya interaction. Phys. Rev. Lett. 104, 137203 (2010).
Di, K. et al. Direct observation of the Dzyaloshinskii-Moriya interaction in a Pt/Co/Ni film. Phys. Rev. Lett. 114, 047201 (2015).
Stashkevich, A. A. et al. Experimental study of spin-wave dispersion in Py/Pt film structures in the presence of an interface Dzyaloshinskii-Moriya interaction. Phys. Rev. B 91, 214409 (2015).
Nembach, H. T., Shaw, J. M., Weiler, M., Jué, E. & Silva, T. J. Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii-Moriya interaction in metal films. Nat. Phys. 11, 825 (2015).
Sato, T. J. et al. Magnon dispersion shift in the induced ferromagnetic phase of noncentrosymmetric MnSi. Phys. Rev. B 94, 144420 (2016).
Iguchi, Y., Uemura, S., Ueno, K. & Onose, Y. Nonreciprocal magnon propagation in a noncentrosymmetric ferromagnet LiFe5O8. Phys. Rev. B 92, 184419 (2015).
Katsura, H., Nagaosa, N. & Lee, P. A. Theory of the thermal Hall effect in quantum magnets. Phys. Rev. Lett. 104, 066403 (2010).
Ideue, T. et al. Effect of lattice geometry on magnon Hall effect in ferromagnetic insulators. Phys. Rev. B 85, 134411 (2012).
Onose, Y. et al. Observation of the magnon Hall effect. Science 329, 297 (2010).
Matsumoto, R., Shindou, R. & Murakami, S. Thermal Hall effect of magnons in magnets with dipolar interaction. Phys. Rev. B 89, 054420 (2014).
Lee, H., Han, J. H. & Lee, P. A. Thermal Hall effect of spins in a paramagnet. Phys. Rev. B 91, 125413 (2015).
Owerre, S. A. Topological thermal Hall effect in frustrated kagome antiferromagnets. Phys. Rev. B 95, 014422 (2017).
Hirschberger, M., Chisnell, R., Lee, Y. S. & Ong, N. P. Thermal Hall effect of spin excitations in a kagome magnet. Phys. Rev. Lett. 115, 106603 (2015).
Hirschberger, M., Krizan, J. W., Cava, R. J. & Ong, N. P. Large thermal Hall conductivity of neutral spin excitations in a frustrated quantum magnet. Science 348, 106 (2015).
Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098 (1940).
Okuma, N. Magnon spin-momentum locking: various spin vortices and dirac magnons in noncollinear antiferromagnets. Phys. Rev. Lett. 119, 107205 (2017).
Murakawa, H., Onose, Y., Miyahara, S., Furukawa, N. & Tokura, Y. Comprehensive study of the ferroelectricity induced by the spin-dependent d-p hybridization mechanism in Ba2XGe2O7 (X=Mn, Co, and Cu). Phys. Rev. B 85, 174106 (2012).
Cheng, R., Daniels, M. W., Zhu, J.-G. & Xiao, D. Antiferromagnetic spin wave field-effect transistor. Sci. Rep. 6, 24223 (2016).
Gitgeatpong, G. et al. Nonreciprocal magnons and symmetry-breaking in the noncentrosymmetric antiferromagnet. Phys. Rev. Lett. 119, 047201 (2017).
Masuda, T. et al. Instability of magnons in two-dimensional antiferromagnets at high magnetic fields. Phys. Rev. B 81, 100402 (2010).
Iguchi, Y. et al. Microwave non-reciprocity of magnon excitations in a non-centrosymmetric antiferromagnet Ba2MnGe2O7. Phys. Rev. B 98, 064416 (2018).
Murakawa, H., Onose, Y., Miyahara, S., Furukawa, N. & Tokura, Y. Ferroelectricity induced by spin-dependent metal-ligand hybridization in Ba2CoGe2O7. Phys. Rev. Lett. 105, 137202 (2010).
Yi, H. T., Choi, Y. J., Lee, S. & Cheong, S.-W. Multiferroicity in the square-lattice antiferromagnet of Ba2CoGe2O7. Appl. Phys. Lett. 92, 212904 (2008).
Jungwirth, T. et al. The multiple directions of antiferromagnetic spintronics. Nat. Phys. 14, 200 (2018).
Cheng, R., Okamoto, S. & Xiao, D. Spin nernst effect of magnons in collinear antiferromagnets. Phys. Rev. Lett. 117, 217202 (2016).
Zyuzin, V. A. & Kovalev, A. A. Magnon spin nernst effect in antiferromagnets. Phys. Rev. Lett. 117, 217203 (2016).
Hayami, S., Kusunose, H. & Motome, Y. Asymmetric magnon excitation by spontaneous toroidal ordering. J. Phys. Soc. Jpn. 85, 053705 (2016).
Owerre, S. A. Topological magnon bands and unconventional thermal Hall effect on the frustrated honeycomb and bilayer triangular lattice. J. Phys. 29, 385801 (2017).
Owerre, S. A. Noncollinear antiferromagnetic Haldane magnon insulator. J. Appl. Phys. 121, 223904 (2017).
Rückriegel, A., Brataas, A. & Duine, R. A. Bulk and edge spin transport in topological magnon insulators. Phys. Rev. B 97, 081106(R) (2018).
Rückriegel, A. & Kopietz, P. Spin currents, spin torques, and the concept of spin superfluidity. Phys. Rev. B 95, 104436 (2017).
Colpa, J. H. P. Diagonalization of the quadratic boson Hamiltonian. Physica 93A, 327 (1978).
Acknowledgements
We acknowledge discussions with Y. Iguchi and Y. Nii and K. Penc. This work is supported by JSPS KAKENHI Grant Numbers JP17K05533, JP17K05497, JP17H02916, JP16H04008, and JP17H05176.
Author information
Authors and Affiliations
Contributions
Y.O. designed the project, M.K. performed all the calculations and constructed the theory in discussion with C.H. and Y.O. C.H. wrote the manuscript based on mutual discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kawano, M., Onose, Y. & Hotta, C. Designing Rashba–Dresselhaus effect in magnetic insulators. Commun Phys 2, 27 (2019). https://doi.org/10.1038/s42005-019-0128-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0128-6
This article is cited by
-
Magnon thermal Hall effect via emergent SU(3) flux on the antiferromagnetic skyrmion lattice
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.