Abstract
Topological superconductors possess a bulk superconducting gap and boundary gapless excitations, known as “Majorana fermion”. Search for new systems with topological superconductivity is of fundamental and application importance due to the potential application of Majorana fermions in topological quantum computation. Here we show that the Larkin-Ovchinnikov superconducting phase with a finite momentum pairing can emerge in a model of bilayer superconducting topological insulator films, in which superconductivity appears for both the top and bottom surface states, and can be topologically non-trivial. This “topological Larkin-Ovchinnikov phase” is induced by an in-plane magnetic field and possesses a Majorana mode chain along the edge perpendicular to the in-plane magnetic field direction due to its non-trivial \({\Bbb Z}_2\) topological nature. Our theoretical model can be naturally realized in superconductor/topological insulator sandwich structure or in Fe(Te, Se) film, a topological material with superconductivity, and thus provides a route to explore unconventional superconductivity in existing systems.
Similar content being viewed by others
Introduction
Magnetism and superconductivity are two fundamental states of matter in condensed matter physics, and the interplay between them continues to bring us intriguing phenomena. Unlike the conventional Cooper pairs with zero momentum in the Bardeen–Cooper–Schrieffer (BCS) theory, magnetism can induce a superconducting (SCing) state with a finite momentum pairing. The pairing function of such a state can either carry a single finite momentum Q, known as Fulde-Ferrell (FF) state1, or multiple finite momenta Qi (i = 1,2,…), known as Larkin–Ovchinnikov (LO) state2. The FFLO state has been theoretically proposed3,4,5 and experimentally tested in a variety of systems, including heavy fermion superconductors (SCs)6,7, organic SCs8, ultrathin crystalline Al films9, and even in cold atom systems10. Another recent development is to realize topological SCs by integrating magnetism, spin–orbit coupling and superconductivity into one hybrid system11,12,13,14,15,16, in which gapless excitations exist at the boundary or in the vortex core, dubbed “Majorana fermions” or “Majorana zero mode (MZM)”. MZM possess exotic non-Abelian statistics and thus can serve as the building block for topological quantum computation17,18.
Since both finite momentum pairing and topological superconductivity require magnetism and superconductivity, it is natural to ask if these two SCing phenomena can coexist and if there is any interplay between them. In particular, one may ask (1) if topological SC phases can exist for FF or LO state with finite momentum pairing; (2) how to find an experimentally feasible system for a robust realization of such state; and (3) what types of boundary modes can emerge in such system. Recent theoretical developments have revealed the possibility of two-dimensional (2D) topological FF (tFF) phase with a non-zero Chern number in the bulk and chiral Majorana modes at the boundary in cold atom systems19,20,21,22. More recently, it was proposed that half-vortex in certain type of topologically trivial LO phase is able to host MZMs23.
In this work, we propose a topologically non-trivial LO (tLO) state in a model system of bilayer SCing topological insulator (TI) thin films under an in-plane magnetic field. Based on the self-consistent gap equation and Ginzburg–Landau free energy, we construct the phase diagram of superconductivity in this model system and demonstrate the existence of LO phase in a wide parameter range. The topological nature of this LO phase is revealed by the calculation of edge modes and the non-trivial \({\Bbb Z}_2\) topological invariant in the D class. In the tLO phase, a chain of numerous MZMs, dubbed “MZM chain”, is predicted along the edge perpendicular to the in-plane magnetic field. The unique experimental signature for probing such MZM chain through scanning tunneling microscope (STM) is proposed to distinguish from other topological SCing phase (e.g., tFF phase). The possible material realization of tLO phase in the SC/TI sandwich structure or in the newly discovered Fe(Te, Se) films with topological surface states is also discussed.
Results
Bilayer SCing TI film
Our model system consists of a TI film under an in-plane magnetic field, in which both top and bottom surface states (bilayer) are in proximity to the conventional s-wave SC pairing, as shown in Fig. 1a. The low energy physics of this system is described by the Hamiltonian
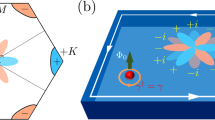
Sketch of the bilayer system and phase diagram. a Illustration of the superconductor/topological insulator/superconductor (SC/TI/SC) heterostructure under an in-plane magnetic field Bx (big green arrow) possessing Majorana zero mode (MZM) chain (marked by the green spheres) at the boundary. b Illustration of the two Fermi surfaces with opposite spin textures (green arrows) for bilayer TI thin films with m0 = m1 = 0 in Eq. (2) under an in-plane magnetic field Bx. c Phase diagram of superconducting TI film in the absence of magnetic field, as a function of intra-layer interaction U and inter-layer interaction V. It consists of one metallic phase and three superconducting phases: the intra-layer A1g pairing \(\hat c_{t \uparrow }\hat c_{t \downarrow } + \hat c_{b \uparrow }\hat c_{b \downarrow }\), the inter-layer A1u pairing \(\hat c_{t \uparrow }\hat c_{b \downarrow } - \hat c_{b \uparrow }\hat c_{t \downarrow }\), and the intra-layer A2u pairing \(\hat c_{t \uparrow }\hat c_{t \downarrow } - \hat c_{b \uparrow }\hat c_{b \downarrow }\)
Here, \({\cal H}_0\) describes the surface states at the top and bottom surfaces under an in-plane magnetic field along the x direction and is given by24,25
where \(\tilde c = \left( {\hat c_{t, \uparrow },\hat c_{t, \downarrow },\hat c_{b, \uparrow },\hat c_{b, \downarrow }} \right)^{\mathrm{T}}\) are the electron annihilation operators, \((\hat p_x,\hat p_y)\) are in-plane momentum operators, v is the Fermi velocity, and σ and τ are Pauli matrices, representing spin and pseudo-spin (top(t) and bottom(b) surfaces), respectively. For the Hamiltonian (2), the first term \(\left( {m = m_0 + m_1{\hat{\mathbf p}}^2} \right)\) describes the tunneling between the two surface states (called inter-layer tunneling below), the second term is the Dirac Hamiltonian for two surface states, and the third term gives the Zeeman coupling between electron spin and in-plane magnetic fields. The sketch of the Fermi surface is shown in Fig. 1b. For simplicity, we have absorbed the parameters \(\hbar\) into v and gμB into Bx. In the calculation, we define \(m_{\mathrm{F}} = m_0 + m_1p_{\mathrm{F}}^2\), which gives rise to \(\mu ^2 = m_{\mathrm{F}}^2 + v^2p_{\mathrm{F}}^2\) in the absence of magnetic field. In this work, our calculation are based on realistic parameters for the model Hamiltonian \({\cal H}_0\), which are described in Supplementary Note 4. To include the SC pairing, we consider electron–electron attractive interaction term26
where \(\hat n_\tau ({\mathbf{r}}) = \mathop {\sum}\nolimits_{\sigma = \uparrow , \downarrow } \hat n_{\tau ,\sigma }({\mathbf{r}})\) is the electron density operator on layer τ = t, b.
The phase diagram of SCing phases can be constructed by minimizing Ginzburg–Landau (GL) free energy \({\cal L}\) obtained from the microscopic Hamiltonian (1)27. The quadratic GL free energy reads,
where the the superconductivity susceptibility is
where \({\cal G}_e(\omega ,{\mathbf{p}})\) and \({\cal G}_h(\omega , - {\mathbf{p}})\) are the single-particle Green’s functions of electrons and holes, and γ represents the superconducting pairing matrix: γ ∈ {sy, τxsy, τysx, τzsy, τy, τysz}. The linearized gap function is derived from \(\partial {\cal L}_2/\partial {\mathrm{\Delta }}_i = 0\) and can be used to construct the phase diagram. More technical details of constructing the phase diagram and the realistic parameters of the microscopic model24,28,29,30,31,32 are discussed in Supplementary Note 3. At zero magnetic field Bx = 0, the Hamiltonian (1) has D3d group symmetry, which possesses three one- dimensional (1D) irreducible representations: A1g, A1u, and A2u; and one 2D irreducible representation: Eu. Consequently, the momentum-independent SCing pairing forms can be classified26. According to the linearized gap equation (See Supplementary Note 2), the stable SCing phases are shown as a function of interaction parameters U and V in Fig. 1c. It is found that intra-layer A1g pairing \(\hat c_{t \uparrow }\hat c_{t \downarrow } + \hat c_{b \uparrow }\hat c_{b \downarrow }\) is favored for a strong attractive U while inter-layer A1u pairing \(\hat c_{t \uparrow }\hat c_{b \downarrow } - \hat c_{b \uparrow }\hat c_{t \downarrow }\) (intra-layer A2u pairing \(\hat c_{t \uparrow }\hat c_{t \downarrow } - \hat c_{b \uparrow }\hat c_{b \downarrow }\)) can appear for a strong attractive (repulsive) V. More precisely, the phase boundary between A1g and A1u is, \(\frac{U}{V} = 1 - \frac{{2m_{\mathrm{F}}^2}}{{\mu ^2}}\); and the boundary between A1g and A2u is U = −V. However, in the realistic materials, we expect the intra-layer interaction U dominates over the inter-layer interaction V and thus gives rise to superconductivity described by A1g pairing in the phase diagram.
Next, we focus on the case with a strong attractive U term below and set V = 0, which is most common, and discuss the T – Bx phase diagram. With magnetic field Bx, two intra-layer superconducting pairings, \({\mathrm{\Delta }}_{A_{1g}}\sim s_y\) and \({\mathrm{\Delta }}_{A_{2u}}\sim \tau _zs_y\), can be mixed with each other. In addition, an in-plane magnetic field is possible to induce the superconducting pairing with the finite momentum q = (0, Q). Therefore, we consider the following three types of pairing forms: (1) BCS state with pairing function \({\mathrm{\Delta }}_{{\mathrm{BCS}}} = {\mathrm{\Delta }}_0\sqrt {1 - b^2} \sigma _y + b\tau _z\sigma _y\), (2) FF state \({\mathrm{\Delta }}_{{\mathrm{FF}}} = {\mathrm{\Delta }}_0\,{\mathrm{exp}}(iQy)\sqrt {1 - b^2} \sigma _y + b\tau _z\sigma _y\) and (3) LO state \({\mathrm{\Delta }}_{{\mathrm{LO}}} = {\mathrm{\Delta }}_0 - i\sqrt {1 - b^2} {\mathrm{sin}}(Qy)\sigma _y + b\,{\mathrm{cos}}\,(Qy)\tau _z\sigma _y\), in which Δ0 and b are parameters to be determined. Based on these three pairing forms, we can minimize the GL free energy with additional forth order terms numerically with respect to the parameters Δ0 and b (see Supplementary Note 3 for details of the numerical procedure) and construct the T − Bx phase diagram, shown in Fig. 2a. Four phases, including (I) BCS state, (II) FF state, (III) LO state and (IV) normal metallic state, are identified in the phase diagram of Fig. 2a. For a small Bx, the BCS state is energetically favored. As Bx increases, the self-consistently calculated momentum Q of the pairing becomes non-zero at a critical magnetic field Bc, as shown in the inset of Fig. 2b, leading a first-order phase transition to a finite momentum pairing state. For Bx far above the critical value Bc, we find that the momentum Q of the pairing can be approximated by 2Bx/v. Two possible finite momentum pairings, FF and LO states, are considered. Our calculation suggests that the LO state is energetically favored at a large Bx (phase III in Fig. 2a), while the FF state only exists in a small region (phase II in Fig. 2a) between the BCS and LO states. This small region for FF state may disappear for a smaller \(m_{\mathrm{F}} = m_0 + m_1p_{\mathrm{F}}^2\) where pF is the Fermi momentum (see Supplementary Note 3 for the analytical calculation in the mF = 0 limit). The critical Bc depends on the coupling strength mF, as shown by different color lines in the inset of Fig. 2b. Figure 2b depicts the dependence of Bc on mF, from which one can see that Bc can be greatly decreased when mF is reduced toward zero.
Bx − T phase diagram. a Phase diagram of Hamiltonian (1) for the set-up in Fig. 1a, in parameter space of in-plane magnetic field Bx and temperature T, in unit of Tc,0 (the superconducting transition temperature at Bx = 0). It comprises conventional Bardeen–Cooper–Schrieffer theory (BCS) phase (I), Fulde-Ferrell(FF) phase (II), Larkin–Ovchinnikov (LO) phase (III), and normal metal (IV). Parameters used here are m0 = −13.5 meV, m1 = 25 eV ⋅ Å2, v = 2.67 eV ⋅ Å, μ = 100 meV, which are probe for NbSe2/Bi2Se3/NbSe2, and UN0 = 0.27, and ωD = 20 meV, so that Tc,0 = 1.134 ωDexp(−1/UN0) = 0.5587 meV. b The critical field Bc/Tc,0 (transition between BCS and LO phase) as function of mF at fixed T/Tc,0 = 0.8. And Bc is reduced if the inter-layer tunneling is reduced. The inset figure shows vQ/Tc,0 as function of Bx/Tc,0 for different values of mF. The non-zero momentum Q develops when the phase transition between BCS and FF or LO occurs. Here, we only consider intra-layer superconducting pairing and ignore inter-layer interaction, namely V = 0
To understand the occurrence of the LO state, we may first consider the energy spectrum of the single-particle Hamiltonian \({\cal H}_0\) in Eq. (2), which is given by \(E_{0,s}({\mathbf{p}}) = \pm \sqrt {v^2p_x^2 + \left( {\sqrt {m_{\mathrm{F}}^2 + v^2p_y^2} + sB_x} \right)^2}\), with s = ±1. In the decoupling limit (mF → 0), the Fermi surfaces of two surface states are shifted with ±Q/2 in the opposite directions with Q = 2Bx/v due to the Zeeman term, as illustrated in Fig. 1b. Spin textures of the surface states are also depicted on the Fermi surfaces, from which one can see that zero momentum pairing can only occur for electrons with the same spin and opposite layers (inter-layer equal spin triplet pairing), while intra-layer spin-singlet pairing is only possible for a finite momentum. In the limit mF → 0, the finite momentum pairing is favored and thus two FF phases with opposite momenta for each surface state appear, similar to the case of bilayer transition metal dichalcogenides (TMDs) system33. A finite mF can induce Josephson coupling between two FF phases at the opposite surfaces and thus drive the whole system into the LO phase. We notice that such coupling also tends to induce the inter-layer pairing (BCS type with zero momentum) between two surfaces in order to lower the free energy \({\cal L}\). As a result, there is a competition between Josephson coupling due to finite mF, which favors BCS pairing, and the momentum shift due to in-plane magnetic fields, which favors FF or LO state. This analysis explains the dependence of the critical magnetic field Bc on mF [See Fig. 2b]. We notice the similarity between our phase diagram (Fig. 2a) and that of 2D Rashba SCs34,35, presumably due to the same spin textures (Fig. 1b) in these two systems.
Majorana zero mode chain
We now study on topological property of the LO phase (phase III in Fig. 2a). We consider the below Bogoliubov-de Gennes (BdG) Hamiltonian,
where \({\cal H}_{ee} = {\cal H}_0(k_x, - i\partial _y)\) and \({\cal H}_{hh} = - {\cal H}_0^ \ast ( - k_x, - i\partial _y)\) with \({\cal H}_0\) given by Eq. (2), and the pairing Hamiltonian \({\cal H}_{eh} = {\mathrm{\Delta }}_{{\mathrm{LO}}}(y) = {\mathrm{\Delta }}_0[ - i\sqrt {1 - b^2} \,{\mathrm{sin}}(Qy)\sigma _y + b\,{\mathrm{cos}}\,(Qy)\tau _z\sigma _y]\). Since ΔLO(y + 2π/Q) = ΔLO(y). We have \({\cal H}_{{\mathrm{BdG}}}(y + 2\pi /Q) = {\cal H}_{{\mathrm{BdG}}}(y)\). Below, the realistic parameters for \({\cal H}_0\) are chosen the same as those in the caption of Fig. 2, while the parameters in ΔLO (Δ0, Q and b) are obtained from the self-consistent calculations at Bx = 0.75Tc,0 and T = 0.8Tc,0.
To investigate the possible gapless modes at the boundary of a finite system, we implement the tight-binding (TB) regularization of the continue Hamiltonian \({\cal H}_{{\mathrm{BdG}}}\) (including both \({\cal H}_0\) and ΔLO) by setting \(p_x \to \frac{1}{{a_{\mathrm{L}}}}{\mathrm{sin}}(p_xa_{\mathrm{L}})\) and \(p_x^2 \to \frac{2}{{a_{\mathrm{L}}^2}}(1 - {\mathrm{cos}}(p_xa_{\mathrm{L}}))\), where aL is the effective lattice constant. With aL = 16 Å, the single-particle energy dispersion of \({\cal H}_0\) reproduces well that of the continuous model near the chemical potential, as depicted in Supplementary Fig. 3 of Supplementary Note 4, thus validating the TB regularization. We numerically diagonalize \({\cal H}_{{\mathrm{BdG}}}\) in a slab configuration which is infinite in the y direction and has open boundary condition along the x direction. We can choose a super-cell with Nx × Ny lattice sites (See Supplementary Note 4 for details), in which Nx labels the width of the slab while \(N_y = \frac{{2\pi }}{{Qa_{\mathrm{L}}}}\) gives the wave length of the LO phase. The energy dispersions of the slab are shown in Fig. 3a for Nx = Ny = 157 (Bx = 2.5 Tesla) and Fig. 3b for Nx = 157,Ny = 39 (Bx = 10 Tesla). Strikingly, flat bands (referred as Majorana flat bands below) appear with the energy close to zero (E0 ~ ± 10−6) for a large Ny (corresponding to a small Bx) in Fig. 3a. The probability distribution for the state in the Majorana flat bands at ky = Q/2 is shown in Fig. 3c, from which localized MZMs are well separated in one super-cell. We find two MZMs located approximately at y = π/2Q, 3π/2Q in one super-cell at each edge of the slab. In addition to the Majorana flat bands at zero energy, there are also Andreev bound states within the SCing gap, which are well separated from MZMs with an energy gap ΔE ~ 0.2Δ0. At large Bx or small Ny, adjacent MZMs are hybridized with each other and the Majorana bands become dispersive, as shown in Fig. 3b, d. We notice that these two Majorana bands cross with each other at ky = Q/2. This crossing is robust against varying magnetic field Bx and implies the possible non-trivial topological nature of these two Majorana bands, which will be discussed in details below.
Majorana zero mode chain. Low eigenenergy spectrum (a, b) and probability distribution of Majorana zero mode (MZM) state (c, d) at ky = Q/2 in the LO phase with \({\mathrm{\Delta }}_0 [- i\sqrt {1 - b^2} {\mathrm{sin}}\,(Qy)\sigma _y + b\,{\mathrm{cos}}\,(Qy)\tau _z\sigma _y]\) where b = 0.77. We find that the variation of b almost doses not affect the results. Open boundary along x-axis and periodic boundary along y-axis are used. In a, c, Bx = 2.5 Tesla so that Q = 2π/157 and the unit cell size is Nx = Ny = 157; MZM chain appears with a large minigap ΔE ~ 0.2Δ0. In b, d, Bx = 10 Tesla so that Q = 2π/39 and the unit cell size is Nx = 157, Ny = 39; Majorana bands disperse due to the hybridization between the intra-edge MZMs, however, two pair of MZMs at ky = Q/2 are protected. Parameters used here are the same as that in Fig. 2: m0 = −13.5 meV, m1 = 25 eV ⋅ Å2, v = 2.67 eV ⋅ Å, μ = 100 meV, g = 23. And other parameters are aL = 16 Å and Δ0 = 1 meV
Topological LO state
To understand the topological nature of the system, we will develop a general theoretical framework for topological LO state. We focus on the general BdG Hamiltonian (6), here \({\cal H}_{ee}\) needs not to be specified. Due to the periodicity of the gap function Δ(y) = Δ(y + 2π/Q) in \({\cal H}_{ee}\), we can expand \({\mathrm{\Delta }}(y) = \mathop {\sum}\nolimits_n {\mathrm{\Delta }}_ne^{inQy}\) with the wave-vector Q and an integer n. Only one Δn is non-zero in the FF state while multiple non-zero Δn exist in the LO state. Consequently, \({\cal H}_{{\mathrm{BdG}}}\) can also be expanded in the momentum space as \(\left( {{\cal H}_{ee}} \right)_{nm} = \delta _{nm}{\cal H}_0(k_x,nQ + k_y)\), \(\left( {{\cal H}_{hh}} \right)_{nm} = - \delta _{nm}{\cal H}_0^ \ast ( - k_x,nQ - k_y)\) and \(\left( {{\cal H}_{eh}} \right)_{nm} = {\mathrm{\Delta }}_{n + m}\) (n, m are integers) on the basis \(\left| {e_n} \right\rangle\) and \(\left| {h_n} \right\rangle\) with the wave-vector nQ. Here, the momentum ky is within the reduced Brillouin zone [0,Q]. The Hamiltonian (6) possesses particle-hole symmetry \({\cal C} = t_x{\cal K}\) where the Pauli matrix tx acts on the particle-hole space and \({\cal K}\) is the complex conjugate. Based on the Hamiltonian (6), we can extract the topological property of FF state, as shown in Supplementary Note 5, which is consistent with the recent results on topological FF state in cold atom systems19,20,21,22.
Next, we focus on the LO state with non-zero Δ±1, for which the Hamiltonian (6) can be split into two decoupled blocks. All the electron part \({\cal H}_0(k_x,nQ + k_y)\) with even (odd) n is only coupled to the hole part \(- {\cal H}_0^ \ast ( - k_x,nQ - k_y)\) with odd (even) n. We call these two blocks as even and odd block, denoted as \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}\) and \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}\), respectively. Here, the even block is written on the basis \(\left| {e_{2n}} \right\rangle\) and \(\left| {h_{2n + 1}} \right\rangle\), while the odd block is written on the basis \(\left| {e_{2n - 1}} \right\rangle\) and \(\left| {h_{2n}} \right\rangle\). The global particle-hole symmetry \({\cal C}\) relates these two blocks, \({\cal C}{\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}{\cal C}^{ - 1} = - {\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}\), and thus there is in general no particle-hole symmetry within one block. However, at the momentum ky = Q/2, a new particle-hole symmetry operator \(\tilde {\cal C}\) can be defined as \(\tilde {\cal C}\left| {e_{2n}} \right\rangle = \left| {h_{2n + 1}} \right\rangle\) and \(\tilde {\cal C}\left| {h_{2n + 1}} \right\rangle = \left| {e_{2n}} \right\rangle\) for the even block \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}\) and \(\tilde {\cal C}\left| {e_{2n - 1}} \right\rangle = \left| {h_{2n}} \right\rangle\) and \(\tilde {\cal C}\left| {h_{2n}} \right\rangle = \left| {e_{2n - 1}} \right\rangle\) for the odd block \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}\), and we have \(\tilde {\cal C}{\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}(k_x,Q/2){\cal C}^{ - 1} = - {\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}( - k_x,Q/2)\) and \(\tilde {\cal C}{\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}(k_x,Q/2)\tilde {\cal C}^{ - 1} = - {\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}( - k_x, Q/2)\), as shown in Supplementary Note 5. The existence of this new particle-hole symmetry \(\tilde {\cal C}\) suggests that the Hamiltonian \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}\) and \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}\) at \(k_y = \frac{Q}{2}\) can be viewed as a 1D SC chain in the D class along the x direction. A \({\Bbb Z}_2\) topological invariant17 can be defined as,
where the anti-unitary matrix A is chosen as the BdG Hamiltonian \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}\) or \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}\) at \(k_y = \frac{Q}{2}\) in the Majorana representation. Here, \({\cal M} = - 1\) is for topologically non-trivial phase with a pair of MZM present, while \({\cal M} = + 1\) is for trivial phase. Thus, we conclude the existence of tLO state characterized by \({\Bbb Z}_2\) topological invariant due to the new particle-hole symmetry \(\tilde {\cal C}\) that is only valid at ky = Q/2.
Based on the above argument, we directly apply this general theory of tLO phase to the Hamiltonian in Eq. (6) that describes the bilayer SCing TI film, and evaluate the \({\Bbb Z}_2\) topological invariant \({\cal M}\) defined in Eq. (7). As we discussed early, there is a robust LO phase existing in this SCing system (see the phase diagram in Fig. 2a), and the corresponding ΔLO satisfies \({\mathrm{\Delta }}_{{\mathrm{LO}}}(y + 2\pi /Q) = {\mathrm{\Delta }}_{{\mathrm{LO}}}(y) = {\mathrm{\Delta }}_0 [- i\sqrt {1 - b^2} {\mathrm{sin}}(Qy)\sigma _y + b\,{\mathrm{cos}}\,(Qy)\tau _z\sigma _y]\), and thus we can directly evaluate \({\Bbb Z}_2\) topological invariant \({\cal M}\). Direct calculation and theoretical analysis described in Supplementary Note 6 suggest that \({\cal M} = - 1\) always exists in our model once the chemical potential is large enough, thus demonstrating the robust realization of the tLO phase in the bilayer SCing TI films. The non-trivial \({\Bbb Z}_2\) topological invariant suggests the existence of Majorana modes at the boundary of the system. As for the two decoupled BdG Hamiltonian (subspace) \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{even}}}\) and \({\cal H}_{{\mathrm{BdG}}}^{{\mathrm{odd}}}\) at \(k_y = \frac{Q}{2}\), there is a non-trivial \({\Bbb Z}_2\) topological invariant in each subspace. Therefore, two degenerate MZMs protected by the new particle-hole symmetry \(\tilde C\) can exist at one edge for the momentum \(k_y = \frac{Q}{2}\), which is consistent with numerical results in Fig. 3. Finally, we emphasize that tLO state with \({\Bbb Z}_2\) topological invariant belongs to a different topological class from tFF state with non-zero Chern number discussed in literature19,20 and thus possesses a different type of boundary mode, the MZM chain.
In the decoupling limit with mF → 0, the LO phase in our system can be viewed as two decoupled FF states, and each FF state can be adiabatically connected to the Fu-Kane model36 by tuning magnetic field to zero. It is well-understood that although Fu-Kane model can host Majorana zero mode inside the vortex core, it does not possess chiral Majorana edge state due to the time reversal symmetry. Since there are two FF states in our system, we expect two Majorana zero modes inside the vortex core and thus the statistics is no longer non-Abelian when exchanging two vortices. Therefore, our system possesses neither chiral (or helical) Majorana edge states nor non-Abelian statistics through exchanging vortex core in the decoupling limit. This also makes the tLO phase found here different from the tFF phase with chiral Majorana edge modes discussed in literature.
Discussion
In this work, we develop a general theory of tLO phase with \({\Bbb Z}_2\) classification and propose its realization in a theoretical model of bilayer SCing TI films. The tLO phase and the corresponding MZM chain also open a new route in the study of MZMs for topological quantum computation. The 1D MZM chain also provides a natural platform to study the interacting Majorana chains37,38. Below we will discuss the possible material realization of our model and the possible unique experimental signatures to distinguish the tLO phase from other topological SCing phase.
Our proposed model can be realized in SC/TI/SC heterostructure30,31,39, e.g., NbSe2/Bi2Te3/NbSe2 heterostructure. With Δ0 = 1 meV, μ = 100 meV, ℏv = 2.67 eV ⋅ Å, the g-factor g = 23, and mF = 20.1 meV, we can estimate the critical field at tricritical point to be about 0.15 Tesla according to gμBBc/kBTc,0 ≈ 0.35 from Fig. 2b. The distance between the two MZMs is estimated as ly = πℏv/4gμBBc ≈ 1.2 μm, which is four times larger than the localization length of MZMs \(\xi \sim \hbar v/{\mathrm{\Delta }}_0 = 0.27\,{\mathrm{\mu}} {\mathrm{m}}\, < \,l_y\). Thus, MZMs in the chain are well separated and can be resolved in a scanning tunneling microscope experiment39. The above estimate is based on Zeeman effect, but we emphasize that the orbital effect of in-plane magnetic fields can also plays a similar role as the Zeeman effect due to the Dirac fermion nature. Compared to the Zeeman effect, we find the orbital effect of an in-plane magnetic field can also induce the FFLO phase (the vector potential may be chosen as \(\vec A = (0, - B_xz,0)\) and set the middle of layers as z = 0 resulting in the opposite momentum shift for the Fermi surface of top and bottom surface states), and it is about \(\pi \hbar vd/2{\mathrm{\Phi }}_0\sim 0.91\,{\mathrm{meV/Tesla}}\) by assuming the space distance between two surfaces d = 3 nm, which is comparable to the Zeeman term with gμB = 1.33 meV/Tesla. One can also consider SC/magnetic TI/SC heterostructure, in which the exchange coupling from magnetic doping takes a similar form as Zeeman effect, but is two orders of magnitude larger than the Zeeman effect25. It should be mentioned that the 1D Z2 topological invariants at ky = Q/2 replies on the translation symmetry and the tLO phase is not robust against strong disorder scattering, thus requiring a relatively clean sample in experiments. We would like to mention a recent experiment on the evidence of finite momentum pairing induced by magnetic fields in HgTe quantum wells40 and 3D TI Bi2Se341 in proximity to superconductivity, and our results suggest the possibility of non-trivial topology of this finite momentum pairing. Based on the above estimate, we conclude that our proposal is feasible under the current experimental conditions.
Our proposal is also applicable to SCing TIs in which topological surface states and bulk superconductivity can coexist. Such materials include Cu doped Bi2Se342,43,44,45, several SCing half-Heusler compounds (e.g., YPtBi, RPdBi)46,47 and Fe(Te, Se) films48,49. We emphasize that the s-wave spin-singlet superconductivity has been demonstrated for the surface states of TI Fe(Te, Se) film49,50, which may provide a natural high-Tc SC platform to realize our model. In addition, odd parity pairing has been proposed in several of the above compounds26,51, and the influence of in-plane magnetic field will be interesting for a future study. Our work provides an example of the interesting interplay between finite momentum pairing and topological physics and similar idea also exists for exciton condensate52.
Finally, we hope to discuss how to unambiguously distinguish the tLO phase from other topological SCing phases, particularly the tFF phase, in experiments. The key difference lies in the fact that the chiral Majorana edge mode in the tFF phase can exist at any edge of the system while the MZM chain in the tLO phase can only exist at the edge perpendicular to the in-plane magnetic field. As shown in Fig. 4, we compare the local density of states (LDOS) at the edge when the in-plane magnetic field is perpendicular (blue lines) or parallel (red line) to the edge. The calculation details of LDOS can be found in Supplementary Note 7. A zero-bias peak is found for the perpendicular magnetic field direction, demonstrating the existence of MZM chain, while a full SCing gap is found for the parallel magnetic field. This calculation suggests that a simple scanning tunneling microscopy measurement of the edge LDOS with parallel and perpendicular magnetic fields can give rise to unambiguous experimental signature to identify the tLO phase and the MZM chain.
Experimental signature. The calculated local density of states (LDOS) \({\cal N}(E)\) at a fixed site (black point illustrated in a). In b, the red line is for the parallel magnetic field direction (By); while the blue line is for the perpendicular magnetic field direction (Bx). Parameters used here are the same as that in Fig. 3a c: m0 = −13.5 meV, m1 = 25 eV ⋅ Å2, v = 2.67 eV ⋅ Å, μ = 100 meV, g = 23, aL = 16 Å, Δ0 = 1 meV and Bx = By = 2.5 Tesla
Methods
In the Supplementary Note 1 and Supplementary Note 2, we review the Ginzburg–Landau theory and use the linearized gap equation to classify the possible SCing pairings of SCing TI thin films in the absence of magnetic field. Then, we show the details for the self-consistent calculation for the T − Bx phase diagram by minimizing the Ginzburg–Landau free energy in Supplementary Note 3, show how to construct the tight-binding model in Supplementary Note 4, analyze the calculation of topological invariant in Supplementary Note 6, and discuss how to calculate LDOS in Supplementary Note 7.
Data availability
The data and codes that support the findings of this study are available from the corresponding author upon reasonable request.
References
Fulde, P. & Ferrell, R. A. Superconductivity in a strong spin-exchange field. Phys. Rev. 135, A550–A563 (1964).
Larkin, A. & Ovchinnikov, I. Inhomogeneous state of superconductors(production of superconducting state in ferromagnet with fermi surfaces, examining green function). Sov. Phys.-JETP 20, 762–769 (1965).
Casalbuoni, R. & Nardulli, G. Inhomogeneous superconductivity in condensed matter and qcd. Rev. Mod. Phys. 76, 263–320 (2004).
Matsuda, Y. & Shimahara, H. Fulde–ferrell–larkin–ovchinnikov state in heavy fermion superconductors. J. Phys. Soc. Jpn. 76, 051005 (2007).
Radzihovsky, L. & Sheehy, D. E. Imbalanced feshbach-resonant fermi gases. Rep. Progress. Phys. 73, 076501 (2010).
Hatakeyama, Y. & Ikeda, R. Antiferromagnetic order oriented by fulde-ferrell-larkin-ovchinnikov superconducting order. Phys. Rev. B 91, 094504 (2015).
Kim, D. Y. et al. Intertwined orders in heavy-fermion superconductor cecoin5. Phys. Rev. X 6, 041059 (2016).
Agosta, C. C. et al. Calorimetric measurements of magnetic-field-induced inhomogeneous superconductivity above the paramagnetic limit. Phys. Rev. Lett. 118, 267001 (2017).
Adams, P. W., Nam, H., Shih, C. K. & Catelani, G. Zeeman-limited superconductivity in crystalline al films. Phys. Rev. B 95, 094520 (2017).
Kinnunen, J. J., Baarsma, J. E., Martikainen, J. -P. & Törmä, P. The fulde–ferrell–larkin–ovchinnikov state for ultracold fermions in lattice and harmonic potentials: a review. Rep. Progress. Phys. 81, 046401 (2018).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Tanaka, Y., Sato, M. & Nagaosa, N. Symmetry and topology in superconductors–odd-frequency pairing and edge states–. J. Phys. Soc. Jpn. 81, 011013 (2011).
Alicea, J. New directions in the pursuit of majorana fermions in solid state systems. Rep. Progress. Phys. 75, 076501 (2012).
Elliott, S. R. & Franz, M. Colloquium. Rev. Mod. Phys. 87, 137–163 (2015).
Sato, M. & Ando, Y. Topological superconductors: a review. Rep. Progress. Phys. 80, 076501 (2017).
Qi, X. -L., Hughes, T. L. & Zhang, S. -C. Chiral topological superconductor from the quantum hall state. Phys. Rev. B 82, 184516 (2010).
Kitaev, A. Y. Unpaired majorana fermions in quantum wires. Phys.-Uspekhi 44, 131 (2001).
Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Qu, C. et al. Topological superfluids with finite-momentum pairing and majorana fermions. Nat. Commun. 4, 2710 (2013).
Zhang, W. & Yi, W. Topological fulde–ferrell–larkin–ovchinnikov states in spin–orbit-coupled fermi gases. Nat. Commun. 4, 2711 (2013).
Wu, F., Guo, G. -C., Zhang, W. & Yi, W. Unconventional superfluid in a two-dimensional fermi gas with anisotropic spin-orbit coupling and zeeman fields. Phys. Rev. Lett. 110, 110401 (2013).
Cao, Y. et al. Gapless topological fulde-ferrell superfluidity in spin-orbit coupled fermi gases. Phys. Rev. Lett. 113, 115302 (2014).
Chan, C. et al. Generic theory for majorana zero modes in 2d superconductors. Phys. Rev. Lett. 119, 047001 (2017).
Lu, H. -Z., Shan, W. -Y., Yao, W., Niu, Q. & Shen, S. -Q. Massive dirac fermions and spin physics in an ultrathin film of topological insulator. Phys. Rev. B 81, 115407 (2010).
Yu, R. et al. Quantized anomalous hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Fu, L. & Berg, E. Odd-parity topological superconductors: Theory and application to cuxbi2se3. Phys. Rev. Lett. 105, 097001 (2010).
Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239 (1991).
Wang, M. -X. et al. The coexistence of superconductivity and topological order in the bi2se3 thin films. Science 336, 52–55 (2012).
Chen, Y. et al. Experimental realization of a three-dimensional topological insulator, bi2te3. Science 325, 178–181 (2009).
Xu, J. -P. et al. Artificial topological superconductor by the proximity effect. Phys. Rev. Lett. 112, 217001 (2014).
Xu, J. -P. et al. Experimental detection of a majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor bi 2 te 3/nbse 2 heterostructure. Phys. Rev. Lett. 114, 017001 (2015).
Wang, J. et al. Evidence for electron-electron interaction in topological insulator thin films. Phys. Rev. B 83, 245438 (2011).
Liu, C. -X. Unconventional superconductivity in bilayer transition metal dichalcogenides. Phys. Rev. Lett. 118, 087001 (2017).
Barzykin, V. & Gor’kov, L. P. Inhomogeneous stripe phase revisited for surface superconductivity. Phys. Rev. Lett. 89, 227002 (2002).
Dimitrova, O. & Feigel’man, M. Theory of a two-dimensional superconductor with broken inversion symmetry. Phys. Rev. B 76, 014522 (2007).
Fu, L. & Kane, C. L. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Rahmani, A., Zhu, X., Franz, M. & Affleck, I. Emergent supersymmetry from strongly interacting majorana zero modes. Phys. Rev. Lett. 115, 166401 (2015).
Chiu, C. -K., Pikulin, D. I. & Franz, M. Strongly interacting majorana fermions. Phys. Rev. B 91, 165402 (2015).
Sun, H. -H. et al. Majorana zero mode detected with spin selective andreev reflection in the vortex of a topological superconductor. Phys. Rev. Lett. 116, 257003 (2016).
Hart, S. et al. Controlled finite momentum pairing and spatially varying order parameter in proximitized hgte quantum wells. Nat. Phys. 13, 87–93 (2017).
Chen, A. Q. et al. Finite momentum cooper pairing in three-dimensional topological insulator josephson junctions. Nat. Commun. 9, 3478 (2018).
Wray, L. A. et al. Observation of topological order in a superconducting doped topological insulator. Nat. Phys. 6, 855–859 (2010).
Hor, Y. S. et al. Superconductivity in cuxbi2se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010).
Kriener, M., Segawa, K., Ren, Z., Sasaki, S. & Ando, Y. Bulk superconducting phase with a full energy gap in the doped topological insulator cuxbi2se3. Phys. Rev. Lett. 106, 127004 (2011).
Matano, K., Kriener, M., Segawa, K. & Ando, Y. & Zheng, G.-q. Spin-rotation symmetry breaking in the superconducting state of cuxbi2se3. Nat. Phys. 12, 852–854 (2016).
Lin, H. et al. Half-heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 9, 546–549 (2010).
Nakajima, Y. et al. Topological rpdbi half-heusler semimetals: A new family of noncentrosymmetric magnetic superconductors. Sci. Adv. 1, e1500242 (2015).
Yin, J. et al. Observation of a robust zero-energy bound state in iron-based superconductor fe (te, se). Nat. Phys. 11, 543–546 (2015).
Zhang, P. et al. Observation of topological superconductivity on the surface of an iron-based superconductor. Science 360, 182–186 (2018).
Wang, D. et al. Evidence for majorana bound states in an iron-based superconductor. Science 362, 333–335 (2018).
Nakosai, S., Tanaka, Y. & Nagaosa, N. Topological superconductivity in bilayer rashba system. Phys. Rev. Lett. 108, 147003 (2012).
Seradjeh, B. Topological exciton condensatbilayer system and phasee of imbalanced electrons and holes. Phys. Rev. B 85, 235146 (2012).
Acknowledgements
It is a pleasure to thank Cheung Chan, Chuang Li, James Jun He, Jia-Bin Yu, Jian-Xiao Zhang, and Rui-Xing Zhang for the helpful discussions. C.-X.L. acknowledges the support from Office of Naval Research (Grant No. N00014-15-1-2675 and renewal No. N00014-18-1-2793), as well as the Pennsylvania State University Two-Dimensional Crystal Consortium—Materials Innovation Platform (2DCC-MIP), which is supported by NSF cooperative Agreement No. DMR-1539916. F.-C.Z. is partly supported by NSFC grant 11674278 and National Basic Research Program of China (Grant No. 2014CB921203) and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB28000000) and Beijing Municipal Science & Technology Commission project No. Z181100004218001.
Author information
Authors and Affiliations
Contributions
L.-H.H. performed all the calculation. C.-X.L. and F.-C.Z. supervised this project. All the authors participated in the discussion and the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, LH., Liu, CX. & Zhang, FC. Topological Larkin-Ovchinnikov phase and Majorana zero mode chain in bilayer superconducting topological insulator films. Commun Phys 2, 25 (2019). https://doi.org/10.1038/s42005-019-0126-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0126-8
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.