Abstract
Atomically thin transition metal dichalcogenides can be stacked to van der Waals heterostructures enabling the design of new materials with tailored properties. The strong Coulomb interaction gives rise to interlayer excitons, where electrons and holes are spatially separated in different layers. In this work, we reveal the time- and momentum-dependent elementary processes behind the formation, thermalization and photoemission of interlayer excitons for the exemplary MoSe2–WSe2 heterostructure. We identify tunneling of holes from MoSe2 to WSe2 on a ps timescale as the crucial process for interlayer exciton formation. We also predict a drastic reduction of the formation time as a function of the interlayer energy offset suggesting that interlayer excitons can be externally tuned. Finally, we explain the experimental observation of a dominant photoluminescence from interlayer excitons despite the vanishingly small oscillator strength as a consequence of huge interlayer exciton occupations at low temperatures.
Similar content being viewed by others
Introduction
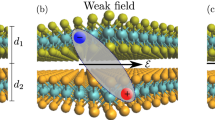
A direct band gap in the optical range, efficient electron-light coupling and a remarkably strong Coulomb interaction make transition metal dichalcogenides (TMDs) highly interesting materials for both fundamental research and technological applications1,2,3,4,5,6. Tightly bound excitons, quasi-particles of Coulomb-bound electron-hole pairs, dominate the optical response of these materials7,8,9,10,11,12,13,14. They have binding energies that are one to two orders of magnitude larger than in conventional materials15,16. As a result, excitonic features are stable at room temperature and dominate the optical response and non-equilibrium dynamics in TMDs. Besides regular bright excitons, TMDs also exhibit a variety of optically forbidden dark excitons17,18,19,20,21,22,23,24, which cannot be addressed optically due to the required momentum transfer or spin flip. The fascinating exciton physics becomes even richer, when considering that atomically thin materials can be vertically stacked to form Van der Waals (vdW) heterostructures1. In these systems the strong Coulomb interaction gives rise to interlayer excitons, where the involved electrons and holes are located in different layers (Fig. 1)25,26,27,28,29. After optical excitation of a regular intralayer exciton (IaX), the hole can tunnel to the other layer forming an interlayer exciton (IeX). Due to an offset in the alignment of the monolayer band structures (type II heterostructures), these interlayer excitons lie energetically below the excitons confined within one layer29 (Fig. 1). Depending on spin and momentum of the states involved, interlayer excitons can be either bright or dark. VdW heterostructures present an emerging field of research, as evidenced by an increasing number of studies, in particular demonstrating the appearance of interlayer excitons in photoluminescence (PL) spectra25,26,28,30,31,32,33,34,35,36,37,38,39. In the low-temperature regime, a pronounced additional resonance is observed at an energy below the intralayer excitons of the single layers26,27,33,40,41. The PL intensity of this low-energy peak is very pronounced compared to the intralayer exciton in the weak excitation regime. This behavior can be traced back to formation of interlayer excitons that due to their spectral position are highly occupied. Furthermore, in time-resolved PL measurements a spectrally narrow resonance was observed exhibiting lifetimes of tens to hundreds of nanoseconds26,27,33,40,41. Theoretical studies of vdW heterostructures have so far been primarily restricted to static observables, such as screening42, excitonic binding energies29, and lattice mismatch effects35. Microscopic insights into the ultrafast dynamics of interlayer excitons have remained literally in the dark yet.
Formation of interlayer excitons. After optically exciting a coherent intralayer exciton (IaX, red oval), incoherent excitons are formed assisted by emission and absorption of phonons. Hole tunneling subsequently converts these into incoherent interlayer excitons (IeX, blue oval). After exciton and thermalization through scattering with phonons, most excitons occupy the energetically lowest interlayer excitonic state EIeX with vanishing center-of mass-momentum. Both IaX and IeX decay radiatively resulting in photoluminescence (PL). The investigated type II heterostructure shows an interlayer energy offset ΔE
In this work, we present a comprehensive microscopic study of the ultrafast kinetics of excitons in vdW heterostructures, in particular revealing the elementary time-resolved and energy-resolved processes behind the formation, thermalization and decay of interlayer excitons. We predict the binding energy of 150 meV for the energetically lowest interlayer excitonic state in the exemplary MoSe2–WSe2 heterostructure, as well as a significant reduction of intralayer binding energies by about 30% due to the increased screening within a heterostructure. Moreover, we shed light on the exciton dynamics demonstrating that excited interlayer excitons are formed via hole tunneling on a picosecond timescale, followed by a phonon-driven relaxation to the ground state on a femtosecond timescale. The radiative interlayer recombination is by orders of magnitude slower reflecting the small oscillator strength of spatially separated excitons. Finally, we provide a microscopic explanation for the recently performed time-resolved photoluminescence experiments demonstrating the surprisingly dominant contribution of interlayer excitons at low temperatures.
Results
Theoretical approach
We investigate the exemplary MoSe2–WSe2 heterostructure on a typical SiO2 substrate. To bring the system into a non-equilibrium, we apply a laser pulse at the energy resonant to the 1s exciton of the MoSe2 layer. We restrict the study to 1s excitons consisting of Coulomb-bound electrons and holes located at the K point of the Brillouin zone.
To provide microscopic access to the dynamics of the coupled excitons, phonons and photons, we apply the density matrix formalism43,44,45,46 and derive the luminescence Bloch equations explicitly including excitonic effects9,44. The emitted luminescence intensity Iω(t) is obtained from the temporal change of the photon density and reads44,47.
Here, \(M_{\mathbf{0}}^{l_{\mathrm{h}}l_{\mathrm{e}}}\) is the optical matrix element for excitons that are composed of electrons in layer le and holes in layer lh. The index 0 indicates that only excitons with vanishing center-of-mass momentum Q = 0 contribute to PL. While the optical matrix element can be obtained analytically using a tight-binding approach for TMD monolayers and adjusting the coupling strength to experimentally measured absorption9,22, first-principle calculations have been performed to determine the coupling for interlayer excitons. The Lorentzian \({\cal L}_\gamma\) accounts for energy conservation, i.e., an exciton decays into a photon with the same energy. We calculate on a microscopic level the components of the dephasing rate γ stemming from exciton-phonon and exciton-photon interactions22,48. At lower temperatures disorder-induced dephasing becomes important and has been accounted for phenomenologically by using the full width at half maximum (FWHM) values measured in ref. 27.
The PL strength is determined by the excitonic polarization \(P_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}(t)\) reflecting the optically driven coherence (often referred to as coherent excitons43,44) and by the exciton occupation \(N_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}\) describing the formation and thermalization of incoherent excitons induced by a non-radiative decay of the excitonic polarization. Equations of motion for \(P_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}(t)\) and \(N_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}\) are derived in the low density regime taking into account exciton-photon coupling giving rise to a spontaneous radiative decay of excitons as well as exciton-phonon coupling allowing for a relaxation of the excited hot exciton distribution into a thermal equilibrium. Furthermore, we take into account the tunneling of carriers between layers. This process is included via the tunneling Hamilton operator \(H_{\mathrm{T}} = \mathop {\sum}\nolimits_{a,b} T^{ab}a_b^\dagger a_b\), where a, b are compound indices containing layer, band and momentum of the electron. The coupling element T is given by the overlap integral 〈Ψa|VT|Ψb〉 of Bloch waves Ψ with the interlayer potential VT. The appearing spatial overlap of the wavefunctions from different layers is obtained from density functional theory calculations that have been carried out using the gpaw package49. More details on the calculation of the tunneling matrix element can be found in the methods section. Finally, applying the Heisenberg equation of motion, we obtain the luminescence Bloch equations for the excitonic polarization \(P_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}(t)\) and the incoherent exciton occupation \(N_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}\), see Eqs. (2) and (3) in the methods section. Numerical solution of this coupled set of differential equations provides microscopic access to time-resolved and momentum-resolved formation, relaxation, and radiative decay dynamics of intralayer and interlayer excitons. It allows us to calculate the photoluminescence of heterostructures as a function of time and energy.
Excitonic band structure
The excitonic eigenenergies and wave functions are obtained by solving the Wannier equation9,43,46 (Equation (1) in the methods section). To obtain the interaction potential between charge carriers in a heterostructure, we generalize the widely used Keldysh potential for the monolayer case9,50. We solve the Poisson equation for two aligned homogeneous slabs (Supplementary Fig. 1 and Supplementary Note 1 for more details). The obtained excitonic band structure and the corresponding excitonic wave functions are shown in Fig. 2 for the three energetically lowest excitonic states (1s, 2s, 3s) for intralayer and interlayer excitons. Here, the electronic band alignment has been extracted from PL measurements26,27. We find that the interlayer exciton is the energetically lowest state at 1.39 eV, while the intralayer excitons lie at 1.65 eV (MoSe2) and 1.75 eV (WSe2), Fig. 2. The resulting excitonic binding energies are displayed in Table 1. As expected, the binding energy for interlayer excitons is reduced (150 meV for 1s) compared to the value for intralayer excitons (205 meV for MoSe2 and 177 eV for WSe2), however it is still much larger than the thermal energy. Thus, interlayer excitons are expected to be stable at room temperature and significantly contribute to the PL. Our calculations also reveal that the binding energy of intralayer excitons is considerably reduced by roughly 30% when the monolayers are stacked into a heterostructure (Table 1). This is due to an increased screening of the Coulomb potential. These results are consistent with previous theoretical studies based on DFT calculations29,37.
Exciton dynamics
Solving the luminescence Bloch equations (the Methods section) we can resolve the dynamics of intralayer and interlayer excitons. Figure 3a shows the temporal evolution of exciton densities, i.e., momentum-integrated exciton occupations \(n = \mathop {\sum}\nolimits_{\mathbf{Q}} N_{\mathbf{Q}}\), at the exemplary temperature of 77 K (Supplementary Fig. 3 and Supplementary Note 3 for 4 K and room temperature). The system is excited by a 100 fs long Gaussian pulse centered at 0.5 ps and a frequency resonant to the intralayer 1s exciton of the MoSe2 layer. We find that the optically excited coherent excitons (dashed red line in Fig. 3) decay on a timescale of hundreds of femtoseconds due to radiative emission and exciton-phonon scattering. The latter leads to the formation of incoherent intralayer excitons (IaX) through the so-called polarization-to-population transfer23,43,51,52. After about 10 ps, these intralayer excitons are completely transferred to interlayer excitons (IeX). This occurs through tunneling between energetically resonant states of the two layers and results in a transfer of holes to the WSe2 layer (Fig. 1). The subsequent phonon-induced relaxation of holes in the WSe2 layer to the valence band maximum effectively traps the holes within that layer, since tunneling back to MoSe2 is energetically forbidden. The resulting interlayer excitons have lifetimes orders of magnitudes longer than the intralayer excitons, since recombination mechanisms are suppressed due to the spatial separation of Coulomb-bound electrons and holes. We predict an interlayer exciton lifetime in the range of hundreds of microseconds at 77 K. Experimentally measured sub-nanosecond values27 suggest that the investigated radiative decay is not the dominant channel, but rather non-radiative decay e.g., induced by disorder might play the crucial role.
Momentum-integrated exciton dynamics. a Evolution of the MoSe2 intralayer (IaX) and the interlayer (IeX) 1s exciton density at 77 K after resonant excitation of the MoSe2 layer. The optical pulse is denoted by the blue-shaded Gaussian. The dashed line represents coherent excitons in the MoSe2 layer. The interlayer exciton formation occurs on a ps timescale. The radiative lifetime determining the decay of exciton densities is in the order of microseconds. b IeX formation time τ as a function of the interlayer energy offset ΔE and the temperature T. The vertical dashed line denotes the interlayer energy offset of the investigated MoSe2–WSe2 heterostructure
To provide the microscopic background of the exciton formation and thermalization process, we now show the time-resolved and energy-resolved dynamics of incoherent intralayer and interlayer excitons. Figure 4a illustrates how 1s intralayer excitons (IaX) are created in the MoSe2 layer after optical excitation at 0.5 ps. The process is followed by a phonon-assisted thermalization and tunneling-driven depletion of these excitons. The main features of these dynamics are illustrated in representative snapshots along the energy axis at fixed times (Fig. 4b). At 0.6 ps, a significant number of excitons is still located in the MoSe2 layer. The distribution is in a strong non-equilibrium due to the efficient polarization-to-population transfer, i.e., the excitonic polarization is converted into incoherent exciton occupations with non-vanishing center-of-mass momentum. This is the origin of the observed peaks (green line in Fig. 4b) corresponding to the position of intersections of exciton and phonon dispersion. After the coherence has decayed (1 ps), the occupation starts to thermalize into a Boltzmann distribution (blue line). The occupation within the light cone centered around the exciton dispersion minimum E0 = 1.65 eV is lowered as a result of radiative recombination. Furthermore, tunneling of holes to the WSe2 layer causes a considerable decay of the intralayer exciton occupation (black line). Finally, the temporal evolution of the exciton occupation at a fixed energy corresponding to the 1s resonance of intralayer excitons (1.65 eV) is shown in Fig. 4c. This occupation represents the optically active exciton with vanishing center-of-mass momentum. We see how intralayer excitons are created already during the optical excitation and how they decay on a ps timescale due to tunneling of holes into the neighboring WSe2 layer.
Energy-resolved and time-resolved intralayer exciton dynamics. Temporal evolution of the intralayer exciton (IaX) occupation N at 77 K after resonant excitation of the MoSe2 monolayer. a The surface plot shows N as a function of time and energy, while b, c illustrate exemplary snapshots along energy and time axes (corresponding to dashed lines in a), respectively. Through exciton-phonon scattering the system equilibrates into a Boltzmann-like distribution, which decreases in amplitude due to radiative recombination and interlayer tunneling
Figure 5a illustrates the corresponding dynamics of interlayer excitons (IeX). They first emerge at E = E0 corresponding to the energy of intralayer excitons in MoSe2. The exciton population generated at this discrete energy consequently relaxes to the band minimum of the interlayer dispersion mostly by emitting LO and TO phonons in MoSe2, which have approximately a constant energy of 36 meV. This yields a cascade-like redistribution of excitons through intermediate energy levels after a series of optical phonon emissions. The slow interaction with acoustic phonons, which provide a continuous range of energies, leads to a smoothing of the occupation distribution, but on a much larger time-scale. The energy conserving nature of the tunneling interaction eventually forces the entire system into a single Boltzmann-like distribution as can be seen in Fig. 5b, spanning over both intralayer and interlayer excitonic states.
Energy-resolved and time-resolved interlayer exciton dynamics. Temporal evolution of the interlayer exciton (IeX) occupation N at 77 K after resonant excitation of the MoSe2 monolayer. a The surface plot shows N as a function of time and energy, while b, c illustrate exemplary snapshots along energy and time axes (corresponding to dashed lines in a), respectively. After appearing around E0 from interlayer tunneling, the interlayer excitons relax through phonon scattering
Figure 5c is analogous to Fig. 4c, and depicts the temporal evolution of interlayer excitons at fixed energies. The green curve first shows how the interlayer exciton occupation at the energy 1.65 eV resonant to the intralayer exciton rises with its intralayer counterpart. Driven by scattering with phonons, excitons then accumulate at the minimum of the dispersion at 1.39 eV (orange curve).
It should be noted that the exciton-phonon scattering has an important effect on the effective tunneling rate. Since the tunneling interaction is symmetric, the effective interlayer tunneling rate is quenched by back-tunneling from energy-allowed states. On a short timescale, the impact is mostly determined by the rate of the phonon-induced down-scattering (Fig. 5). As the Boltzmann distribution is formed (Fig. 5b), the temperature starts becoming an important factor. The spectral width of the IeX distribution increases at enhanced temperatures, leading to more excitons available for back-tunneling. Nevertheless, for the investigated heterostructure the change in temperature has still a relatively small effect on the IeX formation time τ. We find a reduction of τ by approximately 200 fs from 4 K to 200 K, after which it remains nearly constant up to room temperature (Fig. 3b).
The interlayer energy offset ΔE in type II heterostructures (Fig. 1) turns out to be a crucial quantity for the IeX formation time. For the investigated MoSe2–WSe2 heterostructure, the offset reads 315 meV and results in an IeX formation time τ = 2.61 ps at room temperature. The latter is defined as the elapsed time between the pump pulse maximum and the IeX density reaching 1 − e−1 of its maximum value. Increasing (decreasing) the offset by 100 meV, the formation time becomes considerably enhanced to τ = 4.91 ps (reduced to τ = 0.69 ps). This behavior can be ascribed to the reduced (enhanced) tunneling rate reflecting the increased (decreased) momentum transfer, as the interlayer energy offset ΔE becomes larger (smaller). To put it in other words, the spectral overlap of the wavefunctions of the involved states in different layers is highly sensitive to ΔE. The larger the overlap (small ΔE), the more efficient is the tunneling and the faster is the formation time. The disorder-assisted momentum transfer function (Methods) also decreases with increasing ΔE. For this reason tunneling to the higher excitonic states might be non-negligible considering their lower binding energies, and will have to be addressed in a future study.
A modification of the interlayer energy offset could be e.g., achieved by introducing a doping of a single layer26 suggesting that the IeX formation time in heterostructures can be externally tuned. Furthermore, the interlayer wavefunction overlap and the tunneling rate could be tuned by modifying the substrate-induced screening. The smaller the dielectric constant, the stronger is the Coulomb interaction and the broader are the excitonic wavefunctions in the reciprocal space resulting in a more efficient tunneling. Finally, different layer stackings can also have a significant effect on the tunneling rate, as demonstrated by ref. 38 predicting formation times ranging from ps to sub-ps timescales.
Photoluminescence
The exciton dynamics discussed above determines the light emission from the heterostructure. Figure 6a shows the time-resolved and energy-resolved PL spectrum at the exemplary temperature of 77 K in (Supplementary Fig. 4 and Supplementary Note 3 for 4 and 300 K). We find that in the first few ps, the emission from intralayer excitons (IaX) at 1.65 eV clearly dominates the PL. However, after approximately 41 ps, the contribution of interlayer excitons becomes pronounced. To better understand the underlying processes, we show again snapshots at fixed times and energies in Fig. 6b, c, respectively. The emission stemming from the intralayer exciton at 1.65 eV (red line in Fig. 6c) shows a maximum PL intensity in the first hundreds of femtoseconds originating from the efficient coherent emission (radiative decay of polarization on a fs timescale). The following slower decay on a time scale of tens of ps reflects the decrease of intralayer excitons due to hole tunneling to the WSe2 layer. In this time, interlayer excitons are formed (solid blue line in Fig. 6c). After approximately 41 ps, the contribution of the interlayer exciton surpasses the emission from the intralayer exciton. Snapshots of the energy-dependent PL along these characteristic times further demonstrate by far most pronounced coherent IaX emission (orange line, 0.6 ps), the reduced emission due to incoherent IaX (red, 1 ps), equal IaX and IeX emission (blue, 41 ps), and finally the dominant IeX emission (purple, 65 ps).
Time-resolved and energy-resolved photoluminescence. PL of the investigated heterostructure at 77 K plotted a over time and energy (logarithmic) and showing snapshots taken at specific b times and c energies. The chosen energies correspond to the position of the interlayer (IeX) and MoSe2 intralayer (IaX) exciton resonance, respectively. The solid lines in c represent the signals stemming from the interlayer or intralayer emission only, while the dashed lines also include the spectral overlap with the respective other peak
After 60 ps an equilibrium situation is reached that is characterized by a constant IaX–IeX intensity ratio of approximately 100 (dashed lines in Fig. 6c). This is determined by the ratio of the square of the corresponding optical matrix elements |MIeX|2/|MIaX|2 and exciton occupations \(N_0^{{\mathrm{IeX}}}/N_0^{{\mathrm{IaX}}}\) within the light cone. Since the occupations are described by a Boltzmann distribution in equilibrium, we can explicitly calculate the temperature, at which the PL ratio is 1. We find that the interlayer exciton emission dominates until approximately 200 K. Above this temperature, the thermal occupation of energetically higher intralayer excitons increases and considering the significantly larger optical matrix element for intralayer emission, the intralayer peak exceeds the emission from the interlayer exciton.
A recent DFT study37 on MoSe2/WSe2 heterostructures suggests that the interlayer coupling might shift the Λ valley below the K valley in both layers, giving rise to a momentum mismatch between the lowest conduction and the highest valence band in the heterostructure. The resulting enhanced occupation of momentum-forbidden dark interlayer excitons and their impact on luminescence spectra (e.g., via phonon-assisted recombination) is of particular interest for future studies. In particular, for tungsten-based heterostructures the inclusion of other high-symmetry points of the Brillouin zone is expected to be important to capture the entire interlayer exciton dynamics41,53,54
Discussion
In conclusion, we have presented a microscopic view on the dynamics of inter- and intralayer excitons in van der Waals heterostructures. Solving the Wannier equation, we report a binding energy of 150 meV for the interlayer exciton as well as a clear 30% reduction of the binding energy of the intralayer excitons due to the enhanced screening within a heterostructure. Solving the luminescence Bloch equations, we reveal the time-resolved and energy-resolved processes behind the formation, thermalization, and decay of interlayer excitons. We predict that tunneling of holes from the optically excited into the neighboring layer is the dominant formation channel occurring on a picosecond timescale. We demonstrate the crucial role of phonons in both their formation and subsequent relaxation dynamics. Furthermore, we suggest a possibility to externally tune the formation time of interlayer excitons by changing the interlayer energy offset in the type II heterostructure. Finally, we show that although the light emission from interlayer excitons is strongly quenched due to the spatial separation of charge carriers, they actually dominate the photoluminescence spectrum of heterostructures at temperatures below 200 K. The gained insights will trigger new experimental studies on van der Waals heterostructures. In particular, the predicted formation dynamics of interlayer excitons can be experimentally addressed by pumping and probing the intralayer exciton transition in different layers, where a clear bleaching is expected due to the efficient interlayer tunneling.
Methods
Binding energies
To model the interlayer exciton dynamics in heterostructures, we derive the luminescence Bloch equations for the excitonic polarization \(P_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}(t) = \mathop {\sum}\nolimits_{\mathbf{q}} \varphi _{\mathbf{q}}^{ \ast l_{\mathrm{h}}l_{\mathrm{e}}}\left\langle {v_{{\mathbf{q}} + \beta ^{l_{\mathrm{h}}l_{\mathrm{e}}}{\mathbf{Q}}}^{\dagger l_{\mathrm{h}}}c_{{\mathbf{q}} - \alpha ^{l_{\mathrm{h}}l_{\mathrm{e}}}{\mathbf{Q}}}^{l_{\mathrm{e}}}} \right\rangle\) and the incoherent exciton occupation \(N_{\mathbf{Q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}(t) = \mathop {\sum}\nolimits_{{\mathbf{q,q}}\prime } \varphi _{{\mathbf{q}}\prime }^{ \ast l_{\mathrm{h}}l_{\mathrm{e}}}\phi _{\mathbf{q}}^{l_{\mathrm{h}}l_{\mathrm{e}}}\delta \left\langle {c_{{\mathbf{q}} - \alpha ^{l_{\mathrm{h}}l_{\mathrm{e}}}{\mathbf{Q}}}^{\dagger l_{\mathrm{e}}}v_{{\mathbf{q}} + \beta ^{l_{\mathrm{h}}l_{\mathrm{e}}}{\mathbf{Q}}}^{l_{\mathrm{h}}}v_{{\mathbf{q}}\prime + \beta ^{l_{\mathrm{h}}l_{\mathrm{e}}}{\mathbf{Q}}}^{\dagger l_{\mathrm{h}}}c_{{\mathbf{q}}\prime - \alpha ^{l_{\mathrm{h}}l_{\mathrm{e}}}{\mathbf{Q}}}^{l_{\mathrm{e}}}} \right\rangle (t)\) corresponding to electron-hole pair correlations44. Here, we have introduced φq as excitonic wavefunctions in momentum space, \(v^{(\dagger )},c^{(\dagger )}\) as operators for annihilation (creation) of valence- and conduction band electrons as well as relative q and center-of-mass momenta Q with the coefficients α = me/(mh + me) and β = mh/(mh + me) describing the relative electron and hole masses.
To obtain the excitonic binding energies and wave functions, we solve the Wannier equation9,43,46
where μ is the reduced mass, Eb the excitonic binding energy, and \(V_{\mathbf{k}}^{l_{\mathrm{h}}l_{\mathrm{e}}}\) the Coulomb matrix element for the electron-hole interaction. Solving the Poisson equation for two aligned homogeneous slabs, we obtain an effective 2D Coulomb potential \(V_{\mathbf{k}}^{l_{\mathrm{h}}l_{\mathrm{e}}} = \frac{{e_0^2}}{{k\varepsilon _0\varepsilon ^{l_{\mathrm{h}}l_{\mathrm{e}}}({\mathbf{k}})}}\) with a dielectric function \(\varepsilon ^{l_{\mathrm{h}}l_{\mathrm{e}}}({\mathbf{k}})\), depending on the momentum transfer k and the overall composition of the heterostructure, Supplementary Note 1 for more details.
Dynamics
Equations of motion for the exciton polarization and the exciton occupations are derived taking into account all relevant interaction mechanisms in the low density regime. The carrier-phonon matrix elements are taken from DFT calculations55 and are treated in analogy to refs. 22,23,52. The interaction mechanism that distinguishes the exciton dynamics in a vdW heterostructure from the dynamics in a bare TMD monolayer is the tunneling of carriers between layers. This process is included via the tunneling Hamilton operator \(H_T = \mathop {\sum}\nolimits_{a,b} T^{ab}a_b^\dagger a_b\), where a, b are compound indices containing layer, band and momentum of the electron. The coupling element T is given by the overlap integral 〈Ψa|VT|Ψb〉 of Bloch waves Ψ with the interlayer potential VT. The latter can be separated into an out-of-plane component Vz and an in-plane disorder potential Vρ56. The first is given by a step function, which is only non-zero within the region between the two layers and its value was fixed to 5 eV corresponding to the ionization energy of TMD monolayers57,58. The tunneling matrix element can then be expressed as Tab = Vρ(|kb − ka|)Vz 〈ua|ub〉uc, where u are the lattice-periodic parts of the Bloch waves, which are integrated over one unit cell (uc). This integral was obtained from density functional theory calculations, yielding an overlap of approximately 1 × 10−2. The calculations were carried out using the gpaw package49. The wave function was expanded on a grid and exchange-correlation effects were represented using the PBE exchange-correlation functional59. The details behind this process are written in Supplementary Note 4. Finally, the Fourier transform of the in-plane component of the disorder potential reads56 \(V_\rho (|{\mathbf{k}}_b - {\mathbf{k}}_a|) = \sqrt \pi L_{\mathrm{C}}/\left( {1 + \frac{{|{\mathbf{k}}_b - {\mathbf{k}}_a|^2L_{\mathrm{C}}^2}}{2}} \right)^{\frac{3}{4}}\) with LC as the correlation length. It has been set to 1 nm in accordance with the excitonic Bohr radius60, an approximation that applies for short-range disorder61,62.
Applying the Heisenberg equation of motion, we obtain the luminescence Bloch equations for vdW heterostructures
where the excitonic compound indices α, β contain center of mass momentum and electron/hole layers. The dynamics of the exciton polarization Pα(t) is determined by the Rabi frequency Ωα containing the driving optical pump pulse and the decay processes stemming from radiative damping \(\left( {\gamma _{\mathrm{r}}^\alpha } \right)\) and exciton-phonon interaction \(\left( {\Gamma _{\mathrm{P}}^{\alpha \beta }} \right)\). The latter has been obtained by truncating the electron-phonon interaction by a second order Born-Markov approximation44,46, giving rise to energy-dependent scattering rates. Those incorporate all exciton-phonon scattering channels, i.e., all energy allowed exciton transitions, weighted by the excitonic scattering cross-sections, electron-phonon couplings and the occupations of involved phonon modes. The dynamics of the incoherent exciton occupation Nα(t) is determined by formation processes driven by phonon-assisted decay of the excitonic polarization, the radiative decay, and exciton-phonon scattering \(\left( {N_\alpha ^{{\mathrm{scatt}}}} \right)\) driving the excited system towards an equilibrium Boltzmann distribution23,52. Note that that radiative decay scales with Nα,0 = NαδQ,0, where only states within the light cone with a nearly zero center-of-mass momentum Q = 0 can contribute. Finally, \(\Gamma _{\mathrm{T}}^{\alpha \beta }\) describes resonant tunneling between different layers. It depends on the occupation difference (ΔNαβ = Nβ − Nα) of the involved excitonic states and causes the formation of interlayer excitons. It was obtained by applying the same methodology as for \(\Gamma _{\mathrm{P}}^{\alpha \beta }\). The explicit form of the scattering rates is given in Supplementary Note 5.
Code availability
The code used to calculate the findings of this study is available from the corresponding author upon request.
Data availability
The data that supports the findings of this study is available from the corresponding author upon request.
References
Geim, A. K. & Grigorieva, I. V. Van der waals heterostructures. Nature 499, 419–425 (2013).
Wang, Q. H. et al. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2d semiconductor transition metal dichalcogenides. Nat. Photonics 10, 216–226 (2016).
Schaibley, J. R. et al. Valleytronics in 2d materials. Nat. Rev. Mater. 1, 16055 (2016).
Lopez-Sanchez, O. et al. Ultrasensitive photodetectors based on monolayermos2. Nat. Nanotechnol. 8, 497–501 (2013).
Pospischil, A. & Mueller, T. Optoelectronic devices based on atomically thin transition metal dichalcogenides. Appl. Sci. 6, 78 (2016).
Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012).
He, K. et al. Tightly bound excitons in monolayer wse2. Phys. Rev. Lett. 113, 026803 (2014).
Berghäuser, G. & Malic, E. Analytical approach to excitonic properties of mos2. Phys. Rev. B 89, 125309 (2013).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thinmos2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014).
Li, Y. et al. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: Mos2, mose2, ws2, and wse. Phys. Rev. B 90, 205422 (2014).
Steinhoff, A. et al. Efficient excitonic photoluminescence in direct and indirect band gap monolayer mos2. Nano Lett. 15, 6841–6847 (2015).
Wang, G. et al. Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Hanbicki, A. T., Currie, M., Kioseoglou, G., Friedman, A. L. & Jonker, B. T. Measurement of high exciton binding energy in monolayer transition-metal dichalcogenides ws2 and wse2. Solid State Commun. 203, 16–20 (2015).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic rydberg series in monolayer ws2. Phys. Rev. Lett. 113, 076802 (2014).
Arora, A. et al. Excitonic resonances in thin films ofwse2: from monolayer to bulk material. Nanoscale 7, 10421–10429 (2015).
Arora, A., Nogajewski, K., Molas, M., Koperski, M. & Potemski, M. Exciton band structure in layeredmose2: from a monolayer to the bulk limit. Nanoscale 7, 20769–20775 (2015).
Zhang, X.-X., You, Y., Zhao, S. Y. F. & Heinz, T. F. Experimental evidence for dark excitons in monolayer wse2. Phys. Rev. Lett. 115, 257403 (2015).
Zhang, X.-X. et al. Magnetic brightening and control of dark excitons in monolayer wse2. Nat. Nanotechnol. 12, 883–888 (2017).
Molas, M. R. et al. Brightening of dark excitons in monolayers of semiconducting transition metal dichalcogenides. 2D Mater. 4, 021003 (2017).
Selig, M. et al. Excitonic linewidth and coherence lifetime in monolayer transition metal dichalcogenides. Nat. Commun. 7, 13279 (2016).
Selig, M. et al. Dark and bright exciton formation, thermalization, and photoluminescence in monolayer transition metal dichalcogenides. 2D Mater. 5, 035017 (2018).
Feierabend, M., Berghäuser, G., Knorr, A. & Malic, E. Proposal for dark exciton based chemical sensors. Nat. Commun. 8, 14776 (2017).
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der waals heterostructures. Nat. Commun. 5, 4555 (2014).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2-Wse2 heterostructures. Nat. Commun. 6, 6242 (2015).
Nagler, P. et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 4, 025112 (2017).
Gao, S., Yan, L. & Spataru, C. D. Interlayer coupling and gate-tunable excitons in transition metal dichalcogenide heterostructures. Nano Lett. 17, 7809 (2017).
Latini, S., Winther, K. T., Olsen, T. & Thygesen, K. S. Interlayer excitons and band alignment in mos2/hbn/wse2 van der waals heterostructures. Nano Lett. 17, 938–945 (2016).
Yu, Y. et al. Equally efficient interlayer exciton relaxation and improved absorption in epitaxial and nonepitaxial mos2/ws2 heterostructures. Nano Lett. 15, 486 (2015).
Calman, E. V. et al. Indirect excitons in van der waals heterostructures at room temperature. Nat. Commun. 9, 1895 (2018).
Förg, M. et al. Cavity-control of bright and dark interlayer excitons in van der waals heterostructures. Preprint at https://arxiv.org/abs/1710.00990 (2017).
Nagler, P. et al. Giant zeeman splitting inducing near-unity valley polarization in van der waals heterostructures. Nat. Commun. 8, 1551 (2017).
Chaves, A., Azadani, J. G., Özçelik, V. O., Grassi, R. & Low, T. Electrical control of inter-layer excitons in van der waals heterostructures. Phys. Rev. B 98, 121302 (2018).
Wu, F., Lovorn, T. & MacDonald, A. H. Theory of optical absorption by interlayer excitons in transition metal dichalcogenide heterobilayers. Phys. Rev. B 97, 035306 (2018).
Manolatou, C., Wang, H., Chan, W., Tiwari, S. & Rana, F. Radiative and nonradiative exciton energy transfer in monolayers of two-dimensional group-vi transition metal dichalcogenides. Phys. Rev. B 93, 155422 (2016).
Gillen, R. & Maultzsch, J. Interlayer excitons in mose2/wse2 heterostructures from first principles. Phys. Rev. B 97, 165306 (2018).
Zhang, J. et al. Interlayer-state-coupling dependent ultrafast charge transfer in mos2/ws2 bilayers. Adv. Sci. 4, 1700086 (2017).
Hong, X. et al. Ultrafast charge transfer in atomically thin mos2/ws2 heterostructures. Nat. Nanotechnol. 9, 682–686 (2014).
Rivera, P. et al. Valley-polarized exciton dynamics in a 2d semiconductor heterostructure. Science 12, 688–691 (2016).
Miller, B. et al. Long-lived direct and indirect interlayer excitons in van der waals heterostructures. Nano Lett. 17, 5229–5237 (2017).
Florian, M. et al. The dielectric impact of layer distances on exciton and trion binding energies in van der waals heterostructures. Nano Lett. 18, 2725–2732 (2018).
Kira, M. & Koch, S. W. Many-body correlations and excitonic effects in semiconductor spectroscopy. Quantum Electron. 30, 155–296 (2006).
Thränhardt, A., Kuckenburg, S., Knorr, A., Meier, T. & Koch, S. W. Quantum theory of phonon-assisted exciton formation and luminescence in semiconductor quantum wells. Phys. Rev. B 62, 2706 (2000).
Rossi, F. & Kuhn, T. Theory of ultrafast phenomena in photoexcited semiconductors. Rev. Mod. Phys. 74, 895 (2002).
Haug, H. & Koch, S. W. Quantum Theory of the Optical and Electronic Properties of Semiconductors. 5 edn, (World Scientific Publishing Co. Pre. Ltd., Singapore, 2004).
Kira, M., Jahnke, F., Hoyer, W. & Koch, S. W. Quantum theory of spontaneous emission and coherent effects in semiconductor microstructures. Quantum Electron. 23, 189–279 (1999).
Moody, G. et al. Intrinsic homogeneous linewidth and broadening mechanisms of excitons in monolayer transition metal dichalcogenides. Nat. Commun. 6, 8315 (2015).
Enkovaara, J. et al. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. J. Phys. 22, 253202 (2010).
Keldysh, L. V. Coulomb interaction in thin semiconductor and semimetal films. JETP Lett. 29, 658 (1978).
Koch, S. W., Kira, M., Khitrova, G. & Gibbs, H. M. Semiconductor excitons in new light. Nat. Mater. 5, 523–531 (2006).
Brem, S., Berghaeuser, G., Selig, M. & Malic, E. Exciton relaxation cascade in two-dimensional transition-metal dichalcogenides. Sci. Rep. 8, 8238 (2018).
Kunstmann, J. et al. Momentum-space indirect interlayer excitons in transition-metal dichalcogenide van der waals heterostructures. Nat. Phys. 14, 801–805 (2018).
Hanbicki, A. T. et al. Double indirect interlayer exciton in a mose2/wse2 van der waals heterostructure. ACS Nano 12, 4719–4726 (2018).
Jin, Z., Li, X., Mullen, J. T. & Kim, K. W. Intrinsic transport properties of electrons and holes in monolayer transition-metal dichalcogenides. Phys. Rev. B 90, 045422 (2014).
Li, M. O., Esseni, D., Snider, G., Jena, D. & Xing, H. G. Single particle transport in two-dimensional heterojunction interlayer tunneling field effect transistor. J. Appl. Phys. 115, 074508 (2013).
Keyshar, K. et al. Experimental determination of the ionization energies ofmose2, ws2, and mos2 on sio2 using photoemission electron microscopy. ACS Nano 11, 8223–8230 (2017).
McDonnell, S. et al. Hole contacts on transition metal dichalcogenides: Interface chemistry and band alignments. ACS Nano 8, 6265–6272 (2014).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Wang, H. et al. Radiative lifetimes of excitons and trions in monolayers of the metal dichalcogenide mos2. Phys. Rev. B 93, 045407 (2016).
Hoffmann, K. H. & Schreiber, M. Computational Statistical Physics: From Billiards to Monte Carlo. 1 edn, (Springer, Berlin Heidelberg, 2002).
Stefano, O. D., Savasta, S. & Girlanda, R. Theory of local optical spectroscopy of quantum wires with interface fluctuations. Phys. Rev. B 93, 2302 (2016).
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 696656. Furthermore, we acknowledge financial support from the Swedish Research Council (VR), Stiftelsen Olle Engkvist, and the Deutsche Forschungsgemeinschaft (DFG) through SFB 951 and the School of Nanophotonics (SFB 787).
Author information
Authors and Affiliations
Contributions
E.M. conceived and supervised the project. S.O. derived the theory and developed the code, based on previous work by S.B. and M.S. C.L., M.K., and P.E. performed the DFT calculations. S.O. wrote the main bulk of the manuscript, with the help of multiple revisions by mainly S.B. and E.M. T.K. provided fruitful discussions and experimental data to compare to.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ovesen, S., Brem, S., Linderälv, C. et al. Interlayer exciton dynamics in van der Waals heterostructures. Commun Phys 2, 23 (2019). https://doi.org/10.1038/s42005-019-0122-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0122-z
This article is cited by
-
Multilayer WS2 for low-power visible and near-infrared phototransistors
Discover Nano (2024)
-
Dipolar many-body complexes and their interactions in stacked 2D heterobilayers
Nature Reviews Physics (2024)
-
Amplification of interlayer exciton emission in twisted WSe2/WSe2/MoSe2 heterotrilayers
npj 2D Materials and Applications (2024)
-
Twist angle dependent interlayer transfer of valley polarization from excitons to free charge carriers in WSe2/MoSe2 heterobilayers
npj 2D Materials and Applications (2023)
-
Interface engineering of charge-transfer excitons in 2D lateral heterostructures
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.