Abstract
Quantum key distribution (QKD) can offer communication with unconditional security and is a promising technology to protect next generation communication systems. For QKD to see commercial success, several key challenges have to be solved, such as integrating QKD signals into existing fiber optical networks. In this paper, we present experimental verification of QKD co-propagating with a large number of wavelength division multiplexing (WDM) coherent data channels. We show successful secret key generation over 24 h for a continuous-variable QKD channel jointly transmitted with 100 WDM channels of erbium doped fiber amplified polarization multiplexed 16-ary quadrature amplitude modulation signals amounting to a datarate of 18.3 Tbit/s. Compared to previous co-propagation results in the C-band, we demonstrate more than a factor of 10 increase in the number of WDM channels and more than 90 times higher classical bitrate, showing the co-propagation with Tbit/s data-carrying channels.
Similar content being viewed by others
Introduction
Recent advances in quantum computing are threatening the security of today’s communication networks1. It is expected that current systems will be upgraded with post-quantum public key cryptography designed to be resilient against quantum computing attacks2,3. Unfortunately, even post-quantum cryptography cannot be provably secure against so-called “store now, decrypt later” attacks in which an attacker can undetectably wiretap a link and store the information until sufficient technological advances have been made to break the encryption4. This is especially a threat for users of sensitive data, that may have secrecy periods of 100 years or more, such as military, healthcare institutions, and government departments4.
Encryption that is secure against an eavesdropper with unbounded computational power can be achieved using one-time pad5, in which the two communicating parties need to share a secret symmetric key. Quantum key distribution (QKD) can provide means to establish the symmetrical secret key between two remote parties regardless of the equipment available to potential attackers of the channel6,7. QKD has been known since the introduction of BB848 and Ekert’s protocol9, and can typically be divided into discrete variable (DV) protocols8,9, relying on properties of single photons, and continuous variable (CV) protocols using coherent or squeezed states10,11,12. Significant effort has been dedicated to both security proofs6,13,14,15,16 and experimental demonstrations17,18,19,20,21,22, showing that QKD is a promising technology to provide security for next generation communication systems4,14,23,24,25,26,27. Notably, QKD has been demonstrated in installed fiber networks28,29,30, over point-to-point free-space optical links31,32, and for satellite links33,34. Commercial QKD solutions are available35,36,37 and QKD has even been employed in real world use cases38,39.
Despite significant research progress, QKD is yet to become a viable technology for widespread use. One obstacle is the cost, including not only the QKD transmitter and receiver, but also rental or deployment cost of optical fibers, which may be higher than that of the QKD system itself. If QKD channels can be integrated into the existing communication network architecture, the total cost of a QKD link may be greatly reduced. This means that QKD channels should be able to co-propagate with classical data channels in the same fiber, using multiplexing techniques such as wavelength division multiplexing (WDM) without suffering significant penalties from crosstalk, and/or compromising the security. Joint transmission of DV-QKD and between one to four on–off keying channels40,41,42,43 has been demonstrated. Further, coexistence of DV-QKD channels propagating at 1300 nm with 20 and 32 coherent modulation channels propagating at 1550 nm, has been demonstrated44,45 as well as joint propagation in the C-band with two 100 Gbit/s coherent channels and 8 unmodulated carriers46.
For practical implementations, CV-QKD has many features which makes it an interesting alternative to the more developed DV-QKD solutions; the receiver is based on shot-noise limited commercially available balanced photodetectors compared to bulky and costly single photon detectors, the local oscillator (LO) acts as a spectral filter, and the transmitter can be built using conventional telecommunication equipment. Coexistence with classical channels is less explored for CV-QKD compared to DV-QKD. It has been shown that CV-QKD has the potential to be more tolerant to noise originating from WDM channels47. Recently, joint transmission of CV-QKD with unmodulated classical intensity carriers48, as well as on–off keying signals49,50,51,52, has been demonstrated.
To keep up with the traffic demands, current generation fiber optical communication systems are leveraging fully populated WDM transmission, which typically carry more than 100 WDM channels53,54. Further, the transponders have moved from simple intensity modulation formats to coherent quadrature amplitude modulation (QAM) techniques with higher spectral efficiency55. These systems most often apply optical amplifiers such as erbium doped fiber amplifiers (EDFAs), that generate wide bandwidth amplified spontaneous emission (ASE) noise. Previous experiments on joint propagation of classical data channels and QKD channels, both CV and DV, have been limited in terms of the number of classical channels. Further, in most cases legacy modulation formats, such as low bitrate on–off keying, have been used, or Tbit/s data-rates are estimated from co-propagating unmodulated high power continuous wave laser tones and not actual data-carrying signals46. Furthermore, to the best of our knowledge, previous demonstrations have not used any optical amplification of the data signals, which is a key component in modern WDM systems. For widespread deployment, it is crucial to demonstrate that QKD channels can co-exist in the current state of the art fiber optical network and not only under very simplified experimental conditions without EDFAs and/or with unmodulated carriers emulating the classical channels.
In this paper, we demonstrate joint propagation of QKD and wideband WDM transmission of classical data-carrying coherent channels. We transmit a CV-QKD channel jointly with 100 coherent polarization-multiplexed (PM) 16QAM WDM channels, amounting to 18.3 Tbit/s classical datarate (assuming 7% forward error correction overhead). The study in this paper is an extension of our initial trials with 18 WDM PM-16QAM channels56. The result of this paper is compared to previous results with implemented data-carrying classical channels in Fig. 1. We report an experimental demonstration of a co-propagating QKD channel with state-of-the-art classical data-rates and number of WDM channels. For co-propagation in the C-band, we show the first demonstration with Tbit/s classical data rate and more than a factor of 10 increase in the number of WDM channels over previously reported results. Compared to any former CV-QKD demonstration, we show co-propagation with two orders-of-magnitude higher data rates. We demonstrate generation of secret keys for 24 h over 10 km of fiber and we confirm that all the classical channels are error free and not affected by the QKD system. We also show that in-band ASE noise stemming from EDFAs for the classical channels, limits the effectiveness of CV-QKD systems and may even prohibit secure communication. However, it is possible to overcome this issue by proper notch filtering of the noise before multiplexing the QKD and the classical channels. The findings in this study represents a big leap forward for QKD technology, demonstrating that it is possible for QKD signals to share the current network infrastructure.
Comparison with previous co-propagation experiments. Comparison of the total classical bitrate and the number of wavelength division multiplexing channels of this paper and previous results with actual data-carrying classical channels. Text annotations show the reference number, the transmission distance and the secret key rate. DV-QKD discrete variable quantum key distribution, CV-QKD continuous variable quantum key distribution
Results
Continuous variable quantum key distribution system in the presence of ASE
The CV-QKD transmitter is shown in Fig. 2 and is based on a distributed feedback (DFB) laser, with a wavelength of 1549.5 nm, pulsed by a 10 MHz electrical signal. We apply discretely modulated CV-QKD based on the so-called four-state protocol57,58. The CV-QKD signals are generated by modulating the pulse train with four discrete phase states, i.e. similar to 4QAM modulation. A pulsed copy of the transmitter laser is shifted in time compared to the CV-QKD signal, and transmitted on orthogonal polarization. This pulsed copy is used in the receiver as LO. The output power of the CV-QKD signal is controlled by a variable optical attenuator (VOA). Also generated is a 100 MHz clock synchronization signal at 1310 nm. The signals are transmitted over 10 km of standard singlemode fiber (SSMF) as shown in Fig. 2. The receiver is based on single quadrature measurements (often referred to as homodyne detection in quantum applications) with random basis selection using the transmitted copy of the signal laser as LO. The receiver performs active polarization and phase tracking. We apply reconciliation based on low-density parity-check (LDPC) codes and evaluate the secret key rate after privacy amplification. For more details see the Methods section.
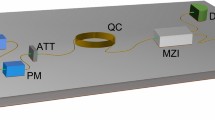
Experimental setup. Outline of the experimental setup for co-propagation of quantum and classical channels showing: The setup of the coherent transmitter generating 24.5 Gbaud polarization multiplexed 16-ary quadrature amplitude modulation (PM-16QAM) signals on 100 carriers with 25 GHz spacing. The notch filter for reducing in-band amplified spontaneous emission (ASE) noise in the continuous variable quantum key distribution (CV-QKD) band. The polarization diverse coherent receiver for detecting each of the classical coherent channels. Further, the CV-QKD transmitter generating four discretely modulated states, followed by the 10 km transmission link based on standard single mode fiber (SSMF), and finally the CV-QKD receiver with automated real-time polarization and optical phase stabilization
In almost all modern fiber optical communication networks, optical amplifiers such as EDFAs, are used. These amplifiers generate broadband amplified spontaneous emission (ASE) noise. For classical communication, the out-of-band ASE noise that leaks to other WDM channels for instance in multiplexing stages, can in most cases be neglected. However, this is not the case for CV-QKD signals which are heavily penalized by any small amount of excess noise in the channel. We investigate the influence of ASE noise on the CV-QKD channel by coupling broadband ASE noise together with the CV-QKD channel, as described in the Methods section. In the experiments in this paper, the ASE noise is originating from amplifiers within the classical transmitters. However, another possible scenario is that the classical channels are transmitted over a periodically amplified multispan link and that the QKD channel is co-propagating over one of the spans in a longer link. Note that the measurements of the ASE noise tolerance is valid for both these cases.
In Fig. 3, we plot the change in secret key rate (SKR) in relation to when no ASE is present, as a function of ASE power. For each measurement point, the SKR is averaged over 10 min. For the points at low in-band ASE power, the SKR is slightly higher than for the case without any ASE noise present. This is due to slowly varying effects on the SKR (which we will see later in this paper where the SKR is measured over 24 h) and attributed to changing external conditions. For in-band ASE noise powers higher than −59.2 dBm/0.1 nm, no secret keys can be generated. This requirement is most likely not fulfilled by currently installed multiplexing equipment where a certain amount of crosstalk between WDM channels is tolerable. In other words, new multiplexing equipment with sufficient extinction of in-band ASE noise for the QKD channels may have to be developed.
Impact of amplified spontaneous emission noise on the secret key rate. Experimentally observed change in the secret key rate as a function of in-band amplified spontaneous emission (ASE) power in relation to no when ASE is present. Markers shows measurements, the orange dashed line shows a third degree polynomial fit of the data points in the slope of the secret key rate, and the purple dotted dashed line shows the reference when no ASE is present
To combat the in-band ASE noise, we construct an optical notch filter that is applied on the classical channels before they are combined with the CV-QKD channel, as shown in Fig. 2. Unfortunately, the roll-off of the filter function of the wavelength selective switches (WSSs) that were used, prohibits us to construct a very narrow filter. While sending ASE noise into the notch filter structure, we increased the notch filter width until we saw no penalty on the CV-QKD channel. The filter width is approximately 4.00 nm and to suppress crosstalk, the same notch is created in the WSS of the transmitter structure generating the classical coherent channels. These two filters remove 20 WDM channels centered around the CV-QKD wavelength. The measured spectra showing the notch, the CV-QKD channel and the classical channels are shown in Fig. 4. Since loss is the main limiting factor for CV-QKD, we place the CV-QKD channel close to 1550 nm to operate at the minimum loss of the SSMF.
Spectra of the transmitted signals. Measured optical spectrum at the input of the fiber link showing both the continuous variable quantum key distribution (CV-QKD) channel and the classical 24.5 Gbaud polarization multiplexed 16-ary quadrature amplitude modulation (PM-16QAM) signals. Purple line shows the two bands of 50 wavelength division multiplexing (WDM) channels each and yellow line the case when 18 WDM channels are used. The power of the CV-QKD channel is amounted by the transmitted pulsed local oscillator
Joint propagation with 100 coherent data channels
The transmitters for the classical coherent signals are shown in Fig. 2. We generate 100 WDM channels of 24.5 Gbaud PM-16QAM with channel spacing of 25 GHz, amounting to a total bitrate of 18.3 Tbit/s assuming 7% forward error correction overhead. The channels are split into two bands of 50 channels located on wavelength on both sides of the CV-QKD channel as shown in the measured spectrum in Fig. 4. The total launch power of the classical channels is 12.9 dBm. In our experiment this power is limited by the maximum output power of the last EDFA (~28 dBm), the loss of the second WSS, and fact that we use a 10% coupler to combine the classical channels with the CV-QKD channels to avoid large amounts of excess loss for the CV-QKD channel.
To evaluate the performance of the CV-QKD system, we perform measurements of the SKR over 24 h, with and without the 100 co-propagating classical channels. The results are shown in Fig. 5. The SKR is slowly changing over time, which is attributed to varying experimental conditions such as temperature in the lab, vibrations from people moving around the setup, polarization changes in the fiber, drifting wavelength of the transmitter laser, etc. The fast dips in the SKR are attributed to the active polarization and phase tracking that sometimes experience fluctuations that are too rapid for the feedback system to handle properly. The mean SKR over 24 h without classical channels is 27.2 kbit/s and when the 100 classical channels are co-propagating it is 28.9 kbit/s. The slightly higher SKR for the case with classical channels is a statistical artifact due to the slowly varying performance of the system. These results show that it is possible to simultaneously transmit a CV-QKD channel with a large number of coherent data channels without reduced performance of the CV-QKD system, given that proper rejection of the in-band ASE noise is achieved. We also performed experiments with 18 WDM channels, placed in the lower wavelength band to facilitate the worst case spontaneous Raman noise case. Also in this case, we did not see any influence on the QKD channel for up to 1.2 dBm launched power per channel (which is higher than optimal for the classical channels). We do notice that the SKR for the case with the classical channels co-propagating, is experiencing a larger variance in the SKR, possibly this could be due to small reflections in the many fiber connectors in the system, which are more prominent when the higher power classical channels are present.
Measured secret key rates. Secret key rates (SKRs) measured over 24 h for the continuous variable quantum key distribution (CV-QKD) channel when no classical channels are co-propagating (green) and when 100 wavelength division multiplexing channels of 24.5 Gbaud polarization multiplexed 16-ary quadrature amplitude modulation (PM-16QAM) are co-propagating (pink)
To investigate the possible nonlinear noise generation, we perform calculations of the spontaneous Raman scattering (SRS) noise, which has been shown to be the dominating nonlinear noise source59. Different noise sources from WDM channels have been studied59. In our case, we can neglect in-band ASE noise and linear crosstalk from the WDM channels since we have tuned the notch filter such that we do not see any impact on the SKR. The calculated Stokes and anti-Stokes SRS is shown in Fig. 6 and the total SRS noise is shown for different transmission distances. The SRS coefficients are selected to reflect the worst case and chosen from Eraerds et al.60. Indicated is also the measured in-band noise levels where the SKR starts to decrease and where no secret keys can be generated (from Fig. 3), translated to the output of the fiber. At 10 km, the expected SRS noise is below the levels that impacts the SKR in our experiments. This supports that the SKR is not affected by the 100 co-propagating channels in our experiment.
Raman scattering. Calculated Stokes and anti-Stokes Raman scattering with parameters matching the experimental conditions. The considered receiver bandwidth is 0.1 nm. Also indicated are the measured noise levels from the experiments where the secret key rate starts to be affected by in-band noise and where no secret key generation is possible. The measured noise levels are translated to the output of the fiber to be comparable to the spontaneous Raman scattering
Performance of the 100 classical coherent channels
For a system co-integrating CV-QKD and classical data channels, the performance of the classical channels should also be addressed. Several sources of possible degradation of the classical channels exist, such as the penalty from any extra multiplexing components (notch filter in our case), possible restrictions on the launch power, and nonlinear crosstalk from the pulsed local oscillator of the CV-QKD system. To assess this, we detect each of the channels using the coherent receiver depicted in Fig. 2. The receiver bandpass filter center wavelength and the wavelength of the LO laser are adjusted to match the channel under test. We apply conventional digital signal processing as outlined in the Methods section. The bit-error-rate (BER) of each of the classical coherent channels with and without the CV-QKD signal on is shown in Fig. 7. The BER of each channel is far below typically assumed forward error correction (FEC) thresholds, e.g. Reed-Solomon codes with 7% FEC overhead with a decoding threshold around BER = 10−3. Further, the BER averaged over all channels is the same with and without the CV-QKD channel co-propagating, showing that no significant nonlinear crosstalk from the pulsed local oscillator to the classical channels occurs.
Performance of the classical channels. Measured bit-error-ratio (BER) of each of the 100 classical coherent polarization multiplexed 16-ary quadrature amplitude modulation (PM-16QAM) channels when the continuous variable quantum key distribution (CV-QKD) channel is off (blue squares) and on (orange circles). Solid blue line shows the mean BER of all channels when the CV-QKD channel is off and orange dotted line the mean BER when it is on
Discussion
We have experimentally demonstrated that CV-QKD can co-exist in WDM fiber optical networks with 100 WDM channels of EDFA amplified coherent 24.5 Gbaud PM-16QAM channels, summing up to a total classical bitrate of 18.3 Tbit/s. To the best of our knowledge, this is the first ever demonstration of joint transmission of QKD and Tb/s classical data-carrying channels in the C-band. The results represent an important step towards practical implementation of QKD technology as we show that it is possible for CV-QKD to share the infrastructure of fiber optical networks in densely populated links with 100 channels. In the following paragraphs, we discuss some implications of our results and propose future studies to bring further insights into different limitations and challenges.
In previous experiments with CV-QKD channels co-propagating with classical channels, it appeared that no optical amplifiers have been incorporated in the transmitter side48,49,50,51. Most fiber optical links today are using amplifiers, such as EDFAs or semiconductor optical amplifiers, which generate ASE noise. Our results show that if we can achieve sufficient suppression of the in-band ASE noise, coexistence of EDFA amplified classical channels and CV-QKD channels is possible. However, further studies on the suppression ratio of conventional multiplexing components, such as those deployed in the field, should be performed. Further, on the transmitter side, the EDFAs are typically placed after the multiplexing components. In other words, the QKD transmitter cannot simply use one port of a WDM multiplexer but will require novel multiplexers after the EDFAs. Simple add-on components for the existing architecture are of interest, and in the long run novel multiplexing components that take QKD channels into account should be investigated for future deployment of new fiber optical links.
The large bandwidth of the notch filter in this experiment is attributed to the characteristics of the employed WSSs. Using a smaller bandwidth notch inferred linear ASE crosstalk to the CV-QKD channel due to the roll-off of the filter function. For conventional communication applications, extremely good suppression is not a major design target as other noise factors such as in-band ASE noise are much more prominent. But as seen in Fig. 3, extreme suppression of ASE noise is needed for the CV-QKD channel. This adds a new design criterion for future notch filters targeting QKD applications. By using sharp roll-off filters with sufficient suppression, future studies should investigate how closely it is possible to place the classical channels to the CV-QKD channel without inflicting penalties, to avoid reducing the spectral efficiency of the system. Further, it should be investigated if placing the classical channels closer will add nonlinear crosstalk to the CV-QKD channel.
The transmission reach in our investigation is mainly limited by the loss that the transmitted LO suffers in both the channel and the components needed for multiplexing with the classical channels, with a total loss of approximately 7 dB compared to the expected loss of 2 dB for the 10 km of fiber. Several techniques exist to increase the reach of CV-QKD, such as for instance employing a true local oscillator with transmitted pilot symbols for phase tracking61,62. However, regarding the influence from the classical channels to the CV-QKD channel, the results in this paper would mostly hold even if the transmission distance is increased. The ASE crosstalk penalty is independent of the reach and nonlinear crosstalk such as cross-phase modulation and four-wave mixing occurs in the beginning of the link where the power is high. An exception is spontaneous Raman scattering which has a peak at distances around 20 km51, see Fig. 6. However, penalty from nonlinear crosstalk could possibly become an issue if it is required to further increase the launched optical power of the classical channels and/or channels are placed closer to the CV-QKD wavelength. To increase the SKR, the pulse repetition rate could be increased. However, this may increase the crosstalk from classical channels since the bandwidth is increased. Another possibility is to also employ WDM for the CV-QKD channels.
Method
Continuous variable quantum key distribution setup
The setup of the QKD system is shown in Fig. 2. For details on the system please see Hirano et al.63. The protocol that is used is based on discretely modulated states57,58, e.g. similar to classical 4-QAM modulation (sometimes referred to as the four state protocol). This protocol benefits from simple signal generation in the transmitter and efficient error correction schemes. However, security has been proven for Gaussian collective attacks but not yet for general attacks63. The modulation is achieved using a digital-to-analog converter that generates four different amplitudes, driving an electro-optic phase modulator. The light source is a distributed feedback (DFB) laser at 1549.5 nm which is directly modulated by a 10 MHz electrical signal to generate a pulse train. The signal is split into two arms, where 1% is directed to the modulation stage and 99% of the pulsed signal is kept unmodulated and delayed in time before being recombined with the modulated signal on orthogonal polarization. This delay is introduced to limit crosstalk between the QKD signal and the phase reference signal. The output power of the CV-QKD signal is adjusted by a variable optical attenuator (VOA) to be approximately 70% of the single photon energy. To synchronize the transmitter and receiver, a sinusoidal signal is generated by directly modulating a DFB laser at 1310 nm using a 100 MHz tone. This eliminates the need for digital clock recovery which is challenging for CV-QKD signals. The clock signal is combined with the 1549.5 nm signal using a 1300 nm/1550 nm WDM coupler.
The CV-QKD receiver starts by demultiplexing the synchronization signal using a 1300 nm/1550 nm WDM coupler where the 1310 nm signal is directed to a photodetector from which the generated electrical signal is used to synchronize the sampling rate of the analog-to-digital converter (ADC) to 100 MHz. The 1549.5 nm signal is first directed to an optical bandpass filter (BPF), with ~1.2 nm in 3dB bandwidth, which suppresses the classical WDM signals. The wider than necessary bandwidth is chosen for two reasons, the first is that it had the lowest loss of the available filters, and the second is that the wavelength of the transmitter laser is observed to be varying by at least ±0.1 nm over time and any excess loss to the CV-QKD channel is directly affecting the SKR. Polarization correction is applied by occasionally measuring the power of the CV-QKD signal arm and minimizing this power by rotating the polarization state before the polarization beam splitter (i.e. minimizing the crosstalk from the polarization multiplexed local oscillator). The CV-QKD signal is directed to a switch which is used to block the CV-QKD signal to characterize the shot noise variance of the receiver. The other arm of the polarization beam splitter contains the pulsed copy of the transmitter laser which will be used as local oscillator. This signal is sent to an electro-optic phase modulator which is driven by a digital-to-analog converter (DAC) that generates a random binary pattern that selects the quadrature to measure (i.e. basis selection). The DAC also generates an adaptive bias signal which is used for phase stabilization. This bias is controlled by feedback from the detected electrical signal. For details on this method please see Hirano et al.63. Other phase referencing methods exist, such as digital phase tracking based on pilot signals and a true local oscillator61,62. Transmitting the local oscillator, as in this paper, relaxes the laser linewidth requirement and enables a phase reference without having to transmit pilot symbols. However, it comes at the cost of lower receiver performance since the local oscillator is affected by the channel loss. The CV-QKD signal and the pulsed local oscillator are combined in a 3 dB coupler whose outputs are sent to a balanced photodetector. The amplified electrical signal is digitized with the ADC board.
CV-QKD protocol operation
The CV-QKD transmitter generates 106 pulses at a time where half of them are used for parameter estimation. The mean value and variance of each of the four coherent states are estimated. These parameters are used to estimate the excess noise and the loss of the channel. Further, from the parameter estimation signals, the phase offset between the CV-QKD signal and the LO can also be estimated63, which is used as a feedback signal to the receiver phase modulator (as explained in the previous paragraph). Reverse reconciliation is performed using non-binary low-density parity-check (LDPC) codes running on a graphics processing unit (GTX 680)64. Privacy amplification is performed using Toeplitz matrix multiplication65. The mutual information between the transmitter and the receiver as well as the Holevo information between the eavesdropper and the receiver are calculated using the estimated excess noise and loss of the channel. Here we assume that an eavesdropper cannot control the internal noise sources in the CV-QKD receiver12. These quantities are used to calculate the compression factor needed for the privacy amplification. For more details on the implemented protocols, please refer to the appendix of the study by Hirano et al.63.
Classical signals: PM-16QAM WDM transmitter and receiver
The light source for the classical coherent channels is an optical frequency comb with 25 GHz carrier spacing. We generate 100 WDM channels using two transmitter structures that produce loading channels and measured test channels. The transmitters are based on dual-polarization (DP) I/Q-modulators driven by arbitrary waveform generators (AWGs) running at 49 Gsample/s. The AWGs generate polarization multiplexed 16-ary quadrature amplitude modulation (PM-16QAM) signals using pulses with a root-raised cosine pulse shape with 0.01 roll-off.
The test band contains 3 modulated carriers while the load channel generates the remaining 97 carriers. The first WSS in the load channel path serves to roughly flatten the power of the carriers from the frequency comb. The second WSS serves four purposes; it removes out of band ASE noise, it generates a notch for the CV-QKD channel (roughly matching the bandwidth of the following notch filter), it flattens the spectrum, and it generates a second notch where the test channels are inserted. The wavelength of this notch is varied depending on which channel that is measured. The modulated channels are sent through 28 km of SSMF to decorrelate the WDM channels using the dispersion.
For the test channels, three neighboring carriers with varying center frequency depending on the measured channel are selected using a BPF. The center channel (which is the channel under test) is sent to one DP-I/Q-modulator while the two neighboring channels are sent to a second DP-I/Q-modulator. The modulators are driven with the same AWG and the signal in the two arms are decorrelated using fibers with different lengths. The testband and the load channels are combined using a 3 dB coupler. The signals are amplified using EDFAs at several places indicated in Fig. 2. For more detailed information on the transmitter setup, please see Puttnam et al.66. Note that for the long term measurements of the CV-QKD performance, we use full load band without inserting the test channels. The main reason for this is that the power of the test band was observed to be slowly varying over time due to polarization effects in the transmitter and we want to avoid that the power of the classical channels decreases during the measurements of the CV-QKD performance.
For measurement of the classical channel quality, we apply a conventional coherent receiver to detect one WDM channel at a time. The receiver applies a tunable bandpass filter that is adjusted to the channel under test (i.e. the center of the generated test band in the transmitter). Further, the receiver local oscillator (100 kHz linewidth tunable external cavity laser (ECL)) is also tuned to approximately the same wavelength as the channel under test. We apply offline digital signal processing (DSP) algorithms: Resampling to two samples per symbol and normalization is followed by a dispersion compensation stage. Polarization de-multiplexing is achieved with a 2 × 2 multiple input multiple output (MIMO) filter structure using 17-tap filters whose coefficients are first updated using a radially directed error function for pre-convergence then switched to a decision-directed least-mean square error-function. Frequency offset estimation and carrier phase estimation based on a decision-directed algorithm with test phase angles is embedded into the equalizer update loop.
In-band ASE measurements
To investigate the in-band ASE noise tolerance of the CV-QKD system, we use the ASE noise generation stage shown in Fig. 8. To be able to generate and accurately measure ASE noise with very low power in CV-QKD spectral band, we use two cascaded WSSs to create wide notches (roughly 6 nm) in the ASE noise. We then measure the spectral power on both sides of the notch and average the power. By knowing the notch attenuation we can calculate the in-band ASE noise power. A manually variable optical attenuator (VOA) is used to change the ASE noise power before the signals are sent to the 10% coupler in the transmitter shown in Fig. 2. The noise power is measured by the optical spectrum analyzer (OSA) indicated in Fig. 2.
Noise loading setup. Outline of the experimental setup for generating in-band amplified spontaneous emission (ASE) noise. The wavelength selective switches (WSSs) are generating a wideband notch with 19 dB attenuation (not using the full attenuation as in the transmission experiments). The power is measured on each side of the notch, using an optical spectrum analyzer, and averaged. By knowing the notch attenuation we can calculate the in-band ASE noise power. EDFA Erbium doped fiber amplifier, WSS wavelength selective switch, VOA Variable optical attenuator, CV-QKD continuous variable quantum key distribution
Notch filter system
As discussed in the results section, in-band ASE noise is detrimental to the performance of CV-QKD signal. Since we have several EDFAs in the transmitter, we need to apply a notch filter in the classical signal arm to remove the ASE noise at the CV-QKD spectral occupancy. To achieve this, we apply two cascaded WSSs with a high power EDFA (28 dBm) in between as indicated in Fig. 2. Both WSSs are programmed to carve a notch that is roughly 4.00 nm in 3 dB bandwidth. This is much larger than what would be necessary with ideal components. However, the filter functions of the WSSs had a slow roll-off and by filtering ASE noise and monitoring the excess noise of the CV-QKD signal, we increased the filter bandwidth until we saw no penalty for the CV-QKD signal. At this point, we further increased the bandwidth slightly to add a margin to account for frequency drifts of the transmitter laser.
Spontaneous Raman scattering noise
The spontaneous Raman scattering noise in the forward direction can be modeled as
where PL is the launched optical power, β(λ) the spontaneous Raman scattering (SRS) coefficient, L the channel length, ηch the transmittance and Δλ the bandwidth59. β(λ) is from ref. 60 to be 4 × 10−9 km−1 nm−1 for the anti-Stokes SRS and 5 × 10−9 km−1 nm−1 for the Stokes SRS. Note that this overestimates the SRS since we use the highest β(λ) within our bandwidth of interest for both cases. Since we use 50 channels in the lower band and 50 channels in the upper band, we divide the total power of 12.9 dBm (measured in the experiments) equally between the two bands. Δλ is chosen to be 0.1 nm, which is much wider than our receiver electrical bandwidth. However, it allows us to directly compare to the noise levels to our measured ASE noise tolerance levels in Fig. 3.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Cesare, C. Encryption faces quantum foe. Nature 525, 167 (2015).
Campagna, M. et al. Quantum Safe Cryptography and Security. ETSI (European Telecommunications Standards Institute) White Paper (2015).
Bernstein, D. J. & Lange, T. Post-quantum cryptography. Nature 549, 188–194 (2017).
Diamanti, E., Lo, H.-K., Qi, B. & Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2, 16025 (2016).
Vernam, G. S. Cipher printing telegraph systems: for secret wire and radio telegraphic communications. J. AIEE 45, 109–115 (1926).
Lo, H.-K. & Chau, H. F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999).
Mayers, D. Unconditional security in quantum cryptography. J. ACM 48, 351–406 (2001).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. In Proc. of the IEEE International Conference on Computers, Systems, and Signal Processing 175–179 (Bangalore, 1984).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991).
Ralph, T. C. Continuous variable quantum cryptography. Phys. Rev. A 61, 010303 (1999).
Hillery, M. Quantum cryptography with squeezed states. Phys. Rev. A 61, 022309 (2000).
Grosshans, F. et al. Quantum key distribution using gaussian-modulated coherent states. Nature 421, 238 (2003).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441 (2000).
Scarani, V. et al. The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301 (2009).
Leverrier, A., Garca-Patrón, R., Renner, R. & Cerf, N. J. Security of continuous-variable quantum key distribution against general attacks. Phys. Rev. Lett. 110, 030502 (2013).
Lim, C. C. W., Curty, M., Walenta, N., Xu, F. & Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002).
Elliott, C. et al. Current status of the darpa quantum network. Def. Secur.: Quantum Inf. Comput. III 5815, 138–150 (2005).
Dynes, J. et al. Stability of high bit rate quantum key distribution on installed fiber. Opt. Express 20, 16339–16347 (2012).
Jouguet, P., Kunz-Jacques, S., Leverrier, A., Grangier, P. & Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 7, 378–381 (2013).
Korzh, B. et al. Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photonics 9, 163 (2015).
Huang, D., Huang, P., Lin, D. & Zeng, G. Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 6, 19201 (2016).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photonics 8, 595 (2014).
Kimble, H. J. The quantum internet. Nature 453, 1023 (2008).
Diamanti, E. & Leverrier, A. Distributing secret keys with quantum continuous variables: principle, security and implementations. Entropy 17, 6072–6092 (2015).
Bedington, R., Arrazola, J. M. & Ling, A. Progress in satellite quantum key distribution. npj Quantum Inf. 3, 30 (2017).
Sasaki, M. Quantum networks: where should we be heading? Quantum Sci. Technol. 2, 020501 (2017).
Peev, M. et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 11, 075001 (2009).
Sasaki, M. et al. Field test of quantum key distribution in the Tokyo QKD network. Opt. Express 19, 10387–10409 (2011).
Tang, Y.-L. et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Phys. Rev. X 6, 011024 (2016).
Schmitt-Manderbach, T. et al. Experimental demonstration of free-space decoy-state quantum key distribution over 144 km. Phys. Rev. Lett. 98, 010504 (2007).
Ursin, R. et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 3, 481 (2007).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43 (2017).
Liao, S.-K. et al. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
ID Quantique. Cerberis3 QKD System https://www.idquantique.com/quantum-safe-security/products/cerberis3-qkd-system/. Accessed 8 January 2019.
QuantumCTek. Quantum key distribution products http://www.quantum-info.com/English/product/quantum/. Accessed 11 June 2018.
Qubitekk. Quantum cryptography. http://qubitekk.com/security/. Accessed 24 May 2018.
ID Quantique. Securing Data Transfer for Elections. https://marketing.idquantique.com/acton/attachment/11868/f-020f/1/-/-/-/-/Geneva%20Govt_%20DCI%20QKD%20Use%20Case.pdf. Accessed 8 January 2019.
Courtland, R. China’s 2,000-km quantum link is almost complete [news]. IEEE Spectr. 53, 11–12 (2016).
Townsend, P. D. Simultaneous quantum cryptographic key distribution and conventional data transmission over installed fibre using wavelength-division multiplexing. Electron. Lett. 33, 188–190 (1997).
Xia, T. J. et al. In-band quantum key distribution (QKD) on fiber populated by high-speed classical data channels. In Optical Fiber Communication Conference (OFC) (Optical Society of America, Anaheim, 2006).
Choi, I. et al. First quantum secured 10-Gb/s DWDM transmission over the same installed fibre. In European Conference on Optical Communication (ECOC) (IEEE, Cannes, 2014).
Patel, K. et al. Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks. Appl. Phys. Lett. 104, 051123 (2014).
Mao, Y. et al. Integrating quantum key distribution with classical communications in backbone fiber network. Opt. Express 26, 6010–6020 (2018).
Wang, L.-J. et al. Long-distance copropagation of quantum key distribution and terabit classical optical data channels. Phys. Rev. A 95, 012301 (2017).
Dynes, J. F. et al. Ultra-high bandwidth quantum secured data transmission. Sci. Rep. 6, 35149 (2016).
Kumar, R., Qin, H. & Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 17, 043027 (2015).
Peters, N. et al. Dense wavelength multiplexing of 1550 nm QKD with strong classical channels in reconfigurable networking environments. New J. Phys. 11, 045012 (2009).
Huang, D. et al. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 23, 17511–17519 (2015).
Huang, D. et al. Field demonstration of a continuous-variable quantum key distribution network. Opt. Lett. 41, 3511–3514 (2016).
Karinou, F. et al. Toward the integration of CV quantum key distribution in deployed optical networks. IEEE Photon. Technol. Lett. 30, 650–653 (2018).
Eriksson, T. A. et al. Coexistence of continuous variable quantum key distribution and 7 × 12.5 Gbit/s classical channels. In IEEE Summer Topical Meeting Series (SUM) (2018).
Rohde, H. et al. Coherent ultra dense WDM technology for next generation optical metro and access networks. J. Light. Technol. 32, 2041–2052 (2014).
Cai, J.-X. et al. 51.5 Tb/s capacity over 17,107 km in C + L bandwidth using single mode fibers and nonlinearity compensation. J. Lightw. Technol. 36, 2135–2141 (2017).
Agrell, E. et al. Roadmap of optical communications. J. Opt. 18, 063002 (2016).
Eriksson, T. A. et al. Joint propagation of continuous variable quantum key distribution and 18 × 24.5 Gbaud PM-16QAM channels. In European Conference on Optical Communication (ECOC) Rome, Italy (2018).
Hirano, T., Yamanaka, H., Ashikaga, M., Konishi, T. & Namiki, R. Quantum cryptography using pulsed homodyne detection. Phys. Rev. A 68, 042331 (2003).
Leverrier, A. & Grangier, P. Unconditional security proof of long-distance continuous-variable quantum key distribution with discrete modulation. Phys. Rev. Lett. 102, 180504 (2009).
Qi, B., Zhu, W., Qian, L. & Lo, H.-K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 12, 103042 (2010).
Eraerds, P., Walenta, N., Legré, M., Gisin, N. & Zbinden, H. Quantum key distribution and 1 Gbps data encryption over a single fibre. New J. Phys. 12, 063027 (2010).
Huang, D., Huang, P., Lin, D., Wang, C. & Zeng, G. High-speed continuous-variable quantum key distribution without sending a local oscillator. Opt. Lett. 40, 3695–3698 (2015).
Kleis, S., Rueckmann, M. & Schaeffer, C. G. Continuous variable quantum key distribution with a real local oscillator using simultaneous pilot signals. Opt. Lett. 42, 1588–1591 (2017).
Hirano, T. et al. Implementation of continuous-variable quantum key distribution with discrete modulation. Quantum Sci. Technol. 2, 024010 (2017).
Kasai, K., Fujisaka, Y. & Onsjö, M. http://qo.phys.gakushuin.ac.jp/kasai/ Accessed 28 May 2018 (2009).
Hayashi, M. & Tsurumaru, T. More efficient privacy amplification with less random seeds via dual universal hash function. IEEE Trans. Inf. Theory 62, 2213–2232 (2016).
Puttnam, B. J. et al. High capacity transmission systems using homogeneous multi-core fibers. J. Light. Technol. 35, 1157–1167 (2017).
Acknowledgements
This work was partly funded by ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan) and JSPS KAKENHI Grant Number JP18H01157, JP18H05237 and JP17H01281.
Author information
Authors and Affiliations
Contributions
T.E., T.H. and B.P. carried out the main experiments. T.E. and B.P. performed the measurements of the classical channels. T.H. and R.N. developed setup and protocols for the CV-QKD system. B.P., G.R. and R.L. developed the classical coherent communication system. T.E., T.H., B.P., M.F., M.T. and M.S. planned the experiments. Y.A., M.T., N.W. and M.S. coordinated the project and supervised the work. T.E. wrote the paper with extensive contributions from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eriksson, T.A., Hirano, T., Puttnam, B.J. et al. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun Phys 2, 9 (2019). https://doi.org/10.1038/s42005-018-0105-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0105-5
This article is cited by
-
ChaQra: a cellular unit of the Indian quantum network
Scientific Reports (2024)
-
Continuous-mode quantum key distribution with digital signal processing
npj Quantum Information (2023)
-
Quantum key distribution in a packet-switched network
npj Quantum Information (2023)
-
Optical soliton based long-haul data transmission over MMF employing OAM multiplexing technology
Optical and Quantum Electronics (2023)
-
Sub-Gbps key rate four-state continuous-variable quantum key distribution within metropolitan area
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.