Abstract
Patterning nanomagnets in three-dimensions presents a new paradigm in condensed matter physics and allows access to a plethora of phenomena including robust spin textures, magnetic metamaterials home to defects carrying magnetic charge and ultrahigh density devices that store information in three-dimensions. However, the nanostructuring of functional magnetic materials into complex three-dimensional geometries has thus far proven to be a formidable challenge. Here we show magnetic nanowires can be arranged into 3D frustrated magnetic nanowire lattices by using a combination of 3D polymer nanoprinting and metallic deposition. The fabricated nanowires are single domain and they switch via nucleation and propagation of domain walls. Deep nanoscale magnetic imaging and finite element simulations elucidate the spin texture present on the 3D nanostructured lattice. Our study demonstrates a generic platform for the production of 3D nanostructured magnetic materials allowing the realisation of racetrack memory devices and 3D nanostructured systems that mimic bulk frustrated crystals.
Similar content being viewed by others
Introduction
Frustration is defined as the inability for all pairwise interactions to be simultaneously satisfied1 and is a phenomenon that impacts a wide variety of areas. For example, frustration is important in the production of solar flares2, in the folding of biological molecules3 and in the bonding of water ice4. Realising model systems for studying frustration will help to elucidate a range of complex phenomena in science. One such model system is the spin-ice materials, which have a pyrochlore structure with Ising spins located on corner-sharing tetrahedra5. The crystal field forces the spins to point along the local [111] direction and frustration leads to a local ordering principle known as the ice-rule5, whereby two spins point into a tetrahedron and two spins point out. This leads to an extensive ground state degeneracy and an associated residual entropy found at low temperature. In addition, spin-ice systems have been found to harbour monopole-like defects that propagate through the material and interact via a magnetic Coulomb’s law6,7. In 2006, it was shown that arranging magnetic nanowires into frustrated geometries allows much of the physics of spin-ice to be captured8. In order to emulate the geometry of spin-ice, magnetic nanowires were arranged in a square lattice with four spins meeting at a vertex. Since magnetic nanowires are essentially bipolar, they are considered effective Ising spins8. The advantage of these “artificial spin-ice” (ASI) systems is that the magnetic islands have dimensions of order 100 nm and thus can be probed with magnetic microscopy. This has led to a wealth of studies9 probing the physics of ordering8,10,11,12,13,14,15, thermodynamics16,17 and the nature of monopole-like defects in these systems18,19,20,21,22,23,24,25. However, it was acknowledged early on that square ASI is not a perfect analogy with the bulk counterpart, because the energy of interaction between neighbouring islands depends upon those chosen8. Layered ASI systems have partially solved this problem17,18,26. By offsetting one of the sublattices by some height such that the energy of interaction between all nearest neighbours becomes equivalent, a magnetic Coulomb phase has been realised27. Unfortunately, such layered systems still do not capture the physics of bulk systems. This is due to the magnetic islands not being arranged in the exact geometry of the spins in the bulk material, along the local [111] direction18. Ideally one would like to produce a diamond-bond 3D nanostructured magnetic lattice, which maps perfectly onto the spin-ice system.
Quite separately, there has been a recent surge in the interest upon 3D nanostructured magnetic materials28. This has partially been driven by theoretical studies that show 3D nanostructuring of magnetic materials28 offers a new means to control the arrangement of spins in ordered magnetic materials by harnessing geometry-dependent magnetic energies and those provided by more subtle curvature-driven effects29. In addition, applications-driven research remains, with the realisation that 3D nanostructuring of magnetic materials will directly enable new racetrack-type memories30.
Thus far there have been three main ways to realise 3D magnetic nanostructures. The simplest involves electrodeposition of a magnetic material into a porous template and this usually yields pure nanowires of cylindrical geometry31,32,33. Here, utilising electrodeposition allows a large variety of magnetic materials to be used in filling the templates providing enormous flexibility. A disadvantage of this approach is that the templates usually have cylindrical pores, limiting the exploration of more complex 3D geometries. Focussed electron beam deposition (FEBD)34 is a newer methodology that harnesses the interaction between an electron beam and a chemical precursor. The reaction takes place at the point of electron focus and by moving this with respect to the substrate, 3D nanostructures can be fabricated. The method is powerful since it allows the realisation of almost any 3D geometry, potentially allowing one to probe the rich physics in 3D magnetic nanostructured systems. However, when the beam interacts with the chemical precursor and any background gases within the chamber, it also leads to the deposition of nonmagnetic contaminants, such as carbon and oxygen. These become embedded within the nanowire and impact the magnetic properties of the system. Despite this, a number of ground-breaking studies have explored the use of FEBD in the realisation of 3D magnetic nanostructures. In a pioneering study, Co nanowires in 3D geometries were produced and measured using magneto-optical Kerr effect (MOKE) and magnetic force microscopy35. Unfortunately, the nanowires were found to be only 85% Co and the nanowires exhibited irreproducible switching characteristics. More recent studies have focussed upon the growth of more complex 3D nano-cube and nano-tree geometries36,37. Here, detailed micro-Hall measurements were used to measure the magnetic switching within the structures36,37. Unfortunately, the structures were found to be 64% metal (Co and Fe) and measurements indicated the individual nanowires were not behaving single domain36. A further study by the same authors also concluded the magnetisation within nanowires was inhomogeneous with curling magnetisation states37. Recent work has shown that FEBD of Pt when coupled with NiFe evaporation can yield planar magnetic nanowires in 3D geometries, which switch via domain wall motion38. The magnetic switching within these simple systems was measured using a novel dark-field magneto-optical Kerr effect magnetometry technique. This methodology is very exciting but has not been applied to the manufacture of complex 3D nanostructured lattices. Finally, two-photon lithography and electrodeposition have been used to fabricate complex 3D magnetic nanostructures39,40 which were also very pure (>95% Co). Unfortunately, the structures made within this study were relatively large (>400 nm) and shown to be multi-domain39.
Measurement of the 3D spin texture within magnetic materials is also a significant challenge. A recent ground-breaking measurement demonstrated the use of hard X-ray tomography to produce a 3D reconstruction of the spin-texture within a micron sized GdCo2 cylinder41. Combining 3D lithography techniques with nanoscale magnetic imaging offers the possibility of directly visualising ground state ordering in complex 3D artificial crystals. In particular, replicating the exact spin arrangement seen in the bulk frustrated materials known as spin-ice5 will allow realisation of new model systems for studying frustration.
Here we demonstrate a new methodology to realise single domain magnetic nanowires within complex-frustrated 3D nanostructured lattices (3DNL). With these newly realised samples, we directly observe via optical magnetometry and finite element simulations, switching by domain wall motion through the 3DNL. In addition, simulations and nanoscale magnetic imaging allows the determination of the exact spin texture upon the 3DNL. Our results suggest these systems may be considered a 3D ASI system.
Results
3D nanowire lattice design
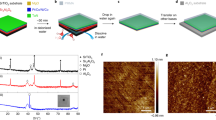
The fabrication methodology is sketched in Fig. 1. Two-photon lithography (TPL) is used to manufacture the desired 3D geometric network. Any geometry can be chosen so long as the upper surface of the desired nanowires is not masked. For this study, a diamond-bond lattice geometry has been chosen to demonstrate that complex nanowire networks can be created and also to capture the geometric arrangement of spins within spin-ice5. After the polymer network has been created, evaporation is used to deposit a magnetic material (Ni81Fe19) upon the nanowires. Evaporation onto a curved geometry yields magnetic nanowires of crescent-shaped cross-section42,43 (Fig. 1d inset).
Schematic of fabrication methodology. a Negative-tone resist is drop cast onto the substrate. b Two-photon lithography is used to define a diamond-bond lattice within the resist. c Development removes unexposed resist revealing the freestanding diamond lattice structure. d Magnetic material is evaporated onto the lattice structure. The exposed surface of the lattice is coated yielding a 3D network of magnetic nanowires. Inset: The nanowires have a crescent-shaped geometry as shown
The nanowire network of interest is 10 μm above the substrate minimising the stray field from any magnetic material on the planar substrate.
Physical characterisation
The 3DNL arrays have dimensions 50 μm × 50 μm × 10 μm (Fig. 2a). The Ni81Fe19 nanowires have an inner radius of curvature of 80 nm yielding an effective outer arc length of 330 nm and have length of ~1000 nm. Since evaporation is used to deposit the magnetic material, the resulting magnetic nanowires are continuous for three sub-lattice layers (L1, L2 and L3) into the z-direction (Fig. 2b). Figure 2c, d shows angled views of the nanowire network. Both images show the 3D geometry of the network. In Fig. 2c it is clear that the polymer nanowire geometry deviates from the perfect cylindrical geometry proposed in Fig. 1 and the nanowires are found to have a greater axial size than lateral size. This effect is well known in two-photon lithography and it is due to the ellipsoidal point-spread function of the laser at focus39. Some methodologies allow this to be optimised (see Discussion) but in this study, since evaporation simply coats the top surface of the polymer nanowire, it is not a concern. A schematic of the grown 3DNL is shown in Fig. 2e (rotating view shown in Supplementary Movie 1), with an individual wire cross-section, based upon SEM data shown in the inset. The Ni81Fe19 is seen to subtend an arc of ~80° either side of the centre, beyond which the polymer has vertical sidewalls. In Fig. 2e the continuity of the L1, L2 and L3 layers can be seen within the lattice. The fourth layer (L4) is seen to have a discontinuity at the lower junction as a direct result of shadowing from L1. Below L4 the polymer nanowires are perfectly shadowed by layers above, to within the positional reproducibility of the TPL galvanometer (~20 nm). From geometric considerations, any magnetic material present on L5 or lower is expected to have a magnetic moment of less than 10-16 Am2. Accordingly, we find that the dipolar energy of interaction between L5 and L4 wires is two orders of magnitude lower than the energy of interaction between wires on upper layers. Thus, we conclude that any dipolar interaction between potential material upon L5 or lower, and nanowires L1, L2, L3 and L4, is negligible. Figure 2e also shows the interesting geometry of the lattice at junctions (for example between L1 and L2). Due to the extended axial nanowire dimension, a constriction is expected at the junction, which may impact domain wall propagation within the lattice.
Physical and material properties of the 3D magnetic nanowire lattice. a Scanning electron microscope image of the entire array (Top view). Scale indicates 10 μm. b Close-up image of the nanowire lattice. L1, L2 and L3 indicate the different sub-lattice layers. Scale indicates 2 μm. c, d Angled images of the 3D nanowire lattice. The dotted box in c indicates a single bipod unit. Scale bar in c is 1 μm and in d it is 10 μm. e A schematic of the realised 3D magnetic nanowire lattice. Inset: Cross-sectional geometry of the nanowires. Yellow depicts polymer and grey depicts Ni81Fe19. f Energy dispersive X-ray spectroscopy images for carbon (scale indicates 20 μm), g for nickel (scale indicates 20 μm), h for nickel at higher magnification (scale indicates 1 μm) and i for iron (scale indicates 20 μm). j Atomic force microscopy image of the nanowire lattice. Scale indicates 1 μm and is preserved in both directions
Energy dispersive X-ray spectroscopy (EDX) allows one to visualise the chemical constituents upon the 3DNL. The main constituent of the resist is carbon and mapping this element (Fig. 2f) yields an image of the underlying polymer template. The slight deformation of the array edge is due to long exposure to an electron beam (~8 h), which was required to obtain sufficient signal. Mapping the Ni content across the array (Fig. 2g, h) shows that the deposited magnetic material is taking the 3D form of the polymer template and that the magnetic nanowire network is continuous. Finally, obtaining the Fe signal (Fig. 2i) allows the composition of the magnetic nanowires to be determined. The ratio of nickel to iron using EDX analysis is found to be 4.26, in excellent agreement with the composition of Ni81Fe19. Careful optimisation of feedback parameters also allows direct atomic force microscopy of the 3DNL surface (Fig. 2j). Both the upper L1 and lower L2 nanowire layers are resolved.
A key question with such lattices is the extent to which nanowire quality (eg. geometry, composition and roughness) varies with sub-lattice layers. The polymer nanowires were written utilising a power compensation routine to ensure minimal difference between exposure for different layers. SEM analysis shows mean nanowire widths of 252 ± 7, 255 ± 7, 264 ± 7, 260 ± 8 and 269 ± 5 nm for L1 (highest), L2, L3, L4 and L5 (lowest), respectively (see Supplementary Figure 1). This indicates that the power compensation routine is working correctly and minimal variation in width is observed between layers. Surface roughness of wires is more difficult to measure for all layers. Visual inspection of each layer with SEM does not show any qualitative variation. Atomic force microscopy images were used to carry out roughness analysis upon L1 and L2 nanowires, yielding values of 10.8 ± 4.3 and 16.1 ± 3.2 nm, respectively. This suggests that the nanowire roughness across different layers does not vary significantly within error.
Finite-element simulations and optical magnetometry
Finite element simulations were performed in order to investigate the switching within the underlying nanowires. For details of geometry construction see Supplementary Figure 2. We start by allowing the nanowire magnetisation to relax in the absence of an applied magnetic field. The result is a single domain state, with magnetisation lying along the long axis of the wire (Fig. 3a). Planar magnetic nanowires are well known to switch via domain wall motion44 and the domain wall type depends upon wire width and thickness45. The nanowires that make up the 3DNL are distinct from their planar counterparts since they have both a graded thickness and cross-sectional curvature. A simulation was performed in order to investigate the domain wall type seen within crescent-shaped nanowires. A vortex domain wall relaxes in the region between two opposing magnetisation directions (Fig. 3b). Figure 3c shows a simulated hysteresis loop of the nanowire when the field is applied at an angle of 35° with respect to the long axis. This field geometry matches the angle of the field with respect to upper wires in optical magnetometry experiments. The loop exhibits an abrupt transition, indicative of domain wall motion, at a magnetic field of ~50 mT. Rotating the magnetic field by 90° such that it has no component along the wire long-axis, yields a hard-axis type loop with low remanence (Fig. 3d), demonstrating the high shape anisotropy exhibited by the wire.
Finite element simulations and experimental magnetometry upon the 3D magnetic nanowire lattice. a Simulated remanent magnetisation profile after relaxation. Inset: The geometry of the magnetic nanowires. b Simulated relaxation with opposing magnetisation showing a vortex domain wall. c Simulated hysteresis loop of single magnetic nanowire with field applied at 35° to the wire long axis. An abrupt switching transition is seen, indicative of domain wall motion. d Simulated loop with field applied perpendicular to long axis projection. e Longitudinal magneto-optical Kerr effect loop of the thin-film upon the substrate (blue) and the 3D nanowire lattice (black: up sweep, red: down sweep). The nanowire lattice is found to have a coercivity one order of magnitude higher than the film as expected for a nanostructured magnetic system. Green arrows indicate the polar magneto-optical Kerr effect signal. f Simulated loop for bipod structure with field applied as shown in inset
Measuring the magnetic properties of 3D magnetic nanostructures is a key challenge. Here, focussed MOKE magnetometry is utilised to measure the switching of the 3DNL. A distinct advantage of realising dense 3DNL samples is the optical scattering centres provided by buried wires. Such a system significantly reduces the specular reflection from the substrate. In order to probe the in-plane magnetisation of the 3DNL, MOKE measurements were performed with the wave vector at 45° angle of incidence and with the field (H1) in the substrate plane (Fig. 3e red/black curve). After careful alignment of the laser spot, we measure the 3DNL with only minimal signal from the substrate. The loop exhibits a sharp transition indicative of domain wall motion, an enhanced coercive field of approximately 8.2 mT, indicative of nanostructuring and a high remanence. The loop also exhibits peaks close to the coercive field (green arrow, Fig. 3e) due to the polar MOKE effect (see Supplementary Note 1). Moving the laser spot off the 3DNL and onto the sheet film produces a loop characteristic of bulk Ni81Fe19 (Fig. 3e blue). A key question with respect to the MOKE measurement upon the 3DNL is the extent to which it is probing each of the individual layers. In order to answer this question, the experimental data was compared to simulated bipod and tetrapod loops. A tetrapod is a unit cell for combined L1 and L2 layers and its simulated loop (see Supplementary Figure 3) has an extended tail leading to saturation, as well as a low remanence (<0.5Ms), not seen in our experimental data. The simulated bipod loop (Fig. 3f) has both longitudinal (Mx) and polar (Mz) contributions that, when superimposed, qualitatively matches our measured loop, indicating MOKE in this configuration is only sensitive to the L1 layer.
Magnetic force microscopy
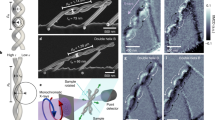
Further experiments and simulations were performed in order to examine the magnetisation configuration in the 3DNL. Figure 4a shows a magnetic force microscopy (MFM) image of the 3DNL surface after a saturating field along H1. For clarity, the image has been processed to improve the contrast in the upper nanowires. Raw data are shown in Supplementary Figure 4. The upper-most layer of the lattice terminates in a series of bipod structures (L1 in Fig. 2b, c). Strong contrast of the same complex pattern is measured in each bipod unit. Identical contrast is also observed after a saturating field in the plane of the substrate but perpendicular to H1 (see Supplementary Figure 5). In order to confirm the contrast is truly magnetic in origin and not an artefact of the topography, an image was measured in the same sample area but with a reversed tip magnetisation, as shown in Fig. 4b. Here it is expected that positive colour contrast (yellow) should now be measured as negative colour contrast (black) and vice-versa. Close examination of individual bipod units in the two tip configurations (Fig. 4c, d) show they have inverted contrast, confirming that the method is truly imaging the magnetic configuration of the 3DNL surface. Interestingly, contrast at the vertices (Fig. 4e, f), where four wires meet, also exhibits an inversion of MFM contrast upon reversing the tip magnetisation. Raw data also show this inversion of contrast as shown in Supplementary Figure 6.
Determining the magnetic configuration upon the 3D nanostructured lattice. a Magnetic force microscopy image of the 3D lattice surface after field has been applied along projection of upper wire long axis (H1). Scale bar indicates 2 μm. b Image of same area but with reversed tip magnetisation. Scale bar indicates 2 μm. c Magnetic contrast of an individual bipod unit upon the surface. d Magnetic contrast of bipod unit after tip magnetisation has been reversed. e Magnetic contrast taken at vertex, where four wires meet. f Magnetic contrast taken at vertex after tip magnetisation has been reversed. g–j Finite element simulations of bipod structures whereby the wires were allowed to relax with magnetisation in head-to-tail arrangement and tail-to-tail arrangement, respectively. k–m Finite element simulations showing low energy 2-in/2-out states that can be realised within a magnetic tetrapod structure composed of single domain wires. n–q Finite element simulations showing higher energy 3-in/1-out and 3-out/1-in states. Red and yellow indicate MFM contrast ρ = ∇∙M
Discussion
Figure 4g–j shows simulated remanent states for a bipod structure whereby the individual nanowire magnetisation vectors were relaxed in the same and in opposing directions, respectively. The red and yellow colour contrast represents the divergence of the magnetisation (∇ • M), which is an effective simulation of the MFM signal46. Comparison between Fig. 4c, h shows good agreement, confirming the nanowires within the 3DNL are single domain. A more detailed vector plot of the magnetisation distribution within the bipod unit (Fig. 4g) shows that the magnetisation smoothly rotates at the upper vertex area. Here the change in sign of Mz yields MFM contrast at the vertex area as observed experimentally. Further discussion of MFM contrast can be found in Supplementary Note 2.
Figure 4i, j shows a two-out state for the upper bipod unit. This high energy state consists of a vortex domain wall pinned on the vertex. When examining the hysteresis loop obtained from the lattice (Fig. 3e), a single abrupt transition is obtained suggesting the wall nucleation field is sufficient to overcome any pinning at the vertex. This matches previous studies where it has been noted that in 2D connected ASI structures within the vortex regime, vertex pinning is not observed21.
Magnetic nanowires of crescent-shaped cross-sectional geometry have not been considered extensively within the literature and certainly not in complex diamond lattice geometries. A key question here is the extent to which this nanowire geometry impacts the available remanent states when compared to a more idealised cylindrical shell geometry. In such a geometry, the vertex will have the idealised four-fold rotational symmetry lending itself to complete degeneracy of the ice-rule states (2-in/2-out states). One concern here is that the broken symmetry in our structures will yield different energies for ice-rule states. More symmetric structures are technologically very challenging and would require both the use of advanced non-linear optical techniques to obtain a spherical point spread function during the TPL process and a vapour-based deposition method to ensure all sidewalls are coated. Figure 4k–q shows the remanent state for tetrapod structures with all possible magnetisation configurations, except those that can be obtained by simple rotational transformations. To aid comparison with 2DASI literature, we have adopted the same vertex nomenclature. The vertex types where four-magnetisation vectors point in/out of a vertex were unstable and these instead relaxed into lower energy configurations. All simulations yield single domain nanowires indicating that the nanowires within our 3D nanolattice can approximate Ising spin behaviour allowing parallels to be drawn with spin-ice5. We emphasise that the nanowire configuration within our lattice maps directly onto the spin-ice lattice, allowing analogy with this bulk frustrated material. Contrary to what is seen in 2DASI where type 1 and type 2 vertices have different energy, computation of the energies (Supplementary Figure 7) in our structures shows that all type 1 and type 2 vertex energies agree to within 10%. This result is very exciting since it allows the possibility of realising a magnetic Coulomb phase, seen previously in layered systems27. However, in our system we note that replicating the geometry of the spin-ice lattice will yield a vanishing string tension between monopole excitations.
The simulated MFM contrast at the vertex within each of the configurations shown in Fig. 4k–q is distinct and depends upon the magnetisation within each of the underlying nanowires. Only one of the configurations (Fig. 4m) shows adjacent lobes of inverted contrast at the vertex, matching the experimental signature shown in Fig. 4e, f. Thus, upon reducing the saturating field along H1 to remanence, the upper wires remain aligned with the field as expected, but 3D dipolar interactions within this frustrated geometry forces the lower wires to adopt the preferred low energy state. Overall, this yields one of the low energy ice-rule configurations whereby two spins point into a vertex and two spins point out. Now that it has been demonstrated that 3D nanostructured frustrated lattices can be fabricated and that the spin texture can be measured via conventional magnetic microscopy, it opens up a huge array of potential experiments, analogous to those carried out upon 2D artificial spin-ice whereby the vertex type and correlations are measured in order to determine the rigidity of the ice-rule and long range ordering. Such experiments would require the development and rigorous testing of demagnetisation or thermalisation routines for 3D nanostructured samples but may ultimately provide deep insight into ground state ordering within bulk frustrated magnets.
In conclusion, we have demonstrated the fabrication and measurement of a 3D frustrated nanowire lattice. We have shown that the individual nanowires are single domain; magnetic switching of the lattice is dominated by the nucleation and propagation of vortex domain walls, and this can be probed directly using optical magnetometry. Finite element simulations show that the low energy ice-rules states corresponding to type 1 and type 2 vertices in 2DASI are close in energy, suggesting our system is a candidate 3D ASI material. Furthermore, we show directly using magnetic force microscopy experiments and finite element simulations that the vertex contrast can be used to elucidate the spin texture upon the lattice surface. Ice-rule violating defects within bulk spin-ice materials may be considered free monopoles in M and H. We note that the 3D symmetry of the lattice in our system will allow the realisation of analogous magnetic charges6 that propagate freely and with the absence of any string tension seen in 2D artificial materials. The simplicity of our approach also lends itself to the realisation of a thermal 3DASI, by utilising thin NiFe layers. Finally, we note that our study will enable new avenues for the investigation of domain wall propagation through 3D magnetic nanowire lattices, allowing one to readily realise 3D magnetic racetrack systems as originally envisaged30.
Methods
Fabrication
Glass coverslips (22 mm × 22 mm) with thickness varying between 0.16–0.19 mm were used as substrates for this study. They were cleaned using acetone and isopropyl alcohol (IPA) solutions before immersion oil (Immersol 518 F) and a negative-tone photoresist (IPL-780) were drop cast onto the lower and upper faces, respectively. A diamond lattice covering a volume of 50 µm × 50 µm × 10 µm was then exposed within the photoresist using a two-photon lithography procedure. The samples were developed in propylene glycol monomethyl ether acetate for 20 min, removing any unexposed photoresist. Finally, the samples were cleaned in IPA and dried with a compressed air gun.
Permalloy (Ni81Fe19) of 99.99% purity was deposited via line of sight deposition. Samples were mounted at the top of a thermal evaporator. A 0.06 g ribbon of Ni81Fe19, cleaned in Isopropyl Alcohol, was placed in an alumina evaporation boat before evacuation of the chamber to a base pressure below 10−6 mbar. A uniform 50 nm film was deposited at a rate of 0.2 nm/s.
Scanning electron microscopy (SEM) and energy dispersive X-ray analysis (EDX)
Imaging was performed using a Zeiss Sigma HD Field Emission Gun Analytical SEM. Images were taken from top view as well as at a 45° tilt with respect to the substrate plane. Samples were mounted upon a SEM stub using carbon paint, which was placed in the SEM chamber. Prior to imaging, the chamber pressure was brought below 1 × 10−4 mbar. EDX compositional mapping was performed upon a sample using a 5 kV accelerating voltage for an extended period of time in order to maximise the resolution. Spectra from 10 locations were averaged to verify the intended 81:19 ratio of Ni:Fe in the sample.
Magnetic force microscopy (MFM)
MFM on the three-dimensional nanowire network was taken using a Bruker Dimension 3100 atomic force microscope (AFM) operated in tapping mode. Prior to mounting, the commercial low-moment MFM tips were magnetised parallel to the tip axis using a 0.5 T permanent magnet. To magnetise the sample, a bespoke electromagnet was mounted on the surface of the AFM stage, allowing the application of a uniform magnetic field. The MFM tip was raised by several millimetres before application of the field. Images were taken, such that the fast scan axis was at an angle of 45° to layer L1 of the lattice. MFM data were captured using a lift height of 100 nm. MFM images were only taken once the feedback settings had been carefully optimised to ensure sample topography was being accurately measured.
Magneto-optical Kerr effect magnetometry (MOKE)
A 100-mW, 637-nm wavelength laser was attenuated to a power of ~6 mW, expanded to a diameter of 1 cm, and passed through a Glan–Taylor polarizer to obtain an s-polarized beam. The beam was then focussed onto the sample using an achromatic doublet (f = 10 cm), to obtain a spot size of approximately 10 μm2. The reflected beam was also collected using an achromatic doublet (f = 10 cm) and passed through a second Glan–Taylor polarizer, from which the transmitted and deflected beams were directed onto two amplified Si photodetectors, yielding the Kerr and reference signals, respectively. A variable neutral density filter was used to ensure that the reference and Kerr signals were of similar values. Subtraction of the reference from the Kerr signal compensates for any change in the laser intensity drift and also eliminates any small transverse Kerr effect from the signal.
Finite element simulations
A series of micro-magnetic simulations using finite element method discretisation were performed using the NMAG code47. These simulations are performed by numerical integration of the Landau-Liftshitz equation upon a finite element mesh. Typical Ni81Fe19 parameters were used, i.e. MS = 0.86 × 106 A m−1, A = 13 × 10−12 J m−1 with zero magnetocrystalline anisotropy. The simulations were performed at a temperature of 0 K that has previously been shown to capture the correct spin-texture seen in room temperature measurements, but a systematic difference in coercivity (factor of ~5) is observed. The wire cross-section is a crescent shape where the arcs subtend a 160° angle. The inner arc is defined from a circle with 80 nm radius corresponding to the 160 nm lateral feature size of the TPL system. Line of sight deposition results in a film thickness proportional to the scalar product of the deposition direction and the surface normal; therefore, the outer arc is based on an ellipse with a minor radius of 80 nm and major radius of 130 nm. The length of the wires is set to 780 nm, due to computational restraints and the wires are arranged as single wires, bipod and tetrapod structures. A comprehensive description of the geometries is given in Supplementary Note 3. The geometries were meshed using adaptive mesh spacing with a lower limit of 3 nm and upper limit of 5 nm.
Data availability
Information on the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalogue at https://doi.org/10.17035/d.2018.0050718074.
References
Bramwell, S. T. et al. Spin-ice state in frustrated magnetic pyrochlore materials. Science 294, 1495 (2001).
Pustil’nik, L. A. Solar flare phenomena as phase transition caused by frustration of current percolation. Astrophys. Space Sci. 264, 171–182 (1998).
Ferreiro, D. U., Komives, E. A. & Wolynes, P. G. Frustration in biomolecules. Q. Rev. Biophys. 47, 285–363 (2014).
Pauling, L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 57, 2680–2684 (1935).
Ramirez, A. P. et al. Zero-point entropy in ‘spin ice’. Nature 399, 333–335 (1999).
Castelnovo, C., Moessner, R. & Sondhi, S. Magnetic monopoles in spin ice. Nature 451, 42–45 (2008).
Giblin, S. R. et al. Creation and measurement of long-lived magnetic monopole currents in spin ice. Nat. Phys. 7, 252–258 (2011).
Wang, R. F. et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).
Nisoli, C., Moessner, R. & Schiffer, P. Colloquium: artificial spin ice: designing and imaging magnetic frustration. Rev. Mod. Phys. 85, 1473–1490 (2013).
Qi, Y., Brintlinger, T. & Cumings, J. Direct observation of the ice rule in an artificial kagome spin ice. Phys. Rev. B 77, 094418 (2008).
Tanaka, M. et al. Magnetic interactions in a ferromagnetic honeycomb nanoscale network. Phys. Rev. B 73, 052411 (2006).
Farhan, A. et al. Direct observation of thermal relaxation in artificial spin ice. Phys. Rev. Lett. 111, 057204 (2013).
Zhang, S. et al. Crystallites of magnetic charges in artificial spin ice. Nature 500, 553–557 (2013).
Kapaklis, V. et al. Thermal fluctuations in artificial spin ice. Nat. Nanotechnol. 9, 514–519 (2014).
Branford, W. R. et al. Emerging chirality in artificial spin ice. Science 335, 1597–1600 (2012).
Nisoli, C. et al. Ground state lost but degeneracy found: the effective thermodynamics of artificial spin ice. Phys. Rev. Lett. 98, 217203 (2007).
Moller, G. & Moessner, R. Artificial square ice and related dipolar nanoarrays. Phys. Rev. Lett. 96, 237202 (2006).
Mol, L. A. S., Moura-Melo, W. A. & Pereira, A. R. Conditions for free magnetic monopoles in nanoscale square arrays of dipolar spin ice. Phys. Rev. B 82, 054434 (2010).
Ladak, S. et al. Direct observation and control of magnetic monopole defects in an artificial spin-ice material. New J. Phys. 13, 063032 (2011).
Ladak, S. et al. Direct observation of magnetic monopole defects in an artificial spin-ice system. Nat. Phys. 6, 359–363 (2010).
Ladak, S. et al. Disorder-independent control of magnetic monopole defect population in artificial spin-ice honeycombs. New J. Phys. 14, 045010 (2012).
Ladak, S. et al. Monopole defects and magnetic Coulomb blockade. New J. Phys. 13, 023023 (2011).
Phatak, C. et al. Nanoscale structure of the magnetic induction at monopole defects in artificial spin-ice lattices. Phys. Rev. B 83, 174431 (2011).
Zeissler, K. et al. The non-random walk of chiral magnetic charge carriers in artificial spin ice. Nat. Sci. Rep. 3, 1252 (2013).
Walton, S. K. et al. Limitations in artificial spin ice path selectivity: the challenges beyond topological control. New J. Phys. 17, 013054 (2015).
Chern, G., Reichhardt, C. & Nisoli, C. Realizing three-dimensional artificial spin ice by stacking planar nano-arrays. Appl. Phys. Lett. 104, 4861118 (2014).
Perrin, Y., Canals, B. & Rougemaille, N. Extensive degeneracy, Coulomb phase and magnetic monopoles in artificial square ice. Nature 540, 410–413 (2016).
Fernandez-Pacheco, A. et al. Three-dimensional nanomagnetism. Nat. Commun. 8, 15756 (2017).
Streubel, R. et al. Magnetism in curved geometries. J. Phys. D.Appl. Phys. 49, 363001 (2016).
Parkin, S. S. P., Hayashi, M. & Thomas, L. Magnetic domain-wall racetrack memory. Science 320, 190–194 (2008).
Da Col, S. et al. Nucleation, imaging, and motion of magnetic domain walls in cylindrical nanowires. Appl. Phys. Lett. 109, 4961058 (2016).
Da Col, S. et al. Observation of Bloch-point domain walls in cylindrical magnetic nanowires. Phys. Rev. B 89, 180405 (2014).
Ivanov, Y. P. et al. Single crystalline cylindrical nanowires—toward dense 3D arrays of magnetic vortices. Sci. Rep. 6, 23844 (2016).
De Teresa, J. M. et al. Review of magnetic nanostructures grown by focused electron beam induced deposition (FEBID). J. Phys. D. Appl. Phys. 49, 243003 (2016).
Fernandez-Pacheco, A. et al. Three dimensional magnetic nanowires grown by focused electron-beam induced deposition. Sci. Rep. 3, 1492 (2013).
Keller, L. et al. Direct-write of free-form building blocks for artificial magnetic 3D lattices. Sci. Rep. 8, 6160 (2018).
Al Mamoori, M. K. I. et al. Magnetic characterization of direct-write free-form building blocks for artificial magnetic 3D lattices. Materials 11, 289 (2018).
Sanz-Hernandez, D. et al. Fabrication, detection, and operation of a three-dimensional nanomagnetic conduit. ACS Nano 11, 11066–11073 (2017).
Williams, G. I. et al. Two photon lithogrpahy for 3D magnetic nanostructure fabrication. Nano Research 11, 845–854 (2018).
Sahoo, S. et al. Ultrafast magnetization dynamics in a nanoscale three-dimensional cobalt tetrapod structure. Nanoscale 10, 9981–9986 (2018).
Donnelly, C. et al. Three-dimensional magnetization structures revealed with X-ray vector nanotomography. Nature 547, 328 (2017).
Albrecht, M. et al. Magnetic multilayers on nanospheres. Nat. Mater. 4, 203–206 (2005).
Streubel, R. et al. Magnetically capped rolled-up nanomembranes. Nano Lett. 12, 3961–3966 (2012).
Atkinson, D. et al. Magnetic domain-wall dynamics in a submicrometre ferromagnetic structure. Nat. Mater. 2, 85–87 (2003).
McMichael, R. D. & Donahue, M. J. Head to head domain wall structures in thin magnetic strips. IEEE Trans. Magn. 33, 4167–4169 (1997).
Hartman, U. Magnetic force microscopy. Annu. Rev. Mater. Sci. 29, 53 (1999).
Fischbacher, T. et al. A systematic approach to multiphysics extensions of finite-element-based micromagnetic simulations: Nmag. IEEE Trans. Magn. 43, 2896–2898 (2007).
Acknowledgements
S.L. acknowledges funding from the EPSRC (EP/R009147/1), as well as discussions with Prof Sean Giblin and Prof Wolfgang Langbein. We gratefully acknowledge technical support from Duncan Muir during EDX acquisition. We gratefully acknowledge support from Advanced Research Computing at Cardiff (ARCCA).
Author information
Authors and Affiliations
Contributions
S.L. conceived of the study and wrote the manuscript. A.M. carried out fabrication of 3D nanolattice samples, performed SEM, EDX, AFM and MFM upon the samples. M.H. carried out SEM and MOKE upon the samples. A.V. created the geometries and carried out finite element simulations upon single wire geometries, bipod geometries and tetrapod geometries and also performed SEM upon samples. A.H. carried out SEM and EDX analysis. All authors contributed to the final draft.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
May, A., Hunt, M., Van Den Berg, A. et al. Realisation of a frustrated 3D magnetic nanowire lattice. Commun Phys 2, 13 (2019). https://doi.org/10.1038/s42005-018-0104-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0104-6
This article is cited by
-
Ultrastrong magnon-magnon coupling and chiral spin-texture control in a dipolar 3D multilayered artificial spin-vortex ice
Nature Communications (2024)
-
Exploring the phase diagram of 3D artificial spin-ice
Communications Physics (2023)
-
Nonlinear multi-magnon scattering in artificial spin ice
Nature Communications (2023)
-
Combining two-photon lithography with laser ablation of sacrificial layers: A route to isolated 3D magnetic nanostructures
Nano Research (2023)
-
Direct observation of a dynamical glass transition in a nanomagnetic artificial Hopfield network
Nature Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.