Abstract
Quantum memory capable of stopping flying photons and storing their quantum coherence is essential for scalable quantum technologies. A room-temperature broadband quantum memory will enable the implementation of large-scale quantum systems for real-life applications. Due to either intrinsic high noises or short lifetime, it is still challenging to find a room-temperature broadband quantum memory beyond conceptual demonstration. Here, we present a far off-resonance Duan–Lukin–Cirac–Zoller (FORD) protocol and demonstrate the broadband quantum memory in room-temperature atoms. We observe a low unconditional noise level of 10−4 and a cross-correlation up to 28. A strong violation of Cauchy–Schwarz inequality indicates high-fidelity generation and preservation of non-classical correlation. Furthermore, the achieved cross-correlation in room-temperature atoms exceeds the key boundary of 6, above which quantum correlation is able to violate Bell’s inequality. Our results open up the door to an entirely new realm of memory-enabled quantum applications at ambient conditions.
Similar content being viewed by others
Introduction
Quantum technologies, incorporating quantum mechanics into communication, information processing and metrology, promise spectacular quantum-enhanced advantages beyond what can be done classically1. However, quantum states are very fragile and easily get lost to the environment; meanwhile, their generation and quantum operations are mostly probabilistic. These problems make it exponentially hard to build long-distance quantum channel for quantum communications2,3 and large quantum systems for quantum computing4,5. Quantum memory6 allows quantum states to be stored and retrieved in a programmable fashion, therefore providing an elegant solution to the probabilistic nature and associated limitation by coordinating asynchronous events7,8,9.
Enormous advances in quantum memory have been made by developing various photon storage protocols and their physical implementations, such as electromagnetically induced transparency (EIT)10,11,12, Duan–Lukin–Cirac–Zoller (DLCZ) memory8,13,14, off-resonant Faraday interaction15, controlled reversible inhomogeneous broadening16,17, atomic frequency combs18 and Raman memory19,20. In order to have quantum memory practicable for efficient synchronization and physical scalability, considerable efforts have been dedicated to meet key features known as high efficiency, low noise level, large time bandwidth product (lifetime divided by pulse duration) and operating at room temperature6.
It has proven very difficult to satisfy all the requirements simultaneously. Especially, in the regime of large bandwidth and room temperature, noise and/or decoherence become dominant, therefore memories cannot work in quantum regime21,22 or can do so only in short times23,24,25,26. At room temperature, EIT and near off-resonance Raman memory have a collision-induced fluorescence noise that cannot be filtered out because of being identical to the signal photons21. By applying larger detuning, far off-resonance Raman is found to be able to well eliminate the fluorescence noise and posses a large storage bandwidth. Unfortunately, noise rising from spontaneous Raman scattering process becomes dominant, which is intrinsic and proportional to the detuning22.
Here we present FORD (far off-resonance Duan–Lukin–Cirac–Zoller) protocol where we exploit spontaneous Raman scattering process to generate and store an excitation rather than taking it as noise. We demonstrate a genuine broadband quantum memory that can simultaneously meet aforementioned key features (see Supplementary Fig. 1, Supplementary Table 1 and Supplementary Notes 1 and 2 in Supplementary Information). We have observed an unconditional noise level (the noise counts divided by the trial number of read process without write process) of 10−4 and a cross-correlation between heralding Stokes photon and retrieved anti-Stokes photon up to 28. A violation of Cauchy–Schwarz inequality27 up to 20 standard deviations indicates high-fidelity generation and preservation of non-classical correlation in room-temperature atoms. Furthermore, the achieved cross-correlation in room-temperature atoms exceeds the key boundary of 6, above which quantum correlation are able to violate Bell’s inequality28,29. A time bandwidth product of 700 can be promptly employed to build large-scale quantum networks.
Results
FORD quantum memory scheme
As is shown in Fig. 1a, in contrast to “mapping in and out” of external photons in other quantum memory protocols, DLCZ memory creates one collective excitation directly inside the atoms by a classical write pulse via spontaneous Raman process, and, meanwhile, emits a Stokes photon that can herald the successful storage with intrinsic unit efficiency8,30. With a programmable delay, a read pulse can retrieve the stored excitation as an anti-Stokes photon with a process similar to Raman memory protocol, which has also been demonstrated with the potential to approach a unit efficiency using a strong enough read pulse19.
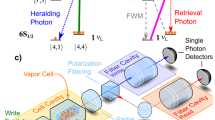
Experimental setup and FORD scheme. a The caesium cell is packed in a three-layer magnetic shielding and is heated up to 61.3 °C. The write and read pulses (red envelopes) are generated with a programmed time delay and are both prepared in horizontal polarization (see Methods for more details). The created Stokes photons (green envelope) and retrieved anti-Stokes photons (blue envelope) are both in vertical polarization. A Wollaston prism (WP) is employed as polarization filter to separate the output photons from the write and read pulses. The two sets of cascaded cavities serve as strong spectrum filters and contribute an extinction ratio up to 107. The colours are a guide to the eye. HWP half-wave plate, QWP quarter-wave plate, PBS polarization beam splitter. b The write process of FORD quantum memory. The blurred grey belt denotes broadband virtual excited state induced by write pulse. The green dash lines represent wide transition band of a Stokes photon. ΔS = 9.2 GHz is the ground state hyperfine splitting of caesium. c The read process of FORD quantum memory. The blue dash lines represent wide transition band of an anti-Stokes photon. d The time sequence for generation, storage and retrieval of non-classical correlation. Ellipsis implies repeated sequences afterward
By combining far off-resonance atomic configuration and standard DLCZ process, an excited virtual energy level near the two-photon resonance can be created by the strong write/read pulse, see Fig. 1b–d. The linewidth of the excited virtual energy level is proportional to the intensity of the write/read laser and the effective optical depth of atomic ensemble. In our experiment, we use broadband write and read pulse with a pulse duration of 2 ns and detune them to a very far off-resonance region. The detuning in linear frequency ΔW and ΔR are larger than 13.2 and 4 GHz, respectively, which is about one order higher than narrowband DLCZ quantum memory protocol. We adopt caesium atoms 133Cs to realize large optical depth relying on its high vapour pressure. With 75-mm-long cell and 10 Torr Ne buffer gas, an optical depth larger than 1000 is obtained at a temperature of 61.3 °C. The storage bandwidth is expected to be near GHz level and its central frequency is tunable by detuning the write and read pulse simultaneously.
A simplified three-level Λ-type configuration is illustrated in Fig. 1b, c. The lower two energy states \(\left| g \right\rangle \left( {6S_{1/2},F = 3} \right)\) and \(\left| s \right\rangle \left( {6S_{1/2},F = 4} \right)\) are the hyperfine ground states of caesium, and the higher energy state \(\left| e \right\rangle \left( {6P_{3/2},F\prime = 2,3,4,5} \right)\) is the excited state. Initially, a pumping laser resonant with the transition of 6S1/2, F = 4 → 6P3/2, F′ = 5 prepare all the atoms into the state \(\left| g \right\rangle\) as
where N is the total number of atoms that participate in interaction. After the initial state is prepared, a strong write pulse with a detuning ΔW creates a single excitation among billions of atoms, and, meanwhile, induces a broadband Stokes photon via spontaneous Raman scattering8,31 (see Methods). In this process, appropriate energy of the write pulse is adopted to ensure that only a single Stokes photon is emitted per attempt and high-order emissions are negligible. Then, the collective excitation state can be expressed as32
where kW is the wave vector of the write pulse, kS is the wave vector of the Stokes photon and rn is the position of the nth atom. After a programmable delay, a strong read pulse with a detuning ΔR and wave vector kR illuminates the caesium cell and transform the collective excitation into a broadband anti-Stokes photon whose wave vector is denoted by kAS.
The write and read pulse are coaxial, which implies kW = kR, in order to maximise the spin wave lifetime of atomic excitation33. It has been theoretically demonstrated that the Stokes photons are mainly inside a small cone around the direction of the write pulse31. According to the phase-matching condition kW + kR = kS + kAS, we infer that the Stokes and anti-Stokes photons are approximately coaxial as well. As shown in Fig. 1a, both Stokes and anti-Stokes photons are polarized orthogonally to the write/read pulse34 and therefore can be separated from the strong addressing light with a high-extinction Wollaston polariser (see Supplementary Notes 3 and 4 in Supplementary Information for more details). Two sets of homemade cascaded cavities composed of three Fabry–Perot cavities are tuned resonant with Stokes and anti-Stokes photons, respectively. Each cavity has a transmission rate of about 90% and contributes an extinction ratio more than 500. Together with a polarising beam splitter and a quarter-wave plate, we realize a dichroic-mirror-like functioning for an extremely small frequency difference of 9.2 GHz (see Methods for more details). A standard Hanbury–Brown and Twiss interferometer composed of three avalanched photodiodes and a 50:50 fibre beam splitter are employed to perform photon statistics and correlation detection.
Observation of broadband quantum memory in room-temperature atoms
Unconditional noise is a key parameter that can be used to benchmark the noise level of optical memory and whether it can work at quantum regime. We measure unconditional noise by retrieving anti-Stokes photons in the absence of the write pulse. As a result of the novel protocol and experimental configuration, we observe a low unconditional noise level of 10−4. We obtain a value of 7.79(5) × 10−5 when we address atoms with the read pulse energy of 30 pJ, see Fig. 2a. A distinct manifestation of such a low unconditional noise level presents a strong non-classical correlation between the heralding Stokes photon and the retrieved atomic excitation anti-Stokes photon. It turns out to be a high cross-correlation \(g_{{\mathrm{S}} - {\mathrm{AS}}}^{(2)}\) and a violation of Cauchy–Schwarz inequality \(\left( {g_{{\mathrm{S - AS}}}^{(2)}} \right)^2 \le g_{{\mathrm{S - S}}}^{(2)} \cdot g_{{\mathrm{AS - AS}}}^{(2)}\)27. We obtain an auto-correlation of \(g_{{\mathrm{S - S}}}^{{\mathrm{(2)}}}\) = 1.97 ± 0.13 (\(g_{{\mathrm{AS - AS}}}^{{\mathrm{(2)}}}\) = 1.87 ± 0.20) for Stokes photons (anti-Stokes photons) and cross-correlation of 7.83 ± 0.18, with the detuning ΔR at 4 GHz, the write/read pulse energy 129 pJ and the delay time 30 ns. The Cauchy–Schwarz inequality is violated up to 20 standard deviations (see Supplementary Note 5 in Supplementary Information for the calculation formula), which clearly indicates a high-fidelity generation and preservation of non-classical correlation in our quantum memory.
Experimental results on the noise level and nonclassicality. a The measured unconditional noise level as a function of the read pulse energy. b The measurement of cross-correlation in a large detuning from near to far off-resonance region, ΔR from 2 to 15 GHz, correspondingly ΔW = ΔR + 9.2 GHz. c Influence of the write/read pulse energy. \(g_{{\mathrm{S - AS}}}^{(2)}\) above the boundary (the dashed line) implies non-classical correlation. Error bars are derived on the basis of the Poisson distribution of single-photon detectors. d The relation between excitation probability λ and the write pulse energy
It is important but technically challenging to investigate storage performance depending on detuning of addressing light. For every detuning data point in Fig. 2b, we realize this by detuning and locking the write/read frequency far away from the transition line of caesium, and also initialising the resonance for all cascaded cavities. We have made measurement of cross-correlation in a large detuning range ΔR from 2 to 15 GHz. For broadband optical memory at room temperature, the performance ranging from near to far off-resonance is identified. Our results show a “sweet spot”, but inconsistent with previous results in narrowband Raman memory experiments which identify 1.3 GHz as the optimal detuning35. Apart from the detuning around 0 or 9.2 GHz where the leakage of fluorescence through cascaded cavities is not negligible, FORD quantum memory shows the ability of working well at quantum regime in a wide spectrum (see Supplementary Note 2 in Supplementary Information). We also made the measurement of cross-correlation and created probability of atomic excitation by scanning the write/read pulse energy, which reveals a higher cross-correlation up to 20 at lower excitation probability, see Fig. 2c, d.
In order to obtain the bandwidth of our quantum memory, we develop a convolution-based approach. We measure the total transmission spectra of cascaded cavities by scanning a narrowband classical light, see Fig. 3a, b. We then count Stokes and anti-Stokes photons while scanning the detuning of the write/read light, shown in Fig. 3c, d. By using convolution theorem and Fourier transform (see Methods), we can deduce the frequency spectra of Stokes and anti-Stokes photons shown in Fig. 3e, f. With the write/read pulse energy of 96 pJ, the measured bandwidth of Stokes and anti-Stokes photons are 504 and 537 MHz, respectively, which is about two order higher than the bandwidth obtained in cold atoms10,11,12.
Experimental results of convolution-based bandwidth measurement. We measure the total transmission windows of cascaded cavities for Stokes (a) and anti-Stokes photons (b). We then detune the write/read light to get another transmission spectra for Stokes (c) and anti-Stokes photons (d). We deduce the frequency spectra of Stokes (e) and anti-Stokes photons (f) by using convolution theorem and Fourier transform
The time bandwidth product is a key figure of merit of quantum memory endowed with the capacity of synchronization. This parameter sets the limit of the times that we can synchronize within the lifetime of stored correlations. We measure \(g_{{\mathrm{S - AS}}}^{{\mathrm{(2)}}}\) as a function of storage time, see Fig. 4a. The data is fitted with the form \(g_{{\mathrm{S - AS}}}^{{\mathrm{(2)}}}\) = 1 + C/(1 + At2 + Bt), where At2 results from atomic random motion33 and Bt is a correction term that reflects the effect of the background noise of write and read light (see Supplementary Table 2 and Supplementary Note 6 in Supplementary Information for more details). The lifetime is defined with the cross-correlation dropping to 1/e, which is found to reach 800 ns, see Fig. 4a. The fitting function reveals that at this stage the lifetime is limited by the nonzero background of addressing light and the motion-induced loss of atoms. Through enlarging the mode field of both the write/read pulse, we achieve a prolonged lifetime to 1400 ns and obtain a time bandwidth product up to 700, see Fig. 4b. We also observe a higher cross-correlation of up to 28, and being higher than 2 until time delay is 6000 ns.
Lifetime measurement. a The measured cross-correlation as a function of storage time. The data are obtained under the condition of a write/read beam waist of 90 μm, pulse energy about 100 pJ and the detuning ΔR = 4 GHz. b The observed improvement of lifetime and cross-correlation by expanding the beam waist to 240 μm. Error bars are derived on the basis of the Poisson distribution of single-photon detectors. The red curve is a theoretical fit of the form \(g_{{\mathrm{S - AS}}}^{{\mathrm{(2)}}}\) = 1 + C/(1 + At2 + Bt)
Discussion
The distinct feature of the FORD scheme is that we exploit a spontaneous Raman scattering process to generate and store an excitation rather than taking it as noise at the write process. It means the write process is completely free of noise. The read process of the FORD scheme is the same as the far off-resonance Raman scheme suffering from the four-wave mixing noise. Another distinct feature of the FORD scheme is that we apply differential coupling strength via detuning for the write and read process. The spontaneous Raman scattering can be well suppressed in the read process because the read field strongly couples with atoms and retrieves the stored excitation back to photon with a probability as high as possible. We identify the performance ranging from the near to far off-resonance. Our results show a “sweet spot” of detuning that is different from the value adopted in previous experiments. At the optimal detuning, the four-wave mixing noise is well suppressed. We therefore are able to observe a low unconditional noise level of 10−4.
The off-resonance Raman process has been proven to be able to reach unit retrieval efficiency19. Our current retrieval efficiency, conditional on registering a Stokes photon, is around 10%. We attribute the gap to the noise, the limited read pulse energy and the mode mismatch of coupling Stokes and anti-Stokes photons. It should be noticed that in our experiment a single pulse laser acts as both the write and read field. The stored photon has the chance to be retrieved instantaneously during the write process, which may set an upper limit for storage efficiency. However, the correlated coupling can be suppressed by employing two control lasers so that the momentum, frequency, bandwidth and intensity of the write and read pulse can be tuned individually, which makes it possible to optimize one without disturbing the other. Further improvements include increasing the read pulse energy19, shaping the read pulse36 and cavity enhancement37.
Although the time bandwidth product has already been very high, a longer absolute lifetime means fewer quantum repeater nodes for a given quantum communication distance7,32. The dominant factor of decoherence mechanism in our current setup is random motion-induced loss, which may be solved by using a small-diameter cell to keep atoms always staying in the interaction region. Meanwhile, anti-relaxation coating should be adopted to keep atomic polarization during its collision with the cell. The lifetime of Zeeman populations and coherences in excess of 60 s has been reported in ref. 38, making it potential for realizing longer storage lifetime (see Supplementary Note 7 in Supplementary Information).
Apart from quantum repeaters, more importantly, quantum memory-enabled synchornization is crucial to build large-scale multi-photon and quantum entanglement states for quantum computing, quantum simulation and quantum metrology. Our quantum memory is more straightforward for experimental implementation (i.e. physically more scalable) and therefore suitable for such applications.
In summary, we have demonstrated a broadband DLCZ quantum memory in room-temperature atoms. Low unconditional noise level, strong nonclassicality preserved among heralding photon and stored excitation, and large time bandwidth product and ability of operating at room temperature make FORD quantum memory promising for future scalable quantum technologies1,39, and promptly applicable in building large-scale quantum networks40.
Methods
Programmable generation of high-intensity write/read pulse
Far off-resonance DLCZ quantum memory requires broadband and high-intensity write/read pulse. We cannot generate it directly from a high-power continuous laser since the required peak power exceeds the threshold of fast electro optic modulator (EOM). A customised commercial Ti:sapphire laser may provide the required bandwidth and intensity. However, fixed periodic generation of pulse means incapability to write and read on-demand, resulting in inadequate exploitation of time bandwidth product of quantum memory. We develop a system to generate high-intensity pulse with tunable central frequency, bandwidth, and more importantly, generation time. An external cavity diode laser locked to the transition 6S1/2, F = 4 → 6S3/2, F′ = 4 co 5 line of caesium serves as reference called MASTER. Another distributed Bragg reflector (DBR) laser called SLAVE are locked to MASTER in an arbitrarily set frequency difference by comparing their frequency on a Fabry–Perot etalon. A fast EOM trigged by electronic pulses from field-programmable gate array is used to chop SLAVE to short pulses. The generated pulses are fed into a homemade tapered amplifier (TA) to boost their power by 17 dB. In order to eliminate the spontaneous emission from the TA, we employ a ruled diffraction grating to spread beam out and spatially pick the stimulated radiation with irises. In our experiment, full-width at half-maximum (FWHM) of the write/read pulse is about 2 ns, measured by a fast photodiode whose rise time is tens of picoseconds.
The excitation is shared among billions of atoms
Many theories and experiments have confirmed the collective enhancement of signal-to-noise ratio during write process and collective interference effect during read process. These collective effects verify that the excitation is shared among a large number of atoms rather than a single atom. The well-known references have been included in the main text8,31,32.
The atomic number density n can be roughly estimated by \(n = {\textstyle{{4\pi d} \over {\lambda ^2L}}}\), where optical depth d is about 5000, wavelength λ ≈ 852 nm and cell length L = 75 mm. The estimated number density is about 1.15 × 1018/m3. We can estimate the total atomic number among the interaction region (the beam waist of laser is on the order of 100 μm) as
So the excitation is shared among billions of atoms.
In each write process, there is a small probability λ to emit a Stokes photon denoted by \(\left| {1_{\mathrm{p}}} \right\rangle\) corresponding to a collective excitation denoted by \(\left| {1_{\mathrm{a}}} \right\rangle\) stored in the atomic ensemble. The total wave function can be written as8
where O(λ3/2) represents the high-order terms with more excitations whose probabilities are equal to or smaller than λ3/2. The excitation probability λ shown in Fig. 2d is controlled by the energy of the write pulse. We can see that the excitation probability is linear to the energy of the write pulse, which is consistent with the statement of cold atoms based experiments, for example, in ref.41.
Cascaded cavities
Collinear configuration of writing and reading offers longer spin wave lifetime while making single photons very hard to be filtered out of strong addressing light. We develop two sets of cascaded cavities composed of three Fabry–Perot cavities tuned resonant with Stokes and anti-Stokes respectively. Every cavity is a monolithic plank-convex glass. Both sides are coated to give an overall transmission window FWHM about 380 MHz. Careful alignment is necessary to optimise mode matching between cavity and incident light, which determines the performance in terms of transmission and extinction ratio. The transmission frequency can be tuned by setting the temperature of the cavity. We use an active feedback system to set the temperature and also lock it within ±3 mK. For each cavity, we obtain a transmission rate of more than 90% and an extinction ratio of more than 500. With three cavities together we have a transmission rate over 70% and total extinction ratio up to 107.
How the frequency filter works
The frequency filter composed of a polarization beam splitter, a quarter-wave plate and two sets of cascaded cavities, which are resonant with Stokes and anti-Stokes photons, respectively. After the Wollaston polarizer, Stokes and anti-Stokes photons are coupled into a single mode fibre. Then the photons with horizontal polarization pass through the polarization beam splitter and encounter the filter. Firstly the photons encounter the Stokes-resonant cavity, the Stokes photons pass through the Stokes-resonant cavity, but the anti-Stokes photons are reflected by the front surface of the Stokes-resonant cavity. Then, the reflected anti-Stokes photons pass through the quarter-wave plate again. Note that, double pass of a quarter-wave plate is equivalent to a half-wave plate. The anti-Stokes photons therefore flip its polarization to vertical and reflected by the polarization beam splitter, and finally pass through the anti-Stokes-resonant cavity. We can see that the Stokes photons and anti-Stokes photons pass through different set of cavities, respectively. There is no 50% loss of photons.
The transmission windows of cavities shown in Fig. 3a, b are measured with a weak classical light from a DBR laser. Single photons are not the best choice for measuring transmission windows of cavities since the fluctuations of single photons and ambient noise will bring considerably difficulty to adjust and optimize the cavities. On the other hand, high intensive light is also not suitable since the cavities will be warmed by the intensive light and the transmission windows of cavities will shift away from their correct frequency position.
Convolution-based bandwidth measurement
As shown in Fig. 3a, b, the total transmission windows of the cascaded cavities are fitted by using
where T0, A, B, C, d, h, g and f0 are fitting parameters. Detuning refers to frequency difference f − f0. The grey circles are experimental data and the green lines are fitting curves. Figure 3c, d are fitted by using
where a, b, d and U0 are fitting parameters. The grey columns are experimental data and the blue lines are fitting curves. It is reasonable to consider U0 as noise rather than signal photons, so it is U(f) − U0 rather than U(f) that describes real convolutions. If function S(f) is assumed to be the frequency spectra of Stokes photons or anti-Stokes photons, then
Applying the convolution theorem, we achieve
where F{S(f)} is the Fourier transform of S(f), similarly for F{U(f) − U0} and F{T(f)}. By applying inverse Fourier transform to F{S(f)}, we derive out the spectrum S(f) of Stokes photons or anti-Stokes photons. The spectra are shown in Fig. 3e, f.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
O’Brien, J. L., Furusawa, A. & Vučković, J. Photonic quantum technologies. Nat. Photon. 3, 687–695 (2009).
Jin, X.-M. et al. Experimental free-space quantum teleportation. Nat. Photon. 4, 376–381 (2010).
Gisin, N. & Thew, R. Quantum communication. Nat. Photon. 1, 165–171 (2007).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nat. Phys. 8, 285–291 (2012).
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nat. Photon. 3, 706–714 (2009).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Nunn, J. et al. Enhancing multiphoton rates with quantum memories. Phys. Rev. Lett. 110, 133601 (2013).
Chanelière, T. et al. Storage and retrieval of single photons transmitted between remote quantum memories. Nature 438, 833–836 (2005).
Eisaman, M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837–841 (2005).
Zhang, H. et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nat. Photon. 5, 628–632 (2011).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
Chrapkiewicz, R., Dabrowski, M. & Wasilewski, W. High-capacity angularly multiplexed holographic memory operating at the single-photon level. Phys. Rev. Lett. 118, 063603 (2017).
Julsgaard, B., Sherson, J., Cirac, J. I., Fiuŕašek, J. & Polzik, E. S. Experimental demonstration of quantum memory for light. Nature 432, 482–486 (2004).
Moiseev, S. A. & Kröll, S. Complete reconstruction of the quantum state of a single-photon wave packet absorbed by a Doppler-broadened transition. Phys. Rev. Lett. 87, 173601 (2001).
Alexander, A. L., Longdell, J. J., Sellars, M. J. & Manson, N. B. Photon echoes produced by switching electric fields. Phys. Rev. Lett. 96, 043602 (2006).
Afzelius, M., Simon, C., de Riedmatten, H. & Gisin, N. Multimode quantum memory based on atomic frequency combs. Phys. Rev. A. 79, 052329 (2009).
Reim, K. F. et al. Multi-pulse addressing of a Raman quantum memory: configurable beam splitting and efficient readout. Phys. Rev. Lett. 108, 263602 (2012).
Ding, D.-S. et al. Raman quantum memory of photonic polarized entanglement. Nat. Photon. 9, 332–338 (2015).
Manz, S., Fernholz, T., Schmiedmayer, J. & Pan, J.-W. Collisional decoherence during writing and reading quantum states. Phys. Rev. A. 75, 040101(R) (2007).
Michelberger, P. S. et al. Interfacing GHz-bandwidth heralded single photons with a warm vapour Raman memory. N. J. Phys. 17, 043006 (2015).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
England, D. G. et al. Storage and retrieval of THz-bandwidth single photons using a room-temperature diamond quantum memory. Phys. Rev. Lett. 114, 053602 (2015).
Kaczmarek, K. T. et al. High-speed noise-free optical quantum memory. Phys. Rev. A. 97, 042316 (2018).
Finkelstein, R., Poem, E., Michel, O., Lahad, O. & Firstenberg, O. Fast, noise-free memory for photon synchronization at room temperature. Sci. Adv. 4, 8598 (2018).
Clauser, J. F. Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect. Phys. Rev. D 9, 853–860 (1974).
de Riedmatten, H. et al. Direct measurement of decoherence for entanglement between a photon and stored atomic excitation. Phys. Rev. Lett. 97, 113603 (2006).
Bao, X.-H. et al. Efficient and long-lived quantum memory with cold atoms inside a ring cavity. Nat. Phys. 8, 517–521 (2012).
Afzelius, M., Gisin, N. & de Riedmatten, H. Quantum memory for photons. Phys. Today 68, 42–47 (2015).
Duan, L.-M., Cirac, J. I. & Zoller, P. Three-dimensional theory for interaction between atomic ensembles and free-space light. Phys. Rev. A 66, 023818 (2002).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Zhao, B. et al. A millisecond quantum memory for scalable quantum networks. Nat. Phys. 5, 95–99 (2009).
Nunn, J. Quantum Memory in Atomic Ensembles. Ph.D. thesis 481–487 (University of Oxford, 2008).
Bashkansky, M., Fatemi, F. K. & Vurgaftman, I. Quantum memory in warm rubidium vapor with buffer gas. Opt. Lett. 37, 142–144 (2012).
Novikova, I., Phillips, N. B. & Gorshkov, A. V. Optimal light storage with full pulse-shape control. Phys. Rev. A 78, 021802(R) (2008).
Nunn, J. et al. Theory of noise suppression in Λ-type quantum memories by means of a cavity. Phys. Rev. A 96, 012338 (2017).
Balabas, M. V., Karaulanov, T., Ledbetter, M. P. & Budker, D. Polarized alkali-metal vapor with minute-long transverse spin-relaxation time. Phys. Rev. Lett. 105, 070801 (2010).
Whiting, D. J. et al. Single-photon interference due to motion in an atomic collective excitation. Phys. Rev. Lett. 118, 253601 (2017).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Chou, C. W., Polyakov, S. V., Kuzmich, A. & Kimble, H. J. Single-photon generation from stored excitation in an atomic ensemble. Phys. Rev. Lett. 92, 213601 (2004).
Acknowledgements
We thank Jian-Wei Pan and Hui-Jun Li for helpful discussions. This work was supported by National Key R&D Program of China (2017YFA0303700); National Natural Science Foundation of China (NSFC) (11374211, 61734005, 11690033); Shanghai Municipal Education Commission (SMEC) (16SG09, 2017-01-07-00-02-E00049); Science and Technology Commission of Shanghai Municipality (STCSM) (15QA1402200, 16JC1400405, 17JC1400403). X.-M.J. acknowledges support from the National Young 1000 Talents Plan.
Author information
Authors and Affiliations
Contributions
X.-M.J. conceived the project. J.-P.D, A.-L.Y. and X.-M.J. designed the experiment. J.-P.D., A.-L.Y., M.-Y.D., D.L., J.G., L.-F.Q., H.L., X.-L.P., Z.F. and H.T. performed the experiment. X.-M.J. and J.-P.D. analysed the data and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dou, JP., Yang, AL., Du, MY. et al. A broadband DLCZ quantum memory in room-temperature atoms. Commun Phys 1, 55 (2018). https://doi.org/10.1038/s42005-018-0057-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0057-9
This article is cited by
-
Entangling motional atoms and an optical loop at ambient condition
npj Quantum Information (2023)
-
Towards entanglement distillation between atomic ensembles using high-fidelity spin operations
Communications Physics (2022)
-
Enhancing photon generation rate with broadband room-temperature quantum memory
Scientific Reports (2022)
-
Room-temperature single-photon source with near-millisecond built-in memory
Nature Communications (2021)
-
Multipartite entanglement of billions of motional atoms heralded by single photon
npj Quantum Information (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.