Introduction

A monolayer transition metal dichalcogenide (TMD) is formed by a layer of transition metal atoms sandwiched between two layers of chalcogen atoms in the trigonal prismatic structure1. Because of its two-dimensional nature, high electron mobility, and massive Dirac energy spectrum, TMD materials are considered as candidates for next-generation transistors2,3,4,5,6. Moreover, since the crystal structure of TMD has no inversion symmetry but respects the out-of-plane mirror symmetry, the strong atomic spin−orbit coupling (SOC) field in TMD materials gives rise to a special type of SOC that we referred to as Ising SOC7,8,9,10,11,12. In sharp contrast to Rashba SOC that pins electrons spins to in-plane directions13,14, the Ising SOC acts as an effective Zeeman field that pins electron spins to opposite out-of-plane directions for electrons with opposite momentum. As TMD materials possess strong Ising SOC, the novel optical and transport phenomena related to the Ising SOC are under intense studies15,16,17.

Recently, several TMD materials such as MoS2, MoSe2, WS2, NbSe2 are found to be superconducting18,19,20 even down to atomic thickness. More importantly, it was shown that monolayer superconducting MoS27,8 and NbSe29,10 possess extremely high in-plane upper critical field Hc2, more than six times higher than the Pauli limit. It was explained that the enhancement of Hc2 is due to the presence of the strong Ising SOC7,8,9,10. The Ising SOC pins electron spins of the Cooper pairs to the out-of-plane directions, preventing the electron spins from being aligned with external in-plane magnetic fields and hence protects the superconductivity. While it is intriguing that Ising SOC can enhance the upper critical fields of superconductors, it is not yet understood whether Ising SOC can induce novel superconducting phases.

In this work, we show that, due to the strong Ising SOC and the fact that Hc2 of superconducting TMDs is strongly enhanced, a superconducting monolayer TMD can be easily driven to a nodal topological phase by an in-plane magnetic field. Using monolayer NbSe2 as an example, we demonstrate that the nodal topological phase occupies a large part of the phase diagram, and the predicted nodal topological regime has been achieved in recent experiments9,21,22. In the nodal topological phase, bulk nodal points located on Γ−M lines are created by an in-plane magnetic field and these nodal points are connected by Majorana flat bands. We further show that the Majorana flat bands can be detected by tunneling experiments. The realization of Majorana fermions in monolayer NbSe2 is experimentally more accessible than other current schemes in semiconductor nanowire/superconductor heterostructures23 and quantum anomalous Hall/superconductor heterostructures24, which have provided evidence of Majorana fermions in 1D and 2D fully gapped topological superconductors25,26,27,28. This is due to the fact that driving the system to the nodal topological phase by an external magnetic field does not require the engineering of heterostructures nor the fine-tuning of experimental parameters. Furthermore, our study applies to other TMDs such as monolayer superconducting TaS229,30.

Results

Band structure in normal state

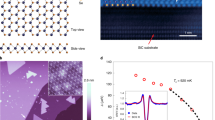
A monolayer NbSe2 is formed by a layer of Nb atoms with triangular lattice sandwiched by two layers of Se atoms with triangular lattices. The material has a hexagonal lattice structure when viewed from the out-of-plane direction but with broken A−B sublattice symmetry as shown in Fig. 1a. Therefore, an in-plane mirror symmetry along the y-direction is broken and this gives rise to the Ising SOC that pins electron spins to the out-of-plane directions and splits the energy bands31. The band structure of a monolayer NbSe2 is obtained through first-principle calculations taking into account SOC using ABINIT package (http://www.abinit.org). The results are presented in Fig. 1b. As expected, the shape of the band structure is almost identical to the band structures of monolayer MoS2, MoSe2, WSe2 and WTe2 found in previous works32. However, unlike Mo- and W-based materials which are insulating intrinsically, an Nb atom has one less d-electron in the outer most shell than Mo and W atoms and the chemical potential of NbSe2 lies in the valence band. The band splitting at the K points due to Ising SOC is about 150 meV. Importantly, the band splitting is significant at the Fermi energy even though the Fermi surface is far away from the K points. As we show in the next section, this Ising SOC at the Fermi energy plays a crucial role in protecting the superconductivity from the paramagnetic effects of in-plane magnetic fields.

Fig. 1
figure 1

The crystal structure and electronic bands for monolayer NbSe2. a Lattice structure of monolayer NbSe2 (left) and its top view (right). Mx denotes the in-plane mirror symmetry. b The band structure for the normal state of monolayer NbSe2 from DFT calculations. c The energy contour at the Fermi level from tight-binding model

Full size image

In order to study the superconducting properties of the material, we construct a six-band tight-binding model that consists of the \(d_{z^2}\), dxy and \(d_{{x^2}\, - \,{y^2}}\) orbitals32,33 of the Nb atoms. Including the third-nearest-neighbor hoppings, the band structure of the DFT calculations can be well explained. The details of the tight-binding model HN(k) can be found in Supplementary Note 1 with the fitting parameters shown in Supplementary Table 1. The Fermi surfaces from the tight-binding model are shown in Fig. 1c. At the Fermi level, there are Fermi pockets around Γ, K, and −K points. In general, the bands are split by Ising SOC except for the states lying along the Γ−M lines. It is important to note that the Fermi surfaces of NbSe2 as depicted in Fig. 1c have been observed through angle-resolved photoemission spectroscopy12,34.

Ising superconductivity in monolayer NbSe2

It is well-known that bulk NbSe2 is superconducting with Tc of 7 K35. However, monolayer NbSe2 was shown to be superconducting only very recently with Tc on-set at about 5 K and zero resistance appears at about 3 K9,21,34,36. In bulk NbSe2, magnetic field can create vortices that eventually destroy superconductivity with Hc2 of about 14.5 T37. In the monolayer case, the orbital effects of in-plane magnetic fields are completely suppressed and the magnetic field can suppress superconductivity only through Zeeman coupling with electron spins.

Similar to the gated superconducting MoS2, NbSe2 was shown to have strongly enhanced Hc2 at 35 T even though the Tc is much lower than the bulk Tc. While the experimental data in MoS2 can be well explained by solving the self-consistence gap equations by taking into account the Ising SOC and Rashba SOC induced by gating, a microscopic theory for explaining the Hc2 data of monolayer NbSe2 is still lacking due to the more complicated band structures in the valence bands. In this work, with the tight-binding model introduced in the method section, we can take into account all the three Fermi pockets shown in Fig. 1c to explain the experimental data. An intra-orbital attractive interaction U between the electrons is introduced. U is determined by the self-consistent gap equation \({\mathrm{\Delta }} = U/V\mathop {\sum}\nolimits_{{\boldsymbol{k}},o} \left\langle {c_{{\boldsymbol{k}}, \downarrow ,o}c_{ - {\boldsymbol{k}}, \uparrow ,o}} \right\rangle\) at zero magnetic field. Here, Δ = 1.76 kBTc is the pairing gap at zero temperature, V is the area of the sample and ck,↑/↓,o is the electron annihilation operator for orbital o.

After finding U at zero magnetic field, we can determine Δ as a function of magnetic field by minimizing the free energy density

$${\mathrm{\Omega }} = \left| {\mathrm{\Delta }} \right|^2/U - \frac{1}{V}\mathop {\sum}\limits_{{\boldsymbol{k}},n} \frac{1}{{2\beta }}{\mathrm{ln}}\left( {1 + e^{ - \beta E_{{\boldsymbol{k}},n}}} \right)$$
(1)

with Ek,n the eigenvalue adopted from the Bogoliubov-de Gennes Hamiltonian HBDG as shown in detail in Supplementary Note 2. The phase diagram for this Ising superconductor is determined and shown in Fig. 2, with HP ≈ 1.84Tc the Pauli limit38. As shown in Fig. 2, the calculated Hc2 (solid line) is strongly enhanced. The theoretical values of Hc2, using the parameters from the tight-binding model without any tuning parameters, are higher than the experimental values (the red dots). Such discrepancy can be due to the disorder39 and the fact that the NbSe2 sample has ripples, and the ripples introduce Rashba-type SOC40 which competes with Ising SOC. This Rashba-type SOC can lower the in-plane Hc2 as in the case of gated superconducting MoS27, and a tiny small Rashba SOC is enough to match the in-plane Hc2 with the experimental data, shown as the red line in Fig. 2. We ignore the effects of ripples in this work. To highlight the importance of Ising SOC, the Hc2 in the absence of Ising SOC is denoted by the dashed line in Fig. 2. It is evident that the Ising SOC enhances Hc2 so that it becomes much higher than the Pauli limit.

Fig. 2
figure 2

The magnetic field-temperature phase diagram for the superconducting monolayer NbSe2. The red dots represent the experimental data from ref. 9. The calculated Hc2 is denoted by the black solid line and it is much higher than the Pauli limit which is denoted by the dashed line. When the applied in-plane magnetic field is higher than the Pauli limit but lower than Hc2, the system can go through a phase transition from a fully gapped superconducting phase to a nodal topological phase. The sample ripples-induced Rashba spin−orbit coupling is further considered in the Hc2 calculation denoted by red solid line, which agrees well with the experimental data

Full size image

Nodal topological phase

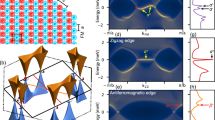
From Fig. 2, one can see that superconductivity survives in the regime where the applied magnetic field is higher than the Pauli limit field. The question is: what are the properties of the superconducting phase under strong magnetic fields? To answer this question, the spectral function \(A\left( {E,{\mathbf{R}}} \right) = - ({1}/{\pi }){\mathrm{Tr}}\left[ {{\mathrm{Im}}G\left( {E,{\boldsymbol{R}}} \right)} \right]\) of the a semi-infinite NbSe2 stripe is calculated. Here, E is energy and R is a point on the armchair edge and G is the Green’s function of the BdG Hamiltonian defined in Supplementary Note 2. The armchair edges are parallel to the y-direction and subject to periodic boundary conditions. The in-plane magnetic field applied is chosen to be H = 3HP. In the bulk Brillouin zone, it can be seen that there are six pairs of nodal points lying in the Γ−M line, as is shown in Fig. 3a. After projecting onto the edge Brillouin zone along ky, there are four pairs of projected nodal points. The outer two pairs of projected nodal points are connected by two sections of Majorana flat bands respectively. The inner two pairs of projected nodal points are from the middle four pairs of nodal points in Fig. 3a, so they are connected by two sections of doubly degenerated Majorana flat bands. In the edge Brillouin zone, the four projected nodal points as well as the four sections of Majorana flat bands are shown in Fig. 3b. Other finite energy modes emerging below the bulk continuum spectrum in Fig. 3b are the trivial edge modes, which can be removed by local potentials.

Fig. 3
figure 3

The nodal topological superconducting monolayer NbSe2 driven by in-plane magnetic field with H = 3HP. a The position for the six pairs of point nodes. They project into four pairs of nodal points on the armchair edges as shown in b. b The logarithmic plot of the spectral function A(E, R) on the armchair edge in a semi-infinite strip of NbSe2 with open boundary condition in the x-direction and periodic boundary condition in the y-direction. The Majorana flat bands connecting the point nodes at the sample edge. The insert shows a pair of nodal points connected by a Majorana flat band. Here \(b = \sqrt 3 a\) and a the lattice constant

Full size image

To understand this nodal topological phase, we use an effective Hamiltonian approach and understand the system from a symmetry point of view. Before writing down the effective Hamiltonian near the Fermi energy, we note that the Ising SOC near the K points is very strong as shown in Fig. 1b. Therefore, the superconducting states near K points are hardly affected by the in-plane magnetic field at \(H = 3H_p \ll H_{c2}\). Therefore, to understand the gap closing effect of the in-plane magnetic field, we only need to focus on the states in the Γ pocket where the Ising SOC is weaker.

Around the Γ pocket, the \(d_{z^2}\) orbital dominates32,33. In the basis of [ck,↑, ck,↓] and in the absence of external magnetic fields, the Hamiltonian has to satisfy the point group symmetries Mz = −iσz, Mx = −iσx, \(C_3 = e^{ - i({\pi }/{3})\sigma _z}\) and time-reversal symmetry T = iσyK. These symmetries restrict the effective Hamiltonian, up to third order in k, to have the form:

$${\cal H}_0 = \left[ {\frac{{k_x^2 + k_y^2}}{{2m}} - \mu } \right]\sigma _0 + \lambda _{{\mathrm{SOC}}}\left( {k_ + ^3 + k_ - ^3} \right)\sigma _z.$$
(2)

Here, μ is the chemical potential and k± = kx ± iky. It is important to note that λSOC term vanishes along the Γ − M lines as dictated by symmetries, consistent with the calculations in Fig. 1c.

Including the in-plane magnetic field, spin-singlet pairing Δ, and in the basis of \(\left[ {c_{k, \uparrow },c_{k, \downarrow },c_{ - k, \uparrow }^\dagger ,c_{ - k, \downarrow }^\dagger } \right]\), the Hamiltonian in the superconducting phase can be written as:

$$\begin{array}{*{20}{l}} {{\cal H}_s} \hfill & = \hfill & {\left[ {\frac{{k_x^2 + k_y^2}}{{2m}} - \mu } \right]\tau _z + \lambda _{{\mathrm{SOC}}}\left( {k_ + ^3 + k_ - ^3} \right)\sigma _z} \hfill \\ {} \hfill & {} \hfill & { + \frac{1}{2}\mu _BgH_x\tau _z\sigma _x + \frac{1}{2}\mu _BgH_y\sigma _y + {\mathrm{\Delta }}\tau _y\sigma _y.} \hfill \end{array}$$
(3)

Here, τi denotes Pauli matrices in the particle-hole basis. Hx and Hy are magnetic fields in the x- and y-directions respectively, μB is the Bohr magneton and g is the electron’s gyromagnetic ratio. Along the Γ−M line where the Ising SOC vanishes, the electrons’ spins are all in-plane polarized by the in-plane magnetic field, so the spin-singlet Cooper pairs from the time-reversal partners are strongly suppressed. Once the Zeeman energy \(\frac{1}{2}\mu _BgH\) exceeds Δ the pairing gap closes along the Γ−M line. However, away from the Γ−M line, the Ising SOC pins the time-reversal partners’ spin to the opposite direction along z and thus the spin-singlet Cooper pair will condensate so that the pairing gap remains finite. As a result, there will be six pairs of point nodes split out along the Γ−M line as the in-plane magnetic field is gradually applied, as is shown in Fig. 3a.

The six pairs of point nodes are protected by the chiral symmetry. Even though time-reversal is broken by the external magnetic field, \({\cal H}_s\) respects a time-reversal like symmetry \(U_T{\cal H}_s\left( {k_x,k_y} \right)U_T^{ - 1} = {\cal H}_s\left( { - k_x,k_y} \right)\) with UT = MzTτz and ky unchanged under the symmetry operation. Moreover, \({\cal H}_s\) respects a 1D particle-hole like symmetry \(U_P{\cal H}_s\left( {k_x,k_y} \right) U_P^{ - 1} = - {\cal H}_s\left( { - k_x,k_y} \right)\) with UP = τxK. Therefore, \({\cal H}_s\) respects the chiral symmetry \(C{\cal H}_s\left( {k_x,k_y} \right)C^{ - 1} = - {\cal H}_s\left( {k_x,k_y} \right)\) where C = τyσx. As a result, for any fixed ky, \({\cal H}_s\) is in the BDI class and the Hamiltonian can be topologically nontrivial41,42,43,44. For the range of ky where \({\cal H}_s\) is nontrivial, there are Majorana zero energy modes on the edge of the system as shown in Fig. 3b. By tuning ky as a parameter, the system can undergo a topological phase transition from a trivial regime to a nontrivial regime by closing the bulk gap. These topological phase transition ky points are the nodal points in Fig. 3b. The nodal points and the Majorana flat bands shown in Fig. 2 can be reproduced by the simple Hamiltonian Hs in Eq. 3.

Detection

In this section, we discuss the experimental detection of the nodal topological superconducting phase in NbSe2. As discussed above, superconducting NbSe2 can be driven from a fully gapped superconducting phase to a nodal superconducting phase by an in-plane magnetic field. As in the case of \(d_{x^2 - y^2}\)-wave superconductors, we expect the density of states of the system as a function of energy to be V-shape near zero energy when the system is nodal. From the low-energy bulk spectrum of the effective Hamiltonian \({\cal H}_s\), the density of states near zero energy can be found to be \(N({{2\pi \left| E \right|}})/({{v_xv_y}})\), where E is the energy and vx,vy denote the Fermi velocity in the x,y-directions near the nodal points and N is the number of nodal points. Thus, the bulk density of states near zero energy is indeed linearly proportional to |E|.

Using the real space version of the six-band tight-binding model HBDG defined in Supplementary Note 1, including pairing and the in-plane magnetic field, we calculate the local density of states in the bulk of the sample.

$$\rho \left( E \right) = - \frac{1}{\pi }{\mathrm{Tr}}\left[ {{\mathrm{Im}}G^{\mathrm{R}}\left( E \right)} \right],$$
(4)

here GR(E) = (E + iη − HBdG)−1 is the retarded Green’s function. The local density of states for a point in the bulk is shown in Fig. 4a. When the applied in-plane field is lower than the Pauli limit, the density of states as a function of energy is U-shape (blue curve) near zero energy indicating a fully gapped superconducting state. On the other hand, the density of states is changed to V-shape (red curve) when the system is driven to the nodal phase as expected. Even though the V-shape density of states in the bulk is only the signature of a nodal phase, not necessarily a nodal topological phase, the observation of the fully gapped to nodal phase transition can be important for identifying the topological phase transition point.

Fig. 4
figure 4

The signature for topological phase transition from the local density of states (DOS). a The DOS in the bulk in the fully gapped regime (blue curve) and the nodal regime (red curve) respectively. The in-plane magnetic field changes the DOS from U-shape H = 0.5HP to V-shape H = 3HP. b The DOS on the armchair edge in the nodal topological phase with H = 3HP. The zero energy DOS is strongly enhanced due to the zero energy Majorana modes associated with the Majorana flat bands (red curve)

Full size image

Moreover, in the nodal topological phase, there are a large number of zero energy Majorana modes residing on the edges of the sample. These zero energy modes strongly enhance the local density of states on the edge of the superconductor. The local density of states at the edge of the sample, before and after the topological phase transition, are shown in Fig. 4b. It is evident that, in the nodal topological phase with in-plane field stronger than the Pauli limit field, the zero energy density of states are strongly enhanced (red curve). Both the bulk density of states and the edge density of states can be detected by tunneling spectroscopy experiments.

Interestingly, due to the zero energy Majorana modes, the pairing correlations induced on the edge of the superconductor are indeed spin-triplet. To show this, we calculated the pairing correlation for a site on the armchair edge of the sample. The pairing correlation can be parametrized as11,14,45:

$$F_{\sigma \sigma \prime }\left( E \right) = - i\mathop {\sum}\limits_o {\int}_{\hskip -5pt 0}^\infty e^{i\left( {E + i0^ + } \right)t}\left\langle {\left\{ {c_{\sigma ,o}\left( t \right),c_{\sigma \prime ,o}\left( 0 \right)} \right\}} \right\rangle {\mathrm d}t$$
(5)

where σ and o are the spin and orbital indices respectively. In the matrix form, the pairing correlation is written as:

$$F\left( E \right) = \left( {\psi + {\boldsymbol{d}} \cdot {\boldsymbol{\sigma }}} \right)i\sigma _y.$$
(6)

Here, the so-called d-vector characterizes the triplet pairing correlation and ψ characterizes the spin-singlet pairing correlation. In Fig. 5a, it is shown that the triplet pairing correlation at zero energy on the armchair edge of the sample is nonzero only when the Zeeman energy \(V_z = ({1}/{2})\mu _{\mathrm B}g|H|\) is larger than Δ. Figure 5b shows the spatial variation of |d| across the sample for a strip of NbSe2 which has a width of 200-sites in the x-direction (perpendicular to the armchair edge). It is evident that |d| is significant only near the two edges of the sample. On the other hand, the singlet pairing correlation amplitude ψ at zero energy is negligible. Furthermore, we calculated s = i(d × d*)/|d|2 which gives the spin-polarization direction of the Cooper pairs46 as shown in Fig. 5c. This indicates that the Cooper pairs injected into the superconductor by the normal lead are spin-polarized with spin pointing to s-direction44,47. As a result, even though the lead attached to the superconductor is nonmagnetic, the current from the lead to the superconductor is spin-polarized. In other words, the Majorana modes can act as spin filters and only allow electrons with spin pointing to s-direction to tunnel into the superconductor. We believe this property of monolayer NbSe2 may lead to applications in superconducting spintronics48,49.

Fig. 5
figure 5

The triplet pairing correlation. a The triplet pairing correlation amplitude |d| on the armchair edge of the sample, as a function of Vz/Δ where \(V_z = ({1}/{2})\mu _{\mathrm B}gH\). It becomes nonzero after the Majorana flat bands emerge when Vz > Δ. b The spatial dependence of |d| in the nodal topological phase with H = 3HP. Here the site are along the x-direction. c The spin-polarization direction s of the Cooper pair at the armchair edge. s depends on the direction of the applied magnetic field H. The vector s with certain color is determined by the vector −H of the same color

Full size image

Discussion

We would like to discuss some important points about the nodal topological phase mentioned above. First, the large number of Majorana zero energy modes associated with the Majorana flat band in Fig. 2b are protected against on-site disorder. This is in sharp contrast to the \(d_{x^2 - y^2}\)-wave superconductor in which the zero energy fermionic modes can be lifted to finite energy by disorder. One can show that the zero energy Majorana modes are not protected by the bulk gap (since the system is nodal) but by the chiral symmetry C = τyσx of Hs in Eq. 350,51,52,53,54,55. In the presence of the chiral symmetry, the band topology can be characterized by net chirality number, which is defined as the difference between number of states with chirality +1 and −1 50. For the finite energy modes, states with opposite chirality number ±1 always come in pairs so the net chirality is zero. In contrast, Majorana zero modes along the same edge have a nonzero net chirality number seen in Supplementary Note 3. Since the on-site disorder respects the chiral symmetry, perturbations due to the on-site disorder can only excite pairs of zero energy states with chirality number ±1 to finite energy modes. Thus, a finite number of Majorana edge modes always exist as long as the bulk topology is not changed. This is similar to the toy model studied in ref. 43, where an in-plane magnetic field creates Majorana flat bands in a time-reversal invariant p ± ip topological superconductor.

Second, we emphasize that the Γ pocket is essential for creating the nodal topological phase. In the case of gated MoS2 or WS2, superconductivity appears in the conduction bands near the K pockets only. Therefore, the nodal phase discussed above cannot be found in those superconductors. On the other hand, intrinsic superconductors NbSe2, NbS2, TaSe2 and TaS2 are candidate materials for realizing the nodal topological superconducting phase found in this work.

Third, the armchair edge is not essential for the observation of the Majorana flat bands as long as the edge is not parallel to the zig-zag edge (kx direction in Fig. 2a). On the zig-zag edge, the projection of the bulk nodal points can cancel each other such that there are no topologically nontrivial regimes for all kx parallel to the zig-zag edge. For all other edges, one can find finite sections of Majorana flat bands along the edges when the system is driven to the nodal topological phase.

Methods

Tight-binding Hamiltonians

In the basis of \(\left[ {c_{{\boldsymbol{k}},d_{z^2}, \uparrow },c_{{\boldsymbol{k}},d_{xy}, \uparrow },c_{{\boldsymbol{k}},d_{x^2 - y^2}, \uparrow },c_{{\boldsymbol{k}},d_{z^2}, \downarrow },c_{{\boldsymbol{k}},d_{xy}, \downarrow },c_{{\boldsymbol{k}},d_{x^2 - y^2}, \downarrow }} \right]\), the six-band model used has the form32

$$\begin{array}{*{20}{l}} {H_{\mathrm{N}}\left( {\boldsymbol{k}} \right)} \hfill & = \hfill & {\sigma _0 \otimes H_{{\mathrm{TNN}}}\left( {\boldsymbol{k}} \right) + \sigma _z \otimes \frac{1}{2}\lambda L_z} \hfill \\ {} \hfill & {} \hfill & { + \frac{1}{2}\mu _{\mathrm B}g{\boldsymbol{H}} \cdot {\boldsymbol{\sigma }} \otimes I_3} \hfill \end{array}$$
(7)

with

$$H_{{\mathrm{TNN}}}\left( {\boldsymbol{k}} \right) = \left( {\begin{array}{*{20}{c}} {V_0} & {V_1} & {V_2} \\ {V_1^ \ast } & {V_{11}} & {V_{12}} \\ {V_2^ \ast } & {V_{12}^ \ast } & {V_{22}} \end{array}} \right),L_z = \left( {\begin{array}{*{20}{c}} 0 & 0 & 0 \\ 0 & 0 & { - i} \\ 0 & i & 0 \end{array}} \right),$$
(8)

where In means the n × n identity matrix. The details about these matrix elements can be found in Supplementary Note 1. Then the Bogliubov-de Gennes Hamiltonian in Nambu spinor representation can be written as

$$H_{{\mathrm{BdG}}}\left( {\boldsymbol{k}} \right) = \left( {\begin{array}{*{20}{c}} {H_{\mathrm{N}}\left( {\boldsymbol{k}} \right) - \mu I_6} & { - i{\mathrm{\Delta }}\sigma _y \otimes I_3} \\ {i{\mathrm{\Delta }}\sigma _y \otimes I_3} & { - H_{\mathrm{N}}^ \ast \left( { - {\boldsymbol{k}}} \right) + \mu I_6} \end{array}} \right).$$
(9)

The real space version of HTNN and HBdG can be found in Supplementary Note 2.

Data availability

The data supporting the findings of this study are available within the paper, its Supplementary Information files, and from the corresponding author upon reasonable request.