Abstract
Magnetic skyrmions are topologically protected nanoscale spin textures exhibiting fascinating physical behaviors. Recent observations of room temperature Néel-type skyrmions in magnetic multilayer films are an important step towards their use in ultra-low power devices. Here, we investigate the magnetization reversal in [Pt/Co/Ta]n multilayer samples under a tilted magnetic field using in-situ Lorentz transmission electron microscopy. On decreasing the magnetic field, individual skyrmions appear to subsequently evolve into snake-like structures growing in the direction opposite to the in-plane magnetic field. We show that this unusual relation between the velocity vector and the magnetic field is dominated by the chirality of the Néel-type skyrmions. It allows one to extract the sign of the Dzyaloshinskii–Moriya constant. We also demonstrate that high concentration of skyrmions can be achieved on increasing the in-plane component of the field or increasing the disorder of the film. Our micromagnetic simulations agree with our experimental results.
Similar content being viewed by others
Introduction
Magnetic skyrmions are nanoscale, relatively stable chiral spin textures that are protected topologically1,2,3,4. Owning to their topological property, small size, and high mobility, skyrmions can be manipulated by much lower current densities than the current densities needed to manipulate magnetic domains3,5,6,7,8,9. Skyrmions have been therefore proposed as promising candidates for the next generation, low power spintronic devices, such as non-volatile information storage3,10,11, spin transfer nano-oscillators12,13 and logic devices14,15.
Skyrmions were first observed in B20 materials in which the Dzyaloshinskii–Moriya interaction (DMI) originates from a non-centrosymmetric crystalline structure and leads to the formation of the intriguing spin texture5,16,17,18,19,20,21,22,23,24,25,26. In these B20 materials, the skyrmions are Bloch-type and can only exist at relatively low temperatures4,27,28. To create room temperature skyrmions suitable for industrial applications, hetero-structured magnetic thin-films were developed, in which the DMI is produced by breaking of the inversion symmetry at the interfaces of ferromagnetic layers and heavy metal layers with large spin–orbit coupling27,29,30,31,32,33,34,35,36,37. This interfacial DMI can result in the formation of the Néel-type skyrmions, which has been widely observed in various thin-film stacks at room temperature27,29,30,31,32,33,34,35,36,37. Furthermore, the formation and dynamics of the Néel-type skyrmions driven by the current have been investigated, which manifested an important step towards application of skyrmions in devices9,11,33,35,38. Usually, the out-of-plane magnetic field is very important for stabilization of skyrmions, thus, the study of the out-of-plane magnetic field on the skyrmions became one of the foci in this area4,28. However, the magnetization reversal and its dynamics are also governed by the in-plane magnetic field9,36,39,40,41,42,43, especially for the films with very weak perpendicular magnetic anisotropy (PMA). Consequently, the study of the effects induced by the in-plane magnetic field has fundamental importance.
An important method of the identification of the chirality of magnetic structures with DMI has been recently developed by Legrand et al.44 and Chauleau45. They have demonstrated that X-ray resonant magnetic scattering (XRMS) permits a straightforward determination of the winding characteristics of magnetic textures, such as, chirality, Néel-type vs Bloch-type, etc. Another interesting observation made by these authors is the possibility of the re-orientation of the chirality inside magnetic textures of multilayered structures that leads to, e.g., a composite chiral Néel-Bloch domain wall. These works have been mainly focused on domain walls but also suggested the possibility of mixed-chirality skyrmion textures. While such a possibility exists for our system, micromanetic simulations results reveal that it does not have much influence on our samples (see Supplementary Note 1). Thus, it is not considered in our work that uses Lorentz transmission electron microscopy (L-TEM). L-TEM has been one of the most direct methods with high spatial resolution to observe the magnetic domain structures, domain walls, and skyrmions, especially for objects with the Bloch-type spin rotation. Moreover, the chirality of the Bloch-type skyrmions can also be determined by the L-TEM images4,22,23,25,26,46, while observation of the Néel-type domain walls and skyrmions in the materials with PMA requires tilting of the sample and does not permit identification of the chirality of skyrmions from the L-TEM images alone36,47.
In this work, we report the determination of the chirality of Néel-type skyrmions from the magnetization reversal behavior in [Pt/Co/Ta]n multilayers with weak PMA by introducing the in-plane magnetic field in the L-TEM imaging. We find that the in-plane magnetic field contributes to the creation of skyrmions and that high concentration of skyrmions can be achieved by increasing the in-plane field. Further micromagnetic simulations reveal that not only the in-plane-field, but also the disorder, facilitates the creation of skyrmions. Note that chirality-dependent expansion of magnetic bubbles in a direction determined by the mutual orientation of the DMI vector and the in-plane magnetic field has been observed in the past39,48. However, observation of the warm-like structures growing along the lines of the magnetic field has not been reported before.
Results
Characterization of the samples
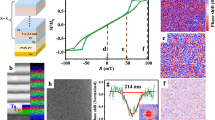
Figure 1a shows the high resolution, high-angle annular dark-field scanning transmission electron microscopy (HADDF-STEM) image of the cross-section of the multilayer, which exhibits a clear stack structure. The electron energy loss spectroscopy (EELS) mapping spectrum (Fig. 1b) further reveals a periodic tri-layered structure showing that each tri-layer is composed of a Co layer sandwiched by Pt and Ta layers. Magnetic properties of the multilayers were characterized using a SQUID-VSM magnetometer at room temperature. Figure 1c shows the normalized out-of-plane and in-plane hysteresis loops, which indicate that the sample possesses a weak PMA with an in-plane saturation field μ0Hk of only 0.206 T. This observation suggests that the sample should be very sensitive to the in-plane field. Moreover, both loops show almost zero remanence. To explore the difference in the magnetic structures in the remanent states after the sample was saturated in the presence of out-of-plane and in-plane fields, the magnetic force microscopy (MFM) measurements were performed at zero fields after each hysteresis loop measurement. The corresponding MFM images are shown in Fig. 1d, e. As expected for the films with both PMA and DMI, a typical labyrinth domain structure is clearly seen after saturation by a perpendicular field. Interestingly, aligned and stripe-like domains, sharply different from the labyrinth domain structure, were observed in the remanent state after the in-plane saturation, although the magnetization within the domains was still perpendicular to the film plane.
Structure analysis and magnetic properties. a HADDF-STEM image and b EELS mapping spectrum of the cross-section of the Ta(5 nm)/[Pt(4 nm)/Co(1.4 nm)/Ta(1.8 nm)]11 multilayer sample. c Normalized out-of-plane and in-plane hysteresis loops of the sample. d, e MFM images at zero fields after the d out-of-plane and e in-plane saturation fields. f Schematic diagram of a Néel-skyrmion on a tilting sample for L-TEM imaging. The blue/red contrast represents areas with negative/positive magnetization along z. The corresponding xy plane projection is indicated with the brown arrows. The green arrows indicate the Lorenz force when electrons pass through the skyrmion. The expected Fresnel contrast is shown at the right side and the distance between the intensity minimum and density maximum represents the skyrmion size
To understand the effect of the in-plane field on the magnetization reversal in the multilayer sample, in situ L-TEM measurements were performed. In L-TEM mode, the magnetic field parallel to the electron beam can be easily applied through the objective lens of the TEM. By tilting the sample, an in-plane field can also be applied. The ratio of the in-plane and out-of-plane field can be tuned by varying the tilt angle (θ)36,47. For the Bloch-type skyrmions, it is not necessary to tilt the sample to create the contrast in the L-TEM images. Depending on the sign of D, the core (shell) shows bright (dark) or dark (bright) contrast25. However, for the Néel-type skyrmions, the sample tilting is essential36,47. Here, we introduce briefly the physics of the L-TEM imaging for Néel-type skyrmions. Figure 1f shows the top view schematic diagram of the L-TEM imaging. The sample is tilted from the xy plane to the x′y′ plane. Blue, white and red contrasts represent the outside, the boundary and the inside of a skyrmion with negative, zero and positive magnetization along the z′ axis. The corresponding xy plane projection of the magnetization is indicated with the brown arrows. The green arrows indicate the corresponding Lorenz force when electrons pass through the skyrmion. It is clear that the skyrmion edge does not show any intensity contrast in the L-TEM image because the intensity change caused by the Lorenz force at any point in this zone is compensated or cancelled. The intensity contrast is formed in the L-TEM images due to the contributions from both the outside and the core of the skyrmion. Therefore, the resulted image for the skyrmion should be of dark-bright contrast with dark at the top side and bright at the bottom side just under the Néel-skyrmion edge, as is shown in the right side of Fig. 1f. The distance between the intensity minimum and the density maximum represents the skyrmion size.
Magnetization reversal under a tilted magnetic field
We start with the tilting angles of α = 23° and β = −20° for the L-TEM imaging. Here, α is the tilting angle around the y axis and β around the x axis. The z axis is chosen to be parallel to the TEM cylinder. Thus, the total tilt angle θ = 30° \(\left( {\cos \left( \theta \right) = \cos \left( \alpha \right) \cdot \cos \left( \beta \right)} \right)\). Before imaging, the sample was saturated in the down direction (−z) while the direction of the in-plane (x′y′ plane) component of the magnetic field pointed to the top left as indicated by the arrow in up-right corner of Fig. 2a. The evolution of the domain structure was imaged at the defocus of 7.62 mm by varying the magnetic field from the negative saturation field to the positive saturation field as is shown in Fig. 2a (see the detailed reversal process in Supplementary Movie 1). When the magnetic field was changed to about −1320 Oe (the out-of-plane component Hout = 1143 Oe and in-plane component Hin = 660 Oe), an isolated skyrmion, with size of about 110 nm (this is just an approximate value because of the very large defocus distance), emerged as marked by the green circle with the contrast of bright at upper right and dark at lower left. By continually varying the field, more skyrmions appeared (such as at −1280 Oe) and began to evolve into snake-like structures as is shown in the image obtained at −1170 Oe. The maximum skyrmion density before the formation of the snake-like structures is denoted as dmax1. By changing the field further (from −1170 Oe to −1050 Oe), the length of the snake-like structures increases. Meanwhile, some new skyrmions appeared (as indicated by yellow arrows in the image obtained at −1160 Oe) and rapidly extended to the snake-like structures. We compared the two images obtained at −1170 Oe and −1160 Oe and marked the structure differences with green dashed ellipses. Interestingly, we found that the snake-like structures mainly extended along the directions that are opposite to the direction of the in-plane field. Finally, the density of the snake-like structures achieved maximum over the entire film at about −540 Oe, forming an almost aligned arrangement. When the field approached zero, the in-plane field became zero too, the oriented stripe domains became less aligned. With increasing the field in the positive direction the in-plane field increases in the opposite direction. The stripe domains become better oriented again as seen in the image obtained at 860 Oe. When increasing the field to 1120 Oe, the orientated domain structures fractured and a mixed state of skyrmions and snake-like structures appeared. Eventually, all snake-like domains broke into skyrmions at 1380 Oe. The maximum skyrmion density obtained in this image was defined as dmax2. With increasing the field further, the skyrmions annihilated gradually (1470 Oe) and the film was finally saturated to a ferromagnetic state at 1570 Oe.
In-situ L-TEM observation of reversal behaviors. a In-situ L-TEM observation of the [Pt/Co/Ta]11 multilayer’s reversal behaviors. The images were taken at a tilt angle of α = 23o and β = −20° and the direction of in-plane component field is marked by the black arrow. b, c L-TEM images of the snake-like structures extension taken during changing the magnetic field from negative saturation field to zero with the tilting angles of (b) α = 0°; β = −20° and (c) α = −28°; β = −20°
In-plane field induced anisotropic growth behaviors
To explore the correlation between the in-plane field direction and the preferred extension direction of the snake-like domains, more experiments were performed with different tilting angles and directions, and the same phenomena were observed. Note that the extension of the snake-like structures is driven by the out-of-plane component of the field, but their anisotropic formation is induced by the in-plane field. Figures 2b, c show the L-TEM images of the extending snake-like structures taken while changing the magnetic field from negative saturation field to zero with the tilting angles of α = 0°; β = −20° and α = −28°; β = −20°, respectively. The corresponding directions of in-plane fields are indicated by black arrows. Similarly, we indicated the changes in the images with green dashed ellipses. It is clear that for both Fig. 2b, c, the snake-like structures preferred to grow along the directions opposite to that of the in-plane fields and finally formed an almost aligned arrangement.
The observation of the preferred extension direction governed by the in-plane field may become a useful and reliable approach to determine the skyrmion chirality, which is of great importance for manipulating skyrmions as well as for establishing the sign of the DMI constant4. To further understand this phenomenon and also determine the chirality of skyrmions, micromagnetic simulations were performed with the mumax3 software49. As an example, we first studied a system with an interfacial DMI of positive D. Following the experimental protocol, we created some skyrmions randomly and stabilized them with a magnetic field applied in the −z direction. Figure 3a shows the evolution of the magnetic structure when decreasing the magnetic field with the tilt angles of θ = 0° and θ > 0°. In the case of θ = 0°, when no in-plane field is applied, the skyrmions extended isotropically, leading to a typical labyrinth domain structure, as we observed experimentally (Fig. 1d). However, at θ > 0◦, when a non-zero in-plane field component was applied along the +x axis, an anisotropic growth of the skyrmions was clearly observed. An important finding is that the snake-like structures grow parallel to the in-plane magnetic field. We also found that the growing speed in the −x direction is much greater than in the +x direction. Thus, we concluded that the preferred extension direction is opposite to the direction of the in-plane magnetic field, when the magnetization of the skyrmion core points up for an interfacial DMI with positive D.
Micromagnetic simulations. a Magnetic structure evolution when increasing magnetic field from negative saturation to zero with a tilt angle of θ = 0 and θ > 0. b Four kinds of skyrmions and c the expected L-TEM contrast for Bloch-type skyrmion without tilting the sample and for Néel-type skyrmion on a tilt sample. d Magnetic structure when apply an in-plane field. e The preferred direction when the in-plane field is in the +x direction. f The final orientated domain structure at zero fields
More simulations were performed for both Bloch-type skyrmions and Néel-type skyrmions with different sign of D. The results are summarized in Fig. 3b–f. Figure 3b shows the spin texture of the four types of skyrmions whose magnetization at the skyrmion core is pointing up. For a Bloch-type skyrmion, the in-plane spin components rotate clockwise for positive D and counter-clockwise for negative D, while for the Néel-type skyrmions, the in-plane component spins point inside (positive D) or outside (negative D). Based on the principle of the contrast formation in the L-TEM imaging, it is not necessary to tilt the sample to create the contrast in the L-TEM images for the Bloch-type skyrmions and their chirality could be distinguished from the contrast (bright or dark) under the skyrmion core (Fig. 3c), while for the Néel-type skyrmions, the sample tilting is essential for the L-TEM imaging and same contrasts (Fig. 3c) will be observed regardless of the sign of D. Therefore, their chirality cannot be identified by the normal L-TEM imaging. However, we could solve this problem by applying an in-plane magnetic field. The in-plane field (+x direction here) breaks the symmetry of the magnetization distribution of a skyrmion as is shown in Fig. 3d, because the region with spins parallel to the in-plane component of the field grows while the region with the opposite spins shrinks. Though the in-plane component of the fields is in the +x direction for all the four cases, it is found that the preferred extension directions are all different as marked in Fig. 3e. For samples with bulk DMI, the preferred extension directions are in the +y or −y direction depending on the sign of D. The final domain structure at zero field is thus an orientated structure in the y directions, as is shown in Fig. 3f. This behavior has been observed experimentally50. For the interfacial DMI, the preferred extension direction is collinear with the in-plane field. By comparing theoretical prediction with experimental data on the relationship between the preferred extension direction and the in-plane field direction, we were able to identify the chirality of the skyrmions (or the sign of D). It is evident that D > 0 in our [Pt/Co/Ta]11 multilayers.
In-plane field and disorder effect on the skyrmions creation
In Fig. 2, we can see that the achieved skyrmion densities are different for different tilting angles (or in-plane field). To understand this phenomenon, we increased the tilt angle θ from 7° to 46°, and studied the magnetization reversal using the in-situ L-TEM (see details in Supplementary Figs. 4-8). As has been discussed in Fig. 2a, the skyrmions appeared twice when the magnetic field was swept from negative saturation field to positive saturation filed. The first emergence of skyrmions corresponded to the nucleation from the ferromagnetic state at negative field and the second emergence corresponded to the creation of skyrmions by breaking the labyrinth domains by the positive field. Figure 4 shows the maximum densities dmax1 and dmax2 as functions of the tilt angle and it also shows the corresponding L-TEM images. One can see that when the tilt angle is very small (i.e., 7°, consequently, the in-plane field is very small), dmax1 is almost zero and the snake-like structures are created directly. However, many more skyrmions were created at the breaking process, when the field was increased from zero to positive saturation. The reason why dmax2 is much larger than dmax1 over the whole range of tilt angles is that the breaking process is energetically more favorable than the nucleation process. Interestingly, with increasing the tilt angle (increasing the in-plane field), we found that both dmax1 and dmax2 increase, which indicates that the in-plane field favors the creation of skyrmions. This can be understood in the following way. It has been shown that skyrmion density increased with increasing the critical material parameter\(\kappa = \pi {\it{D}}{\mathrm{/}}4\sqrt {{\it{AK}}_{eff}}\)34,37, where A is the exchange stiffness, Keff is the effective perpendicular anisotropy and D is the DMI constant. Application of the in-plane field will actually weaken the role of the perpendicular anisotropy, while keeping D and A unchanged, which leads to the increase of κ.
Relationship between skyrmion densities and tilt angles. The maximum skyrmion densities dmax1 and dmax2 as functions of the tilt angles. The top shows the corresponding L-TEM images. The scale bar corresponds to 1 μm. The error-bars represent the calculated standard deviation from 9 areas of one square micron
To further investigate skyrmion creation assisted by the in-plane field and also to have deep understanding of the relationship between skyrmions density and critical material parameter κ, Ta(5 nm)/[Pt(3 nm)/Co(x nm)/Ta(2 nm)]11 with x = 2.05, 2.1, and 2.15 were deposited on Si3N4 membranes. Figure 5a shows the L-TEM images obtained when the skyrmion densities reach the maximum in the breaking process at tilt angles of 10°, 20°, 30°, and 42° for a x = 2.15 sample (see the results for x = 2.05 and 2.1 samples in Supplementary Fig. 9). It is clear that, for all these three samples, the skyrmions density increases with the tilt angles (see Supplementary Fig. 10a). Moreover, we found that the skyrmions density also increases with increase of x at the same tilt angle. According to our experiments, Keff decreases with increasing x from 2.05 and 2.15 (see Supplementary Fig. 10b–d), thus κ also increases. Therefore, our experimental results agree well with the equation predicting that skyrmions density increases with increasing of κ.
Control skyrmion densities by tilt angles and the disorder. a L-TEM images obtained when the skyrmion densities reach the maximum in the breaking process by decreasing the field from 0 Oe to negative saturation field at tilt angles of 10°, 20°, 30°, and 42° for a Ta(5 nm)/[Pt(3 nm)/Co(2.15 nm)/Ta(2 nm)]10 sample. b, c Micromagnetic simulations of the evolution of the domain structure with increasing the out-of-plane field at the tilt angle of 30o for (b) a disorder-free sample and (c) a disordered sample with the strength Ku and direction of magnetic anisotropy axis varying within 20%. d The maximum skyrmion densities as a function of tilt angle for Ku and magnetic anisotropy axis amplitude variation of 0, 10, 20, and 30%. All simulations were performed at room temperature
In addition micromagnetic simulations have been performed. Figure 5b shows evolution of the domain structure with the increasing out-of-plane field at the tilt angle of 30° for a pure (disorder-free) sample at room temperature. It can be seen that only 3 skyrmions were created. Since our samples are polycrystalline, the disorder of the film should be considered. Figure 5c shows the results for a disordered sample with the strength Ku and the direction of the magnetic anisotropy axis varied by 20%. Obviously, more skyrmions are created. Subsequently we did more simulations for different amplitude of disorder and tilt angles as is shown in Fig. 5d. It could be see that the skyrmion density increases with both the tilt angle and the amplitude of disorder, which reveals that, except for the intrinsic magnetic parameters, both the in-plane magnetic field and the disorder could also be used to control the skyrmions density. Note that the in-plane field should not be too large or the rotational symmetry of the skyrmion will be broken9.
Discussion
The demonstration of the possibility to measure chirality of the magnetic structure by L-TEM is one of our main results. Another important result is our finding that the vector of the speed V with which Néel skyrmion snakes are growing in a certain direction (or the vector indicating that direction), is determined by the vector of the in-plane magnetic field Hin, implying the relation V = p Hin between the directions of the two vectors, with p being a scalar function. For most physical systems such a relation is prohibited by symmetry because V changes sign under spatial reflection, r →−r, while Hin does not. One must have a pseudo-scalar in the system, that is, a scalar function p that changes sign under spatial reflection, in order to have the direction of the velocity determined by the direction of the magnetic field. In our system that pseudo-scalar originates from the chirality of the skyrmion that is determined by the sign of the Dzyaloshinskii-Moriya constant D in a non-centrosymmetric crystal. Thus, observation in which direction the skyrmion snakes are growing allows one to extract the skyrmions type and the sign of D. Furthermore, we found that both the in-plane field and the disorder facilitates the creation of skyrmions and increases their concentration.
Methods
Sample preparation
The PMA multilayer stacks Ta(5 nm)/[Pt(4 nm)/Co(1.4 nm)/Ta(1.8 nm)]11 were deposited simultaneously both on thermally oxidized Si substrates and carbon membranes by DC magnetron sputtering at room temperature. Ta(5 nm)/[Pt(3 nm)/Co(x nm)/Ta(2 nm)]10 with x = 2.05, 2.1, and 2.15 were further deposited on Si3N4 membranes with the same method. The pressure of the Ar gas was 0.4 Pa. The base pressure was lower than ~2 × 10−5 Pa. The films grown on thermally oxidized Si substrates were used for the SQUID-VSM and MFM measurements. The films on carbon/Si3N4 membranes were used for the in-situ L-TEM measurements.
Transmission electron microscopy (TEM)
TEM sample was prepared using focused ion beam (FIB) from the sample deposited on thermally oxidized Si substrates. The High angle annular dark field scanning TEM (HADDF-STEM) images and Electron energy loss spectroscopy (EELS) mapping spectrum were employed to analyze the structure of sample in a FEI TEM (Titan 60–300).
L-TEM measurements
In-situ Lorentz transmission electron microscopy (L-TEM) imaging was carried out by using a FEI Titan Cs Image TEM in Lorentz mode (the Fresnel imaging mode) at 300 kV. A double holder was used for the measurements. The magnetic field parallel to the electron beam can be easily applied and tuned by varying the current passing though the microscope’s objective lens. By tilting the sample, an in-plane field can also be applied. The ratio of the in-plane and out-of-plane field can be tuned by varying the tilt angle (θ).
MFM measurements
The magnetic force microscopy (MFM) experiments were performed using an Agilent 5500 Scanning Probe Microscope in tapping/lift mode.
Micromagnetic stimulations
mumax3 software package was used for the micromagnetic simulations. First, full three-dimensional multilayer simulations were performed to investigate the domain wall variation along the vertical direction, and the mesh size was set to 5 × 5 × 1.4 nm3. To reduce the computational resources and speed up the simulations, an effective medium approach proposed by Woo et al.33, was used to model the multilayer film as a single uniform layer to perform the other simulations and the mesh size is set to 5 × 5 × 5 nm3. The values of saturation magnetization Ms and the effective perpendicular anisotropy Keff, were obtained from the magnetization loops with out-of-plane and in-plane magnetic fields, using SQUID-VSM. The exchange stiffness A and interfacial DMI constant D used in this paper are the same as in ref. 33. A 1 × 1 × 0.07 μm2 square system with 2D periodic boundary conditions was used as a material system and the following parameters were chosen: Ms = 8.8 × 105 A m−1, Ku = 5.0 × 105 J m−3, A = 1.0 × 10−11 J m−1 and T = 300 K. For comparison, both bulk DMI and interfacial DMI were considered and its magnitude was set to D = 1.3 × 10−3 J m−2. Our samples are polycrystalline, so the disorder in the film is induced by the grain structure. Here, the grain size is set to 20 nm. Each grain varied in Ku and magnetic anisotropy axis in the range from 0 to 30%. The exchange coupling between grains was set at 90%. To generate skyrmions by a tilted field, we increased magnetic field with the step size of 20 Oe, and the relaxation time of 2 ns was used for each step.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91 (1960).
Fert, A., Cros, V. & Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 8, 152–156 (2013).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Jonietz, F. et al. Spin transfer torques in MnSi at ultralow current densities. Science 330, 1648–1651 (2010).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 8, 742–747 (2013).
Sampaio, J., Cros, V., Rohart, S., Thiaville, A. & Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 8, 839–844 (2013).
Schulz, T. et al. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 8, 301–304 (2012).
Jiang, W. et al. Blowing magnetic skyrmion bubbles. Science 349, 283–286 (2015).
Tomasello, R. et al. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 4, 6784 (2014).
Yu, G. et al. Room-temperature skyrmion shift device for memory application. Nano. Lett. 17, 261–268 (2016).
Zhang, S. et al. Current-induced magnetic skyrmions oscillator. New J. Phys. 17, 023061 (2015).
Garcia-Sanchez, F., Sampaio, J., Reyren, N., Cros, V. & Kim, J. A skyrmion-based spin-torque nano-oscillator. New J. Phys. 18, 075011 (2016).
Zhang, X., Ezawa, M. & Zhou, Y. Magnetic skyrmion logic gates: conversion, duplication and merging of skyrmions. Sci. Rep. 5, 9400 (2015).
Xia, H. et al. Control and manipulation of antiferromagnetic skyrmions in racetrack. J. Phys. D 50, 505005 (2017).
Grigoriev, S. et al. Helical spin structure of Mn1−yFeySi under a magnetic field: Small angle neutron diffraction study. Phys. Rev. B 79, 144417 (2009).
Pappas, C. et al. Chiral paramagnetic skyrmion-like phase in MnSi. Phys. Rev. Lett. 102, 197202 (2009).
Münzer, W. et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 81, 041203 (2010).
Yu, X. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Kanazawa, N. et al. Large topological Hall effect in a short-period helimagnet MnGe. Phys. Rev. Lett. 106, 156603 (2011).
Yu, X. et al. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 10, 106–109 (2011).
Tonomura, A. et al. Real-space observation of skyrmion lattice in helimagnet MnSi thin samples. Nano. Lett. 12, 1673–1677 (2012).
Yu, X. et al. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 3, 988 (2012).
Milde, P. et al. Unwinding of a skyrmion lattice by magnetic monopoles. Science 340, 1076–1080 (2013).
Shibata, K. et al. Towards control of the size and helicity of skyrmions in helimagnetic alloys by spin–orbit coupling. Nat. Nanotechnol. 8, 723–728 (2013).
Park, H. S. et al. Observation of the magnetic flux and three-dimensional structure of skyrmion lattices by electron holography. Nat. Nanotechnol. 9, 337–342 (2014).
Jiang, W. et al. Skyrmions in magnetic multilayers. Phys. Rep. 704, 1–49 (2017).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Schlenhoff, A. et al. Magnetic nano-skyrmion lattice observed in a Si-wafer-based multilayer system. ACS Nano 9, 5908–5912 (2015).
Boulle, O. et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotechnol. 11, 449–454 (2016).
Moreau-Luchaire, C. et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 11, 444–448 (2016).
Pulecio, J. F. et al. Hedgehog Skyrmion Bubbles in Ultrathin Films with Interfacial Dzyaloshinskii-Moriya Interactions. arXiv preprint arXiv:1611.06869 (2016).
Woo, S. et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Yu, G. et al. Room-temperature creation and spin–orbit torque manipulation of skyrmions in thin films with engineered asymmetry. Nano. Lett. 16, 1981–1988 (2016).
Legrand, W. et al. Room-temperature current-induced generation and motion of sub-100 nm skyrmions. Nano. Lett. 17, 2703–2712 (2017).
Pollard, S. D. et al. Observation of stable Néel skyrmions in cobalt/palladium multilayers with Lorentz transmission electron microscopy. Nat. Commun. 8, 14761 (2017).
Soumyanarayanan, A. et al. Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers. Nat. Mater. 16, 898–904 (2017).
Zhang, S. et al. Direct writing of room temperature and zero field skyrmion lattices by a scanning local magnetic field. Appl. Phys. Lett. 112, 132405 (2018).
Hrabec, A. et al. Measuring and tailoring the Dzyaloshinskii–Moriya interaction in perpendicularly magnetized thin films. Phys. Rev. B 90, 020402 (2014).
Lin, S.-Z. & Saxena, A. Noncircular skyrmion and its anisotropic response in thin films of chiral magnets under a tilted magnetic field. Phys. Rev. B 92, 180401 (2015).
Leonov, A. & Kézsmárki, I. Skyrmion robustness in noncentrosymmetric magnets with axial symmetry: the role of anisotropy and tilted magnetic fields. Phys. Rev. B 96, 214413 (2017).
Leonov, A. & Kézsmárki, I. Asymmetric isolated skyrmions in polar magnets with easy-plane anisotropy. Phys. Rev. B 96, 014423 (2017).
Loudon, J. C., Leonov, A., Bogdanov, A., Hatnean, M. C. & Balakrishnan, G. Direct observation of attractive skyrmions and skyrmion clusters in the cubic helimagnet Cu2OSeO3. Phys. Rev. B 97, 134403 (2018).
Legrand, W. et al. Resolving thickness-dependent reorientation of chiral hybrid textures in magnetic multilayers for spin-torque engineering. arXiv preprint arXiv:1712.05978 (2017).
Chauleau, J.-Y. et al. Chirality in magnetic multilayers probed by the symmetry and the amplitude of dichroism in X-ray resonant magnetic scattering. Phys. Rev. Lett. 120, 037202 (2018).
Wang, W. et al. A centrosymmetric hexagonal magnet with superstable biskyrmion magnetic nanodomains in a wide temperature range of 100–340 K. Adv. Mater. 28, 6887–6893 (2016).
Benitez, M. et al. Magnetic microscopy and topological stability of homochiral Néel domain walls in a Pt/Co/AlOx trilayer. Nat. Commun. 6, 8957 (2015).
Je, S.-G. et al. Asymmetric magnetic domain-wall motion by the Dzyaloshinskii-Moriya interaction. Phys. Rev. B 88, 214401 (2013).
Vansteenkiste, A. et al. The design and verification of MuMax3. AIP Adv. 4, 107133 (2014).
Wang, C. et al. Enhanced stability of the magnetic skyrmion lattice phase under a tilted magnetic field in a two-dimensional chiral magnet. Nano. Lett. 17, 2921–2927 (2017).
Acknowledgements
This publication is based on research supported by the King Abdullah University of Science and Technology (KAUST), Office of Sponsored Research (OSR) and under the Award No. OSR-2016-CRG5-2977.
Author information
Authors and Affiliations
Contributions
S.F.Z. and X.X.Z. conceived and coordinated the project. S.F.Z. fabricated the samples and performed the MFM measurements and the micromagnetic simulations. J.W.Z. performed the L-TEM measurements. S.F.Z., X.X.Z., J.W.Z., Y.W., and E.M.C. interpreted the results. S.F.Z., X.X.Z., and E.M.C. wrote the paper. The study was supervised by X.X.Z. All authors contributed to the discussion and preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, S., Zhang, J., Wen, Y. et al. Determination of chirality and density control of Néel-type skyrmions with in-plane magnetic field. Commun Phys 1, 36 (2018). https://doi.org/10.1038/s42005-018-0040-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0040-5
This article is cited by
-
Distinct skyrmion phases at room temperature in two-dimensional ferromagnet Fe3GaTe2
Nature Communications (2024)
-
Electric-field control of skyrmions in multiferroic heterostructure via magnetoelectric coupling
Nature Communications (2021)
-
Néel-type skyrmion in WTe2/Fe3GeTe2 van der Waals heterostructure
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.