Abstract
The high signal throughput of Fourier transform spectroscopy has proved a boon to overcoming the difficulties of otherwise overwhelming detector noise in chemical infrared spectroscopy and near-infrared Raman spectroscopy, and is desirable for in situ measurement. Here we introduce a stationary channel dispersed Fourier transform (CDFT) spectrometer that efficiently utilizes two-dimensional imagers to obtain high-resolution input spectra in low-pixel-density imagers. By angularly dispersing a vertical one-dimensional interference pattern along a horizontal axis, an array of bandlimited interferogram channels is measured with reduced sampling constraints in each channel. CDFT spectrometers can use existing imagers to measure spectra with 0.0025 cm−1 resolution over an 800 cm−1 bandwidth. Moreover, this approach reduces the quantization noise present in low dynamic range imagers significantly. To demonstrate the utility of CDFT spectroscopy, broadband spectral domain optical coherence and multicolor quantum dot photoluminescence are measured in low-pixel-density imagers.
Similar content being viewed by others
Introduction
The in situ detection of trace features of analyte in a complex environment requires an accurate sensor capable of measuring low levels of indicator signal in real time, and with limited capability for sample filtration, must resolve signal traces with specific discrimination from background markers. Optical spectroscopy excels at chemical identification and is ubiquitous in the sciences as a highly specific and noninvasive probe of molecular structure1,2,3,4,5,6,7. In Fourier transform (FT) spectroscopy, the high signal throughput has proved a boon to overcoming the difficulties of otherwise overwhelming detector noise in infrared spectroscopy and near-infrared Raman spectroscopy, and is desirable for in situ measurement8,9,10,11,12. In contrast with benchtop mirror-driven spectrometers, stationary FT spectrometers utilize multichannel detector arrays to record spatial interferograms for spectral recovery13,14,15,16,17,18,19,20,21,22,23,24,25, and while favorable for in situ FT spectroscopy, the fixed length of the detector array and pixel size fundamentally limit their spectral resolving power. To improve the spectral resolution of stationary FT spectrometers, we introduce a channel dispersed Fourier transform (CDFT) spectrometer that records two-dimensional spatial interferograms using imaging detectors in a single-frame snapshot to recover high-resolution spectra.
By spectrally dispersing the one-dimensional interference pattern, an array of bandlimited interferograms is measured in real time, relaxing sampling constraints within each spectral channel. Bandlimited channels also reduce centerburst contrast, lowering the quantization noise set by detector dynamic range. To demonstrate the CDFT spectrometer, broadband spectral domain optical coherence and multicolor quantum dot photoluminescence are measured using low-pixel-density detectors. Through efficient use of the full pixel count in imaging detectors, the resolution improvement of CDFT spectrometers offers a route to a compact and precise in situ spectrometer, useful for environmental management, medicine, and security26,27,28,29,30,31.
Results
Principle of operation
The CDFT spectrometer can be understood as an extension of the well developed stationary FT spectrometer. For stationary FT spectrometers, the 1D interferogram spans a detector column by path delay as shown in Fig. 1a, and for a zero path delay (or center burst) at the column center, the total path difference is inversely proportional to the minimum resolvable spectral element. Sampling rate is determined by the optical path difference equal to pixel pitch, or equivalently, the number of detector pixels sampling the interferogram. For two-sided spectrum signal bandwidth of KB and desired resolution Δk the following equation is valid:
where Npx is the number of pixels along the interferogram direction. Hence, for a fixed signal resolution, decreasing signal bandwidths results in a stationary FT spectrometer with lower pixel density in fixed-size detector arrays in order to recover the spectrum without aliasing.
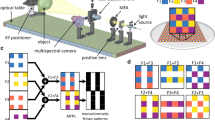
A stationary Fourier transform spectrometer measures the spatial interference pattern of a signal in a single dimension (a) and obtains the spectrum by Fourier transformation. While increasing the interference angle will squeeze more fringes into the detector column and increase the interferogram window, the sampling rate along the delay axis is simultaneously reduced by the fixed pixel width, and a full-bandwidth Nyquist rate limits the recovered spectral resolution for un-aliased spectra. Spectral dispersion in a CDFT spectrometer (b) creates an array of narrowband interferograms in the detector columns that partition the signal spectrum. Measurement and Fourier transformation of each channel (column) interference pattern, unwrapping around the carrier frequency, and summation recovers the total spectrum signal. Since the bandwidth in each channel is reduced by the partition factor, the interference window can be increased proportionally over the one-dimensional counterpart. Schematic diagram of a CDFT spectrometer (c). Spatial interference is generated by Sagnac interferometric arm; interference angle is determined by tuning mirror tilt. Periscope assembly rotates the interference plane by 90° to allow for dispersion in the propagation plane. Dispersive arm spreads the signal interference pattern into sub-band spectral channels to form the CDFT interferogram and is recorded by a 2D imager (Detector)
The CDFT spectrometer design optically disperses the one-dimensional interferogram pattern across a two-dimensional detector array. The spectral dispersion can be generated by prism, diffractive element, or any similar dispersive spectral mapping component. With the spatial interference pattern oriented along the detector columns, the pattern image is dispersed perpendicularly in horizontal direction and resolved along the rows of the detector array. In this two-dimensional interference pattern, shown in Fig. 1b, each column interference pattern, or “spectral channel” is formed by a sub-band of the signal spectrum and can be Fourier transformed to recover the sub-band spectrum32. After processing for carrier frequency aliasing and background, the recovered sub-band spectra can be added to recover the full signal power spectrum. While each spectral channel can be of a single-pixel width, channels with multi-pixel widths can be binned to a column with single-pixel width. Once the spectral channels are defined, the band limits are determined by both the dispersion angle subtended by the column extent. For a total signal bandwidth spread evenly across Npy spectral channels, the tradeoff can be described as follows:
Since each spectral channel bandwidth now occupies a smaller fraction of the total signal bandwidth, the minimum number of pixels along the interference axis needed to avoid aliasing is now lowered by the number of channel divisions Npy. A more detailed analysis and derivation of the CDFT advantage is presented elsewhere (see Supplementary Note 1).
For comparison, we consider a long-wave infrared (LWIR) spectrum measured from 1450 to 650 cm−1 (roughly 7–15 µm, matching the responsivity of an uncooled infrared focal plane array). For a stationary FT spectrometer that uses a linear array with 640 pixels, the highest generally achievable resolution without aliasing is 1.3 cm−1, or 13 nm for spectral features near 10 µm. Because the sampling rate is fixed by the pixel count of the detector array, increasing the interferogram window also results in reduced sampling rates, towards the Nyquist limit. In contrast, for a CDFT spectrometer, a large-format focal plane array with 640 by 512 pixel dimensions can recover spectra with 0.0025 cm−1 resolution or 0.025 nm for spectral features near 10 µm. Through spectral dispersion, the bandwidth per channel is reduced by the number of channels partitioning the total signal bandwidth; the minimum sampling rate of the interference pattern in each channel is reduced by the number of pixels (or channels) in the introduced detector axis, and the interferogram window can be increased proportionally to maximize the spectral resolution.
To calibrate bandpass sampling, an unwrapping algorithm is performed by passing two known spectrally separate and narrowband sources through the CDFTS system and extrapolating the spectral dispersion across the camera. As the interference angle is increased from co-linear to highly sheared, the fringe density is increased, and the calibration source lines increase in sampling frequency towards the Nyquist edge. As the interference angle is further increased, we observe wrapping, where the lines will cross the sampling edge and fold back into the sampling space, moving back towards DC (this is undersampling). For each angle, a linear correspondence is made between the discrete wavenumber [pix−1] spacing of the measured sources and the known spectral frequency spacing of the sources. Absolute wavenumber position is established by the known center frequency of each source. The number of wraps can be measured by sweeping the interference angle and observing the two spectral lines.
In practice, it is critical that the shearing angle of the interference pattern is chosen such that the channel bandwidth is not itself aliased32. In particular this is the condition that an integer multiple of the sampling rate does not directly fall into the channel band, this condition can be met by translational alignment of the detector along the dispersion axis, or by fine tuning of the shearing angle to move the sampling rate to a channel band edge. Moreover, the system optical transfer function lower bounds the minimum resolvable linewidth. While the interior angle of the interference waves can be increased within the bandpass sampling limit, system apertures will restrict the visibility of higher spatial frequency components of the FT interferometric pattern, and lower the SNR of high frequency components in the recovered spectra. Moreover, wideband system noise (both shot and detector) is itself aliased in bandpass sampling, and noise is introduced into the signal band with decreasing sampling rates to further lower the SNR. Judicial design of the optical system and selection of its elements is necessary to compensate for higher order errors. Simulations illustrate advantage of CDFTS in avoiding undersampling corruption and the reduction of signal dynamic range (see Supplementary Notes 2 and 3, and Supplementary Figures 1 and 2).
Experiment
The experimental implementation of CDFT spectrometer is shown in Fig. 1c. An interferometric arm based on a Sagnac interferometer splits a collimated signal beam into two beams with an interior interference angle proportional to the tuning mirror tilt; at 45° to the beam path, optical beams exiting the ring are collinear, and for tilt displacements of θ, the interior angle of the emerging beams will be 2θ. This topology has been thoroughly studied as an interferometer and stationary FT spectrometer33. The typical stationary FT spectrometers interference pattern is shown schematically in Fig. 1a. Based on the interior angle, control of the tuning mirror tilt allows for variable shearing of the counter-propagating beams in the Sagnac ring and thus fringe density in the final interferogram. While the Sagnac generated interference plane is initially along the table, a periscope element rotates the plane by 90° out of the table prior to prism input; the interference plane is then perpendicular to the table. A prism is used to spectrally disperse the broadband spatial interference pattern into a spread array of bandlimited interference patterns, and is resolved by an imaging camera. Recorded interferograms are then binned into spectral channels, and 1D Fourier transforms of the channel interferograms are computed by fast Fourier transform (FFT) in MATLAB; high pass filters are applied to each channel interferogram to remove out-of-band baseline noise spectra while preserving in-band channel components. For low sampling rates, aliased spectral channels are unwrapped from un-aliased components into an empty half space and summed to reconstruct the complex spectrum; recovery of the power spectrum is obtained from the spectral magnitude. A CDFT spectrometer was constructed according to the previously described schematic to measure the spectrum of modulated xenon arc lamp emission. Since the advantage of CDFT spectrometers is in measuring broadband spectra with narrow spectral features, we use this technique to evaluate the spectrum of a broadband xenon arc lamp output from a Michelson interferometer. Increasing displacement of the delay mirror from the point of zero optical path difference introduces a sinusoidal modulation of the optical spectrum with increasing spectral fringe density. This technique is the basis for depth imaging in spectral domain optical coherence tomography, for spectral evaluation, and it is useful for generating arbitrarily dense spectral features over a broad signal bandwidth. In this experiment, the broadband signal is used to demonstrate the effect of aliasing in undersampled interferograms of stationary FT spectrometers, and how channel dispersion in CDFT spectrometers can recover and restore the narrow spectral features.
The modulated xenon spectrum was passed through the CDFT spectrometer as described in Fig. 1, and was recorded as a 2D interferogram by the CMOS imager with 1900 × 1200 pixel format (per row, per column) and 5.86 micron square pixel pitch; the interference pattern runs along the columns. To demonstrate the efficacy of the system as a low-pixel-density stationary interferometer, two binned formats are processed, with 128 × 1200 (row, column) and 128 × 300, corresponding to un-aliased and aliased spectra, respectively. In Fig. 2, experimental recovery for 128 × 1200 format is shown. The raw interferogram for the 128 × 1200 format is obtained (Fig. 2a), and the spectral channel interferograms in each column (Fig. 2b) are first zero-padded for interpolation in the spectral domain and then individually Fourier transformed by FFT. The recovered normalized magnitudes of the channel spectra are shown in Fig. 2c; with increasing channel number, the center wavelength is shown to increase, corresponding to the spectral dispersion in the CDFT interferogram. Moreover, the dispersion also partitions the total spectrum between the pixel columns, and the recovered channel spectra can be seen to be localized to a narrowband about their center frequency. Owing to the linearity of the center frequency dispersion, it is evident that the signal is not aliased owing to the sufficient sampling of the interferometric axis by 1200 pixels, and recovery of the full spectrum is achieved by computing the magnitude in sum (Fig. 2d). Calibration of the sample wavenumber spacing was performed as described above by measuring the interference patterns passing through the CDFTS system for a helium neon laser (λ = 633 nm) and an LED (λ = 780 nm), and extrapolating the linear wavenumber spacing per frequency sample in the Fourier transformed interferogram. To factor out spectral distortion from speckle-induced zeros in the laser interferogram, a smoothing window is applied to the recovered spectrum (100-point moving average window on a 12,000 point linearly interpolated spectrum) to clearly identify the peak spectral position of the laser line.
Experimental 1200 × 128 pixel (column, row) CDFT interferogram of a broadband Xe lamp spectrum modulated by a Michelson interferometer to generate narrow spectral lines (a) with dispersion channels across the columns and interference along the rows. Each column contains a sampled interferogram (b) that is band-limited by the dispersion across the column width. Fourier transform of each channel results in the recovery of a sub-band of the total spectrum, and the normalized magnitudes are shown in (c). Without aliasing, evidenced by the linear dispersion of the channel center frequencies, summation of the complex channel Fourier transforms yields the recovered signal spectrum magnitude shown in (d)
Because of the sufficient density of pixels along the interferometric axis (1200 pixels), recovery in this case does not provide a sampling advantage over the 1D stationary FT spectrometer, as the interferogram is oversampled for all channels. Since there is no aliasing between the spectral channels or spectral overlap, the summation of recovered channel spectra is equivalent to the summation or binning of channel interferograms into a single 1200 × 1 array. In this case, alias-free recovery is enabled by the high density of pixels along the interferometric vertical axis of the detector.
The CDFT sampling advantage is evident in low-pixel-density detectors where undersampling occurs. This sampling advantage can be shown in the experimental recovery of a 128 × 300 (row, column) format CDFT interferogram, where using a 1D stationary spectrometer of the longest pixel dimension is insufficient to sample the entire 500 nm bandwidth of the visible band while retaining the single nanometer features. At the same shearing angle as before for identical spectral resolution, the binning of the native detector format brought the signal to a 128 × 300 format is obtained with each column as a spectral channel sampling the interference pattern with 300 detectors. After zero-padding interpolation as before, the channel spectra are recovered by FFT and shown in magnitude in Fig. 3a: here, the low-density of pixels shows aliasing to occur for small signal wavelengths. As a result of undersampling, simple summation (Fig. 3b) of the channel spectra results in an aliased signal spectrum, identical to 1D stationary FT spectrometer signal recovery. Since the channel center-frequencies are linearly dispersed, the wrapping or “reflecting” of the dispersion back into the sampling bandwidth is symptomatic of aliasing and cannot generally be distinguished for dense spectra in the 1D case. Owing to the channel separation in CDFT interferograms, these wrapped spectral channels can be uniquely separated from overlapping channels, and unwrapped or reflected across the Nyquist frequency into an empty half space as in Fig. 3c. Following this processing, the channel summation of recovered sub-bands can be repeated, and the alias-free CDFT recovery of the total spectrum is shown in Fig. 3d.
Experimental 300 × 128 pixel (column, row) CDFT interferogram of spectrally modulated Xe lamp. The Fourier transform recovered channel spectra magnitudes (a) show wrapping of the linear dispersion about the Nyquist zone for short wavelengths, indicative of undersampling and aliasing in these channels. When simply added, irreversible aliasing is observed in the magnitude (b) as shorter wavelengths are reflected across the critical sampling frequency to overlap with longer wavelengths; this is equivalent to the spectrum recovered from the 1D interferogram of a stationary Fourier transform spectrometer. CDFT spectrometers allow the separation of the aliased components from overlapping channel spectra. Linear dispersion of the spectral channels is restored by unwrapping the aliased channels into an empty half space (c) and recovery by summation recovery (d)
To test the applicability of low-pixel-density CDFT interferograms, multicolor quantum dot fluorescence measurements over a broad spectral range were measured. With the increasing sophistication of both laboratory and consumer imaging systems, multicolor/channel detection of fluorescent tags is an important direction towards high throughput analysis in immunoassay and biological sensing as a whole. A simple side collection fluorescence measurement was performed in a 1 mm path length glass cell, and a 400 mW Ar-ion laser was used to excite QD luminescence. Solutions of 6 nm diameter CdSe/ZnS quantum dots (1 mM in toluene) with emission lines at 540, 575, and 630 nm were individually measured for PL in both high (128 × 1200) and low (128 × 64) pixel-density environments by camera binning. A final measurement of a quantum dot mixture (300 µM each) was performed in both pixel-density environments, and processed spectra of individual QDs and mixture are shown in Fig. 4. Spectral dispersion was maintained along the constant 128 pixel axis, while interferogram sampling was variable between high and low-pixel-density environments. In the high pixel-density imager, alias-free spectra are obtained, as the sampling of the interferogram is well within the Nyquist rate (Fig. 4a). In the case of the low-pixel-density environments, the spectral channels can be observed to overlap (Fig. 4b) and the equivalent 1D interferogram is shown to recover an aliased signal spectrum (Fig. 4c). Using the unwrapping routine allowed by CDFT spectrometers, the overlapped spectral channels can be flipped into the empty spectral-half space (Fig. 4d) and superimposed to recover the unwrapped spectra (Fig. 4e). As a result of multiple undersampling wraps about the Nyquist edge in the severe 64 pixel sampling case, longer wavelengths are measured as higher spatial frequencies in the observable sampling space. Calibration by the spectral line sources as described earlier tracks the number of wrapping events, and linearly extrapolates the relation of physical wavenumber spacing to the sample space.
CDFT spectral measurements of CdZnSe quantum dot luminescence spectra. In a high pixel-density configuration (a), 128 binned spectral channels with 1200 pixel path delay sampling each are used to measure and recover monodisperse quantum dot PL (colored curves) at λem = 540, 575, and 630 nm. A mixture of the quantum dots is measured to recover broadband PL (gray). In a low-pixel-density configuration, the 128 spectralchannels are further binned to a 64 pixel sampling. As the carrier Nyquist rate is undersampled, spectral wrapping in the channel magnitudes is observed (b) resulting in an aliased spectrum recovery (c). CDFT spectrometer separation of the channel spectra in measurement allows for unwrapping of the overlapped bands (d) to reconstruct the alias-free signal spectrum (e). Uncertainty in calibration by spectral peak maximum results in a shift in the 64 pixel sampled spectrum (solid black) relative to the overlayed oversampled 1200 pixel sampled spectrum (dotted black); spectral shape is shown to be preserved with a shifted (dotted magenta)
Discussion
In our derivation, it was shown that by dispersion, the total signal bandwidth in a single interferogram can be divided into sub-bands that can sample the interferogram at a lower rate without aliasing. In particular, for a given number of pixels Npy along the interferometric axis, the critical Nyquist sampling rate can be lowered by a factor of Npx, the number of dispersion channels. This allows the detector to measure proportionally larger path delays to allow for a resolution increase by a factor of Npx. While the carrier frequency, or channel center frequency, is more readily aliased as a value invariant with the number of spectral channels, knowing the dispersion center in each channel allows the recovered spectra to be uniquely unwrapped from about the Nyquist edges and restored without aliasing; this was demonstrated in our experiment for aliasing across a single Nyquist edge. For highly undersampled interferograms, aliasing can potentially occur across both Nyquist edges, and more rigorous methods for spectral unwrapping will be necessary. To calibrate this process, known broadband spectra with dense features such as the spectrally modulated Xe lamp used in our experiment can be used to determine the number of wraps across Nyquist edges by tracking the channel spectra with increasing interference angle. In particular, the center frequency for each sub-band can be followed in each channel as the interference angle increases, and at the target angle for the desired spectral resolution, the center frequency of each sub-band will determine the number of reflections to make across each Nyquist edge.
Using the width of observed fringes generated by the modulated Xe lamp as a standard, we estimate 3 nm resolution (at 600 nm) for our current setup. In this particular system, the Sagnac interferometer while conferring stability, has an upper limit on interference angle for the given beam size owing to the finite aperture of our optical components. Higher spatial frequencies can be measured with increasing interference angle, which is possible with a modified Sagnac interferometer (using larger mirror optics to accommodate larger shear angles. Alternatively, Mach Zehnder configurations can be applied with special care taken to ensure optical component fixation and stability to make the system both compact and vibration insensitive. While these measurements show that the resolution can be improved beyond the Nyquist limit set by the pixel count in 1D, the measured 3 nm resolution is still less than the ideally achievable resolution which is on the order of 0.1 nm (limited by the finite length of the camera as the maximum OPD). This is because of the contrast loss induced by pixel area sampling rather than discrete time sampling in the case of time scanned FT spectrometers (see Supplementary Note 4). Namely, OPD doubling from increasing interference angle results in a resolution improvement by a factor of 2 (Supplementary Eqn. 4), but also lowers signal power owing to multiple fringe averaging in a single-pixel (Supplementary Eqns. 10, 11). This can be mitigated by placing a pinhole in front of each camera pixel in a pinhole array akin to those found in Hartmann sensors, or by using a stronger source. Similar optical elements that sample the wavefront discretely without sacrificing signal power can be proposed.
Calibration of photometric transfer function and wavenumber accuracy are necessary for high fidelity spectral acquisition. Imperfection in the source and spectrally dependent contrast loss contribute to spectral distortion and inaccuracy, which are particularly prevalent for severe undersampling, evident in the PL spectra for 128 × 64 pixels in Fig. 4e. For our measurements, speckle in the He–Ne laser interference pattern after passing through the optical system distorts the spectral position with spurious zero crossings. To correct this, the FT of the interference pattern was smoothed to find the peak center. A 100-point moving average smoothing window (on a linearly interpolated 12,000 sample spectrum) was applied to the Fourier recovered spectrum was performed for smoothing the laser source since only this source produced speckle, allowing for a better estimate of the spectral center of the laser line. While this smoothing method helps the peak position to be more clearly identified for calibrating the oversampled case (128 × 1200 pixels), the undersampled speckle (128 × 64 pixels) loses signal contrast (see Supplementary Figure 3) that can cause error in the peak position when similarly smoothed. This makes this calibration method increasingly more ambiguous for spectral accuracy in severely undersampled interferograms. To circumvent this issue, an extremely robust calibration could be performed with a single mode tunable laser. When the source is swept, not only would the spatial frequency be mapped to the tuned spectral frequency, but the variable loss in spectral power would also be calibrated, i.e. calibrate the transfer function and apodization due to undersampling (see Supplementary Note 4 and Supplementary Figure 3); this would improve the photometric accuracy of our spectrometer and correct for the FWHM errors.
We have demonstrated a CDFT spectrometer and have shown that spectral dispersion of the 1D stationary FT interferogram allows for the interferogram to be undersampled in proportion to the number of spectral channels introduced. CDFT spectral evaluation allows for high spectral resolution to be achieved for stationary infrared FT spectrometers in a format native to sensitive low-pixel-density imagers that populate much of the mid-IR and far-IR range. Conversely, with the reduced dependence on linear pixel-density, high pixel-density imagers in the visible and NIR can be partitioned for hyperspectral imaging by integration with a compact implementation of parallel CDFT spatial filters. Moreover, high speed cameras that scan rapidly over a limited number of detector elements can also benefit from channel dispersion, and in applications such as optical coherence tomography, CDFT spectrometers can improve the speed of A-scan readouts in the spectral domain without sacrificing dynamic range or resolution.
Methods
The CDFT spectrometer is an extension of the Sagnac interferometer. As described in Fig. 1c, the signal beam is split by a 50:50 beam-splitter reflected across the same three mirrors forming the ring, in opposite circuits to create two beam paths; adjustable in-plane tilt in the central mirror creates angularly displaces the two paths for an interference pattern (see Supplementary Note 5). A lens (L1) is then used to form an intermediate spatial Fourier (SF) transform plane, allowing for separation of the two beams for spatial filtering and background calibration. Prior to dispersion, a periscope assembly is used to rotate the interference plane by 90° out of the table-plane; this allows the now out-of-plane interference pattern to be dispersed in the table-plane along the detector. The lens focal lengths are 6” each with 2” Ø clear apertures (both L1 and L2 in schematic). The second lens is placed 12” after the first lens, with an intermediate Fourier plane formed at the midpoint for inspection of the background. Steering mirrors are silver with 1” Ø clear apertures. Two interferometer mirrors have 3” Ø clear apertures, while the other two are 1” Ø clear apertures, and all are silver. The fiber used for the measurement was a 0.22 NA patch cable with 200 micron core diameter. Similar system topologies are employed in pulse characterization system34,35,36, where in CDFT spectrometers, the aim is to distribute the spectral information across all detectors in an imaging detector and maximize spectral resolution (see Fig. 1b). The dispersive element is a Pelin-Broca prism (Thorlabs) for 90° dispersion, and the spectrally dispersed interference pattern is resolved by a cylindrical mirror with curvature in the dispersion plane onto the CMOS imager (Point Grey Blackfly, 2.3 MP monochrome) with 5.6 micron square pixel pitch.
Data availability
Supporting data can be made available from corresponding author upon request.
References
Henderson, B. & Imbusch, G. F. Optical spectroscopy of inorganic solids. Vol. 44 (Oxford University Press, Oxford, UK, 2006).
Movasaghi, Z., Rehman, S. & Rehman, I. U. Raman spectroscopy of biological tissues. Appl. Spectrosc. Rev. 42, 493–541 (2007).
Bao, J. & Bawendi, M. G. A colloidal quantum dot spectrometer. Nature 523, 67 (2015).
Huang, E., Ma, Q. & Liu, Z. Etalon Array Reconstructive Spectrometry. Sci. Rep. 7, 40693 (2017).
Redding, B., Liew, S. F., Sarma, R. & Cao, H. Compact spectrometer based on a disordered photonic chip. Nat. Photonics 7, 746–751 (2013).
Redding, B., Alam, M., Seifert, M. & Cao, H. High-resolution and broadband all-fiber spectrometers. Optica 1, 175–180 (2014).
Freeman, L. M., Smolyaninov, A., Pang, L. & Fainman, Y. Simulated Raman correlation spectroscopy for quantifying nucleic acid-silver composites. Sci. Rep. 6, 23535 (2016).
Griffiths, P. R. & De Haseth, J. A. Fourier transform infrared spectrometry. vol. 171 (John Wiley & Sons, Hoboken, NJ, 2007).
Baker, M. J. et al. Using Fourier transform IR spectroscopy to analyze biological materials. Nat. Protoc. 9, 1771–1791 (2014).
Movasaghi, Z., Rehman, S. & ur Rehman, D. I. Fourier transform infrared (FTIR) spectroscopy of biological tissues. Appl. Spectrosc. Rev. 43, 134–179 (2008).
Ferraro, J. R. & Basile, L. J. Fourier transform infrared spectra: applications to chemical systems (Academic press, Cambridge, MA, 2012).
Siesler, H. W., Ozaki, Y., Kawata, S. & Heise, H. M. Near-infrared spectroscopy: principles, instruments, applications (John Wiley & Sons, Hoboken, NJ, 2008).
August, I., Oiknine, Y., AbuLeil, M., Abdulhalim, I. & Stern, A. Miniature compressive ultra-spectral imaging system utilizing a single liquid crystal phase retarder. Sci. Rep. 6, 23524 (2016).
Le Coarer, E. et al. Wavelength-scale stationary-wave integrated Fourier-transform spectrometry. Nat. Photonics 1, 473–478 (2007).
Cheben, P., Powell, I., Janz, S. & Xu, D.-X. Wavelength-dispersive device based on a Fourier-transform Michelson-type arrayed waveguide grating. Opt. Lett. 30, 1824–1826 (2005).
Junttila, M.-L., Kauppinen, J. & Ikonen, E. Performance limits of stationary Fourier spectrometers. JOSA A. 8, 1457–1462 (1991).
Rommeluère, S. et al. Infrared focal plane array with a built-in stationary Fourier-transform spectrometer: basic concepts. Opt. Lett. 33, 1062–1064 (2008).
Hashimoto, M. & Kawata, S. Multichannel Fourier-transform infrared spectrometer. Appl. Opt. 31, 6096–6101 (1992).
Barducci, A., Cosmo, De V., Marcoionni, P. & Pippi, I. ALISEO: a new stationary imaging interferometer for earth observation. In Proc. SPIE 5546, Imaging Spectrometry X, (15 October 2004); https://doi.org/10.1117/12.557191.
Ishimaru, I., Kawashima, N. & Hosono, S. Built-in hyperspectral camera for smartphone in visible, near infrared and middle infrared lights region (first report): trial products of beans-size Fourier-spectroscopic line-imager and feasibility experimental results of middle infrared spectroscopic imaging. In Proc. SPIE 9855, Next-Generation Spectroscopic Technologies IX, 985504, vol. 9855 (SPIE, Baltimore, 2016).
Thomas, F. et al, Fourier Transform Spectroscopy. In Proc Light, Energy and the Environment. p. FTh2C–2 v (Optical Society of America, Germany, 2016)
Madi, M. et al. Lippmann waveguide spectrometer with enhanced throughput and bandwidth for space and commercial applications. Opt. Express 26, 2682–2707 (2018).
Froehly, C., Lacourt, A. & Vienot, J. C. Time impulse response and time frequency response of optical pupils.: experimental confirmations and applications. Nouv. Rev. Opt. 4, 183 (1973).
Thomas, F. et al. First results in near and mid IR lithium niobate-based integrated optics interferometer based on SWIFTS-Lippmann concept. J. Light. Technol. 32, 3736–3742 (2014).
Souza, M. C., Grieco, A., Frateschi, N. C. & Fainman, Y. Fourier transform spectrometer on silicon with thermo-optic non-linearity and dispersion correction. Nat. Commun. 9, 665 (2018).
Zanella, A., Bui, N., Castellani, A., Vangelista, L. & Zorzi, M. Internet of things for smart cities. IEEE Internet Things J. 1, 22–32 (2014).
Fang, S. et al. An integrated system for regional environmental monitoring and management based on internet of things. IEEE Trans. Ind. Inform. 10, 1596–1605 (2014).
Rateni, G., Dario, P. & Cavallo, F. Smartphone-based food diagnostic technologies: a review. Sensors 17, 1453 (2017).
Rodriguez-Saona, L. & Allendorf, M. Use of FTIR for rapid authentication and detection of adulteration of food. Annu. Rev. Food Sci. Technol. 2, 467–483 (2011).
Zhu, H., Isikman, S. O., Mudanyali, O., Greenbaum, A. & Ozcan, A. Optical imaging techniques for point-of-care diagnostics. Lab. Chip. 13, 51–67 (2013).
López-López, M. & García-Ruiz, C. Infrared and Raman spectroscopy techniques applied to identification of explosives. TrAC Trends Anal. Chem. 54, 36–44 (2014).
Vaughan, R. G., Scott, N. L. & White, D. R. The theory of bandpass sampling. IEEE Trans. Signal Process. 39, 1973–1984 (1991).
Barnes, T. Photodiode array Fourier transform spectrometer with improved dynamic range. Appl. Opt. 24, 3702–3706 (1985).
Trebino, R. Measuring the seemingly immeasurable. Nat. Photonics 5, 189–192 (2011).
Panasenko, D., Putilin, S. & Fainman, Y. Tunable spectral interferometry for broadband phase detection by use of a pair of optical parametric amplifiers. JOSA B. 22, 922–929 (2005).
Kovács, A., Szipöcs, R., Osvay, K. & Bor, Z. Group-delay measurement on laser mirrors by spectrally resolved white-light interferometry. Opt. Lett. 20, 788–790 (1995).
Acknowledgements
This work was supported in part by the National Science Foundation (NSF), the Office of Naval Research (ONR), the Army Research Office (ARO), DARPA, Cymer Corporation, and the San Diego Nanotechnology Infrastructure (SDNI) supported by the NSF National Nanotechnology Coordinated Infrastructure (grant ECCS-1542148).
Author information
Authors and Affiliations
Contributions
B.H., F.M., and Y.F. developed the project idea, carried out experiments, and analyzed results described.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hong, B., Monifi, F. & Fainman, Y. Channel dispersed Fourier transform spectrometer. Commun Phys 1, 34 (2018). https://doi.org/10.1038/s42005-018-0036-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0036-1
This article is cited by
-
Scalable integrated two-dimensional Fourier-transform spectrometry
Nature Communications (2024)
-
An integrated broadband spectrometer on thin-film lithium niobate
Nature Photonics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.