Abstract
Excitons in semiconductors and insulators consist of fermionic subsystems, electrons and holes, whose attractive interaction facilitates bound quasiparticles with quasi-bosonic character. In the presence of a degenerate electron gas, such excitons dissociate due to free carrier screening. Despite their absence, we found pronounced emission traces in the below-band-edge region of bulk, germanium-doped GaN up to a temperature of 100 K, mimicking sharp spectral features at high free electron concentrations (3.4E19–8.9E19 cm−3). Our interpretation of the data suggests that a degenerate, three-dimensional electron gas stabilizes a novel class of quasiparticles, which we name collexons. These many-particle complexes are formed by exchange of electrons with the Fermi gas. The potential observation of collexons and their stabilization with rising doping concentration is enabled by high crystal quality due to the almost ideal substitution of host atoms with dopants.
Similar content being viewed by others
Introduction
Many striking thermodynamic effects in nature are based on the reduction of the repulsive interaction between fermions or even on the bosonization of fermions and fermion complexes1. Prominent examples are macroscopic quantum phenomena such as superfluidity2 and superconductivity3. Besides in the ground state, such phenomena can also be observed in excited states, for example, of non-metallic matter with quasi-bosonic, excitonic excitations4,5 in the low-excitation-density limit. Here, an ideal bosonic behaviour is prevented by electron–electron, hole–hole and electron–hole interaction, hampering the system of interacting fermions to be condensed into a system of entirely massless, non-interacting bosons6,7.
Even more intriguing is the interaction of such quasi-bosonic excitons with a dedicated, degenerate Fermi system in its ground or even excited state—another fundamental phenomenon in many-body physics—leading to exciton cooling8 or even the short-lived stabilization (≈25 ps) of extended aggregates like the dropleton9 in an electron–hole plasma at a temperature of 10 K. In contrast, excitons in bulk semiconductors commonly dissociate in the presence of a degenerate electron gas due to screening of the Coulomb interaction, leaving behind only the optical traces of band-to-band transitions10.
The influence of high free carrier concentrations on electronic states in heavily doped semiconductors is well known10. Rising free carrier concentrations alter the optical characteristics of the semiconductor via the competing effects of the Burstein–Moss shift11,12 (BMS) and the band-gap renormalization (BGR)13, while also a Pauli blocking of the optical transitions occurs14. In the limit of high free carrier concentrations, decreasing exciton binding energies facilitate a transition to Mahan-like excitons15 at the Fermi edge singularity16. Excitonic excitations above the band edge have already been discussed for bulk systems17 above the Mott density18—the onset of a metal-like state. Ultimately, the quasi-bosonic character of excitons is lost upon their dissociation into their purely fermionic constituents (electron and hole). The spatial confinement inherent to nanostructures19,20,21 like quantum dots22,23 and quantum wells8,24 can stabilize quasiparticle complexes causing distinct optical features even under intermediate free carrier concentrations, with recent papers even reporting trions in two-dimensional MoS2 crystals25,26.
Here, we provide evidence for what we interpret as a novel class of exciton-like particles, which we suggest to call collexons. Within our interpretation, these collexons can increasingly be stabilized with rising density of a degenerate electron gas in a bulk semiconductor (GaN) up to a temperature of 100 K due to many-particle effects. Upon optical excitation long-lived (> 250 ps), strongly localized quasiparticles are formed, which do not only comprise a single electron–hole pair, but a collective excitation coupled to the entire degenerate electron gas in the high-density limit. In contrast to the common behaviour of heavily doped semiconductors, the entire emission intensifies and its decay time increases towards an increasing free electron concentration, while the collexonic emission narrows spectrally, as long as no free-carrier compensation occurs. We suggest a model of this intricate many-particle problem that is consistent with all of our experimental findings, demonstrating an increasing bosonization of the collexons with rising electron concentration. We conclude that the most likely interpretation of our results are collexons, that is, fundamental many-particle excitations in the presence of a degenerate electron gas irrespective of the particular semiconductor host material.
Results
Photoluminescence signature of heavily Ge-doped GaN
Figure 1 shows the photoluminescence (PL) signal of a highly germanium-doped, n-type GaN film at a temperature of 1.8 K (free electron concentration: n = 5.1E19 cm−3). Despite the present high doping level, two pronounced peaks stand out at \(E_{{\mathrm{N}}^ \ast }^{\mathrm{L}}\) = 3.492 eV and \(E_{\mathrm{N}}^{\mathrm{U}}\) = 3.505 eV, which we will label XL and XU. We emphasize that emission lines with such low half-width at half-maximum (HWHM) values, with \(\gamma _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\)= 4.50 ± 0.05 meV and \(\gamma _{\mathrm{N}}^{\mathrm{U}}\) = 3.0 ± 0.1 meV, represent a highly unusual observation at the given doping level. Both emission lines originate from the doped GaN:Ge layer as outlined in Supplementary Note 1. In addition, a well-known characteristic band-to-band luminescence27 evolves with the doping level as illustrated in the inset of Fig. 1. Here, the spectra range from a non-intentionally doped GaN reference sample (bottom, green line) up to a free electron concentration of n = 8.9E19 cm−3 (top, black line) as obtained by Hall effect measurements in conjunction with an in-detail Raman analysis. While the luminescence of the pure GaN sample is still dominated by donor bound excitons28, any rise of the germanium concentration (nGe) causes a spectral broadening, as frequently observed for various semiconductor compounds29,30. Once the free electron concentration suffices, the corresponding Fermi energy passes the conduction band and causes above band-gap luminescence due to the BMS, while the simultaneous shift of the luminescence towards lower energies is caused by the BGR. The corresponding critical carrier density is the Mott density that corresponds to an electron concentration of about n = 7E18–1E19 cm−3 in GaN27,31.
Exciton-like complex stabilization monitored by photoluminescence. Optical signature of a highly Ge-doped GaN sample showing the typical band-gap renormalization (BGR) and Burstein–Moss shift (BMS) along with two pronounced peaks XL and XU associated to many-particle complexes stabilized by the Fermi sea of electrons—the collexons. The inset shows a corresponding doping series starting with a non-intentionally doped (NID) sample featuring bound-excitonic emission. Upon rising doping concentration, the spectra broaden and the Fermi edge appears, before the two peaks XL and XU start to dominate the spectrum
Several observations based on Fig. 1 contradict the standard model for the behaviour of highly doped semiconductors. First, the high doping level in the present case causes the appearance of distinct peaks (XL and XU), and second, the entire luminescence intensity in the band-edge region rises with nGe due to the present high crystal quality. Additionally, the lifetime τBMS of the band-to-band transitions close to the Fermi edge increases with nGe—a clear sign of negligible compensation of free carriers. A combination of secondary ion mass spectrometry (SIMS), Hall effect, Raman, transmission, reflection, and PL measurements (see Supplementary Note 2) proves that the set of highly germanium-doped GaN samples exhibits only minor compensation effects as only a well-tolerable concentration of, for example, extended structural defects and deep carrier traps is introduced32,33. Hence, the free electron concentration \(n\) scales with the dopant concentration nGe in an almost linear fashion, with the highest doped sample as the sole exception. The main reason for the overall high crystalline quality is given by the similarity of the Ge4+ and Ga3+ cores and bonds with N in GaN34. The only significant doping-induced difference is the additional valence electron of Ge, which leads to the Fermi sea formation—an ideal, textbook-like doping situation.
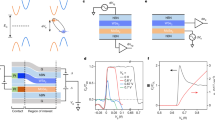
The effect of the high doping concentration in combination with low compensation is directly revealed by the particular luminescence characteristics of XL and XU (see Table 1). The spectral splitting between both peaks—the binding energy of XL (\(E_{{\mathrm{bind}}}\) = \(E_{\mathrm{N}}^{\mathrm{U}}\,-\,{E}_{{\mathrm{N}}^ \ast }^{\mathrm{L}}\)) in regard to XU—diminishes with rising free electron concentration. Simultaneously, the line broadenings \(\gamma _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right)\) and \(\gamma _{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) (HWHM values) decrease, indicating a new stabilization mechanism. In addition, the time-resolved PL (TRPL) measurements from Fig. 2a reveal a characteristic scaling behaviour of the associated decay times, indicating particular quasiparticle conversion processes as studied in more detail based on PL excitation (PLE) spectroscopy in Fig. 2b. All these observations underline the novel characteristics of the elementary excitations that are not inhibited, but instead stabilized by a degenerate electron gas.
Doping-driven balance between the fundamental excitations XU and XL. a Time-resolved PL analysis of XL and XU for three doping concentrations. All transients (circles) can be approximated by a simple fitting model (solid lines) yielding the characteristic decay times (\(\tau _{\mathrm{D}}\)) and rise times (\(\tau _{\mathrm{R}}\)). b Photoluminescence excitation (PLE) spectra (top) along with the corresponding PL spectrum (bottom) showing XL and XU along with the defect-related band at around 3.425 eV (n = 8.9E19 cm−3). All PLE spectra show energy differences in regard to at the given free electron concentration in order to eliminate the influence of strain. While XU only shows a weak trace of a single excitation channel, XL features four excitation channels related to the topmost three valence bands of GaN and XU. The emission band at 3.425 eV is excited predominantly via XL and XU. Interestingly, an increase in the free electron concentration enhances the excitation channel related to XU → XL (the PLE spectra are not shifted horizontally)
Doping-driven balance of the fundamental excitations
The decay times of the XL and XU excitations as listed in Table 1 surpass the value of the background BGR and BMS luminescence, which indicates a binding or stabilization mechanism induced by the Fermi sea of electrons (compare Supplementary Note 3). Interestingly, the decay times of the BGR and BMS luminescence increase with rising doping concentration in accordance with the evolution of the decay times \(\tau _{\mathrm{D}}^{\mathrm{L}}\) and \(\tau _{\mathrm{D}}^{\mathrm{U}}\) (see Table 1). While the high energy peak (XU) features a fast rise time (\(\tau _{\mathrm{R}}^{\mathrm{U}}\) < 10 ps) in all transients shown in Fig. 2a (blue and red data points), its low energy counterpart (XL) exhibits a well-resolvable rise time \(\tau _{\mathrm{R}}^{\mathrm{L}}\) that diminishes with rising doping concentration (see Table 1). All transients in Fig. 2a represent differential transients, showing only the temporal evolution of XU and XL because the partially BGR-induced and BMS-induced background was subtracted (see Supplementary Note 3 for details). The solid lines in Fig. 2a represent the results of a biexponential fitting model, taking into consideration rise and decay times. Only the highest doped sample requires the inclusion of a second decay time due to the onset of compensation and structural defect formation leading to non-radiative decays28.
Figure 2b (top) shows the PLE spectra with detection energies directly associated to XL, XU, and a defect-related feature in the regime of the BGR luminescence unique to the sample with the highest free electron concentration (n = 8.9E19 cm−3). All relative PLE detection energies are assigned to the corresponding absolute PL energies by vertical, dashed lines, see Fig. 2b (bottom). We show such differential PLE detection energies in order to eliminate the minor influence of varying strain levels in our samples as discussed in Supplementary Note 2. The PLE spectrum of XU (blue) suggests one excitation channel comprising a hole from the A-valence band and an electron in the conduction band forming a first excited state (\({\mathrm{X}}_{{\mathrm{A}}\left( {{{n}} = 2} \right)}^{\mathrm{U}}\)) of an electron–hole pair complex—a situation similar to the excited A-exciton in high-quality, undoped GaN samples (see Supplementary Figure 6) now augmented by the interaction with the degenerate electron gas in the conduction band35,36,37. In contrast, the PLE spectra related to XL appear as much less perturbed due to an enhanced binding mechanism. In the displayed high-energy regime, two additional excitation channels appear, comprising holes from the B-valence (\({\mathrm{X}}_{\mathrm{B}}^{\mathrm{U}}\)) and C-valence (\({\mathrm{X}}_{\mathrm{C}}^{\mathrm{U}}\)) band along with an electron in the ground state. In addition, close-to-resonant excitation of XU boosts the intensity of XL, driving a quasiparticle conversion process, whose dynamics is quantified by \(\tau _{\mathrm{R}}^{\mathrm{L}}\) extracted from the time-resolved analysis. Thereby, the intensity of the excitation channel related to XU rises with doping concentration, while the entire PLE spectrum of XL gets more distinct. This observation, in addition to the particular scaling behaviour of the rise time (\(\tau _{\mathrm{R}}^{\mathrm{L}}\)) with doping concentration (see Table 1), supports our interpretation of XU and XL as the exciton-like complex, called collexon, and the four-particle complex, the bicollexon, both stabilized by the Fermi sea.
Shifting the PLE detection towards lower energies (e.g. 3.425 eV) yields a PLE spectrum that exhibits resonances in close energetic vicinity to XU and XL. The energy shift in between the PLE resonances related to XU and XL and the corresponding luminescence features are clear indications for a light self-absorption process28,38 as described in Supplementary Note 4. Nevertheless, the assignment between the luminescence peaks and the corresponding excitation channels is apparent from Fig. 2b, showing that holes from the three topmost valence bands contribute to XL, while the complexes related to XU possess an efficient conversion pathway towards XL. Naturally, both complexes can dissociate and therefore contribute to any luminescence at lower energies as their components—electrons and holes—relax towards the corresponding defect bands (see Fig. 2b).
Alternative interpretations for XU and XL as, for example, classical bound excitons related to germanium can be excluded. No discrete emission peaks with linewidths in the meV regime should occur for this case because high dopant concentrations should create a broad39, Ge-related defect band comprising a wide energy spectrum for bound excitons. Additionally, the reflectivity is heavily altered in energetic vicinity to XU and XL, indicating a high concentration of bound elementary excitations. Their thermalization behaviour even reveals the stability of XU and XL up to a temperature of 100 K (see Supplementary Notes 1 and 5).
Interpretation
All experimental observations point to the formation of many-particle complexes (see Supplementary Methods for further comments). We suggest to identify the XU emission peak as an electron–hole pair complex interacting with the Fermi sea that achieves its stabilization by exchange of electrons. This interpretation is supported by the fact that the most important energy gain mechanism providing stability of an electron gas is particle exchange14. Our understanding of the complex formation mechanisms and the associated exchange stabilization are illustrated in the upper, left panel of Fig. 3a. The second low energy peak XL is correspondingly interpreted as a more extended many-particle complex, capturing an electron–hole pair from the Fermi sea (see upper, right panel of Fig. 3a). In contrast to the interband electron–hole pair forming the complex XU—the collexon—the additionally captured electron–hole pair is of an intraband nature. The resulting four-particle complex in interaction with the excited Fermi sea, called the bicollexon, is consequently stabilized by electron exchange and Coulomb attraction. Its total excitation energy is lowered by the effective binding energy of the additional intraband electron–hole pair, that is, the full binding energy of the collexon complex minus the excitation energy of an electron from the Fermi sea above the Fermi level, leaving a hole behind.
Suggested collexonic excitations in the Fermi sea. a The electronic ground state (G) is formed by the degenerate electron gas—the Fermi sea—in the Γ7c conduction band of GaN:Ge. Upon optical excitation, interband excitations are formed and stabilized by the Fermi sea of electrons giving rise to the first excited state, the collexon (XU) with a decay rate γU. In the high-density regime, such collexons scatter with electrons in the Fermi sea (γU→L), enabling the formation of the bicollexon (XL). Hence, the bicollexon represents a mixed complex of interband and intraband electron–hole pairs that decays (γL), forming the second excited state. b Based on our modelling and the fitting function extracted from the imaginary part of Eq. 1 (solid, red lines), we can approximate the PL data (symbols) related to XU and XL. All spectra are displaced horizontally for clarity
In contrast to trions8,23,24,26,40, the predicted (bi-)collexon is electrically neutral, spinless, and of bosonic nature. PL measurements in the presence of a magnetic field up to 5 T (not shown) do not reveal any shift or splitting of the collexon lines from Figs. 1 and 2b. We cannot exclude the formation of even larger complexes with more than one intraband electron–hole pair, but only slightly smaller excitation energies in comparison to the bicollexon. Indeed, in Supplementary Figure 9 the XL peak exhibits a prominent line-shape asymmetry below 10 K that may be caused by additional bound intraband electron–hole pairs. The theoretical picture developed for low or moderately doped semiconductor nanostructures as quantum wells, wires, or dots cannot be applied in the present case. The measured free electron concentrations (n = 3.4E19, 5.1E19 and 8.9E19 cm−3) correspond to Fermi energies of \(\varepsilon _{\mathrm{F}} = \hbar ^2k_{\mathrm{F}}^2{\mathrm{/}}2m_{\mathrm{e}}^ \ast =\) 166, 217 and 315 meV in the conduction band with a Fermi wave vector of \(k_{\mathrm{F}} = \left( {3\pi ^2n} \right)^{1/3} =\) 1.00, 1.15 and 1.38 nm−1, if an isotropic effective electron mass \(m_{\mathrm{e}}^ \ast =\) 0.231\(m_{\mathrm{e}}\) is assumed27. Direct comparison with the Bohr radius of an A-exciton in GaN (hydrogen-like \(a_{{\mathrm{ex}}} =\) 3.58 nm) shows that the high-density limit \(a_{{\mathrm{ex}}}k_{\mathrm{F}} \gg\) 1 beyond the Mott density is reached, where free excitons and their charged, trionic counterparts are completely dissociated, nullifying their relevance for optical data in the high-density regime.
The extraordinary role of the degenerate electron gas for the formation of XU and XL is illustrated in Fig. 3a. The ground state (G) of the system is given by the Fermi sea in the Γ7c conduction band of GaN:Ge. Upon optical, interband excitation, the predicted collexon is formed as an electron–hole pair well below the Burstein–Moss edge, but strongly coupled to the degenerate electron gas and scattered by the N electrons present in the ground state (G) in the conduction band. Within our model, the collexon forms a first excited state stabilized by the Fermi sea of electrons through unscreened electron exchange as likely stabilization mechanism (illustrated by the arrows in Fig. 3a). It is protected against interactions with polar optical phonons, since the Fröhlich coupling41,42 almost vanishes because of the strong free carrier screening. The formation of the larger complex XL as a second excited state with a lower excitation energy is consequently explained by a two-step procedure. First, virtually, a collexon is excited. Second, scattering of the collexon in the Fermi sea excites an electron from the gas and leaves a hole behind, yielding a bicollexon complex, which emits at lower energies with respect to the collexon. Following this idea, XL is a highly unconventional, mixed complex constituting intraband as well as interband excitations that originate from the optical excitation and the subsequent exciton–electron scattering (γU→L) and coupling mechanism to the Fermi sea. The optical decay of a bicollexon leaves an intraband excitation behind that will relax rapidly towards the G state—the unperturbed Fermi sea in the conduction band.
This described mechanism is totally different from the formation of excitons, the primary response of an undoped non-metal solid to light. However, it is also completely different from the formation of surface excitons in a metal43,44. Despite the presence of a Fermi sea in this case, the excitons of metal surfaces are confined in normal direction by the image potential. In addition, the screening of the electron–hole attraction is dominated by the image potential effects. The presence of the electron gas only determines the strength of the image potential near the surface, but does not stabilize the exciton formation itself. The predicted particular formation process of the bicollexon XL explains the occurrence of the rise time (\(\tau _{\mathrm{R}}^{\mathrm{L}}\)) in the corresponding PL transients in Fig. 2a and the particular excitation channel in close energetic vicinity to the collexon XU, see Fig. 2b (top). The rising free electron concentration promotes the excitation channel associated to XU as the probability for electron exchange events is enhanced, see Fig. 2b (top). The increasing stabilization mechanism via electron exchange is described by\(\,\tau _{\mathrm{R}}^{\mathrm{U}}\) and \(\tau _{\mathrm{R}}^{\mathrm{L}}\) and their particular scaling behaviour with rising doping concentration (see Table 1), being in good qualitative agreement with the spectral narrowing shown in Fig. 1. The characteristic rise times are generally larger than the common rise times for exciton formation in GaN28, ZnO45, and GaAs46,47.
Discussion
Even the most sophisticated theory focused on solving the Bethe–Salpeter equations for electron–hole polarization functions coupled to a degenerate electron gas is difficult to formulate directly for collexon-like excitation complexes with two or four particles coupled to a degenerate electron gas14,16. The challenges arise mainly due to the need for possible inclusion of vertex corrections to the integral kernel and non-particle-conserving interactions (see Supplementary Methods). Ideas for such an in-detail many-body approach are outlined in Supplementary Methods section 'Collexon from first principles' but are difficult to provide conclusive results. Therefore, an intuitive physically theory is used in the following. More detailed arguments can be found in Supplementary Methods section 'Phenomenological approach'. In the low-excitation limit, the absorption and emission properties are dominated by bound states, for example, of free 1s excitons14,48 or trions49,50,51, and can be simulated by the imaginary part of a frequency-dependent optical susceptibility \(\chi \left( \omega \right)\) as a sum of such quantities in oscillator form with poles at their eigenenergies14,48,49. We follow such an approach to describe also the collexon and bicollexon contributions in the PL and absorption spectra by
Here, \(E_{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) and \(\gamma _{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) denote the density-dependent excitation energy and the line broadening of the collexon XU (see Table 1). The capture process of an additional intraband electron–hole pair constituting the bicollexon (XL) is described by a self-energy \(\mathop {\sum }\limits_{{\mathrm{N}}^ \ast }^{\mathrm{L}} \left( n \right)\)50,51. Its negative real part \(E_{{\mathrm{bind}}}\left( n \right) = - {\mathrm{Re}}\mathop {\sum }\limits_{{\mathrm{N}}^ \ast }^{\mathrm{L}} \left( n \right)\) is interpreted as the effective binding energy of the additional intraband electron–hole pair affected by the degenerate electron gas, \({E}_{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right) = {E}_{\mathrm{N}}^{\mathrm{U}}\left( n \right) + {\mathrm{Re}}\mathop {\sum }\limits_{{\mathrm{N}}^ \ast }^{\mathrm{L}} \left( n \right)\), while the negative imaginary part \(- {\mathrm{Im}}\mathop {\sum }\limits_{{\mathrm{N}}^ \ast }^{\mathrm{L}} \left( n \right)\) characterizes the modification of the bicollexon’s line broadening \(\gamma _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right) = \gamma _{\mathrm{N}}^{\mathrm{U}}\left( n \right) + {\mathrm{Im}}\mathop {\sum }\limits_{{\mathrm{N}}^ \ast }^{\mathrm{L}} \left( n \right)\). The density-dependent envelope functions \(\phi _{\mathrm{N}}^{\mathrm{U}}\left( 0 \right)\) and \(\phi _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( 0 \right)\) of the many-particle complexes XU and XL appear in real space at vanishing relative particle coordinates similar to the exciton case, because the optical transition matrix element \({{M}}\) is approximated by its value at the Γ-point14,48. The squares of the envelope functions characterize the localization of the many-particle complexes with rising electron density. The index \({\mathrm{N}}\) labels the stabilizing degenerate gas with \({\mathrm{N}}\) electrons, the corresponding index \({\mathrm{N}}^ \ast\) indicates that the intraband electron gas is excited with an electron above the Fermi level and a hole in the Fermi sea, while the pre-factors \(N^{\mathrm{U}}\) and \(N^{\mathrm{L}}\) describe the number of corresponding complexes.
The fits of PL spectra based on the imaginary part of the model function in Eq. 1 are displayed in Fig. 3b, considering slightly varying strain levels. The most important parameters of the excitations are fitted self-consistently with the free electron concentration n. These are the relative positions of the two peaks \(E_{\mathrm{N}}^{\mathrm{U}}\) and \({E}_{{\mathrm{N}}^ \ast }^{\mathrm{L}}\), the line broadenings \(\gamma _{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) and \(\gamma _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right)\), as well as the relative oscillator strengths \(I_{\mathrm{N}}^{\mathrm{U}}\left( n \right) = N_{\mathrm{U}}\left| {\phi _{\mathrm{N}}^{\mathrm{U}}\left( 0 \right)} \right|^2\gamma _{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) and \(I_{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right) = N_{\mathrm{L}}\left| {\phi _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( 0 \right)} \right|^2\gamma _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right)\). Despite the stabilization tendency evoked by the electron gas, \(E_{{\mathrm{bind}}}\left( n \right)\) of the additional intraband electron–hole pair decreases with rising n (see Fig. 3b and Table 1), since increasing intraband excitation energies that scale with the Fermi energy. The HWHM values of both emission lines \(\gamma _{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) and \(\gamma _{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right)\) reduce with rising n in accordance with a decay time prolongation—a statement particularly true for XU (see Table 1 and Supplementary Note 2). Naturally, the inverse of the decay times \(\tau _{\mathrm{D}}^{{\mathrm{U}}/{\mathrm{L}}}\) is always much smaller than \(\gamma _{\mathrm{N}}^{{\mathrm{U}}/{\mathrm{L}}}\) considering the time-energy uncertainty, due to parasitic, for example, Auger and phononic process.
The entire set of lifetime and emission line width trends unequivocally confirm the stabilizing action of the degenerate electron gas. The bicollexon emission line broadens in comparison to its collexon counterpart due to the increase of \({\mathrm{Im}}\mathop {\sum }\limits_{{\mathrm{N}}^ \ast }^{\mathrm{L}} \left( n \right) =\) 1.0, 1.5, and 1.9 meV (see Table 1). Interestingly, while the relative intensities \(I_{{\mathrm{N}}^ \ast }^{\mathrm{L}}\left( n \right)/I_{\mathrm{N}}^{\mathrm{U}}\left( n \right)\) remain almost constant with rising \(n\) in accordance with the PL spectra (see Fig. 3b). Despite its higher complexity, the bicollexon contribution to the PLE spectra dominates over the collexon peak. This result directly illustrates the efficiency of the binding mechanism of the intraband electron–hole pair, a process that can only be overcome under extreme optical pump conditions (>10 MW cm−2). In summary, the fit of the PL spectra in Fig. 3b by means of the imaginary part of Eq. 1 supports our interpretation of XU and XL as neutral and spinless electronic excitations called collexon and bicollexon that are both stabilized by the degenerate electron gas.
After the doping-induced complete dissociation of the quasi-bosonic excitons into their fermionic constituents, a bosonic revival, collexons, occurs due to the stabilizing action of the degenerate electron gas. In general, we propose that the two fundamental excitations that motivated us to conduct this study should occur in the optical signature of any highly doped and at the same time lowly compensated semiconductor with an overall high crystalline quality. No additional spatial confinement of carriers as in quantum well and quantum dot structures is needed50,51,52. In contrast, the formation of collexons could even be favoured in bulk material due to the interaction with the degenerate three-dimensional Fermi gas. Nevertheless, both a sufficiently high doping level and low compensation would not suffice alone for the observation of collexons. Additionally, the material quality of the undoped semiconductor must be high, which can be confirmed by the appearance of luminescence related to the free A-exciton and B-exciton and low HWHM values for the Raman modes (≈1.3 ± 0.1 cm−1)33. We believe that all, for example, n-dopants that achieve a close-to-perfect substitution of the corresponding host atom should lead to near perfect, doped crystals comprising a degenerate electron gas as in GaN:Ge. Other possible candidates are Ge dopants occupying Ga-sites in Ga2O3 or Sn dopants on In sites in InN and In2O3. Therefore, more experimental but especially theoretical investigations are welcome to improve our understanding of the data and hopefully support our proposed stabilization mechanisms which we suggest to result in the novel electronic complexes.
Methods
The GaN:Ge samples were grown by metalorganic vapour phase epitaxy on (0001) sapphire substrates (0.25° off-oriented towards the m-direction) with germane as Ge source as reported by Fritze et al.32 Room temperature Hall effect measurements33 were performed based on the standard van der Pauw method.
The PL and PLE experiments were performed in one setup comprising a He bath cryostat providing a base temperature of 1.8 K. For the continuous wave PL measurements, a HeCd laser (325 nm) was used, while the PLE measurements were conducted with a dye laser (100 Hz repetition rate, pumped by a XeCl excimer laser) containing 2-methyl-5-t-butyl-p-quaterphenyl as the active medium. The luminescence signal was dispersed by an additive double monochromator (Spex 1404–0.85 m focal length, 1200 groves mm−1, 500 nm blaze) equipped with an ultra-bialkali photomultiplier tube (Hamamatsu, H10720-210). For the TRPL measurements, the sample was excited with the fourth harmonic of a picosecond Nd:YAG laser (266 nm, 76 MHz repetition rate) in a Janis micro-cryostat (ST-500) at a temperature of 5 K. The PL was spectrally and temporally analysed by a subtractive double monochromator (McPherson 2035–35 cm focal length, 2400 groves mm−1, 300 nm blaze) attached to a multichannel plate photomultiplier (Hamamatsu R3809U-52) providing a laser pulse width limited temporal resolution of 55 ps. Standard photon counting electronics were applied in order to derive the final histograms. Standard deconvolution techniques were employed in order to fit the measured transients.
Details regarding the theoretical treatment of electronic excitations in the Fermi sea can be found in the Supplementary Methods.
Data availability
The data that support the findings of this study are available from the authors on reasonable request, see author contributions for specific data sets.
References
Gogolin, A. O., Nersesyan, A. A. & Tsvelik, A. M. Bosonization and Strongly Correlated Systems 1st edn (Cambridge University Press, Cambridge, 2004).
London, F. The λ-phenomenon of liquid helium and the Bose–Einstein degeneracy. Nature 141, 643–644 (1938).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Frenkel, J. On the transformation of light into heat in solids. Phys. Rev. 37, 17–44 (1931).
Wannier, G. H. The structure of electronic excitation levels in insulating crystals. Phys. Rev. 52, 191–197 (1937).
Blatt, J. M., Böer, K. W. & Brandt, W. Bose–Einstein condensation of excitons. Phys. Rev. 126, 1691–1692 (1962).
Kasprzak, J. et al. Bose–Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006).
Bigenwald, P., Kavokin, A. & Gil, B. Excitons and trions confined in quantum systems: from low to high injection regimes. Phys. Stat. Sol. Appl. Res. 195, 587–591 (2003).
Almand-Hunter, A. E. et al. Quantum droplets of electrons and holes. Nature 506, 471–475 (2014).
Shklovskii, B. I. & Efros, A. L. Electronic Properties of Doped Semiconductors 1st edn (Springer, Berlin, 1984).
Burstein, E. Anomalous optical absorption limit in InSb. Phys. Rev. 93, 632–633 (1954).
Moss, T. S. The interpretation of the properties of indium antimonide. Proc. Phys. Soc. Sect. B 67, 775–782 (1954).
Berggren, K. F. & Sernelius, B. E. Band-gap narrowing in heavily doped many-valley semiconductors. Phys. Rev. B 24, 1971–1986 (1981).
Bechstedt, F. Many-Body Approach to Electronic Excitations 1st edn (Springer, Berlin, 2015).
Mahan, G. D. Excitons in degenerate semiconductors. Phys. Rev. 153, 882–889 (1967).
Schleife, A., Rödl, C., Fuchs, F., Hannewald, K. & Bechstedt, F. Optical absorption in degenerately doped semiconductors: Mott transition or Mahan excitons? Phys. Rev. Lett. 107, 236405 (2011).
Thomas, G. A. & Rice, T. M. Trions, molecules and excitons above the Mott density in Ge. Solid State Commun. 23, 359–363 (1977).
Mott, N. F. Metal–insulator transition. Rev. Mod. Phys. 40, 677–683 (1968).
Kheng, K. et al. Observation of negatively charged excitons X− in semiconductor quantum wells. Phys. Rev. Lett. 71, 1752–1755 (1993).
Finkelstein, G., Shtrikman, H. & Bar-Joseph, I. Optical spectroscopy of a two-dimensional electron gas near the metal–insulator transition. Phys. Rev. Lett. 74, 976–979 (1995).
Shields, A. J., Pepper, M., Ritchie, D. A., Simmons, M. Y. & Jones, G. A. C. Quenching of excitonic optical transitions by excess electrons in GaAs quantum wells. Phys. Rev. B 51, 18049–18052 (1995).
Warming, T. et al. Hole–hole and electron–hole exchange interactions in single InAs/GaAs quantum dots. Phys. Rev. B 79, 125316 (2009).
Xu, X. Enhanced trion emission from colloidal quantum dots with photonic crystals by two-photon excitation. Sci. Rep. 3, 3228 (2013).
Esser, A., Runge, E., Zimmermann, R. & Langbein, W. Photoluminescence and radiative lifetime of trions in GaAs quantum wells. Phys. Rev. B 62, 8232–8239 (2000).
Lui, C. H. et al. Trion-induced negative photoconductivity in monolayer MoS2. Phys. Rev. Lett. 113, 166801 (2014).
Scheuschner, N. et al. Photoluminescence of freestanding single- and few-layer MoS2. Phys. Rev. B 89, 125406 (2014).
Feneberg, M. et al. Band gap renormalization and Burstein–Moss effect in silicon- and germanium-doped wurtzite GaN up to 1020 cm−3. Phys. Rev. B 90, 75203 (2014).
Callsen, G. et al. Optical signature of Mg-doped GaN: Transfer processes. Phys. Rev. B 86, 75207 (2012).
Arnaudov, B., Paskova, T., Goldys, E., Evtimova, S. & Monemar, B. Modeling of the free-electron recombination band in emission spectra of highly conducting n-GaN. Phys. Rev. B 64, 045213 (2001).
De-Sheng, J., Makita, Y., Ploog, K. & Queisser, H. J. Electrical properties and photoluminescence of Te-doped GaAs grown by molecular beam epitaxy. J. Appl. Phys. 53, 999–1006 (1982).
Binet, F., Duboz, J. Y., Off, J. & Scholz, F. High-excitation photoluminescence in GaN: Hot-carrier effects and the Mott transition. Phys. Rev. B 60, 4715–4722 (1999).
Fritze, S. et al. High Si and Ge n-type doping of GaN doping—limits and impact on stress. Appl. Phys. Lett. 100, 122104 (2012).
Nenstiel, C. et al. Germanium—the superior dopant in n-typeGaN. Phys. Stat. Sol. 9, 716–721 (2015).
Bogusławski, P. & Bernholc, J. Doping properties of C, Si, and Ge impurities in GaN and AlN. Phys. Rev. B 56, 9496–9505 (1997).
Volm, D. et al. Exciton fine structure in undoped GaN epitaxial films. Phys. Rev. B 53, 16543–16550 (1996).
Rodina, A. et al. Free excitons in wurtzite GaN. Phys. Rev. B 64, 11–14 (2001).
Alemu, A., Gil, B., Julier, M. & Nakamura, S. Optical properties of wurtzite GaN epilayers grown on A-plane sapphire. Phys. Rev. B 57, 3761–3764 (1998).
Broser, I., Gutowski, J. & Riedel, R. Excitation spectroscopy of the donor–acceptor-pair luminescence in CdS. Solid State Commun. 49, 445–449 (1984).
Taniyasu, Y., Kasu, M. & Makimoto, T. An aluminium nitride light-emitting diode with a wavelength of 210 nanometres. Nature 441, 325–328 (2006).
Lui, C. H. et al. Trion-induced negative photoconductivity in monolayer MoS2. Phys. Rev. Lett. 113, 166801 (2014).
Fröhlich, H., Pelzer, H. & Zienau, S. XX. Properties of slow electrons in polar materials. Philos. Mag. 41, 221–242 (1950).
Fröhlich, H. Electrons in lattice fields. Adv. Phys. 3, 325–361 (1954).
Cui, X. et al. Transient excitons at metal surfaces. Nat. Phys. 10, 505–510 (2014).
Silkin, V. M., Lazić, P., Došlić, N., Petek, H. & Gumhalter, B. Ultrafast electronic response of Ag(111) and Cu(111)surfaces: from early excitonic transients to saturated image potential. Phys. Rev. B. 92, 155405 (2015).
Wagner, M. R. et al. Bound excitons in ZnO: structural defect complexes versus shallow impurity centers. Phys. Rev. B 84, 035313 (2011).
Huber, R. et al. How many-particle interactions develop after ultrafast excitation of an electron–hole plasma. Nature 414, 286–289 (2001).
Leitenstorfer, A., Huber, R., Tauser, F. & Brodschelm, A. How fast do charged particles get dressed? Phys. Stat. Sol. B 238, 455–461 (2003).
Haug, H. & Koch, S. W. Quantum Theory of the Optical and Electronic Properties of Semiconductors 5th edn (World Scientific, Singapore, 2009).
Esser, A., Zimmermann, R. & Runge, E. Theory of trion spectra in semiconductor nanostructures. Phys. Stat. Sol. B 227, 317–330 (2001).
Suris, R. A. et al. Excitons and trions modified by interaction with a two-dimensional electron gas. Phys. Stat. Sol. B 227, 343–352 (2001).
Suris, R. A. Optical Properties of 2D Systems with Interacting Electrons SE-9. NATO Science Series Vol. 119, 111–124 (Springer, Netherlands, 2003).
Koudinov, A. V. et al. Suris tetrons: possible spectroscopic evidence for four-particle optical excitations of a two-dimensional electron gas. Phys. Rev. Lett. 112, 147402 (2014).
Acknowledgements
We acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) within the Collaborative Research Center 787 (CRC 787). We thank M. Müller and Prof. J. Christen for fruitful discussions and experimental support.
Author information
Authors and Affiliations
Contributions
C.N. and G.C. contributed equally to this work, wrote the manuscript and measured as well as interpreted the majority of all data. F.N. and T.K. provided significant experimental support and supported the scientific debate. S.S. and N.J. undertook the cathodoluminescence measurements and analysis. M.P.H. recorded and analysed the SIMS data. S.F., A.D. and A.K. provided the GaN:Ge samples. F.B. performed the modelling and has a most significant contribution to the overall interpretation. M.R.W. and A.H. have strongly supported the interpretation of the experimental data and guided the project together with G.C., C.N. and F.B.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nenstiel, C., Callsen, G., Nippert, F. et al. Electronic excitations stabilized by a degenerate electron gas in semiconductors. Commun Phys 1, 38 (2018). https://doi.org/10.1038/s42005-018-0033-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0033-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.