Abstract
In conventional energy harvesting systems, energy can be extracted from a fixed-level source at a constant rate at best. The resulting growth of harvested energy is bound by a linear function. Here we show that exponential energy harvesting can be achieved in a system of reconfigurable energy storage elements. The exponential extraction results from the positive feedback of the system potential energy due to repetitive system reconfigurations. The concept is studied theoretically and validated with results from systems of droplet capacitors. A device with three 300 μL mercury drops can generate an exponentially growing voltage that reaches 168 V within a few cycles of a low-level and low-frequency mechanical excitation. The same device with water drops can generate a similarly growing voltage that reaches 56 V. This concept holds potential in DC power generation and may be applied in other energy domains.
Similar content being viewed by others
Introduction
Rapid technological advancements have made the world inextricably dependent on energy. Extensive efforts have been devoted to improving energy-related science and technology, ranging from the development of advanced storage devices1,2,3,4 and effective harvesting schemes5,6,7,8,9,10 to the establishment of modernized policies and regulations11,12. Of particular interest to this study is the energy harvesting methodology, which dates back to ancient times as demonstrated by antique watermills that utilized hydropower to sustain the functions of the mills. Because electricity has become the primary form of power supply in the modern world, energy harvesting often refers to electricity generation. More recently, the need for reliable, in situ power generation in distributed and autonomous systems has spawned tremendous research in harvesting energy from the ambient environment13,14,15,16,17,18.
In principle, electricity generation involves cross domain energy transfer. Table 1 shows a list of conventional energy harvesting technologies. Except in the photovoltaics-based technologies, energy that can be extracted and converted to electricity is determined by certain macroscopic variations of the states of an energy source, such as mechanical oscillations in electromechanical technologies, temperature differences in thermoelectric technologies, and concentration gradients in electrochemical technologies. To sustain a continuous conversion process, energy from an environmental source must be coupled continuously into a harvesting system, resulting in a repetitive response from the harvester, e.g., the vibrations of a cantilever beam in an electromechanical energy harvester or the rotations of turbine blades on a windmill. In these conventional technologies, the energy coupled into the harvester in a cycle is converted to electricity and then exits the harvesting system-either delivered to storage or consumed by electric loads. Removal of the harvested energy from the system is necessary because the harvester needs to return to its original state to continue with the next harvesting cycle. Therefore, the harvested energy does not assist with the harvesting process, i.e. no energy feedback is established. An energy source with a fixed level creates a fixed response for the harvester, leading to a constant energy extraction rate at best. The growth of the harvested energy is bound by a linear function19,20,21,22. In low-level ambient sources, the extraction rates of conventional methods usually become too low to be of practical use because the generated electricity is not sufficient to satisfy the conditioning requirements for storage or consumption.
In this study, a method is developed so that the normally destabilizing nature of positive feedback is utilized to extract energy from an external source at an exponentially increasing rate. It is shown that in a system of reconfigurable energy storage elements, a positive feedback mechanism can be created through an appropriate, repetitive reconfiguration process of the system. The external energy source, which enables the reconfiguration, is both harvested exponentially and stored without rectification in the system. Because of the exponentially increasing rate of energy extraction, this method is particularly effective for distributed devices to scavenge energy from low-level ambient sources, i.e. the local environment, thus enabling self-powered operation. If applied to systems with elements of high energy and power densities, this method may become a viable way of large-scale power generation.
Results
Concept
Consider a reconfigurable system of interconnected energy storage elements, in which environmental energy is harvested through positive work done on the system and then stored in the system as potential energy. Figure 1a schematically shows the exponential growth of the harvested energy when the system is repetitively switched between two configurations and positive external work is performed only in one configuration. Assume without loss of generality that an energy harvesting cycle starts from the equilibrium state of configuration 1, energy is harvested in configuration 2, and the cycle completes when the system is switched from configuration 2 back to the equilibrium state of configuration 1. The system energy U(1) and U(2), i.e. the harvested energy, evolve as \(U^{(w)}(i + 1) = \gamma _{w,i}^2U^{(w)}(i)\), where w = 1, 2 indicating the configurations, \(\gamma _{1,i} = \sqrt {{\mathrm{\Gamma }}_i\eta _{12,i}\eta _{21,i}}\), and \(\gamma _{2,i} = \sqrt {{\mathrm{\Gamma }}_i\eta _{21,i}\eta _{12,i + 1}}\). The gain on the system energy due to external work is represented by Γ i . Because a system cannot move to an equilibrium state of a higher energy level without positive work from an external source, η12,i, η12,i+1, η21,i ≤ 1 representing the energy loss during reconfiguration. The system energy will grow exponentially if γ1,i, γ2,i > 1, i.e. Γ i > max{(1/η12,i × 1/η21,i), (1/η12,i+1 × 1/η21,i)}, which implies that the positive external work is sufficient to compensate the loss. Consider the two-configuration system of n + 1 capacitors shown in Fig. 1b. The two possible configurations are: Config. 1, in which n capacitors (sinks) with capacitances C1,C2 … C n are connected in series and then in parallel to the source capacitor (C0), and Config. 2, in which all capacitors are connected in parallel with capacitances changed to \(C_0^\prime ,C_1^\prime ,C_2^\prime \cdots C_n^\prime\). When the system is switched repetitively between the two configurations and positive work of the external source is done in Config. 2 to change the capacitances while keeping the same amount of electrical charge carried by individual capacitors, the total summation of the charge in the system follows Q(i + 1) = γQ(i), where
where r l = \(C_l^\prime\)/C l , l = 0, 1, 2 … n, \(C_{{\mathrm{eqv}}}^\prime = \mathop {\sum}\nolimits_{k = 0}^n {\kern 1pt} C_{\mathrm{k}}^\prime\) and s = C0/Csr in which \(C_{{\mathrm{sr}}} = 1{\mathrm{/}}\left( {\mathop {\sum}\nolimits_{k = 1}^n {\kern 1pt} 1{\mathrm{/}}C_k} \right)\). When n > 1 and \(r_0 > \mathop {\sum}\nolimits_{k = 1}^n {\kern 1pt} r_k\) so that γ > 1, the total amount of charge grows exponentially. The corresponding electrostatic energy stored in the system grows exponentially with a base of γ2. When C1 = C2 = …C n = C and \(C_1^\prime\) = \(C_2^\prime\) = …\(C_n^\prime\) = C′, it follows that
where α = \(C_0^\prime\)/C′, β = C/C0. Therefore, any arbitrary amount of initial charge in the system will start an exponential growth of charge if γ > 1.
A generalized result can be obtained for any reconfigurable system, composed of one-port, two-terminal energy storage elements with generalized across and through variables. The across variable of an element is a monotonic, single-valued function of the generalized through variable, which describes the constitutive law of the element23. One element is referred to as the source element and all others as sinks. One of the configurations is defined as the duplicative configuration, in which the change of the through variable of every sink is the negation of that of the source element. The other is defined as the distributive configuration, in which the total amount of through variables in the system is conserved. According to the principle of minimum potential energy, the summation of the across variables of the sinks at equilibrium in the duplicative state is equivalent to the across variable of the source element, whereas the across variable of every sink at equilibrium in the distributive state is that of the source element. Assume that the system is repetitively switched between the two configurations. Denote the total amount of the through variables as Q(1)(i) and Q(2)(i) for the duplicative and the distributive states in the ith cycle, respectively; ΔQ(12)(i) = ζ(12)(i)Q(1)(i), ΔQ(21)(i) = ζ(21)(i)Q(2)(i) represent the changes of the total amount of through variables corresponding to the transition from the duplicative state to the distributive state and vice versa. The following relationships are obtained.
where γ1(i) = [1 + ζ(12)(i)][1 + (n − 1)ζ(21)(i)] and γ2(i) = [1 + ζ(12)(i)][1 + (n − 1)ζ(21)(i + 1)]. When n ≥ 1 and ζ(12)(i), ζ(21)(i) > 0 for all cycles, γ1(i), γ2(i) > 1, leading to the exponential growth of not only the through variables, but ultimately the across variables and the harvested energy. Note that the same result applies for systems in which the roles of the across and the through variables are switched.
Prototype device
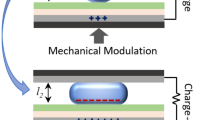
The results from generators fabricated with droplet-based variable capacitors are presented in this section. The simplest generator utilizes one source capacitor and two sink capacitors. A 3D rendered model of a device is shown in Fig. 2a. A commercial ceramic capacitor is used here as the source capacitor C0 for simplicity. An equivalent circuit for the generator is shown in Fig. 2b. The working principle of the device is illustrated in Fig. 2c–f. A typical sink capacitor can be fabricated on a doped silicon wafer, one side of which is covered by a layer of silicon dioxide. An amorphous fluoropolymer, CYTOP, is applied to silicon dioxide such that the resulting hydrophobic surface contains two regions of equal area but different thicknesses. When a free-standing conductive liquid drop is placed on the surface, a variable capacitor is formed. The drop and the doped silicon substrate function as the electrodes of the capacitor. The capacitance will change if the drop moves across the junction because of the thickness variation. More specifically, C > C′, where C and C′ represent the capacitances associated with the thinner and the thicker sides, respectively. Metal contacts that do not chemically interact with the drop are used at both sides as passive switches to facilitate the connectivity required for the reconfigurations. When both drops touch the metal contacts on the thinner side of the CYTOP coating, the device enters the duplicative state (Fig. 2c), which corresponds to closing SW1 while keeping SW2 and SW3 open in the equivalent circuit. Charge flows from the source capacitor to the sinks. The drops then move to the thicker side so that the device enters the distributive state (Fig. 2d), which corresponds to opening SW1 while closing SW2 and SW3. Charge then flows back to the source capacitor because of the reduction in sink capacitances. If the capacitance variation satisfies αβ = C/C′ > 2 (Eq. (2)), the subsequent motions of the drops back to the thinner side (Fig. 2e) and then to the thicker side (Fig. 2f) will create a geometric growth of total charge in the system. More sink capacitors can be used to increase the base of the exponential growth. Additional liquid drops have been used in this study as passive switches to facilitate the connectivity required by 3 or more sink capacitors (Supplementary Fig. 1).
Prototype device with two sink capacitors and one source capacitor. a A three-dimensional (3D) rendered model of the device. b An equivalent circuit of the device. c–f Working principle of the device. c Liquid drops on the thinner side of the amorphous fluoropolymer (CYTOP) coating with the maximum sink capacitance. Sink capacitors are connected in series. d Drops on thicker side with the minimum sink capacitance. Sink capacitors connected in parallel. e Drops back to the thinner side again ((i + 1)th cycle) with increased charge. f Drops to thicker side again ((i + 1)th cycle) with more charge flowing to the source capacitor
Because the length scale of the contact area is much larger than that of the thicknesses of the dielectric materials, the droplet capacitor can be reasonably modeled as a parallel-plate capacitor. The effect of the thickness difference of the CYTOP layers on the electric output is shown in Fig. 3. The results correspond to devices with fixed source capacitors, i.e. C0 = \(C_0^\prime\). Both the silicon dioxide layer and the thinner layer of CYTOP have been assumed to be 200 nm thick. The condition αβ > 2 requires a minimal value of 2.57 for the ratio between the thicknesses of the CYTOP layers. It is seen that the base γ increases monotonically and converges as the thickness ratio increases. A smaller capacitance of the source capacitor (i.e. larger β) leads to a larger limit value of γ with a lower converging rate. Therefore, it may not be practical to achieve the limit values corresponding to very low source capacitances. For example, if the capacitance of the source capacitor is one-tenth of that of the droplet capacitor when the drop is on the thinner side, i.e. β = 10, it will require a thickness difference larger than 5000 times to achieve the limit γ = 1.833. The size of the liquid drops also affects the amount of electrical energy harvested. A larger liquid drop creates a larger contact area that leads to a higher capacitance. However, there will be no size effect on the base of the exponential growth of the charge in the system or the voltages across the capacitors if the ratios between capacitances (α and β) are fixed. While it may be favorable to use larger drops because more charge will be collected due to higher capacitances, the largest size of the drops is limited by the physical constraints of the device and ultimately by the surface energy of the liquid. It is noted that the equivalent circuits shown are RC circuits in reality. However, the effect of resistances can be ignored when the frequency of switching is low compared to the time constants of the RC circuits so that the equilibrium state of each configuration is established before subsequent switching. Therefore, the conductivity of the liquid drops does not affect the base of the exponential growth of the electric output in low-frequency applications, which implies that mechanism depends only on the position of the drops, and thus, the speed of the drops does not affect the electric output.
Contact electrification and charge trapping
If a liquid drop is brought into contact with an initially uncharged CYTOP surface and then separated for the first time, the surface will be electrified due to contact electrification. Subsequent oscillatory motions of the drop on the surface will cause the surface charge to increase to a saturated value, which will be different for the two sides because of the molecular-scale fluctuations of surface properties24,25,26,27,28,29. The two sides will consequently behave as electrets possessing a different amount of negative surface charge as illustrated in Fig. 2. Electrostatic induction will then become the dominating mechanism that determines the charge distribution on the liquid drop24,28,29. The effect of electrostatic induction can be modeled by a fixed amount of charge, Qc, which is transferred to or removed from the drop when it moves from one side to the other (Supplementary Fig. 2). Because of variations of surface properties, this charge is in general different for droplet capacitors fabricated with an identical procedure. The charge can be estimated as30 Qc(i) = sgn(q(i))[σtk(i)−σtn(i)]A(i), where q(i) represents the charge carried by the ith drop, σtn(i) and σtk(i) the surface charge densities of the thinner and the thicker CYTOP side for the ith capacitor, respectively, and A(i) represents the contact area.
The contacts between a charged liquid drop and the CYTOP surface will also induce charge trapping at the surface, which limits the amount of charge that can move with the drop. However, the fact that the trapped charge can be annihilated by grounding the drop suggests that trapping occurs on the surface rather than in the insulator31,32,33. Because of the internal connectivity of the system, the drop is charged when it is on the thinner side and almost completely discharged when moving to the thicker side. Therefore, charge trapping is negligible for the thicker side. The trapping on the thinner side can be accurately modeled with a parasite capacitor Cp, connected in parallel to the effective capacitor (\(\tilde C\)) associated with the thinner side. In this study, the parasite capacitance was determined experimentally (Supplementary Fig. 3). The total capacitance of an individual capacitor in the duplicative state is then \(C = \tilde C + C_{\mathrm{p}}\). Therefore, the summations of the charge of all capacitors in the ith cycle for the duplicative and the distributive states are different, which are obtained as follows
where w = 1, 2 representing the duplicative and the distributive state, respectively. The effect of charge trapping on the growth of the total charge is represented by γp = (n − 1)δ/[(n + α)(n + β)], where δ = Cp/C′, \(\bar Q_{\mathrm{c}} = \frac{1}{n}\mathop {\sum}\nolimits_{i = 1}^n {\kern 1pt} Q_{\mathrm{c}}(i)\), and \(\xi ^{(1)} = \frac{{n\alpha (n - 1)}}{{n + \alpha }}\frac{{1 + \beta }}{{n + \beta }}\) for the duplicative state and \(\xi ^{(2)} = \frac{{n(n - 1)}}{{n + \beta }}\) for the distributive state.
Performance of prototype generators
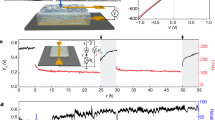
Figure 4 shows the results obtained from generators involving multiple 150 μL mercury drops. Commercial capacitors with fixed capacitances were used in different devices as the source capacitors. The devices were manually rocked at a frequency of approximately 0.25 Hz and the tilting angle was within ±5° so that the drops were synchronously driven to touch the metal contacts. The growth of the voltages across the source capacitors is shown in Fig. 4a–c for cases corresponding to two, three, and four sink capacitors, respectively. Four devices were evaluated in every case, each with a different source capacitor. The experimental results agree very well with the theoretical predictions from Eq. (4). The ratio between the maximum and minimum capacitances of the sinks was kept unchanged in all cases considered, i.e. αβ = C/C′ = 10.15. Under this condition, αopt = βopt = 3.18 will lead to the maximum \(\hat \gamma\). For a 150 μL mercury drop, the maximum capacitance was measured to be approximately C = 2.74 nF, corresponding to the optimal source capacitor of C0 = 0.86 nF. Therefore, out of the four source capacitors used, C0 = 0.94 nF provided the largest \(\hat \gamma\). It is worth noting that for any device in which αβ is fixed, there exists an optimal number of sinks that will result in the maximum base of the exponential growth \(\hat \gamma\). The optimal number of sinks was found theoretically (Eq. (4)) and verified experimentally to be nopt = 3 (Fig. 4d). The results obtained for devices with water drops, 300 μL each, are presented in Fig. 5. The ratio of the maximum and the minimum capacitances was kept at αβ = 7.82 for all relevant experiments. The voltages across the source capacitors are shown in Fig. 5a–c. The theoretical and experimental results showing the optimal number of the sink capacitors are presented in Fig. 5d. The optimal number of sink capacitors for this case was also three. In addition to plain water, deionized water with the conductivity of 0.055 μS cm−1and 1 mol L−1 (1 M) sodium chloride solution were also used in this study. Very close values of \(\hat \gamma\) were obtained for the three cases, indicating a negligible effect of the ion concentration on the base of the exponential growth. This is expected for low-frequency vibrations. The ion concentration, however, has been shown to influence the charge due to electrostatic induction28,34. The time histories of the output voltages were thus different for the three cases due to different charge (\(\bar Q_{\mathrm{c}}\)) resulting from electrostatic induction (Supplementary Fig. 4).
Results obtained from generators with mercury drops, 150 μL each. a Voltage accumulation when two sinks were used. b Voltage accumulation when three sinks were used. c Voltage accumulation when four sinks were used. d Relations between the exponential base and β = C/C0. Markers and lines represent respectively the experimental results and those obtained with Eq. (4)
Results obtained from generators with water drops, 300 μL each. a Voltage accumulation when two sinks were used. b Voltage accumulation when three sinks were used. c Voltage accumulation when four sinks were used. d Relations between the exponential base and β = C/C0. Markers and lines represent respectively the experimental results and those obtained with Eq. (4)
The method has also been applied to generators fabricated with parallel-plate variable capacitors that use air as the dielectric. Passive switching has been realized by metal-metal contacts. While charge trapping is negligible when air is used as the dielectric, the metal-metal contacts play a similar role to that of the induction process due to different work functions35. Three two-sink devices have been fabricated using three different source capacitors. The theoretical results obtained from Eq. (4) agree excellently with those from experiments (Supplementary Fig. 5).
Finally, generators made from three identical droplet-based variable capacitors (one source and two sinks) have been used to drive commercial light-emitting diodes (LEDs) under low-frequency mechanical vibrations. A schematic diagram of the three-drop generators is shown in Fig. 6a. Vibrations of 2.5 Hz were used in the experiment to simulate the vibrations induced by human walking. After a few initial cycles of energy accumulation, the voltage output of the device with three 300 μL mercury drops reached 168 V when the system was in the distributive state. The energy extracted per cycle was sufficient for illuminating 60 green LEDs connected in series (Fig. 6b, Supplementary Movie 1). Under the same condition, the device with water drops of the same size could generate 56 V, sufficient to illuminate 20 green LEDs connected in series (Fig. 6c, Supplementary Movie 2). Because both the source and sink capacitors had the same position-dependent capacitances, the resulting base of the exponential growth (\(\hat \gamma _{}^{}\)) was much higher than those of the cases shown in Figs. 4 and 5, in which the source capacitors had fixed capacitances. More specifically, in this case, \(\hat \gamma _{}^{}\) was 1.674 for mercury drops and 1.669 for water drops. It is noted that αβ = 10.152 in this case, which is an order of magnitude higher than those in the cases of a fixed source capacitor. The effects of charge trapping for mercury and water drops were considerably reduced because of the dramatically decreased γp. The actual resulting values of \(\hat \gamma\) for mercury and water drops were thus very close. While mercury and water are both liquids at room temperature, the charge carriers are different36,37,38. The voltages due to contact electrification were 4.69 and 2.72 V for mercury and water, respectively. Therefore, the voltage across the source capacitor of the device with mercury drops reached 168 V after 7 cycles and it took the device with water drops 6 cycles to reach 56 V.
Generators of three droplet capacitors illuminating light-emitting diodes (LEDs) connected in series under moderate vibrations of 2.5 Hz. a Schematic diagram of a three-drop generator. b A generator with three mercury drops (300 μL each) illuminating 60 LEDs. c. A generator with three water drops (300 μL each) illuminating 20 LEDs
Discussion
It has been shown that if energy storage elements are used as the primary energy harvesting components of a system, appropriate reconfigurations of the system can create a positive feedback of the potential energy in the elements, leading to an exponential growth of the energy that is harvested as the elemental potential energy. The efficacy of this method has been demonstrated with droplet generators. Consider the device with a fixed source capacitor of 0.94 nF and three 150 μL mercury drops and the device with a fixed source capacitor of 1.26 nF and three 300 μL water drops. In the experiments conducted, the tilting angle of the wafer was within ±5°. The total available energy was calculated to be 83.2 μJ for the mercury drops and 15.4 μJ for the water drops by adding the two peak values of the potential energy of the drops in a cycle. It has been shown that devices with mercury drops and those with water drops can sustain a continuous operation at 168 and 56 V, respectively. If operated at these voltages, the device with mercury drops can harvest energy at the rate of 10.2 μJ per cycle, corresponding to a harvesting efficiency of 12.2% and the values for the device with three water drops will be 1.2 μJ per cycle and 7.9%. Because energy is harvested as electric potential energy in this method, the harvesting efficiency is independent of the electrical load to which the energy can be delivered. The efficiencies of the prototype devices fabricated in this study far exceed those of the droplet generators reported in the literature, which are on the order of 0.01% under the optimal condition29. The devices can be operated at a higher energy level with a higher efficiency. However, since energy is harvested only in the distributive state in this study, the efficiency is limited to 50% per cycle when the total potential energy in both states is considered.
Although the experimental study has been limited to scavenging low-level vibration energy, this method can be applied at a larger scale. If applied to high-capacitance devices1,3,6,39,40,41 driven by abundant environmental sources42,43,44, this concept may lead to efficient, large-scale and possibly grid-level DC power supply systems. In this regard, it is envisioned this report will stimulate the emergence of new research areas, e.g., supercapacitors with a wide range of adjustable capacitances. Because the concept of exponential energy harvesting is not domain specific, it may lead to new research in directional energy transfer systems in various energy domains.
Methods
Device fabrication
The capacitors were fabricated on 2-in doped silicon wafers (with resistivity of 1–10 Ω ⋅ cm), one capacitor per wafer. The doped silicon was used as the back electrode. A layer of 200 nm silicon dioxide was grown on one side of the wafer. Cytop was spin-coated on silicon dioxide to create a hydrophobic layer. Additional Cytop was manually applied to the spin-coated layer to create an area of a thicker Cytop layer. The thicknesses were 200 nm and 3 μm for devices using mercury drops and 400 nm and 4 μm for devices using water drops. For every capacitor in which a water drop of approximately 300 μL was used as the moving electrode, the maximum and the minimum capacitances were measured to be 3.52 and 0.45 nF, respectively. The parasite capacitance accounting for charge trapping was experimentally determined to be approximately 0.76 nF. For capacitors in which a mercury drop of 150 μL was used, the maximum and the minimum capacitances were 2.74 and 0.27 nF, respectively. The parasite capacitance was approximately 0.40 nF. Measurements were obtained using a Tektronix© electrometer (6517B). Tap water was used to form the droplets used in the experiments. The ion concentration of the water was measured to be 220 p.p.m. The experiments were conducted in an ambient atmosphere of 1 atm, 25 °C with a moisture content of 50–70%. The LEDs had a nominal forward voltage of 3.0 V.
Derivation of Eq. (1)
Assume without loss of generality that a cycle starts from the equilibrium state when the system is in Config. 1. For the ith cycle, the charge is distributed such that \(q_k^{(1)} = \bar q^{(1)}(i),k = 1,2 \cdots n\) and \(q_0^{(1)}(i) = C_0/C_{{\mathrm{sr}}}^{(1)}\bar q^{(1)}(i)\), \(C_{{\mathrm{sr}}}^{(1)} = 1{\mathrm{/}}\left( {\mathop {\sum}\nolimits_{k = 1}^n {\kern 1pt} 1{\mathrm{/}}C_k} \right)\), where the superscripts indicate the configurations. The total electrical potential energy of the system is
where \(Q(i) = q_0^{(1)}(i) + n\bar q^{(1)}(i)\) and \(s = C_0{\mathrm{/}}C_{{\mathrm{sr}}}^{(1)}\). After the system is switched to Config. 2 and equilibrium is reached, the charge distribution is
where \(\bar \eta _k^{(2)} = C_k{\mathrm{/}}C_{{\mathrm{eqv}}}^{(2)}\) and \(C_{{\mathrm{eqv}}}^{(2)} = \mathop {\sum}\nolimits_{l = 0}^n {\kern 1pt} C_l\). The system energy is
If the external energy is coupled into the system parametrically, i.e. the capacitances are changed from C k to \(C_k^\prime\), which leads to an increase in the system energy, the total system energy becomes
where \(C_{{\mathrm{eqv}}}^\prime = \mathop {\sum}\nolimits_{l = 0}^n {\kern 1pt} C_l^\prime\). The charge is redistributed as
where \(\hat \eta _k^{(2)} = C_k^\prime {\mathrm{/}}C_{{\mathrm{eqv}}}^\prime\).
The system is then switched back to Config. 1 and the capacitances revert to the original values. The total charge after equilibrium is reached is the total charge for the start of the (i + 1)th cycle and the charge is distributed as
where
where r l = \(C_l^\prime\)/C l , l = 0, 1, 2…n. Therefore,
Derivation of Eq. (3)
Assume without loss of generality that the ith cycle starts from the duplicative state after equilibrium is reached. For the kth element, the energy and the through variable are denoted as \(U_k^{(1)}(i)\) and \(q_k^{(1)}(i)\), respectively. The total system energy and the summation of all through variables are denoted as \(U^{(1)}(i) = \mathop {\sum}\nolimits_{l = 0}^n {\kern 1pt} U_l^{(1)}(i)\) and \(Q^{(1)}(i) = \mathop {\sum}\nolimits_{l = 0}^n {\kern 1pt} q_l^{(1)}(i)\), respectively. The cycle completes when equilibrium is established after the system is switched to the distributive state. The energy and the through variable of the kth element for the distributive state are denoted as \(U_k^{(2)}(i)\) and \(q_k^{(2)}(i)\), respectively. The change of the total through variables in the transition from the duplicative state to the distributive state is denoted by ΔQ(12)(i) = ζ(12)(i)Q(1)(i). The through variables can be determined using the Lagrangian defined as
where λ(i) is the Lagrange multiplier, \(U^{(2)}(i) = \mathop {\sum}\nolimits_{l = 0}^n {\kern 1pt} U_l^{(2)}(i)\), and \(Q^{(2)}(i) = \mathop {\sum}\nolimits_{k = 0}^n {\kern 1pt} q_k^{(2)}(i)\). According to the principle of minimum potential energy,
The through variable of each element can be obtained as
When the system is subsequently switched to the duplicative state, which is the start of the i + 1th cycle, a new Lagrangian is defined as
where ΔQ(21)(i) = ζ(21)(i)Q(2)(i) denotes the change of the total through variables required for equilibrium. Therefore,
The total through variables in the i + 1th cycle are obtained as
where γ1(i) = [1 + ζ(12)(i)][1 + (n − 1)ζ(21)(i)] and γ2(i) = [1 + ζ(12)(i)][1 + (n − 1)ζ(21)(i + 1)].
Derivation of Eq. (4)
Assume that the variable capacitors are identical, the capacitances of the parasite capacitors are the same and they are connected in parallel to the sink capacitors in Config. 1 so that the total capacitance of every sink capacitor is \(C = \tilde C + C_{\mathrm{p}}\), where \(\tilde C\) denotes the effective capacitance. It is further assumed that a cycle starts when the system reaches equilibrium in Config. 1. At the start of the ith cycle every drop carries the same amount of charge, q(1)(i), and the sum of the charge on all capacitors is \(Q^{(1)}(i) = q_0^{(1)}(i) + nq^{(1)}(i) + nq_{\mathrm{p}}^{(1)}(i)\), where q denotes the charge that can move with the drop and qp the charge stored in the parasite capacitor. Define \(\tilde s = C_0{\mathrm{/}}C_{{\mathrm{sr}}}\), where Csr = C/n and \(\tilde \eta = \tilde C{\mathrm{/}}C\). The following relationships are established.
When the drops move to the other sides of the surface, and immediately before the connectivity is established such that the system is in Config. 2, due to contact electrification, the total charge becomes
After the capacitances change from \(\tilde C\) to C′ and then the capacitors are connected so that the system is in Config. 2, the charge is distributed as
The system is then switched back to Config. 1 and the capacitances revert to the original values. At equilibrium, the summation of the total charge in the system becomes
where \(\tilde q^{(1)}(i + 1) = q^{(1)}(i + 1) + q_{\mathrm{p}}^{(1)}(i + 1)\) and
Therefore,
where α = C0/C′ and β = C/C0. Define δ = Cp/C′. The following relationship is obtained.
where
The total charge in Config. 2 follows
where
Data availability
All data generated or analysed during this study are included in this published article and its Supplementary Information files.
References
Conway, B. E. Transition from supercapacitor to battery behavior in electrochemical energy-storage. J. Electrochem. Soc. 138, 1539–1548 (1991).
Nie, A. et al. Twin boundary-assisted lithium ion transport. Nano. Lett. 15, 610–615 (2015).
Sheberla, D. et al. Conductive mof electrodes for stable supercapacitors with high areal capacitance. Nat. Mater. 16, 220–224 (2017).
Rustomji, C. S. et al. Liquefied gas electrolytes for electrochemical energy storage devices. Science 356, eaal4263 (2017).
DiSalvo, F. J. Thermoelectric cooling and power generation. Science 285, 703–706 (1999).
Brogioli, D. Extracting renewable energy from a salinity difference using a capacitor. Phys. Rev. Lett. 103, 058501 (2009).
Ma, T. W., Zhang, H. & Xu, N. S. A novel parametrically excited nonlinear energy harvester. Mech. Syst. Signal Pr. 28, 323–332 (2012).
Zuo, L. & Zhang, P. S. Energy harvesting, ride comfort, and road handling of regenerative vehicle suspensions. J. Vib. Acoust. 135, 011002 (2013).
Swarnkar, A. et al. Quantum dot–induced phase stabilization of α-CsPbI3 perovskite for high-efficiency photovoltaics. Science 354, 92–95 (2016).
Cognet, V., Courrech du Pont, S., Dobrev, I., Massouh, F. & Thiria, B. Bioinspired turbine blades offer new perspectives for wind energy. Proc R Soc London A 473 20160726 (2017).
Lilliestam, J., Labordena, M., Patt, A. & Pfenninger, S. Empirically observed learning rates for concentrating solar power and their responses to regime change. Nature Energy https://doi.org/10.1038/nenergy.2017.94 (2017).
Stokes, L. C. & Warshaw, C. Renewable energy policy design and framing influence public support in the united states. Nature Energy https://doi.org/10.1038/nenergy.2017.107 (2017).
Wang, Z. L. & Song, J. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 312, 242–246 (2006).
Donelan, J. M. et al. Biomechanical energy harvesting: generating electricity during walking with minimal user effort. Science 319, 807–810 (2008).
White, B. E. Energy-harvesting devices: beyond the battery. Nat. Nano 3, 71–72 (2008).
Karami, M. A. & Inman, D. J. Powering pacemakers from heartbeat vibrations using linear and nonlinear energy harvesters. Appl. Phys. Lett. 100, 042901 (2012).
Niu, S. et al. Theoretical study of contact-mode triboelectric nanogenerators as an effective power source. Energy Environ. Sci. 6, 3576–3583 (2013).
Hwang, G.-T. et al. Self-powered cardiac pacemaker enabled by flexible single crystalline pmn-pt piezoelectric energy harvester. Adv. Mater. 26, 4880–4887 (2014).
Radousky, H. B. & Liang, H. Energy harvesting: an integrated view of materials devices and applications. Nanotechnology 23, 502001 (2012). (35pp).
Halvorsen, E. Fundamental issues in nonlinear wideband-vibration energy harvesting. Phys. Rev. E 87, 042129 (2013).
Yang, Y. et al. Charging-free electrochemical system for harvesting low-grade thermal energy. Proc. Natl Acad. Sci. 111, 17011–17016 (2014).
Ma, T. W. & Zhang, H. Reaping the potentials of nonlinear energy harvesting with tunable damping and modulation of the forcing functions. Appl. Phys. Lett. 104, 214104 (2014).
Firestone, F. A. A new analogy between mechanical and electrical systems. J. Acoust. Soc. Am. 4, 249–267 (1933).
Lowell, J. & Rose-Innes, A. Contact electrification. Adv. Phys. 29, 947–1023 (1980).
Horn, R. G. & Smith, D. T. Contact electrification and adhesion between dissimilar materials. Science 256, 362 (1992).
Horn, R. G., Smith, D. & Grabbe, A. Contact electrification induced by monolayer modification of a surface and relation to acid-base interactions. Nature 366, 442–443 (1993).
Baytekin, H. T. et al. The mosaic of surface charge in contact electrification. Science 333, 308–312 (2011).
Lin, Z.-H., Cheng, G., Lin, L., Lee, S. & Wang, Z. L. Water-solid surface contact electrification and its use for harvesting liquid-wave energy. Angew. Chem. Int. Ed. 52, 12545–12549 (2013).
Lin, Z.-H., Cheng, G., Lee, S., Pradel, K. C. & Wang, Z. L. Harvesting water drop energy by a sequential contact-electrification and electrostatic-induction process. Adv. Mater. 26, 4690–4696 (2014).
Yu, J., Ma, E. & Ma, T. Harvesting energy from low-frequency excitations through alternate contacts between water and two dielectric materials. Sci. Rep. https://doi.org/10.1038/s41598-017-17522-8 (2017).
Verheijen, H. J. J. & Prins, M. W. J. Reversible electrowetting and trapping of charge: model and experiments. Langmuir 15, 6616–6620 (1999).
Kilaru, M. K., Heikenfeld, J., Lin, G. & Mark, J. E. Strong charge trapping and bistable electrowetting on nanocomposite fluoropolymer: Batio3 dielectrics. Appl. Phys. Lett. 90, 212906 (2007).
Krupenkin, T. & Taylor, J. A. Reverse electrowetting as a new approach to high-power energy harvesting. Nat. Commun. https://doi.org/10.1038/ncomms1454 (2011).
Choi, D. et al. A smart pipet tip: triboelectricity and thermoelectricity assisted in situ evaluation of electrolyte concentration. Nano Energy 38, 419–427 (2017).
Varpula, A., Laakso, S. J., Havia, T., Kyynäräinen, J. & Prunnila, M. Harvesting vibrational energy using material work functions. Sci. Rep. https://doi.org/10.1038/srep06799 (2014).
Yatsuzuka, K., Mizuno, Y. & Asano, K. Electrification phenomena of pure water droplets dripping and sliding on a polymer surface. J. Electrost. 32, 157–171 (1994).
Amin, M. S., Peterson, T. F. & Zahn, M. Advanced faraday cage measurements of charge and open-circuit voltage using water dielectrics. J. Electrost. 64, 424–430 (2006).
Santos, L. P., Ducati, T. R. D., Balestrin, L. B. S. & Galembeck, F. Water with excess electric charge. J. Phys. Chem. C. 115, 11226–11232 (2011).
Conway, B., Birss, V. & Wojtowicz, J. The role and utilization of pseudocapacitance for energy storage by supercapacitors. J. Power Sources 66, 1–14 (1997).
La Mantia, F., Pasta, M., Deshazer, H. D., Logan, B. E. & Cui, Y. Batteries for efficient energy extraction from a water salinity difference. Nano. Lett. 11, 1810–1813 (2011).
Lee, S. W. et al. An electrochemical system for efficiently harvesting low-grade heat energy. Nat. Commun. https://doi.org/10.1038/ncomms4942 (2014).
Norman, R. S. Water salination: a source of energy. Science 186, 350–352 (1974).
Heremans, J. P. Thermoelectricity: the ugly duckling. Nature 508, 327–328 (2014).
Uihlein, A. & Magagna, D. Wave and tidal current energy-a review of the current state of research beyond technology. Renew. Sustain. Energy Rev. 58, 1070–1081 (2016).
Beeby, S. P., Tudor, M. J. & White, N. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 17, R175–R195 (2006).
Arnold, D. P. Review of microscale magnetic power generation. IEEE. Trans. Magn. 43, 3940–3951 (2007).
Calio, R. et al. Piezoelectric energy harvesting solutions. Sensors 14, 4755–4790 (2014).
Boisseau, S., Despesse, G. & Seddik, B. A. Electrostatic conversion for vibration energy harvesting. Preprint at https://arxiv.org/abs/1210.5191v1 (2012).
Wang, Z. L., Chen, J. & Lin, L. Progress in triboelectric nanogenerators as a new energy technology and self-powered sensors. Energy Environ. Sci. 8, 2250–2282 (2015).
Cuadras, A., Gasulla, M. & Ferrari, V. Thermal energy harvesting through pyroelectricity. Sens. Actuators A. 158, 132–139 (2010).
Bowen, C. R., Kim, H., Weaver, P. & Dunn, S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 7, 25–44 (2014).
Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321, 1457–1461 (2008).
Sootsman, J. R., Chung, D. Y. & Kanatzidis, M. G. New and old concepts in thermoelectric materials. Angew. Chem. Int. Ed. 48, 8616–8639 (2009).
Achilli, A., Cath, T. Y. & Childress, A. E. Power generation with pressure retarded osmosis: an experimental and theoretical investigation. J. Memb. Sci. 343, 42–52 (2009).
Post, J. W. et al. Salinity-gradient power: evaluation of pressure-retarded osmosis and reverse electrodialysis. J. Memb. Sci. 288, 218–230 (2007).
Rica, R. A. et al. Capacitive mixing for harvesting the free energy of solutions at different concentrations. Entropy 15, 1388–1407 (2013).
Gratzel, M. Photoelectrochemical cells. Nature 414, 338–344 (2001).
Fahrenbruch, A. & Bube, R. Fundamentals of solar cells: photovoltaic solar energy conversion (Elsevier, New York, NY, 2012).
Acknowledgements
The research was supported by the National Science Foundation (Grant No.: CMMI 0758632), State of Hawaii Department of Transportation and the University of Hawaii.
Author information
Authors and Affiliations
Contributions
T. M. conceived the idea. T. M. and J. Y. designed all experiments. J. Y. fabricated the capacitors. J. Y., E. M., and T. M. performed measurements and data analysis. T. M., J. Y., and E. M. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
A patent application has been filed based on the results in the manuscript.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yu, J., Ma, E. & Ma, T. Exponential energy harvesting through repetitive reconfigurations of a system of capacitors. Commun Phys 1, 9 (2018). https://doi.org/10.1038/s42005-018-0010-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0010-y
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.